Joint Efficient UAV Trajectory and Velocity Optimization for IoT Data Collection Using a New Projection Algorithm †
Abstract
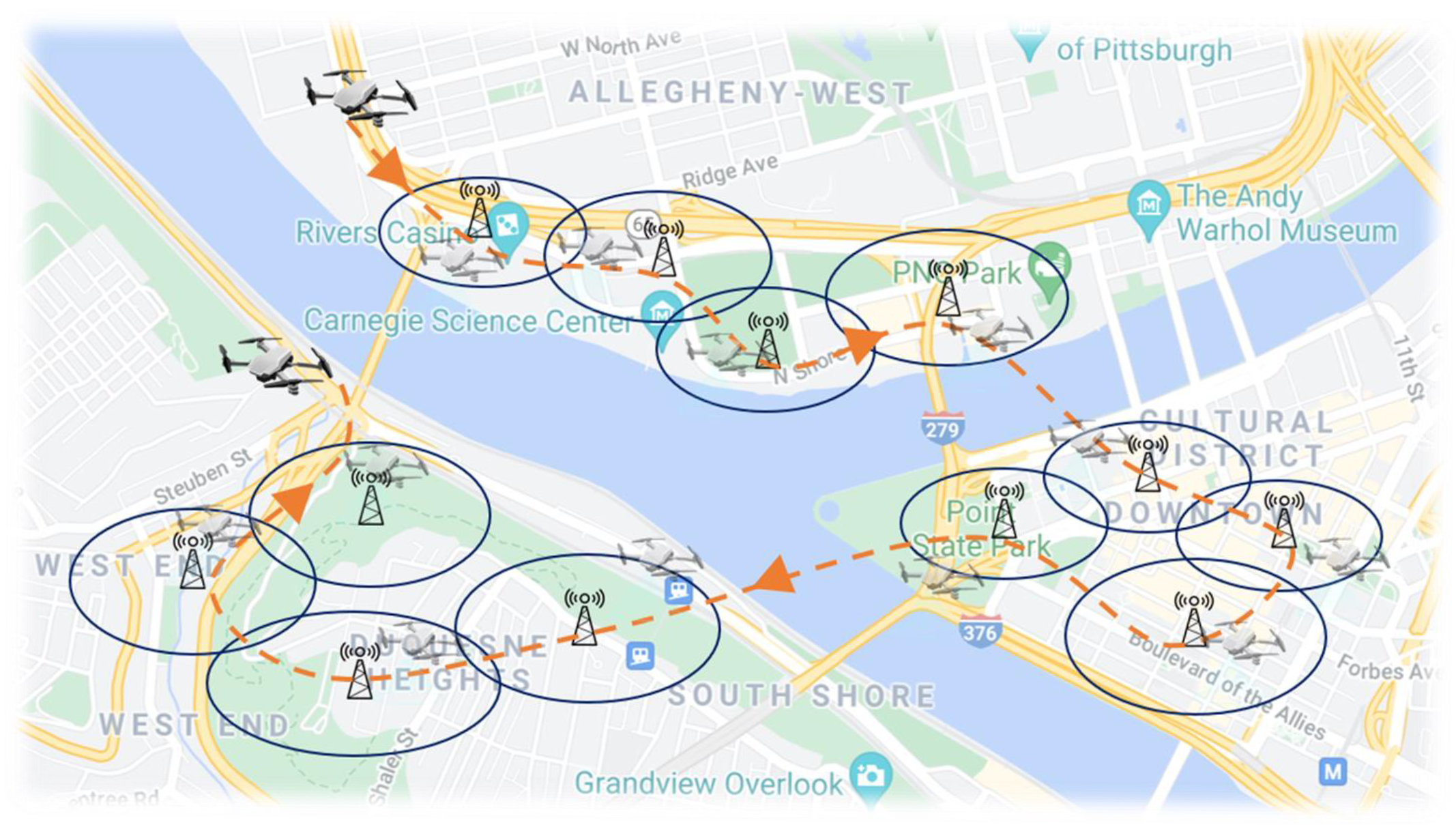
1. Introduction
- In the previous studies, the UAV velocity optimization is only based on the relationship between speed and power, which we found may not always lead to the best energy efficiency. As a key finding in this paper, we also analyzed the relationship between speed and energy consumption per unit distance, and found that there should be different speed selection strategies under different flying scenarios (i.e., fixed-time cases or fixed-distance cases), leading to much better UAV energy efficiency.
- We propose CirCo, a novel algorithm to jointly optimize the trajectory and velocity of the UAV for minimized total energy consumption while meeting all communication task requirements. It adopts an original projection method to convert the 3D scenario to the 2D plane corresponding to the transmission ranges and time requirements of GNs, which greatly reduces the complexity of the problem. Then CirCo leverages a speed selection strategy to determine the most energy-efficient speed and the corresponding path within the constraint range derived by the projection method.
- We verify the effectiveness of CirCo through experiments with real UAV data. Simulation results show that CirCo can save as much as energy and in flight times and it is very close to the lower bounds of energy–flight time consumption to complete the transmission tasks.
2. Materials and Models
2.1. Energy Consumption Model
2.2. System Model
2.3. Problem Formulation
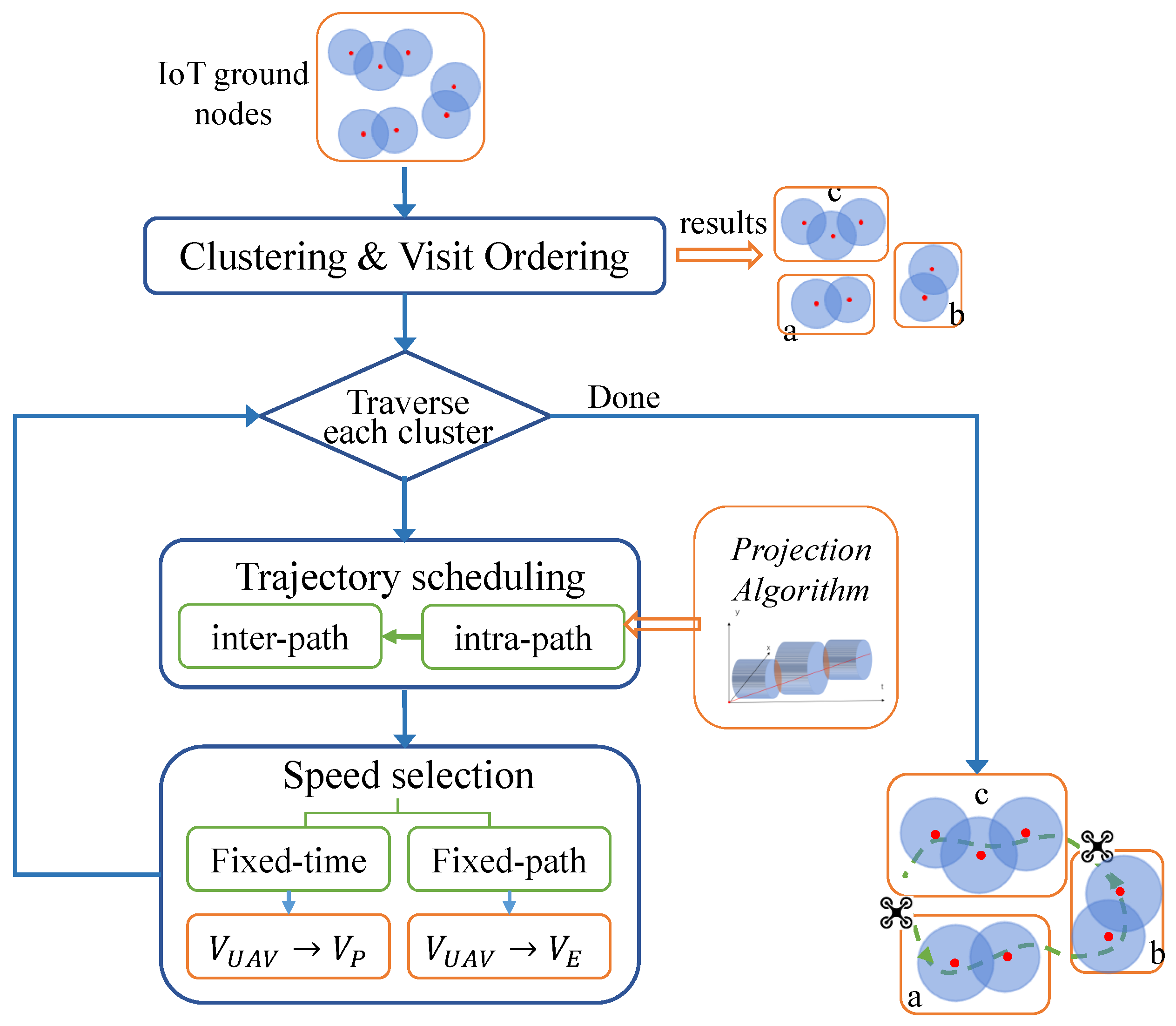
3. CirCo Methods
3.1. Cluster and Order Determination
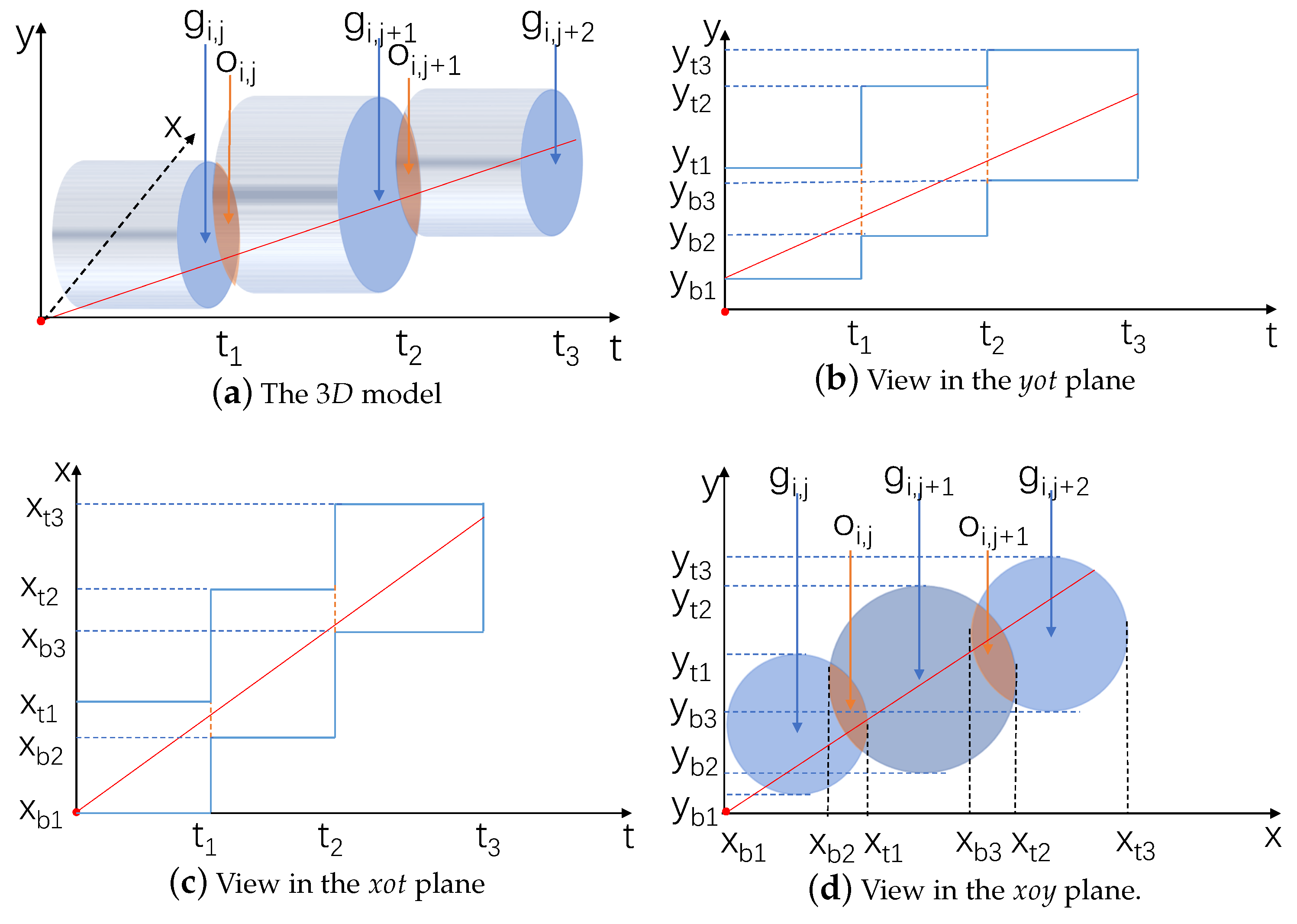
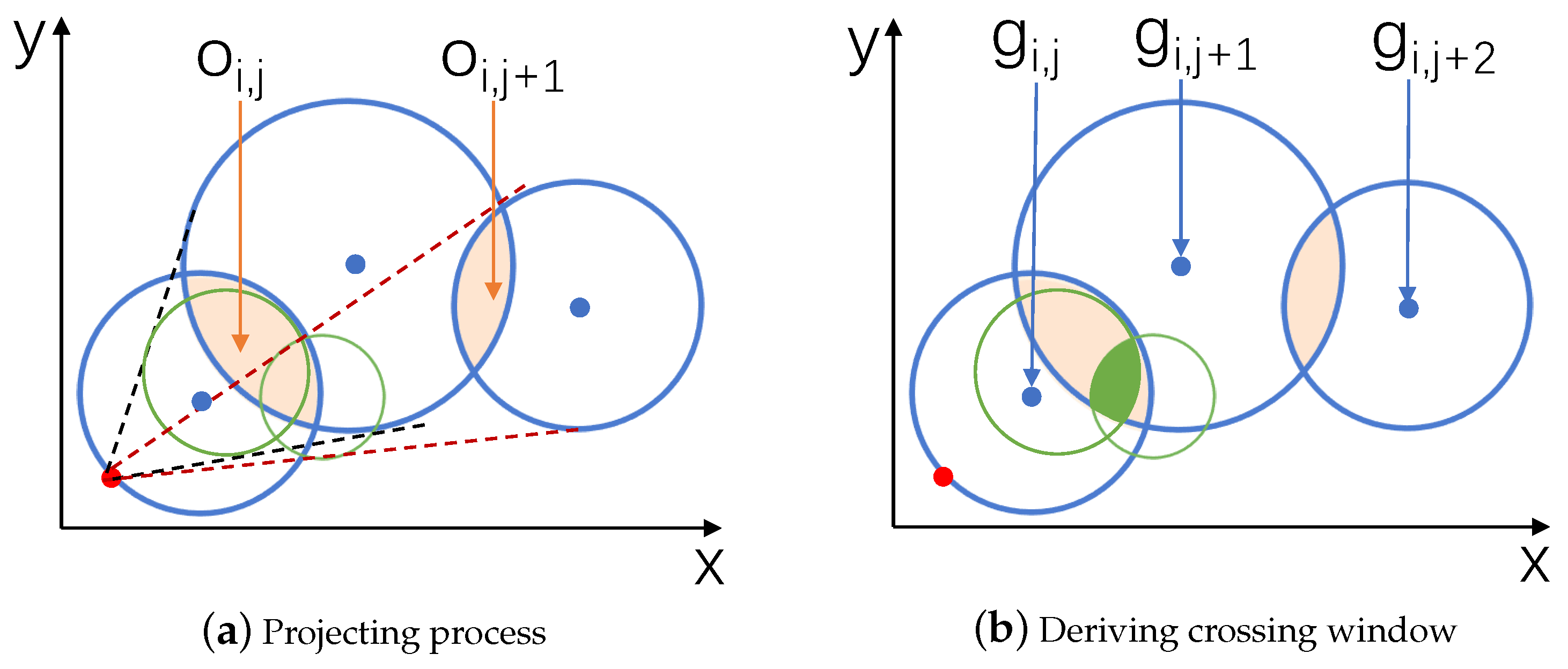
3.2. Design of the Projection Method
3.3. Algorithm of CirCo
| Algorithm 1 The CirCo algorithm in the jth intra-GNC part |
Input:
Output: the speed and route of the UAV in the jth GNC |
3.4. Computation Complexity Analysis
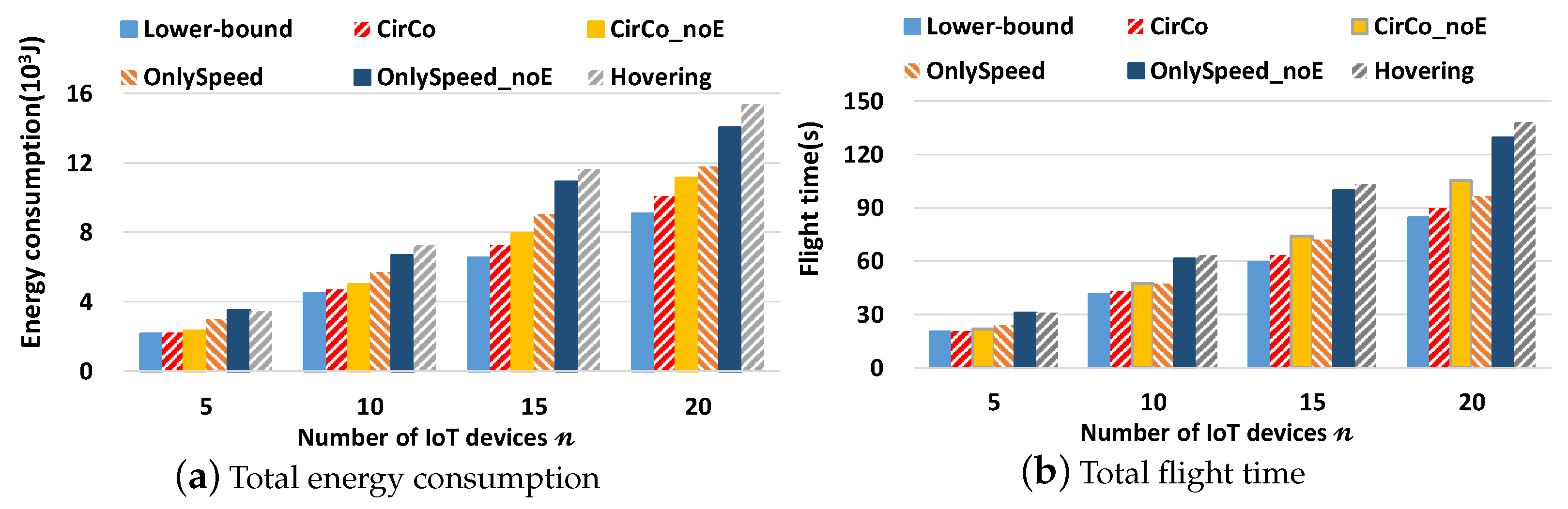
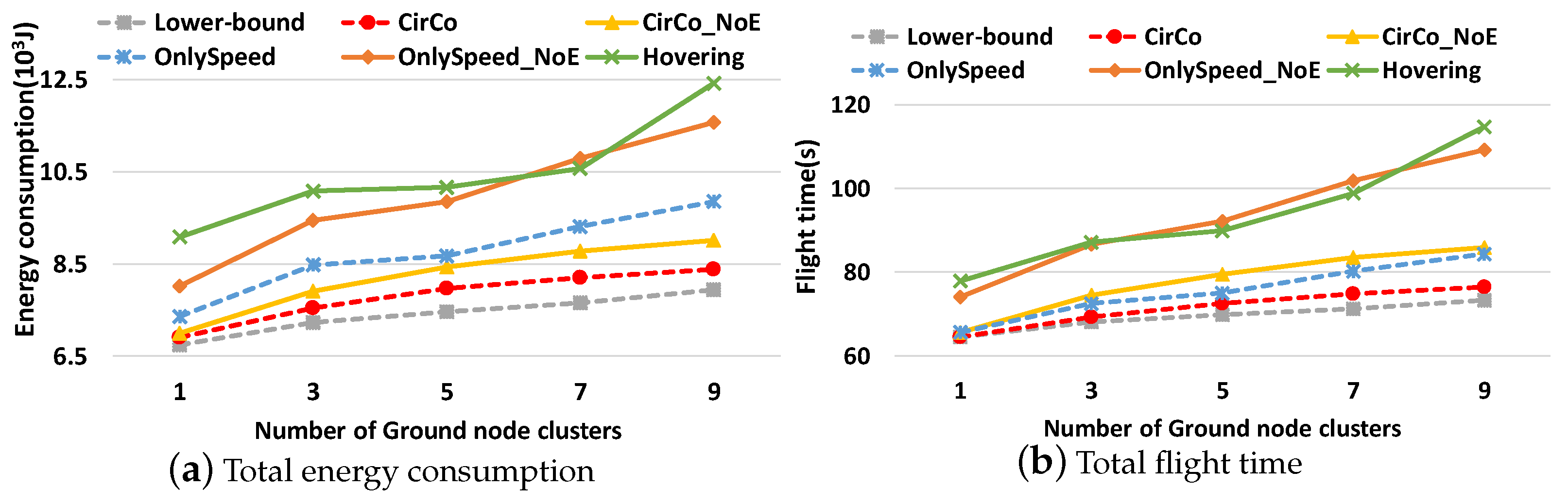
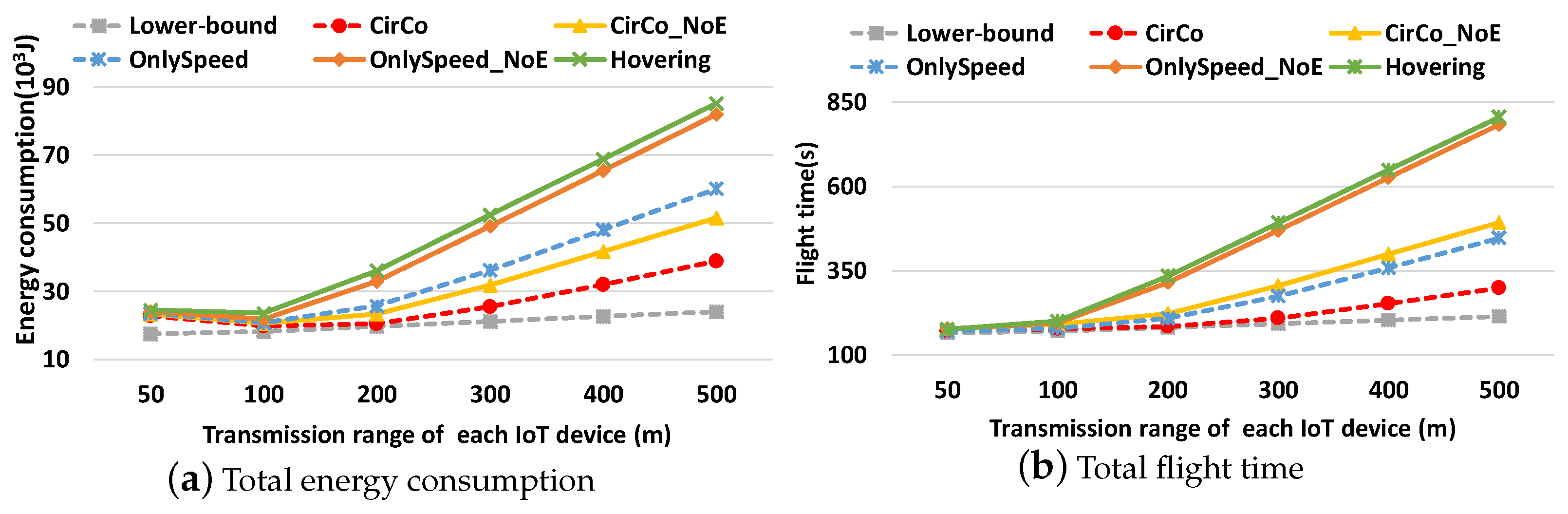
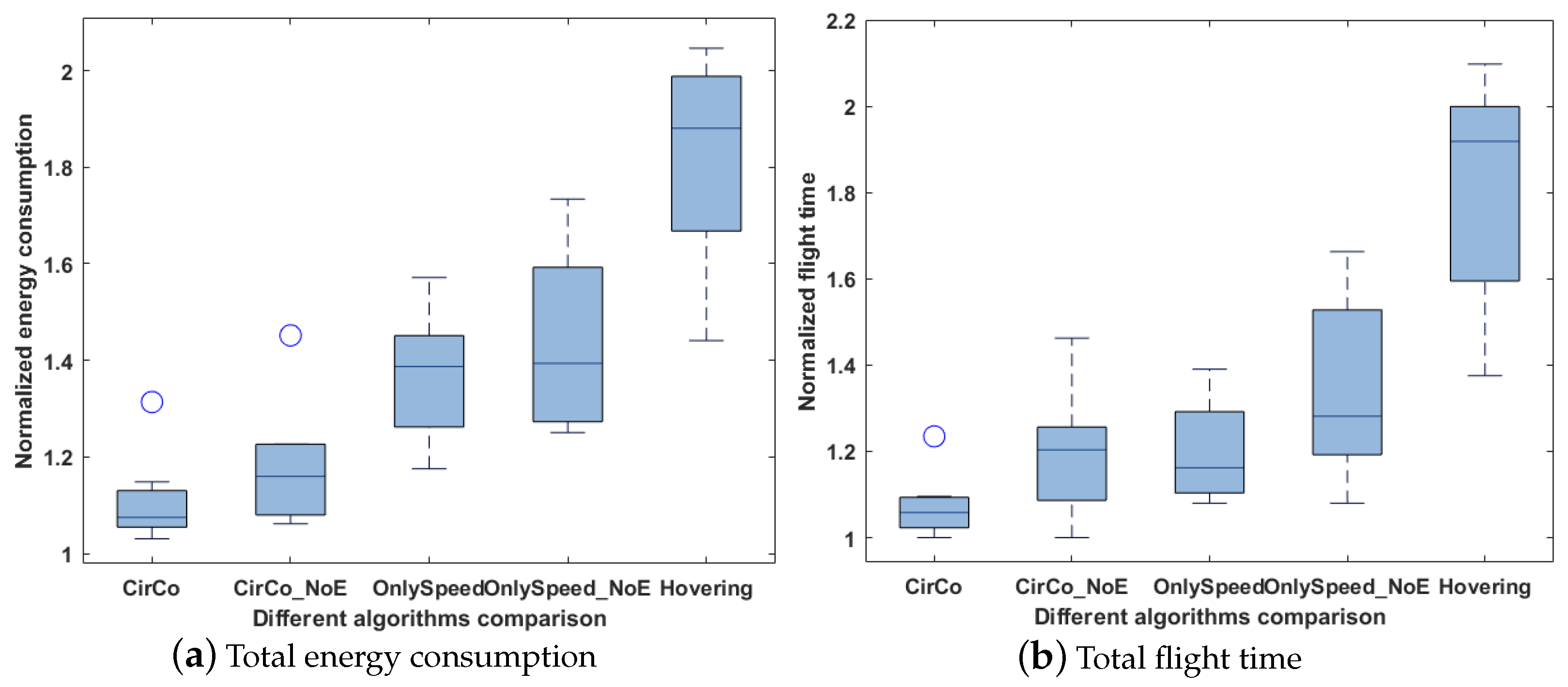
4. Experiment Evaluation
4.1. Experimental Settings
- OnlySpeed [31]: An algorithm of speed optimization. The UAV passes through the location of the GNs in turn. When the UAV reaches the communication range of the next GN, the UAV starts the next data collection task immediately. In addition, the speed of the UAV is chosen as close as while ensuring the completion of the data collection tasks.
- OnlySpeed_noE: A variant of OnlySpeed, which does not consider the relationship between energy consumption per unit distance and velocity. Moreover, the UAV speed is set as close as while ensuring the completion of the data collection tasks.
- CirCo_noE: A variant of CirCo, such as OnlySpeed_noE, CirCo_noE does not consider the relationship between energy consumption per unit distance and velocity when optimizing the velocity of the UAV.
- Lower-bound: A theoretical (may be infeasible) baseline with the minimum energy consumption of the joint trajectory and speed optimization problem. The energy consumption of its intra-GNC (inter-GNC) part is the product of the minimum transmission time (distance) of the corresponding optimal speed (). The energy consumption of the inter-GNC part is the product of the minimum distance among GNCs times the corresponding optimal speed .
- Hovering [36]: A joint speed and path optimization. It leverages the UAV to fly in the nearest line at a speed that minimizes the power of the UAV. If the UAV cannot finish the current transmission task when out of the current transmission range, the UAV hovers at the border until the task is finished. Moreover, Hovering does not consider the relationship between energy consumption per unit distance and velocity when optimizing the velocity of the UAV.
4.2. Energy Consumption and Flight Time Performance Comparison
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| UAV | unmanned aerial vehicle |
| IoT | Internet of Things |
| GN | ground node |
| GNC | ground node cluster |
References
- Ma, Z.; Zhou, Z.; Zhao, M.; Zheng, K. WinCross: Find the Energy-efficient Crossing Window for UAV with Joint Optimization of Path and Speed. In Proceedings of the 2021 International Conference on Space-Air-Ground Computing (SAGC), Huizhou, China, 23–25 October 2021; pp. 137–142. [Google Scholar]
- Lin, T.J.; Stol, K.A. Autonomous Surveying of Plantation Forests Using Multi-Rotor UAVs. Drones 2022, 6, 256. [Google Scholar] [CrossRef]
- Unal, G. Visual target detection and tracking based on Kalman filter. J. Aeronaut. Space Technol. 2021, 14, 251–259. [Google Scholar]
- Kiyak, U. Small aircraft detection using deep learning. Aircr. Eng. Aerosp. Technol. 2021, 93, 671–681. [Google Scholar] [CrossRef]
- Trotta, A.; Andreagiovanni, F.D.; Di Felice, M.; Natalizio, E.; Chowdhury, K.R. When UAVs ride a bus: Towards energy-efficient city-scale video surveillance. In Proceedings of the INFOCOM, Honolulu, HI, USA, 16–19 April 2018. [Google Scholar]
- Vecchi, E.; Tavasci, L.; De Nigris, N.; Gandolfi, S. GNSS and Photogrammetric UAV Derived Data for Coastal Monitoring: A Case of Study in Emilia-Romagna, Italy. J. Mar. Sci. Eng. 2021, 9, 1194. [Google Scholar] [CrossRef]
- Huang, H.; Savkin, A.V.; Huang, C. Round Trip Routing for Energy-Efficient Drone Delivery Based on a Public Transportation Network. IEEE Trans. Transp. Electrif. 2020, 6, 1368–1376. [Google Scholar] [CrossRef]
- Zhao, M.; Ma, Z.; Zhou, Z.; Zheng, K. WSpeed: Drone Energy Optimization for Multiple-Package Delivery Considering Weight Changes. In Proceedings of the 2021 International Conference on Space-Air-Ground Computing (SAGC), Huizhou, China, 23–25 October 2021; pp. 1–6. [Google Scholar]
- Tan, T.; Zhao, M.; Zhu, Y.; Zeng, Z. Joint Offloading and Resource Allocation of UAV-assisted Mobile Edge Computing with Delay Constraints. In Proceedings of the ICDCSW, Washington, DC, USA, 7–10 July 2021. [Google Scholar]
- Bai, T.; Wang, J.; Ren, Y.; Hanzo, L. Energy-efficient computation offloading for secure UAV-edge-computing systems. IEEE Trans. Veh. Technol. 2019, 68, 6074–6087. [Google Scholar] [CrossRef]
- Liu, Q.; Sun, S.; Rong, B.; Kadoch, M. Intelligent Reflective Surface Based 6G Communications for Sustainable Energy Infrastructure. IEEE Wirel. Commun. 2021, 28, 49–55. [Google Scholar] [CrossRef]
- Fu, S.; Tang, Y.; Wu, Y.; Zhang, N.; Gu, H.; Chen, C.; Liu, M. Energy-efficient UAV-enabled data collection via wireless charging: A reinforcement learning approach. IEEE Internet Things J. 2021, 8, 10209–10219. [Google Scholar] [CrossRef]
- Liu, D.; Xu, Y.; Xu, Y.; Sun, Y.; Anpalagan, A.; Wu, Q.; Luo, Y. Opportunistic data collection in cognitive wireless sensor networks: Air–ground collaborative online planning. IEEE Internet Things J. 2020, 7, 8837–8851. [Google Scholar] [CrossRef]
- Hinke, J.T.; Giuseffi, L.M.; Hermanson, V.R.; Woodman, S.M.; Krause, D.J. Evaluating Thermal and Color Sensors for Automating Detection of Penguins and Pinnipeds in Images Collected with an Unoccupied Aerial System. Drones 2022, 6, 255. [Google Scholar] [CrossRef]
- Bai, T.; Ben-Othman, J.; Han, S.; Kadoch, M.; Li, W.; Rong, B. Guest Editorial: Ubiquitous IoT with Integrated Space, Air, Ground, and Ocean Networks. IEEE Netw. 2021, 35, 98–99. [Google Scholar] [CrossRef]
- Mignardi, S.; Marini, R.; Verdone, R.; Buratti, C. On the performance of a uav-aided wireless network based on nb-iot. Drones 2021, 5, 94. [Google Scholar] [CrossRef]
- Baek, J.; Han, S.I.; Han, Y. Energy-efficient UAV routing for wireless sensor networks. IEEE Trans. Veh. Technol. 2019, 69, 1741–1750. [Google Scholar] [CrossRef]
- Gong, J.; Chang, T.H.; Shen, C.; Chen, X. Flight time minimization of UAV for data collection over wireless sensor networks. IEEE J. Sel. Areas Commun. 2018, 36, 1942–1954. [Google Scholar] [CrossRef]
- Liu, J.; Tong, P.; Wang, X.; Bai, B.; Dai, H. UAV-aided data collection for information freshness in wireless sensor networks. IEEE Trans. Wirel. Commun. 2020, 20, 2368–2382. [Google Scholar] [CrossRef]
- Gaur, A.; Scotney, B.; Parr, G.; McClean, S. Smart city architecture and its applications based on IoT. Procedia Comput. Sci. 2015, 52, 1089–1094. [Google Scholar] [CrossRef]
- Wang, J.; Su, J.; Hua, R. Design of a smart independent smoke sense system based on NB-IoT technology. In Proceedings of the 2019 International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS), Changsha, China, 12–13 January 2019. [Google Scholar]
- Klein Hentz, Â.M.; Kinder, P.J.; Hubbart, J.A.; Kellner, E. Accuracy and optimal altitude for physical habitat assessment (PHA) of stream environments using unmanned aerial vehicles (UAV). Drones 2018, 2, 20. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, X.; Huang, X.; Shen, L.; Huang, J.; Chang, X.; Xing, G. Understanding power consumption of NB-IoT in the wild: Tool and large-scale measurement. In Proceedings of the 26th Annual International Conference on Mobile Computing and Networking, London, UK, 21–25 September 2020. [Google Scholar]
- Xie, L.; Feng, X.; Zhang, C.; Dong, Y.; Huang, J.; Cheng, J. A Framework for Soil Salinity Monitoring in Coastal Wetland Reclamation Areas Based on Combined Unmanned Aerial Vehicle (UAV) Data and Satellite Data. Drones 2022, 6, 257. [Google Scholar] [CrossRef]
- Erdelj, M.; Natalizio, E. UAV-assisted disaster management: Applications and open issues. In Proceedings of the 2016 international conference on computing, networking and communications (ICNC), Kauai, HI, USA, 15–18 February 2016; pp. 1–5. [Google Scholar]
- Liu, M.; Yang, J.; Gui, G. DSF-NOMA: UAV-assisted emergency communication technology in a heterogeneous Internet of Things. IEEE Internet Things J. 2019, 6, 5508–5519. [Google Scholar] [CrossRef]
- Pádua, L.; Guimarães, N.; Adão, T.; Sousa, A.; Peres, E.; Sousa, J.J. Effectiveness of sentinel-2 in multi-temporal post-fire monitoring when compared with UAV imagery. ISPRS Int. J. Geo-Inf. 2020, 9, 225. [Google Scholar] [CrossRef]
- Fu, X.; Ding, T.; Peng, R.; Liu, C.; Cheriet, M. Joint UAV channel modeling and power control for 5G IoT networks. EURASIP J. Wirel. Commun. Netw. 2021, 2021, 106. [Google Scholar] [CrossRef]
- Zhou, Z.; Ma, Z.; Zhao, M.; Zheng, K. E-Cube: Energy-efficient UAV Trajectory Scheduling with Height and Speed Optimization. In Proceedings of the 2021 International Conference on Space-Air-Ground Computing (SAGC), Huizhou, China, 23–25 October 2021; pp. 12–17. [Google Scholar]
- Yang, Z.; Xu, W.; Shikh-Bahaei, M. Energy efficient UAV communication with energy harvesting. IEEE Trans. Veh. Technol. 2019, 69, 1913–1927. [Google Scholar] [CrossRef]
- Shan, F.; Luo, J.; Xiong, R.; Wu, W.; Li, J. Looking before Crossing: An Optimal Algorithm to Minimize UAV Energy by Speed Scheduling with a Practical Flight Energy Model. In Proceedings of the INFOCOM, Toronto, ON, Canada, 6–9 July 2020. [Google Scholar]
- Abeywickrama, H.V.; Jayawickrama, B.A.; He, Y.; Dutkiewicz, E. Comprehensive Energy Consumption Model for Unmanned Aerial Vehicles, Based on Empirical Studies of Battery Performance. IEEE Access 2018, 6, 58383–58394. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Debbah, M. Mobile Unmanned Aerial Vehicles (UAVs) for Energy-Efficient Internet of Things Communications. IEEE Trans. Wirel. Commun. 2017, 16, 7574–7589. [Google Scholar] [CrossRef]
- Baek, J.; Han, S.I.; Han, Y. Optimal UAV route in wireless charging sensor networks. IEEE Internet Things J. 2019, 7, 1327–1335. [Google Scholar] [CrossRef]
- Zhan, C.; Lai, H. Energy Minimization in Internet-of-Things System Based on Rotary-Wing UAV. IEEE Wirel. Commun. Lett. 2019, 8, 1341–1344. [Google Scholar] [CrossRef]
- Zeng, Y.; Xu, J.; Zhang, R. Energy Minimization for Wireless Communication With Rotary-Wing UAV. IEEE Trans. Wirel. Commun. 2019, 18, 2329–2345. [Google Scholar] [CrossRef]
- Wang, C.N.; Yang, F.C.; Nguyen, V.T.T.; Vo, N.T. CFD analysis and optimum design for a centrifugal pump using an effectively artificial intelligent algorithm. Micromachines 2022, 13, 1208. [Google Scholar] [CrossRef]
- Ye, W.; Wu, W.; Shan, F.; Yang, M.; Luo, J. Energy-efficient Trajectory Planning and Speed Scheduling for UAV-assisted Data Collection. In Proceedings of the 2020 16th International Conference on Mobility, Sensing and Networking (MSN), Tokyo, Japan, 17–19 December 2020. [Google Scholar]
- Song, D.; Zhai, X.B.; Liu, X.; Tan, C.W. Jointly Optimal Fair Data Collection and Trajectory Design Algorithms in UAV-Aided Cellular Networks. In Proceedings of the 2021 IEEE Wireless Communications and Networking Conference (WCNC), Nanjing, China, 29 March–1 April 2021. [Google Scholar]
- Zhang, J.; Li, Z.; Xu, W.; Peng, J.; Liang, W.; Xu, Z.; Ren, X.; Jia, X. Minimizing the number of deployed UAVs for delay-bounded data collection of IoT devices. In Proceedings of the INFOCOM, Vancouver, BC, Canada, 10–13 May 2021. [Google Scholar]
- Zhan, C.; Zeng, Y.; Zhang, R. Energy-efficient data collection in UAV enabled wireless sensor network. IEEE Wirel. Commun. Lett. 2017, 7, 328–331. [Google Scholar] [CrossRef]
- Ren, X.; Liang, W.; Xu, W. Data collection maximization in renewable sensor networks via time-slot scheduling. IEEE Trans. Comput. 2014, 64, 1870–1883. [Google Scholar] [CrossRef]
- Sial, M.B.; Zhang, Y.; Wang, S.; Ali, S.; Wang, X.; Yang, X.; Liao, Z.; Yang, Z. Bearing-Based Distributed Formation Control of Unmanned Aerial Vehicle Swarm by Quaternion-Based Attitude Synchronization in Three-Dimensional Space. Drones 2022, 6, 227. [Google Scholar] [CrossRef]
- Torky, M.; El-Dosuky, M.; Goda, E.; Snášel, V.; Hassanien, A.E. Scheduling and Securing Drone Charging System Using Particle Swarm Optimization and Blockchain Technology. Drones 2022, 6, 237. [Google Scholar] [CrossRef]



| Notation | Physical Meaning | Simulation Value |
|---|---|---|
| W | Weight of UAV in Newton | 20 |
| Air density () | 1.225 | |
| R | Roter radius (m) | 0.4 |
| n | Number of blades | 4 |
| l | blade chord length (m) | 0.0157 |
| Blade angular velocity (r/s) | 300 | |
| s | Roter solidity, defined as the ratio of the total blade area to the rotor disc area, = | 0.05 |
| Fuselage equivalent flat area () | 0.0151 | |
| Fuselage drag ratio, = | 0.6 | |
| k | Incremental correction factor to induced power | 0.1 |
| Mean rotor induced velocity in hover, = | 0.0157 | |
| Profile drag coefficient | 0.012 |
| Notation | Description |
|---|---|
| The ith ground node cluster (GNCs) | |
| I/J | The total number of GNCs/GNs |
| The location of the center point for the ith GNC | |
| / | The time when the UAV leaves or arrives |
| The vector path from to | |
| The velocity of the UAV between and | |
| The j ground node(GNs) in the ith GNC | |
| The total number of GNs in the ith GNC | |
| The location of | |
| The radius of | |
| The minimum communication time of | |
| The overlapped area between and | |
| / | The starting/endpoint of communication in |
| / | The time when the UAV leaves or arrives at |
| The vector path from to | |
| The velocity of the UAV between and | |
| H | The altitude of the UAV |
| /P | The power/(energy consumption per mile) of UAV |
| / | The UAV velocity corresponding to minimum P/ |
| The total consumption of UAV | |
| / | The consumption of the UAV insides/among GNCs |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, K.; Ma, Z.; Zhao, M.; Zhou, Z.; Zhang, Z.; Li, Y. Joint Efficient UAV Trajectory and Velocity Optimization for IoT Data Collection Using a New Projection Algorithm. Drones 2022, 6, 376. https://doi.org/10.3390/drones6120376
Zheng K, Ma Z, Zhao M, Zhou Z, Zhang Z, Li Y. Joint Efficient UAV Trajectory and Velocity Optimization for IoT Data Collection Using a New Projection Algorithm. Drones. 2022; 6(12):376. https://doi.org/10.3390/drones6120376
Chicago/Turabian StyleZheng, Kuangyu, Zimo Ma, Mingyue Zhao, Zhuyang Zhou, Ziheng Zhang, and Yifeng Li. 2022. "Joint Efficient UAV Trajectory and Velocity Optimization for IoT Data Collection Using a New Projection Algorithm" Drones 6, no. 12: 376. https://doi.org/10.3390/drones6120376
APA StyleZheng, K., Ma, Z., Zhao, M., Zhou, Z., Zhang, Z., & Li, Y. (2022). Joint Efficient UAV Trajectory and Velocity Optimization for IoT Data Collection Using a New Projection Algorithm. Drones, 6(12), 376. https://doi.org/10.3390/drones6120376






