Accuracy Assessment of Direct Georeferencing for Photogrammetric Applications Based on UAS-GNSS for High Andean Urban Environments
Abstract
1. Introduction
2. Materials and Methods
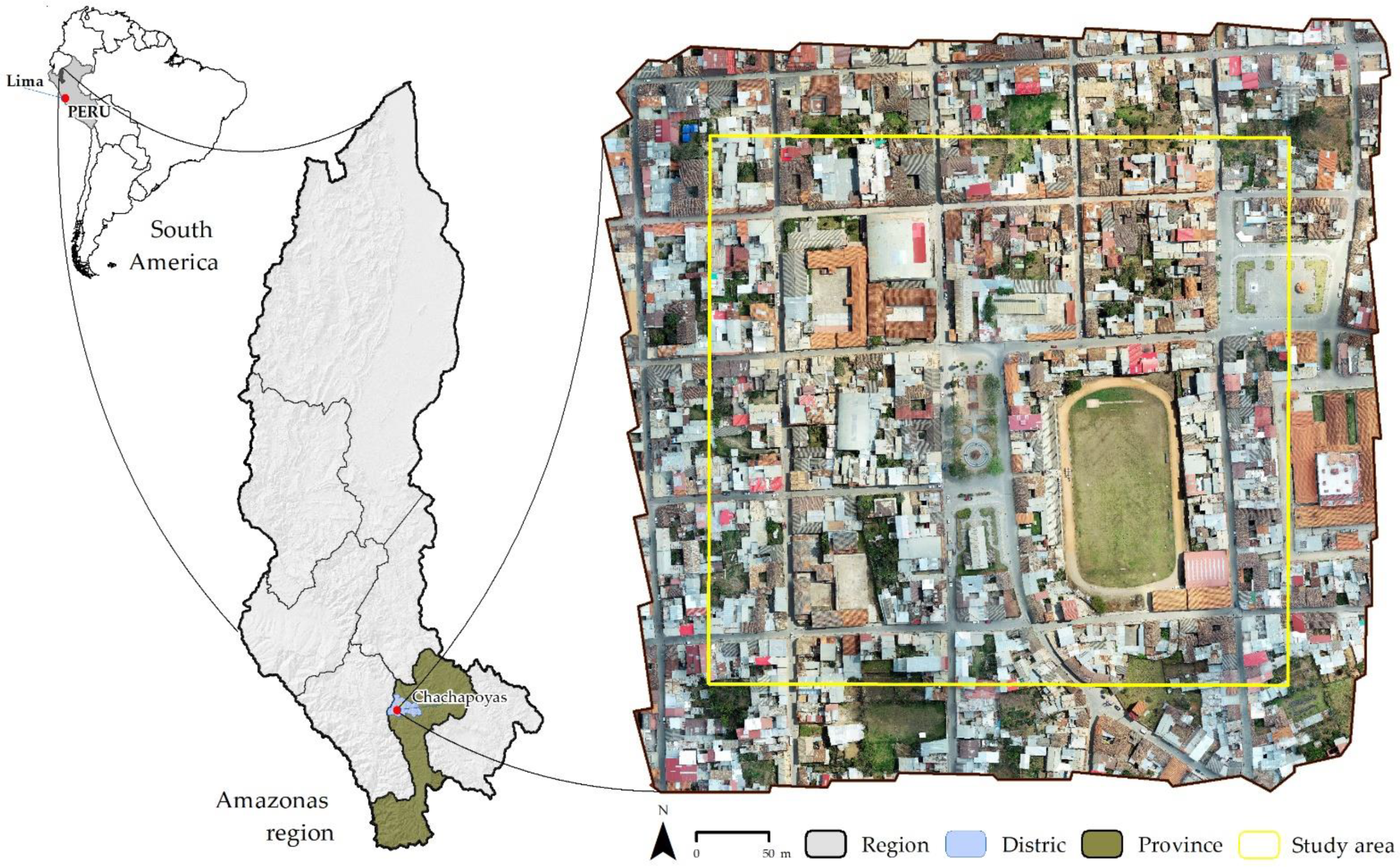
2.1. Study Area
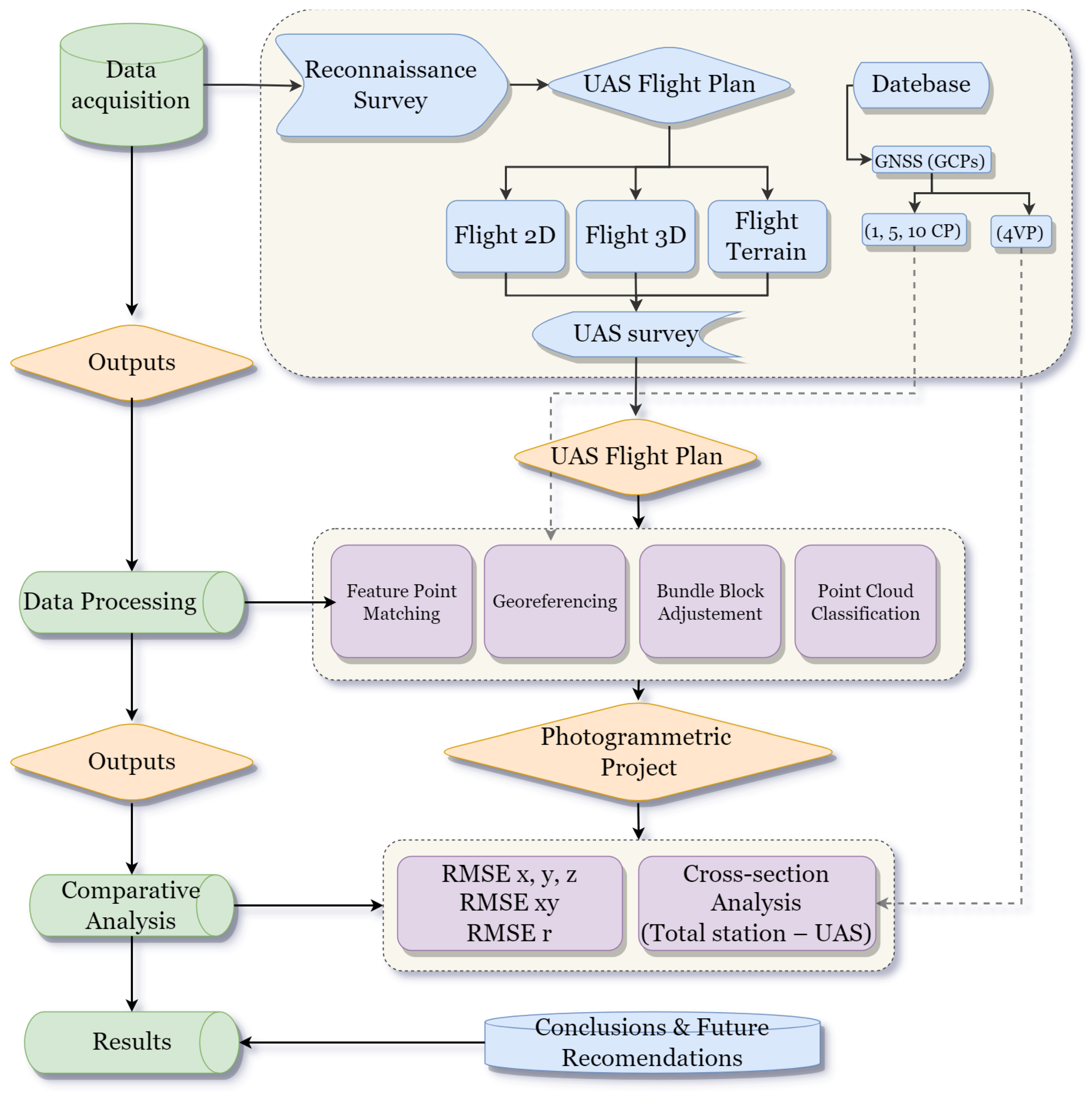
2.2. Data Acquisition
2.2.1. GNSS Survey
2.2.2. UAS Planning
2.3. Positioning Configurations Adopted during Flight Tests
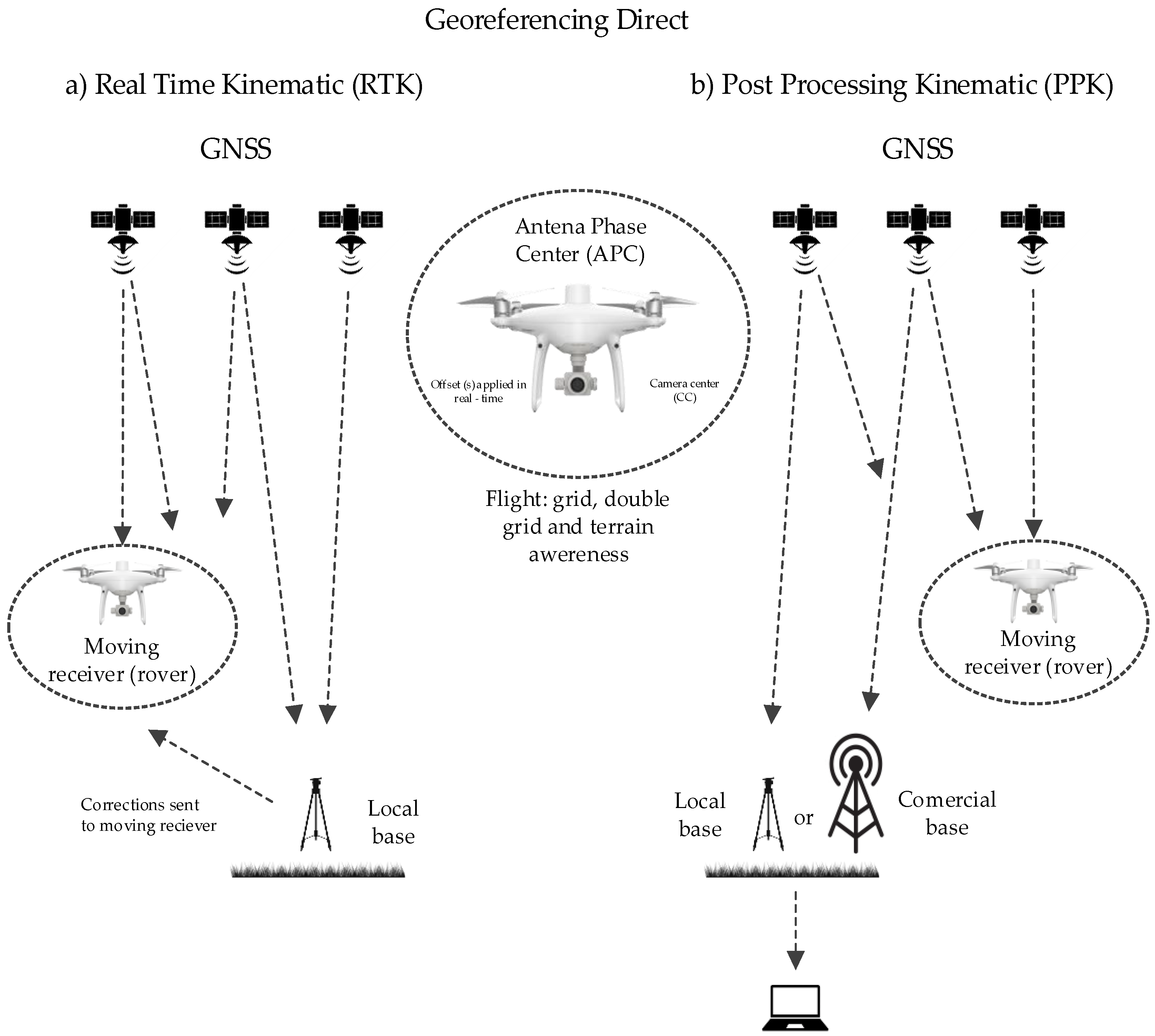
2.3.1. UAS-RTK Surveying
2.3.2. UAS-PPK Surveying
2.4. Photogrammetric Processing of the Acquired Data
2.5. Comparative Analysis
2.5.1. Accuracy Assessment
2.5.2. Cross-Section Analysis
3. Results
3.1. Geometric Accuracy of Aerial Photographic Mosaics
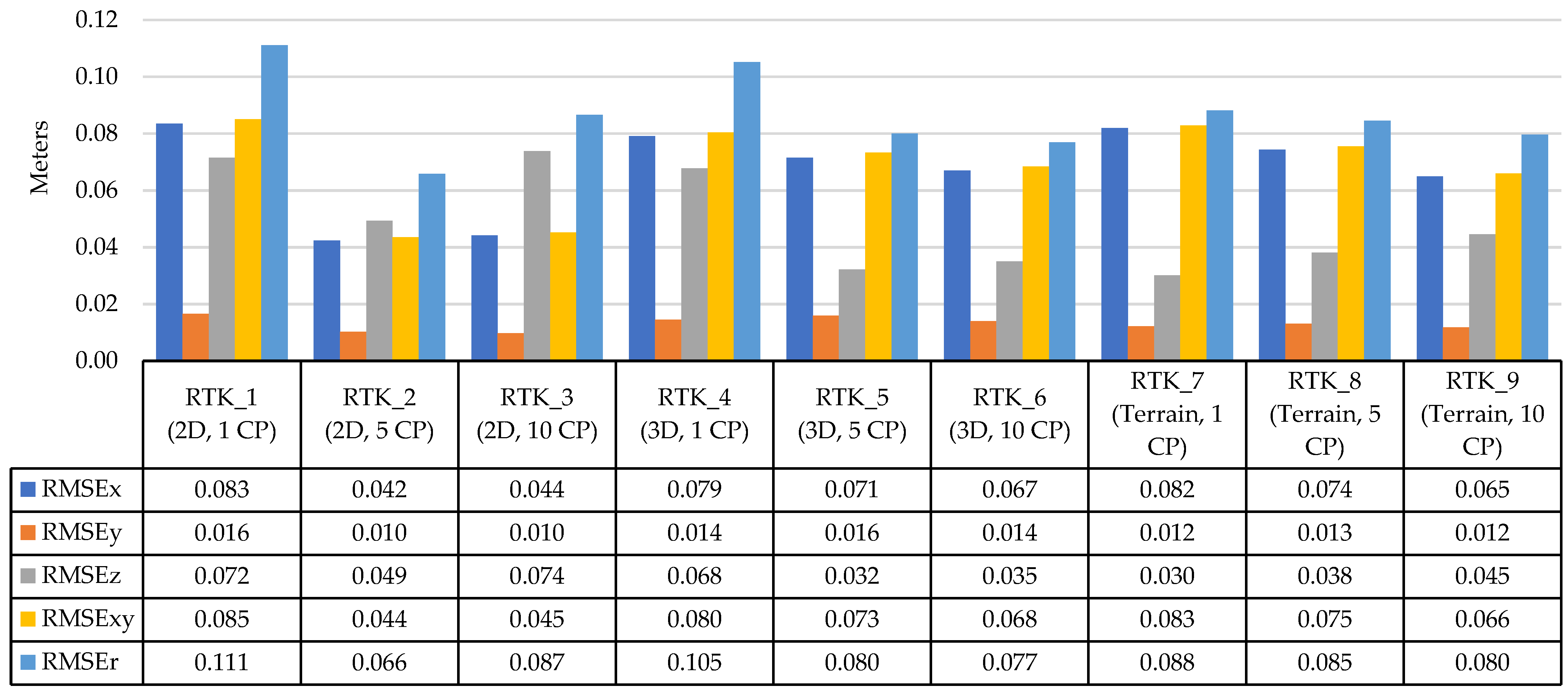
3.1.1. RTK Accuracy
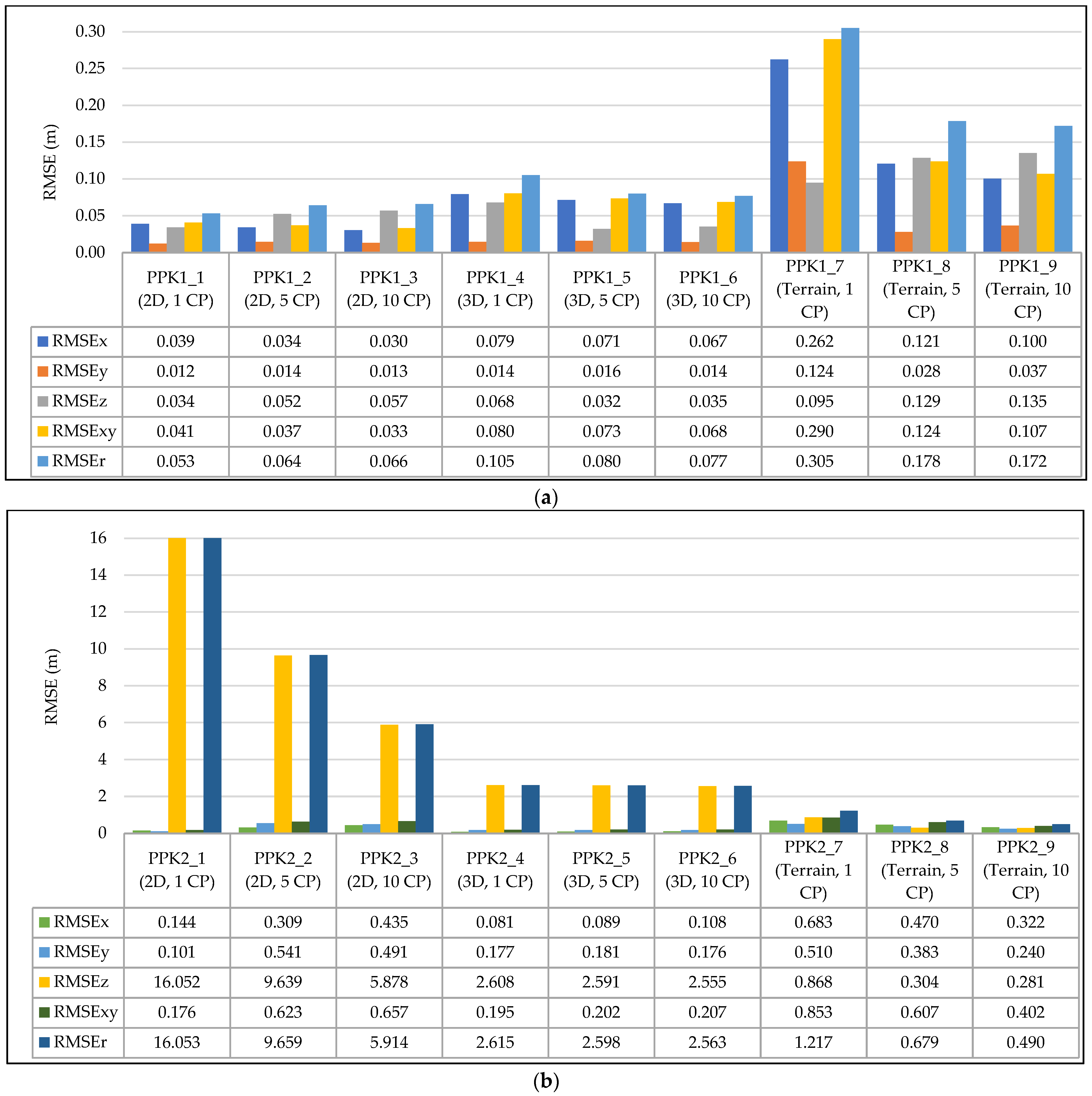
3.1.2. PPK1 and PPK2 Accuracy
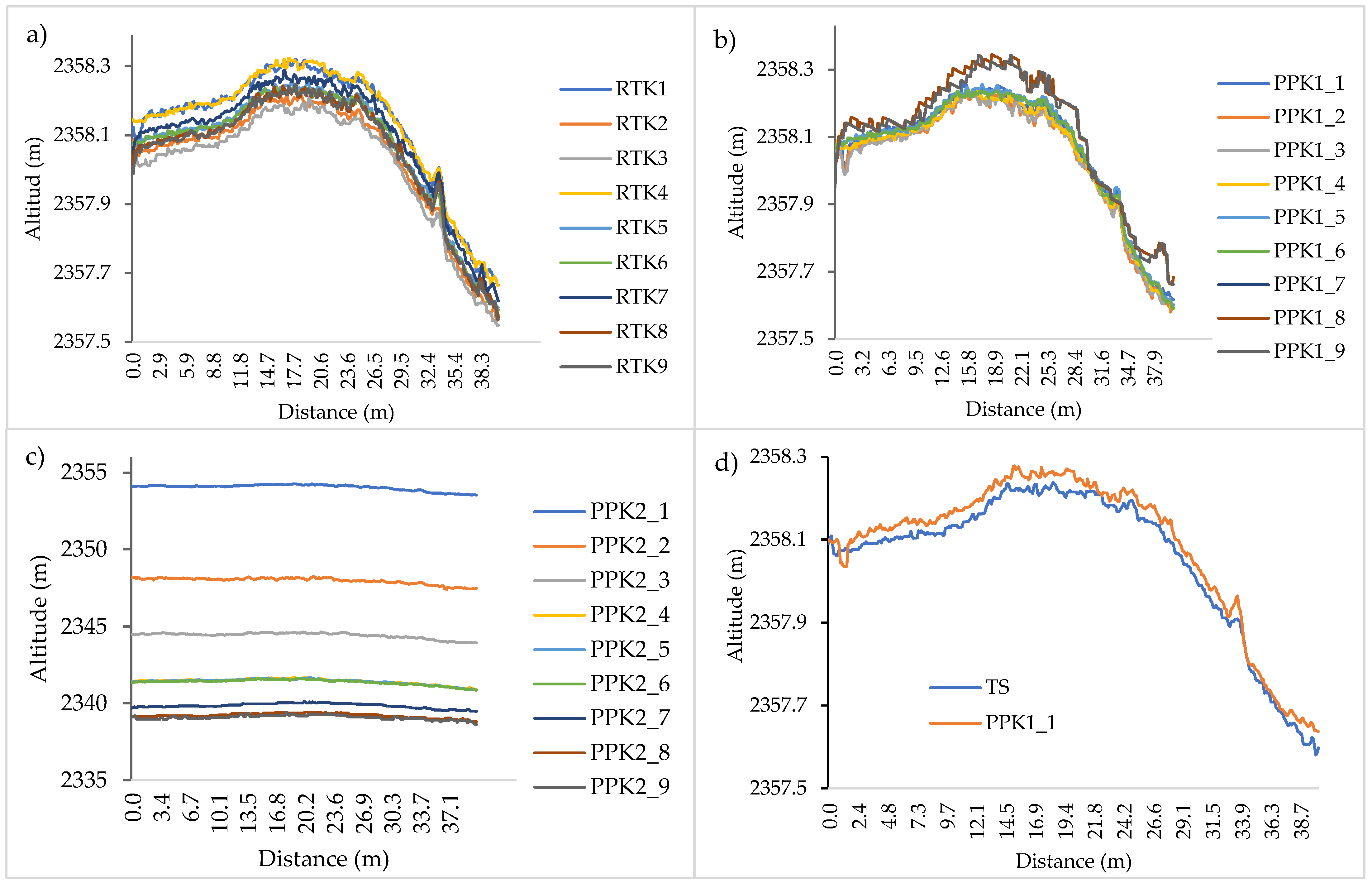
3.2. Cross-Section
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Koslowski, R.; Schulzke, M. Drones along Borders: Border Security UAVs in the United States and the European Union. Int. Stud. Perspect. 2018, 19, 305–324. [Google Scholar] [CrossRef]
- Blázquez, M.; Colomina, I. Relative INS/GNSS aerial control in integrated sensor orientation: Models and performance. ISPRS J. Photogramm. Remote Sens. 2012, 67, 120–133. [Google Scholar] [CrossRef]
- Kerle, N.; Nex, F.; Gerke, M.; Duarte, D.; Vetrivel, A. UAV-Based Structural Damage Mapping: A Review. ISPRS Int. J. Geo-Inf. 2019, 9, 14. [Google Scholar] [CrossRef]
- Jiang, S.; Jiang, C.; Jiang, W. Efficient structure from motion for large-scale UAV images: A review and a comparison of SfM tools. ISPRS J. Photogramm. Remote Sens. 2020, 167, 230–251. [Google Scholar] [CrossRef]
- Grubesic, T.H.; Nelson, J.R. UAVs and Urban Spatial Analysis; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Mozas-Calvache, A.T.; Pérez-García, J.L. Analysis and Comparison of Lines Obtained from GNSS and UAV for Large-Scale Maps. J. Surv. Eng. 2017, 143, 04016028. [Google Scholar] [CrossRef]
- Roberts, J.; Koeser, A.; Abd-Elrahman, A.; Wilkinson, B.; Hansen, G.; Landry, S.; Perez, A. Mobile Terrestrial Photogrammetry for Street Tree Mapping and Measurements. Forests 2019, 10, 701. [Google Scholar] [CrossRef]
- Xu, S.; Vosselman, G.; Elberink, S.O. Multiple-entity based classification of airborne laser scanning data in urban areas. ISPRS J. Photogramm. Remote Sens. 2014, 88, 1–15. [Google Scholar] [CrossRef]
- Pepe, M.; Fregonese, L.; Scaioni, M. Planning airborne photogrammetry and remote-sensing missions with modern platforms and sensors. Eur. J. Remote Sens. 2018, 51, 412–435. [Google Scholar] [CrossRef]
- Jones, C.A.; Church, E. Photogrammetry is for everyone: Structure-from-motion software user experiences in archaeology. J. Archaeol. Sci. Rep. 2020, 30, 102261. [Google Scholar] [CrossRef]
- Vasuki, Y.; Holden, E.-J.; Kovesi, P.; Micklethwaite, S. Semi-automatic mapping of geological Structures using UAV-based photogrammetric data: An image analysis approach. Comput. Geosci. 2014, 69, 22–32. [Google Scholar] [CrossRef]
- Taddia, Y.; Corbau, C.; Zambello, E.; Russo, V.; Simeoni, U.; Russo, P.; Pellegrinelli, A. UAVs to Assess the Evolution of Embryo Dunes. In Proceedings of the International Conference on Unmanned Aerial Vehicles in Geomatics, Bonn, Germany, 23 August 2017; Volume 42, pp. 363–369. [Google Scholar]
- Taddia, Y.; Pellegrinelli, A.; Corbau, C.; Franchi, G.; Staver, L.; Stevenson, J.; Nardin, W. High-Resolution Monitoring of Tidal Systems Using UAV: A Case Study on Poplar Island, MD (USA). Remote Sens. 2021, 13, 1364. [Google Scholar] [CrossRef]
- Gaitani, N.; Burud, I.; Thiis, T.; Santamouris, M. High-resolution spectral mapping of urban thermal properties with Unmanned Aerial Vehicles. Build. Environ. 2017, 121, 215–224. [Google Scholar] [CrossRef]
- Tokarczyk, P.; Leitao, J.P.; Rieckermann, J.; Schindler, K.; Blumensaat, F. High-quality observation of surface imperviousness for urban runoff modelling using UAV imagery. Hydrol. Earth Syst. Sci. 2015, 19, 4215–4228. [Google Scholar] [CrossRef]
- Salvo, G.; Caruso, L.; Scordo, A. Urban Traffic Analysis through an UAV. Procedia Soc. Behav. Sci. 2014, 111, 1083–1091. [Google Scholar] [CrossRef]
- Zhang, M.; Rao, Y.; Pu, J.; Luo, X.; Wang, Q. Multi-Data UAV Images for Large Scale Reconstruction of Buildings. In Proceedings of the Multi Media Modeling 26th International Conference, MMM 2020, Daejeon, Republic of Korea, 5–8 January 2020; Springer: Cham, Switzerland, 2020; Volume 11962, pp. 254–266. [Google Scholar]
- Nex, F.; Remondino, F. UAV for 3D mapping applications: A review. Appl. Geomat. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Diaz-Varela, R.; Angileri, V.; Loudjani, P. Tree height quantification using very high resolution imagery acquired from an unmanned aerial vehicle (UAV) and automatic 3D photo-reconstruction methods. Eur. J. Agron. 2014, 55, 89–99. [Google Scholar] [CrossRef]
- Casapia, X.T.; Falen, L.; Bartholomeus, H.; Cárdenas, R.; Flores, G.; Herold, M.; Coronado, E.N.H.; Baker, T.R. Identifying and Quantifying the Abundance of Economically Important Palms in Tropical Moist Forest Using UAV Imagery. Remote Sens. 2020, 12, 9. [Google Scholar] [CrossRef]
- Westoby, M.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. ‘Structure-from-Motion’ photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- Kalacska, M.; Lucanus, O.; Arroyo-Mora, J.; Laliberté, E.; Elmer, K.; Leblanc, G.; Groves, A. Accuracy of 3D Landscape Reconstruction without Ground Control Points Using Different UAS Platforms. Drones 2020, 4, 13. [Google Scholar] [CrossRef]
- Cledat, E.; Jospin, L.; Cucci, D.; Skaloud, J. Mapping quality prediction for RTK/PPK-equipped micro-drones operating in complex natural environment. ISPRS J. Photogramm. Remote Sens. 2020, 167, 24–38. [Google Scholar] [CrossRef]
- Trujillo, M.M.; Darrah, M.; Speransky, K.; DeRoos, B.; Wathen, M. Optimized flight path for 3D mapping of an area with structures using a multirotor. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016. [Google Scholar] [CrossRef]
- Backes, D.; Schumann, G.; Teferele, F.N.; Boehm, J. Towards a High-Resolution Drone-Based 3D Mapping Dataset to Optimise Flood Hazard Modelling. In Proceedings of the ISPRS Geospatial Week 2019, Enschede, The Netherland, 10–14 June 2019; Volume 42, pp. 181–187. [Google Scholar]
- Gabrlik, P. The Use of Direct Georeferencing in Aerial Photogrammetry with Micro UAV. IFAC-Pap. 2015, 48, 380–385. [Google Scholar] [CrossRef]
- Agüera-Vega, F.; Carvajal-Ramírez, F.; Martínez-Carricondo, P. Assessment of photogrammetric mapping accuracy based on variation ground control points number using unmanned aerial vehicle. Measurement 2017, 98, 221–227. [Google Scholar] [CrossRef]
- Martínez-Carricondo, P.; Agüera-Vega, F.; Carvajal-Ramírez, F.; Mesas-Carrascosa, F.J.; García-Ferrer, A.; Pérez-Porras, F.-J. Assessment of UAV-photogrammetric mapping accuracy based on variation of ground control points. Int. J. Appl. Earth Obs. Geoinf. 2018, 72, 1–10. [Google Scholar] [CrossRef]
- Sanz-Ablanedo, E.; Chandler, J.H.; Rodríguez-Pérez, J.R.; Ordóñez, C. Accuracy of unmanned aerial vehicle (UAV) and SfM photogrammetry survey as a function of the number and location of ground control points used. Remote Sens. 2018, 10, 1606. [Google Scholar] [CrossRef]
- Heipke, C.; Jacobsen, K.; Wegmann, H.; Andersen, Ø.; Nilsen, B. Test Goals and Test Set up for the OEEPE Test. In Integrated Sensor Orientation; OEEPE Official Publication: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Bilker, M.; Honkavaara, E.; Jaakkola, J. GSPS Supported Aerial Triangulation Using Untargeted Ground Control. Int. Arch. Photogramm. Remote Sens. 1998, 32, 2–9. [Google Scholar]
- Ip, A.; El-Sheimy, N.; Mostafa, M. Performance Analysis of Integrated Sensor Orientation. Photogramm. Eng. Remote Sens. 2007, 73, 89–97. [Google Scholar] [CrossRef]
- Cramer, M.; Stallmann, D.; Haala, N. Direct Georeferencing Using GPS/Inertial Exterior Orientations for Photogrammetric. Int. Arch. Photogramm. Remote Sens. 2000, 33, 198–205. [Google Scholar]
- Losè, L.T.; Chiabrando, F.; Tonolo, F.G. Boosting the Timeliness of UAV Large Scale Mapping. Direct Georeferencing Approaches: Operational Strategies and Best Practices. ISPRS Int. J. Geo-Inf. 2020, 9, 578. [Google Scholar] [CrossRef]
- Xiang, T.-Z.; Xia, G.-S.; Zhang, L. Mini-unmanned aerial vehicle-based remote sensing: Techniques, applications, and prospects. IEEE Geosci. Remote Sens. Mag. 2019, 7, 29–63. [Google Scholar] [CrossRef]
- Zhang, H.; Aldana-Jague, E.; Clapuyt, F.; Wilken, F.; Vanacker, V.; Van Oost, K. Evaluating the potential of post-processing kinematic (PPK) georeferencing for UAV-based structure- from-motion (SfM) photogrammetry and surface change detection. Earth Surf. Dyn. 2019, 7, 807–827. [Google Scholar] [CrossRef]
- Benassi, F.; Dall’Asta, E.; Diotri, F.; Forlani, G.; Morra Di Cella, U.; Roncella, R.; Santise, M. Testing Accuracy and Repeatability of UAV Blocks Oriented with GNSS-Supported Aerial Triangulation. Remote Sens. 2017, 9, 172. [Google Scholar] [CrossRef]
- Rehak, M.; Skaloud, J. FIXED-WING Micro Aerial Vehicle for Accurate Corridor Mapping. In Proceedings of the International Conference on Unmanned Aerial Vehicles in Geomatics, Toronto, ON, Canada, 30 August–2 September 2015; Volume 2, pp. 23–31. [Google Scholar]
- Stöcker, C.; Nex, F.; Koeva, M.; Gerke, M. Quality Assessment of Combined IMU/GNSS Data for Direct Georeferencing in the Context of UAV-Based Mapping. In Proceedings of the International Conference on Unmanned Aerial Vehicles in Geomatics, Bonn, Germany, 4–7 September 2017; Volume 42, pp. 355–361. [Google Scholar]
- Rehak, M.; Mabillard, R.; Skaloud, J. A Micro Aerial Vehicle with Precise Position and Attitude Sensors. Photogramm. -Fernerkund. -Geoinf. 2014, 4, 239–251. [Google Scholar] [CrossRef]
- Cucci, D.A.; Rehak, M.; Skaloud, J. Bundle adjustment with raw inertial observations in UAV applications. ISPRS J. Photogramm. Remote Sens. 2017, 130, 1–12. [Google Scholar] [CrossRef]
- Rabah, M.; Basiouny, M.; Ghanem, E.; Elhadary, A. Using RTK and VRS in direct geo-referencing of the UAV imagery. NRIAG J. Astron. Geophys. 2018, 7, 220–226. [Google Scholar] [CrossRef]
- Hugenholtz, C.; Brown, O.; Walker, J.; Barchyn, T.; Nesbit, P.; Kucharczyk, M.; Myshak, S. Spatial Accuracy of UAV-Derived Orthoimagery and Topography: Comparing Photogrammetric Models Processed with Direct Geo-Referencing and Ground Control Points. Geomatica 2016, 70, 21–30. [Google Scholar] [CrossRef]
- Forlani, G.; Diotri, F.; Morra Di Cella, U.; Roncella, R. UAV Block Georeferencing and Control by ON-BOARD GNSS Data. In Proceedings of the XXIV ISPRS Congress, Nice, France, 31 August–2 September 2020; Volume 43, pp. 9–16. [Google Scholar]
- DJI Phantom 4 RTK, User Manual v2.4. Available online: https://www.dji.com/downloads/products/phantom-4-rtk (accessed on 3 May 2022).
- Przybilla, H.-J.; Bäumker, M.; Luhmann, T.; Hastedt, H.; Eilers, M. Interaction between direct georeferencing, control point configuration and camera self-calibration for rtk-based uav photogrammetry. In Proceedings of the XXIV ISPRS Congress, Nice, France, 31 August–2 September 2020; pp. 485–492. [Google Scholar]
- Taddia, Y.; Stecchi, F.; Pellegrinelli, A. Coastal Mapping Using DJI Phantom 4 RTK in Post-Processing Kinematic Mode. Drones 2020, 4, 9. [Google Scholar] [CrossRef]
- Štroner, M.; Urban, R.; Reindl, T.; Seidl, J.; Brouček, J. Evaluation of the Georeferencing Accuracy of a Photogrammetric Model Using a Quadrocopter with Onboard GNSS RTK. Sensors 2020, 20, 2318. [Google Scholar] [CrossRef]
- Losè, L.T.; Chiabrando, F.; Tonolo, F.G. Are measured ground control points still required in uav based large scale mapping? Assessing the positional accuracy of an RTK multi-rotor platform. In Proceedings of the XXIV ISPRS Congress, Nice, France, 31 August–2 September 2020; pp. 507–514. [Google Scholar]
- American Society for Photogrammetryand Remote Sensing (ASPRS). ASPRS Positional Accuracy Standards for Digital Geospatial Data. Photogramm. Eng. Remote Sens. 2015, 81, A1–A26. [Google Scholar] [CrossRef]
- Whitehead, K.; Hugenholtz, C.H. Applying ASPRS Accuracy Standards to Surveys from Small Unmanned Aircraft Systems (UAS). Photogramm. Eng. Remote Sens. 2015, 81, 787–793. [Google Scholar] [CrossRef]
- Agüera-Vega, F.; Carvajal-Ramírez, F.; Martínez-Carricondo, P. Accuracy of Digital Surface Models and Orthophotos Derived from Unmanned Aerial Vehicle Photogrammetry. J. Surv. Eng. 2017, 143, 04016025. [Google Scholar] [CrossRef]
- Rscón, J.; Angeles, W.G.; Oliva, M.; Huatangari, L.Q.; Grurbillon, M.A.B. Determinación de Las Épocas Lluviosas y Secas En La Ciudadde Chachapoyas Para El Periodo de 2014–2018. Rev. Climatol. 2020, 20, 15–28. [Google Scholar]
- Municipalidad Provincial de Chachapoyas (MPCH). Plan de Desarrollo Urbano de La Ciudad de Chachapoyas; Scribd: Chschapoyas, Peru, 2013.
- Instituto Geográfico Nacional (IGN). Norma Técnica Geodésica: Especificaciones Técnicas Para Posicionamiento Geodésico Estático Relativo Con Receptores Del Sistema Satelital de Navegación Global; IGN: Lima, Peru, 2015. [Google Scholar]
- TRIMBLE. Trimble R10 GNSS Receiver User Guide; IGN: Lima, Peru, 2014. [Google Scholar]
- DJI. D-RTK 2 High Precision GNSS Mobile Station Release Notes; DJI: Shenzhen, China, 2021. [Google Scholar]
- Takasu, T.; Yasuda, A. Development of the Low-Cost RTK-GPS Receiver with an Open Source Program Package RTKLIB. In International Symposium on GPS/GNSS; International Convention Center Jeju Korea: Seogwipo-si, Korea, 2009; Volume 1, pp. 1–6. [Google Scholar]
- REDcatch. REDtoolbox v2.77 User Manual; REDcatch: Fulpmes, Austria; pp. 1–29.
- Agisoft Metashape User Manual, Standard Edition, Version 1.7. Available online: https://www.agisoft.com/downloads/user-manuals/ (accessed on 3 May 2021).
- Congalton, R.G. Thematic and Positional Accuracy Assessment of Digital Remotely Sensed Data. In Proceedings of the Seventh Annual Forest Inventory and Analysis Symposium, Portland, ME, USA, 3–6 October 2005; pp. 149–154. [Google Scholar]
- Taddia, Y.; Stecchi, F.; Pellegrinelli, A. Using Dji Phantom 4 Rtk Drone for Topographic Mapping of Coastal Areas. In Proceedings of the ISPRS Geospatial Week 2019, Enschede, The Netherlands, 10–14 June 2019; Volume 42, pp. 625–630. [Google Scholar]
- Tenedório, J.A.; Estanqueiro, R.; Lima, A.M.; Marques, J. Remote Sensing from Unmanned Aerial Vehicles for 3D Urban Modelling: Case Study of Loulé, Portugal. In Back to the Sense of the City: International Monograph Book; Centre de Política de Sòl i Valoracions: Loulé, Portugal, 2016. [Google Scholar]
- Instituto Geográfico Nacional. Diario el Peruano Resolución Jefatural No. 149-2022_IGN_DIG_SDPG; Normas y Documentos Legales; Gobierno Del Perú: Lima, Peru, 2022.
- Trajkovski, K.K.; Grigillo, D.; Petrovič, D. Optimization of UAV Flight Missions in Steep Terrain. Remote Sens. 2020, 12, 1293. [Google Scholar] [CrossRef]
- Forlani, G.; Dall’Asta, E.; Diotri, F.; di Cella, U.M.; Roncella, R.; Santise, M. Quality Assessment of DSMs Produced from UAV Flights Georeferenced with On-Board RTK Positioning. Remote Sens. 2018, 10, 311. [Google Scholar] [CrossRef]

| Flight Configuration ID 1 | Positioning Solution | Photogrammetric Projects According to N° CP | ||
|---|---|---|---|---|
| 1 | 3 | 5 | ||
| A | RTK (Refined position due to corrections sent by a GNSS base station in the field, the D-RTK 2 receiver placed at a point of known coordinates) | RTK_1, RTK_4, RTK_7. | RTK_2, RTK_5, RTK_8 | RTK_3, RTK_6, RTK_9, |
| B | PPK1 (Refined position due to post-process corrections by a GNSS base station in cabinet, Trimble R10 receiver placed at a point of known coordinates) | PPK1_1, PPK1_4, PPK1_7. | PPK1_2, PPK1_5, PPK1_8. | PPK1_3, PPK1_6, PPK1_9. |
| PPK2 (Refined position due to post-process corrections by a GNSS base station in a cabinet, the commercial receiver AMA01 established by IGN) | PPK2_1, PPK2_4, PPK2_7. | PPK2_2, PPK2_5, PPK2_8. | PPK2_3, PPK2_3, PPK2_9. | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salas López, R.; Terrones Murga, R.E.; Silva-López, J.O.; Rojas-Briceño, N.B.; Gómez Fernández, D.; Oliva-Cruz, M.; Taddia, Y. Accuracy Assessment of Direct Georeferencing for Photogrammetric Applications Based on UAS-GNSS for High Andean Urban Environments. Drones 2022, 6, 388. https://doi.org/10.3390/drones6120388
Salas López R, Terrones Murga RE, Silva-López JO, Rojas-Briceño NB, Gómez Fernández D, Oliva-Cruz M, Taddia Y. Accuracy Assessment of Direct Georeferencing for Photogrammetric Applications Based on UAS-GNSS for High Andean Urban Environments. Drones. 2022; 6(12):388. https://doi.org/10.3390/drones6120388
Chicago/Turabian StyleSalas López, Rolando, Renzo E. Terrones Murga, Jhonsy O. Silva-López, Nilton B. Rojas-Briceño, Darwin Gómez Fernández, Manuel Oliva-Cruz, and Yuri Taddia. 2022. "Accuracy Assessment of Direct Georeferencing for Photogrammetric Applications Based on UAS-GNSS for High Andean Urban Environments" Drones 6, no. 12: 388. https://doi.org/10.3390/drones6120388
APA StyleSalas López, R., Terrones Murga, R. E., Silva-López, J. O., Rojas-Briceño, N. B., Gómez Fernández, D., Oliva-Cruz, M., & Taddia, Y. (2022). Accuracy Assessment of Direct Georeferencing for Photogrammetric Applications Based on UAS-GNSS for High Andean Urban Environments. Drones, 6(12), 388. https://doi.org/10.3390/drones6120388











