Low-Altitude Sensing of Urban Atmospheric Turbulence with UAV

Abstract

The capabilities of a quadcopter in the hover mode for low-altitude sensing of atmospheric turbulence with high spatial resolution in urban areas characterized by complex orography are investigated. The studies were carried out in different seasons (winter, spring, summer, and fall), and the quadcopter hovered in the immediate vicinity of ultrasonic weather stations. The DJI Phantom 4 Pro quadcopter and AMK-03 ultrasonic weather stations installed in different places of the studied territory were used in the experiment. The smoothing procedure was used to study the behavior of the longitudinal and lateral spectra of turbulence in the inertial and energy production ranges. The longitudinal and lateral turbulence scales were estimated by the least-square fit method with the von Karman model as a regression curve. It is shown that the turbulence spectra obtained with DJI Phantom 4 Pro and AMK-03 generally coincide, with minor differences observed in the high-frequency region of the spectrum. In the inertial range, the behavior of the turbulence spectra shows that they obey the Kolmogorov–Obukhov “5/3” law. In the energy production range, the longitudinal and lateral turbulence scales and their ratio measured by DJI Phantom 4 Pro and AMK-03 agree to a good accuracy. Discrepancies in the data obtained with the quadcopter and the ultrasonic weather stations at the territory with complex orography are explained by the partial correlation of the wind velocity series at different measurement points and the influence of the inhomogeneous surface.

1. Introduction

Recently, unmanned aerial vehicles (UAVs) have become widespread in our life, and they are now an important component of the airspace. Analysis and forecast of modern trends in their use show that, in the next decade, there will be an explosive growth in the number of commercial and military UAVs. This growth will require efficient systems capable of controlling UAV traffic, in particular, under bad weather conditions [1,2,3,4,5,6]. Atmospheric turbulence is the main factor that most strongly affects the efficiency of future UAV traffic management systems. Many UAVs are small in size and light in weight. As a result, their trajectory can deviate significantly in a turbulent atmosphere, and loss of control is highly probable in this case.

Most UAVs fly at altitudes of up to 500 m. The atmospheric boundary layer at these altitudes is considerably affected by local orography. For example, for flights in an urban environment, i.e., an environment with complex orography, atmospheric turbulence is characterized by strong spatial inhomogeneity due to the presence of buildings, park zones, highways, etc.

The main technologies to obtain information about turbulence profiles of the urban atmosphere are lidar, sodar, and radar sensing methods. For these sensing technologies, the spatial resolution is determined by the size of the sensing volume. It ranges from a few tens to hundreds of meters [7,8,9,10,11,12,13,14,15]. Spatial variations of turbulent air flows can reach several meters, which is much smaller than the spatial resolution of lidars, sodars, and radars. This discrepancy between the spatial resolution of the applied technologies and the scale of turbulent flows in the atmosphere can lead to their significant averaging and, consequently, to significant errors in atmospheric turbulence measurements. Thus, the future UAV traffic management systems must use data on the turbulent atmosphere obtained with high spatial resolution.

Acoustic anemometry methods can be used to obtain atmospheric data with high spatial resolution [11,16,17]. Complete information about the state of the atmosphere at different heights can be obtained with acoustic anemometry methods if acoustic devices are set on weather towers or a tethered balloon, which is not always possible in an urban environment.

One of the main trends in low-altitude sensing, i.e., to heights of about 500 m, is the development of methods for diagnostics of the turbulent atmosphere with UAVs. The results of diagnostics of the speed of air mass flows with UAVs are reported in [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35]. In [36,37,38,39,40,41,42,43,44,45,46,47], the fundamental possibility of measuring the turbulence spectra with fixed-wing UAVs of various sizes and weights was shown. In the process of sensing, UAVs of this type move in space for a long time. The typical flight pattern in a turbulence measurement experiment consists of straight sections about one kilometer long [47]. As a result, the spatial resolution in measurement of the turbulence spectrum is approximately comparable with the length of a straight section. Thus, for the non-even and non-homogeneous underlying surface and in the non-stationary atmosphere, the use of a fixed-wing UAV can lead, as in the case of lidars, sodars, and radars, to significant averaging and, as a consequence, to significant errors in measurements of atmospheric turbulence.

In contrast to a fixed-wing UAV, a quadcopter can hover at a needed point in space for a long time and obtain atmospheric data with the high spatial resolution in an area characterized by complex orography. The results of studying the turbulence spectrum in the inertial and energy production ranges with the DJI Mavic Mini quadcopter in the altitude hold mode are reported in [48]. The measurements were carried out over territory characterized by a flat and uniform surface with a slight slope; it bordered a cottage village on one side and a forest on the other side. The results obtained are in a good agreement with the theory of homogeneous and isotropic turbulence and the data measured by the methods of acoustic anemometry.

Knowledge of the state of atmospheric turbulence allows us to study its effect on the efficiency of UAV management systems. It is well-known that turbulence reduces the possibility of efficient use of wind energy and causes accelerated wear. Techniques of low-altitude sensing of the atmospheric state, including turbulence, allow us to estimate the climate change caused by urban growth and are needed to address current and future urbanization challenges.

In addition to turbulent fluctuations of the wind velocity field in the atmosphere, there are random temperature oscillations. These oscillations lead to random fluctuations of the refractive index, which should be taken into account when studying the propagation of optical radiation in the atmosphere. Turbulent fluctuations of the wind velocity field and temperature in the atmosphere are correlated. For example, the relation between the turbulence scales that characterize fluctuations of wind velocity and temperature is given in [49]. The results of investigation of the structure characteristic of turbulent fluctuations of the refractive index with UAV and acoustic anemometry methods are reported in [50,51].

When atmospheric turbulence is studied over a territory with complex orography, diagnostic methods providing data with high spatial resolution are preferable. As already mentioned, a quadcopter—in contrast to fixed-wing UAV [36,37,38,39,40,41,42,43,44,45,46,47] and to lidars, sodars, and radars—allows us to obtain atmospheric data with high spatial resolution. Quadcopter capabilities under ideal conditions were examined in [48], in particular, to compare theory with experiment. In this paper, we study the capabilities of a quadcopter for monitoring the state of atmospheric turbulence in an urban area over a territory with complex orography. One of the main fundamental parameters that describe the state of atmospheric turbulence quite completely and accurately and that is investigated in this paper is the turbulence spectrum [52,53,54,55,56]. The theoretical part of the paper describes the coordinate systems, introduces the concept of a spectral tensor of turbulence, and presents the Taylor hypothesis, which allows us to obtain a relationship between the spatial and temporal spectra of turbulence and the basic equations of the von Karman model. In this part, we derive the equations for the wind velocity components measured with the quadcopter in the hover mode, as well as the equations for longitudinal and lateral velocity fluctuations.

The second part of the paper provides general information about the experiment, presents the results of measurements of the quadcopter speed and the longitudinal and lateral components of the wind velocity measured with the DJI Phantom 4 Pro quadcopter and AMK-03 ultrasonic weather stations [16,17]. In addition, longitudinal and lateral turbulence spectra measured with the DJI Phantom 4 Pro and AMK-03 are presented, and their behavior in the inertial and energy production ranges is studied. In conclusion, the main results are summarized.

2. Theory of a Quadcopter in a Turbulent Atmosphere

In the sensing of the mean wind velocity, its projections onto the axes of the coordinate system used in meteorology are of particular interest. In contrast to diagnostics of the mean wind, the fluctuation wind velocity is studied in the coordinate system, one of whose axes is directed along the mean wind. In this section, we examine theoretically the ideal hovering of a quadcopter in a turbulent atmosphere as applied to the problem of sensing of wind velocity fluctuations in the case of horizontal air mass transfer in the coordinate system related to the mean horizontal wind.

2.1. Coordinate Systems

Figure 1 shows schematically the arrangement of the equipment and the direction of the average wind speed during the experiments. It can be seen that the AMK-03 weather station and the quadcopter are oriented differently relative to each other and relative to the direction of the average wind. The ultrasonic weather station is oriented in space along the cardinal points, and the quadcopter can be oriented arbitrarily. Thus, in the case of AMK-03, the measured wind speed data correspond to the {E, N} coordinate system used in meteorology in which one axis is directed to the east (E) and the other axis is directed to the north (N) [53,54].

The quadcopter dynamics may be described in a coordinate system other than the {E, N} meteorological system. The coordinate system in which the quadcopter dynamics is described is denoted as $\left\{x,y\right\}$. The axes of this coordinate system are shown as $x$ and $y$ in Figure 1 [21,31,57,58].

In the theory of turbulence [52,53,54], fluctuations of the wind velocity are described in the coordinate system related to the mean wind. In the coordinates system related to the mean horizontal wind, one axis is directed along the mean wind, and the two other coordinate axes are directed normally to the mean wind. As a result of this choice of the coordinate system, one longitudinal and two lateral fluctuations of the wind velocity are clearly distinguished.

2.2. Taylor Hypothesis

It is well known that, in the atmosphere, the horizontal air mass transfer often prevails over the vertical motion. The average vertical component of the wind speed is small and can be neglected. Thus, we can take into account only the horizontal component. In this case, one of the axes of the coordinate system can be directed along the mean horizontal wind. Two other axes are directed normally to the mean horizontal wind, and one of them lies in a horizontal plane, while another is directed vertically upward. As a result, in this coordinate system related to the mean horizontal wind, the velocity field of the turbulent air flow at the point $r=\left\{\xi ,0,0\right\}$ has the form [52,53,54]:

$$\mathrm{u}\left(r,t\right)=\langle \mathrm{u}\rangle +{\mathrm{u}}^{\prime }\left(r,t\right),$$

(1)

$$\mathrm{v}\left(r,t\right)={\mathrm{v}}^{\prime }\left(r,t\right),$$

(2)

$$\mathrm{w}\left(r,t\right)={\mathrm{w}}^{\prime }\left(r,t\right),$$

(3)

where $\langle \mathrm{u}\rangle$ is the mean wind speed, ${\mathrm{u}}^{\prime }\left(r,t\right)$, ${\mathrm{v}}^{\prime }\left(r,t\right)$, and ${\mathrm{w}}^{\prime }\left(r,t\right)$ are fluctuations of the wind speed, $\langle \dots \rangle$ is the operator of statistical averaging. It can be seen from Equations (1)–(3) that longitudinal fluctuations of the wind speed ${\mathrm{u}}^{\prime }\left(r,t\right)$ are directed along the direction of the mean wind speed and that two lateral fluctuations of the wind speed ${\mathrm{v}}^{\prime }\left(r,t\right)$ and ${\mathrm{w}}^{\prime }\left(r,t\right)$ are directed normally to the mean wind speed. The component ${\mathrm{v}}^{\prime }\left(r,t\right)$ lies in the horizontal plane, and the component ${\mathrm{w}}^{\prime }\left(r,t\right)$ is directed vertically upward and describes vertical fluctuations.

In the mathematical description of fluctuations of the velocity field, the concepts of the second-rank correlation tensor and the turbulence spectrum tensor are introduced [52,53,54]. For isotropic turbulence, the diagonal elements of the correlation tensor can be written in the form

$$B_{\mathrm{u}}\left(\xi ;t\right)=\langle {\mathrm{u}}^{\prime }\left(\xi ,0,0;t\right){\mathrm{u}}^{\prime }\left(0,0,0;0\right)\rangle ,$$

(4)

$$B_{\mathrm{v}}\left(\xi ;t\right)=\langle {\mathrm{v}}^{\prime }\left(\xi ,0,0;t\right){\mathrm{v}}^{\prime }\left(0,0,0;0\right)\rangle ,$$

(5)

$$B_{\mathrm{w}}\left(\xi ;t\right)=\langle {\mathrm{w}}^{\prime }\left(\xi ,0,0;t\right){\mathrm{w}}^{\prime }\left(0,0,0;0\right)\rangle .$$

(6)

The diagonal components of the one-dimensional spatial spectral tensor of turbulence take the form

$${\mathsf{\varphi }}_{\mathrm{u}}\left(\kappa \right)=\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{B}_{\mathrm{u}}\left(\xi ;t\right)e^{2\pi i\kappa \xi }d\xi ,$$

(7)

$${\mathsf{\varphi }}_{\mathrm{v}}\left(\kappa \right)=\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{B}_{\mathrm{v}}\left(\xi ;t\right)e^{2\pi i\kappa \xi }d\xi ,$$

(8)

$${\mathsf{\varphi }}_{\mathrm{w}}\left(\kappa \right)=\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{B}_{\mathrm{w}}\left(\xi ;t\right)e^{2\pi i\kappa \xi }d\xi ,$$

(9)

and the diagonal components of the temporal spectral tensor of turbulence are determined by the following equations:

$${\mathsf{\Phi }}_{\mathrm{u}}\left(f\right)=\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{B}_{\mathrm{u}}\left(\xi ;t\right)e^{2\pi ift}dt,$$

(10)

$${\mathsf{\Phi }}_{\mathrm{v}}\left(f\right)=\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{B}_{\mathrm{v}}\left(\xi ;t\right)e^{2\pi ift}dt,$$

(11)

$${\mathsf{\Phi }}_{\mathrm{w}}\left(f\right)=\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{B}_{\mathrm{w}}\left(\xi ;t\right)e^{2\pi ift}dt,$$

(12)

The diagonal components of the temporal spectral tensor of turbulence ${\mathsf{\Phi }}_{\mathrm{u}}\left(f\right)$ and ${\mathsf{\Phi }}_{\mathrm{v}}\left(f\right)$ are the longitudinal and lateral spectra of turbulence, and those of ${\mathsf{\Phi }}_{\mathrm{w}}\left(f\right)$ form the vertical spectrum of turbulence.

In the coordinate system related to the mean wind, we have the opportunity to use Taylor’s hypothesis of "frozen" turbulent fluctuations [52,53,54]. The essence of this hypothesis is that the entire spatial turbulent pattern moves in time with the mean wind speed $\langle \mathrm{u}\rangle$. The application of Taylor’s hypothesis leads to the relation between the spatiotemporal and purely spatial characteristics of fluctuations of the wind velocity field in the form

$${\mathrm{u}}^{\prime }\left(\xi ,0,0;t\right)={\mathrm{u}}^{\prime }\left(\xi -\langle \mathrm{u}\rangle t,0,0\right),$$

(13)

$${\mathrm{v}}^{\prime }\left(\xi ,0,0;t\right)={\mathrm{v}}^{\prime }\left(\xi -\langle \mathrm{u}\rangle t,0,0\right),$$

(14)

$${\mathrm{w}}^{\prime }\left(\xi ,0,0;t\right)={\mathrm{w}}^{\prime }\left(\xi -\langle \mathrm{u}\rangle t,0,0\right).$$

(15)

The application of Taylor’s hypothesis (13)–(15) to Equations (7)–(9) with allowance for Equations (10)–(12) leads to the well-known relation between the spatial and temporal spectra

$${\mathsf{\varphi }}_{\mathrm{u}}\left(\kappa \right)=\langle u\rangle {\mathsf{\Phi }}_{\mathrm{u}}\left(f\right),$$

(16)

$${\mathsf{\varphi }}_{\mathrm{v}}\left(\kappa \right)=\langle u\rangle {\mathsf{\Phi }}_{\mathrm{v}}\left(f\right),$$

(17)

$${\mathsf{\varphi }}_{\mathrm{w}}\left(\kappa \right)=\langle u\rangle {\mathsf{\Phi }}_w\left(f\right).$$

(18)

The relation between the spatial and temporal frequencies is given as $\kappa =f/\langle \mathrm{u}\rangle$. In experiments, we measure temporal spectra, while the theory deals with spatial spectra. Thus, Equations (16)–(18) allow us to compare the behavior of experimentally measured temporal spectra with theoretical results.

2.3. Model of Atmospheric Turbulence

One of the most commonly used turbulence spectra models is the von Karman model [52,53,54,55,56,58], which allows us to study the behavior of the spectrum in the energy production and inertial ranges. In addition to the von Karman model, a suitable approximation in problems of UAV dynamics in a turbulent atmosphere is the Dryden turbulence model [52,56,58]. Other models, such as the unified turbulence model, can also be used to describe atmospheric turbulence [56].

In this study, we use the von Karman model to analyze turbulence spectra. With allowance for Equations (16)–(18), the equations for the longitudinal, lateral, and vertical temporal spectra of turbulence for the von Karman model have the form

$$\frac{{\mathsf{\Phi }}_{\mathrm{u}}\left(f\right)}{{\mathsf{\sigma }}_{\mathrm{u}}^2}=\frac{2{\mathrm{L}}_{\mathrm{u}}}{\pi }\frac{1}{{\left[1+{\left(1.339{\mathrm{L}}_{\mathrm{u}}·2\pi f/\langle \mathrm{u}\rangle \right)}^2\right]}^{5/6}},$$

(19)

$$\frac{{\mathsf{\Phi }}_{\mathrm{v}}\left(f\right)}{{\mathsf{\sigma }}_{\mathrm{v}}^2}=\frac{2{\mathrm{L}}_{\mathrm{v}}}{\pi }\frac{1+\raisebox{1ex}{$8$}\!\left/ \!\raisebox{-1ex}{$3$}\right.{\left(2.678{\mathrm{L}}_{\mathrm{v}}·2\pi f/\langle w\rangle \right)}^2}{{\left[1+{\left(2.678{\mathrm{L}}_{\mathrm{v}}·2\pi f/\langle \mathrm{u}\rangle \right)}^2\right]}^{11/6}},$$

(20)

$$\frac{{\mathsf{\Phi }}_{\mathrm{w}}\left(f\right)}{{\mathsf{\sigma }}_{\mathrm{w}}^2}=\frac{2{\mathrm{L}}_{\mathrm{w}}}{\pi }\frac{1+\raisebox{1ex}{$8$}\!\left/ \!\raisebox{-1ex}{$3$}\right.{\left(2.678{\mathrm{L}}_{\mathrm{w}}·2\pi f/\langle w\rangle \right)}^2}{{\left[1+{\left(2.678{\mathrm{L}}_{\mathrm{w}}·2\pi f/\langle \mathrm{u}\rangle \right)}^2\right]}^{11/6}},$$

(21)

where ${\mathrm{L}}_{\mathrm{u}}$ is the longitudinal turbulence scale, ${\mathrm{L}}_{\mathrm{v}}$ is the lateral turbulence scale, and ${\mathrm{L}}_{\mathrm{w}}$ is the vertical turbulence scale and ${\mathsf{\sigma }}_{\mathrm{u}}^2$, ${\mathsf{\sigma }}_{\mathrm{v}}^2$, and ${\mathsf{\sigma }}_{\mathrm{v}}^2$ are turbulence intensities.

2.4. Wind Velocity Components

The dynamic equations for the quadcopter’s center of gravity can be written in the inertial coordinates associated with the Earth as [21,31,57]

$$\ddot{x}=\left(s_{\varphi }{s}_{\psi }+c_{\varphi }{s}_{\theta }{c}_{\psi }\right)\frac{T}{m}+\frac{F_x}{m}$$

(22)

$$\ddot{y}=\left(-s_{\varphi }{c}_{\psi }+c_{\varphi }{s}_{\theta }{s}_{\psi }\right)\frac{T}{m}+\frac{F_y}{m}$$

(23)

$$\ddot{z}=c_{\varphi }{c}_{\theta }\frac{T}{m}-g+\frac{F_z}{m}$$

(24)

where $s_{(•)}=\sin (•); c_{(•)}=\cos (•); \varphi$ is the roll angle; $\theta$ is the pitch angle; $\psi$ is the yaw angle; $T$ is the aerodynamic force generated by propellers; $F_x$, $F_y$, and $F_z$ are the drag force components along the $x$, $y$, and $z$ axes; $m$ is the quadcopter mass; and $g$ is the acceleration due to gravity.

The components of the drag force along the x, y, and z axes, which arise during the quadcopter flight, have the form [18,21,31,57]

$$F_j=-c_j\left(v_j-w_j\right)$$

(25)

in the linear case, and

$$F_j=-\frac{1}{2}\rho C_j{A}_j\mathrm{sgn}\left(v_j-w_j\right)\times {\left(v_j-w_j\right)}^2$$

(26)

in the square-law case. In Equations (25) and (26), $c_j$ and $C_j$ are the drag coefficient along the x, y, and z axes; $j$ is the subscript for enumeration of the orthogonal components of vectors, i.e., $j\in \left\{x,y,z\right\}; v_j$ are the quadcopter speed components; and $w_j$ are components of the turbulent flow velocity in the atmosphere in the coordinate system $\left\{x,y\right\}; \rho$ is the air density; $A_j$ are the projections of the quadcopter area on the corresponding axes; and $\mathrm{sgn}(•)$ is the sign function.

Let us consider the case of ideal hover, which can be achieved by compensating all the forces acting on the quadcopter and at $v_j=0$. Equations (22)–(24) can be transformed to the case of ideal hover through their linearization. The roll, pitch, and yaw angles in a turbulent atmosphere are sums of the average and fluctuation components: $\varphi =\langle \varphi \rangle +{\varphi }^{\prime }$, $\theta =\langle \theta \rangle +{\theta }^{\prime }$ and $\psi =\langle \psi \rangle +{\psi }^{\prime }$. In the small-angle approximation, $\varphi ,\theta \ll \pi$ and at ${\psi }^{\prime }\ll \pi$, as well as if the conditions $\ddot{x}=\ddot{y}=\ddot{z}=0$ and $v_j=0$ are fulfilled, the equations for estimation of the horizontal velocity components of the wind velocity field $w_x$ and $w_y$ take the form

$$w_x=-\frac{mg}{c_x}\left(\langle \phi \rangle s_{\langle \psi \rangle }+\langle \theta \rangle c_{\langle \psi \rangle }\right)-\frac{mg}{c_x}\left({\phi }^{\prime }{s}_{\langle \psi \rangle }+{\theta }^{\prime }{c}_{\langle \psi \rangle }\right),$$

(27)

$$w_y=-\frac{mg}{c_y}\left(-\langle \phi \rangle c_{\langle \psi \rangle }+\langle \theta \rangle s_{\langle \psi \rangle }\right)-\frac{mg}{c_y}\left(-{\phi }^{\prime }{c}_{\langle \psi \rangle }+{\theta }^{\prime }{s}_{\langle \psi \rangle }\right)$$

(28)

in the linear case, and

$$w_x=-\mathrm{sgn}\left(\langle \phi \rangle s_{\langle \psi \rangle }+\langle \theta \rangle c_{\langle \psi \rangle }\right)\sqrt{\frac{2mg}{\rho C_x{A}_x}\left|\left(\langle \phi \rangle s_{\langle \psi \rangle }+\langle \theta \rangle c_{\langle \psi \rangle }\right)\right|}\left\{1+\frac{{\phi }^{\prime }{s}_{\langle \psi \rangle }+{\theta }^{\prime }{c}_{\langle \psi \rangle }}{2\left(\phi s_{\langle \psi \rangle }+\theta c_{\langle \psi \rangle }\right)}\right\},$$

(29)

$$w_y=-\mathrm{sgn}\left(-\langle \phi \rangle c_{\langle \psi \rangle }+\langle \theta \rangle s_{\langle \psi \rangle }\right)\sqrt{\frac{2mg}{\rho C_x{A}_x}\left|\left(-\langle \phi \rangle c_{\langle \psi \rangle }+\langle \theta \rangle s_{\langle \psi \rangle }\right)\right|}\left\{1+\frac{-{\phi }^{\prime }{c}_{\langle \psi \rangle }+{\theta }^{\prime }{s}_{\langle \psi \rangle }}{2\left(-\phi c_{\langle \psi \rangle }+\theta s_{\langle \psi \rangle }\right)}\right\}$$

(30)

in the square-law case.

It follows from Equations (27)–(30) that, regardless of the model of the drag force, the estimates of the horizontal components of the turbulent flow velocity are the sum of the regular and fluctuation parts. The regular part of the estimates is determined by the average values of the roll, pitch, and yaw angles, whereas the fluctuation part is proportional to the fluctuations of the roll ${\phi }^{\prime }$ and pitch ${\theta }^{\prime }$ angles.

2.5. Longitudinal and Lateral Velocity Fluctuations

In the case of predominance of the horizontal air mass transfer over the vertical motion, the longitudinal and lateral turbulent fluctuations of the wind velocity take the form

$${\mathrm{u}}^{\prime }=n_E{w}_E^{\prime }+n_N{w}_N^{\prime },$$

(31)

$${\mathrm{v}}^{\prime }=-n_N{w}_E^{\prime }+n_E{w}_N^{\prime }$$

(32)

$$n=\left\{n_E,n_N,0\right\}=\{\frac{\langle w_E\rangle }{\langle \mathrm{u}\rangle },\frac{\langle w_N\rangle }{\langle \mathrm{u}\rangle },0\}$$

(33)

for the ultrasonic weather station, and

$${\mathrm{u}}^{\prime }=n_x{w}_x^{\prime }+n_y{w}_y^{\prime }$$

(34)

$${\mathrm{v}}^{\prime }=-n_x{w}_y^{\prime }+n_y{w}_x^{\prime }$$

(35)

$$n=\left\{n_x,n_y,0\right\}=\{\frac{\langle w_x\rangle }{\langle \mathrm{u}\rangle },\frac{\langle w_y\rangle }{\langle \mathrm{u}\rangle },0\}$$

(36)

for the quadcopter. Here, $w_E^{\prime }$ and $w_N^{\prime }$ are fluctuations of wind velocity components along the E and N axes, i.e., data of the ultrasonic weather station; $w_x^{\prime }$ and $w_y^{\prime }$ are fluctuations of the wind velocity components obtained from the results of quadcopter telemetry; $\langle w_E\rangle$ and $\langle w_N\rangle$ are the average components of the horizontal velocity along the E and N axes; $\langle w_x\rangle$ and $\langle w_y\rangle$ are estimates of the velocity components along the $x$ and $y$ axes. Thus, Equations (31)–(36) allow us to compare the longitudinal and lateral turbulence spectra measured by the quadcopter and the ultrasonic weather station.

3. Experiment

Usually, turbulence spectra are studied experimentally over territories having a flat and uniform underlying surface and under weather conditions corresponding to the stationary state of the atmosphere. At such a territory and under such weather conditions, obtained experimental data agree well with theoretical results. The capabilities of a hovering quadcopter as applied to the study of homogeneous and isotropic turbulence were examined in [48]. It was shown that the obtained results are in a good agreement with the theory of homogeneous and isotropic turbulence and the data measured by acoustic anemometry methods. However, from the practical point of view, it is interesting to analyze the capabilities of a hovering quadcopter when studying atmospheric turbulence over an urban territory with complex orography in different seasons: winter, spring, summer, and fall. From the viewpoint of the theory of turbulence, the behavior of the turbulence spectrum for this territory and under bad weather conditions is poorly studied. Therefore, the quadcopter data were compared with the data of ultrasonic weather stations.

3.1. General Information about the Experiment

Experimental studies were carried out at the territory of the Institute for Monitoring of Climatic and Ecological Systems of the Siberian Branch of the Russian Academy of Sciences (IMCES SB RAS), which is located in Academgorodok, one of the districts of the city of Tomsk (Russian Federation). This area is a territory with complex orography: it is a forested area with the buildings of the Academgorodok institutes and highways. Figure 2 shows a Google map of the experimental area. The arrows show the location of the used AMK-03 ultrasonic weather stations, and the measurement dates are indicated.

The studies were carried out in different seasons: winter (4 February 2020), spring (17 March 2020), summer (13 August 2020), and fall (15 November 2020). The quadcopter hovered at different places of the territory with complex orography: over the building of the Geophysical Observatory and the IMCES SB RAS main building, as well as in the immediate vicinity of a small grove where a 30 m weather tower is installed (see Figure 2 and Figure 3). In the experiment on February 20, the launch point of the DJI Phantom 4 Pro quadcopter was chosen in close proximity to the foundation of the Geophysical Observatory building, and on August 13 the quadcopter started from the foundation of the 30 m weather tower. During the measurements on March 17 and November 15, the quadcopter took off in the immediate vicinity of the foundation of the IMCES SB RAS main building.

The AMK-03 ultrasonic weather station serves to measure and record the wind speed and direction using acoustic anemometry methods, as well as recording temperature, relative air humidity, and atmospheric pressure [16,17]. We used AMK-03 data of two types, which recorded the wind speed and direction with a frequency of 10 and 80 Hz. The locations of the weather stations of different types are shown by the arrows in Figure 2. The data on the state of the quadcopter in the flight logs were recorded at a frequency of 10 Hz in CSV format.

Figure 4 shows the quadcopter’s flight paths during the experiments.

Table 1. Date and time of the start and end of the study and the hover height.

Date	Start, UTC	End, UTC	Hover Height, m
4 February 2020	10:21	10:42	27
17 March 2020	05:10	05:28	22
13 August 2020	07:01	07:23	27
15 November 2020	05:38	06:01	28

presents the dates and times of the start and end of the experiments, as well as the DJI Phantom 4 Pro quadcopter’s flight heights. After takeoff, the quadcopters flew up to the AMK-03 ultrasonic weather stations located on the roofs of the buildings and on the weather tower. After the end of the experiments, the quadcopters returned to the starting point.

According to the data of the Tomsk International Airport spaced by ~10 km from IMCES SB RAS, the following weather conditions were observed during the experiments. On February 4, weather conditions were satisfactory in terms of the quadcopter flight: south–south-west wind, speed of 3 m/s, air temperature of −4 °C, air humidity of 86%, light snow, horizontal visibility range of 8 km. On March 17, good weather conditions were recorded: variable wind, speed of 1 m/s, air temperature of −1 °C, air humidity of 55%, no precipitation, horizontal visibility range of 10 km or more. On August 13, the weather in the airport was excellent: southeast wind, speed of 4 m/s, air temperature of 27 °C, air humidity of 42%, no precipitation, horizontal visibility range of 10 km or more. On November 15, the weather in the airport was satisfactory in terms of the quadcopter flight: south–south-west wind, speed of 2 m/s, air temperature of −9 °C, air humidity of 90%, no precipitation, horizontal visibility range of 10 km or more.

Thus, the experiments were carried out in different seasons, under different weather conditions, and the hover took place at different places of the IMCES SB RAS territory, which is characterized by complex orography.

3.2. Quadcopter Velocity

Figure 5 shows the dynamics of the $v_x$, $v_y$, and $v_z$ components of the quadcopter velocity during hovering. It can be seen that, generally, the quadcopter velocity components are equal to zero during the measurements. In short periods of time, the forces acting on the quadcopter exceed the capabilities of the control system and high-precision positioning is disrupted. After regaining control, the quadcopter begins to move to its original position and, upon reaching this position, it stops.

Thus, the periods in which the precision positioning of the quadcopter in space is disrupted can be neglected due to their insignificance, and we can believe that ideal hovering was observed during the experiment.

3.3. Longitudinal and Lateral Wind Velocity Components

Let us consider the behavior of the estimates of the longitudinal and lateral components of the wind velocity from the quadcopter data in the altitude hold mode in the turbulent atmosphere and compare it with the results obtained from the data of the AMK-03 ultrasonic weather station.

Figure 6 shows the temporal dynamics of the longitudinal and lateral wind velocity components measured with AMK-03 (red curves) and DJI Phantom 4 Pro (black curves) on (a) 4 February, (b) 17 March, (c) 13 August, and (d) 15 November 2020. It follows from Figure 6 that the time series of u and v measured in different ways generally coincide, and discrepancies are observed only in the high-frequency range of fluctuations.

The difference between the two different ways of wind velocity measurement can be characterized by the variance defined as ${\sigma }_{\mathrm{u}}=\sqrt{{\langle \left({\mathrm{u}}^{\mathrm{Dron}}-{\mathrm{u}}^{\mathrm{AMK}-03}\right)}^2}\rangle$ and ${\sigma }_{\mathrm{v}}=\sqrt{{\langle \left({\mathrm{v}}^{\mathrm{Dron}}-{\mathrm{v}}^{\mathrm{AMK}-03}\right)}^2\rangle }$. Here, ${\mathrm{u}}^{\mathrm{Dron}}$, ${\mathrm{u}}^{\mathrm{AMK}-03},$ and ${\mathrm{v}}^{\mathrm{Dron}}$, ${\mathrm{v}}^{\mathrm{AMK}-03}$ are the longitudinal and lateral wind velocity components measured by the quadcopter and the weather station.

Table 2. Variances ${\sigma }_{\mathrm{u}}$ and ${\sigma }_{\mathrm{v}}$.

Date	Longitudinal Component		Lateral Component
	No Smoothing	Smoothing	No Smoothing	Smoothing
4 February 2020	0.63	0.24	0.66	0.18
17 March 2020	0.64	0.36	0.59	0.22
13 August 2020	0.93	0.32	1.00	0.25
15 November 2020	0.60	0.21	0.72	0.31
Average	0.7	0.28	0.74	0.24

presents the variances ${\sigma }_{\mathrm{u}}$ and ${\sigma }_{\mathrm{v}}$ calculated for original and smoothed time series. It can be seen from Table 2 that, for the original time series, the variances range within 0.60–0.93 for the longitudinal component and 0.59–1.00 for the lateral component. When the time series are smoothed by moving average for the period of 60 s, which corresponds to suppression of the high-frequency part of the spectrum, ${\sigma }_{\mathrm{u}}$ and ${\sigma }_{\mathrm{v}}$ decrease down to 0.21–0.36 and 0.18–0.31 for, respectively, the longitudinal and lateral components.

Other parameters characterizing the difference between the two measurement methods are the correlation coefficients.

Table 3. Correlation coefficients.

Date	Longitudinal Component		Lateral Component
	No Smoothing	Smoothing	No Smoothing	Smoothing
4 February 2020	0.55	0.87	0.48	0.83
17 March 2020	0.54	0.72	0.73	0.95
13 August 2020	0.59	0.90	0.52	0.86
15 November 2020	0.63	0.88	0.37	0.61
Average	0.58	0.84	0.53	0.81

presents the calculated coefficients of correlation between the wind velocities measured by the quadcopter and the weather station for the original and smoothed time series. It can be seen from Table 3 that, for the original time series, the correlation coefficients range within 0.54–0.63 for the longitudinal component and 0.37–0.73 for the lateral component. When the time series are smoothed by moving average for the period of 60 s, which corresponds to suppression of the high-frequency part of the spectrum, the correlation coefficients increase up to 0.72–0.90 and 0.61–0.95 for, respectively, the longitudinal and lateral components.

It follows from Table 2 and Table 3 that, upon smoothing, the variance decreases 2.5–3.1 times, while the correlation increases 1.5 times. This leads to a decrease of the average variances from ${\sigma }_{\mathrm{u}}=0.70$ and ${\sigma }_{\mathrm{v}}=0.74$ down to ${\sigma }_{\mathrm{u}}=0.28$ and ${\sigma }_{\mathrm{v}}=0.24$, whereas the average correlation coefficients increase from 0.58 and 0.53 up to 0.84 and 0.81 for the longitudinal and lateral components of the wind velocity, respectively. Thus, the smoothing suppresses the high-frequency component of the signal, which is accompanied by a significant decrease in the variances and an increase in the correlation. Taking this into account, we can conclude that the quadcopter data well describe the behavior of the large-scale turbulent vortices. Small-scale vortices, due to their low energy and quadcopter inertia, do not always give the correct response to the resulting signal.

Table 4. Average values of the longitudinal, lateral, and vertical wind velocity components and their maximal values.

Date	$\langle \mathbf{u}\rangle$, m/s	$\langle \mathbf{v}\rangle$, m/s	$\mathbf{m}\mathbf{a}\mathbf{x} \left(\mathbf{u}\right), \mathbf{m}/\mathbf{s}$	$\mathbf{m}\mathbf{a}\mathbf{x} \left(\mathbf{v}\right), \mathbf{m}/\mathbf{s}$	$\langle \mathbf{w}\rangle$, m/s
4 February 2020	1.78	0	4.9	2.6	0.3
17 March 2020	0.89	0	3.03	2.76	0.04
13 August 2020	1.36	0	5.20	3.91	−0.1
15 November 2020	1.35	0	4.13	2.58	0.15

presents the average values of the longitudinal, lateral, and vertical components of the wind velocity measured with AMK-03 in the experiments. It can be seen that the average wind speed $\langle \mathrm{u}\rangle$ differs from the corresponding values observed at the airport. This difference is explained by two circumstances. First, the airport is located approximately 10 km from the IMCES SB RAS buildings. Second, the airport territory, where the measurements were carried out, has a flat underlying surface, whereas the IMCES SB RAS territory has complex orography.

It can also be seen from Table 4 that, in the experiment, the horizontal transfer of air masses predominated over the vertical motion, i.e., $\langle \mathrm{w}\rangle \approx 0$. The fulfillment of the condition $\langle \mathrm{w}\rangle \approx 0$ in the experiment means that the assumption of the predominance of the horizontal air mass transfer over the vertical motion when calculating longitudinal and lateral turbulent fluctuations of the wind velocity using Equations (31)–(36) is justified. It should be noted that the maximal values of the longitudinal and lateral components of the wind velocity exceed the average wind, which is indicative of strong turbulence during measurements.

3.4. Spectra of Turbulence

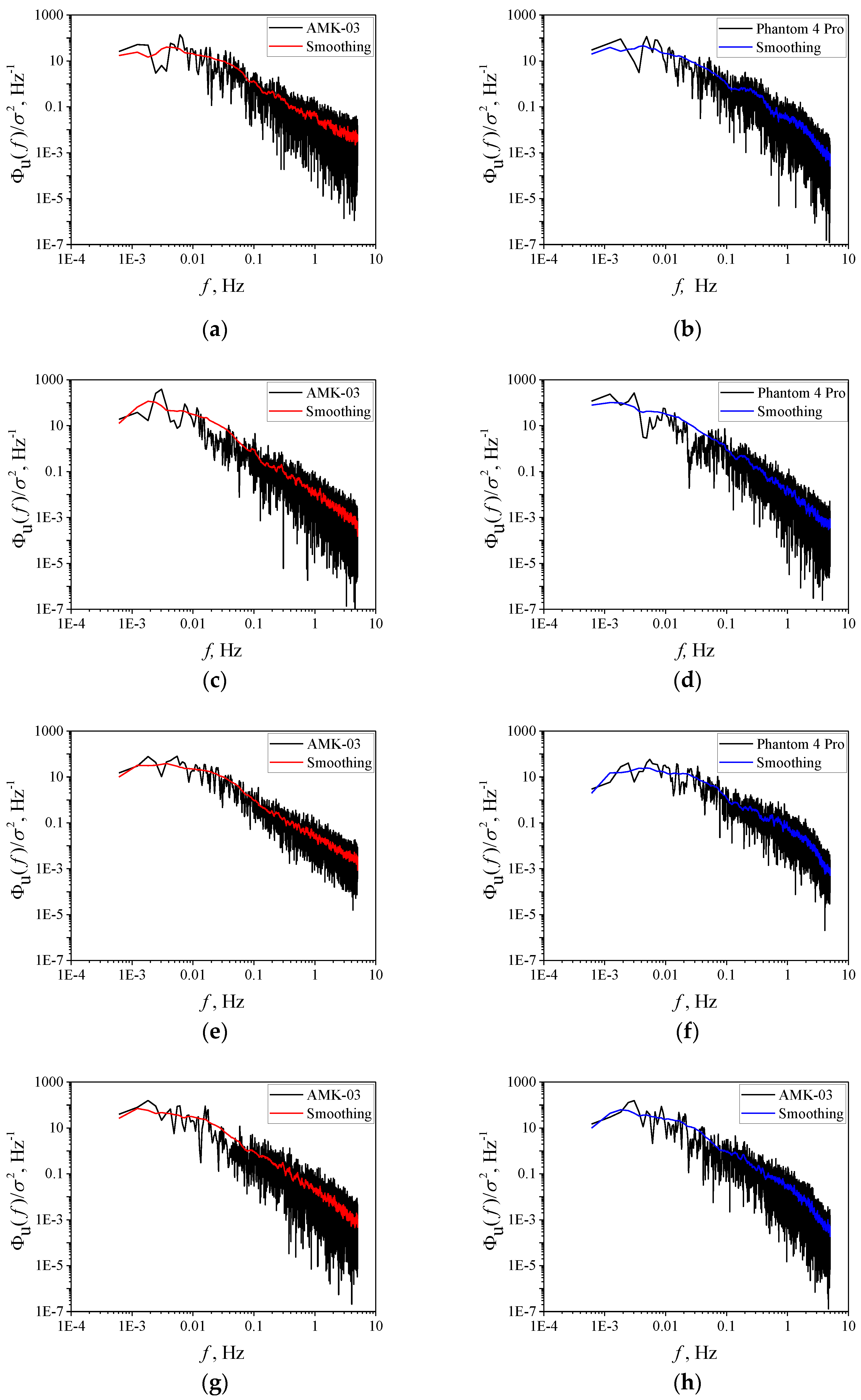
Turbulence spectra were calculated by the well-known methods with standard FFT software. Figure 7 and Figure 8 show the results of measurements of the longitudinal and lateral relative turbulence spectra ${\mathsf{\Phi }}_{\mathrm{u}}\left(f\right)$ and ${\mathsf{\Phi }}_{\mathrm{v}}\left(f\right)$. The turbulence spectra obtained from the data of the AMK-03 ultrasonic weather station and the DJI Phantom 4 Pro quadcopter are shown by the black curves, ${\sigma }^2$ is the normalization coefficient.

It can be seen from Figure 7 and Figure 8 that the values of spectra ${\mathsf{\Phi }}_{\mathrm{u}}\left(f\right)$ and ${\mathsf{\Phi }}_{\mathrm{v}}\left(f\right)$ vary significantly at minor variations of the frequency $f$. These variations are random oscillations about the main regularities of the turbulence spectra. To reveal these regularities in the turbulence spectra, a smoothing procedure was used.

The result of applying the smoothing procedure is shown in Figure 7 and Figure 8 by continuous colored curves: red and blue curves for the turbulence spectra of the longitudinal velocity component ${\mathsf{\Phi }}_{\mathrm{u}}\left(f\right)$ and pink and purple curves for the turbulence spectra of the lateral velocity component ${\mathsf{\Phi }}_{\mathrm{v}}\left(f\right)$. Figure 7a,c,e,g and Figure 8a,c,e,g depict the results of the application of the smoothing procedure of the relative turbulence spectra obtained from the data of the AMK-03 ultrasonic weather station, while Figure 7b,d,f,h and Figure 8b,d,f,h show those for the DJI Phantom 4 Pro quadcopter data. The figures correspond to the following dates: (a, b) 4 February, (c, d) 17 March, (e, f) 13 August, and (g, h) 15 November 2020.

Figure 9 compares the smoothed turbulence spectra obtained from the AMK-03 and DJI Phantom 4 Pro data. Similarly to the case in Figure 7 and Figure 8, red and blue curves represent the turbulence spectra of the longitudinal velocity component ${\mathsf{\Phi }}_{\mathrm{u}}\left(f\right)$ and pink and purple curves represent the turbulence spectra of the lateral velocity component ${\mathsf{\Phi }}_{\mathrm{v}}\left(f\right)$. It can be seen from Figure 9 that the turbulence spectra obtained from the AMK-03 and DJI Phantom 4 Pro data generally coincide, and slight differences are observed in the high-frequency range of the spectrum.

It is well known [52,54] that the turbulence spectrum has three main spectral ranges: the energy production range, the inertial range, and the dissipation range. In the energy production range, which contains the main part of the turbulent energy, the energy is generated by buoyancy and shear. In the inertial range, the energy is neither generated nor dissipated but transferred from large scales to smaller ones. In the dissipation range, the kinetic energy is converted into the internal energy. Next, we consider the behavior of the turbulence spectra in the inertial and energy production ranges.

3.5. Inertial and Energy Production Ranges

In the inertial range, the turbulence spectrum obeys the Kolmogorov–Obukhov “5/3” law [52,53,54,55,56], which was found from dimensional considerations. The von Karman model is a generalization of the "5/3" law to the frequencies of the energy production range. Therefore, the Kolmogorov–Obukhov law can be found from model (19)–(21) at ${\mathrm{L}}_{\mathrm{u}}f/\langle \mathrm{u}\rangle \gg 1$, ${\mathrm{L}}_{\mathrm{v}}f/\langle \mathrm{u}\rangle \gg 1$ and ${\mathrm{L}}_{\mathrm{w}}f/\langle \mathrm{u}\rangle \gg 1$. In the inertial range, the spectral curve has the form

$$\frac{{\mathsf{\Phi }}_{\mathrm{u}}\left(f\right)}{{\mathsf{\sigma }}_{\mathrm{u}}^2} ~ f^{-5/3},$$

(37)

$$\frac{{\mathsf{\Phi }}_{\mathrm{v}}\left(f\right)}{{\mathsf{\sigma }}_{\mathrm{v}}^2} ~ f^{-5/3},$$

(38)

$$\frac{{\mathsf{\Phi }}_{\mathrm{w}}\left(f\right)}{{\mathsf{\sigma }}_{\mathrm{w}}^2} ~ f^{-5/3}.$$

(39)

In Figure 9, the dashed curves show the turbulence spectra corresponding to the Kolmogorov–Obukhov “5/3” law, which, as already noted, holds true for a homogeneous surface. It was already mentioned that the IMCES SB RAS territory is not homogeneous and has complex orography. Despite the complex orography, the turbulence spectrum in the inertial range obeys the $f^{-5/3}$ law, as is clearly seen from Figure 9.

Studying the behavior of turbulence spectra in the inertial range by the least-squares fit method with the frequency dependence of the turbulence spectrum in the form $f^{-\gamma }$ taken as a regression curve, it follows from Equations (37) to (39) that $\gamma =5/3\approx 1.7$.

Table 5. Exponents ${\gamma }_{\mathrm{u}}$ and ${\mathsf{\gamma }}_{\mathrm{v}}$ and frequency ranges $\mathsf{\Delta }{f}_{\mathrm{u}}$ and $\mathsf{\Delta }{f}_{\mathrm{v}}$.

	Longitudinal Spectra		Lateral Spectra
	${\mathit{\gamma }}_{\mathbf{u}}$	$\mathsf{\Delta }{\mathit{f}}_{\mathbf{u}}$	${\mathsf{\gamma }}_{\mathbf{v}}$	$\mathsf{\Delta }{\mathit{f}}_{\mathbf{v}}$
4 February 2020
AMK-03	1.7	$\left[0.0281, 0.639\right]$	1.6	$\left[0.0281, 0.639\right]$
DJI Phantom 4 Pro	1.6	$\left[0.0281, 0.639\right]$	1.7	$\left[0.0281, 0.639\right]$
17 March 2020
AMK-03	1.7	$\left[0.0281, 0.639\right]$	1.8	$\left[0.0281, 0.944\right]$
DJI Phantom 4 Pro	1.8	$\left[0.0281, 0.639\right]$	1.7	$\left[0.0281, 0.639\right]$
13 August 2020
AMK-03	1.7	$\left[0.0281, 0.639\right]$	1.7	$\left[0.0281, 0.639\right]$
DJI Phantom 4 Pro	1.7	$\left[0.0372, 0.251\right]$	1.6
15 November 2020
AMK-03	1.7	$\left[0.0281, 0.639\right]$	1.8	$\left[0.0617, 0.672\right]$
DJI Phantom 4 Pro	1.8	$\left[0.0281, 0.639\right]$	1.7	$\left[0.0220, 0.639\right]$

presents the exponents ${\gamma }_{\mathrm{u}}$ and ${\mathsf{\gamma }}_{\mathrm{v}}$ calculated for the longitudinal and lateral turbulence spectra, respectively, and the frequency ranges $\mathsf{\Delta }{f}_{\mathrm{u}}$ and $\mathsf{\Delta }{f}_{\mathrm{v}}$ used in the least-squares fit. It can be seen from Table 5 that the exponents ${\gamma }_{\mathrm{u}}$ and ${\mathsf{\gamma }}_{\mathrm{v}}$ for the longitudinal and lateral turbulence spectra agree with the theoretical results within the statistical error. In some cases, the frequency ranges corresponding to the inertial range differ for the different measurement methods. Insignificant discrepancies are explained by additional vortices arising as a result of the turbulent flow around the IMCES SB RAS buildings or near the small grove where the 30 m weather tower is installed.

The main characteristics of the energy production range include the longitudinal and lateral scales of turbulence ${\mathrm{L}}_{\mathrm{u}}$ and ${\mathrm{L}}_{\mathrm{v}}$, respectively. The information about these scales is contained in relative turbulence spectra. In the case of an isotropic atmosphere, the equation for the scale ratio has the form

$$\frac{{\mathrm{L}}_{\mathrm{v}}}{{\mathrm{L}}_{\mathrm{u}}}=0.5$$

(40)

To estimate the scales ${\mathrm{L}}_{\mathrm{u}}$ and ${\mathrm{L}}_{\mathrm{v}}$, the von Karman model is used in the approximation of experimental data. The values of the turbulence scales are determined by the equations relating the turbulence scales and the values of the maxima of the functions $f{\mathsf{\Phi }}_{\mathrm{u}}\left(f\right)$ and $f{\mathsf{\Phi }}_{\mathrm{v}}\left(f\right)$ [51]. In this study, we used the least-square fit method for approximation of the experimental data with the von Karman model as the regression curve. In contrast to [55], the maximum was not sought, and the scales ${\mathrm{L}}_{\mathrm{u}}$ and ${\mathrm{L}}_{\mathrm{v}}$ were determined directly as the parameters of the best fit when applying the least-square fit method. The calculation procedure used in this study is equivalent to the approach outlined in [55].

The values of the turbulence scales are given in

Table 6. Integral scales of turbulence.

	${\mathbf{L}}_{\mathbf{u}}$	${\mathbf{L}}_{\mathbf{v}}$	${\mathbf{L}}_{\mathbf{v}}/{\mathbf{L}}_{\mathbf{u}}$
4 February 2020
AMK-03	9.2	7.2	0.78
DJI Phantom 4 Pro	12.9	9.5	0.74
17 March 2020
AMK-03	9.6	7.1	0.74
DJI Phantom 4 Pro	9.4	7.2	0.77
13 August 2020
AMK-03	8.0	6.3	0.79
DJI Phantom 4 Pro	6.9	4.9	0.71
15 November 2020
AMK-03	14.7	10.3	0.70
DJI Phantom 4 Pro	16.0	11.5	0.72

. Keeping in mind that the IMCES SB RAS territory is not homogeneous and has complex orography, we can conclude that the scale ratio is also true to a good accuracy. In Figure 9, the colored dashed curves are for the best fit curves, red and blue curves are for the turbulence spectra of the longitudinal component ${\mathsf{\Phi }}_{\mathrm{u}}\left(f\right)$, and pink and purple curves are for the turbulence spectra of the lateral component ${\mathsf{\Phi }}_{\mathrm{v}}\left(f\right)$. Figure 9 demonstrates the good agreement for the best fit curves for the turbulence spectra obtained from the ANK-03 and DJI Phantom 4 Pro data.

4. Discussion

The problem of ideal hovering of a quadcopter in a turbulent atmosphere in the case of horizontal air mass transfer as applied to sensing of wind velocity fluctuations is considered in this paper based on dynamic equations. From the viewpoint of the theory of turbulence and correct calculation of the turbulence spectrum, the coordinate system, one of whose axes is directed along the mean wind, is of interest. In this paper, the equations for fluctuations of the longitudinal and lateral wind speed, which characterize random air mass motions in the coordinate system with the axis directed along the mean horizontal wind, are obtained. It is shown that fluctuations of the longitudinal and lateral wind velocity are proportional to fluctuations of the pitch and roll angles.

The studies of the use of DJI Phantom 4 Pro in the hover mode in combination with the AMK-03 ultrasonic weather stations show that the quadcopter allows us to obtain turbulence spectra with high spatial resolution in the atmosphere in areas with complex orography in hard-to-reach places, under various weather conditions, as well as in different seasons: winter, spring, summer, and fall.

The measured values of the longitudinal and lateral spectra vary significantly with insignificant variations of the frequency. Therefore, we used the smoothing procedure to study the main regularities in the behavior of turbulence in the inertial and energy production ranges. To estimate the longitudinal and lateral scales of turbulence, the least square fit method was used with the von Karman model as a regression curve.

The longitudinal and lateral turbulence spectra obtained with the DJI Phantom 4 Pro and AMK-03 are generally the same, with minor differences observed in the high-frequency range of the spectrum. Discrepancies in the high-frequency spectral range are also observed in the behavior of the time series of the longitudinal and lateral components of wind velocity measured by different methods. The behavior of the turbulence spectra in the inertial range shows that they obey the Kolmogorov–Obukhov “5/3” law. In the energy production range, the longitudinal and lateral turbulence scales and their ratio measured by both the DJI Phantom 4 Pro and AMK-03 coincide to a good accuracy.

Discrepancies in the behavior of the turbulence spectra obtained experimentally by different methods can be explained as follows. First, for safety reasons, the quadcopter was at a distance of ~10 m from AMK-03 during the experiment. Measurements of the integral turbulence scales show that they are of the same order of magnitude as the distance from AMK-03 to DJI Phantom 4 Pro. This relation between the scales and the distances means that the wind velocity fields at the AMK-03 and quadcopter locations are partially correlated. Therefore, it makes no sense to talk about complete equality of the measured data and, consequently, the turbulence spectra should differ.

Second, experimental studies were carried out at a territory with complex orography. The presence of the park zone, institute buildings, and highways means that the territory is inhomogeneous, which leads to significant deviations from homogeneity and isotropy. As a result, the behavior of the wind velocity field and its characteristics is different for the AMK-03 and quadcopter locations. This difference is most pronounced in the behavior of the ratio of turbulence scales. For the homogeneous and isotropic atmosphere, this ratio is ${\mathrm{L}}_{\mathrm{v}}/{\mathrm{L}}_{\mathrm{u}}=0.5$, but in our experiment, as can be seen from Table 6, ${\mathrm{L}}_{\mathrm{v}}/{\mathrm{L}}_{\mathrm{u}}~ 0.8$ for AMK-03 and ${\mathrm{L}}_{\mathrm{v}}/{\mathrm{L}}_{\mathrm{u}}~ 0.7$ for DJI Phantom 4 Pro on August 13.

It was shown in [48] that the results of investigation of the turbulence spectra in the inertial and energy production ranges with the quadcopter in the altitude holding mode over a homogeneous territory are in a good agreement with the theory of homogeneous and isotropic turbulence and with the measurement data obtained using acoustic anemometry. This study allows us to conclude that, in these ranges, at the territory with complex orography, the behavior of the turbulence spectrum measured by the quadcopter agrees with objective data on the state of atmospheric turbulence. Thus, the results obtained allow us to assert that a rotary-wing UAV can serve as a tool having great potential for diagnostics of the atmospheric boundary layer. Due to the capability of providing data on the state of atmospheric turbulence with high spatial resolution, the quadcopter is a promising tool for solving problems of controlling the UAV movement under bad weather conditions, as well as problems of wind energy, climatic measurements in an urban environment, etc.

From the scientific and practical points of view, it is of great interest to monitor the state of atmospheric turbulence at various spatial points of the studied area. From this point of view, further work on the use of a quadcopter for low-altitude sensing is associated with the use of a quadcopter swarm to determine profiles of atmospheric turbulence in both the vertical and horizontal planes.