Singular Zone in Quadrotor Yaw–Position Feedback Linearization

Abstract

Feedback linearization-based controllers are widely exploited in stabilizing a tilt rotor (eight or twelve inputs); each degree of freedom (six degrees of freedom in total) is manipulated individually to track the desired trajectory, since no singular decoupling matrix is introduced while applying this method. The conventional quadrotor (four inputs), on the other hand, is an under-actuated MIMO system that can directly track four independent degrees of freedom at most. Common selections of these outputs can be yaw–position and attitude–altitude. It is reported that no singularity is found in the decoupling matrix while applying feedback linearization in the yaw–position-tracking problem. However, in this research, we argue the existence of the ignored singular zone within the range of interest, which can cause the failure in the controller design. This paper visualizes this noninvertible area and details the process of deduction for the first time. An attempt (switch controller) to avert the singular problem is later discussed with the verification by simulation in Simulink and MATLAB. All the results are sketched in the roll–pitch diagram.

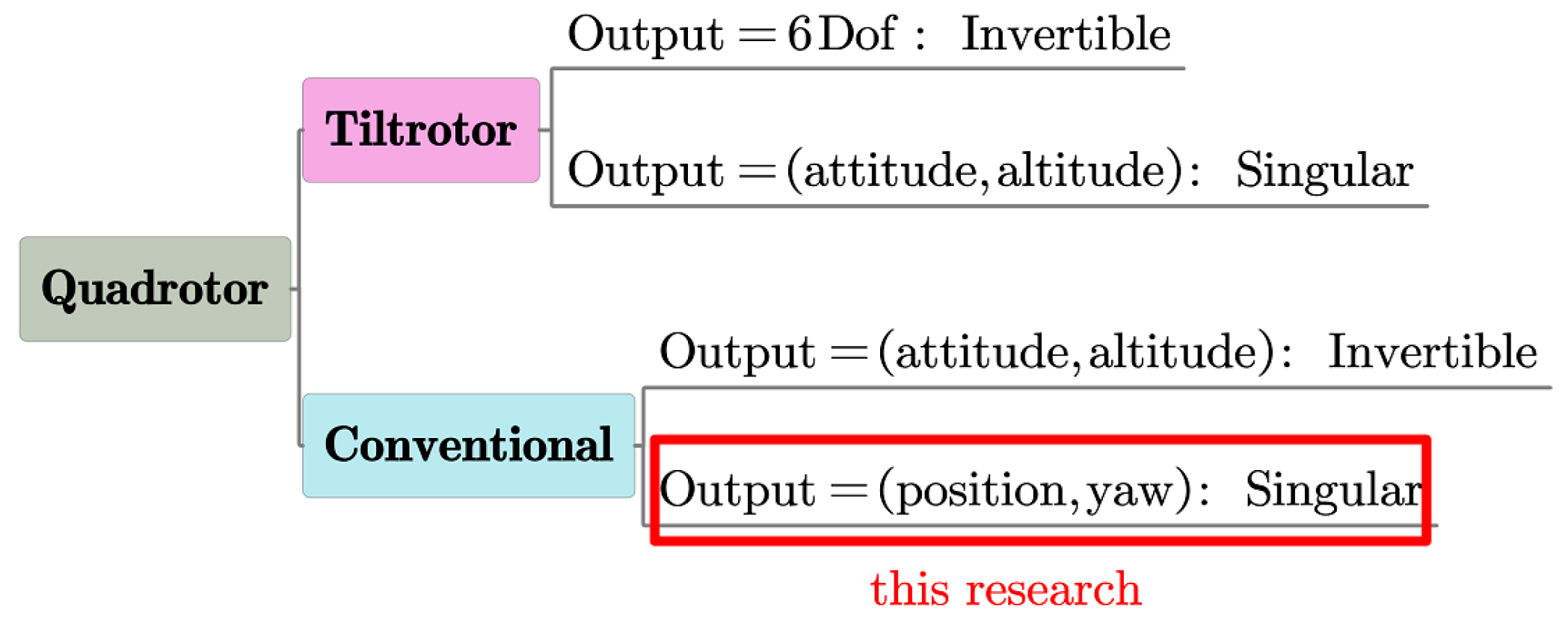
1. Introduction

With the higher demands on the performance of the conventional quadrotor (four inputs) in trajectory tracking, the effects of the controllers based on the linearization at the equilibrium state are reduced. Several nonlinear controllers have been developed to stabilize the quadrotor. References [1,2,3,4,5] applied feedback linearization equipped with a PID controller. References [6,7,8,9] employed the backstepping method, which guarantees stability using the Lyapunov criteria. References [10,11,12,13] developed a sliding mode controller. References [14,15,16,17] utilized MPC.

Among these controllers, the feedback linearization method is relatively special, since it transfers the original nonlinear system into a linear one compatible with the linear controllers. With the development of the concept of the tilt rotor [18,19,20] in the last decade, feedback linearization [4,18,20,21,22] and sliding mode control [13,23] have reclaimed their high popularity.

Although feedback linearization yields convenience in designing the exterior loop controller, several problems may hinder its application. One requirement is that the control signal and the state variable should not activate the constraints; hitting the input saturation or non-negative constraint are strictly prohibited in the exchange to hold the relevant stability criteria. To meet this requirement, References [24,25,26,27] put forward Reference Governor.

Another potential issue is the singular decoupling matrix; a singular matrix can block the application of the feedback linearization, though some methods, e.g., PCH [28], dynamic approximation [29], etc., are put forward to avert this issue.

Interestingly, the singular decoupling matrix does not universally exist in the dynamics of a quadrotor or tilt rotor. The conclusion can differ from the choices of the independent outputs directly tracked, even for the same type of tilt rotor or quadrotor.

It was proved in Reference [19] that feedback linearization produces no singular decoupling matrix for tilt rotors (eight inputs) if all the degrees of freedom (six) are tracked independently. Notice that this solution can cause a state drift phenomenon [30].

For the same dynamics (eight-input tilt rotor), Reference [31] points out that feedback linearization is hindered by a singular decoupling matrix at several specific attitudes, if only four degrees of freedom (attitude and altitude) are controlled independently. These attitudes are calculated and visualized in Reference [31].

As for the conventional quadrotor, the number of inputs (six) is less than the number of degrees of freedom (four). Based on this, four degrees of freedom, at most, can be tracked independently for a quadrotor. The typical choices of these degrees of freedom can are yaw–position and attitude–altitude.

In feedback linearization, attitude–altitude ($\mathsf{\varphi },\mathsf{\theta },\mathsf{\psi },\mathrm{and}\mathrm{z}$) are the independent tracking variables, and the conventional quadrotor introduces no singular decoupling matrix; the delta matrix in Reference [32] is strictly a full rank within the range of interest.

The other choices of independent variables are yaw (ψ) and position (x, y, and z) combinations. By applying two integrators as the input signal, Reference [1] showed their results in a simulation with the conclusion that the singularity does not exist once the attitude is in the zone of interest. That is: ϕ∈(−π/2,π/2) and θ∈(−π/2,π/2).

On the contrary, we will report the extra singular zone ignored by previous research in feedback linearization by selecting yaw–position $\left(\mathsf{\psi },\mathrm{x},\mathrm{y},\mathrm{and}\mathrm{z}\right)$ as the independent controlled variables in this paper.

It is worth mentioning that Reference [33] tried feedback linearization of the quadrotor dynamics based on yaw–position and seemed to successfully avert the noninvertible problem. While the fundamental reason for its success was an estimation of the dynamics, a linearization at the equilibrium–attitude was applied before the feedback linearization process. This approach, however, lost the essence of the dynamic inversion. As tested in Reference [34], this approximation is only applicable to the controllers within a specific range of attitude.

Notice that the number of selected independent controlled variables in a quadrotor can be less than three; Reference [35] used a cascade control structure with three controlled variables for each layer to control all six variables. The singularity problem is also avoided in this way. However, these choices are beyond the scope of this research.

There are sophisticated works focusing on singularity avoidance, escape, and penetration in gyro systems [36,37]. While designing a sophisticated controller to escape the singular zone for our system is not the primary objective of this research, the main focus of this research is to provide sound proof of the existence of the singular zone in quadrotor yaw–position feedback linearization. A potential solution, a preliminary attempt, specifically, to avert this reported singular zone is put forward after deducing the singular zone later in this paper; a switch control strategy attempts to cancel the effect of this zone, achieving stability within a particular attitude zone.

The remainder of this paper is organized as follows. In Section 2, previous works on the dynamics and feedback linearization applied to a quadrotor are introduced. Section 3 deduces the ignored singular area within the zone of interest. This noninvertible zone is visualized in Section 4. A potential approach to avoid this singular zone is put forward and simulated in Section 5. Finally, there are the conclusions and further discussions in Section 6.

2. Dynamics and Feedback Linearization in UAV Control

This section briefs the feedback linearization control in Reference [1]. The details in deducing the dynamics can be seen in Reference [1].

The input vector is given by

$${\left[{\mathrm{u}}_1{\mathrm{u}}_2{\mathrm{u}}_3{\mathrm{u}}_4\right]}^{\mathrm{T}}$$

(1)

where ${\mathrm{u}}_1$ is the total thrust generated by four propellers, ${\mathrm{u}}_2$ is the difference of thrust between the left rotor and the right rotor, ${\mathrm{u}}_3$ is the difference of thrust between the front rotor and the back rotor, and ${\mathrm{u}}_4$ is the difference of torque between the two clockwise-turning rotors and the two counterclockwise-turning rotors.

As introduced in Reference [1], the virtual inputs are

$${\left[{\overline{\mathsf{u}}}_1{\overline{\mathsf{u}}}_2{\overline{\mathsf{u}}}_3{\overline{\mathsf{u}}}_4\right]}^{\mathrm{T}}$$

(2)

where

$${\overline{\mathsf{u}}}_1=\dot{\mathsf{\xi }},$$

(3)

$$\mathsf{\xi }=\dot{\mathsf{\zeta }},$$

(4)

$$\mathsf{\zeta }={\mathrm{u}}_1,$$

(5)

$${\overline{\mathsf{u}}}_2={\mathrm{u}}_2,$$

(6)

$${\overline{\mathsf{u}}}_3={\mathrm{u}}_3,$$

(7)

$${\overline{\mathsf{u}}}_4={\mathrm{u}}_4.$$

(8)

The dynamics of the quadrotor are then written as

$$\dot{\overline{\mathsf{x}}}=\mathrm{f}\left(\overline{\mathsf{x}}\right)+{\displaystyle \sum }_{\mathrm{i}=1}^4{\mathrm{g}}_{\mathrm{i}}\left(\overline{\mathsf{x}}\right)·{\overline{\mathsf{u}}}_{\mathrm{i}}$$

(9)

where $\overline{\mathsf{x}}$ is the augmented state vector,

$$\overline{\mathsf{x}}=[\mathrm{x},\mathrm{y},\mathrm{z},\mathsf{\psi },\mathsf{\theta },\mathsf{\varphi },\dot{\mathrm{x}},\dot{\mathrm{y}},\dot{\mathrm{z}},\mathsf{\zeta },\mathsf{\xi },\mathrm{p},\mathrm{q},\mathrm{r}]{}^{\mathrm{T}},$$

(10)

where $\mathrm{x},\mathrm{y},\mathrm{and}\mathrm{z}$ are the positions with respect to the earth frame; $\mathsf{\psi },\mathsf{\theta },\mathrm{and}\mathsf{\varphi }$ are the yaw angle, pitch angle, and roll angle, respectively, $\mathrm{and} \mathrm{p},\mathrm{q},\mathrm{and}\mathrm{r}$ are the angular velocities along the body-fixed x-axis, y-axis, and z-axis, respectively.

${\mathrm{g}}_{\mathrm{i}}\left(\overline{\mathsf{x}}\right)$ is defined as

$${\mathrm{g}}_1\left(\overline{\mathsf{x}}\right)={\left[0,0,0,0,0,0,0,0,0,0,1,0,0,0\right]}^{\mathrm{T}},$$

(11)

$${\mathrm{g}}_2\left(\overline{\mathsf{x}}\right)={\left[0,0,0,0,0,0,0,0,0,0,0,\frac{\mathrm{d}}{{\mathrm{I}}_{\mathrm{x}}},0,0\right]}^{\mathrm{T}},$$

(12)

$${\mathrm{g}}_3\left(\overline{\mathsf{x}}\right)={\left[0,0,0,0,0,0,0,0,0,0,0,0,\frac{\mathrm{d}}{{\mathrm{I}}_{\mathrm{y}}},0\right]}^{\mathrm{T}},$$

(13)

$${\mathrm{g}}_4\left(\overline{\mathsf{x}}\right)={\left[0,0,0,0,0,0,0,0,0,0,0,0,0,\frac{\mathrm{d}}{{\mathrm{I}}_{\mathrm{z}}}\right]}^{\mathrm{T}},$$

(14)

where $\mathrm{d}$ is the length of each arm, $\mathrm{and} {\mathrm{I}}_{\mathrm{x}},{\mathrm{I}}_{\mathrm{y}},{\mathrm{and}\mathrm{I}}_{\mathrm{z}}$ are the rotational inertia along the body-fixed x-axis, y-axis, and z-axis, respectively.

$\mathrm{f}\left(\overline{\mathsf{x}}\right)$ is defined as

$$\mathrm{f}\left(\overline{\mathsf{x}}\right)=\left[\begin{array}{c}\dot{\mathrm{x}}\\ \dot{\mathrm{y}}\\ \dot{\mathrm{z}}\\ \frac{\mathrm{s}\mathsf{\varphi }}{\mathrm{c}\mathsf{\theta }}·\mathrm{q}+\frac{\mathrm{c}\mathsf{\varphi }}{\mathrm{c}\mathsf{\theta }}·\mathrm{r}\\ \mathrm{c}\mathsf{\varphi }·\mathrm{q}-\mathrm{s}\mathsf{\varphi }·\mathrm{r}\\ \mathrm{p}+\mathrm{s}\mathsf{\varphi }·\mathrm{t}\mathsf{\theta }·\mathrm{q}+\mathrm{c}\mathsf{\varphi }·\mathrm{t}\mathsf{\theta }·\mathrm{r}\\ {\mathrm{g}}_1^7·\mathrm{\zeta }\\ {\mathrm{g}}_1^8·\mathrm{\zeta }\\ {\mathrm{g}}_1^9·\mathrm{\zeta }+\mathrm{g}\\ \mathrm{\xi }\\ 0\\ \frac{{\mathrm{I}}_{\mathrm{y}}-{\mathrm{I}}_{\mathrm{z}}}{{\mathrm{I}}_{\mathrm{x}}}·\mathrm{q}·\mathrm{r}\\ \frac{{\mathrm{I}}_{\mathrm{z}}-{\mathrm{I}}_{\mathrm{x}}}{{\mathrm{I}}_{\mathrm{y}}}·\mathrm{p}·\mathrm{r}\\ \frac{{\mathrm{I}}_{\mathrm{x}}-{\mathrm{I}}_{\mathrm{y}}}{{\mathrm{I}}_{\mathrm{z}}}·\mathrm{p}·\mathrm{q}\end{array}\right]$$

(15)

where $\mathrm{s}\mathsf{\Lambda },\mathrm{c}\mathsf{\Lambda },\mathrm{and}\mathrm{t}\mathsf{\Lambda }$ represent $\sin \left(\mathsf{\Lambda }\right)$, $\cos \left(\mathsf{\Lambda }\right)$, and $\tan \left(\mathsf{\Lambda }\right),$ respectively, $\mathrm{g}$ is the gravitational acceleration, $\mathrm{and} {\mathrm{g}}_1^7,{\mathrm{g}}_1^8,{\mathrm{and}\mathrm{g}}_1^9$ are defined as

$$\begin{array}{lll}{\mathrm{g}}_1^7& =& -\frac{1}{\mathrm{m}}·\left(\mathrm{c}\mathsf{\varphi }·\mathrm{c}\mathsf{\psi }·\mathrm{s}\mathsf{\theta }+\mathrm{s}\mathsf{\varphi }·\mathrm{s}\mathsf{\psi }\right)\\ & \triangleq & -\frac{1}{\mathrm{m}}·{\mathrm{A}}_1,\end{array}$$

(16)

$$\begin{array}{lll}{\mathrm{g}}_1^8& =& -\frac{1}{\mathrm{m}}·\left(\mathrm{c}\mathsf{\varphi }·\mathrm{s}\mathsf{\psi }·\mathrm{s}\mathsf{\theta }-\mathrm{s}\mathsf{\varphi }·\mathrm{c}\mathsf{\psi }\right)\\ & \triangleq & -\frac{1}{\mathrm{m}}·{\mathrm{A}}_2,\end{array}$$

(17)

$$\begin{array}{lll}{\mathrm{g}}_1^9& =& -\frac{1}{\mathrm{m}}·\mathrm{c}\mathsf{\theta }·\mathrm{c}\mathsf{\varphi }\\ & \triangleq & -\frac{1}{\mathrm{m}}·{\mathrm{A}}_3\end{array}$$

(18)

where $\mathrm{m}$ is the mass of the quadrotor, ${\mathrm{and}\mathrm{A}}_1=\mathrm{c}\mathsf{\varphi }·\mathrm{c}\mathsf{\psi }·\mathrm{s}\mathsf{\theta }+\mathrm{s}\mathsf{\varphi }·\mathrm{s}\mathsf{\psi }$, ${\mathrm{A}}_2=\mathrm{c}\mathsf{\varphi }·\mathrm{s}\mathsf{\psi }·\mathrm{s}\mathsf{\theta }-\mathrm{s}\mathsf{\varphi }·\mathrm{c}\mathsf{\psi }$, $\mathrm{and} {\mathrm{A}}_3=\mathrm{c}\mathsf{\theta }·\mathrm{c}\mathsf{\varphi }$.

The four independent controlled variables (${\mathrm{y}}_1,{\mathrm{y}}_2,{\mathrm{y}}_3,\mathrm{and}{\mathrm{y}}_4$) are selected as

$$\left[\begin{array}{c}{\mathrm{y}}_1\\ {\mathrm{y}}_2\\ {\mathrm{y}}_3\\ {\mathrm{y}}_4\end{array}\right]=\left[\begin{array}{c}\mathrm{x}\\ \mathrm{y}\\ \mathrm{z}\\ \mathsf{\psi }\end{array}\right].$$

(19)

To apply the feedback linearization, Reference [1] calculated the higher derivative of the controlled variables and received

$$\begin{array}{c}\left[\begin{array}{c}{\mathrm{y}}_1{}^{\left(4\right)}\\ {\mathrm{y}}_2{}^{\left(4\right)}\\ {\mathrm{y}}_3{}^{\left(4\right)}\\ {\ddot{\mathrm{y}}}_4\end{array}\right]=\left[\begin{array}{c}{\mathrm{x}}^{\left(4\right)}\\ {\mathrm{y}}^{\left(4\right)}\\ {\mathrm{z}}^{\left(4\right)}\\ \ddot{\mathsf{\psi }}\end{array}\right]\\ =\mathrm{Ma}\left(\overline{\mathsf{x}}\right)+\Delta \left(\overline{\mathsf{x}}\right)·\left[\begin{array}{c}{\overline{\mathsf{u}}}_1\\ {\overline{\mathsf{u}}}_2\\ {\overline{\mathsf{u}}}_3\\ {\overline{\mathsf{u}}}_4\end{array}\right]\end{array}$$

(20)

where both $\mathrm{Ma}\left(\overline{\mathsf{x}}\right)\mathrm{and}\Delta \left(\overline{\mathsf{x}}\right)$ are a 4 × 4 matrix of state (10).

Once $\Delta \left(\overline{\mathsf{x}}\right)$ is invertible, the feedback linearization can be further applied. It was concluded in Reference [1] that $\Delta \left(\overline{\mathsf{x}}\right)$ is always invertible given that ϕ∈(−π/2,π/2), θ∈(−π/2,π/2), $\mathsf{\zeta }\ne 0$.

However, based on our deductions, this condition does not hold within the entire space above. The additional requirement for $\Delta \left(\overline{\mathsf{x}}\right)$ and its proof are given in the next section.

3. Invertibility Analysis

3.1. Necessary and Sufficient Condition to Be Invertible

$\Delta \left(\overline{\mathsf{x}}\right)$ is invertible within the region ϕ∈(−π/2,π/2), θ∈(−π/2,π/2), $\mathsf{\zeta }\ne 0$ if and only if

$$-1+{\cos }^2\mathsf{\theta }·{\cos }^2\mathsf{\varphi }-{\cos }^2\mathsf{\theta }·\cos \mathsf{\varphi }·\sin \mathsf{\varphi }\ne 0.$$

(21)

3.2. Proof of The Invertible Condition

This section details the process of deduction for receiving Equation (21).

The necessary and sufficient condition for receiving an invertible $\Delta \left(\overline{\mathsf{x}}\right)$ is

$$\left|{\mathrm{P}}^{4\times 4}·\Delta \left(\overline{\mathsf{x}}\right)·{\mathrm{Q}}^{4\times 4}\right|\ne 0,\left(\mathrm{P}\mathrm{and}\mathrm{Q}\mathrm{are}\mathrm{invertible}\right).$$

(22)

Before finding $\mathrm{P}$ and $\mathrm{Q}$, we start with calculating $\Delta \left(\overline{\mathsf{x}}\right)$ analytically in Equation (16). Firstly, ${\mathrm{y}}_1{}^{\left(4\right)}$, ${\mathrm{y}}_2{}^{\left(4\right)}$, ${\mathrm{y}}_3{}^{\left(4\right)}$, and ${\ddot{\mathrm{y}}}_4$ are to be calculated.

${\mathrm{y}}_1{}^{\left(4\right)}$ is calculated as follows:

$${\ddot{\mathrm{y}}}_1=-\frac{1}{\mathrm{m}}·{\mathrm{A}}_1·\mathsf{\zeta },$$

(23)

$${\mathrm{y}}_1{}^{\left(3\right)}=-\frac{1}{\mathrm{m}}·{\dot{\mathrm{A}}}_1·\mathsf{\zeta }-\frac{1}{\mathrm{m}}·{\mathrm{A}}_1·\mathsf{\xi },$$

(24)

$${\mathrm{y}}_1{}^{\left(4\right)}=-\frac{1}{\mathrm{m}}·{\ddot{\mathrm{A}}}_1·\mathsf{\zeta }-\frac{2}{\mathrm{m}}·{\dot{\mathrm{A}}}_1·\mathsf{\xi }-\frac{1}{\mathrm{m}}·{\mathrm{A}}_1·{\overline{\mathsf{u}}}_1.$$

(25)

${\mathrm{y}}_2{}^{\left(4\right)}\mathrm{and}{\mathrm{y}}_3{}^{\left(4\right)}$ are deduced in a similar way:

$${\mathrm{y}}_2{}^{\left(4\right)}=-\frac{1}{\mathrm{m}}·{\ddot{\mathrm{A}}}_2·\mathsf{\zeta }-\frac{2}{\mathrm{m}}·{\dot{\mathrm{A}}}_2·\mathsf{\xi }-\frac{1}{\mathrm{m}}·{\mathrm{A}}_2·{\overline{\mathsf{u}}}_1,$$

(26)

$${\mathrm{y}}_3{}^{\left(4\right)}=-\frac{1}{\mathrm{m}}·{\ddot{\mathrm{A}}}_3·\mathsf{\zeta }-\frac{2}{\mathrm{m}}·{\dot{\mathrm{A}}}_3·\mathsf{\xi }-\frac{1}{\mathrm{m}}·{\mathrm{A}}_3·{\overline{\mathsf{u}}}_1.$$

(27)

${\ddot{\mathrm{y}}}_4$ is deduced in Equation (28):

$$\begin{array}{cc}\hfill \ddot{\mathsf{\psi }}& ={\left(\frac{\mathrm{s}\mathsf{\varphi }}{\mathrm{c}\mathsf{\theta }}·\mathrm{q}+\frac{\mathrm{c}\mathsf{\varphi }}{\mathrm{c}\mathsf{\theta }}·\mathrm{r}\right)}^{\prime }\hfill \\ & ={\mathrm{A}}_4\left(\mathsf{\varphi },\mathsf{\theta },\mathrm{p},\mathrm{q},\mathrm{r}\right)+\frac{\mathrm{s}\mathsf{\varphi }}{\mathrm{c}\mathsf{\theta }}·\frac{\mathrm{d}}{{\mathrm{I}}_{\mathrm{y}}}·{\overline{\mathsf{u}}}_3+\frac{\mathrm{c}\mathsf{\varphi }}{\mathrm{c}\mathsf{\theta }}·\frac{\mathrm{d}}{{\mathrm{I}}_{\mathrm{z}}}·{\overline{\mathsf{u}}}_4\hfill \end{array}$$

(28)

where ${\mathrm{A}}_4\left(\mathsf{\varphi },\mathsf{\theta },\mathrm{p},\mathrm{q},\mathrm{r}\right)$ are the remaining terms without containing ${\overline{\mathsf{u}}}_3$ or ${\overline{\mathsf{u}}}_4$.

Notice that ${\mathrm{A}}_1,{\mathrm{A}}_2,\mathrm{and}{\mathrm{A}}_3$ are the functions of ($\mathsf{\psi },\mathsf{\theta },\mathrm{and}\mathsf{\varphi }$). Thus, ${\dot{\mathrm{A}}}_1,{\dot{\mathrm{A}}}_2,{\mathrm{and}\dot{\mathrm{A}}}_3$ are the functions of the state $\overline{\mathsf{x}}$ in Equation (10), containing no ${\overline{\mathsf{u}}}_1$, ${\overline{\mathsf{u}}}_2$, or ${\overline{\mathsf{u}}}_3$. Consequently, the terms $-2/\mathrm{m}·{\dot{\mathrm{A}}}_{\mathrm{i}}·\mathsf{\xi }$ in Equations (25)–(27) do not contribute to the coefficients of ${\overline{\mathsf{u}}}_1,{\overline{\mathsf{u}}}_2, \mathrm{and} {\overline{\mathsf{u}}}_3$.

On the other hand, ${\ddot{\mathrm{A}}}_1$, ${\ddot{\mathrm{A}}}_2$, and ${\ddot{\mathrm{A}}}_3$ are calculated by differentiating the state $\overline{\mathsf{x}}$ in Equation (10), which generates ${\overline{\mathsf{u}}}_1,{\overline{\mathsf{u}}}_2,\mathrm{and}{\overline{\mathsf{u}}}_3$. Notice the forms of Equations (25)–(28); calculating ${\ddot{\mathrm{A}}}_1,{\ddot{\mathrm{A}}}_2, \mathrm{and}{\ddot{\mathrm{A}}}_3$ is necessary to receive the coefficients of ${\overline{\mathsf{u}}}_1,{\overline{\mathsf{u}}}_2,\mathrm{and}{\overline{\mathsf{u}}}_3$. In the following, we found the terms containing ${\overline{\mathsf{u}}}_1$, ${\overline{\mathsf{u}}}_2$, and ${\overline{\mathsf{u}}}_3$ in ${\ddot{\mathrm{A}}}_1,{\ddot{\mathrm{A}}}_2,\mathrm{and}{\ddot{\mathrm{A}}}_3$.

We start with finding ${\ddot{\mathrm{A}}}_1$.

Firstly, ${\dot{\mathrm{A}}}_1$ is calculated as

$${\dot{\mathrm{A}}}_1=-\mathrm{s}\mathsf{\psi }·\mathrm{s}\mathsf{\theta }·\mathrm{c}\mathsf{\varphi }·\dot{\mathsf{\psi }}+\mathrm{c}\mathsf{\psi }·\mathrm{c}\mathsf{\theta }·\mathrm{c}\mathsf{\varphi }·\dot{\mathsf{\theta }}-\mathrm{c}\mathsf{\psi }·\mathrm{s}\mathsf{\theta }·\mathrm{s}\mathsf{\varphi }·\dot{\mathsf{\varphi }}+\mathrm{c}\mathsf{\psi }·\mathrm{s}\mathsf{\varphi }·\dot{\mathsf{\psi }}+\mathrm{s}\mathsf{\psi }·\mathrm{c}\mathsf{\varphi }·\dot{\mathsf{\varphi }}.$$

(29)

Substituting $\dot{\mathsf{\psi }}$, $\dot{\mathsf{\theta }}$, and $\dot{\mathsf{\phi }}$ in Equation (9), we receive

$${\dot{\mathrm{A}}}_1={\mathrm{M}}_1·\left(\frac{\mathrm{s}\mathsf{\varphi }}{\mathrm{c}\mathsf{\theta }}·\mathrm{q}+\frac{\mathrm{c}\mathsf{\varphi }}{\mathrm{c}\mathsf{\theta }}·\mathrm{r}\right)+{\mathrm{N}}_1·\left(\mathrm{p}+\mathrm{s}\mathsf{\varphi }·\mathrm{t}\mathsf{\theta }·\mathrm{q}+\mathrm{c}\mathsf{\varphi }·\mathrm{t}\mathsf{\theta }·\mathrm{r}\right)+{\mathrm{O}}_1·\left(\mathrm{c}\mathsf{\varphi }·\mathrm{q}-\mathrm{s}\mathsf{\varphi }·\mathrm{r}\right)$$

(30)

where ${\mathrm{M}}_1,{\mathrm{N}}_1,\mathrm{and}{\mathrm{O}}_1$ are defined as

$${\mathrm{M}}_1=\mathrm{c}\mathsf{\psi }·\mathrm{s}\mathsf{\varphi }-\mathrm{s}\mathsf{\psi }·\mathrm{s}\mathsf{\theta }·\mathrm{s}\mathsf{\varphi },$$

(31)

$${\mathrm{N}}_1=\mathrm{s}\mathsf{\psi }·\mathrm{c}\mathsf{\varphi }-\mathrm{c}\mathsf{\psi }·\mathrm{s}\mathsf{\theta }·\mathrm{s}\mathsf{\varphi },$$

(32)

$${\mathrm{O}}_1=\mathrm{c}\mathsf{\psi }·\mathrm{c}\mathsf{\theta }·\mathrm{c}\mathsf{\varphi }.$$

(33)

Further, we calculated the terms containing ($\dot{\mathrm{p}},\dot{\mathrm{q}},\dot{\mathrm{r}}$) in ${\ddot{\mathrm{A}}}_1$ based on the result of ${\dot{\mathrm{A}}}_1$ in Equation (30). The sum of the terms containing $\dot{\mathrm{p}}$, $\dot{\mathrm{q}}$, and $\dot{\mathrm{r}}$, which generate ${\overline{\mathsf{u}}}_2$, ${\overline{\mathsf{u}}}_3$, and ${\overline{\mathsf{u}}}_4,$ respectively, in ${\ddot{\mathrm{A}}}_1$ is illustrated as

$${\mathrm{R}}_{{\mathrm{A}}_1}={\mathrm{N}}_1·\dot{\mathrm{p}}+\left({\mathrm{M}}_1·\frac{\mathrm{s}\mathsf{\varphi }}{\mathrm{c}\mathsf{\theta }}+{\mathrm{N}}_1·\mathrm{s}\mathsf{\varphi }·\mathrm{t}\mathsf{\theta }+{\mathrm{O}}_1·\mathrm{c}\mathsf{\varphi }\right)·\dot{\mathrm{q}}+\left({\mathrm{M}}_1·\frac{\mathrm{c}\mathsf{\varphi }}{\mathrm{c}\mathsf{\theta }}+{\mathrm{N}}_1·\mathrm{c}\mathsf{\varphi }·\mathrm{t}\mathsf{\theta }-{\mathrm{O}}_1·\mathrm{s}\mathsf{\varphi }\right)·\dot{\mathrm{r}}.$$

(34)

As a result, the coefficient of ${\overline{\mathsf{u}}}_1$ in Equation (25) is $-1/\mathrm{m}·{\mathrm{A}}_1$. The coefficient of ${\overline{\mathsf{u}}}_2$ in Equation (25) confirmed by Equation (34) is $-\mathsf{\zeta }/\mathrm{m}·{\mathrm{N}}_1·\frac{\mathrm{d}}{{\mathrm{I}}_{\mathrm{x}}}$. The coefficient of ${\overline{\mathsf{u}}}_3$ in Equation (25) confirmed by Equation (34) is $-\mathsf{\zeta }/\mathrm{m}·\left({\mathrm{M}}_1·\mathrm{s}\mathsf{\varphi }/\mathrm{c}\mathsf{\theta }+{\mathrm{N}}_1·\mathrm{s}\mathsf{\varphi }·\mathrm{t}\mathsf{\theta }+{\mathrm{O}}_1·\mathrm{c}\mathsf{\varphi }\right)·\mathrm{d}/{\mathrm{I}}_{\mathrm{y}}$. The coefficient of ${\overline{\mathsf{u}}}_4$ in Equation (25) confirmed by Equation (34) is $-\mathsf{\zeta }/\mathrm{m}·\left({\mathrm{M}}_1·\mathrm{c}\mathsf{\varphi }/\mathrm{c}\mathsf{\theta }+{\mathrm{N}}_1·\mathrm{c}\mathsf{\varphi }·\mathrm{t}\mathsf{\theta }-{\mathrm{O}}_1·\mathrm{s}\mathsf{\varphi }\right)·\mathrm{d}/{\mathrm{I}}_{\mathrm{z}}$. So far, we have received the results of the coefficients of ${\overline{\mathsf{u}}}_1,{\overline{\mathsf{u}}}_2,{\overline{\mathsf{u}}}_3,\mathrm{and}{\overline{\mathsf{u}}}_4$ in ${\mathrm{y}}_1{}^{\left(4\right)}$.

A similar procedure is conducted to calculate the coefficients of ${\overline{\mathsf{u}}}_1,{\overline{\mathsf{u}}}_2,{\overline{\mathsf{u}}}_3,\mathrm{and}{\overline{\mathsf{u}}}_4$ in ${\mathrm{y}}_2{}^{\left(4\right)}$ in Equation (26). It starts with finding

$${\dot{\mathrm{A}}}_2={\mathrm{M}}_2·\left(\frac{\mathrm{s}\mathsf{\varphi }}{\mathrm{c}\mathsf{\theta }}·\mathrm{q}+\frac{\mathrm{c}\mathsf{\varphi }}{\mathrm{c}\mathsf{\theta }}·\mathrm{r}\right)+{\mathrm{N}}_2·\left(\mathrm{p}+\mathrm{s}\mathsf{\varphi }·\mathrm{t}\mathsf{\theta }·\mathrm{q}+\mathrm{c}\mathsf{\varphi }·\mathrm{t}\mathsf{\theta }·\mathrm{r}\right)+{\mathrm{O}}_2·\left(\mathrm{c}\mathsf{\varphi }·\mathrm{q}-\mathrm{s}\mathsf{\varphi }·\mathrm{r}\right)$$

(35)

where ${\mathrm{M}}_2,{\mathrm{N}}_2,\mathrm{and}{\mathrm{O}}_2$ are defined as

$${\mathrm{M}}_2=\mathrm{s}\mathsf{\psi }·\mathrm{s}\mathsf{\varphi }+\mathrm{c}\mathsf{\psi }·\mathrm{s}\mathsf{\theta }·\mathrm{s}\mathsf{\varphi },$$

(36)

$${\mathrm{N}}_2=-\mathrm{c}\mathsf{\psi }·\mathrm{c}\mathsf{\varphi }-\mathrm{s}\mathsf{\psi }·\mathrm{s}\mathsf{\theta }·\mathrm{s}\mathsf{\varphi },$$

(37)

$${\mathrm{O}}_2=\mathrm{s}\mathsf{\psi }·\mathrm{c}\mathsf{\theta }·\mathrm{c}\mathsf{\varphi }.$$

(38)

Further, we calculated the terms containing ($\dot{\mathrm{p}},\dot{\mathrm{q}},\dot{\mathrm{r}}$) in ${\ddot{\mathrm{A}}}_2$ based on the result of ${\dot{\mathrm{A}}}_2$ in Equation (35). The sum of the terms containing $\dot{\mathrm{p}}$, $\dot{\mathrm{q}}$, and $\dot{\mathrm{r}}$, which generate ${\overline{\mathsf{u}}}_2$, ${\overline{\mathsf{u}}}_3$, and ${\overline{\mathsf{u}}}_4$, respectively, in ${\ddot{\mathrm{A}}}_2$ is

$${\mathrm{R}}_{{\mathrm{A}}_2}={\mathrm{N}}_2·\dot{\mathrm{p}}+\left({\mathrm{M}}_2·\frac{\mathrm{s}\mathsf{\varphi }}{\mathrm{c}\mathsf{\theta }}+{\mathrm{N}}_2·\mathrm{s}\mathsf{\varphi }·\mathrm{t}\mathsf{\theta }+{\mathrm{O}}_2·\mathrm{c}\mathsf{\varphi }\right)·\dot{\mathrm{q}}+\left({\mathrm{M}}_2·\frac{\mathrm{c}\mathsf{\varphi }}{\mathrm{c}\mathsf{\theta }}+{\mathrm{N}}_2·\mathrm{c}\mathsf{\varphi }·\mathrm{t}\mathsf{\theta }-{\mathrm{O}}_2·\mathrm{s}\mathsf{\varphi }\right)·\dot{\mathrm{r}}.$$

(39)

As a result, the coefficient of ${\overline{\mathsf{u}}}_1$ in Equation (26) is $-1/\mathrm{m}·{\mathrm{A}}_2$. The coefficient of ${\overline{\mathsf{u}}}_2$ in Equation (26) confirmed by Equation (39) is $-\mathsf{\zeta }/\mathrm{m}·{\mathrm{N}}_2·\mathrm{d}/{\mathrm{I}}_{\mathrm{x}}$. The coefficient of ${\overline{\mathsf{u}}}_3$ in Equation (26) confirmed by Equation (39) is $-\mathsf{\zeta }/\mathrm{m}·\left({\mathrm{M}}_2·\mathrm{s}\mathsf{\varphi }/\mathrm{c}\mathsf{\theta }+{\mathrm{N}}_2·\mathrm{s}\mathsf{\varphi }·\mathrm{t}\mathsf{\theta }+{\mathrm{O}}_2·\mathrm{c}\mathsf{\varphi }\right)·\mathrm{d}/{\mathrm{I}}_{\mathrm{y}}$. The coefficient of ${\overline{\mathsf{u}}}_4$ in Equation (26) confirmed by Equation (39) is $-\mathsf{\zeta }/\mathrm{m}·\left({\mathrm{M}}_2·\mathrm{c}\mathsf{\varphi }/\mathrm{c}\mathsf{\theta }+{\mathrm{N}}_2·\mathrm{c}\mathsf{\varphi }·\mathrm{t}\mathsf{\theta }-{\mathrm{O}}_2·\mathrm{s}\mathsf{\varphi }\right)·\mathsf{d}/{\mathrm{I}}_{\mathrm{z}}$.

A similar procedure is conducted to calculate the coefficients of ${\overline{\mathsf{u}}}_1,{\overline{\mathsf{u}}}_2,{\overline{\mathsf{u}}}_3,\mathrm{and}{\overline{\mathsf{u}}}_4$ in ${\mathrm{y}}_3{}^{\left(4\right)}$ in Formula (27).

As a result, the coefficient of ${\overline{\mathsf{u}}}_1$ in Equation (27) is $-1/\mathrm{m}·{\mathrm{A}}_3$. The coefficient of ${\overline{\mathsf{u}}}_2$ in Equation (27) is $-\mathsf{\zeta }/\mathrm{m}·{\mathrm{N}}_3·\mathrm{d}/{\mathrm{I}}_{\mathrm{x}}$. The coefficient of ${\overline{\mathsf{u}}}_3$ in Equation (27) is $-\mathsf{\zeta }/\mathrm{m}·\left({\mathrm{N}}_3·\mathrm{s}\mathsf{\varphi }·\mathrm{t}\mathsf{\theta }+{\mathrm{O}}_3·\mathrm{c}\mathsf{\varphi }\right)·\mathrm{d}/{\mathrm{I}}_{\mathrm{y}}$. The coefficient of ${\overline{\mathsf{u}}}_4$ in Equation (27) is $-\mathsf{\zeta }/\mathrm{m}·\left({\mathrm{N}}_3·\mathrm{c}\mathsf{\varphi }·\mathrm{t}\mathsf{\theta }-{\mathrm{O}}_3·\mathrm{s}\mathsf{\varphi }\right)·\mathrm{d}/{\mathrm{I}}_{\mathrm{z}}$. ${\mathrm{N}}_3{\mathrm{and}\mathrm{O}}_3$ are defined as

$${\mathrm{N}}_3=-\mathrm{c}\mathsf{\theta }·\mathrm{s}\mathsf{\varphi },$$

(40)

$${\mathrm{O}}_3=-\mathrm{s}\mathsf{\theta }·\mathrm{c}\mathsf{\varphi }.$$

(41)

As for the coefficients of ${\overline{\mathsf{u}}}_1,{\overline{\mathsf{u}}}_2,{\overline{\mathsf{u}}}_3,\mathrm{and}{\overline{\mathsf{u}}}_4$ in ${\ddot{\mathrm{y}}}_4$, we can find them in Equation (28). As a result, the coefficient of ${\overline{\mathsf{u}}}_1$ in Equation (28) is $0$. The coefficient of ${\overline{\mathsf{u}}}_2$ in Equation (28) is $0$. The coefficient of ${\overline{\mathsf{u}}}_3$ in Equation (28) is $\mathrm{s}\mathsf{\varphi }/\mathrm{c}\mathsf{\theta }·\mathrm{d}/{\mathrm{I}}_{\mathrm{y}}$. The coefficient of ${\overline{\mathsf{u}}}_4$ in Equation (28) is $\mathrm{c}\mathsf{\varphi }/\mathrm{c}\mathsf{\theta }·\mathrm{d}/{\mathrm{I}}_{\mathrm{z}}$.

So far, we have found all the coefficients of ${\overline{\mathsf{u}}}_1$, ${\overline{\mathsf{u}}}_2$, ${\overline{\mathsf{u}}}_3$, and ${\overline{\mathsf{u}}}_4$ in ${\mathrm{y}}_1{}^{\left(4\right)},{\mathrm{y}}_2{}^{\left(4\right)},{\mathrm{y}}_3{}^{\left(4\right)},\mathrm{and}{\ddot{\mathrm{y}}}_4$. Thus, the decoupling matrix (delta matrix), $\Delta \left(\overline{\mathsf{x}}\right)$, in Equation (20) is found. That is

$$\Delta \left(\overline{\mathsf{x}}\right)=\left[\begin{array}{cccc}{\Delta }_{11}& {\Delta }_{12}& {\Delta }_{13}& {\Delta }_{14}\\ {\Delta }_{21}& {\Delta }_{22}& {\Delta }_{23}& {\Delta }_{24}\\ {\Delta }_{31}& {\Delta }_{32}& {\Delta }_{33}& {\Delta }_{34}\\ {\Delta }_{41}& {\Delta }_{42}& {\Delta }_{43}& {\Delta }_{44}\end{array}\right]$$

(42)

where

$${\Delta }_{11}=-\frac{1}{\mathrm{m}}·{\mathrm{A}}_1,$$

$${\Delta }_{21}=-\frac{1}{\mathrm{m}}·{\mathrm{A}}_2,$$

$${\Delta }_{31}=-\frac{1}{\mathrm{m}}·{\mathrm{A}}_3,$$

$${\Delta }_{41}=0,$$

$${\Delta }_{12}=-\frac{\mathsf{\zeta }}{\mathrm{m}}·{\mathrm{N}}_1·\frac{\mathrm{d}}{{\mathrm{I}}_{\mathrm{x}}},$$

$${\Delta }_{22}=-\frac{\mathsf{\zeta }}{\mathrm{m}}·{\mathrm{N}}_2·\frac{\mathrm{d}}{{\mathrm{I}}_{\mathrm{x}}},$$

$${\Delta }_{32}=-\frac{\mathsf{\zeta }}{\mathrm{m}}·{\mathrm{N}}_3·\frac{\mathrm{d}}{{\mathrm{I}}_{\mathrm{x}}},$$

$${\Delta }_{42}=0,$$

$${\Delta }_{13}=-\frac{\mathsf{\zeta }}{\mathrm{m}}·\left({\mathrm{M}}_1·\frac{\mathrm{s}\mathsf{\varphi }}{\mathrm{c}\mathsf{\theta }}+{\mathrm{N}}_1·\mathrm{s}\mathsf{\varphi }·\mathrm{t}\mathsf{\theta }+{\mathrm{O}}_1·\mathrm{c}\mathsf{\varphi }\right)·\frac{\mathrm{d}}{{\mathrm{I}}_{\mathrm{y}}},$$

$${\Delta }_{23}=-\frac{\mathsf{\zeta }}{\mathrm{m}}·\left({\mathrm{M}}_2·\frac{\mathrm{s}\mathsf{\varphi }}{\mathrm{c}\mathsf{\theta }}+{\mathrm{N}}_2·\mathrm{s}\mathsf{\varphi }·\mathrm{t}\mathsf{\theta }+{\mathrm{O}}_2·\mathrm{c}\mathsf{\varphi }\right)·\frac{\mathrm{d}}{{\mathrm{I}}_{\mathrm{y}}},$$

$${\Delta }_{33}=-\frac{\mathsf{\zeta }}{\mathrm{m}}·\left({\mathrm{N}}_3·\mathrm{s}\mathsf{\varphi }·\mathrm{t}\mathsf{\theta }+{\mathrm{O}}_3·\mathrm{c}\mathsf{\varphi }\right)·\frac{\mathrm{d}}{{\mathrm{I}}_{\mathrm{y}}},$$

$${\Delta }_{43}=\frac{\mathrm{s}\mathsf{\varphi }}{\mathrm{c}\mathsf{\theta }}·\frac{\mathrm{d}}{{\mathrm{I}}_{\mathrm{y}}},$$

$${\Delta }_{14}=-\frac{\mathsf{\zeta }}{\mathrm{m}}·\left({\mathrm{M}}_1·\frac{\mathrm{c}\mathsf{\varphi }}{\mathrm{c}\mathsf{\theta }}+{\mathrm{N}}_1·\mathrm{c}\mathsf{\varphi }·\mathrm{t}\mathsf{\theta }-{\mathrm{O}}_1·\mathrm{s}\mathsf{\varphi }\right)·\frac{\mathrm{d}}{{\mathrm{I}}_{\mathrm{z}}},$$

$${\Delta }_{24}=-\frac{\mathsf{\zeta }}{\mathrm{m}}·\left({\mathrm{M}}_2·\frac{\mathrm{c}\mathsf{\varphi }}{\mathrm{c}\mathsf{\theta }}+{\mathrm{N}}_2·\mathrm{c}\mathsf{\varphi }·\mathrm{t}\mathsf{\theta }-{\mathrm{O}}_2·\mathrm{s}\mathsf{\varphi }\right)·\frac{\mathrm{d}}{{\mathrm{I}}_{\mathrm{z}}},$$

$${\Delta }_{34}=-\frac{\mathsf{\zeta }}{\mathrm{m}}·\left({\mathrm{N}}_3·\mathrm{c}\mathsf{\varphi }·\mathrm{t}\mathsf{\theta }-{\mathrm{O}}_3·\mathrm{s}\mathsf{\varphi }\right)·\frac{\mathrm{d}}{{\mathrm{I}}_{\mathrm{z}}},$$

$${\Delta }_{44}=\frac{\mathrm{c}\mathsf{\varphi }}{\mathrm{c}\mathsf{\theta }}·\frac{\mathrm{d}}{{\mathrm{I}}_{\mathrm{z}}}.$$

It can be concluded from this that $\mathsf{\zeta }$ should be nonzero if we expect the delta matrix to be a full rank.

The next step is to find a proper invertible matrix ${\mathrm{P}}^{4\times 4}$ and ${\mathrm{Q}}^{4\times 4}$ in Equation (22). This step is designed to simplify the delta matrix to the form that we can calculate the determinant based on easily.

Notice that

$${\mathrm{P}}^{4\times 4}·\Delta \left(\overline{\mathsf{x}}\right)·{\mathrm{Q}}^{4\times 4}=\left[\begin{array}{cccc}{\mathrm{D}}_{11}& \mathrm{s}\mathsf{\psi }·\mathrm{c}\mathsf{\varphi }& \mathrm{c}\mathsf{\psi }& 0\\ {\mathrm{D}}_{21}& -\mathrm{c}\mathsf{\psi }·\mathrm{c}\mathsf{\varphi }& \mathrm{s}\mathsf{\psi }& 0\\ 0& \mathrm{s}\mathsf{\varphi }& \mathrm{s}\mathsf{\theta }& 0\\ 0& 0& 0& 1\end{array}\right]$$

(43)

where

$${\mathrm{D}}_{11}=\mathrm{c}\mathsf{\psi }·\mathrm{s}\mathsf{\theta }·\mathrm{c}\mathsf{\varphi }-\mathrm{c}\mathsf{\psi }·\mathrm{s}\mathsf{\theta }·\mathrm{s}\mathsf{\varphi }+\mathrm{s}\mathsf{\psi }·\mathrm{s}\mathsf{\varphi }+\mathrm{s}\mathsf{\psi }·\mathrm{c}\mathsf{\varphi },$$

$${\mathrm{D}}_{21}=\mathrm{s}\mathsf{\psi }·\mathrm{s}\mathsf{\theta }·\mathrm{c}\mathsf{\varphi }-\mathrm{s}\mathsf{\psi }·\mathrm{s}\mathsf{\theta }·\mathrm{s}\mathsf{\varphi }-\mathrm{c}\mathsf{\psi }·\mathrm{s}\mathsf{\varphi }-\mathrm{c}\mathsf{\psi }·\mathrm{c}\mathsf{\varphi },$$

$$\mathrm{P}={\mathrm{P}}_1·{\mathrm{P}}_2·{\mathrm{P}}_3,$$

$${\mathrm{P}}_1=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& -\mathrm{c}\mathsf{\theta }& 0\\ 0& 0& 0& 1\end{array}\right],$$

$${\mathrm{P}}_2=\left[\begin{array}{cccc}1& 0& 0& \mathrm{s}\mathsf{\varphi }·\mathrm{s}\mathsf{\psi }·\mathrm{c}\mathsf{\theta }\\ 0& 1& 0& \mathrm{s}\mathsf{\varphi }·\mathrm{s}\mathsf{\psi }·\mathrm{c}\mathsf{\theta }\\ 0& 0& 1& -\mathrm{s}\mathsf{\varphi }·\mathrm{s}\mathsf{\theta }\\ 0& 0& 0& 1\end{array}\right],$$

$${\mathrm{P}}_3=\left[\begin{array}{cccc}1& 0& 0& \frac{\mathsf{\zeta }}{\mathrm{m}}·\mathrm{c}\mathsf{\theta }\\ 0& 1& 0& \frac{\mathsf{\zeta }}{\mathrm{m}}·\mathrm{c}\mathsf{\theta }\\ 0& 0& 1& \frac{\mathsf{\zeta }}{\mathrm{m}}·\mathrm{c}\mathsf{\theta }\\ 0& 0& 0& -\frac{\mathsf{\zeta }}{\mathrm{m}}·\mathrm{c}\mathsf{\theta }\end{array}\right],$$

$$\mathrm{Q}={\mathrm{Q}}_1·{\mathrm{Q}}_2·{\mathrm{Q}}_3,$$

$${\mathrm{Q}}_1=\left[\begin{array}{cccc}-\mathrm{m}& 0& 0& 0\\ 0& -\frac{\mathrm{m}·{\mathrm{I}}_{\mathrm{x}}}{\mathsf{\zeta }·\mathrm{d}}& 0& 0\\ 0& 0& -\frac{\mathrm{m}·{\mathrm{I}}_{\mathrm{y}}}{\mathsf{\zeta }·\mathrm{d}}& 0\\ 0& 0& 0& -\frac{\mathrm{m}·{\mathrm{I}}_{\mathrm{z}}}{\mathsf{\zeta }·\mathrm{d}}\end{array}\right],$$

$${\mathrm{Q}}_2=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& -\frac{\mathrm{s}\mathsf{\varphi }}{\mathrm{c}\mathsf{\varphi }}& 1\end{array}\right],$$

$${\mathrm{Q}}_3=\left[\begin{array}{cccc}1& 0& 0& 0\\ 1& 1& 0& 0\\ 0& \frac{\mathrm{s}\mathsf{\theta }·\mathrm{s}\mathsf{\varphi }}{\mathrm{c}\mathsf{\theta }}& \frac{1}{\mathrm{c}\mathsf{\theta }}& 0\\ 0& 0& 0& \frac{1}{\mathrm{c}\mathsf{\varphi }}\end{array}\right].$$

Further,

$$\left|{\mathrm{P}}^{4\times 4}·\Delta \left(\overline{\mathsf{x}}\right)·{\mathrm{Q}}^{4\times 4}\right|=-1+{\cos }^2\mathsf{\theta }·{\cos }^2\mathsf{\varphi }-{\cos }^2\mathsf{\theta }·\cos \mathsf{\varphi }·\sin \mathsf{\varphi }.$$

(44)

Thus, $\Delta \left(\overline{\mathsf{x}}\right)$ is invertible if and only if the right side of Equation (44) is nonzero, which is exactly Equation (21). This completes the proof.

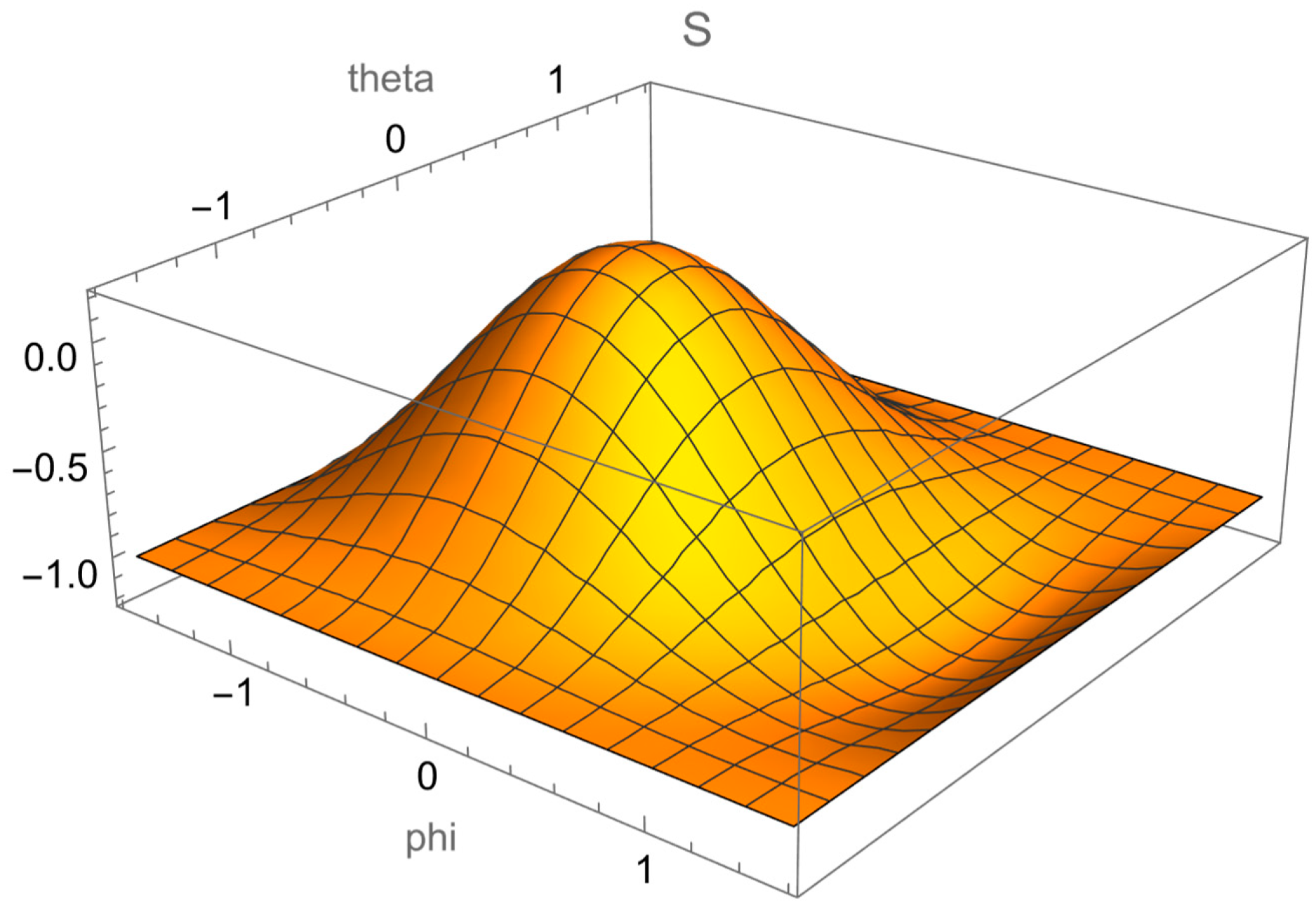
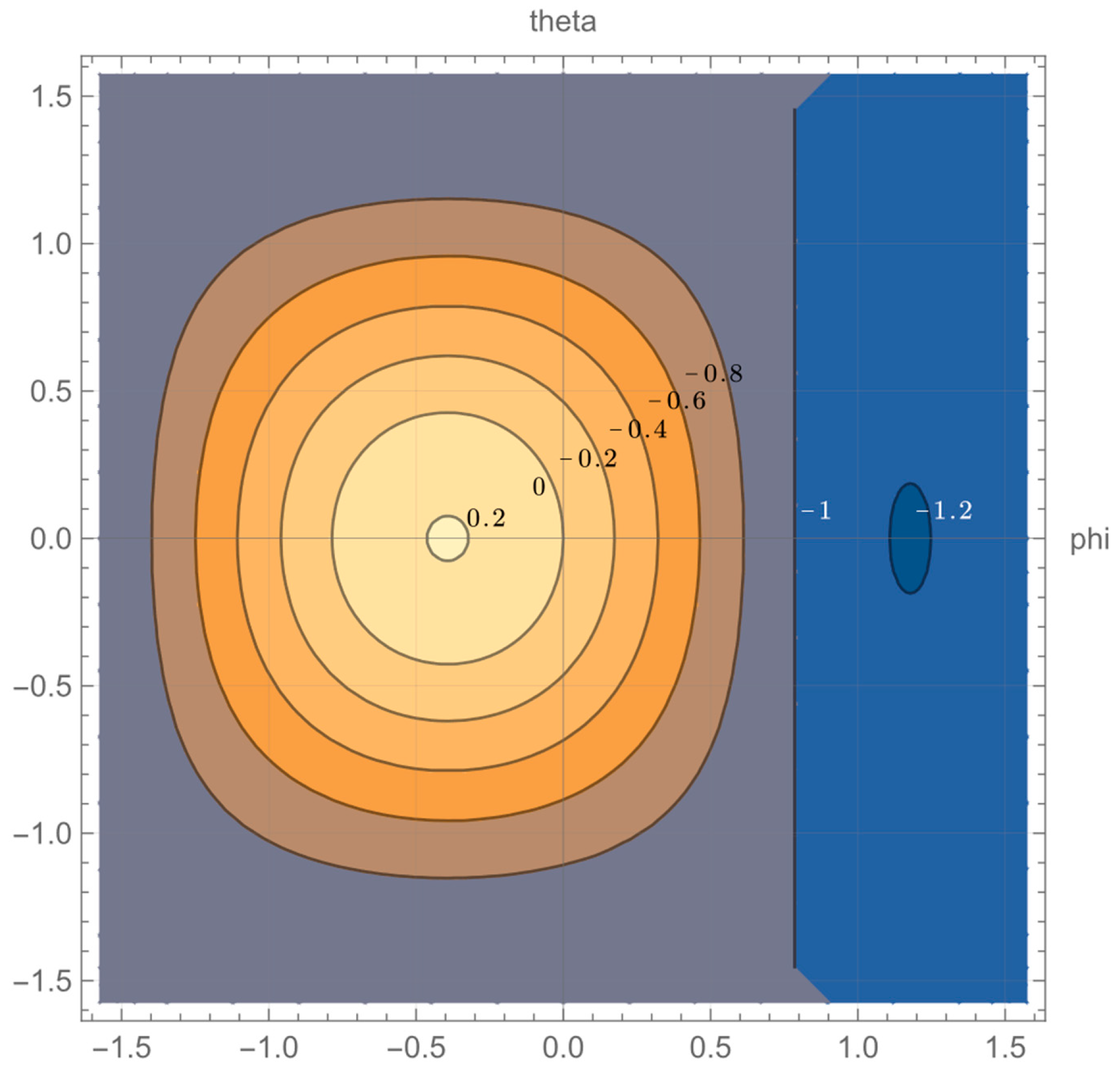
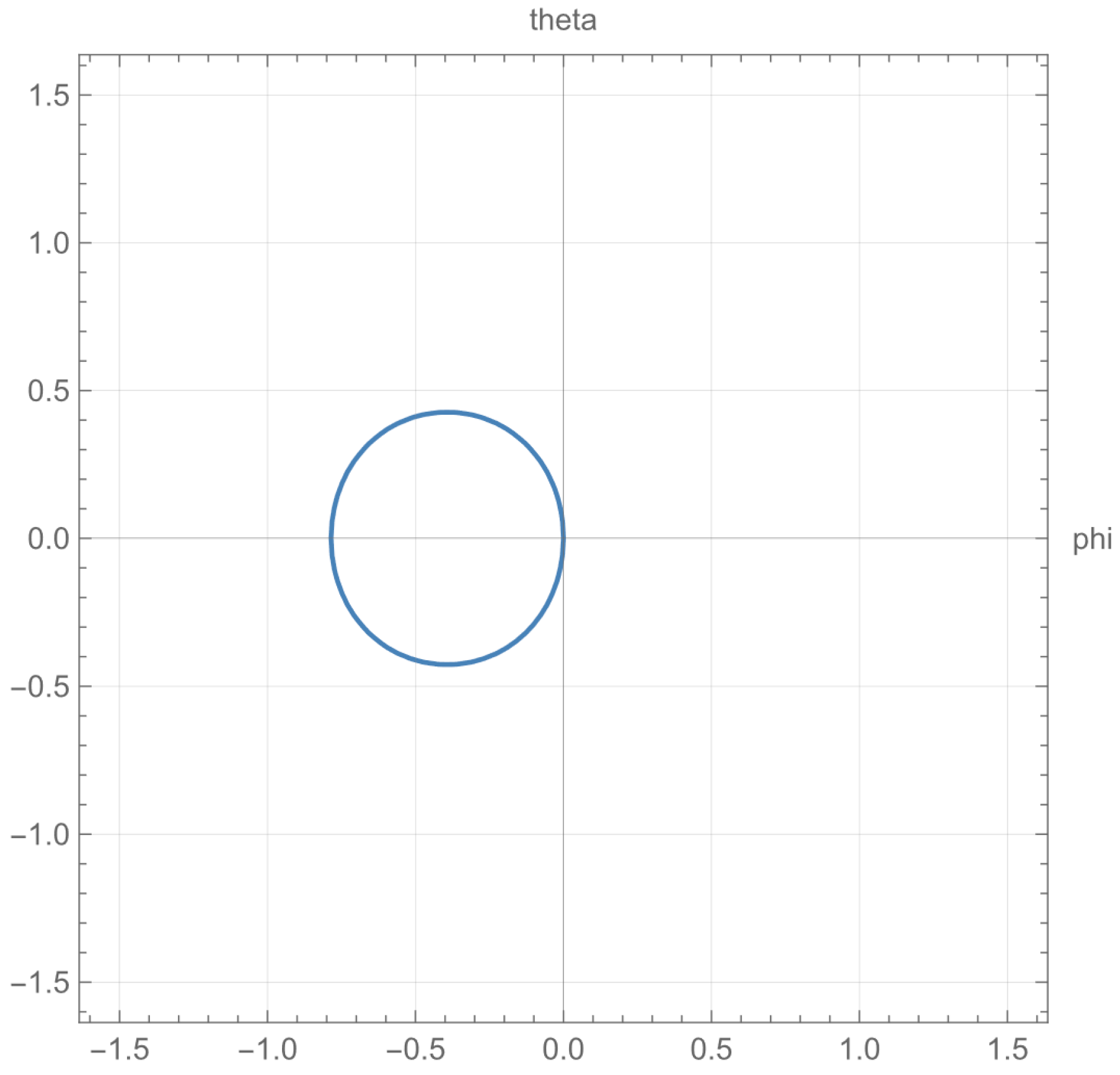
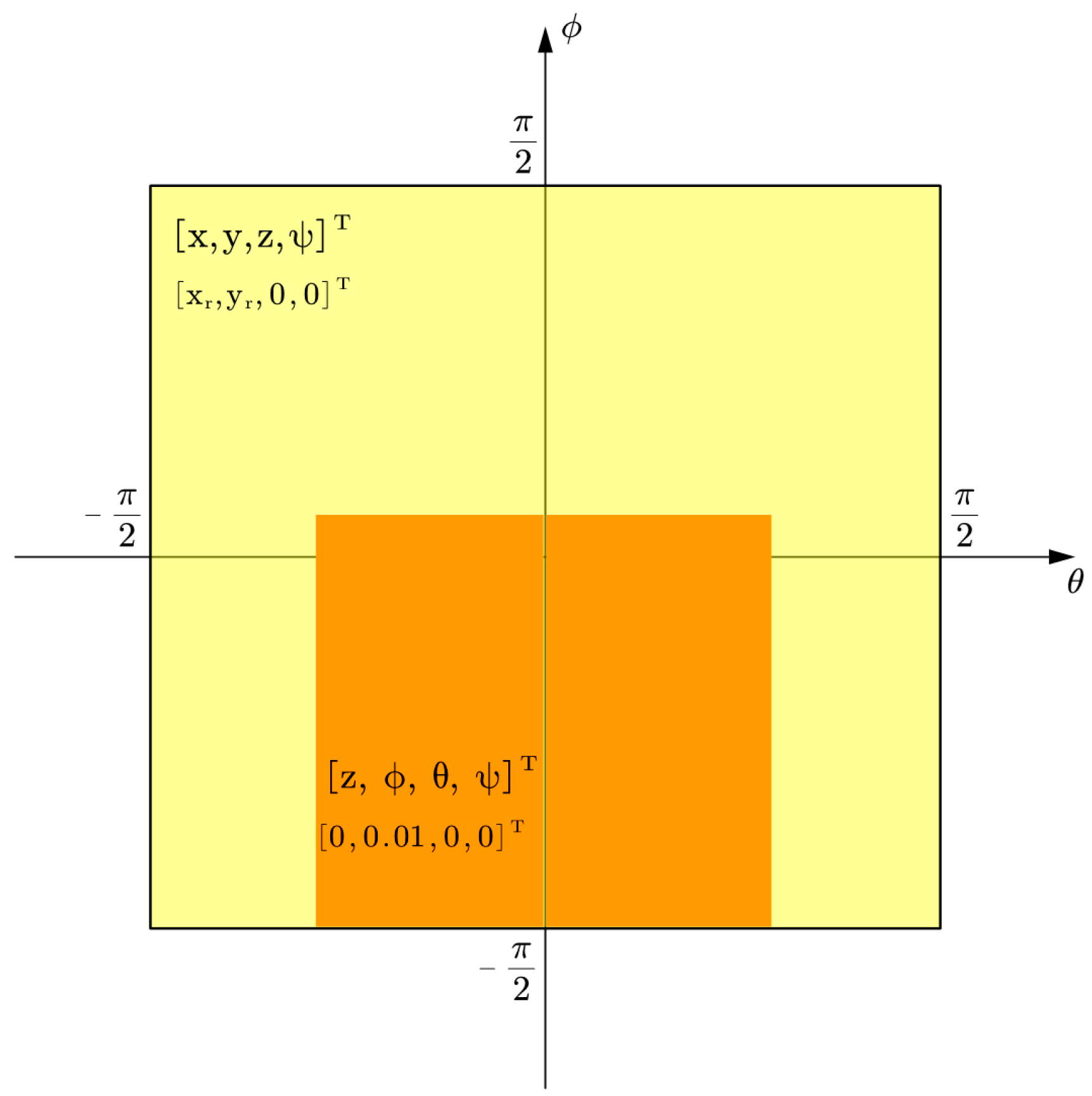
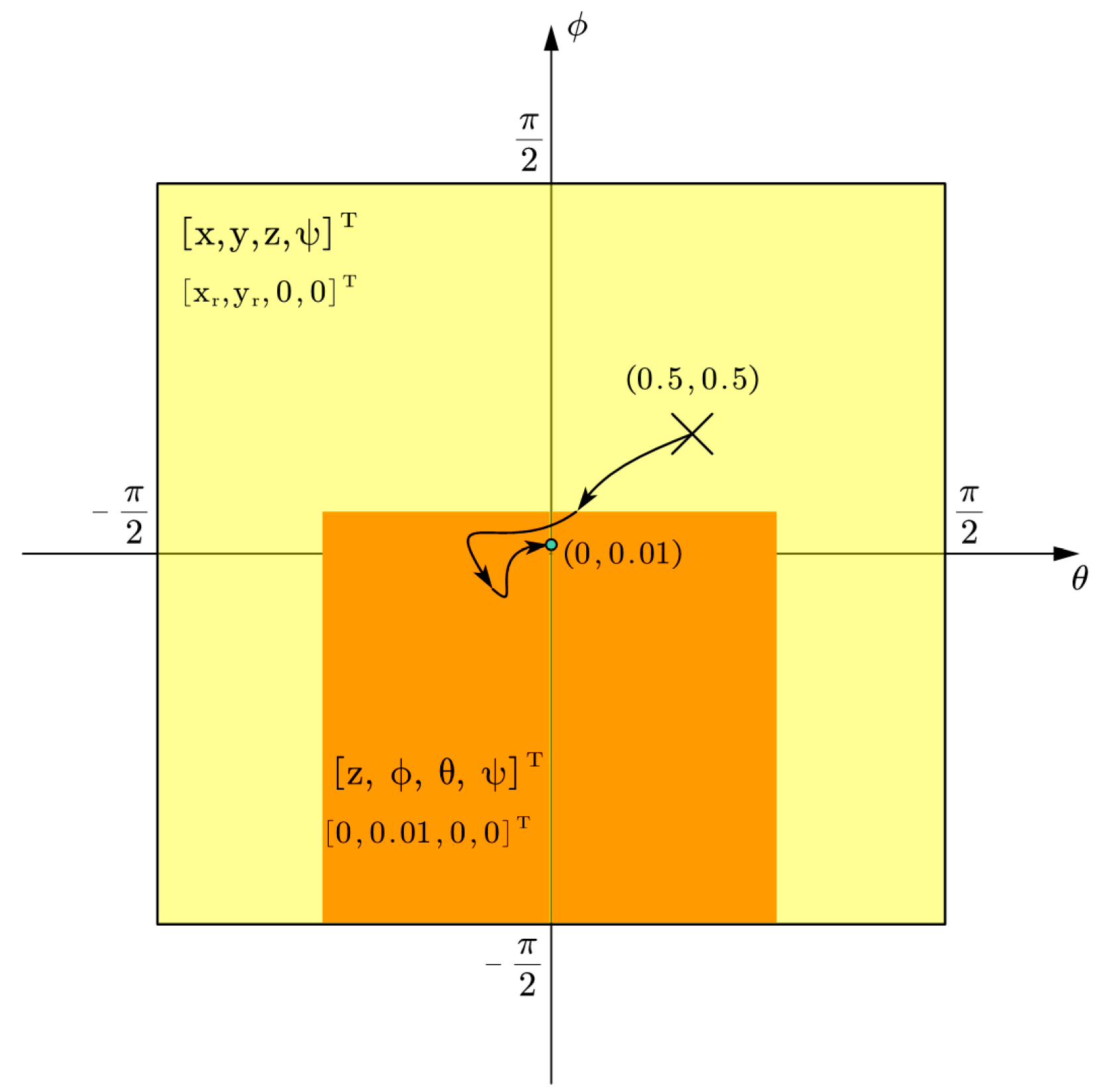
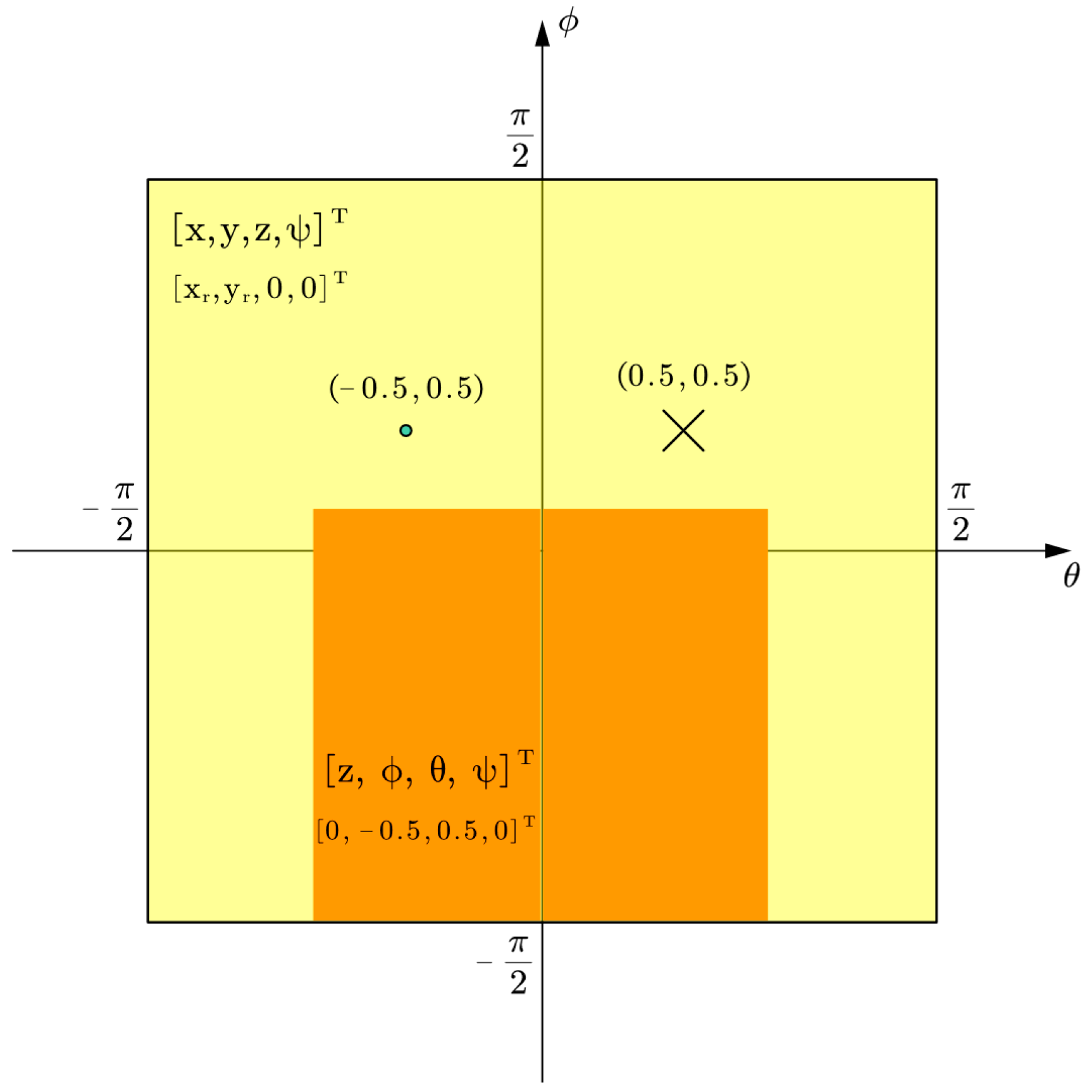
4. Visualize The Singular Zone

The singular space is determined by

$$\left|{\mathrm{P}}^{4\times 4}·\Delta \left(\overline{\mathsf{x}}\right)·{\mathrm{Q}}^{4\times 4}\right|=-1+{\cos }^2\mathsf{\theta }·{\cos }^2\mathsf{\varphi }-{\cos }^2\mathsf{\theta }·\cos \mathsf{\varphi }·\sin \mathsf{\varphi }.$$

(45)

This space is defined by $\mathsf{\varphi }\mathrm{and}\mathsf{\theta }$, which are not controlled independently; the independently controlled variables selected in Equation (19) do not include the roll and pitch. Consequently, avoiding the singular space defined in Equation (45) can be not straightforward or even not feasible for some trajectories.

We visualize the singular space by defining the “determinant surface”:

$$\mathrm{S}\left(\mathsf{\theta },\mathsf{\varphi }\right)=-1+{\cos }^2\mathsf{\theta }·{\cos }^2\mathsf{\varphi }-{\cos }^2\mathsf{\theta }·\cos \mathsf{\varphi }·\sin \mathsf{\varphi }.$$

(46)

We plot $\mathrm{S}\left(\mathsf{\theta },\mathsf{\varphi }\right)$ in Figure 1 (3D) and Figure 2 (contour plot).

Figure 3 plots the singular curve, given $\mathrm{S}\left(\mathsf{\theta },\mathsf{\varphi }\right)=0$, where the attitudes on the curve introduce the singular decoupling matrix. Clearly, there exists a singular region within the space of interest,$\mathsf{\varphi }\in \left(-\mathsf{\pi }/2,\mathsf{\pi }/2\right),\mathsf{\theta }\in \left(-\mathsf{\pi }/2,\mathsf{\pi }/2\right)$.

To avoid touching the singular curve, the quadrotor is either outside the “circular” area in Figure 3 or inside it throughout the entire flight. Crossing the “circular” area is strictly prohibited, since it causes the noninvertible problem in the decoupling matrix.

However, this requirement can be too strict, since we can find in Figure 3 that $\left(\mathsf{\theta },\mathsf{\varphi }\right)=\left(0,0\right)$ is on the singular curve, while the quadrotor is near this state during most flights or even on it, e.g., while hovering.

It is worth mentioning that this result is not influenced by changing the definition of the positive direction of the body-fixed frame; changing the positive direction of the body-fixed frame (e.g., Reference [38]) changes the signs in several rows in the delta matrix, which has no influence on the rank of a matrix.

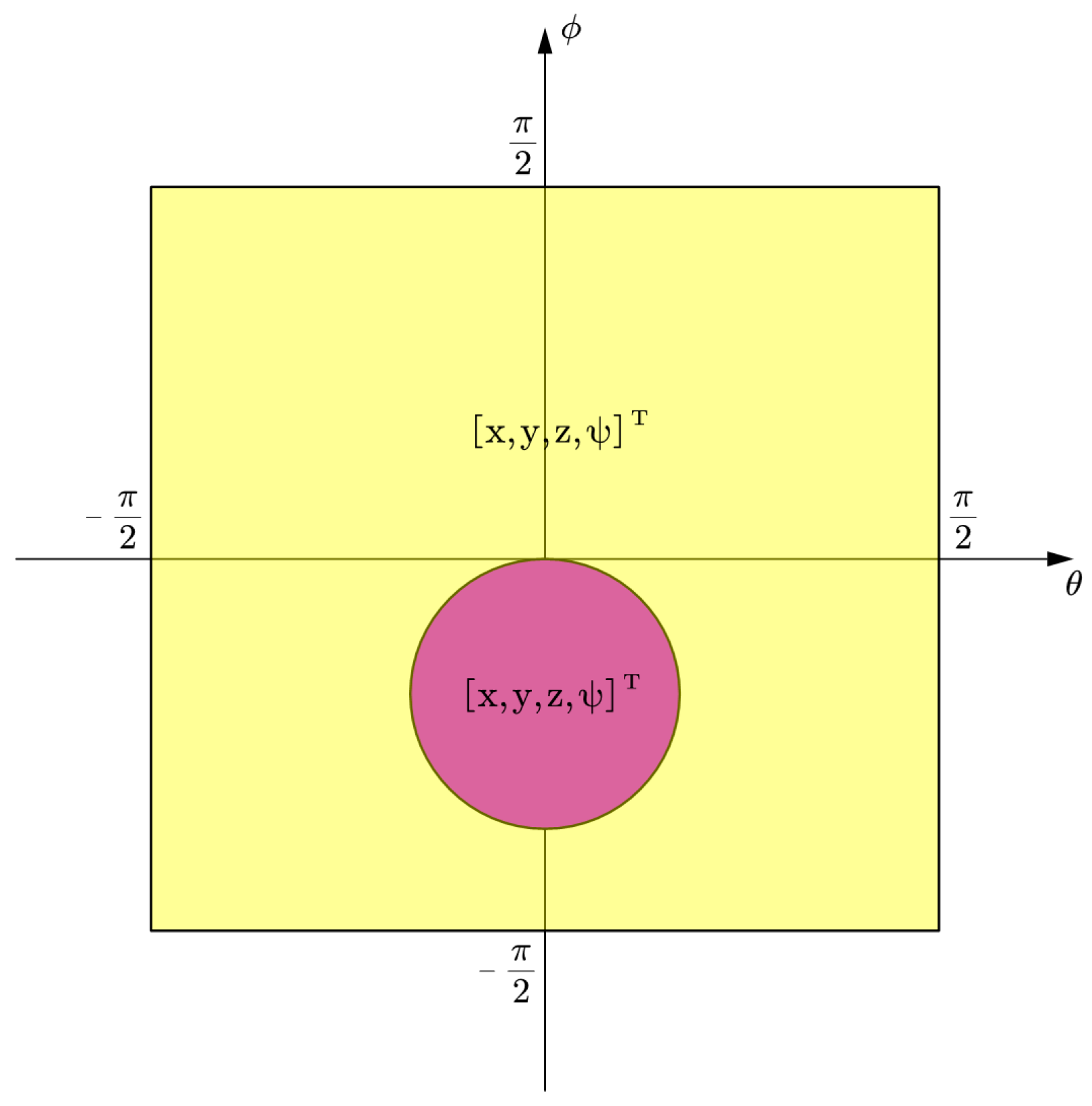
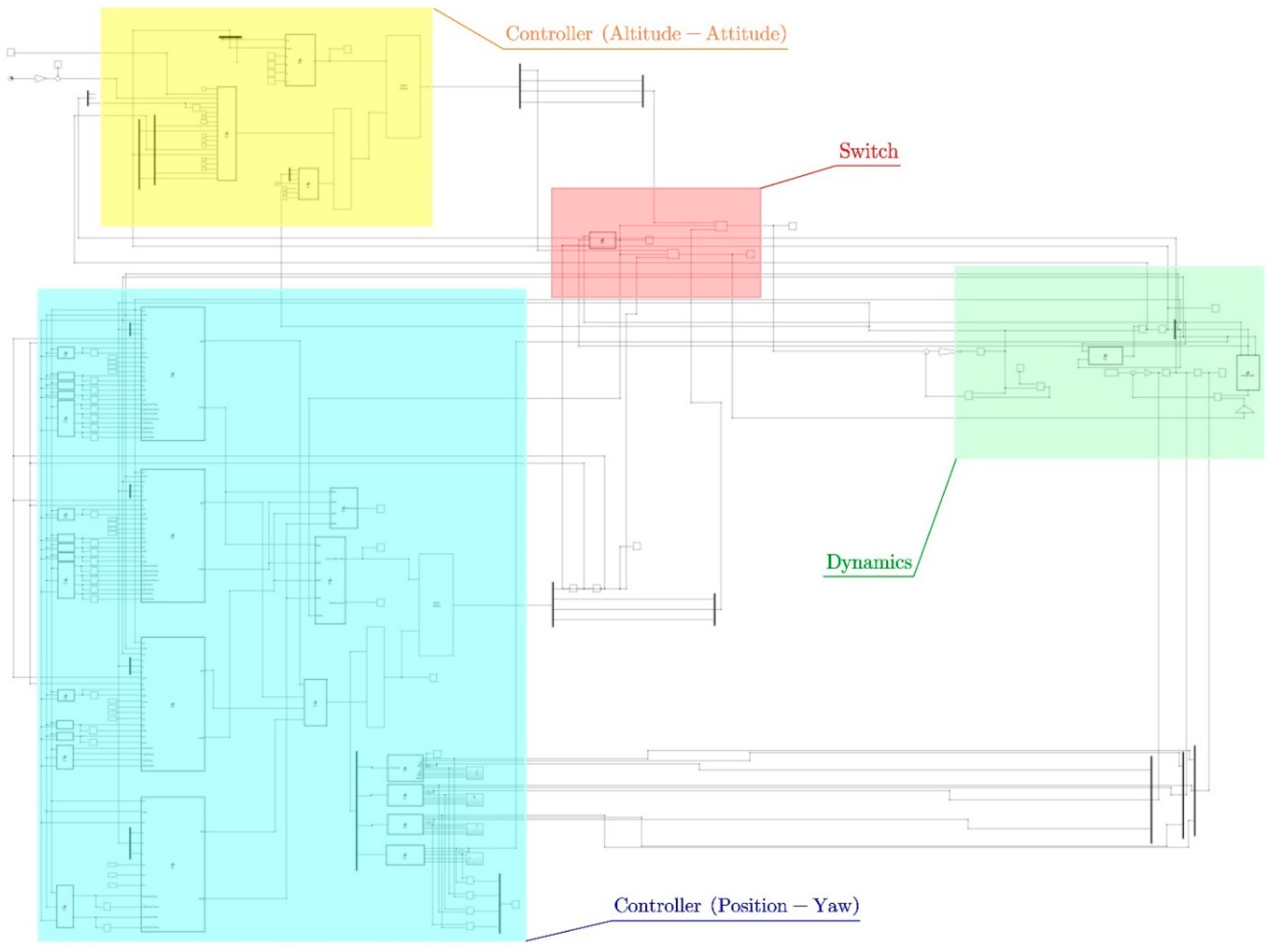
5. Switch Controller

This section puts forward an approach attempting to avoid the above singular zone by switching to another controller when the state is near the singular curve.

Though the previous analysis showed that yaw–position output-based feedback linearization introduces a singular zone, attitude–altitude output-based ($\mathsf{\varphi }$,$\mathsf{\theta }$,$\mathsf{\psi }$,$\mathrm{z}$) feedback linearization does not (see Reference [32]). Inspired by this, we replace the control rule near the singular area.

As illustrated in Figure 4, the attitude lies either within the purple zone or the yellow zone during the entire flight based on the independent output choice ($\mathrm{x},\mathrm{y},\mathrm{z},\mathsf{\psi }$). Crossing the singular curve from the yellow zone to the purple zone is prohibited and vice versa.

To avoid touching the singular curve, we change the controller in some attitudes (Figure 5). In the orange zone, we use another independent output choice ($\mathsf{\varphi },\mathsf{\theta },\mathsf{\psi },\mathrm{z}$) in the feedback linearization, while the independent output choice for the rest of the attitude area (yellow zone) remains unchanged ($\mathrm{x},\mathrm{y},\mathrm{z},\mathsf{\psi }$). Based on this, the singular curve in Figure 4 is eliminated in the entire attitude area. The attitude is allowed to change within the yellow or orange areas or to cross from one to the other.

The attitude zone where the output $\left(\mathsf{\varphi },\mathsf{\theta },\mathsf{\psi },\mathrm{z}\right)$ is chosen, the orange zone in Figure 5, is determined by

$$\{\begin{array}{c}-0.5⩽\mathsf{\theta }⩽0.5\\ -\frac{\mathsf{\pi }}{2}⩽\mathsf{\varphi }⩽0.2\end{array}.$$

(47)

The Simulink block is pictured in Figure 6, where the relevant parts are noted. The parameters of the quadrotor in the simulator are specified in Appendix A (

Table A1. The parameters of the quadrotor in the simulator.

Parameter	Value
mass	0.429 kg
gravitational acceleration	$9.8\mathrm{m}/{\mathrm{s}}^2$
length of the arm	0.1785 m
moment of inertia of the body	$\left[\begin{array}{ccc}2.237568& & \\ & 2.985236& \\ & & 4.80374\end{array}\right]·{10}^{-3}\mathrm{kg}·{\mathrm{m}}^2$
coefficient of the thrust	$8.048\times {10}^{-4}\mathrm{N}·{\mathrm{s}}^2/{\mathrm{rad}}^2$
coefficient of the drag moment	$8.048\times {10}^{-4}\mathrm{N}·\mathrm{m}·{\mathrm{s}}^2/{\mathrm{rad}}^2$

). The adopted controllers are PD controllers for both the altitude–attitude-linearized system and the position–yaw-linearized system. The design and the parameters of the PD controller are demonstrated in Appendix B.

The initial attitude (roll, pitch, and yaw) is set as: $\left({\mathsf{\varphi }}_0,{\mathsf{\theta }}_0,{\mathsf{\psi }}_0\right)=\left(0.5,0.5,0\right)$.

In the first experiment, the position reference and the attitude reference for two controllers are marked in Figure 7. The altitude–attitude reference is set as $\left({\mathrm{z}}_{\mathrm{r}},{\mathsf{\varphi }}_{\mathrm{r}},{\mathsf{\theta }}_{\mathrm{r}},{\mathsf{\psi }}_{\mathrm{r}}\right)=\left(0,0.01,0,0\right)$. The altitude reference and the yaw reference in the independent choice $\left({\mathrm{x}}_{\mathrm{r}},{\mathrm{y}}_{\mathrm{r}},{\mathrm{z}}_{\mathrm{r}},{\mathsf{\psi }}_{\mathrm{r}}\right)$ are set as ${\mathrm{z}}_{\mathrm{r}}={\mathsf{\psi }}_{\mathrm{r}}=0$, while ${\mathrm{x}}_{\mathrm{r}}$ and ${\mathrm{y}}_{\mathrm{r}}$ are specified in Appendix B.

Figure 8 sketches the results of the attitude trajectory. It can be seen that attitude ($\mathsf{\varphi },\mathsf{\theta }$) starts from $\left(0.5,0.5\right)$ under the dominance of the yaw–position controller (yellow zone). After some time, it enters the orange zone governed by the altitude–attitude controller and is captured by this zone before being stabilized at $\left(\mathsf{\varphi },\mathsf{\theta }\right)=\left(0.01,0\right)$.

In the second experiment, the attitude is expected to be stabilized at $\left({\mathsf{\varphi }}_f,{\mathsf{\theta }}_f\right)=\left(0.5,-0.5\right)$. Thus, we set the references for both controllers in Figure 9. The altitude–attitude reference is set as $\left({\mathrm{z}}_{\mathrm{r}},{\mathsf{\varphi }}_{\mathrm{r}},{\mathsf{\theta }}_{\mathrm{r}},{\mathsf{\psi }}_{\mathrm{r}}\right)=\left(0,-0.5,0.5,0\right)$. The altitude reference and the yaw reference in the independent choice $\left({\mathrm{x}}_{\mathrm{r}},{\mathrm{y}}_{\mathrm{r}},{\mathrm{z}}_{\mathrm{r}},{\mathsf{\psi }}_{\mathrm{r}}\right)$ are set as ${\mathrm{z}}_{\mathrm{r}}={\mathsf{\psi }}_{\mathrm{r}}=0$.

Figure 10 sketches the results of the attitude trajectory.

The attitude witnesses several switches in controllers before finally becoming unstable. Although the altitude–attitude control zone (orange zone) tries to let the attitude reach $\left({\mathsf{\varphi }}_{\mathrm{f}},{\mathsf{\theta }}_{\mathrm{f}}\right)=\left(0.5,-0.5\right)$, the altitude–attitude controller is switched to the yaw–position controller once the attitude escapes the orange zone. The yaw–position controller has no effect on driving the attitude roll and pitch, $\mathsf{\varphi }$ and $\mathsf{\theta }$. Thus, the attitude in the yellow zone can escape the area of interest, $\mathsf{\varphi }\in \left(-\mathsf{\pi }/2,\mathsf{\pi }/2\right),\mathsf{\theta }\in \left(-\mathsf{\pi }/2,\mathsf{\pi }/2\right)$, becoming unstable. The relevant attitude signal history is plotted in Figure 11.

6. Conclusions and Discussion

The decoupling matrix in feedback linearization is not always invertible in the entire attitude zone for the yaw–position output combination. Thus, the relevant controller risks encountering the singular decoupling matrix that causes the failure in controlling.

The attitude causing the singularity in the decoupling matrix was presented analytically and visualized in this research.

Substituting part of the yaw–position-based feedback linearization with altitude–attitude-based feedback linearization can avoid the noninvertible problem. The attitude is finally stabilized within the region governed by the altitude–attitude controller. Attempts in driving the attitude to a reference inside the region dominated by the yaw–position controller can be unstable and was not realized in this research.

Figure 12 demonstrates the statue of this work compared with other research discussing the property of the decoupling matrix in the quadrotor while implementing the exact linearization.

There are still several questions worth exploring.

Although we report the singular problem in the decoupling matrix in the yaw–position choice in the outputs, the properties of the decoupling matrices in several other combinations of independent outputs are still waiting to be uncovered by research. Actually, there are 15 (${\mathrm{C}}_6^4$) combinations in total if we pick four outputs as the independent controlled variables. The current research only explored two of them.

Moreover, the number of the combinations increase if we only pick three outputs [35] as the independent controlled variables. There could be 20 (${\mathrm{C}}_6^3$) cases in total, most of which have not been given attention yet.

Discussing the whole picture of the property of the decoupling matrix for each case is helpful for other researchers working on feedback linearization.

Further, we did not successfully stabilize the attitude in the attitude zone governed by the yaw–position controller while applying the exact feedback linearization. Designing a control method that directly avoids this singular space is also a further step.