New Supplementary Photography Methods after the Anomalous of Ground Control Points in UAV Structure-from-Motion Photogrammetry
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
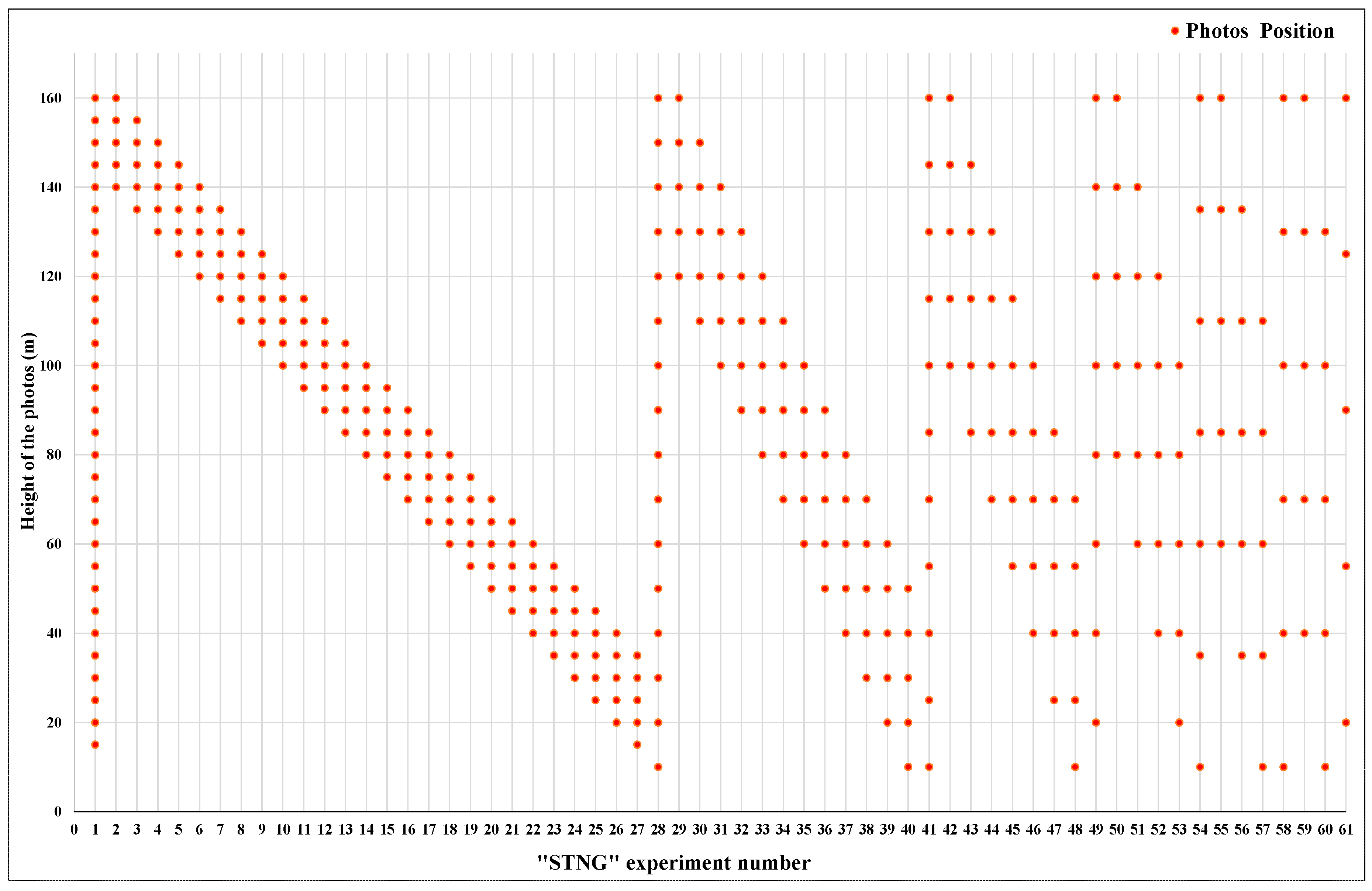
2.2. Overall Workflow
2.3. Data Collection
2.3.1. GNSS Survey
2.3.2. UAV Image Acquisition
2.4. Data Processing
2.5. Accuracy Assessment
3. Results
3.1. Accuracy Based on RMSE
3.2. Point Cloud Evaluation Based on M3C2 Distance
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Šafář, V.; Potůčková, M.; Karas, J.; Tlustý, J.; Štefanová, E.; Jančovič, M.; Cígler Žofková, D. The Use of UAV in Cadastral Mapping of the Czech Republic. ISPRS Int. J. Geo-Inf. 2021, 10, 380. [Google Scholar] [CrossRef]
- Puniach, E.; Bieda, A.; Ćwiąkała, P.; Kwartnik-Pruc, A.; Parzych, P. Use of Unmanned Aerial Vehicles (UAVs) for Updating Farmland Cadastral Data in Areas Subject to Landslides. ISPRS Int. J. Geo-Inf. 2018, 7, 331. [Google Scholar] [CrossRef] [Green Version]
- Chio, S.-H.; Chiang, C.-C. Feasibility Study Using UAV Aerial Photogrammetry for a Boundary Verification Survey of a Digitalized Cadastral Area in an Urban City of Taiwan. Remote Sens. 2020, 12, 1682. [Google Scholar] [CrossRef]
- Alexiou, S.; Deligiannakis, G.; Pallikarakis, A.; Papanikolaou, I.; Psomiadis, E.; Reicherter, K. Comparing High Accuracy t-LiDAR and UAV-SfM Derived Point Clouds for Geomorphological Change Detection. ISPRS Int. J. Geo-Inf. 2021, 10, 367. [Google Scholar] [CrossRef]
- De Marco, J.; Maset, E.; Cucchiaro, S.; Beinat, A.; Cazorzi, F. Assessing Repeatability and Reproducibility of Structure-from-Motion Photogrammetry for 3D Terrain Mapping of Riverbeds. Remote Sens. 2021, 13, 2572. [Google Scholar] [CrossRef]
- Kyriou, A.; Nikolakopoulos, K.; Koukouvelas, I. How Image Acquisition Geometry of UAV Campaigns Affects the Derived Products and Their Accuracy in Areas with Complex Geomorphology. ISPRS Int. J. Geo-Inf. 2021, 10, 408. [Google Scholar] [CrossRef]
- Bakirman, T.; Bayram, B.; Akpinar, B.; Karabulut, M.F.; Bayrak, O.C.; Yigitoglu, A.; Seker, D.Z. Implementation of Ultra-Light UAV Systems for Cultural Heritage Documentation. J. Cult. Herit. 2020, 44, 174–184. [Google Scholar] [CrossRef]
- Berrett, B.E.; Vernon, C.A.; Beckstrand, H.; Pollei, M.; Markert, K.; Franke, K.W.; Hedengren, J.D. Large-Scale Reality Modeling of a University Campus Using Combined UAV and Terrestrial Photogrammetry for Historical Preservation and Practical Use. Drones 2021, 5, 136. [Google Scholar] [CrossRef]
- Teppati Losè, L.; Chiabrando, F.; Giulio Tonolo, F. Documentation of Complex Environments Using 360° Cameras. The Santa Marta Belltower in Montanaro. Remote Sens. 2021, 13, 3633. [Google Scholar] [CrossRef]
- Fraser, B.T.; Congalton, R.G. Estimating Primary Forest Attributes and Rare Community Characteristics Using Unmanned Aerial Systems (UAS): An Enrichment of Conventional Forest Inventories. Remote Sens. 2021, 13, 2971. [Google Scholar] [CrossRef]
- Malachy, N.; Zadak, I.; Rozenstein, O. Comparing Methods to Extract Crop Height and Estimate Crop Coefficient from UAV Imagery Using Structure from Motion. Remote Sens. 2022, 14, 810. [Google Scholar] [CrossRef]
- Pagliai, A.; Ammoniaci, M.; Sarri, D.; Lisci, R.; Perria, R.; Vieri, M.; D’Arcangelo, M.E.M.; Storchi, P.; Kartsiotis, S.-P. Comparison of Aerial and Ground 3D Point Clouds for Canopy Size Assessment in Precision Viticulture. Remote Sens. 2022, 14, 1145. [Google Scholar] [CrossRef]
- Santana, L.S.; Ferraz, G.A.e.S.; Marin, D.B.; Faria, R.d.O.; Santana, M.S.; Rossi, G.; Palchetti, E. Digital Terrain Modelling by Remotely Piloted Aircraft: Optimization and Geometric Uncertainties in Precision Coffee Growing Projects. Remote Sens. 2022, 14, 911. [Google Scholar] [CrossRef]
- Albeaino, G.; Gheisari, M. Trends, benefits, and barriers of unmanned aerial systems in the construction industry: A survey study in the United States. J. Inf. Technol. Constr. 2021, 26, 84–111. [Google Scholar] [CrossRef]
- Esposito, G.; Mastrorocco, G.; Salvini, R.; Oliveti, M.; Starita, P. Application of UAV Photogrammetry for the Multi-Temporal Estimation of Surface Extent and Volumetric Excavation in the Sa Pigada Bianca Open-Pit Mine, Sardinia, Italy. Environ. Earth Sci. 2017, 76, 1–16. [Google Scholar] [CrossRef]
- Hammad, A.; da Costa, B.; Soares, C.; Haddad, A. The Use of Unmanned Aerial Vehicles for Dynamic Site Layout Planning in Large-Scale Construction Projects. Build 2021, 11, 602. [Google Scholar] [CrossRef]
- Lee, S.B.; Song, M.; Kim, S.; Won, J.-H. Change Monitoring at Expressway Infrastructure Construction Sites Using Drone. Sens. Mater. 2020, 32, 3923–3933. [Google Scholar] [CrossRef]
- Rizo-Maestre, C.; González-Avilés, Á.; Galiano-Garrigós, A.; Andújar-Montoya, M.D.; Puchol-García, J.A. UAV + BIM: Incorporation of Photogrammetric Techniques in Architectural Projects with Building Information Modeling Versus Classical Work Processes. Remote Sens. 2020, 12, 2329. [Google Scholar] [CrossRef]
- Bolkas, D. Assessment of GCP Number and Separation Distance for Small UAS Surveys with and without GNSS-PPK Positioning. J. Surv. Eng. 2019, 145, 04019007. [Google Scholar] [CrossRef]
- Hugenholtz, C.; Brown, O.; Walker, J.; Barchyn, T.; Nesbit, P.; Kucharczyk, M.; Myshak, S. Spatial Accuracy of UAV-Derived Orthoimagery and Topography: Comparing Photogrammetric Models Processed with Direct Geo-Referencing and Ground Control Points. Geomatica 2016, 70, 21–30. [Google Scholar] [CrossRef]
- Fazeli, H.; Samadzadegan, F.; Dadrasjavan, F. Evaluating the Potential of Rtk-Uav for Automatic Point Cloud Generation in 3d Rapid Mapping. ISPRS—Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B6, 221–226. [Google Scholar] [CrossRef] [Green Version]
- Forlani, G.; Dall’Asta, E.; Diotri, F.; Cella, U.M.d.; Roncella, R.; Santise, M. Quality Assessment of DSMs Produced from UAV Flights Georeferenced with On-Board RTK Positioning. Remote Sens. 2018, 10, 311. [Google Scholar] [CrossRef] [Green Version]
- Benassi, F.; Dall’Asta, E.; Diotri, F.; Forlani, G.; Morra di Cella, U.; Roncella, R.; Santise, M. Testing Accuracy and Repeatability of UAV Blocks Oriented with GNSS-Supported Aerial Triangulation. Remote Sens. 2017, 9, 172. [Google Scholar] [CrossRef] [Green Version]
- Taddia, Y.; Stecchi, F.; Pellegrinelli, A. Coastal Mapping Using DJI Phantom 4 RTK in Post-Processing Kinematic Mode. Drones 2020, 4, 9. [Google Scholar] [CrossRef] [Green Version]
- Štroner, M.; Urban, R.; Seidl, J.; Reindl, T.; Brouček, J. Photogrammetry Using UAV-Mounted GNSS RTK: Georeferencing Strategies without GCPs. Remote Sens. 2021, 13, 1336. [Google Scholar] [CrossRef]
- Teppati Losè, L.; Chiabrando, F.; Giulio Tonolo, F. Boosting the Timeliness of UAV Large Scale Mapping. Direct Georeferencing Approaches: Operational Strategies and Best Practices. ISPRS Int. J. Geo-Inf. 2020, 9, 578. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S. Mitigating systematic error in topographic models derived from UAV and ground-based image networks. Earth Surf. Processes Landf. 2014, 39, 1413–1420. [Google Scholar] [CrossRef] [Green Version]
- Oniga, V.-E.; Breaban, A.-I.; Pfeifer, N.; Chirila, C. Determining the Suitable Number of Ground Control Points for UAS Images Georeferencing by Varying Number and Spatial Distribution. Remote Sens. 2020, 12, 876. [Google Scholar] [CrossRef] [Green Version]
- Sanz-Ablanedo, E.; Chandler, J.; Rodríguez-Pérez, J.; Ordóñez, C. Accuracy of Unmanned Aerial Vehicle (UAV) and SfM Photogrammetry Survey as a Function of the Number and Location of Ground Control Points Used. Remote Sens. 2018, 10, 1606. [Google Scholar] [CrossRef] [Green Version]
- Ferrer-González, E.; Agüera-Vega, F.; Carvajal-Ramírez, F.; Martínez-Carricondo, P. UAV Photogrammetry Accuracy Assessment for Corridor Mapping Based on the Number and Distribution of Ground Control Points. Remote Sens. 2020, 12, 2447. [Google Scholar] [CrossRef]
- Liu, X.; Lian, X.; Yang, W.; Wang, F.; Han, Y.; Zhang, Y. Accuracy Assessment of a UAV Direct Georeferencing Method and Impact of the Configuration of Ground Control Points. Drones 2022, 6, 30. [Google Scholar] [CrossRef]
- Ulvi, A. The Effect of the Distribution and Numbers of Ground Control Points on the Precision of Producing Orthophoto Maps with an Unmanned Aerial Vehicle. J. Asian Archit. Build. Eng. 2021, 20, 806–817. [Google Scholar] [CrossRef]
- Boon, M.A.; Drijfhout, A.P.; Tesfamichael, S. Comparison of a Fixed-Wing and Multi-Rotor Uav for Environmental Mapping Applications: A Case Study. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, XLII-2/W6, 47–54. [Google Scholar] [CrossRef] [Green Version]
- Reshetyuk, Y.; Mårtensson, S.-G. Generation of Highly Accurate Digital Elevation Models with Unmanned Aerial Vehicles. Photogramm. Rec. 2016, 31, 143–165. [Google Scholar] [CrossRef]
- Context Capture 4.4.10. Available online: https://www.bentley.com/en/products/brands/contextcapture (accessed on 19 February 2022).
- Forsmoo, J.; Anderson, K.; Macleod, C.J.; Wilkinson, M.E.; DeBell, L.; Brazier, R.E. Structure from Motion Photogrammetry in Ecology: Does the Choice of Software Matter? Ecol. Evol. 2019, 9, 12964–12979. [Google Scholar] [CrossRef] [PubMed]
- Manyoky, M.; Theiler, P.; Steudler, D.; Eisenbeiss, H. Unmanned Aerial Vehicle in Cadastral Applications. The International Archives of the Photogrammetry. Remote Sens. Spat. Inf. Sci. 2012, XXXVIII-1/C22, 57–62. [Google Scholar] [CrossRef] [Green Version]
- Agüera-Vega, F.; Carvajal-Ramírez, F.; Martínez-Carricondo, P. Assessment of Photogrammetric Mapping Accuracy Based on Variation Ground Control Points Number Using Unmanned Aerial Vehicle. Measurement 2017, 98, 221–227. [Google Scholar] [CrossRef]
- Rabah, M.; Basiouny, M.; Ghanem, E.; Elhadary, A. Using RTK and VRS in Direct Geo-Referencing of the UAV Imagery. NRIAG J. Astron. Geophys. 2019, 7, 220–226. [Google Scholar] [CrossRef] [Green Version]
- Gerke, M.; Przybilla, H.J. Accuracy Analysis of Photogrammetric UAV Image Blocks: Influence of Onboard RTK-GNSS and Cross Flight Patterns. Photogramm. Fernerkund. Geoinf. (PFG) 2016, 1, 17–30. [Google Scholar] [CrossRef] [Green Version]
- Lalak, M.; Wierzbicki, D.; Kędzierski, M. Methodology of Processing Single-Strip Blocks of Imagery with Reduction and Optimization Number of Ground Control Points in UAV Photogrammetry. Remote Sens. 2020, 12, 3336. [Google Scholar] [CrossRef]
- CloudCompare v2.12. Available online: https://www.danielgm.net/cc/ (accessed on 19 February 2022).
- DiFrancesco, P.-M.; Bonneau, D.; Hutchinson, D.J. The Implications of M3C2 Projection Diameter on 3D Semi-Automated Rockfall Extraction from Sequential Terrestrial Laser Scanning Point Clouds. Remote Sens. 2020, 12, 1885. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S.; Smith, M.W. 3-D Uncertainty-Based Topographic Change Detection with Structure-From-Motion Photogrammetry: Precision Maps for Ground Control and Directly Georeferenced Surveys. Earth Surf. Processes Landf. 2017, 42, 1769–1788. [Google Scholar] [CrossRef]
- Rangel, J.M.G.; Gonçalves, G.R.; Pérez, J.A. The Impact of Number and Spatial Distribution of GCPs on the Positional Accuracy of Geospatial Products Derived from Low-Cost UASs. Int. J. Remote Sens. 2018, 39, 7154–7171. [Google Scholar] [CrossRef]
- Martínez-Carricondo, P.; Agüera-Vega, F.; Carvajal-Ramírez, F.; Mesas-Carrascosa, F.-J.; García-Ferrer, A.; Pérez-Porras, F.-J. Assessment of UAV-Photogrammetric Mapping Accuracy Based on Variation of Ground Control Points. Int. J. Appl. Earth Obs. Geoinf. 2018, 72, 1–10. [Google Scholar] [CrossRef]
- Mesas-Carrascosa, F.J.; Notario Garcia, M.D.; Merono de Larriva, J.E.; Garcia-Ferrer, A. An Analysis of the Influence of Flight Parameters in the Generation of Unmanned Aerial Vehicle (UAV) Orthomosaicks to Survey Archaeological Areas. Sensors 2016, 16, 1838. [Google Scholar] [CrossRef] [Green Version]
- Quoc Long, N.; Goyal, R.; Khac Luyen, B.; Van Canh, L.; Xuan Cuong, C.; Van Chung, P.; Ngoc Quy, B.; Bui, X.-N. Influence of Flight Height on The Accuracy of UAV Derived Digital Elevation Model at Complex Terrain. Inżynieria Miner. 2020, 1, 179–186. [Google Scholar] [CrossRef]
- Casella, V.; Chiabrando, F.; Franzini, M.; Manzino, A.M. Accuracy Assessment of a UAV Block by Different Software Packages, Processing Schemes and Validation Strategies. ISPRS Int. J. Geo-Inf. 2020, 9, 164. [Google Scholar] [CrossRef] [Green Version]
- Wackrow, R.; Chandler, J.H. Minimising Systematic Error Surfaces in Digital Elevation Models Using Oblique Convergent Imagery. Photogramm. Rec. 2011, 26, 16–31. [Google Scholar] [CrossRef] [Green Version]
- Bi, R.; Gan, S.; Yuan, X.; Li, R.; Gao, S.; Luo, W.; Hu, L. Studies on Three-Dimensional (3D) Accuracy Optimization and Repeatability of UAV in Complex Pit-Rim Landforms as Assisted by Oblique Imaging and RTK Positioning. Sensors 2021, 21, 8109. [Google Scholar] [CrossRef]
- Harwin, S.; Lucieer, A.; Osborn, J. The Impact of the Calibration Method on the Accuracy of Point Clouds Derived Using Unmanned Aerial Vehicle Multi-View Stereopsis. Remote Sens. 2015, 7, 11933–11953. [Google Scholar] [CrossRef] [Green Version]
- Sanz-Ablanedo, E.; Chandler, J.H.; Ballesteros-Pérez, P.; Rodríguez-Pérez, J.R. Reducing systematic dome errors in digital elevation models through better UAV flight design. Earth Surf. Processes Landf. 2020, 45, 2134–2147. [Google Scholar] [CrossRef]
- DJI Phantom 4 Pro. Available online: https://www.dji.com/phantom-4-pro/info#specs (accessed on 19 February 2022).














| Project | Max. Flight Altitude (m) | Radius (m) | Camera Oblique Angle β (°) | Heading Angle Interval α (°) | Number of Images |
|---|---|---|---|---|---|
| Flight 1 | 160 | 20 | 78 | 20 | 18 |
| Flight 2 | 140 | 20 | 77 | 20 | 18 |
| Flight 3 | 180 | 20 | 83 | 20 | 18 |
| Experiment Name | Description of the Method | Number of GCPs and CPs |
|---|---|---|
| Group I | Use “STNG” | 5 GCPs + 19 CPs |
| Group II | Oblique and circle | 5 GCPs + 19 CPs |
| Natural feature point (NFP) | Natural feature point used as GCP (replace K2 Point) | 5 GCPs (include 1 NFP) + 19 CPs |
| 4 GCPs | Lose K2 Point | 4 GCPs + 19 CPs |
| 5 GCPs | All GCPs are normal | 5 GCPs + 19 CPs |
| Aero Triangulation Setting | Value |
|---|---|
| Positioning mode | Use control points for adjustment |
| Key point density | Normal |
| Pair selection mode | Default |
| Component construction mode | OnePass |
| Tie points | Compute |
| Position | Compute |
| Rotation | Compute |
| Photogroup estimation mode | MultiPass |
| Focal length | Adjust |
| Principal point | Adjust |
| Radial distortion | Adjust |
| Tangential distortion | Adjust |
| Aspect ratio | Keep |
| Skew | Keep |
| Experiment | RMSEX (mm) | RMSEY (mm) | RMSEZ (mm) |
|---|---|---|---|
| II_140m_20° (18) | 70.70 | 51.80 | 77.90 |
| II_140m_60° (6) | 70.60 | 52.10 | 75.00 |
| II_160m_20° (18) | 71.10 | 51.10 | 87.30 |
| II_160m_60° (6) | 71.30 | 50.70 | 83.00 |
| II_180m_20° (18) | 70.80 | 50.80 | 74.30 |
| II_180m_60° (6) | 70.30 | 53.20 | 84.20 |
| Experiment | RMSEX (mm) | RMSEY (mm) | RMSEZ (mm) |
|---|---|---|---|
| II_140m_60° (6) | 70.60 | 52.10 | 75.00 |
| II_140m_20° (6) | 71.00 | 51.90 | 79.80 |
| II_140m_40° (6) | 70.50 | 52.50 | 86.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Li, X.; Luo, L.; Zhao, L.; Wei, J.; Ma, T. New Supplementary Photography Methods after the Anomalous of Ground Control Points in UAV Structure-from-Motion Photogrammetry. Drones 2022, 6, 105. https://doi.org/10.3390/drones6050105
Yang J, Li X, Luo L, Zhao L, Wei J, Ma T. New Supplementary Photography Methods after the Anomalous of Ground Control Points in UAV Structure-from-Motion Photogrammetry. Drones. 2022; 6(5):105. https://doi.org/10.3390/drones6050105
Chicago/Turabian StyleYang, Jia, Xiaopeng Li, Lei Luo, Lewen Zhao, Juan Wei, and Teng Ma. 2022. "New Supplementary Photography Methods after the Anomalous of Ground Control Points in UAV Structure-from-Motion Photogrammetry" Drones 6, no. 5: 105. https://doi.org/10.3390/drones6050105
APA StyleYang, J., Li, X., Luo, L., Zhao, L., Wei, J., & Ma, T. (2022). New Supplementary Photography Methods after the Anomalous of Ground Control Points in UAV Structure-from-Motion Photogrammetry. Drones, 6(5), 105. https://doi.org/10.3390/drones6050105






