A Wind-Tunnel Assessment of Parameters That May Impact Spray Drift during UAV Pesticide Application
Abstract
:1. Introduction
2. Materials and Methods
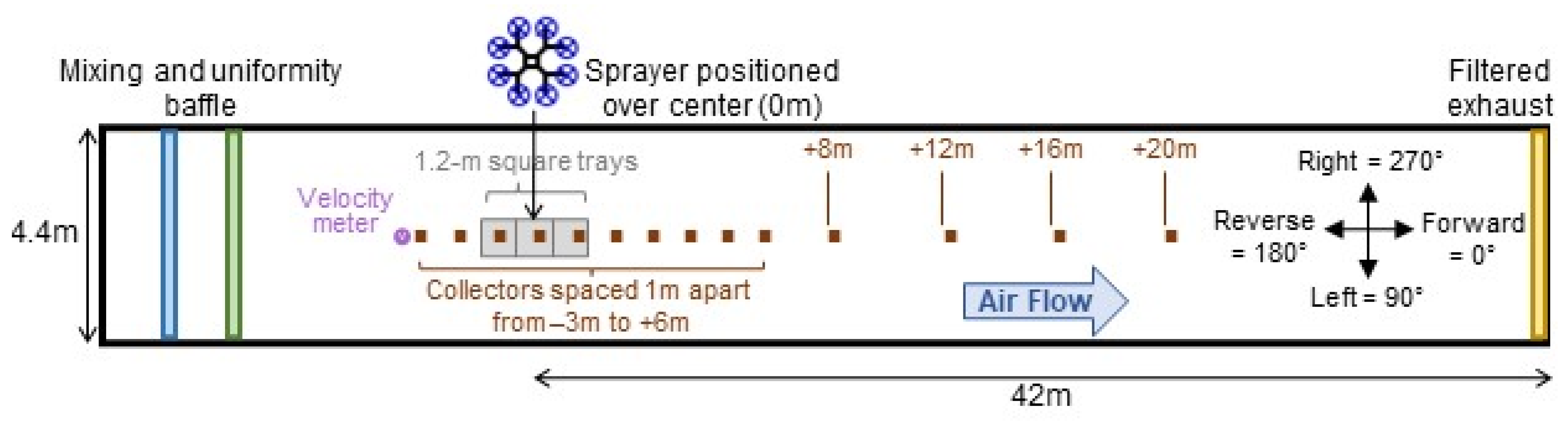
2.1. Wind Tunnel and UAV Setup
2.2. Study Design
2.3. Experimental Setup and Procedure
2.4. Sample Analysis
2.5. Nozzle Characterization
2.6. Meteorological Measurements
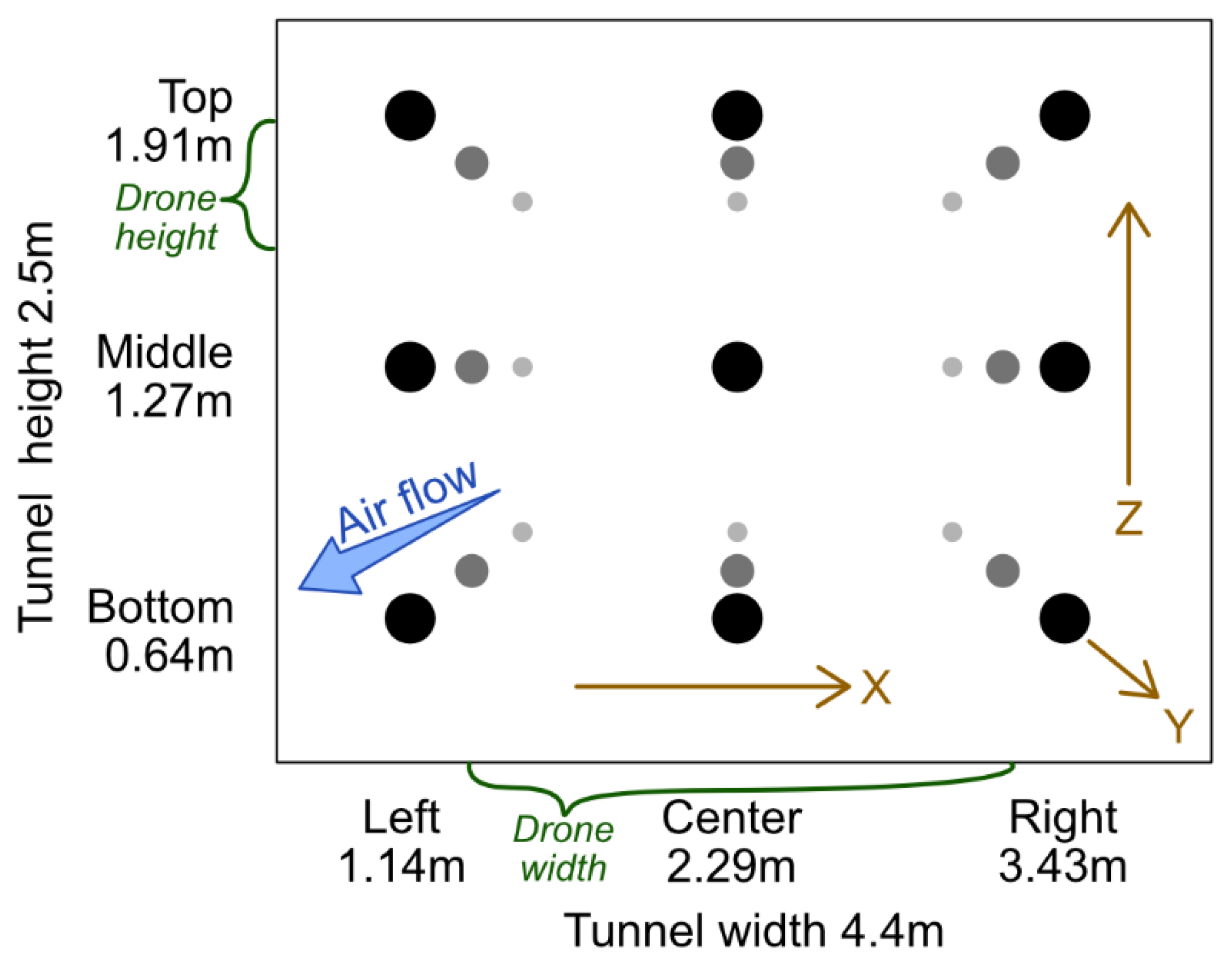
2.7. 3D Anemometer Measurement on a Grid across Tunnel
2.8. Statistical Analysis of Downwind Deposition
3. Results
3.1. Nozzle Characterization
3.2. Meteorological Data Summary
3.3. Upwind and In-Swath Deposition
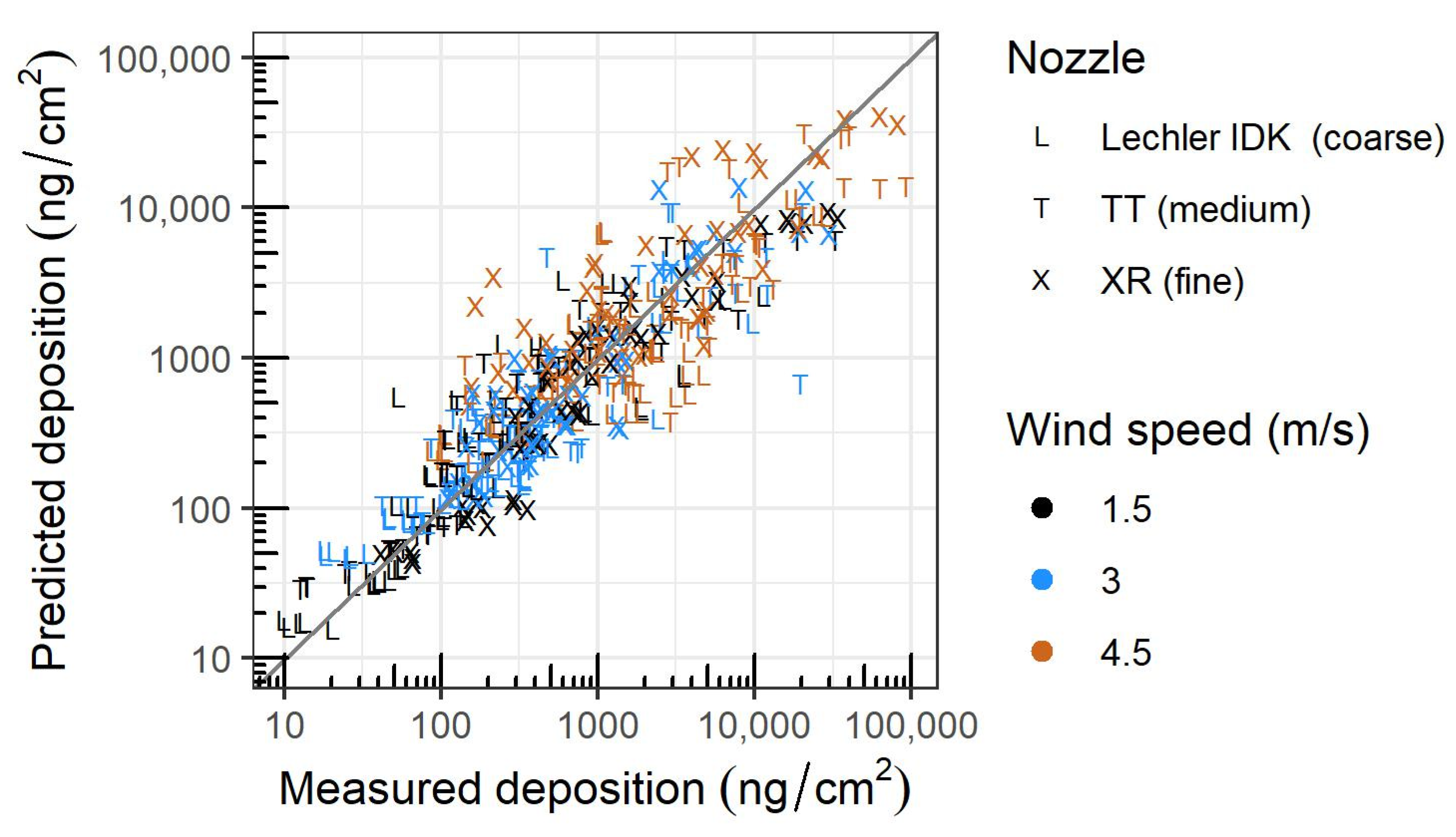
3.4. Downwind Deposition
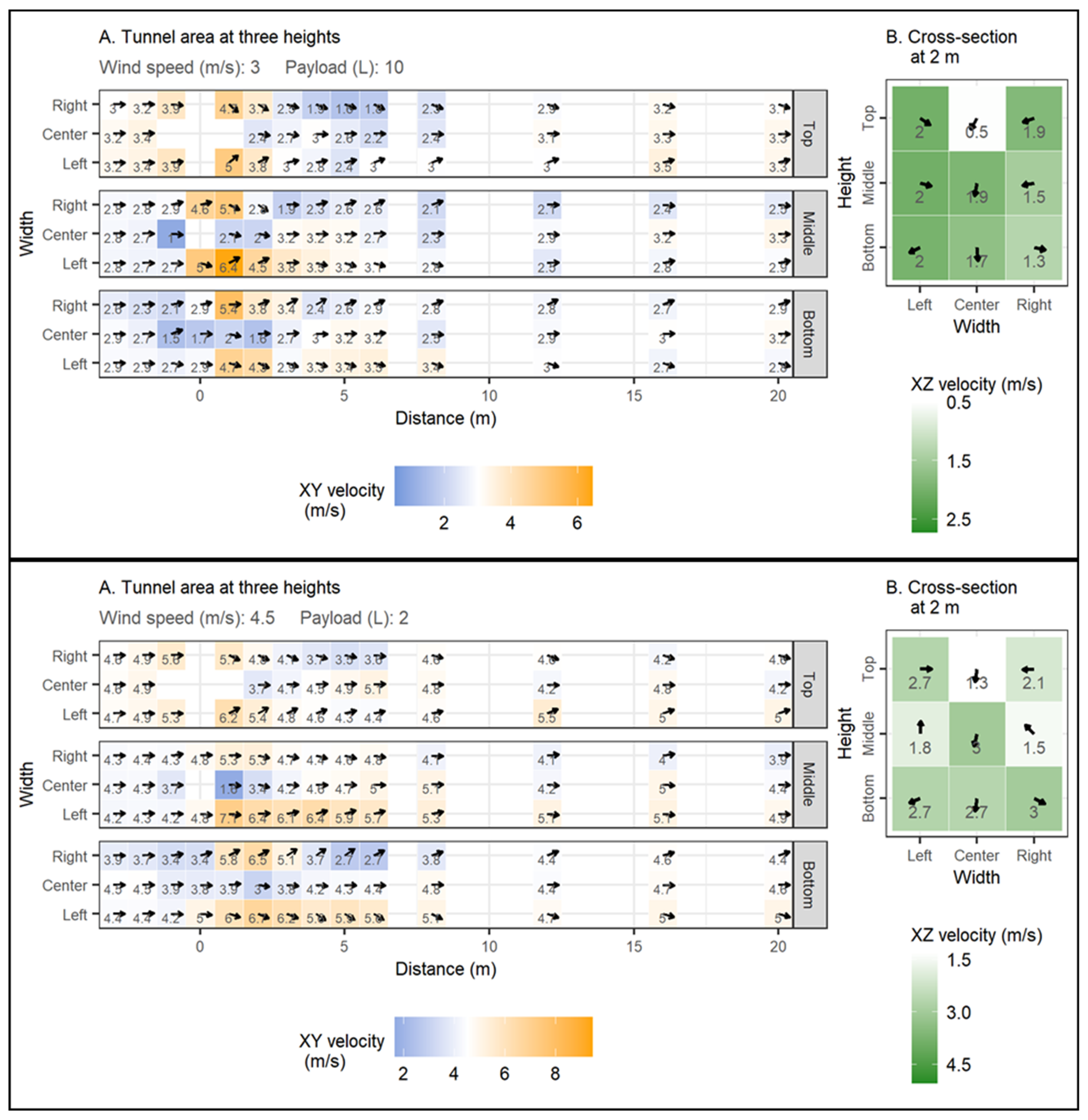
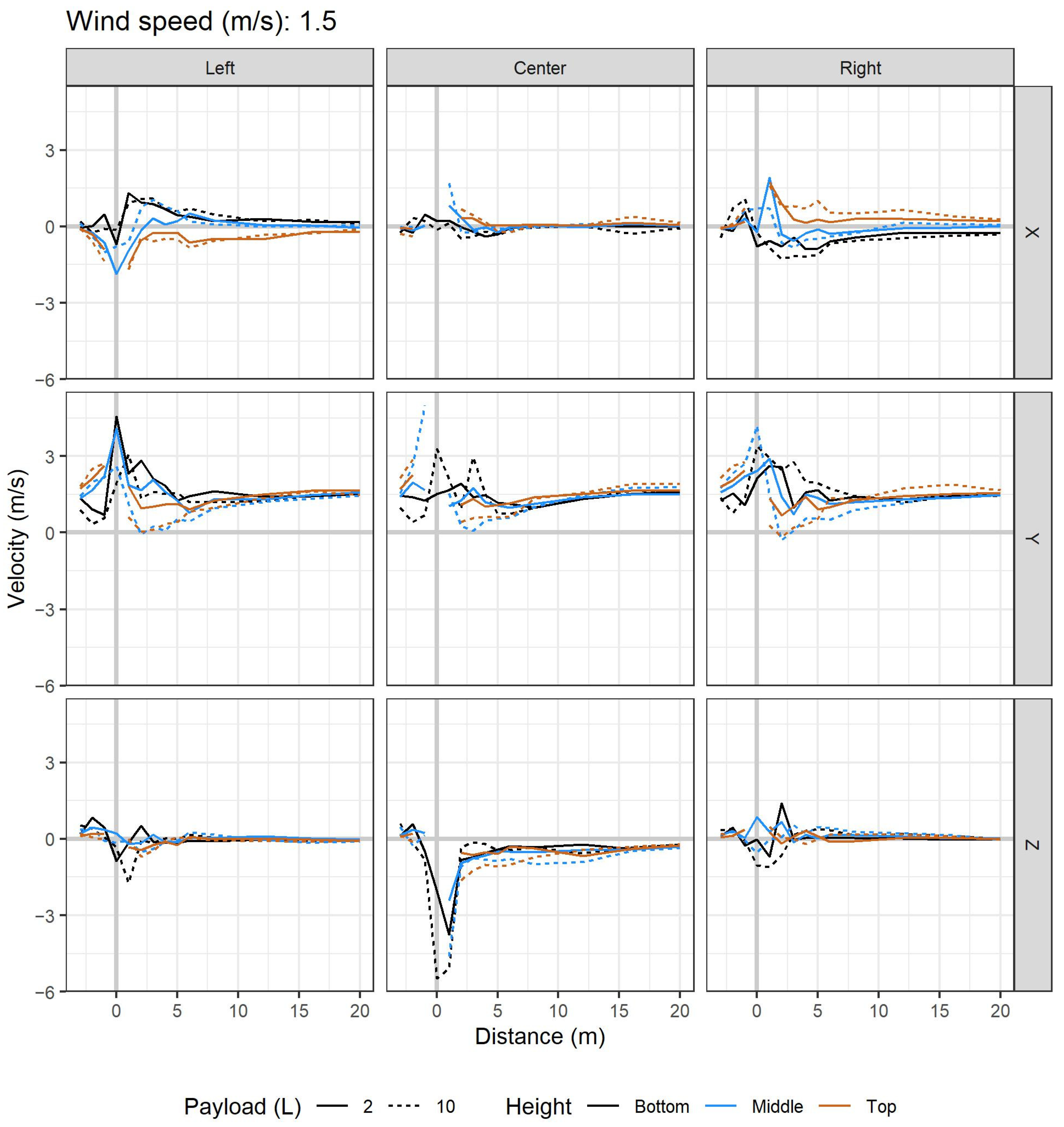
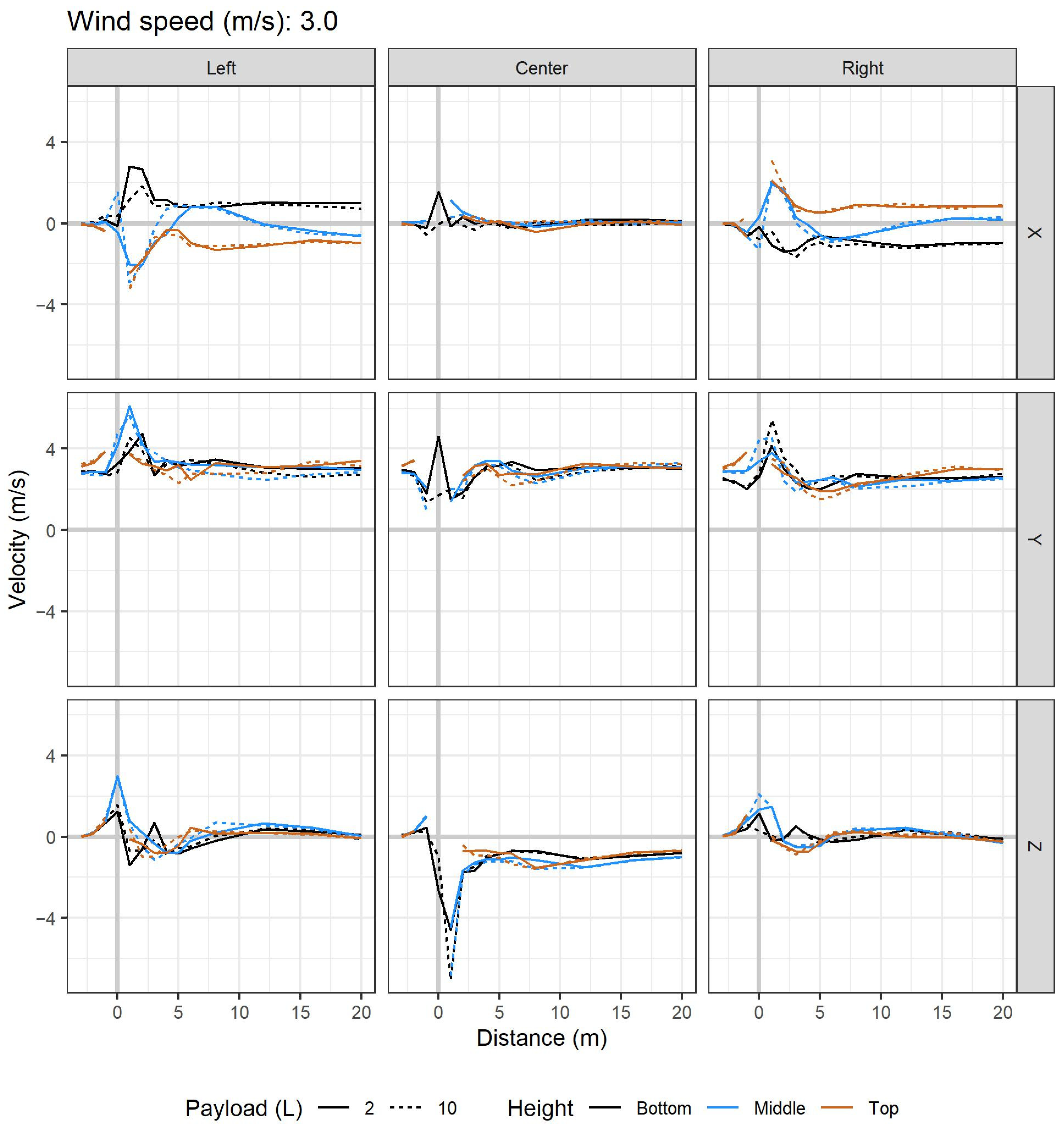
3.5. Wind Direction and Airflow Variability
4. Discussion
4.1. Payload
4.2. 3D Anemometer Data
4.3. Offset vs. Drift
4.4. Aberrations Observed from Operating a UAV in a Wind Tunnel
5. Conclusions
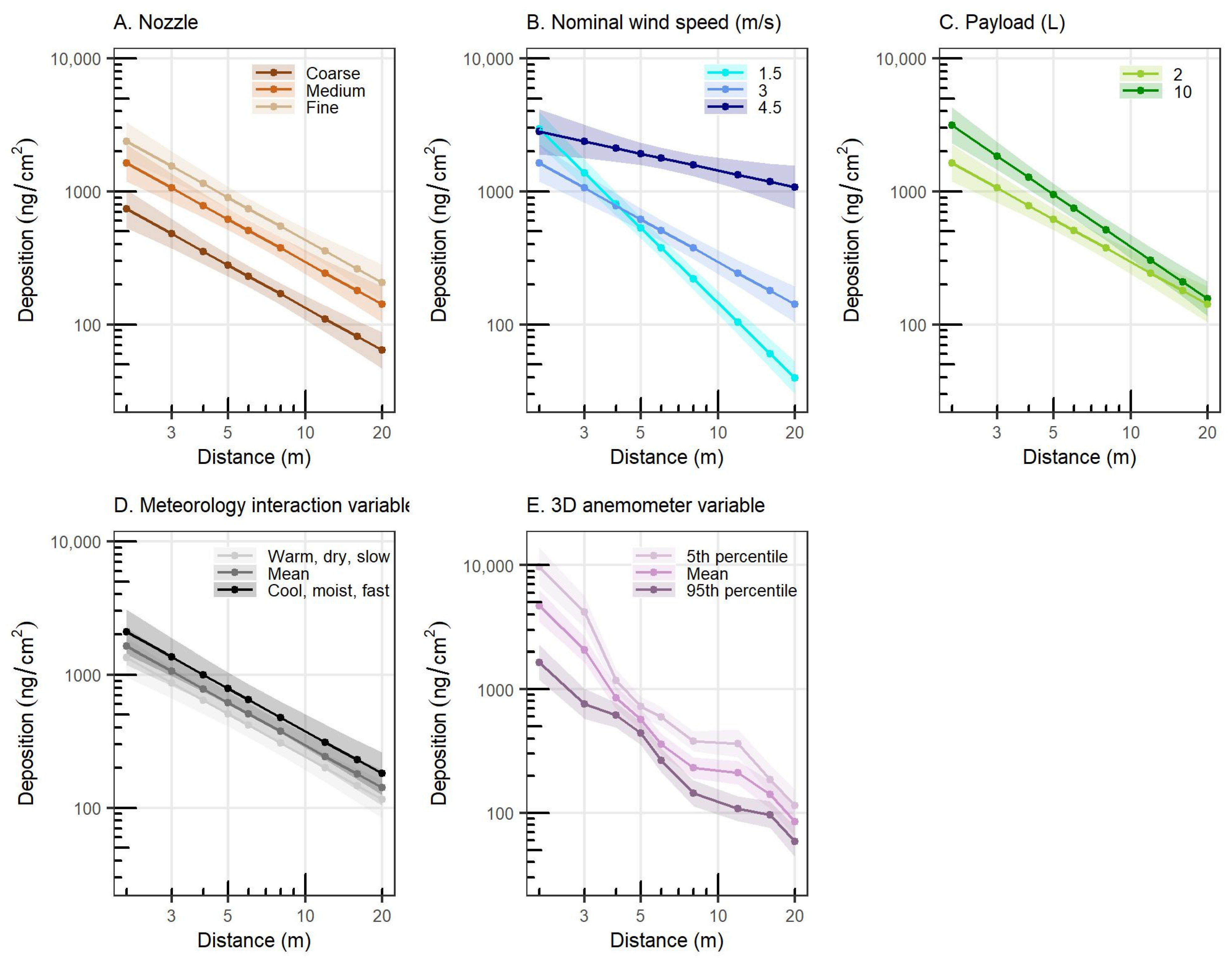
- A multiple linear regression of the three experimental variables and the wind tunnel environmental and wind conditions explained 80% (adjusted R2) of the variability in downwind deposition behavior in the experiment. Among the variables tested, wind speed had the greatest influence on downwind deposition, such that 4.5 m/s produced the most deposition. Drift was more similar between 3.0 and 1.5 m/s but was consistently greater at 3.0 m/s at most distances.
- The nozzle that produced coarse spray droplet sizes resulted in the least downwind drift deposition, and the fine nozzle resulted in the most.
- In general, in-swath deposition was highest when the UAV operated in the 1.5 and 3.0 m/s wind speeds for the coarse and medium nozzles. At the highest wind speed tested and for the fine spray droplets, the swath is displaced in the downwind direction by up to 2 m.
- The experimental result also showed that while there is a statistically significant difference in downwind deposition when starting with a 10 L or 2 L initial payload volumes, the effect is most notable at distances closer to the UAV. This effect is likely due to the difference in downwash forces generated by the UAV operating in the bespoke experimental conditions.
- These experiments allow for the development of optimized operating conditions that limit off-target movement of spray droplets for UAVs as variables such as wind speed can be isolated and controlled.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Location | Wind Speed (m/s) | Turbulence (%) | Variability |
|---|---|---|---|
| Boom | 4.47 | 5.59 | 5.23 |
| Boom | 2.91 | 5.65 | 5.82 |
| Boom | 1.39 | 5.75 | 5.19 |
| 18 m (~60 ft) downwind | 4.78 | 3.70 | 5.53 |
| 36 m (~120 ft) downwind | 4.73 | 3.63 | 4.26 |
| Components | Mass (kg) |
|---|---|
| UAV only (tank empty, no battery) | 10.85 |
| UAV + battery (tank empty) | 14.96 |
| UAV + battery at 2 L tank fill | 16.72 |
| UAV + battery at 10 L tank fill | 24.77 |


| Conversion Step | Formula |
|---|---|
| Convert degrees to radians | Used R package NISTunits [42] |
| Convert radians to X dimension, and take mean of all measurements within 60 s | |
| Convert radians to Y dimension, and take mean of all measurements within 60 s | |
| Back-calculate average angle; returns values between -pi radians to pi radians | |
| Convert radians to degrees | Used R package NISTunits [42] |
| Convert scale from −180 to 180 to 0 to 360 | If degree value was negative, add 360 |
| Convert angle from meteorological convention to math convention | Take reflection of angle over the non-tunnel-width axis |



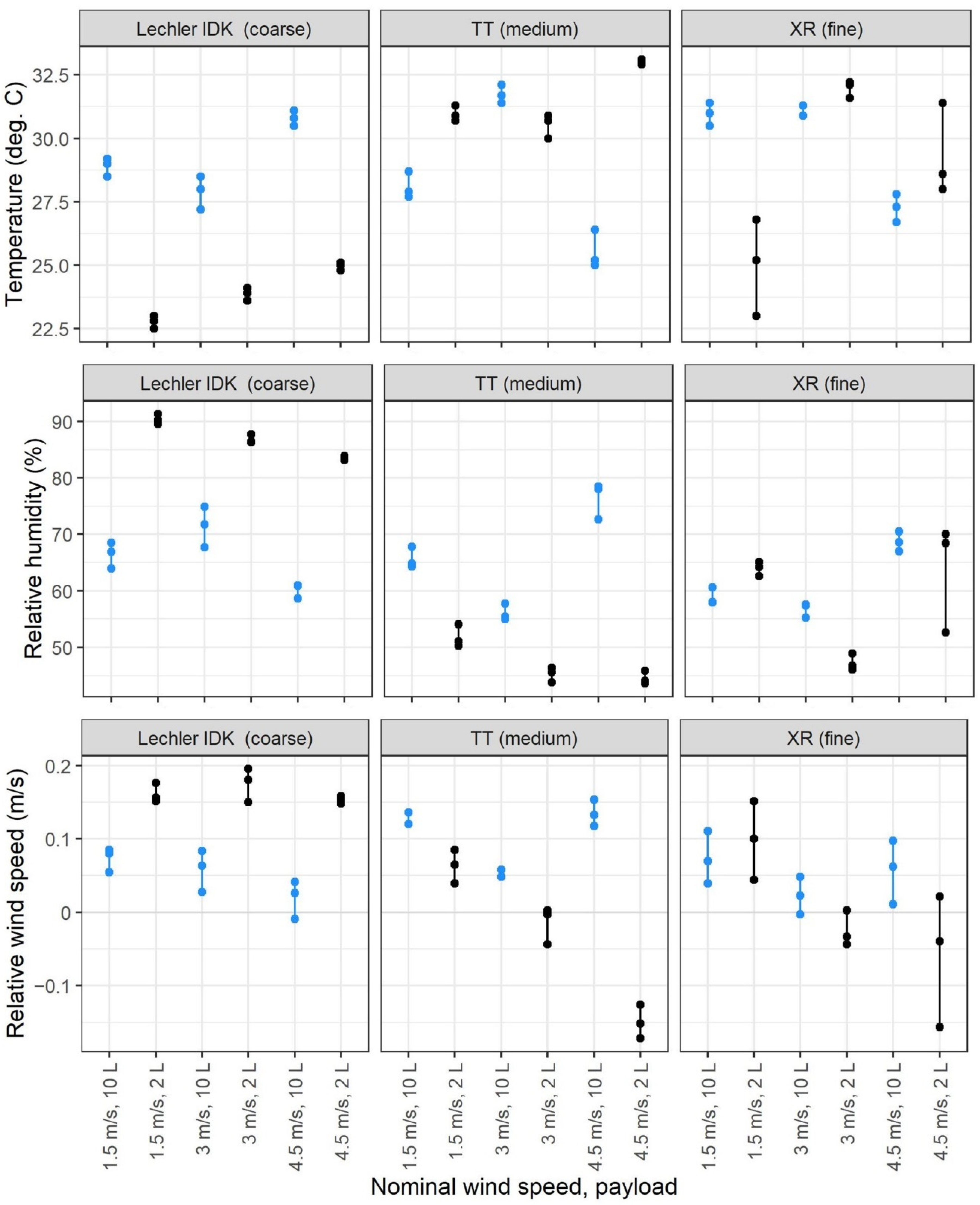
| Nozzle | Wind Speed (m/s) | Payload (L) | Equation to Estimate: Mean Deposition in ng/cm2 = |
|---|---|---|---|
| Lechler IDK (coarse) | 1.5 | 2 | |
| 10 | |||
| 3 | 2 | ||
| 10 | |||
| 4.5 | 2 | ||
| 10 | |||
| TT (medium) | 1.5 | 2 | |
| 10 | |||
| 3 | 2 | ||
| 10 | |||
| 4.5 | 2 | ||
| 10 | |||
| XR (fine) | 1.5 | 2 | |
| 10 | |||
| 3 | 2 | ||
| 10 | |||
| 4.5 | 2 | ||
| 10 |
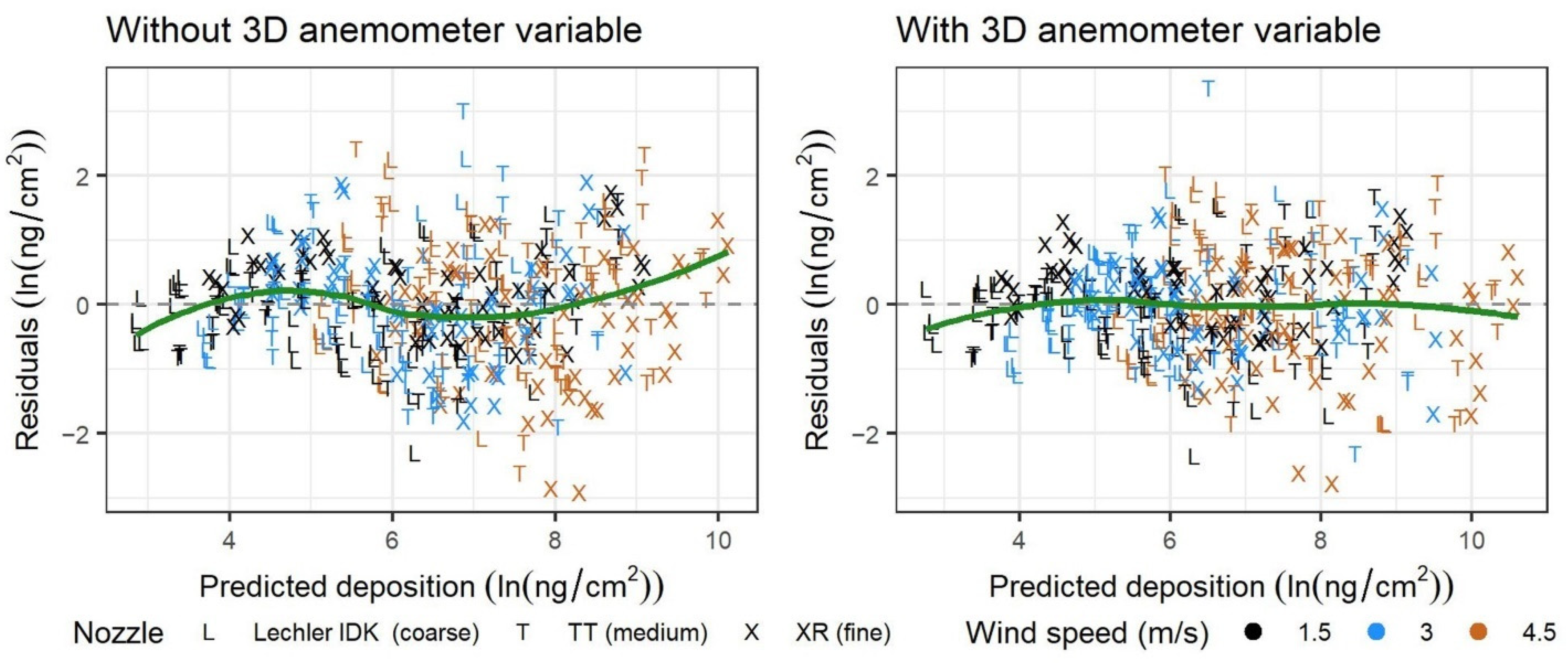
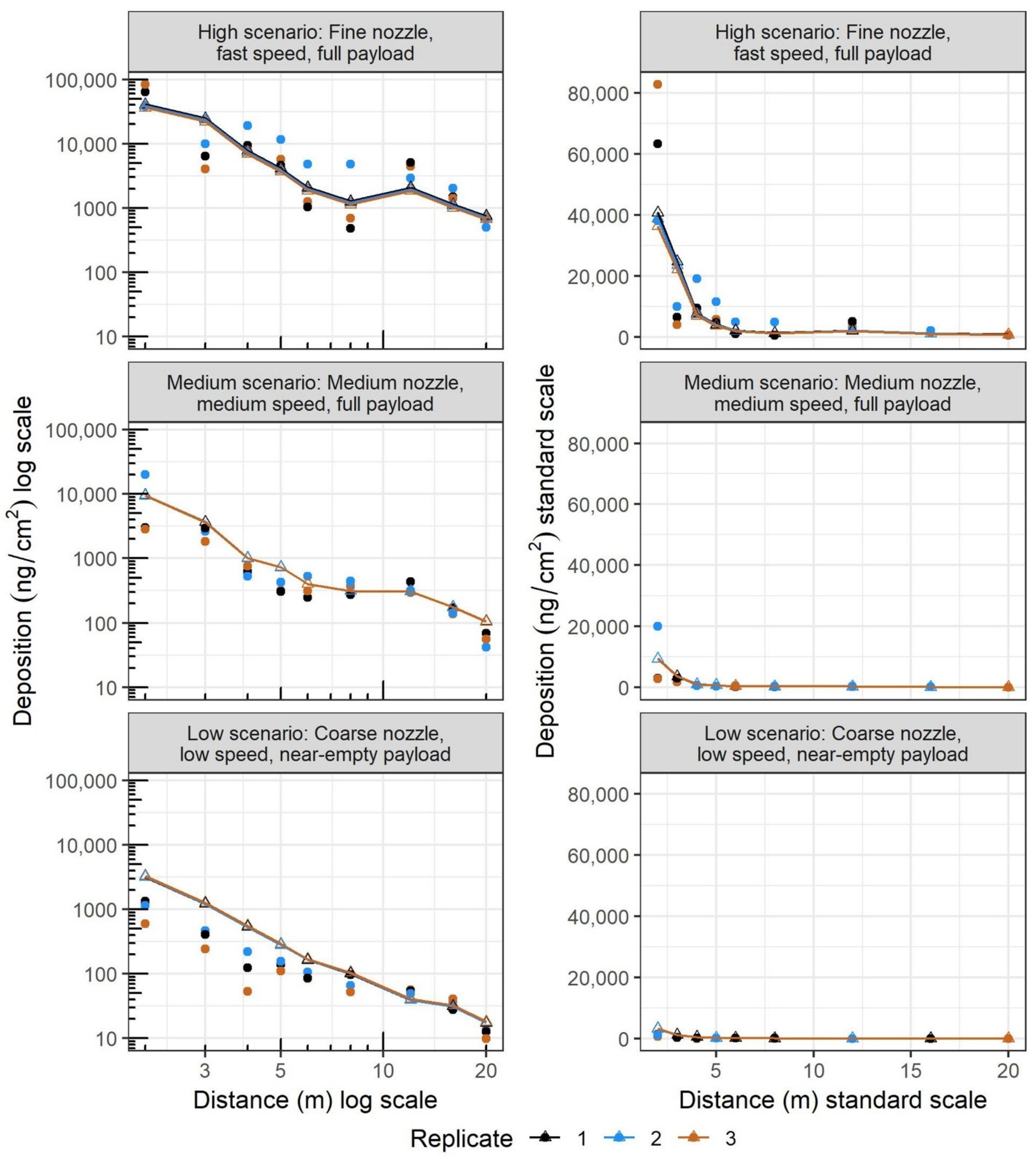
References
- United States Environmental Protection Agency (US EPA). Session 4: UAVs. In Proceedings of the Pesticide Program Dialogue Committee, Arlington, VA, USA, 8–9 May 2019; Available online: https://www.epa.gov/pesticide-advisory-committees-and-regulatory-partners/pesticide-program-dialogue-committee-1 (accessed on 10 April 2020).
- Carvalho, F.; Chechetto, R.; Mota, A.; Antuniassi, U. Challenges of Aircraft and Drone Spray Applications. Outlooks Pest. Manag. 2020, 31, 83–88. [Google Scholar] [CrossRef]
- Crop Life International. Drones Manual—Stewardship Guidance for Use of Unmanned Aerial Vehicles (Uavs) for Application of Crop. Protection Products; Crop Life International: Brussel, Belgium, 2020. [Google Scholar]
- US EPA. Emerging Application Technologies. Available online: https://www.epa.gov/sites/production/files/2018-11/documents/session-3-emerging-application-technologies-l-trossbach.pdf (accessed on 10 April 2020).
- Teske, M.E.; Bird, S.L.; Esterly, D.M.; Ray, S.L.; Perry, S.G. A User’s Guide for Agdrift 2.0.07: A Tiered Approach for the Assessment of Spray Drift of Pesticides. 2003. Available online: https://www.epa.gov/pesticide-science-and-assessing-pesticide-risks/models-pesticide-risk-assessment#AgDrift (accessed on 1 December 2021).
- US EPA. Agdrift®—A Tiered Approach for the Assessment of Spray Drift of Pesticides, 2.1.1; United States Environmental Protection Agency: Washington, DC, USA, 2003. [Google Scholar]
- Ahmad, F.; Qiu, B.; Dong, X.; Ma, J.; Huang, X.; Ahmed, S.; Ali Chandio, F. Effect of Operational Parameters of UAV Sprayer on Spray Deposition Pattern in Target and Off-Target Zones During Outer Field Weed Control Application. Comput. Electr. Agric. 2020, 172, 105350. [Google Scholar] [CrossRef]
- Brown, C.R.; Giles, D.K. Measurement of Pesticide Drift from Unmanned Aerial Vehicle Application to a Vineyard. Trans. ASABE 2018, 61, 1539–1546. [Google Scholar] [CrossRef]
- Chen, S.; Lan, Y.; Zhou, Z.; Ouyang, F.; Wang, G.; Huang, X.; Deng, X.; Cheng, S. Effect of Droplet Size Parameters on Droplet Deposition and Drift of Aerial Spraying by Using Plant Protection UAV. Agronomy 2020, 10, 195. [Google Scholar] [CrossRef]
- Hunter, J.E.; Gannon, T.W.; Richardson, R.J.; Yelverton, F.H.; Leon, R.G. Coverage and Drift Potential Associated with Nozzle and Speed Selection for Herbicide Applications Using an Unmanned Aerial Sprayer. Weed Technol. 2020, 34, 235–240. [Google Scholar] [CrossRef]
- Li, L.; Liu, Y.; He, X.; Song, J.; Zeng, A.; Zhichong, W.; Tian, L. Assessment of Spray Deposition and Losses in the Apple Orchard from Agricultural Unmanned Aerial Vehicle in China. In Proceedings of the 2018 ASABE Annual International Meeting, St. Joseph, MI, USA, 29 July–1 August 2018; p. 1. [Google Scholar]
- Lou, Z.; Xin, F.; Han, X.; Lan, Y.; Duan, T.; Fu, W. Effect of Unmanned Aerial Vehicle Flight Height on Droplet Distribution, Drift and Control of Cotton Aphids and Spider Mites. Agronomy 2018, 8, 187. [Google Scholar] [CrossRef]
- Wang, C.; He, X.; Wang, X.; Wang, Z.; Wang, S.; Li, L.; Bonds, J.; Herbst, A. Testing Method and Distribution Characteristics of Spatial Pesticide Spraying Deposition Quality Balance for Unmanned Aerial Vehicle. Int. J. Agric. Biol. Eng. 2018, 11, 18–26. [Google Scholar] [CrossRef]
- Wang, J.; Lan, Y.B.; Zhang, H.; Zhang, Y.L.; Wen, S.; Yao, W.; Deng, J. Drift and Deposition of Pesticide Applied by UAV on Pineapple Plants under Different Meteorological Conditions. Int. J. Agric. Biol. Eng. 2018, 11, 5–12. [Google Scholar] [CrossRef]
- Wang, X.; He, X.; Song, J.; Wang, Z.; Wang, C.; Wang, S.; Wu, R.; Meng, Y. Drift Potential of UAV with Adjuvants in Aerial Applications. Int. J. Agric. Biol. Eng. 2018, 11, 54–58. [Google Scholar] [CrossRef]
- Wang, X.; He, X.; Wang, C.; Wang, Z.; Li, L.; Wang, S.; Bonds, J.; Herbst, A.; Wang, Z. Spray Drift Characteristics of Fuel Powered Single-Rotor UAV for Plant Protection. Trans. Chin. Soc. Agric. Eng. 2017, 33, 117–123. [Google Scholar] [CrossRef]
- Xue, X.; Kang, T.; Weicai, Q.; Yubin, L.; Huihui, Z. Drift and Deposition of Ultra-Low Altitude and Low Volume Application in Paddy Field. Int. J. Agric. Biol. Eng. 2014, 7, 23–28. [Google Scholar] [CrossRef]
- Martin, D.E.; Woldt, W.E.; Latheef, M.A. Effect of Application Height and Ground Speed on Spray Pattern and Droplet Spectra from Remotely Piloted Aerial Application Systems. Drones 2019, 3, 83. [Google Scholar] [CrossRef]
- Wang, C.; Zeng, A.; He, X.; Song, J.; Herbst, A.; Gao, W. Spray Drift Characteristics Test of Unmanned Aerial Vehicle Spray Unit under Wind Tunnel Conditions. Int. J. Agric. Biol. Eng. 2020, 13, 13–21. [Google Scholar] [CrossRef]
- Wang, L.; Chen, D.; Yao, Z.; Ni, X.; Wang, S. Research on the Prediction Model and Its Influencing Factors of Droplet Deposition Area in the Wind Tunnel Environment Based on UAV Spraying. IFAC-Pap. 2018, 51, 274–279. [Google Scholar] [CrossRef]
- Yang, F.; Xue, X.; Cai, C.; Sun, Z.; Zhou, Q. Numerical Simulation and Analysis on Spray Drift Movement of Multirotor Plant Protection Unmanned Aerial Vehicle. Energies 2018, 11, 2399. [Google Scholar] [CrossRef]
- Zhan, Y.; Chen, P.; Xu, W.; Chen, S.; Han, Y.; Lan, Y.; Wang, G. Influence of the Downwash Airflow Distribution Characteristics of a Plant Protection UAV on Spray Deposit Distribution. Biosyst. Eng. 2022, 216, 32–45. [Google Scholar] [CrossRef]
- Berner, B.; Chojnacki, J. Use of Drones in Crop Protection. In Proceedings of the Farm Machinery and Processes Management in Sustainable Agriculture, IX International Scientific Symposium, Lublin, Poland, 22–24 November 2017; pp. 46–51. [Google Scholar]
- Lv, M.; Xiao, S.; Tang, Y.; He, Y. Influence of UAV Flight Speed on Droplet Deposition Characteristics with the Application of Infrared Thermal Imaging. Int. J. Agric. Biol. Eng. 2019, 12, 10–17. [Google Scholar] [CrossRef]
- Tang, Y.; Hou, C.J.; Luo, S.M.; Lin, J.T.; Yang, Z.; Huang, W.F. Effects of Operation Height and Tree Shape on Droplet Deposition in Citrus Trees Using an Unmanned Aerial Vehicle. Comput. Electr. Agric. 2018, 148, 1–7. [Google Scholar] [CrossRef]
- Zhu, H.; Jiang, Y.; Li, H.; Li, J.; Zhang, H. Effects of Application Parameters on Spray Characteristics of Multi-Rotor UAV. Int. J. Precis. Agric. Aviat. 2019, 2, 18–25. [Google Scholar] [CrossRef]
- Chen, Y.; Hou, C.; Tang, Y.; Zhuang, J.; Lin, J.; Luo, S. An Effective Spray Drift-Reducing Method for a Plant-Protection Unmanned Aerial Vehicle. Int. J. Agric. Biol. Eng. 2019, 12, 14–20. [Google Scholar] [CrossRef]
- ISO 25358; Crop Protection Equipment—Droplet-Size Spectra from Atomizers—Measurement and Classification. International Organization for Standardization: Geneva, Switzerland, 2018; Volume 7.
- R Core Team. R: A Language and Environment for Statistical Computing, 4.2.0; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Wickham, H. Ggplot2 (V3.3.6): Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016. [Google Scholar]
- Fox, J.; Weisberg, S. An R Companion to Applied Regression, 3rd ed.; Companion to Applied Regression (CAR) package v.3.0.13; Sage: Los Angeles, CA, USA, 2019. [Google Scholar]
- Hewitt, A.J.; Johnson, D.R.; Fish, J.D.; Hermansky, C.G.; Valcore, D.L. Development of the Spray Drift Task Force Database for Aerial Applications. Environ. Toxicol. Chem. 2002, 21, 648–658. [Google Scholar] [CrossRef] [PubMed]
- Teske, M.E.; Wachspress, D.A.; Thistle, H.W. Prediction of Aerial Spray Release from Uavs. Trans. ASABE 2018, 61, 909–918. [Google Scholar] [CrossRef]
- Chen, H.; Lan, Y.; Fritz, B.K.; Hoffmann, W.C.; Liu, S. Review of Agricultural Spraying Technologies for Plant Protection Using Unmanned Aerial Vehicle (UAV). Int. J. Agric. Biol. Eng. 2021, 14, 38–49. [Google Scholar] [CrossRef]
- Zhang, H.C.; Zheng, J.; Zhou, H.; Dorr, G.J. Droplet Deposition Distribution and Off-Target Drift During Pesticide Spraying Operation. Nongye Jixie Xuebao Trans. Chin. Soc. Agric. Mach. 2017, 48, 114–122. [Google Scholar] [CrossRef]
- US EPA. Annual Spray Drift Review. Available online: https://archive.epa.gov/scipoly/sap/meetings/web/html/spraydrift.html (accessed on 4 May 2022).
- Wang, G.; Han, Y.; Li, X.; Andaloro, J.; Chen, P.; Hoffmann, W.C.; Han, X.; Chen, S.; Lan, Y. Field Evaluation of Spray Drift and Environmental Impact Using an Agricultural Unmanned Aerial Vehicle (UAV) Sprayer. Sci. Total Environ. 2020, 737, 139793. [Google Scholar] [CrossRef] [PubMed]
- Herbst, A.; Bonds, J.; Wang, Z.; Zeng, A.; He, X.; Goff, P. The Influence of Unmanned Agriculturalaircraft System Design on Spray Drift. J. Für Kult. 2020, 72, 1–11. [Google Scholar] [CrossRef]
- Ferguson, J.C.; Chechetto, R.G.; O’Donnell, C.C.; Dorr, G.J.; Moore, J.H.; Baker, G.J.; Powis, K.J.; Hewitt, A.J. Determining the Drift Potential of Venturi Nozzles Compared with Standard Nozzles across Three Insecticide Spray Solutions in a Wind Tunnel. Pest Manag. Sci. 2016, 72, 1460–1466. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Chen, S.; Wang, G.; Lan, Y. Drift Evaluation of a Quadrotor Unmanned Aerial Vehicle (UAV) Sprayer: Effect of Liquid Pressure and Wind Speed on Drift Potential Based on Wind Tunnel Test. Appl. Sci. 2021, 11, 7258. [Google Scholar] [CrossRef]
- International Organization for Standardization. Equipment for Crop Protection—Methods for the Laboratory Measurement of Spray Drift—Wind Tunnels. ISO 22856; International Organization for Standardization: Geneva, Switzerland, 2008. [Google Scholar]
- Gama, J. NISTunits (v1.0.1). Fundamental Physical Constants and Unit Conversions from NIST; 2016. Available online: https://CRAN.R-project.org/package=NISTunits (accessed on 2 April 2022).




| Droplet Diameter (µm) | |||||
|---|---|---|---|---|---|
| Nozzle | Dv10 | Dv50 | Dv90 | % ≤141 µm | Spray Classification |
| XR11001 | 62.6 | 126.7 | 234.8 | 58.2 | Fine |
| TT11001 | 132.8 | 309.8 | 597.5 | 11.5 | Medium |
| Lechler IDK 120-01 | 258.7 | 526.8 | 950.2 | 2.3 | Coarse |
| Variable | Nominal Tunnel Wind Speed (m/s) | Minimum | Mean | Maximum |
|---|---|---|---|---|
| Temperature (°C) | 1.5 | 22.5 | 27.8 | 31.4 |
| 3 | 23.6 | 29.5 | 32.2 | |
| 4.5 | 24.8 | 28.5 | 33.1 | |
| Relative humidity (%) | 1.5 | 50.3 | 66.2 | 91.3 |
| 3 | 43.8 | 60.6 | 87.7 | |
| 4.5 | 43.6 | 66.2 | 83.9 | |
| Measured wind speed (m/s) | 1.5 | 1.54 | 1.60 | 1.68 |
| 3 | 2.96 | 3.05 | 3.20 | |
| 4.5 | 4.33 | 4.53 | 4.66 |
| Variable Explaining ln(deposition) in ng/cm2 | Coefficient | Standard Error | p Value of Coefficient | ANOVA p Value of Variable |
|---|---|---|---|---|
| Intercept | 8.4026 | 0.2283 | <2.0 × 10−16 | - |
| ln(D): ln of distance (m) | −1.8703 | 0.1027 | <2.0 × 10−16 | <2.0 × 10−16 |
| W3.0: Tunnel wind speed of 3.0 m/s (1 or 0) | −1.1501 | 0.2572 | 9.75 × 10−6 | <2.0 × 10−16 |
| W4.5: Tunnel wind speed of 4.5 m/s (1 or 0) | −1.0552 | 0.2967 | 4.14 × 10−4 | |
| NT: Nozzle TT11001 medium (1 or 0) | 0.7928 | 0.0997 | 1.40 × 10−14 | <2.0 × 10−16 |
| NX: Nozzle XR11001 fine (1 or 0) | 1.1707 | 0.1037 | <2.0 × 10−16 | |
| P: Payload at 10 L (1 or 0) | 0.8146 | 0.2041 | 7.63 × 10−5 | 150 × 10−6 |
| M: Meteorological interaction variable (speed m/s × humidity %/temperature °C) | 0.5032 | 0.1827 | 6.10 × 10−3 | 6.79 × 10−3 |
| Z: 3D anemometer variable of Z dimension at bottom center (m/s) | −1.6886 | 0.1653 | <2.0 × 10−16 | 3.74 × 10−8 |
| ln(D) × W3.0 | 0.8070 | 0.1281 | 6.77 × 10−10 | <2.0 × 10−16 |
| ln(D) × W4.5 | 1.4534 | 0.1502 | <2.0 × 10−16 | |
| ln(D) × P | −0.2380 | 0.1016 | 1.95 × 10−2 | 1.95 × 10−2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grant, S.; Perine, J.; Abi-Akar, F.; Lane, T.; Kent, B.; Mohler, C.; Scott, C.; Ritter, A. A Wind-Tunnel Assessment of Parameters That May Impact Spray Drift during UAV Pesticide Application. Drones 2022, 6, 204. https://doi.org/10.3390/drones6080204
Grant S, Perine J, Abi-Akar F, Lane T, Kent B, Mohler C, Scott C, Ritter A. A Wind-Tunnel Assessment of Parameters That May Impact Spray Drift during UAV Pesticide Application. Drones. 2022; 6(8):204. https://doi.org/10.3390/drones6080204
Chicago/Turabian StyleGrant, Shanique, Jeff Perine, Farah Abi-Akar, Timothy Lane, Brenna Kent, Christopher Mohler, Chris Scott, and Amy Ritter. 2022. "A Wind-Tunnel Assessment of Parameters That May Impact Spray Drift during UAV Pesticide Application" Drones 6, no. 8: 204. https://doi.org/10.3390/drones6080204
APA StyleGrant, S., Perine, J., Abi-Akar, F., Lane, T., Kent, B., Mohler, C., Scott, C., & Ritter, A. (2022). A Wind-Tunnel Assessment of Parameters That May Impact Spray Drift during UAV Pesticide Application. Drones, 6(8), 204. https://doi.org/10.3390/drones6080204






