Abstract
The deployment performance of the unfolded wing determines whether the winged missiles can fly normally after being launched, infecting the attack performance of the winged missiles. The paper proposes a new deployment mechanism with clearance eliminator. Based on the slider-crank principle, the proposed deployment mechanism achieves fast and low-impact deployment of the wings. The proposed clearance eliminator with shape memory alloy (SMA) effectively eliminates the clearance of the sliding pair and improves the support stiffness and stability of the deployed wing. The collision characteristics and the clearance elimination are studied for the deployment mechanism. The influence of the collision force on the motion state of the wing during the deployment is analyzed. The static stiffness of the wing under the clearance state and the deformation is analyzed. The dynamic stiffness under the catapult clearance elimination state is modeled based on the fractal geometry and contact stress theory. The relationship between the locking force and the support stiffness is revealed. The kinetic simulation is used to analyze the motion response during the action of the deployment mechanism. Modal analysis, harmonic response analysis, and random vibration analysis were conducted for the whole wings. A prototype was developed to verify the ejection performance of the wing according to the input load characteristics. The dynamic stiffness of the unfolded wings is tested by the fundamental frequency experiments to verify the performance of the clearance elimination assembly. The experimental results show that the designed deployment mechanism with clearance compensation achieves fast ejection and high stiffness retention of the missile wing.
1. Introduction
Winged missiles have the advantages of good maneuverability, easy control, and both the active and passive segments of the flight trajectory can be controlled. This form has been applied to airborne missiles, anti-ship missiles, anti-tank missiles, and air defense missiles [,,,,]. As winged missiles increase in lethality, strike accuracy, and battlefield deterrence, the number of missiles carried and their launch efficiency are becoming important indicators of the attack capability of modern weapons such as warplanes and ships. If the space occupied by individual missiles can be reduced, the amount of ammunition carried will be significantly increased, and the carrying capacity of the aircraft will be greatly enhanced. Morphing wings can realize flexible maneuvering in different flight environments and maintain high flight efficiency [,,,,,]. The aircraft wing can be divided into the in-plane deformation of the wing [,], the out-plane deformation of the wing [,,,,,], and the wing deformation [,,,]. Winged missiles generally have foldable or retractable wings [,,,,], so that they can be stowed in the launcher in a small footprint and their wings can open automatically when the missile is launched. In order to reduce the lateral dimensions of the missile; facilitate storage, transportation and launch; save storage and transportation space; improve the storage and transportation capacity; and improve the mobility and operational capability of the weapon system, the wings or part of the wings of the missile are often contracted to reduce the wingspan [,,,,]. When the missile flies away from the launch device, the wings automatically unfold to ensure the normal flight of the missile.
The missile wings with the proposed deployment mechanisms are completely folded inside the missile body in the process of storage and transportation, which can effectively increase the loading rate. After the missile flies away from the launching device, the deployment mechanisms push out the wings synchronously and quickly and achieve position locking and stiffness maintenance. It can significantly improve the contraction rate, deployment efficiency, and wing surface stiffness of the missile wing and make the wing provide better aerodynamic force for the missile body. In order to improve the loading capacity and launch efficiency of the missile launch platform, the wing is usually designed to be retractable, and the existing retractable wings have two forms: rotational deployment and direct-acting deployment [,,,,]. According to the rotational direction of the missile wing, the main airfoil is rotated and retracted horizontally and vertically. The rotational deployment radius is large, the aerodynamics of the airfoil during the deployment process is unstable, and the locking stiffness is low after the deployment of the wing. The direct-acting wing refers to the wing moving in a straight line during deployment. The airfoil aerodynamic force is more stable during the unfolding process than that of the rotational deployment, the airfoil is completely stowed inside the missile body when it is folded, and the stowage ratio is large. The direct-acting wing deployment mechanism requires the wing to be fully stowed inside the body in a straight line during retraction, which requires a higher stowage ratio, but the direct-acting wing deployment mechanism has obvious advantages in reducing the lateral dimensions of the missile and expanding the capacity of the magazine. The direct-acting wing deployment mechanism can hide all the wings inside the body of the missile when closing, which is effective in reducing the lateral size of the missile. The use of the telescopic rudder surface is more flexible, and the wings can be controlled before and after deployment. The rudder deflection can be preset or deflected according to the command when the aircraft and missile are separated to control the separation attitude of the rudder, which is more conducive to separation safety.
The deployment performance of the unfolded wing is related to whether the winged missile can fly normally after being launched, which restricts the attack performance of the winged missile. After the wing deployment process, there are inevitably clearances between the wing and the kinematic pair of the missile body, and the influence of the kinematic pair clearance on the wing is often ignored in the traditional design. To improve the dynamic stiffness and stability of the wing, measures should be taken to eliminate the kinematic clearance. Therefore, in order to make the wings of the missile synchronized and to achieve fast deployment as well as reliable operation, the design of the transmission, wing locking, clearance elimination, and stiffness retention mechanisms of the wing deployment scheme are particularly important.
The main contributions and innovations of this paper lie in two aspects: 1. A new deployment mechanism is designed based on the slider-crank principle to achieve the fast and low-impact ejection of the missile wings. 2. A clearance eliminator with shape memory alloy (SMA) is designed for the deployed missile wing to achieve high stiffness and stability. The sections of the paper are organized as the following: Section 2 presents a new deployment mechanism of missile wings. The configuration and operating principle of the drive actuator and the clearance eliminator are introduced. Section 3 analyzes the effect of ejection collision characteristics on the motion of the wings and the stiffness under the clearance locking and unlocking. Section 4 analyzes the dynamic characteristics of the wing and the modalities of the whole mechanism. In Section 5, the ejection performance and the effect of eliminating clearance are investigated through prototype experiments.
2. Structure and Principle of the Missile Wings
2.1. Deployment Mechanism
In order to achieve a large stowage ratio, fast actuation, and high stiffness retention, we propose a new deployment mechanism with clearance eliminator for missile wings. The designed deployment mechanism mainly consists of the drive actuator and the clearance eliminator, as shown in Figure 1. The principle of wing ejection and locking is shown in Figure 2. The operating principle of the deployment mechanism includes three steps: 1. With the command of the unlocking issued, the upper and bottom locking devices realize the unlocking action of the wing through the compression springs. 2. Driven by the torsion spring, the crank slider mechanism of the drive actuator pushes out the wing along a straight line. 3. With the wing fully extended, the clearance eliminator eliminates the clearance of the kinematic pair to improve the wing stiffness.
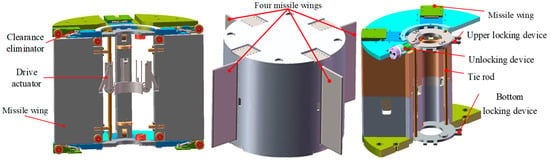
Figure 1.
Deployment mechanism for the missile wings.

Figure 2.
The principle of wing ejection and locking.
2.2. Drive Actuator
The drive actuator consists of a drive element, linkage mechanism, missile wings, and pulley block, as shown in Figure 3. The torsion spring, as the drive source, is mounted on the input shaft to save design space. One arm of force is supported on the base, and the other arm of force acts on linkage and pushes the missile wing out by linkage b. The ejection assembly of the deployment mechanism is based on the slider-crank principle, as shown in Figure 4. When the wing is pushed out, it is subjected to lateral load, resulting in friction resistance that affects the pushing out of the wing. In order to change the sliding friction between the wing and the base into rolling friction, an axial pulley and a lateral pulley are embedded in the root of the wing, and a pair of ball bearings with flanges are installed inside the pulley to enhance the smoothness and stability of the movement and to limit the pulley axially at the same time.
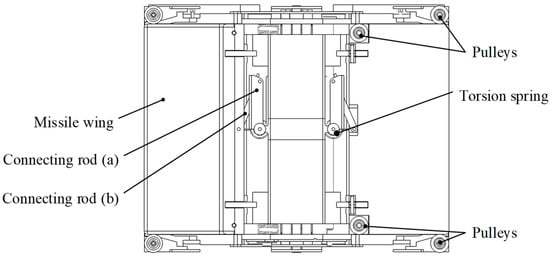
Figure 3.
Structure of drive actuator.

Figure 4.
Working principle of drive actuator.
2.3. Clearance Eliminator
There are clearances between the kinematic pairs of the wing and the missile body to enable the smooth ejection of the wing. In order to improve the dynamic stiffness and stability of the wing, measures should be taken to eliminate the clearance of the kinematic pair. A Clearance eliminator with SMA is proposed to drive a wedge to eliminate the clearance of the kinematic pair between the wing and the base, to generate a locking force to improve the support stiffness of the wing and the base joint, and to improve the resonance frequency and stability of the wing.
The configuration of the clearance eliminator is shown in Figure 5. The end cap and the base are solidly connected to the missile body, and the shape memory alloy driver is hinged to the base at one end and the wedge at the other end. In order to speed up the deformation response of the shape memory alloy material, the memory alloy rod is heated by directly energizing it. The design of the SMA drive requires consideration of insulation and thermal insulation. As shown in Figure 6, conductive sheets are embedded in both ends of the memory alloy rod and heated by electricity. Heat-preserved sleeve made of insulating material is set on the outside of the memory alloy rod to play the role of insulation and heat preservation. A holding sleeve made of alloy steel is set on the outside of the heat-preserved sleeve to enhance the axial stiffness of the alloy rod and prevent destabilization under pressure. The working principle of the clearance eliminator is shown in Figure 7. The wedge is driven by the shape memory alloy to contact the base and the missile wing and generate mutual force. A positive pressure Fy on the contact surface of the wedge and the wing produces an axial locking effect on the wing, and a frictional force Fx on the contact surface of the wedge and the wing produces a lateral locking effect on the wing. By applying the locking force to the wing, the support stiffness of the root of the wing is improved and the stability of the wing is enhanced.
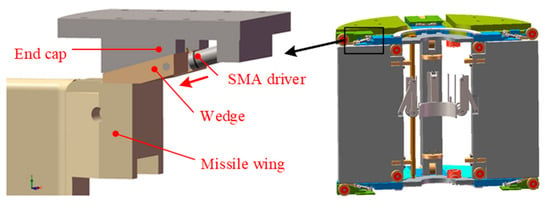
Figure 5.
Configuration of clearance eliminator.
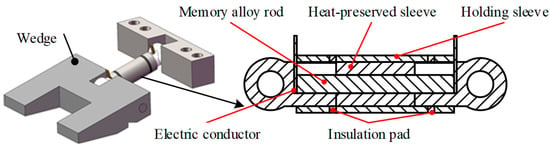
Figure 6.
Configuration of SMA driver.

Figure 7.
Working principle of the clearance eliminator.
3. Missile Wing Deployment and Clearance Elimination Analysis
3.1. Collision Characterization
In the movement of the wing, the joint at the hinge will cause vibration and collision force due to the existence of the clearance, so that the displacement and speed of the wing jitter. During the collision, the contact point can move relative to the collision body, and the collision force passes through the action point. The collision force and the deformation displacement of the collision body satisfy the theory of elasticity, the collision force equations are as follows:
where is the normal contact force, is the equivalent spring force, is the equivalent damping force, is the equivalent joint stiffness coefficient, is the damping coefficient, is the normal puncture depth at the contact point, is the normal relative velocity at the contact point, is an exponent, 1.5 for metallic contacts, is the collision recovery factor, and is the relative velocity before collision.
The tangential friction at the clearance is expressed using the Coulomb friction model in ADAMS as:
where is the sign function, is the relative sliding velocity at the contact point, and is the friction factor.
The elastic force and friction are both simulated by the step function and friction function in Adams to analyze the collision at the hinge of the deployment mechanism. The missile wing and the deployment mechanism are simplified as shown in Figure 8. The collision force at the clearance and the effect of the clearance on the motion of the wing are calculated.

Figure 8.
Simplified model of the wing deployment mechanism.
The stiffness coefficient was taken as 1.2 105 N/m, the damping coefficient was taken as 120 N·s/m, and the static and dynamic friction coefficients were set as 0.3 and 0.25, respectively. The simulations were carried out with the clearance of 0.1 mm, 0.3 mm, and 0.5 mm, respectively. The variation in the contact force in the driving joint and the wing joint with time is shown in Figure 9 and Figure 10. The displacement and velocity of the wing with time are shown in Figure 11 and Figure 12.
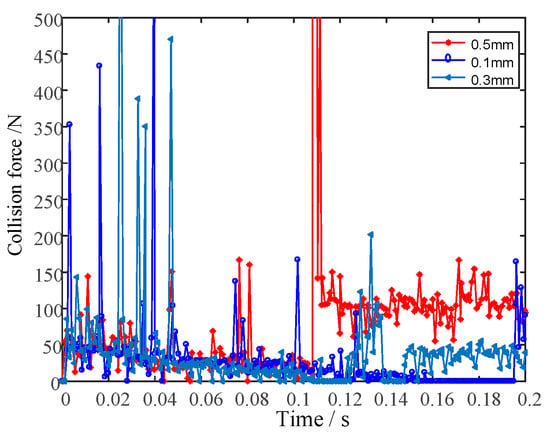
Figure 9.
Collision force at the driving joint.

Figure 10.
Collision force at the wing joint.

Figure 11.
The effect of clearance on the displacement of the wing.

Figure 12.
The effect of clearance on the velocity of the wing.
From the calculation results, it can be seen that when the
clearance is 0.3 mm, the wing deployment time is the shortest. The clearance collision force is smaller, and the collision frequency is lower. The clearance has less influence on the fluctuation of the movement speed of the wing. This analysis result plays an important guiding role in the design of the subsequent joint manufacturing accuracy and the control of the dimensional chain.
3.2. Static Stiffness Characteristics with Clearance
In order to ensure that the wing is pushed out smoothly, the clearance between the wing and the kinematic pair is predetermined, as shown in Figure 13. After the wing is pushed out, due to the existence of the clearance, the wing is in a free state in a certain space and deflects freely under the surface load, and after deflecting a certain displacement, it bends under a certain component of the uniform load. As a result, the static deformation of the wing in the clearance state can be divided into two parts, i.e., the deformation deflection turning angle during the free deflection and the bending deformation and after one end is restrained; then, the static deformation of the wing under the action of the uniform load in the clearance state is the superposition of the two processes of deformation.

Figure 13.
Static stiffness analysis of the missile wing.
From the geometric relationship, we obtain that:
Since the wing is subjected to a uniform load perpendicular to the wing surface as shown in Figure 14, only the transverse bending of the wing is considered, and a unit of arbitrary width in the face is selected for analysis, which can be equated to a cantilever beam with length , width , and height . The equivalent distributed load on it is .
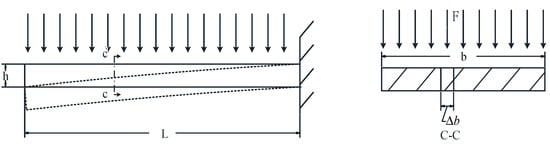
Figure 14.
Schematic of the wing subjected to normal load.
From the deflection characteristics of the cantilever beam, it follows that:
Substituting equations and into the deflection and angle of rotation formulas, it is found that the deflection characteristics can be solved using the cantilever beam formula for any cross-sectional width under the action of a normal uniform load perpendicular to the surface, so the missile wing can be equated to a cantilever beam structure. The equivalent distributed load on it is . Then, the deflection characteristics of the missile wing are as follows:
where is the modulus of elasticity of the material, and is the moment of inertia of the section; then, the maximum angle of rotation of the wing and the maximum deflection at the end of the wing are as follows:
The deflection angle and deflection of the wing under the uniform load are shown in Figure 15 and Figure 16.

Figure 15.
Deflection angle–load relationship.

Figure 16.
Deflection–load relationship.
In accordance with the design index of the wing deployment mechanism, the maximum normal load is 700 N. The airfoil uniform load is , the wing deflection angle is 14.8402 10−6°, and the end deflection is 0.1008 mm. From the static load analysis results, it can be seen that the clearance has a great impact on the deformation of the wing so that there is a certain degree of free deflection of the wing. In order to enhance the stability of the wings, it is necessary to design a clearance eliminator to compensate for the clearance at the kinematic pair of the wings.
3.3. Clearance-Free Locking Stiffness Modeling
When the structure and material of the missile wing deployment mechanism are determined, the mass matrix of the deployment mechanism system is fixed. So, the vibration frequency of the deployment mechanism is mainly affected by the system stiffness. By locking the root of the wing through the clearance eliminator to provide reliable support to the wing root, the system stiffness can be effectively improved, further improving the dynamic stiffness characteristics.
By eliminating the clearance at the kinematic pair of the missile wing using the clearance eliminator, the connection between the root of the missile wing and the base is transformed from the clearance state to the contact state, as shown in Figure 7. In the x direction, the wing contacts the base through the V-shaped contact surface and applies pre-stress to the contact surface in the x direction by applying transverse locking force. In the y direction, the top and bottom ends of the wing contact the base by the wedged force and apply pre-stress to the contact surface in the y direction by applying longitudinal pre-stress.
The wedge interacts with the wing and the base under the action of the driving force of the shape memory alloy . The transverse locking force is generated by the frictional force interacting between the wedge and the missile wing. During the interaction between the wedge and the missile wing, small deformations occur tangentially and normally along the contact surface, and it is known from Coulomb friction theory that the frictional force is proportional to the contact surface load , i.e., and ( is the inclination angle of the wedge). The relationship between the transverse locking force and the driving force of the shape memory alloy can be introduced as:
The frictional force generated at the contact surface under different is obtained by simulation analysis, as shown in Figure 17.

Figure 17.
Relationship between and .
It can be seen that basically varies linearly with . It can be determined by the slope of the image that the parameter , from which the relationship between and can be obtained as:
The wing root is connected to the base through the clearance eliminator. The connection characteristics of the contact surface have a great influence on the dynamic stiffness of the wing. If the root support is reliable, the wing structure can be equivalent to a cantilevered thin plate. Its modal characteristics can be derived according to the finite element method. The inherent frequency is only related to the shape parameters of the wing and the structural material. With the structural material of the wing given, the inherent frequency is constant. Therefore, the dynamic stiffness analysis of the wing focuses on the dynamic stiffness analysis of the connection between the wing root and the base. Assuming that the wing is a rigid body, the relationship between the different locking forces and the frequency response of the wing is established under the clearance elimination state.
The locking force Fx in the x direction generates a lateral contact force Fcx on the V-shaped contact surface, creating a contact stiffness on the V-shaped contact surface. The wing root can be equated to a support structure as shown in Figure 18. The support of the contact surface can be equated to a spring of the same stiffness.
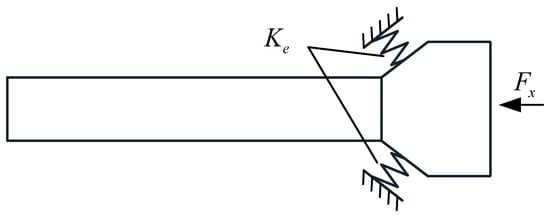
Figure 18.
Equivalent diagram of the support part.
Based on fractal geometry, the normal contact stiffness of the V-shaped contact surface is modeled with reference to the Hertz contact theory. Due to the large area of contact area of the bonding surface, it can be assumed that a small amount of elastic deformation occurs at the bonding surface. is the critical contact deformation of the contact surface from elastic to elasto-plastic deformation. is much smaller than .
According to Hertz contact theory, when the micro-convex body between V-contact surfaces is in elastic contact, the contact load of the micro-convex body can be obtained as follows:
From we can obtain the contact stiffness of micro-convex body as:
where R is an equivalent radius of curvature of the micro-convex body on the contact surface, and E is the composite modulus of elasticity of the material, . and are the modulus of elasticity of the two surface materials, respectively, and and are the corresponding Poisson’s ratios. is the deformation of the contact point.
According to fractal theory, the equivalent radius of curvature of a micro-convex body on a machined contact surface is calculated by the following equation:
where is and intermediate variable, ; is the characteristic factor responding to the contour size, and the height dimension parameter of the milled machined surface is 1.2117 × 10−4 m. is the spatial frequency of the random contour, and = 1.5. is the number of fractal cones of the contour, which is 1.2183. is the hardness of the material, and . is the yield strength of the material. is the average contact surface pressure coefficient, and . is the Poisson’s ratio of the material at the bonding surface.
By Hooke’s law: . Then, the deformation is: , where are the contact surface stress, strain, contact surface normal pressure, contact surface thickness, and contact area, respectively, which in turn leads to:
The angular velocity of vibration of the missile wing root is . Intrinsic frequency at the root support of the missile wing is .
Taking as 6 mm, 2661.5 mm2, and 37.37°, respectively, the relationship between the missile wing vibration frequency and the transverse locking force is derived as shown in Figure 19.

Figure 19.
Vibration frequency versus locking force.
As can be seen from Figure 19, the frequency response of the wing first increases sharply when the locking force increases from 0 under the action of transverse locking. Then, when the locking force reaches 20 N, increase in frequency the wing starts to slow down with the increase in the locking force, and the frequency response of the wing gradually tends to become smooth as the locking force continues to increase. The parameters are optimized by simulation software, and the frequency response of the wing under different lateral locking forces is shown in Figure 20.

Figure 20.
The relationship between the intrinsic frequency of the wing and the locking force.
The simulation results show that when transverse locking is applied, a small locking force can cause the vibration frequency of the root of the wing to stop. The frequency response tends to stabilize with the increase in the locking force. Comparing with the theoretical results, it can be found that both of them have the tendency that the frequency response of the wing starts to increase sharply with the increase in the locking force. The frequency response of the wing gradually tends to be stable with the increase in the locking force. The reason for the difference between the theoretical and simulation results is that the constraint boundary conditions of the wing root are different between theory and simulation. From the perspective of theoretical modeling, the locking force on the wing root will have a great effect on the contact stiffness. While from the simulation analysis, the effect of the locking force on the frequency response of the wing is not obvious because it ignores the surface characteristics of the contact surface. It considers the contact form as unconsolidated once the lateral locking force is applied. Therefore, the effect of the locking force on the frequency response of the missile wing is not obvious.
4. Mechanical Characterization
4.1. Kinetic Characteristics
The state of motion during the deployment of the wing is analyzed. The rolling friction coefficient between the wing and the contact surface during the motion of the wing is set to 0.05. The frictional reaction force generated by the air load during the deployment of the wing is equated by attaching a spring to the wing, and the driving torque is set to 1 Nm. The displacement versus time and velocity versus time during the deployment of the wing are shown in Figure 21 and Figure 22, respectively.

Figure 21.
Displacement versus time.
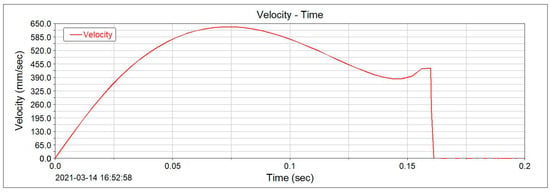
Figure 22.
Velocity versus time.
From the simulation results, it can be seen that the deployment time of the wing is about 0.154 s, which is basically the same as the solution of the kinetic equation. It can be determined that the time to push the wing into place is about 0.150.16 s, which meets the speed requirement of the deployment mechanism.
4.2. Modal Analysis
In the unlocked state, Figure 23 shows the boundary conditions and mesh division according to the loading environment. For convenience, we use free mixed mesh generation in the study. The modal analysis is carried out in the unpreloaded state. The results of the fundamental frequency and the first six orders of frequency are shown in Table 1.
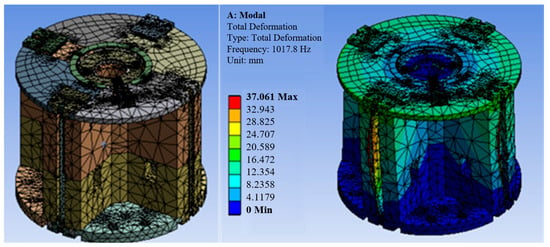
Figure 23.
Mesh division and modal analysis under docking condition.

Table 1.
First six orders of frequency of the whole machine in the unlocked state. (Hz).
After the wing is pushed into place and the clearance eliminator is actuated, the pre-stress-modal analysis is performed on the wing. The pre-stress loading is shown in Figure 24a. The load simulates the driving force of the SMA actuator, and the results of the wing modal analysis are shown in Figure 24b. The first six orders of its inherent frequency are obtained as shown in Table 2.

Figure 24.
Modal analysis with deployment: (a) Pre-stress loading; (b) Results of modal analysis.

Table 2.
First six orders of frequency after the deployment of the missile wing (Hz).
Based on the existing pre-stress modal analysis results, the harmonic response analysis of the missile wing was carried out with the frequency band set to 0~500 Hz and the damping coefficient set to 0.05. In addition, a 700 N uniform normal load was applied on the surface of the wing, and the amplitude versus frequency response was obtained as shown in Figure 25. At resonance, the swept frequency phase angle is set to 90°, as shown in Figure 26, and the maximum deformation of the missile wing is 7.855 mm.
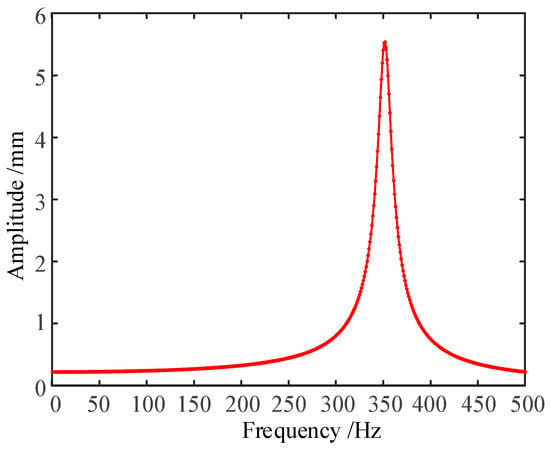
Figure 25.
Amplitude–frequency response characteristics.
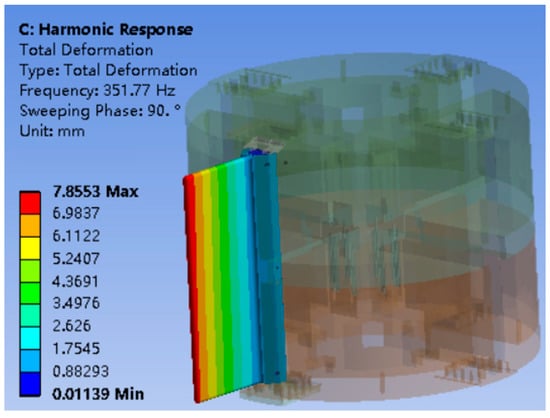
Figure 26.
Schematic diagram of maximum deformation of the wing during resonance.
With the maneuvering flight of the missile, the deployed wing is subjected to complex non-constant aerodynamic effects. The environmental loads on the wing deployment mechanism are mostly manifested as irregular dynamic inputs. In order to evaluate the random vibration fatigue characteristics of the mechanism, the random vibration analysis is performed on the basis of the modal analysis for the wing deployment mechanism. By setting the power spectral density parameters specified in the vibration test standard to simulate the irregular dynamic environmental loads on the mechanism, the random vibration response analysis is performed on the missile wing deployment mechanism.
The results of the modal analysis are used as the initial conditions of the random vibration analysis, and the power spectral density excitation in the xyz direction is set as shown in Figure 27. The displacement response of the device as a whole is obtained, as shown in Figure 28. The maximum deformation of the end of the wing is 0.273 mm, which means that it will not cause structural instability or damage under the large power spectral density excitation.

Figure 27.
Loaded power spectral density.

Figure 28.
Displacement response spectrum.
In order to verify the connection stiffness of the wing deployment mechanism along the x-direction and z-direction, the acceleration response spectrum of a point at the end of the wing is selected, as shown in Figure 29, in which the x-direction’s and z-direction’s input power spectrum densities are the same. The results show that the acceleration responses almost completely overlap, indicating that the transverse connection stiffness of the device is high and the stability is excellent.
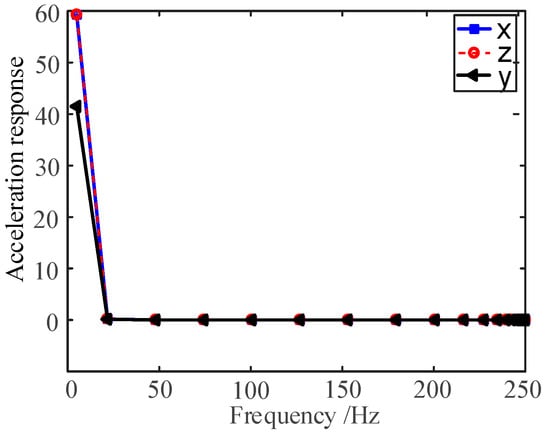
Figure 29.
Acceleration response.
5. Experimental Research
5.1. Verification of Wing Deployment Characteristics
The developed principle prototype is shown in Figure 30. To save costs and improve the test efficiency, only one set of opposing wings was deployed. In order to reduce the weight of the mechanism, except for the key stressed parts which are machined by 40Cr material, the rest of the parts are made of aluminum alloy, and the overall mass of the prototype is about 15 Kg. A high-speed camera is used to record the deployment time of the principle prototype wing, as shown in Figure 31. The deployment process is shown in Figure 32. The complete deployment time of the missile wing is about 0.14 s, which meets the requirement of rapidity. The experiments show that there is a difference of about 6 ms between the deployment times of the two wings. There are three main reasons for this difference: 1. The manufacturing error of the prototype leads to inconsistent clearances. The impact forces acting on the wining are also inconsistent during the deployment process. 2. The assembly error causes the installation position of the torsion spring to shift, such as the assembly error of the shaft hole of the torsion springs. 3. The performance difference of the torsion springs leads to inconsistent driving torques of the deployment mechanisms. The size and stiffness coefficient of the torsion springs cannot be completely consistent.

Figure 30.
Principle prototype of deployment mechanism.

Figure 31.
High-speed camera test system.

Figure 32.
Testing results of the high-speed camera.
According to the design index of the wing deployment mechanism, the wing is subjected to a normal load that varies linearly with the push-out distance during the deployment process. The load was equated to a spring load, and the launch function test was conducted on the missile wing deployment mechanism under loading conditions. The test device is shown in Figure 33. The test of the wing deployment process under the applied load condition, the wing can be pushed out quickly under the normal load that varies linearly with the push-out distance in the range of 0~700 N.

Figure 33.
Wing load test.
5.2. Fundamental Frequency Test
The prototype of the developed clearance eliminator and the built modal test set are shown in Figure 34. The internal SMA driver of the prototype is heated by energizing. The support stiffness of the wing is tested to verify the function of the clearance eliminator and to test the dynamic support stiffness performance after the wing is deployed.

Figure 34.
Modal test experiment.
As shown in Figure 34, the acceleration sensors are arranged at the four corners of the wing, and the vibration characteristics of the wing are measured by the LMS modal test system. The amplitude–frequency characteristics of the wing vibration are shown in Figure 35. The action of the clearance eliminator is obtained by the hammering test, and its mode of vibration is shown in Figure 36. The first-order frequency of the wing is about 220 Hz, which is smaller than the FEM results. There are three main reasons: 1. The rough mesh division of assembly leads to a low accuracy of the calculation results. 2. The material parameters used in assembly simulation cannot be completely consistent with the actual values. 3. There are errors and clearance during processing and assembly. Excessive bolt preload causes component deformation. By analyzing the mode of vibration, the support stiffness of one side of the wing is lower than the other side, indicating that the clearance eliminator on the weaker side has not fully eliminated the clearance of the kinematic pair of the wing. This is because the clearance is too large due to machining errors, exceeding the memory alloy actuator travel. In addition, the prototype has become deformed during the test process, making the clearance larger. According to the overall test results of the wing deployment mechanism, it can be verified that the function of the clearance eliminator meets the design requirements.
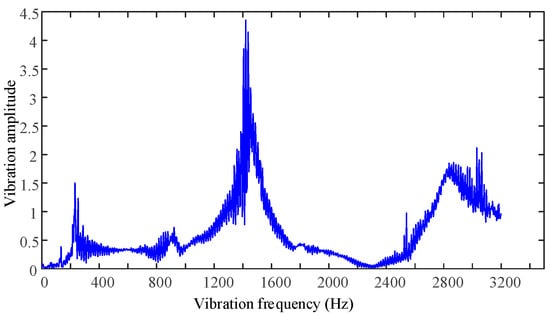
Figure 35.
The amplitude–frequency of the wing vibration.
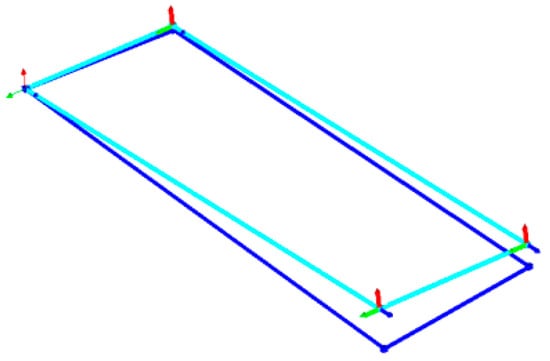
Figure 36.
The mode of wing vibration.
6. Conclusions
In order to achieve rapid ejection and high stiffness retention of the missile wings, a deployment mechanism with clearance elimination is proposed. The deployment performance and wing locking performance are studied through theoretical modeling, simulation and experiment. The static load bearing of the deployment mechanism is analyzed, and the stresses of the overall and internal components of the deployment mechanism are obtained. The static stiffness characteristics of the deployment mechanism are analyzed, and the deflection of the missile wing under load in the clearance state is obtained. The dynamic stiffness characteristics of the wing deployment mechanism are analyzed, and the relationship between the locking force and the dynamic support stiffness of the wing is obtained. The influences of the collision force on the motion state of the wing are analyzed. The kinetic simulations are conducted to obtain the displacement and velocity response to time during the launch of the wing. Static simulation analysis is carried out to obtain the force and deformation of the wing deployment mechanism under static load conditions. The modal analysis, harmonic response analysis, and random vibration analysis are conducted for the locking and clearance elimination states, respectively. The results show that the overall joint stiffness is high and the stability is great. The prototype of the deployment mechanism has been developed with an ejection stroke of 75 mm. High-speed camera recording results show that the deployment time is 0.14 s. Under the simulated load of the springs, the actuation of the deployment mechanism is reliable and stable. The vibration characteristics of the wings are measured by the LMS modal test system. The results show that the first-order frequency of the wing is about 220 Hz after the gap elimination, indicating good dynamic support stiffness is achieved. The designed deployment mechanism with gap compensation achieves fast ejection and high stiffness retention. In future research, we will enhance the performance of the deployment mechanism with a clearance eliminator to improve actuation synchronization and consistency.
Author Contributions
Conceptualization, H.Y. and F.Y.; methodology, Y.Z. and T.L.; software, Y.Z. and Y.G.; validation, X.Y., S.C. and Y.Z.; formal analysis, F.Y. and Y.G.; investigation, S.C. and Y.G.; resources, F.Y.; data curation, S.C. and T.L.; writing—original draft preparation, Y.Z.; writing—review and editing, X.Y. and Y.G.; visualization, X.Y. and T.L.; supervision, F.Y. and S.C.; project administration, H.Y.; funding acquisition, H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (52075118).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The author would like to thank the reviewers and the editors for their valuable comments and constructive suggestions that helped to improve the paper significantly.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Allen, J.M. Aerodynamics of an Axisymmetric Missile Concept Having Cruciform Strakes and In-Line Tail Fins from Mach 0.60 to 4.63, Supplement; NASA: Washington, DC, USA, 2005. [Google Scholar]
- McDaniel, D.R.; Nichols, R.H.; Eymann, T.A.; Starr, R.E.; Morton, S.A. Accuracy and Performance Improvements to Kestrel’s Near-Body Flow Solver. In AIAA Paper 2016–1051; AIAA: San Diego, CA, USA, 2016. [Google Scholar]
- Kim, D.H.; Lee, I.; Paek, S.K. Nonlinear Aeroelastic Instability of a Supersonic Missile Wing with Pitch Axis Freeplay. Int. J. Aeronaut. Space Sci. 2003, 4, 53–62. [Google Scholar] [CrossRef]
- Eidell, M.; Nance, R.; McGowan, G.; Carpenter, J.; Moore, F. Computational Investigation of Roll Damping for Missile Configurations. In Proceedings of the 30th AIAA Applied Aerodynamics Conference, New Orleans, LA, USA, 25–28 June 2012. [Google Scholar]
- Ghoreyshi, M.; Jirasek, A.; Aref, P.; Seidel, J. Computational aerodynamic investigation of long strake-tail missile configurations. Aerosp. Sci. Technol. 2022, 127, 107704. [Google Scholar] [CrossRef]
- Kim, S.I. Analysis of Folding Wing Deployment with Aero and Restraint Effects. J. Korean Soc. Aeronaut. Space Sci. 2015, 43, 533–539. [Google Scholar] [CrossRef]
- Kroyer, R. Wing mechanism analysis. Comput. Struct. 1999, 72, 253–265. [Google Scholar] [CrossRef]
- Yang, J.; Wen, L.; Jiang, B.; Wang, Z. Dynamic Modeling and Flight Simulation of a Folding Wing-Tip UAV. In Proceedings of the 2020 Chinese Control and Decision Conference (CCDC), Hefei, China, 22–24 August 2020. [Google Scholar]
- John, D.; Pawel, C.; Barry, L. Flight Dynamic Simulation Assessment of a Morphable Hyper-Elliptic Cambered Span Winged Configuration. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Austin, TX, USA, 11–14 August 2003. [Google Scholar]
- Matthew, S.P.; Brian, S.; Franklin, E.E.; Geoffrey, F.J. Vibration and Flutter Characteristics of a Folding Wing. J. Aircr. 2009, 46, 791–799. [Google Scholar]
- Obradovic, B.; Subbarao, K. Modeling of flight dynamics of morphing wing aircraft. J. Aircr. 2012, 48, 391–402. [Google Scholar] [CrossRef]
- Samuel, J.B.; Pines, D. Design and testing of a pneumatic telescopic wing for unmanned aerial vehicles. J. Aircr. 2007, 44, 1088–1099. [Google Scholar] [CrossRef]
- Joo, J.J.; Sers, B.; Johnson, T.; Frecker, M.I. Optimal Actuator Location within a Morphing Wing Scissor Mechanism Configuration. In Proceedings of the Conference on Smart Structures and Materials 2006: Modeling, Signal Processing, and Control, San Diego, CA, USA, 27 March 2006. [Google Scholar]
- Xu, H.; Huang, Q.; Han, J.; Yun, H.; Xie, X.P. Calculation of hinge moments for a folding wing aircraft based on high-order panel method. Math. Probl. Eng. 2020, 2020, 8881233. [Google Scholar] [CrossRef]
- Henry, J.; Schwartz, D.R.; Soukup, M.A.; Altman, A. Design, construction, and testing of a folding-wing, tube-launched micro air vehicle. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar]
- Vos, R.; Gurdal, Z.; Abdalla, M. Mechanism for warp-controlled twist of a morphing wing. J. Aircr. 2010, 47, 450–457. [Google Scholar] [CrossRef]
- Manzo, J.; Garcia, E. Demonstration of an in situ morphing hyperelliptical cambered span wing mechanism. Smart Mater. Struct. 2010, 19, 025012. [Google Scholar] [CrossRef]
- Xilun, D.; Anwei, Q.; Kun, X.U. Design and analysis of a scissor-bending deployable and foldable mechanism. J. Mech. Eng. 2020, 56, 55. [Google Scholar]
- Abdulrahim, M.; Lind, R. Flight testing and response characteristics of a variable gull-wing morphing aircraft. AIAA Pap. 2004, 5113, 16–19. [Google Scholar]
- Barbarino, S.; Gandhi, F.; Webster, S.D. Design of extendable chord sections for morphing helicopter rotor blades. J. Intell. Mater. Syst. Struct. 2011, 22, 891–905. [Google Scholar] [CrossRef]
- Brailovski, V.; Terriault, P.; Georges, T.; Coutu, D. SMA actuators for morphing wings. Phys. Procedia 2010, 10, 197–203. [Google Scholar] [CrossRef]
- Woods, B.K.S.; Friswell, M.I.; Wereley, N.M. Advanced kinematic tailoring for morphing aircraft actuation. AIAA J. 2014, 52, 788–798. [Google Scholar] [CrossRef]
- Heo, H.; Ju, J.; Kim, D.M. Compliant cellular structures: Application to a passive morphing airfoil. Compos. Struct. 2013, 106, 560–569. [Google Scholar] [CrossRef]
- Guyot, D.; Schülein, E. Novel Locally Swept Lattice Wings for Missile Control at High Speeds. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit DLR, Reno, NV, USA, 8–11 January 2007. [Google Scholar]
- Jian-guo, G.; Jun, Z. Modeling and Simulation Research of Missile with Morphing Wings. In Proceedings of the 2010 Second International Conference on Intelligent Human-Machine Systems and Cybernetics, Nanjing, China, 26–28 August 2010; IEEE: New York, NY, USA, 2010; Volume 76, pp. 280–283. [Google Scholar]
- Zhan, G.; Gong, Z.; Lv, Q.; Zhou, Z.; Wang, Z.; Yang, Z.; Zhou, D. Flight Test of Autonomous Formation Management for Multiple Fixed-Wing UAVs Based on Missile Parallel Method. Drones 2022, 6, 99. [Google Scholar] [CrossRef]
- Takahashi, T.T.; Spall, R.J.; Turner, D.C.; Birney, M.A. Multi-Disciplinary Survey of Advanced Subsonic Tactical Cruise Missile Configuration. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar]
- Zhang, Y.; Chen, W.; Guo, C.; Zhang, Z.; Li, P. Simulation research on roll attitude initialization algorithm for fixed wing canards. In Proceedings of the 2017 IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 6–9 August 2017; IEEE: New York, NY, USA, 2017; pp. 1292–1296. [Google Scholar]
- Zhang, J.; Yan, J. A Novel Control Approach for Flight-Stability of Fixed-Wing UAV Formation with Wind Field. IEEE Syst. J. 2020, 15, 2098–2108. [Google Scholar] [CrossRef]
- Li, P.; Ni, Y.; Hou, C.; Wan, X.; Zhao, M. Nonlinear aeroelastic modeling of a folding wing structure. J. Phys. Conf. Ser. 2019, 1215, 012009. [Google Scholar] [CrossRef]
- Dowell, E.H.; Tang, D.; Attar, P.J. Nonlinear aeroelastic study for folding wing structure. AIAA J. 2010, 48, 2187–2195. [Google Scholar]
- Tang, D.; Dowell, E.H. Theoretical and experimental aeroelastic study for folding wing structures. J. Aircr. 2008, 45, 1136–1147. [Google Scholar] [CrossRef]
- Otsuka, K.; Wang, Y.; Makihara, K. Deployable wing model considering structural flexibility and aerodynamic unsteadiness for deployment system design. J. Sound Vib. 2017, 408, 105–122. [Google Scholar] [CrossRef]
- Gao, Y.; Hu, M.; Zhao, D.; Gao, X.; Lin, J. Dynamics and reliability analysis of the deployment process of spring folding wing. In Proceedings of the 2020 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering, Xi’an, China, 8–11 October 2020. [Google Scholar]
- Gao, Y.; Hu, M.; Zhou, X.; Zhang, M. Reliability Evaluation for Cable-Spring Folding Wing Considering Synchronization of Deployable Mechanism. Actuators 2021, 10, 99. [Google Scholar] [CrossRef]
- Harris, J.; Slegers, N. Performance of a fire-and-forget anti-tank missile with a damaged wing. Math. Comput. Model 2009, 50, 292–305. [Google Scholar] [CrossRef]
- Wang, B.; Xie, L.; Fan, F.; Ma, H.; Zhao, B.; Li, H. Reliability analysis of folding wing deployable mechanism considering common cause failure. J. Mech. Eng. 2020, 56, 161–171. [Google Scholar]
- Geva, A.; Abramovich, H.; Arieli, R. Investigation of a Morphing Wing Capable of Airfoil and Span Adjustment Using a Retractable Folding Mechanism. Aerospace 2019, 6, 85. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).