ATSUKF-Based Actuator Health Assessment Method for Quad-Copter Unmanned Aerial Vehicles
Abstract
:1. Introduction
2. System Modeling
2.1. Quadcopter UAV Nonlinear System Model
- The UAV is a rigid body, which ignores the elastic vibration and deformation generated during flight.
- The inertia matrix, the gravitational acceleration and the mass are time-invariant.
- Control forces are almost always given in body-fixed frame.
- The geometric center coincides with the center of gravity.
- The effects of the ground effect are ignored.
2.2. Actuator Performance Degradation Model
2.3. State Space Model
3. ATSUKF-Based Actuator Health Assessment Algorithm
3.1. TSUKF-Based Algorithm
3.2. ATSUKF-Based Algorithm
4. Numerical Simulations
4.1. Simulation Parameters
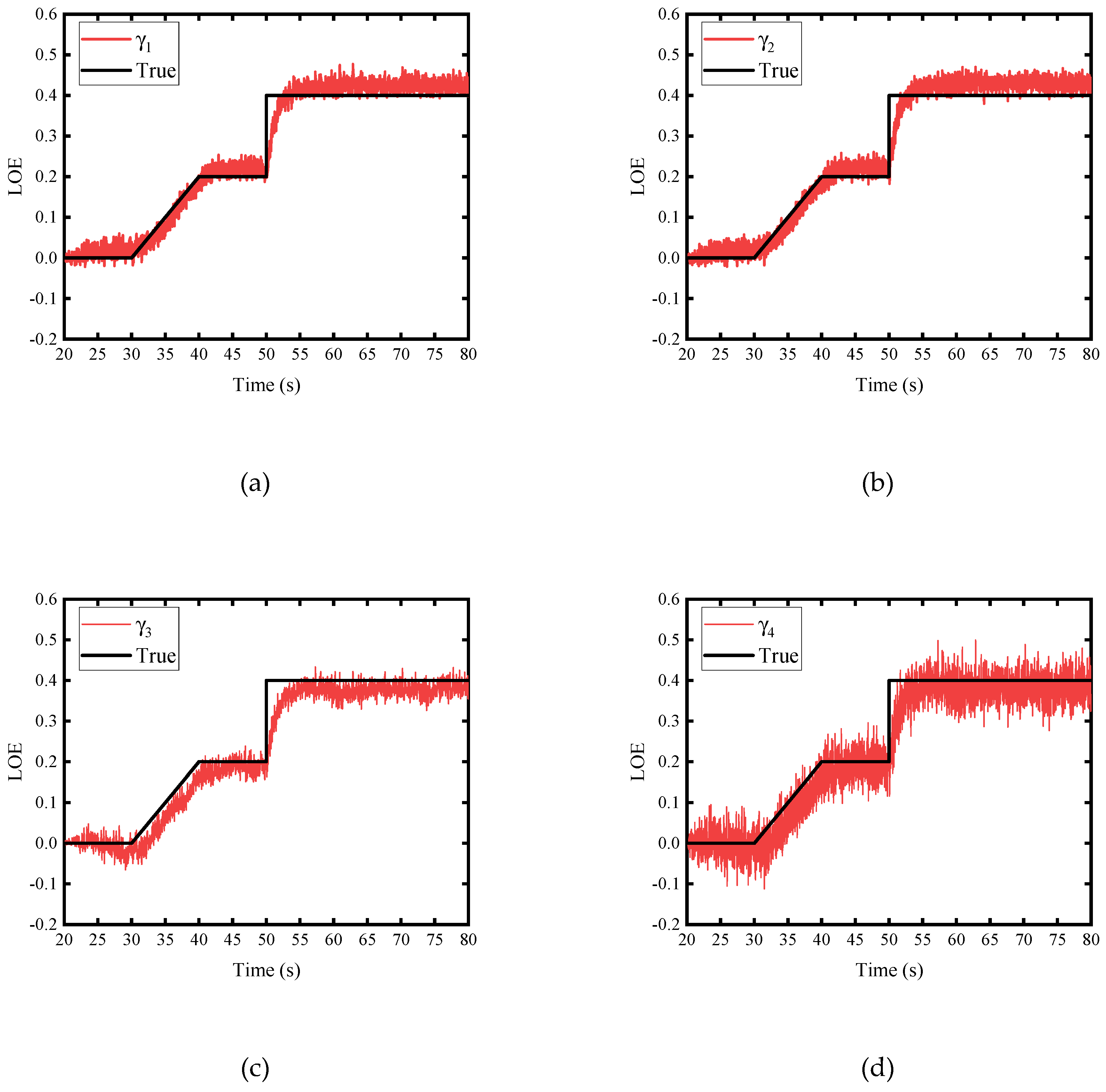
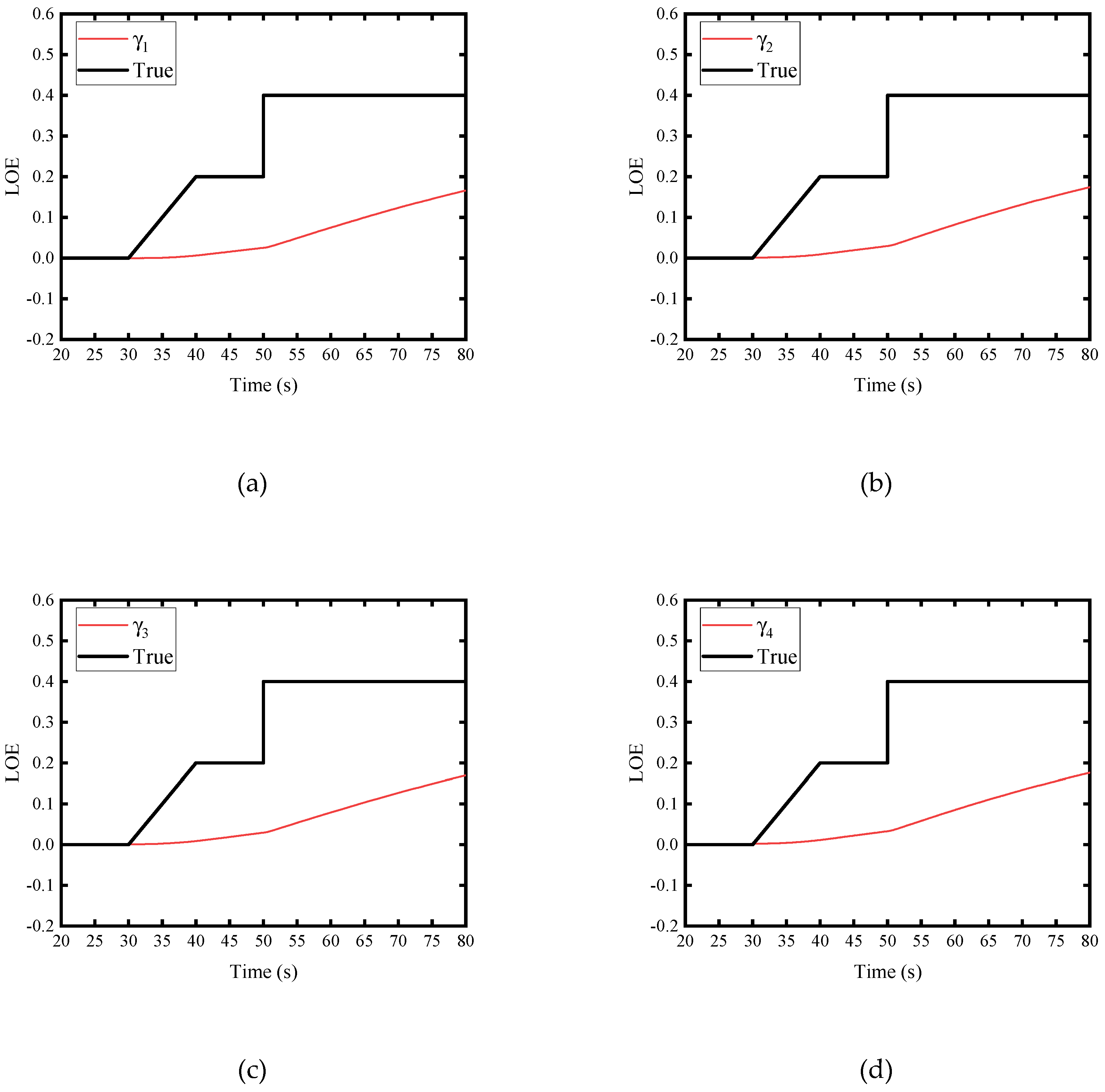
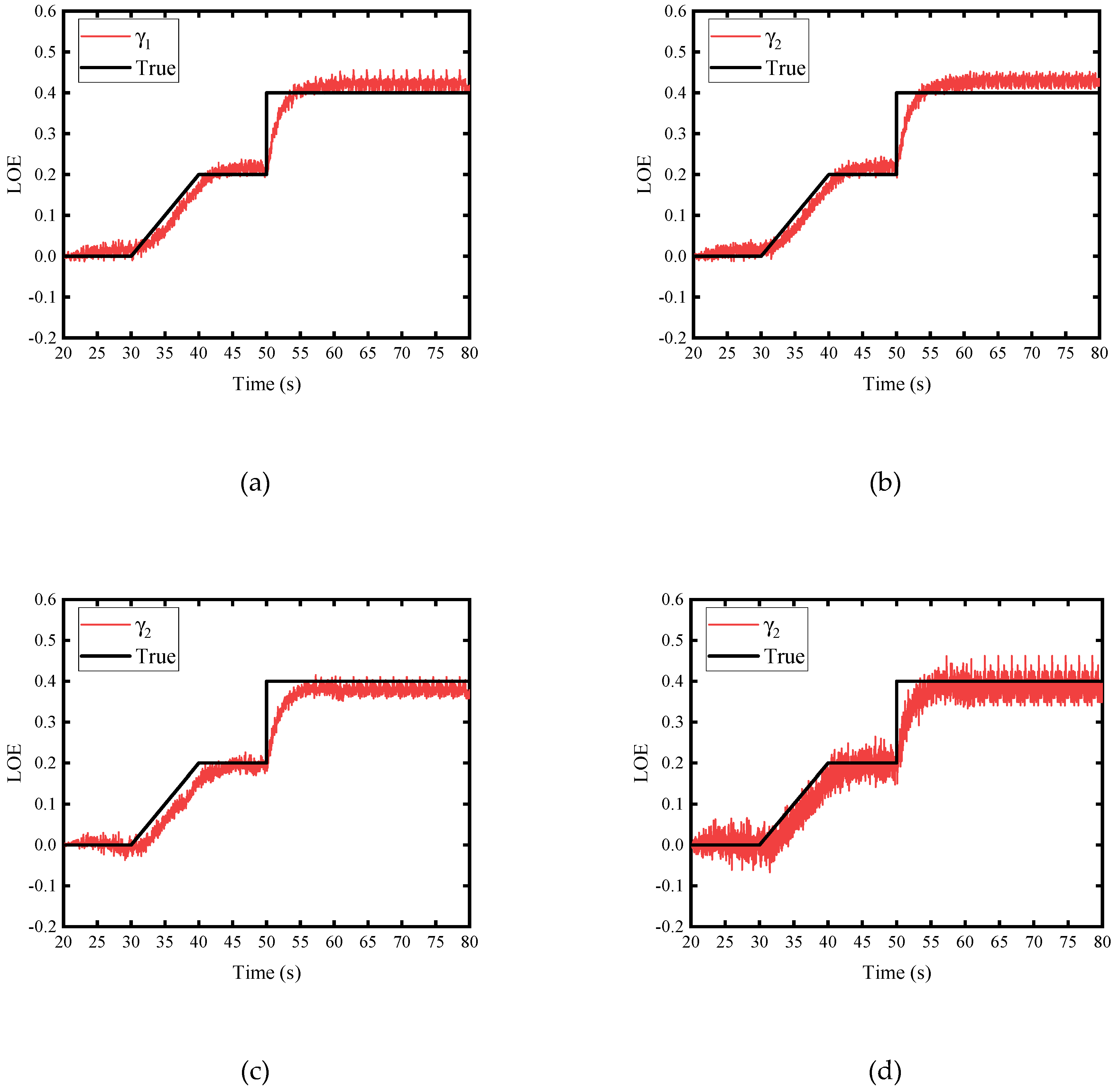
4.2. Simulation Results
4.2.1. Scenario 1: Performance Degradation of a Single Actuator
4.2.2. Scenario 2: Performance Degradation of Multiple Executors
5. Conclusions
- This health assessment method only requires the control input signal and the attitude signal during flight without the real-time operation information of the actuator.
- The actuator health assessment can also be realized without fully understanding the actuator health state and the dynamic model of external interference.
- The nonlinear system model can be directly used in the filtering process through the traceless transformation, and the sensitivity to the changes in the actuator health state is enhanced by combining the filter divergence judgment and covariance matching technology.
- It is not only applicable to single actuator health assessments but also to multiple actuator health assessments.
- It is not only applicable to quad-rotor UAVs but also to other multi-rotor UAVs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hussein, H.; Benjamin, L.; Isabelle, F.; Clovis, F. Data Fusion Fault Tolerant Strategy for a Quadrotor UAV under Sensors and Software Faults. ISA Trans. 2022, 1, 7. [Google Scholar] [CrossRef]
- Alemayehu, T.S.; Kim, J.H.; Yoon, W. Fault-Tolerant UAV Data Acquisition Schemes. Wirel. Pers. Commun. 2020, 114, 1669–1685. [Google Scholar] [CrossRef]
- Iglesis, E.; Horri, N.; Dahia, K.; Brusey, J.; Piet-Lahanier, H. Nonlinear Estimation of Sensor Faults With Unknown Dynamics for a Fixed Wing Unmanned Aerial Vehicle. In Proceedings of the 2021 International Conference on Unmanned Aircraft Systems (ICUAS), Athènes, Grèce, 19 July 2021. [Google Scholar] [CrossRef]
- Iglesis, E.; Horri, N.; Dahia, K.; Brusey, J.; Piet-Lahanier, H. Simultaneous Actuator and Sensor Faults Estimation for Aircraft Using a Jump-Markov Regularized Particle Filter. In Proceedings of the 2021 IEEE International Conference on Prognostics and Health Management (ICPHM), Détroit, MI, USA, 7–9 June 2021. [Google Scholar] [CrossRef]
- Ducard, G. The SMAC Fault Detection and Isolation Scheme: Discussions, improvements, and application to a UAV. In Proceedings of the 2013 Conference on Control and Fault-Tolerant Systems (SysTol), Nice, France, 9–11 October 2013; pp. 480–485. [Google Scholar] [CrossRef]
- Ren, X.L. Observer Design for Actuator Failure of a Quadrotor. IEEE Access 2020, 8, 152742–152750. [Google Scholar] [CrossRef]
- Patton, R.J. Robust model-based fault diagnosis: The state of the art. IFAC Proc. Vol. 1994, 27, 1–24. [Google Scholar] [CrossRef]
- Savkin, A.V.; Petersen, I.R. Model validation for robust control of uncertain systems with an integral quadratic constraint. Automatica 1996, 32, 603–606. [Google Scholar] [CrossRef]
- Friedland, B. Treatment of bias in recursive filtering. IEEE Trans. Autom. Control 1969, 14, 359–367. [Google Scholar] [CrossRef]
- Gillijns, S.; Moor, B.D. Brief paper: Unbiased minimum-variance input and state estimation for linear discrete-time systems. Automatica 2007, 43, 111–116. [Google Scholar] [CrossRef]
- Steven, G.; Moor, B.D. Unbiased minimum-variance input and state estimation for linear discrete-time systems with direct feedthrough. Automatica 2007, 43, 934–937. [Google Scholar] [CrossRef]
- Simon, D.J. Optimal State Estimation: Kalman, H∞, and Nonlinear Approaches; Wiley-Interscience: New York, NY, USA, 2006. [Google Scholar]
- Zhang, H.; Gao, Q.; Pan, F. An Online Fault Diagnosis Method for Actuators of Quadrotor UAV with Novel Configuration Based on IMM. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhang, Y.; Zhang, W.; Zuo, J.; Zhan, H. Robust Actuator Fault Detection and Diagnosis for a Quadrotor UAV with external Disturbances. IEEE Access 2018, 6, 1. [Google Scholar] [CrossRef]
- Gao, J.; Zhang, Q.; Chen, J. EKF-Based Actuator Fault Detection and Diagnosis Method for Tilt-Rotor Unmanned Aerial Vehicles. Math. Probl. Eng. 2020, 1, 1–12. [Google Scholar] [CrossRef]
- Qi, J.T.; Jiang, Z.; Zhao, X.G. Adaptive UKF and Its Application in Fault Tolerant Control of Rotorcraft UAV. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Hilton Head, SC, USA, 20–23 August 2007. [Google Scholar] [CrossRef] [Green Version]
- Bouabdallah, S.; Pierpaolo, M.; Roland, S. Design and control of an indoor micro quadrotor. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004. [Google Scholar] [CrossRef] [Green Version]
- Zio, E. Reliability engineering: Old problems and new challenges. Reliab. Eng. Syst. Saf. 2009, 94, 125–141. [Google Scholar] [CrossRef] [Green Version]
- Botchev, V. Kalman filtering: With real-time applications. Comput. Rev. 2020, 51, 404–405. [Google Scholar] [CrossRef] [Green Version]
- He, Q.; Zhang, W.; Liu, X.; Liu, J. Information Fusion and Reconstruction of Key Sensors in a Flight Control System in Constant Wind Field based on Two Stage EKF. In Proceedings of the 2016 IEEE Chinese Guidance, Navigation and Control Conference (CGNCC), Nanjing, China, 12 August 2016. [Google Scholar] [CrossRef]
- Julier, S.J. Unscented Filtering and Nonlinear Estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef]
- Chen, X.; Sun, R.; Wang, F.; Song, D.; Jiang, W. Two-stage unscented kalman filter algorithm for fault estimation in spacecraft attitude control system. IET Control. Theory Appl. 2018, 12, 1781–1791. [Google Scholar] [CrossRef]
- Li, W.; Wang, C.W. Research on life prediction and life extension method of feedback control system under actuator degradation. IEEE Access 2020, 4, 67. [Google Scholar]
- Sriyanand, H. A simple method for the control of divergence in Kalman-filter algorithms. Int. J. Control 1972, 16, 1101–1106. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, W. A new learning statistic for adaptive filter based on predicted residuals. Prog. Nat. Sci. 2006, 16, 833–837. [Google Scholar] [CrossRef]
- Quan, Q.; Dai, X.; Wang, S. Multicopter Design and Control Practice: A Series Experiments Based on MATLAB and Pixhawk; Springer Nature: Singapore, 2020. [Google Scholar]





| Parameter | Value | Unit |
|---|---|---|
| 1.4 | ||
| 9.8 | ||
| 0.0211 | ||
| 0.0219 | ||
| 0.0366 | ||
| 0.0225 | ||
| 11.18 | ||
| 0.0161 |
| Type | Parameter | Value |
|---|---|---|
| Covariance Matrix Parameters | ||
| Algorithm initial value | ||
| Algorithm initial value | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Zhang, M.; Li, G.; Qin, S.; Xu, C. ATSUKF-Based Actuator Health Assessment Method for Quad-Copter Unmanned Aerial Vehicles. Drones 2023, 7, 12. https://doi.org/10.3390/drones7010012
Zhang Z, Zhang M, Li G, Qin S, Xu C. ATSUKF-Based Actuator Health Assessment Method for Quad-Copter Unmanned Aerial Vehicles. Drones. 2023; 7(1):12. https://doi.org/10.3390/drones7010012
Chicago/Turabian StyleZhang, Zhenxin, Meng Zhang, Guoxi Li, Shilong Qin, and Chunxiao Xu. 2023. "ATSUKF-Based Actuator Health Assessment Method for Quad-Copter Unmanned Aerial Vehicles" Drones 7, no. 1: 12. https://doi.org/10.3390/drones7010012
APA StyleZhang, Z., Zhang, M., Li, G., Qin, S., & Xu, C. (2023). ATSUKF-Based Actuator Health Assessment Method for Quad-Copter Unmanned Aerial Vehicles. Drones, 7(1), 12. https://doi.org/10.3390/drones7010012






