Vision-Based Deep Reinforcement Learning of UAV-UGV Collaborative Landing Policy Using Automatic Curriculum
Abstract
:1. Introduction
- We propose an automatic curriculum learning framework for solving the UAV-UGV landing problem under different conditions of UGV motions and wind interference.
- We design a task difficulty discriminator to schedule the curriculum according to the levels of difficulty.
- We design a streamlined pipeline that enables rapid visual tracking while providing pose estimation for the DRL controller.
2. Preliminaries
2.1. Deep Reinforcement Learning
2.1.1. Reward Function Setup
2.1.2. TD3-Based Landing Controller
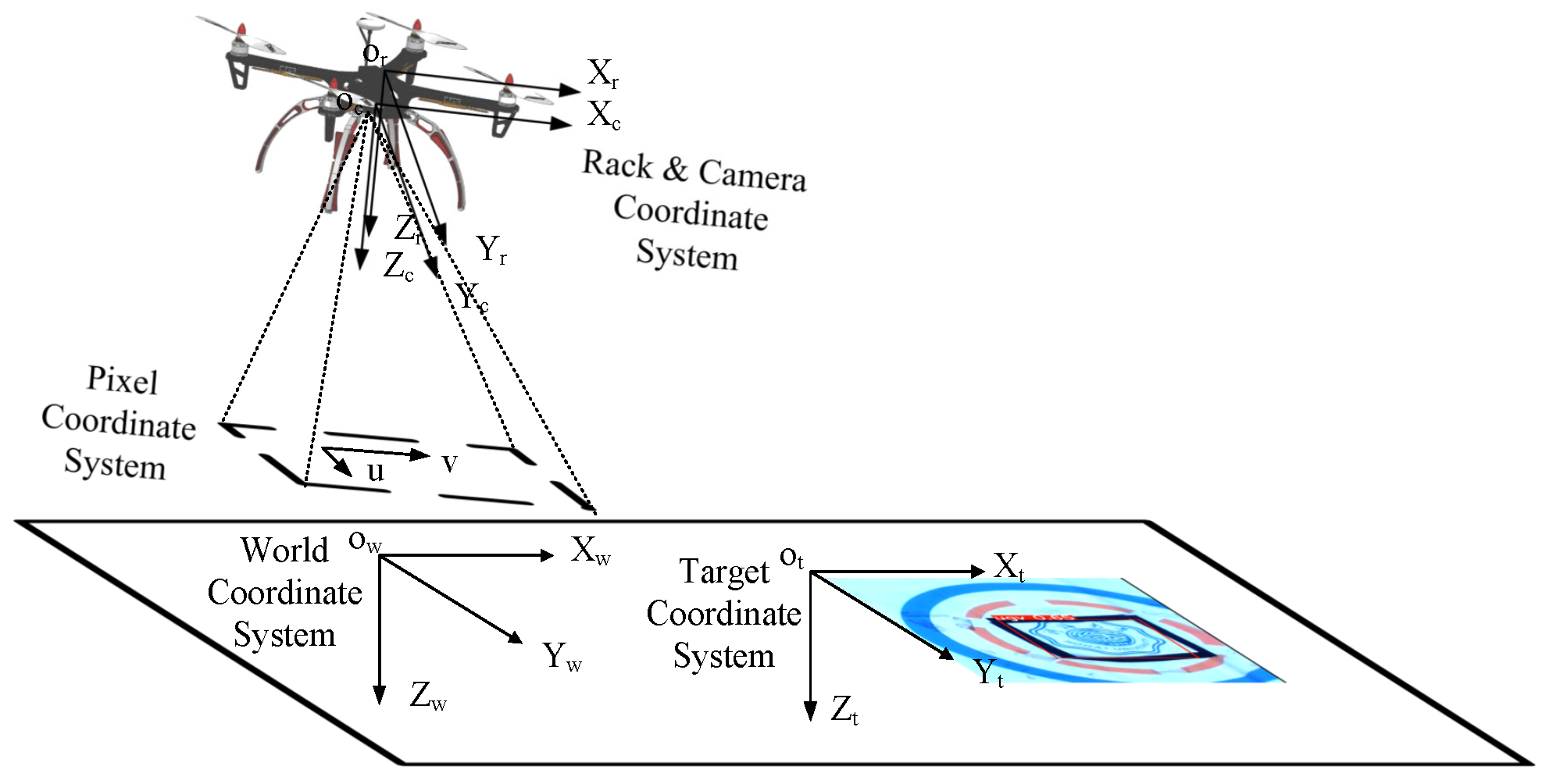
2.2. Coordinate System and the UAV Kinematics
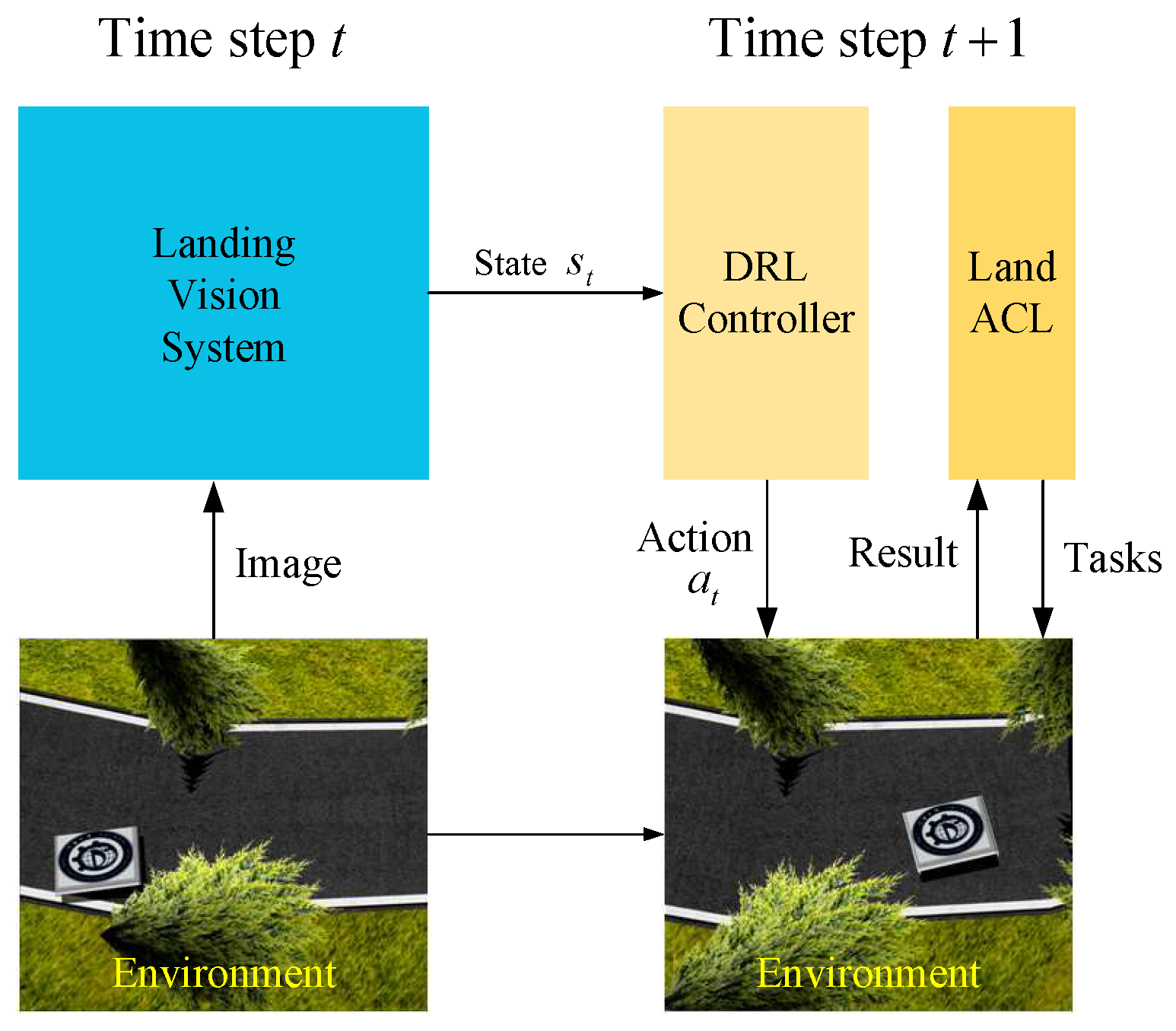
3. Method
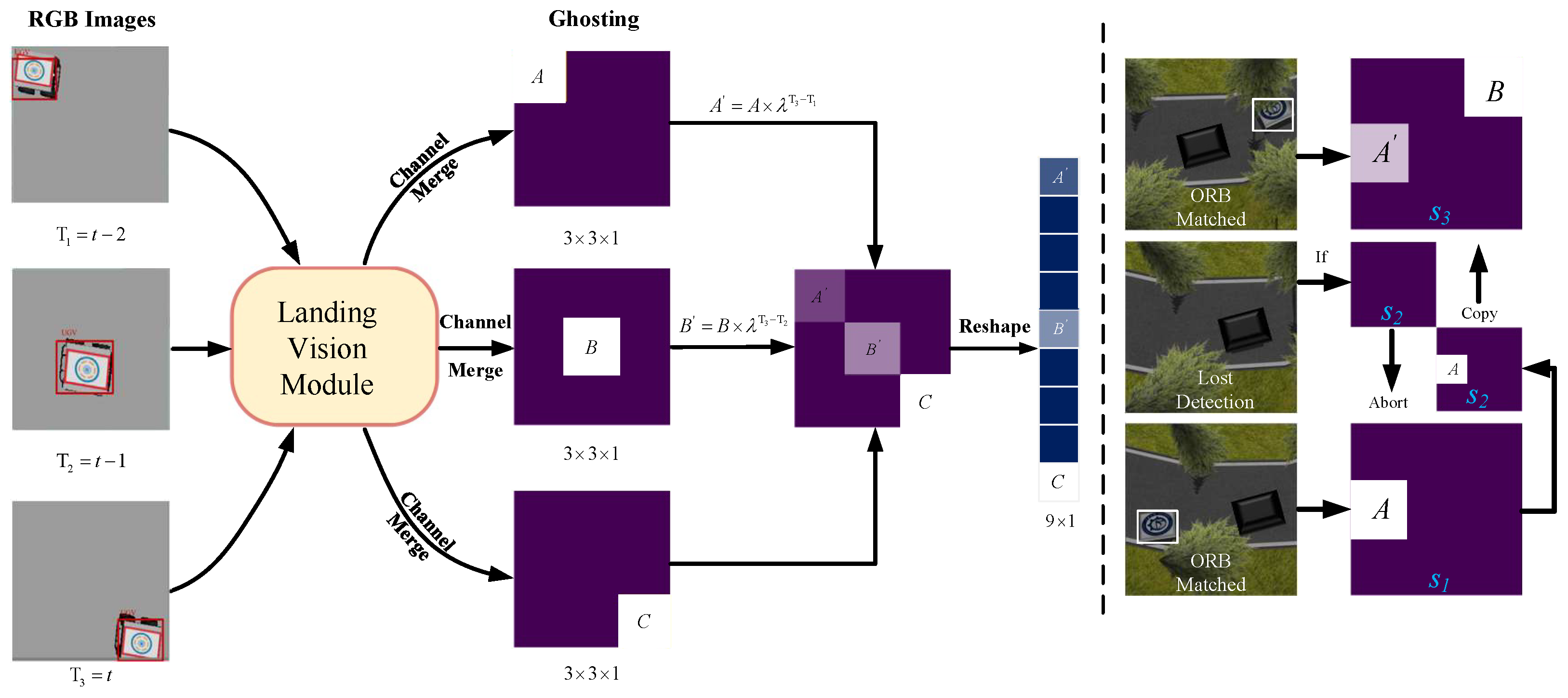
3.1. Landing Vision System
3.2. Automatic Curriculum Learning of the Landing Policy
3.2.1. Task Setup
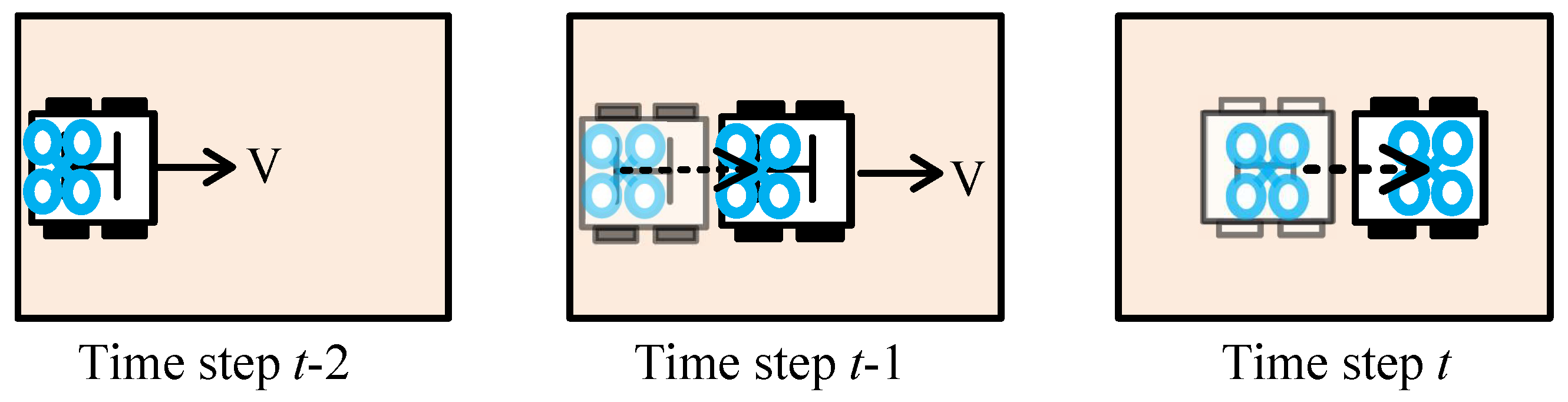
- : We introduce the task to provide the agent with primary signals for learning low-level principles of landing on the UGV. Specifically, the task contains a single variable: the UGV’s linear velocity . By introducing the task, our aim is to facilitate the agent to learn basic landing strategies, as shown in Figure 5. Moreover, the action policy learned in is intended to prepare the agent for the transition from to the subsequent task, addressing the gap that may arise during task switching.
- : The task is designed to facilitate learning to land in complex situations. The task incorporates two additional variables based on the task: angular velocity and speed acceleration , as illustrated in Figure 6. We change the direction of at regular intervals. We intend to enhance the agent’s ability for quick response when dealing with unexpected environmental changes. In addition, the robustness of the landing process can also be improved through adding acceleration and steering.
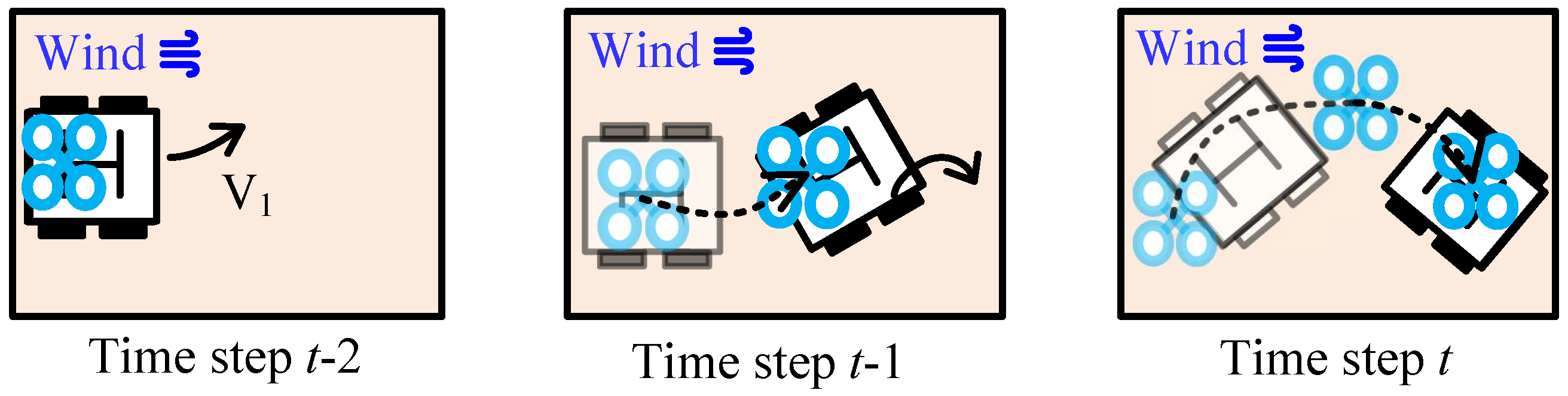
- : In order to further enhance the adaptability to complex environments for the policy, we introduce the task to facilitate learning to land with wind interference, which is simulated using continuous Gaussian noise added to the UAV’s maneuver commands. This Gaussian noise is limited to a magnitude of 0.3 m/s and lasts for a maximum of 2 s. Furthermore, we use the augmentation of as a simulated-to-real strategy to prepare the policy for handling environmental disruptions during real flights.
3.2.2. Land-ACL
| Algorithm 1 Land-ACL |
|
4. Experiments and Results
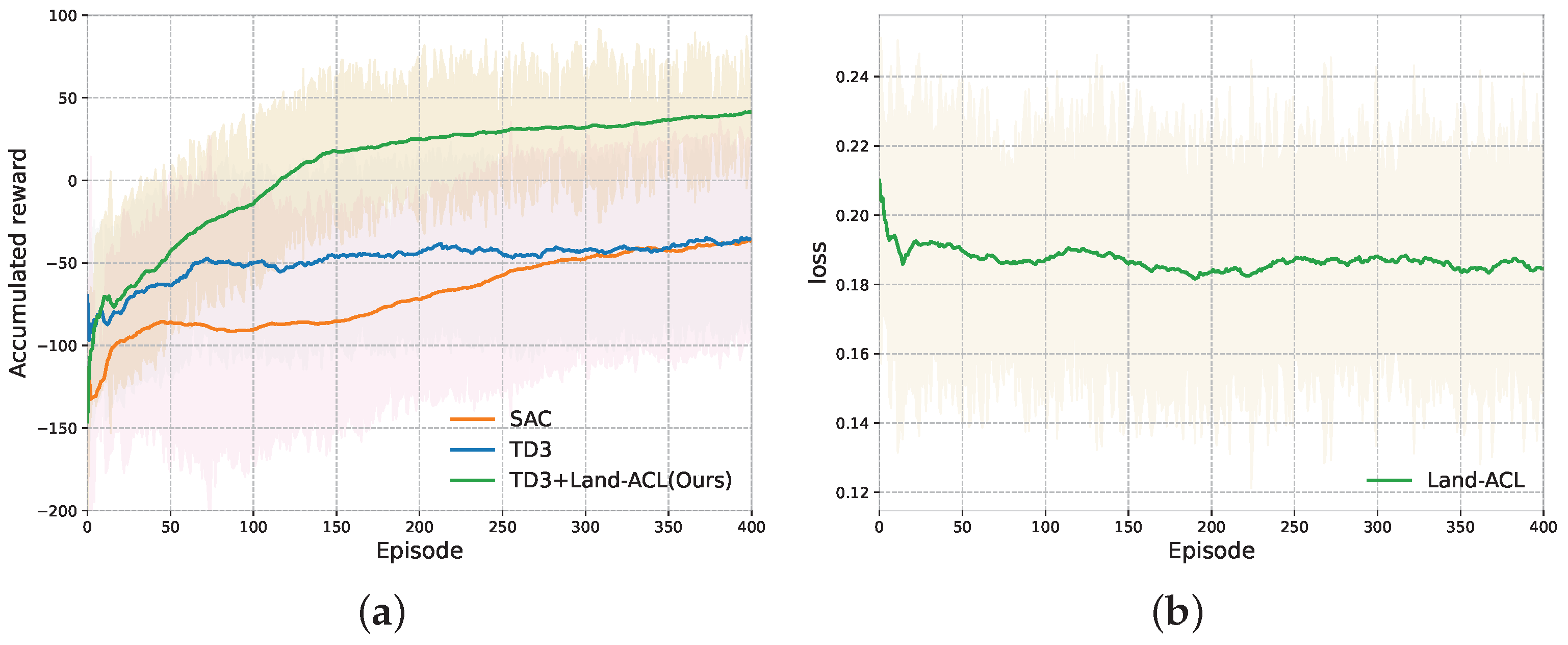
4.1. Simulated Trainings
4.2. Simulated Testings
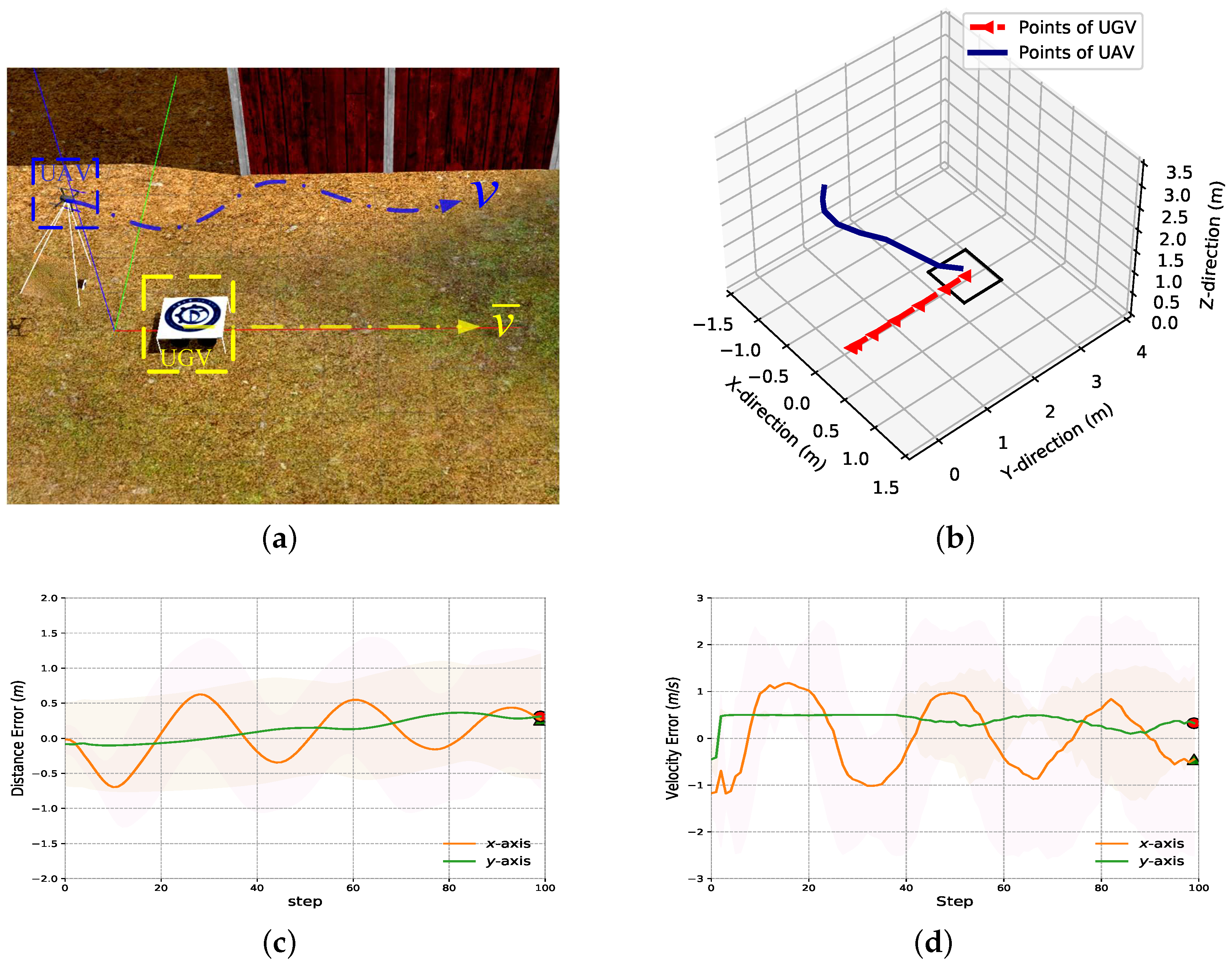
4.2.1. Test Scenario A: UGV Moving along a Straight Trajectory
4.2.2. Test Scenario B: UGV Moving along a Curved Trajectory
4.2.3. Landing Precision
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tokekar, P.; Hook, J.V.; Mulla, D.; Isler, V. Sensor Planning for a Symbiotic UAV and UGV System for Precision Agriculture. IEEE Trans. Robot. 2016, 32, 1498–1511. [Google Scholar] [CrossRef]
- Nex, F.; Remondino, F. UAV for 3D mapping applications: A review. Appl. Geomat. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Liu, P.; Chen, A.Y.; Huang, Y.-N.; Han, J.-Y.; Lai, J.-S.; Kang, S.-C.; Wu, T.-H.; Wen, M.-C.; Tsai, M.-H. A review of rotorcraft Unmanned Aerial Vehicle (UAV) developments and applications in civil engineering. Smart Struct. Syst. 2014, 13, 1065–1094. [Google Scholar] [CrossRef]
- Yin, D.; Yang, X.; Yu, H.; Chen, S.; Wang, C. An Air-to-Ground Relay Communication Planning Method for UAVs Swarm Applications. IEEE Trans. Intell. Veh. 2023, 8, 2983–2997. [Google Scholar] [CrossRef]
- De Souza JP, C.; Marcato AL, M.; de Aguiar, E.P.; Jucá, M.A.; Teixeira, A.M. Autonomous landing of UAV based on artificial neural network supervised by fuzzy logic. J. Control. Autom. Electr. Syst. 2019, 30, 522–531. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, C.; Baek, S.; Rawashdeh, S.; Mohammadi, A. Autonomous Landing of a UAV on a Moving Platform Using Model Predictive Control. Drones 2018, 2, 34. [Google Scholar] [CrossRef]
- Gautam, A.; Sujit, P.B.; Saripalli, S. A survey of autonomous landing techniques for UAVs. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014. [Google Scholar]
- Araar, O.; Aouf, N.; Vitanov, I. Vision Based Autonomous Landing of Multirotor UAV on Moving Platform. J. Intell. Robot. Syst. 2017, 85, 369–384. [Google Scholar] [CrossRef]
- Xin, L.; Tang, Z.; Gai, W.; Liu, H. Vision-Based Autonomous Landing for the UAV: A Review. Aerospace 2022, 9, 634. [Google Scholar] [CrossRef]
- Alam, S.; Oluoch, J. A survey of safe landing zone detection techniques for autonomous unmanned aerial vehicles (UAVs). Expert Syst. Appl. 2021, 179, 115091. [Google Scholar] [CrossRef]
- Wu, L.; Wang, C.; Zhang, P.; Wei, C. Deep Reinforcement Learning with Corrective Feedback for Autonomous UAV Landing on a Mobile Platform. Drones 2022, 6, 238. [Google Scholar] [CrossRef]
- Kakaletsis, E.; Symeonidis, C.; Tzelepi, M.; Mademlis, I.; Tefas, A.; Nikolaidis, N.; Pitas, I. Computer Vision for Autonomous UAV Flight Safety: An Overview and a Vision-based Safe Landing Pipeline Example. ACM Comput. Surv. 2021, 54, 1–37. [Google Scholar] [CrossRef]
- Patruno, C.; Nitti, M.; Petitti, A.; Stella, E.; D’orazio, T. A Vision-Based Approach for Unmanned Aerial Vehicle Landing. J. Intell. Robot. Syst. 2019, 95, 645–664. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Narvekar, S.; Peng, B.; Leonetti, M.; Sinapov, J.; Taylor, M.E.; Stone, P. Curriculum learning for reinforcement learning domains: A framework and survey. J. Mach. Learn. Res. 2020, 21, 7382–7431. [Google Scholar]
- Ren, Z.; Dong, D.; Li, H.; Chen, C. Self-Paced Prioritized Curriculum Learning with Coverage Penalty in Deep Reinforcement Learning. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 2216–2226. [Google Scholar] [CrossRef]
- Morad, S.D.; Mecca, R.; Poudel, R.P.K.; Liwicki, S.; Cipolla, R. Embodied Visual Navigation with Automatic Curriculum Learning in Real Environments. IEEE Robot. Autom. Lett. 2021, 6, 683–690. [Google Scholar] [CrossRef]
- Hu, Z.; Gao, X.; Wan, K.; Wang, Q.; Zhai, Y. Asynchronous Curriculum Experience Replay: A Deep Reinforcement Learning Approach for UAV Autonomous Motion Control in Unknown Dynamic Environments. IEEE Trans. Veh. Technol. 2023, 1–16. [Google Scholar] [CrossRef]
- Xue, H.; Hein, B.; Bakr, M.; Schildbach, G.; Abel, B.; Rueckert, E. Using Deep Reinforcement Learning with Automatic Curriculum Learning for Mapless Navigation in Intralogistics. Appl. Sci. 2022, 12, 3153. [Google Scholar] [CrossRef]
- Wang, Z.; Xuan, J.; Shi, T. Multi-label fault recognition framework using deep reinforcement learning and curriculum learning mechanism. Adv. Eng. Inform. 2022, 54, 101773. [Google Scholar] [CrossRef]
- Yan, C.; Wang, C.; Xiang, X.; Low, K.H.; Wang, X.; Xu, X.; Shen, L. Collision-Avoiding Flocking with Multiple Fixed-Wing UAVs in Obstacle-Cluttered Environments: A Task-Specific Curriculum-Based MADRL Approach. IEEE Trans. Neural Netw. Learn. Syst. 2023, 1–15. [Google Scholar] [CrossRef]
- Clegg, A.; Erickson, Z.; Grady, P.; Turk, G.; Kemp, C.C.; Liu, C.K. Learning to Collaborate From Simulation for Robot-Assisted Dressing. IEEE Robot. Autom. Lett. 2020, 5, 2746–2753. [Google Scholar] [CrossRef]
- Muzio, A.F.V.; Maximo, M.R.O.A.; Yoneyama, T. Deep Reinforcement Learning for Humanoid Robot Behaviors. J. Intell. Robot. Syst. 2022, 105, 1–16. [Google Scholar] [CrossRef]
- Fujimoto, S.; Hoof, H.; Meger, D. Addressing function approximation error in actor-critic methods. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; PMLR: London, UK, 2018; pp. 1587–1596. [Google Scholar]
- Rabelo, M.F.S.; Brandão, A.S.; Sarcinelli-Filho, M. Landing a uav on static or moving platforms using a formation controller. IEEE Syst. J. 2020, 15, 37–45. [Google Scholar] [CrossRef]
- Miller, A.; Miller, B.; Popov, A.; Stepanyan, K. UAV landing based on the optical flow video navigation. Sensors 2019, 19, 1351. [Google Scholar] [CrossRef] [PubMed]
- Wenzel, K.E.; Masselli, A.; Zell, A. Automatic Take Off, Tracking and Landing of a Miniature UAV on a Moving Carrier Vehicle. J. Intell. Robot. Syst. 2011, 61, 221–238. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; PMLR: London, UK, 2018. [Google Scholar]
- Chai, J.; Hayashibe, M. Motor Synergy Development in High-Performing Deep Reinforcement Learning Algorithms. IEEE Robot. Autom. Lett. 2020, 5, 1271–1278. [Google Scholar] [CrossRef]
- Hazarika, B.; Singh, K.; Biswas, S.; Li, C.-P. DRL-Based Resource Allocation for Computation Offloading in IoV Networks. IEEE Trans. Ind. Inform. 2022, 18, 8027–8038. [Google Scholar] [CrossRef]
- Compton, W.; Curtin, M.; Vogt, W.; Scheinker, A.; Williams, A. Deep Reinforcement Learning for Active Structure Stabilization. In Data Science in Engineering, Proceedings of the 40th IMAC, A Conference and Exposition on Structural Dynamics 2022, Florida, USA, 7–10 February 2022; Springer International Publishing: Cham, Switzerland, 2022; Volume 9. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Rodriguez-Ramos, A.; Sampedro, C.; Bavle, H.; de la Puente, P.; Campoy, P. A Deep Reinforcement Learning Strategy for UAV Autonomous Landing on a Moving Platform. J. Intell. Robot. Syst. 2019, 93, 351–366. [Google Scholar] [CrossRef]





| Task | Parameters | Description |
|---|---|---|
| Maximum linear velocity of UGV | ||
| , + | Maximum angular velocity and acceleration of UGV | |
| + | Maximum wind speed |
| Input | Network Dimensions | Output | Operator |
|---|---|---|---|
| , | FC1 | Leaky Relu | |
| FC1 | FC2 | Leaky Relu | |
| FC2 | P | Tanh |
| Scenario | Average Distance Error (m) | Total | Average Velocity Error (m/s) | Total | ||
|---|---|---|---|---|---|---|
| -Axis | -Axis | -Axis | -Axis | |||
| Scenario A | 0.45 ± 0.05 | 0.34 ± 0.04 | 0.56 | 1.12 ± 0.04 | 0.52 ± 0.03 | 1.23 |
| Scenario B | 0.47 ± 0.07 | 0.40 ± 0.05 | 0.62 | 1.15 ± 0.04 | 0.57 ± 0.01 | 1.28 |
| Algorithm | Average Distance (m) | (m) | Successful Landing Rate (%) |
|---|---|---|---|
| SAC | 0.86 | 0.33 | 24 |
| TD3 | 0.78 | 0.31 | 36 |
| TD3+Land-ACL | 91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Wang, J.; Wei, C.; Zhu, Y.; Yin, D.; Li, J. Vision-Based Deep Reinforcement Learning of UAV-UGV Collaborative Landing Policy Using Automatic Curriculum. Drones 2023, 7, 676. https://doi.org/10.3390/drones7110676
Wang C, Wang J, Wei C, Zhu Y, Yin D, Li J. Vision-Based Deep Reinforcement Learning of UAV-UGV Collaborative Landing Policy Using Automatic Curriculum. Drones. 2023; 7(11):676. https://doi.org/10.3390/drones7110676
Chicago/Turabian StyleWang, Chang, Jiaqing Wang, Changyun Wei, Yi Zhu, Dong Yin, and Jie Li. 2023. "Vision-Based Deep Reinforcement Learning of UAV-UGV Collaborative Landing Policy Using Automatic Curriculum" Drones 7, no. 11: 676. https://doi.org/10.3390/drones7110676
APA StyleWang, C., Wang, J., Wei, C., Zhu, Y., Yin, D., & Li, J. (2023). Vision-Based Deep Reinforcement Learning of UAV-UGV Collaborative Landing Policy Using Automatic Curriculum. Drones, 7(11), 676. https://doi.org/10.3390/drones7110676









