Abstract
Unmanned aerial vehicles (UAVs) open new methods for efficient and rapid transportation in urban logistics distribution, where task allocation is a significant issue. In urban logistics systems, the energy status of UAVs is a critical factor in ensuring mission fulfillment. While extensive literature addresses the energy consumption of UAVs during tasks, the feasibility of energy replenishment must be addressed, which introduces additional uncertainty to the task allocation. This paper realizes multi-tasking, considering the energy consumption and replenishment of UAVs, to ensure that the tasks can be accomplished while reducing energy consumption. This paper proposes uniform distribution K-means to realize balanced multi-task grouping. Based on the Monte Carlo tree search (MCTS), a task-allocation-oriented MCTS method is proposed, including improving the selection and simulation process of MCTS. The aim was to collaborate with multiple trees for node selection and record historical simulation information to guide subsequent simulations for better results. Finally, the optimality of the proposed method was validated by comparing it with other relevant MCTS methods through several randomized experiments.
1. Introduction
In recent years, unmanned aerial vehicles (UAVs) have made outstanding progress in structure, control systems, and communication systems [1]. With technological advances and cost reductions, the use of UAVs in areas such as mapping [2], agriculture [3], public safety [4], transportation systems [5], health systems [6], and logistics [7] has been gradually increasing, especially in the logistics sector.
Currently, the logistics industry is experiencing rapid growth, with the number of parcels delivered by various companies increasing annually. However, some inherent limitations and challenges are associated with traditional logistics and transportation methods, such as traffic congestion, transportation time, and high labor costs [8,9]. The emergence of UAVs brings excellent opportunities for change in the logistics industry. First, UAVs are not restricted by ground transportation conditions and can carry out rapid cargo distribution, significantly improving logistics efficiency [10]. Moreover, the flexibility of UAVs enables them to enter areas with complicated terrain or inconvenient transportation options, providing a new solution for logistics supply in remote areas and making up for the gaps that traditional logistics cannot cover [11]. Unlike traditional logistics’ dependence on petroleum resources [12], UAVs use clean energy, reducing energy needs [13,14]. The green and low-carbon application mode of UAVs could help to address problems such as environmental pollution and global warming and meet the needs of green and sustainable development [15,16].
Thanks to the high flexibility, low cost, and eco-friendliness of UAVs [17], many companies are actively exploring the introduction of UAVs into the logistics industry. As the world’s largest e-commerce company, Amazon has launched the Prime Air drone delivery service, aiming to deliver parcels to homes within 30 min [18]. As a globally renowned fast-food giant, Domino’s Pizza is a franchisee that has obtained the right to deliver pizzas by drone. Pizza delivery is strictly limited by local regulators. Therefore, with the authorization of the New Zealand government, they completed a test of drone pizza delivery [19]. The German logistics company Deutsche Post DHL has initiated a project called Parcelcopter, which delivers medical supplies by drone. This service is particularly suitable for remote areas and situations where drugs are urgently needed [20]. In addition, companies like Google, Walmart, and Alibaba are also committed to drone delivery research and have conducted a series of delivery tests [21].
Furthermore, to address the issue of UAV flight time being limited by battery capacity, some enterprises and scholars are focusing on the research of UAV docks [22,23]. UAV docks allow UAVs to land, change batteries automatically, and then take off again [24]. Through such a design, UAVs can undertake multiple tasks consecutively, extending the working hours of UAVs and laying the groundwork for UAV applications in logistics.
In the logistics industry, a core issue is allocating multiple tasks to different UAVs effectively. Allocating multiple tasks to multiple UAVs can be seen as a multi-robot task allocation (MRTA) problem. In the past few years, many studies have proposed various methods for MRTA problems, mainly categorized into methods based on linear programming, heuristic-based methods, and auction algorithms.
The task allocation problem for multiple UAVs or robots working collaboratively is a classic combinatorial optimization problem in mathematics and can be viewed as a 0–1 integer linear programming problem [25]. The primary method for solving linear programming problems in the early days was the Hungarian algorithm [26], which can be used to solve allocation optimization problems with one-to-one matching characteristics. Madridano designed a UAV task allocation system based on the Hungarian algorithm for building emergencies. This system assigned different tasks to UAVs based on parameters such as urgency and distance of the task [27]. Mixed-integer linear programming methods can handle more complex calculations and have been used to solve multi-objective task allocation problems for robots under uncertain conditions [28,29,30]. Linear programming is suitable for problems with solid constraint conditions, requiring the objective function of the problem to be linear.
Heuristic-based methods for solving MRTA problems can find optimal or near-optimal solutions while meeting specific constraints [31]. Based on heuristic information (such as robot positions and capabilities), heuristic methods evaluate and select heuristic information until a condition is met. For instance, the genetic algorithm for solving MRTA problems simulates the evolutionary mechanisms in nature to obtain relevant information during the search process, yielding the best allocation scheme [32,33,34]. Similarly, algorithms like particle swarm optimization (PSO) and ant colony optimization (ACO) can also be used to address MRTA problems [35,36,37]. However, heuristic-based methods converge slowly when faced with problems with large search spaces.
In recent years, increasing research has focused on addressing MRTA problems using auction algorithms [38]. Auction algorithms draw from the concept of market transactions, viewing tasks as bidding objects. Each robot bids based on its capabilities and requirements, ultimately forming an optimized task allocation scheme [31]. Based on auction algorithms, the consensus-based auction algorithm (CBAA) and consensus-based bundle algorithm (CBBA) have been used to solve single-task and multi-task allocation problems [39]. Moreover, Cheng successfully used auction algorithms to solve multi-UAV task allocation problems under multiple constraints [40]. Combining communication situations, some research has delved into impaired communication states’ impact on the performance of auction algorithms [41]. The Robot-Group Assignment Strategy also combines grouping strategies and auction algorithms, effectively solving MRTA problems [42].
With the continuous advancement of UAV technology and the increasing complexity of task allocation scenarios, the methods above have certain limitations when dealing with MRTA problems with various constraints. To address these challenges, some new approaches offer better solutions for MRTA problems, such as the Monte Carlo Tree Search (MCTS). MCTS was initially mainly used to improve computer performance in board games, especially in Go [43]. AlphaGo, developed by Google DeepMind, employed MCTS as its key component [44]. Moreover, MCTS has gradually been applied to broader domains. For instance, in ever-changing factory environments, MCTS can facilitate rapid automated decisions for human–machine collaboration [45]. Based on MCTS, signal control systems at intersections can be optimized, providing an effective solution for urban traffic management [46]. In autonomous driving technology, by combining reinforcement learning with MCTS, the unsafe behaviors of self-driving vehicles can be minimized, enhancing their performance in intricate settings [47]. In UAV-aided wireless systems, UAV planning problems are addressed using the random-MCTS (R-MCTS) strategy [48]. Furthermore, the greedy-MCTS (G-MCTS) strategy and a combined approach of the random–greedy simulation strategy (random–greedy-MCTS, RG-MCTS) can effectively tackle the weighted vertex coloring problem [49]. However, only some studies leverage MCTS to solve UAV task allocation challenges.
The information from the related literature and its method type is summarized in Table 1. Although there have been many studies on task allocation, some aspects have not been considered: (1) excess numbers of tasks can impact decision-making efficacy; (2) UAV task planning is strictly limited by energy and capacity; and (3) energy replenishment services of UAV docks should also be factored in. These aspects will introduce more uncertainties to the task allocation.

Table 1.
Summary of the related literature.
The core objective of this paper was to design an effective multi-task allocation method that considers the need for UAVs to be energized via UAV docks to meet the demands of performing longer-range and longer-time missions in the presence of limited UAV payload capacity and battery energy. In this paper, the process of task assignment was divided into two steps. Firstly, to reduce the search range of task allocation, this paper divided all the tasks into different sub-task groups and performed task allocation within each sub-task group. Secondly, for task allocation, this paper proposes the task allocation MCTS (TA-MCTS) method based on MCTS. TA-MCTS aims to minimize the energy consumption of UAVs, considers the constraints of load capacity and battery energy, and rationally formulates UAV flight strategies. The main methods are as follows:
(1) Based on the K-Means clustering method, this paper constrained the number of elements in each sub-task group so that it not only grouped all tasks but also ensured the same number of tasks were allocated to each sub-task group.
(2) Within the divided sub-task groups, task allocation was realized by multiple trees of MCTS corresponding to multiple UAVs.
(3) In the selection and expansion phase of MCTS, selection and expansion optimization strategies were proposed. By considering the energy state of the UAVs during the execution of the mission, the following possible nodes were selectively expanded to reduce the search range of the MCTS.
(4) In the simulation phase of MCTS, a simulation optimization strategy was proposed. The strategy utilized the simulation results during the multi-UAV task assignment process as heuristic information to guide the selection of tasks in the simulation phase.
2. Problem Description
2.1. Problem Scenario
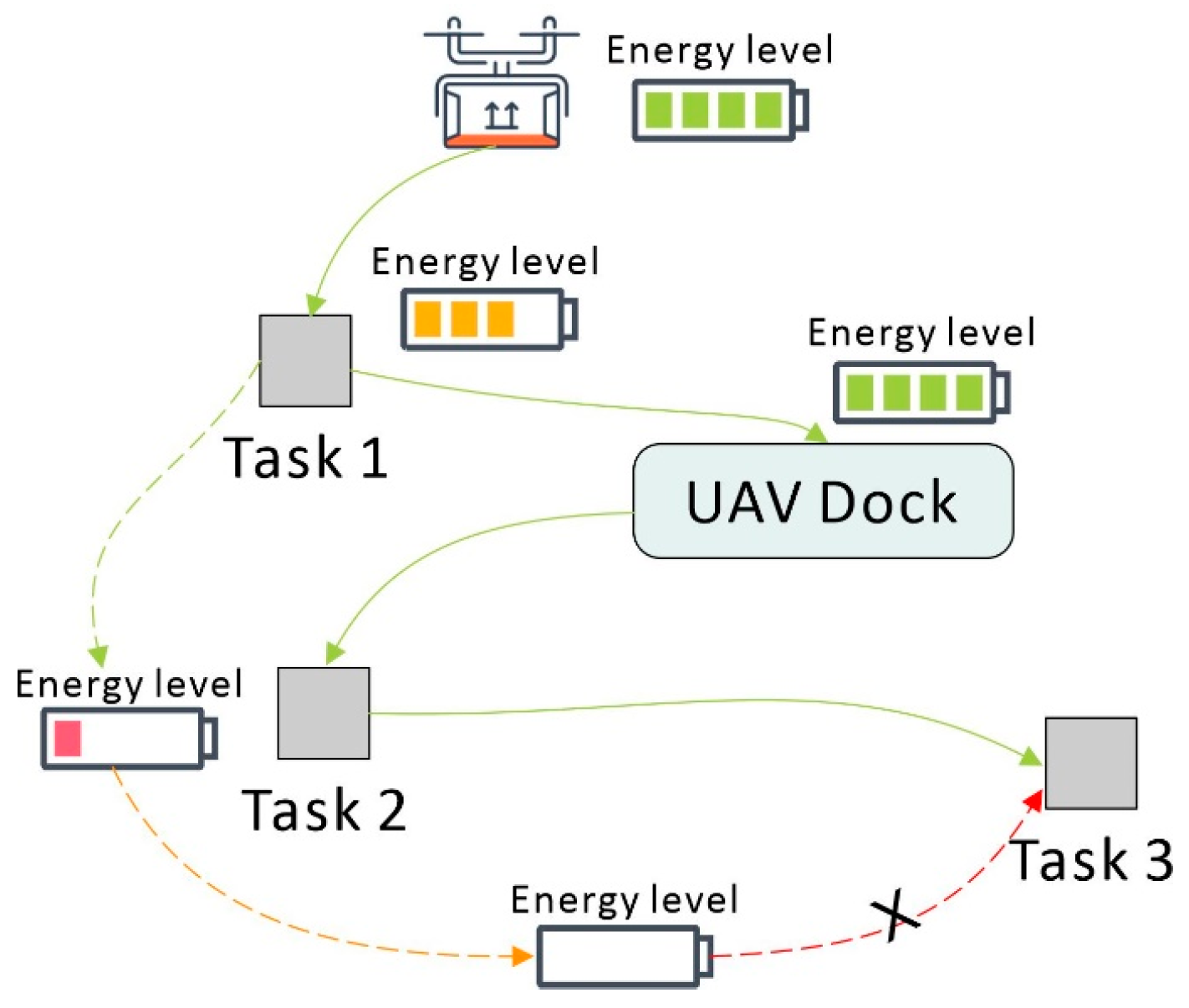
Urban UAV logistics is a complex system involving the interaction of multiple entities, including UAVs, distribution centers (DC), UAV docks, and task locations. In this paper, we mainly considered how to assign multiple tasks to UAVs to minimize energy consumption when UAVs have limited energy and UAV docks are available. As shown in Figure 1, although the energy of the UAV could meet the needs of tasks 1 and 2, it could not perform task 3. Therefore, the UAV should replace the battery at the dock after performing task 1 to reach the energy requirement for performing three tasks. Unlike the traditional allocation method, the consumption of UAV energy affects the task allocation process.
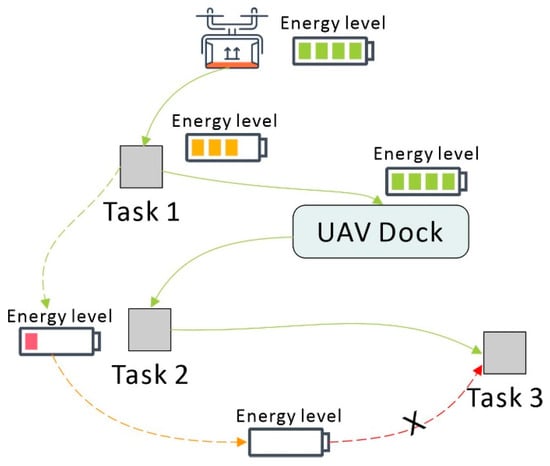
Figure 1.
Task selection considering the energy level.
To simplify the problem, the following assumptions were made in this paper:
- The distribution center covers a specific area, and the distribution targets of the task are distributed in this area.
- UAV docks are distributed in this area and serve as service stations for UAVs to change their batteries.
- The UAVs have limited energy sources, and when low on power, the UAVs need to travel to docks for battery replacement.
- The UAVs have limited carrying capacity, and each can only carry a limited number of items of the same weight.
- The UAVs maintain a consistent flight speed throughout the delivery process, correlating energy consumption per kilometer to the number of items carried.
2.2. Task Model
The task model and symbol are described as follows: Let denote the set of m UAVs, with the UAVs denoted by . Each UAV has the same attributes: average flight speed , average flight altitude , maximum number of items to be carried , maximum battery capacity , and energy consumed per kilometer . Let denote the set of tasks, with the tasks denoted by , and the task location denoted by their coordinates . is defined as Equation (1), where represents the energy consumed by the UAV per kilometer when no items are loaded, and is the number of loaded items. denotes the energy consumed by each item (based on the assumption that the weight of the items is the same).
When task is assigned to UAV , the energy required for UAV to accomplish is shown in Equation (2), where denotes the distance of the UAV from position to position .
In this paper, all tasks are grouped, and each sub-task group is denoted by , with the same number of tasks in each group denoted as . The following constraints are satisfied if the task group is feasible:
where indicates that task is assigned to UAV ; otherwise, . Equation (4) indicates that the number of items carried by each UAV cannot exceed the maximum limit, . Equation (5) indicates that, at most, one UAV is assigned to each task. indicates the energy left after UAV completes task . Equation (7) indicates that after completing the previous task, the UAV should have enough energy to reach the following task location.
Considering that the MRTA problem can be expressed as a minimization objective function, in this paper, the objective function was defined as all the energy consumed by the UAV to perform the tasks, and the objective function is shown in Equation (8) under the above constraints:
3. Methodology
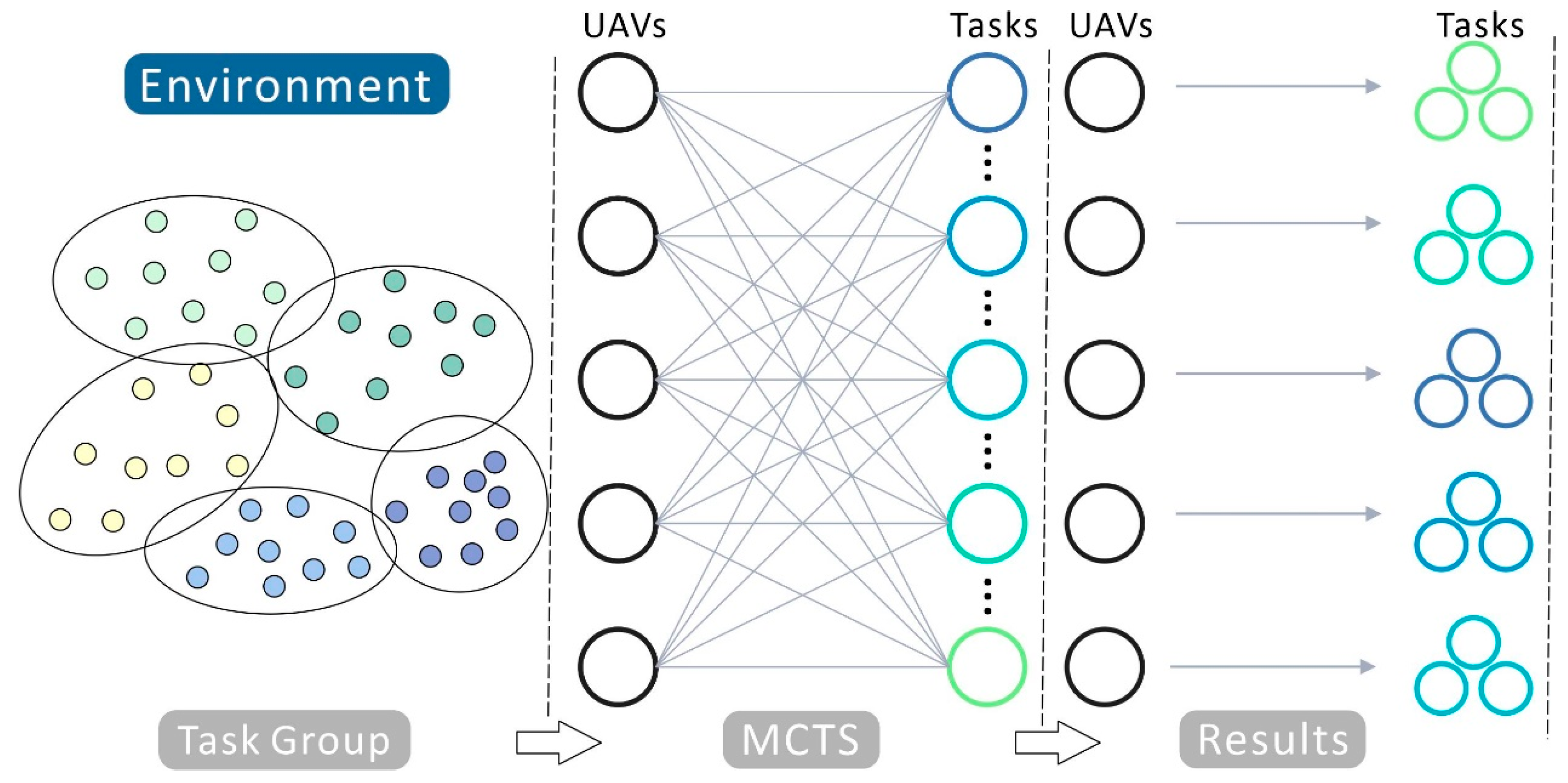
Generally, a DC in an urban area with many required delivery tasks is responsible for a specific area. In order to accomplish all the tasks with minimum energy consumption, the core idea of TA-MCTS proposed in this paper was to group the tasks and solve the multi-task assignment problem by local search, as shown in Figure 2. This consisted of two main aspects. Firstly, the tasks were grouped into multiple sub-task groups by improved K-means. Then, using MCTS, all the tasks contained in each group were assigned to multiple UAVs.
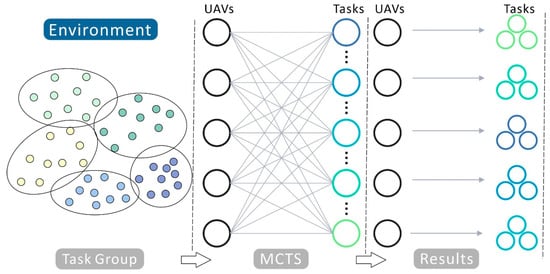
Figure 2.
Methodology of TA-MCTS. Solid circles in different colors representing divided sub-task groups.
3.1. Task Grouping Strategy
A direct assignment of all tasks in DC with many tasks would create a large-scale search range, leading to poor assignment results. Therefore, it was crucial to group all tasks according to UAV characteristics. These sub-task groups directly affected the way the UAV performed its tasks. Moreover, grouping results play a crucial role in reducing energy consumption.
According to the scenario in Section 2.1, the DC set in this paper was surrounded by multiple distribution task locations. Considering the load capacity of UAVs, this paper first clustered the tasks according to their locations. Currently, standard clustering methods include density-based, hierarchical, and partitioning clustering methods.
K-means, among the partitioned clustering methods, is widely used due to its efficiency. The K-means algorithm can randomly assign all tasks to K clusters, with K representing the number of groups. K-means bases its classification on the distances of each element from the center of each cluster without considering the number of elements in each cluster. However, during the task assignment process, if the clustering results in an unequal number of elements, it may result in the number of tasks exceeding the maximum load capacity of the UAV, which will thus fail to complete the task assignment.
In this paper, based on K-means, the uniform distribution K-means (UD-Kmeans) method was proposed to ensure that the number of elements in each cluster was the same according to the payload capacity of the UAV. is calculated as shown in Equation (9), where denotes the number of all sub-task groups, and the meanings of are shown in Section 2.2.
The details of the UD-Kmeans method are described in Algorithm 1. First, a point is randomly selected as the first clustering center from all task locations (Line 2). The shortest distance from each task location to the existing clustering center is calculated. Moreover, we select the next center point with a probability weighted by the square of the distance. The first clustering center is selected by the above method (Lines 3–9). When all the clustering centers are selected, each task is assigned to the nearest center to form a sub-task group (Lines 12–15). After that, whether the item number in each sub-task group exceeds the specified number is checked. If it is exceeded, the task that is farthest from the current is moved out of , and is moved into closest to (Lines 16–20). Then, the mean value of is calculated, and the clustering center is updated (Lines 22–24). The next iteration is carried out until the clustering center does not change.
| Algorithm 1: Uniform Distribution K-Means | |
| 1: | Initialization: |
| 2: | Construct a list of clustering centers |
| 3: | for to do |
| 4: | for each in do |
| 5: | , |
| 6: | end for |
| 7: | |
| 8: | Add new |
| 9: | end for |
| 10: | while is changed do |
| 11: | Clear all elements in |
| 12: | for each in do |
| 13: | |
| 14: | |
| 15: | end for |
| 16: | for each in do |
| 17: | while do |
| 18: | |
| 19: | |
| 20: | end while |
| 21: | end for |
| 22: | for each in do |
| 23: | |
| 24: | end for |
| 25: | end while |
3.2. MCTS Task Allocation
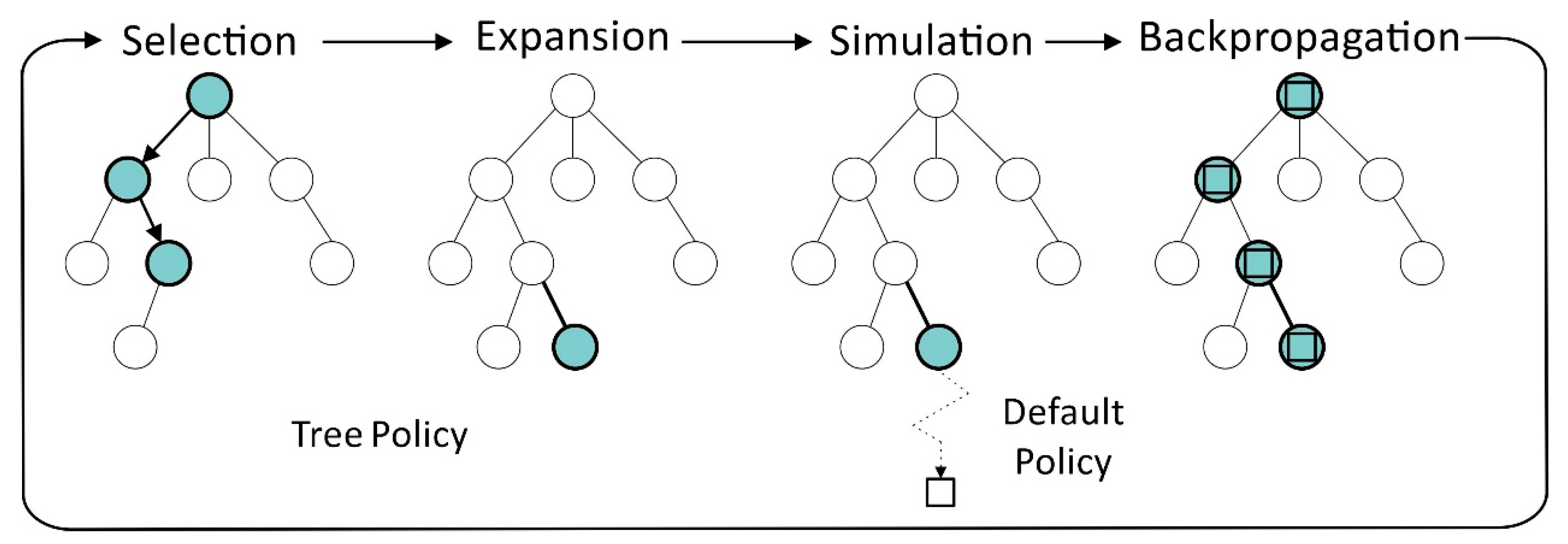
MCTS is widely used as a powerful method in games and decision-making problems. The method constructs a tree and stores information about each action through iterations, allowing for more illuminating decisions to be made in subsequent decisions. Figure 3 shows one complete iteration in MCTS.
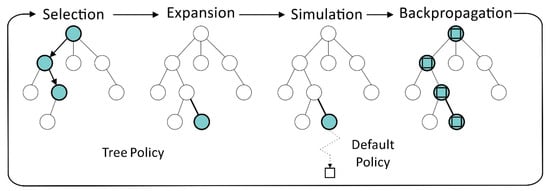
Figure 3.
One iteration of the MCTS approach.
Selection: From the root node, MCTS selects the node with the highest value in each iteration, according to the selection strategy.
Expansion: If a node is found that has not been expanded, one or more child nodes are added to this node to indicate the following possible action.
Simulation: Starting from the selected node, a series of actions are simulated until an end state is reached. Usually, a random or greedy strategy is adopted [50].
Backpropagation: MCTS propagates the simulation results to the root node and updates all nodes on the path.
In the selection phase, the upper confidence bounds for trees (UCT) method is most commonly used to balance exploration and exploitation of the entire tree, as shown in Equation (10):
where denotes the set of actions available in state . denotes the average reward of action in state . denotes the number of executions of action in state . denotes the number of all executions of state . is a constant controlling the balance between exploration and exploitation. A larger implies exploring more unvisited nodes; otherwise, it is more inclined to utilize visited nodes. With the reward value set within the range , favors the construction of the MCTS tree.
In this paper, based on MCTS, the TA-MCTS method was proposed to solve the multi-task assignment problem of UAVs. First, considering that there were multiple UAVs in the scene, constructing only one tree was expected to lead to a sharp increase in the number of nodes, affecting the search speed and efficiency. Therefore, this paper constructs a separate tree for each UAV.
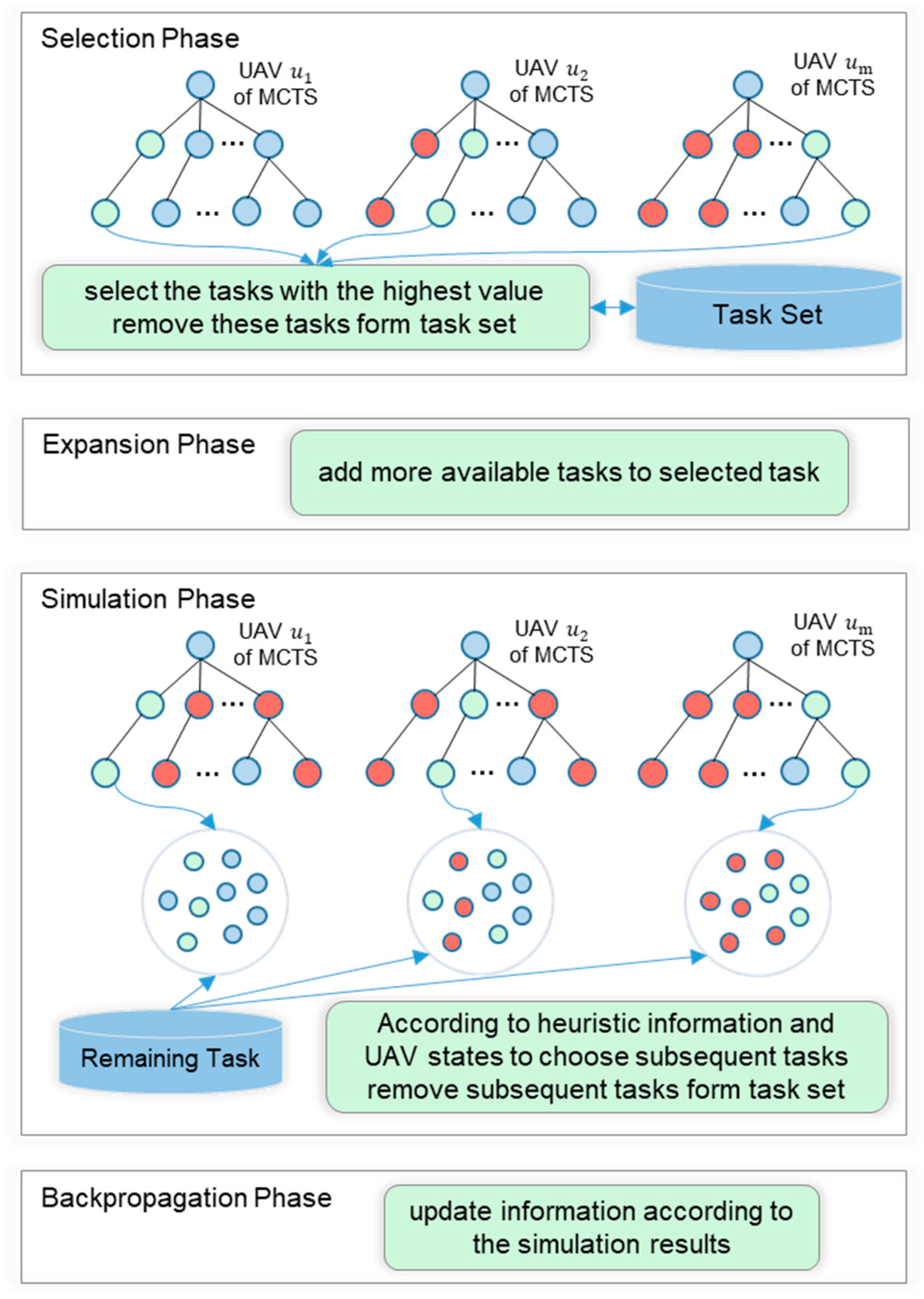
Figure 4 shows the process of TA-MCTS proposed in this paper. When searching multiple trees in TA-MCTS, a public task set is established to record the changes of selected tasks in the TA-MCTS process corresponding to each UAV to prevent task selection conflicts. Firstly, in this paper, we select a TA-MCTS process corresponding to a UAV, and according to the selection rule, a task is selected and removed from the task set to prevent it from being selected by other trees. After that, the node will expand according to the selected tasks. In the simulation phase, based on the historical information generated in the iterative process and the tasks selected by the current tree, the subsequent tasks that may be executed are obtained and removed from the task set. Finally, a backpropagation phase is performed to update the information.
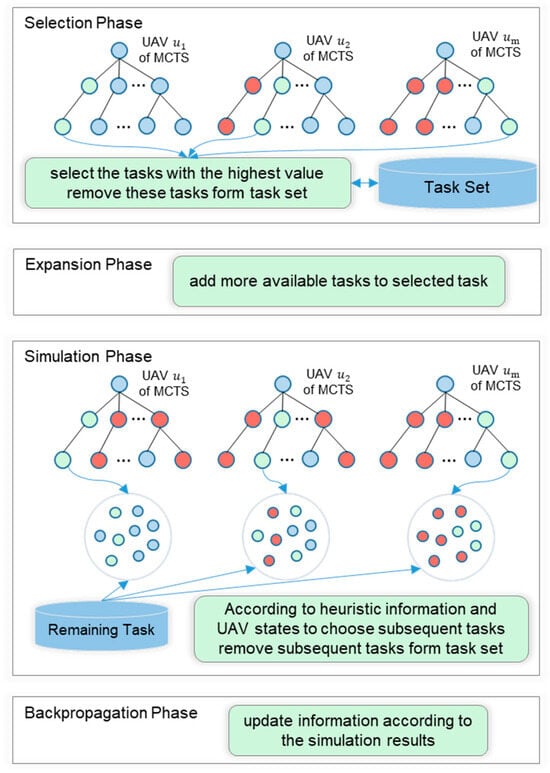
Figure 4.
One iteration of the TA-MCTS method. Blue nodes represent tasks that all UAVs have not selected. The green node represents a task that is currently selected by one of the UAVs. The red node cannot be selected because it represents a task that another UAV has already selected.
The TA-MCTS method has two essential aspects: the selection and expansion optimization strategy and the simulation optimization strategy.
Selection and Expansion Optimization Strategy (SEOS): In the selection phase of the MCTS, this strategy ensures that, in an iteration, in addition to considering the reward values of the nodes, there is no task conflict between each UAV. In the expansion phase, this strategy considers the energy consumption of UAVs and selectively expands the possible tasks according to the current energy status of UAVs. This method can efficiently build different nodes in the tree.
Simulation Optimization Strategy (SOS): During the MCTS tree construction, we recorded each node’s value as heuristic information. This information was used in subsequent simulations to compute more rational results.
Algorithm 2 shows the whole flow of the TA-MCTS method. TA-MCTS builds a search tree for each UAV and sets its state. A public task set is built to represent the tasks visited to avoid task selection conflicts (Lines 3–4). Define the matrix as an information repository to record the information for the simulation optimization strategy (Lines 5). Lines 6–15 represent all the processes during one iteration of TA-MCTS. First, a search tree corresponding to a UAV is selected. Following the node selection strategy, the tree selects and expands a task node. The simulation optimization strategy is used in the simulation process to guide nodes in choosing possible tasks. Finally, the backpropagation process updates the result based on the simulation outcome. During this process, is continuously updated to collaborate with the corresponding trees of different UAVs to prevent task conflicts. The notations and functions involved are further elaborated in Section 3.2.1 and Section 3.2.2.
| Algorithm 2: TA-MCTS | |
| 1: | Initialization: |
| 2: | |
| 3: | representing the DC. |
| 4: | denoting visited tasks |
| 5: | |
| 6: | while iterations are not completed do: |
| 7: | is randomly selected |
| 8: | |
| 9: | |
| 10: | then |
| 11: | |
| 12: | end if |
| 13: | |
| 14: | |
| 15: | end while |
3.2.1. Selection and Expansion Optimization Strategy
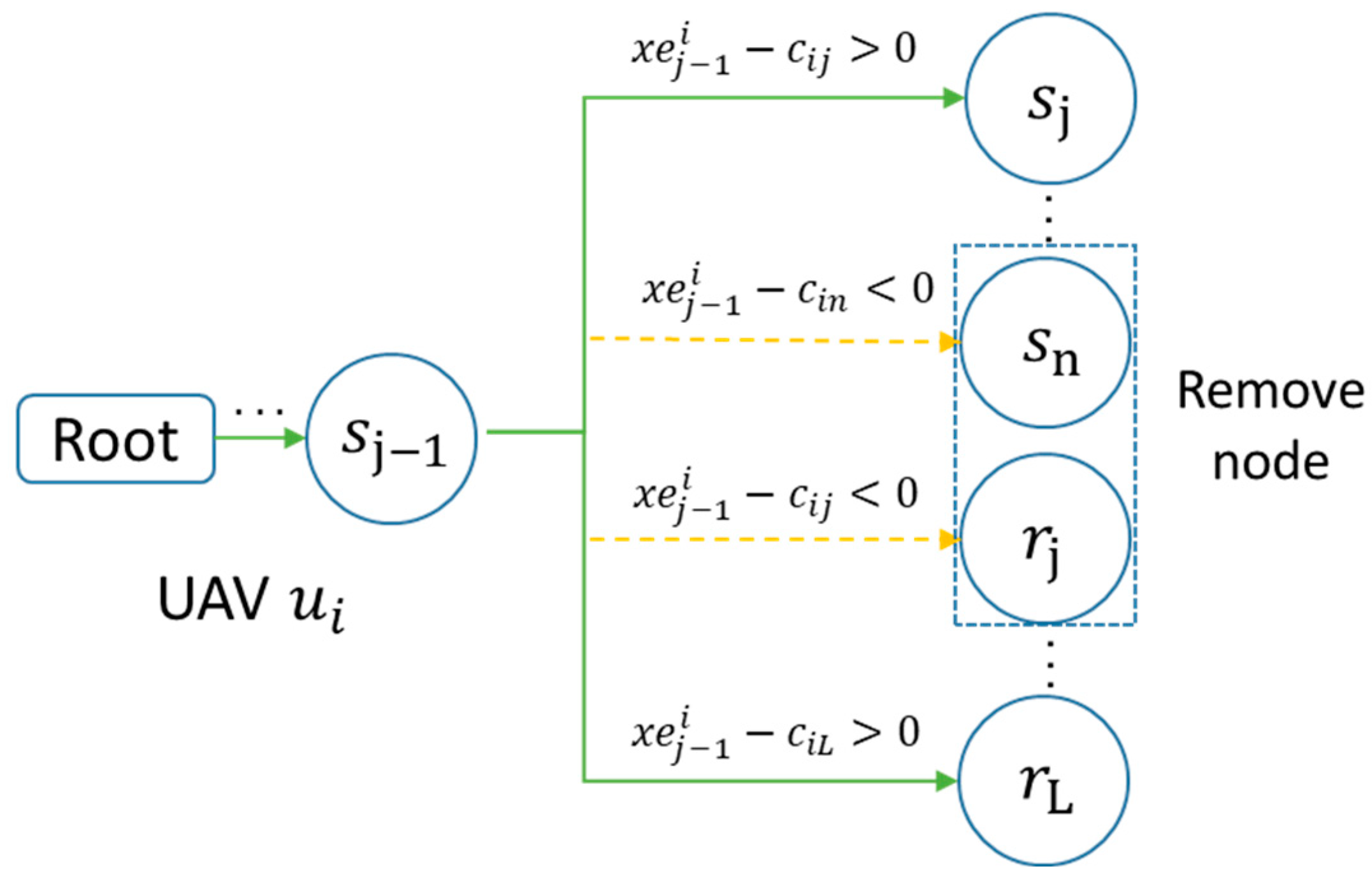
Combined with the energy situation of UAVs, this paper proposes a selection and expansion optimization strategy to optimize the selection and expansion phases of MCTS. Firstly, through SEOS, we ensured that there was no conflict in the task selection of each UAV in the respective node selection phase. Furthermore, during the expansion process, considering that UAV energy has limitations, not all locations satisfy the expansion needs. SEOS selectively added feasible nodes according to the UAV energy status, enabling the following simulation process to be effective and improving the multi-task assignment efficiency for UAVs.
According to the definition in Section 2.2, let denote the set of UAVs, with the UAVs denoted by . denotes the number of items the UAV currently carries. In this paper, task assignments for UAVs were performed in each sub-task group. We used to denote each sub-task group, and the number of tasks in each group is , with the tasks denoted by as shown in Equation (11).
Let denote the set of UAV docks, with the UAV docks denoted by as shown in Equation (12).
The task location of UAV is denoted by , where denotes the UAV docks and task locations. As shown in Equation (13), the energy state of UAV at position is denoted using . When satisfy , it means the UAV has enough energy to fly from the previous position to When belongs to , it means the UAV completes the battery exchange and the energy becomes again.
As shown in Figure 5, when the UAV is in the node expansion phase, it selects tasks that have not been visited. Using Equation (13), it evaluates its energy and selects reachable nodes while removing inaccessible nodes due to insufficient energy. Based on this, we ensured the nodes’ validity and effectively reduced the search tree’s size, minimizing invalid and redundant searches.
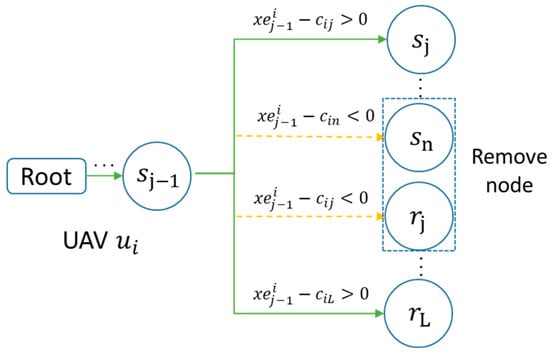
Figure 5.
Expansion process.
Based on the above calculations, SEOS pseudo-code as shown in Algorithm 3.
| Algorithm 3: Selection and Expansion Optimization Strategy | |
| 1: | function |
| 2: | while state of satisfy do |
| 3: | if not fully expanded then |
| 4: | return |
| 5: | else |
| 6: | |
| 7: | end while |
| 8: | return |
| 9: | function |
| 10: | choose |
| 11: | is obtained by Equation (13) |
| 12: | if then |
| 13: | set state and position of the new node according to and |
| 14: | add a new child to |
| 15: | return |
| 16: | else |
| 17: | |
| 18: | end if |
| 19: | function |
| 20: | is obtained by Equation (10) |
| 21: | return |
The above pseudo-code primarily outlines the SEOS method. Lines 1–7 depict the selection function. If a node has not reached its termination status, it means the UAV is currently carrying items not exceeding . If this node is not fully expanded, it will proceed with expansion. Otherwise, the optimal node will be selected. Lines 8–16 illustrate the expansion function. An unvisited task location is chosen, and then is computed based on Equation (13). If , a new node will be generated and added to the child list of the prior node. If not, a new task location that has not been visited will be reselected. Lines 17–19 depict the optimal node computation function, where its reward value is computed through Equation (10).
3.2.2. Simulation Optimization Strategy
Typically, the MCTS simulation phase starts at a selected node and carries out a series of actions, either randomly or according to some strategy, until it reaches the termination state. This process is also referred to as a rollout. However, the traditional simulation approach may not be optimal when faced with the multi-UAV task assignment problem.
The simulation optimization strategy proposed in this paper aims to enhance the simulation phase of MCTS for the multi-UAV task assignment problem. The following is the core idea of the strategy:
In solving the multi-UAV task assignment, the method proposed in this paper builds a separate tree for each UAV. Moreover, as the MCTS iterates the process many times, many different results are formed. This paper recorded and shared these simulation results with all UAVs. These results were used as heuristic information to form an information repository during multiple iterations, which could be used as historical experience to guide action selection in the subsequent simulation process. The simulation phase could be more effective by combining the historical experience with the current state information of a particular UAV. Thus, a stochastic simulation process was transformed into an intelligent simulation that combined historical heuristic information. SOS improved the effectiveness of the simulation phase of MCTS and provided a better solution for MCTS to solve the multi-task assignment problem.
Based on SOS, this paper recorded the results of each iteration in the tree for each UAV and updated the information repository. By defining matrix as the information repository with dimension , is the number of tasks in the sub-task group, and is the number of UAV docks. In matrix , the information between each task position is computed as shown in Equation (14):
where denotes the value of information between positions and during the -th iteration, . The matrix is constantly updated through multiple iterations of multiple UAVs, which guides the simulation process in MCTS.
During the simulation process, the information in the matrix helps guide the algorithm to quickly select the following possible actions based on the existing information to find a suitable allocation scheme. Specifically, the following action is selected in the simulation process according to a certain random probability, and the random probability is calculated as shown in Equation (15):
where denotes the probability of selecting location based on the current location , and denotes the set of locations that have not yet been visited after removing location .
Algorithm 4 is the simulation process of the TA-MCTS method. First, we determined whether node satisfied the termination state, and if it did, we computed directly according to Equation (8). Otherwise, we obtained the set of nodes (Line 4) that had not been visited. We iterated through all the nodes, computed each node’s current probability according to Equation (15), and stored it in the list of (Lines 6–12). Subsequently, the next possible location was obtained based on the generated random number and the list of . A new node was set up based on the current state, and the matrix was updated by Equation (14) (Lines 13–17).
| Algorithm 4: Simulation Optimization Strategy | |
| 1: | function |
| 2: | set |
| 3: | while state of satisfy do |
| 4: | get the set of not visited position |
| 5: | |
| 6: | for each do |
| 7: | is obtained by Equation (13) |
| 8: | if then |
| 9: | by Equation (15) |
| 10: | |
| 11: | end if |
| 12: | end for |
| 13: | |
| 14: | |
| 15: | set state and position of the new node |
| 16: | |
| 17: | update matrix by Equation (14) |
| 18: | end while |
| 19: | according to Equation (8) |
| 20: | return |
In summary, based on the characteristics of multi-task assignment, this paper optimized the MCTS simulation phase. The results of multiple MCTS simulations were utilized to create an information repository, which guided the selection of actions during the simulation phase.
4. Experiments
In order to validate the TA-MCTS method, experiments and comparisons were performed. The experimental running environment was a 2.30 GHz CPU, 16.0 GB of RAM, and a 64-bit operating system.
4.1. Experimental Environment
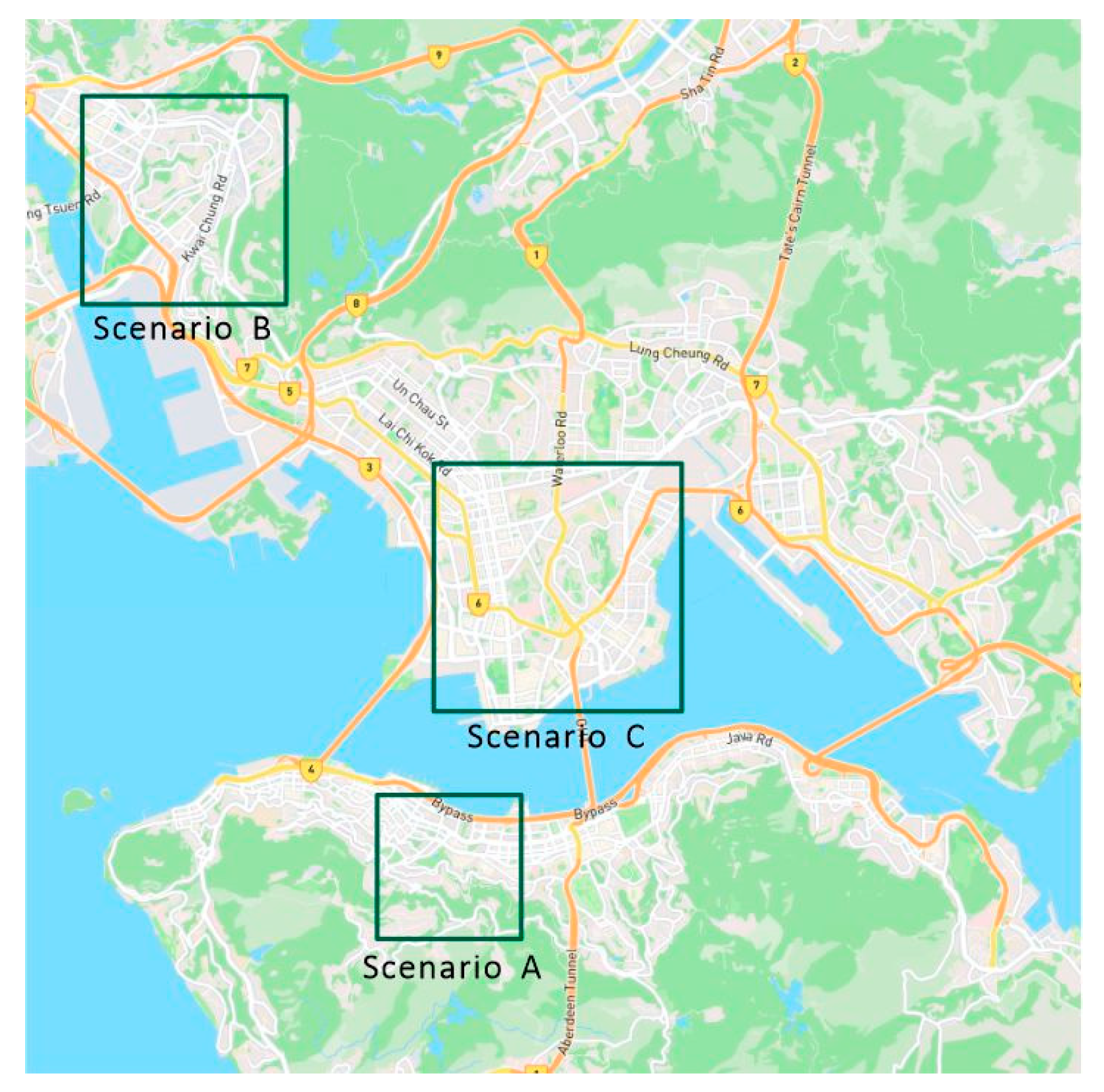
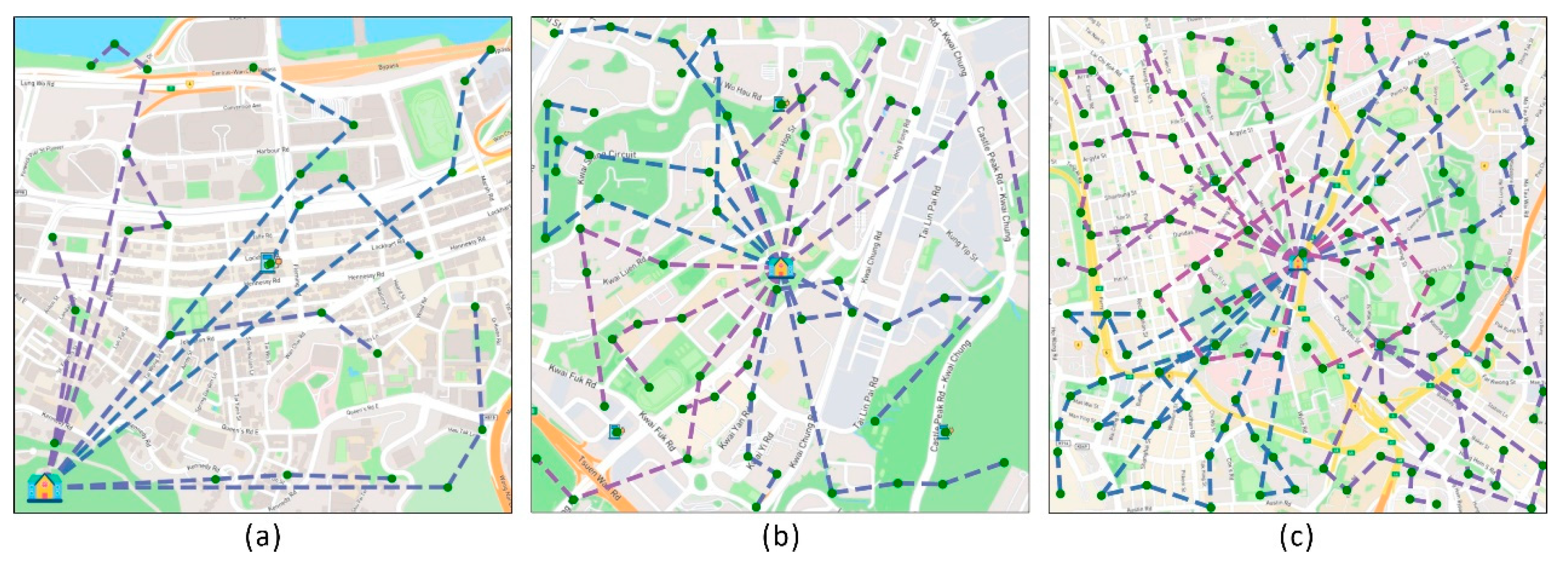
The experimental area of this experiment was part of Hong Kong, as shown in Figure 6. In this paper, three square areas were selected in this region to simulate the experiment.
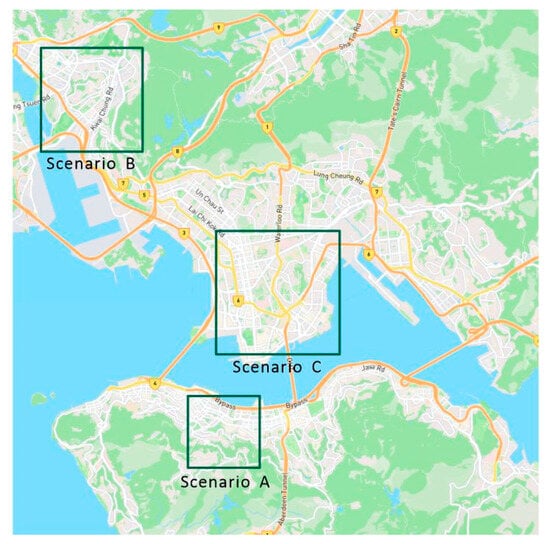
Figure 6.
Selected research area.
Table 2 shows the size and the latitude and longitude of the lower left corner of each scenario selected in this paper. Based on the location of the lower-left corner, this paper defines the local coordinates of the DC and UAV docks concerning the lower-left corner of the scenario. Moreover, a specific number of task locations were randomly generated in the region. With the expansion of scenarios and the increased number of tasks, UAVs need more energy to complete them all. Therefore, broadening the scenario, this paper establishes additional UAV docks. The increase in the number of tasks and UAV docks directly adds to the uncertainty of task allocation, which can more effectively evaluate the applicability and effectiveness of the TA-MCTS method in different environments.

Table 2.
Positions defined in different scenarios.
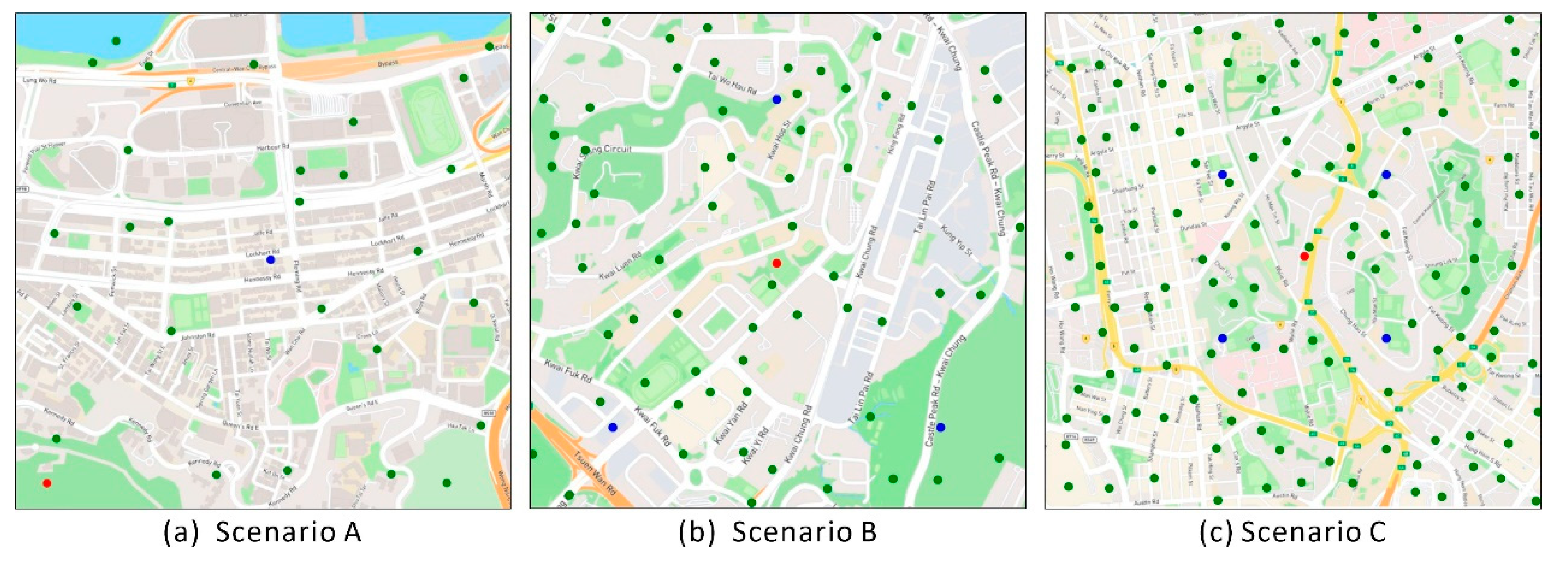
Combining the above settings, the locations of DC, UAV docks, and randomly generated tasks for the three scenarios are shown in Figure 7. The red point represents the DC, the blue point represents the UAV dock, and the green point represents the task location.
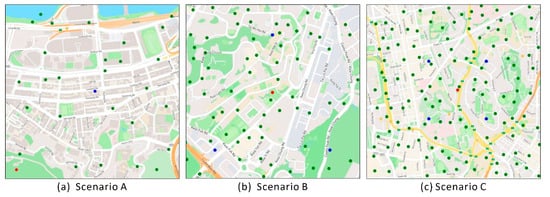
Figure 7.
Position of distribution centers, UAV docks and tasks.
Scenarios A, B, and C cover small to large areas where the number of UAVs involved and their flight capabilities differ. Table 3 shows the parameter settings of the UAVs in the three scenarios, with the number of UAVs as , the maximum battery capacity as , the maximum number of items to be carried as , represents the energy consumed by the UAVs per kilometer when no items are loaded, is the number of loaded items, and denotes the energy consumed by each item. In order to better conform to actual conditions, as the payload capacity of UAVs increases, the required battery capacity and the energy consumption per kilometer also increase accordingly. Moreover, variations in the energy parameters of UAVs directly affect the frequency of their visits to UAV docks.

Table 3.
UAV parameters in different scenarios.
4.2. Task Grouping Comparison
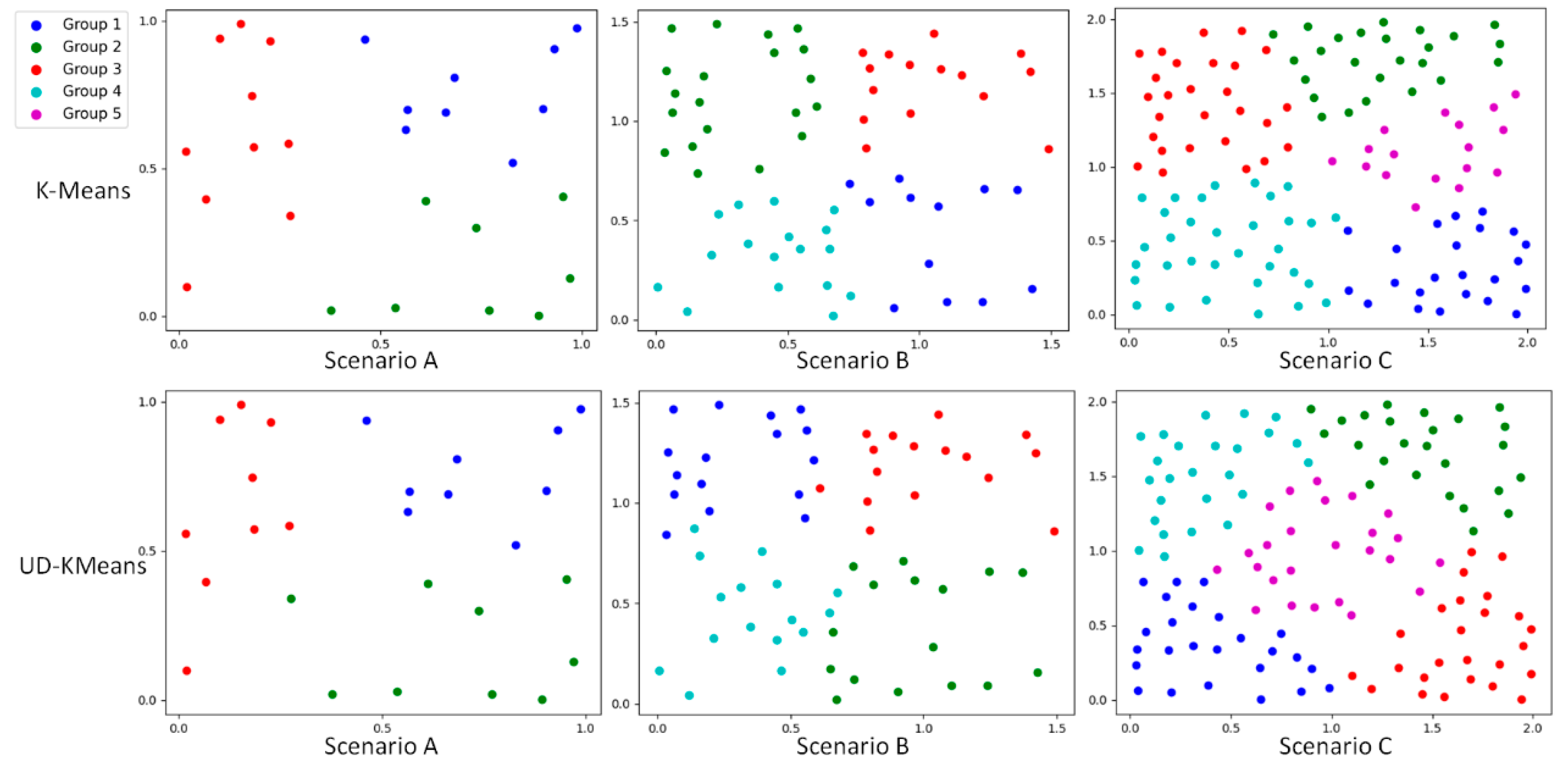
In this paper, we first experimented with the task grouping strategy. Task grouping aims to cluster tasks according to their geographic location, narrowing the search range of task assignments for UAVs and improving the efficiency and accuracy of the assignment. Unlike the traditional K-means, the UD-Kmeans proposed in this paper ensured that the number of tasks within each grouping was consistent, thus creating favorable conditions for subsequent task allocation.
In order to verify the effectiveness of the UD-Kmeans method, this paper conducted group experiments for all tasks within the three scenarios. Based on the maximum load of UAVs and the number of UAVs, this paper determined that the number of groups in scenarios A, B, and C was 3, 4, and 5, respectively, according to Equation (9). The experimental results are shown in Figure 8 and Table 4. Figure 8 indicates the grouping results with different colored dots, and Table 4 directly shows the number of elements in each group. UD-Kmeans made the number of tasks in each grouping result consistent. However, the K-means grouping results indicate inconsistent tasks in each group. Uneven grouping results may lead to difficulties in subsequent task assignments. Therefore, UD-Kmeans contributes to the stability and reliability of subsequent multi-task allocations.
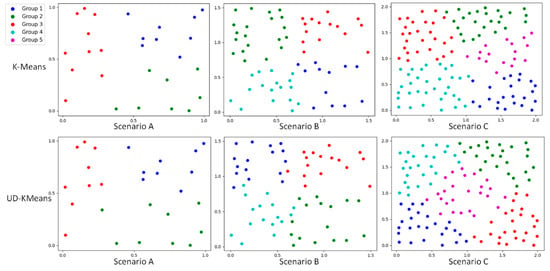
Figure 8.
Comparison of K-Means vs. UN-Kmeans results.

Table 4.
Comparison of K-Means and UD-Kmeans.
4.3. MCTS Comparison
In order to validate the TA-MCTS, we conducted randomized experiments of TA-MCTS with R-MCTS, G-MCTS, and RG-MCTS in three scenarios. For RG-MCTS, the weights of random and greedy simulation strategies were set to 50%.
Compared with the original MCTS method, the TA-MCTS optimized the node selection and simulation strategies. Generally, MCTS builds a separate tree for node selection and simulation. However, in the case of task allocation considering multi-UAV and energy, a separate tree may result in too many nodes and a slow search. Therefore, this paper modified the three MCTS methods mentioned above to use multiple trees.
Due to the randomness of the methods, a single experiment could not fully reflect the differences between different methods. In order to achieve a more precise comparison, this paper executed 50, 100, 150, 200, 1000, and 2000 simulations for each method in each scenario and then analyzed the results comprehensively.
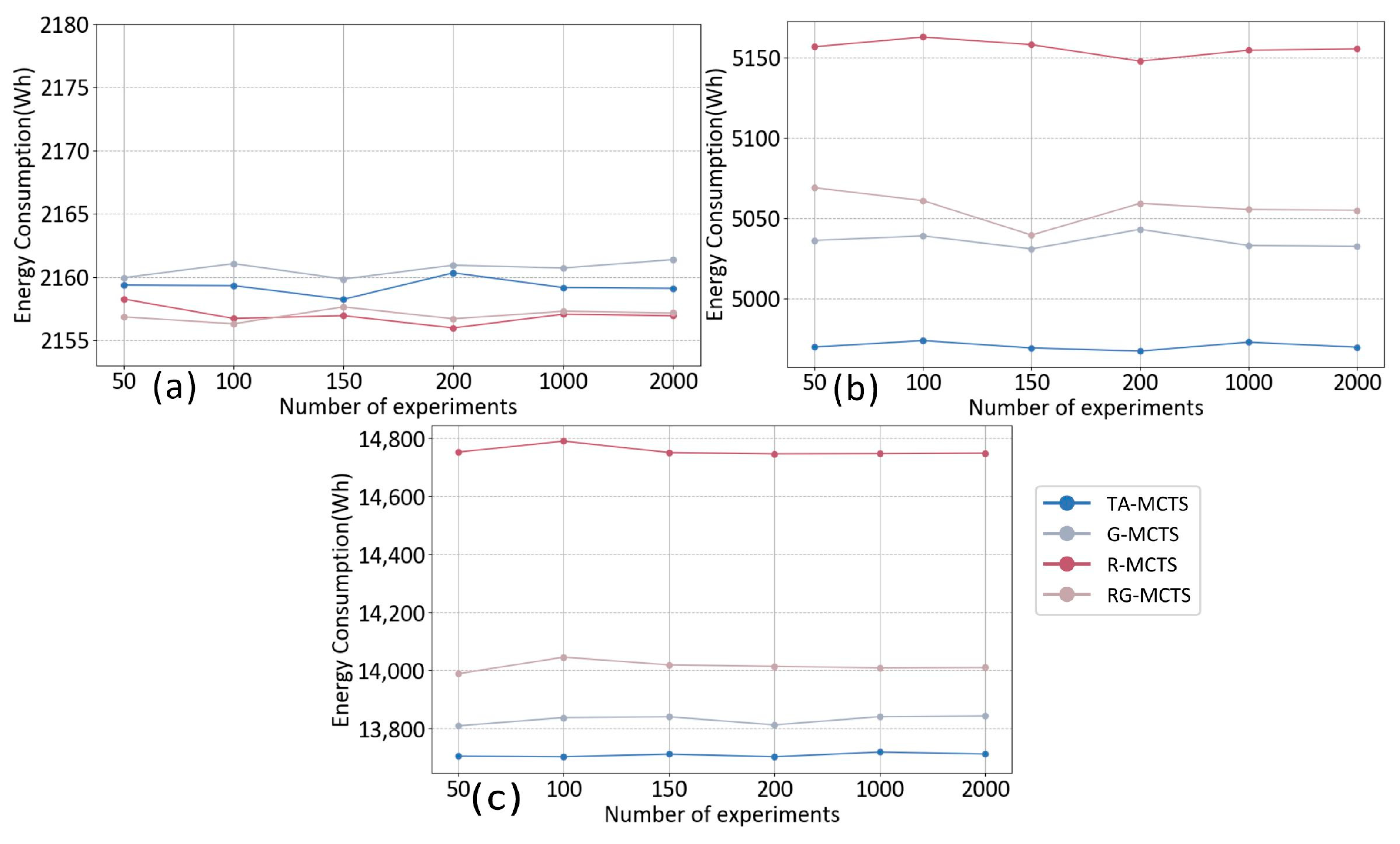
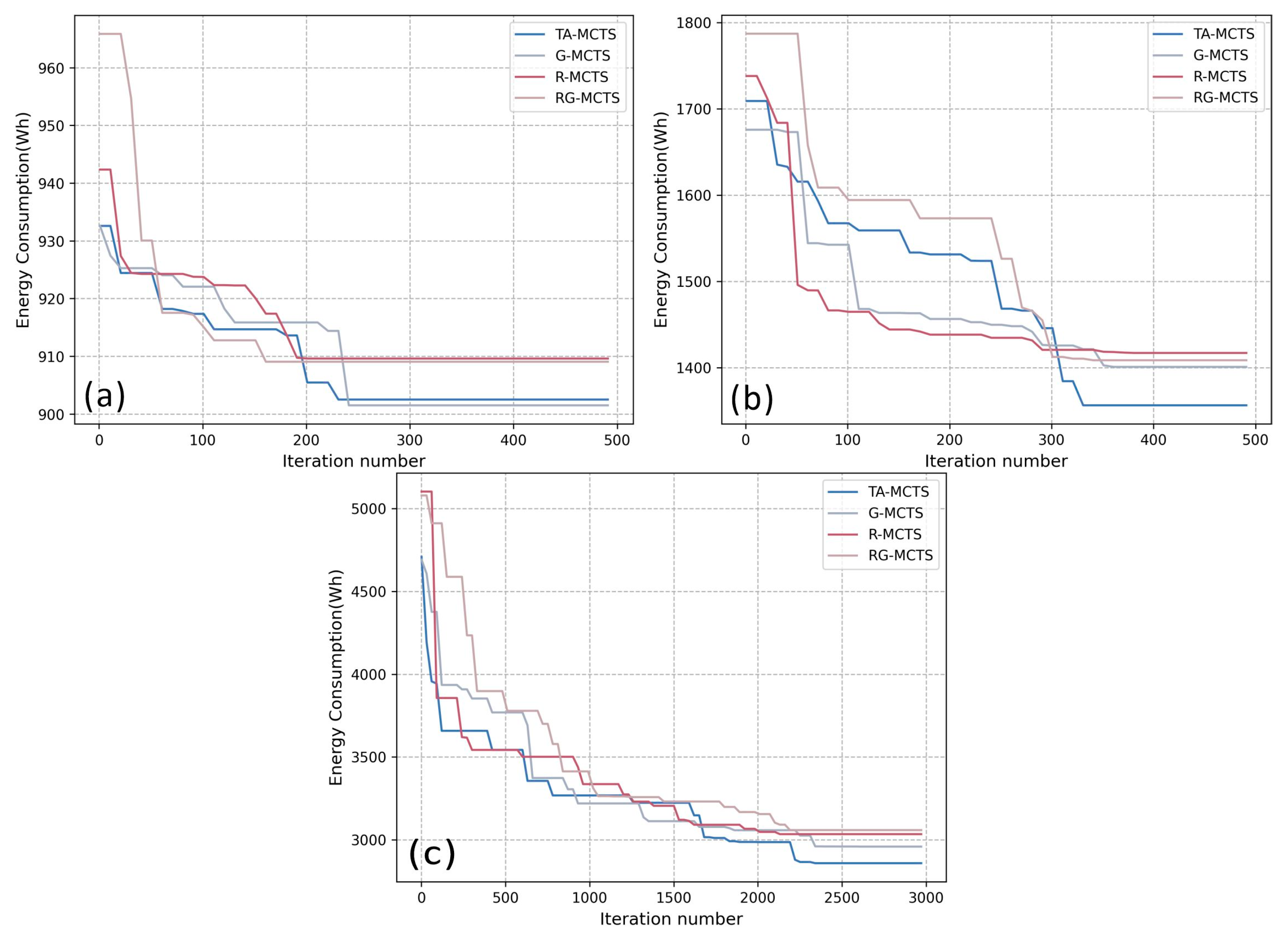
Figure 9 shows the average energy consumption of different algorithms for multiple experiments in different scenarios. Figure 9a–c represent the average energy consumption under scenarios A, B, and C, respectively. The difference between the four methods was relatively slight due to the small area covered by Scenario A. Figure 9b,c show that TA-MCTS consumed less energy on average than the other three methods, regardless of the number of experiments. Moreover, the results obtained by the TA-MCTS method were more stable, while the other three methods were subject to fluctuations.
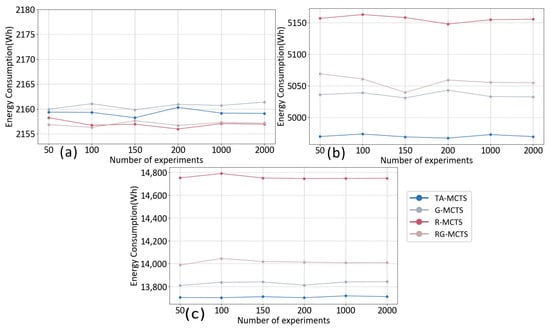
Figure 9.
Comparison of average energy consumption. (a) The average energy consumption in scenario A. (b) The average energy consumption in scenario B. (c) The average energy consumption in scenario C.
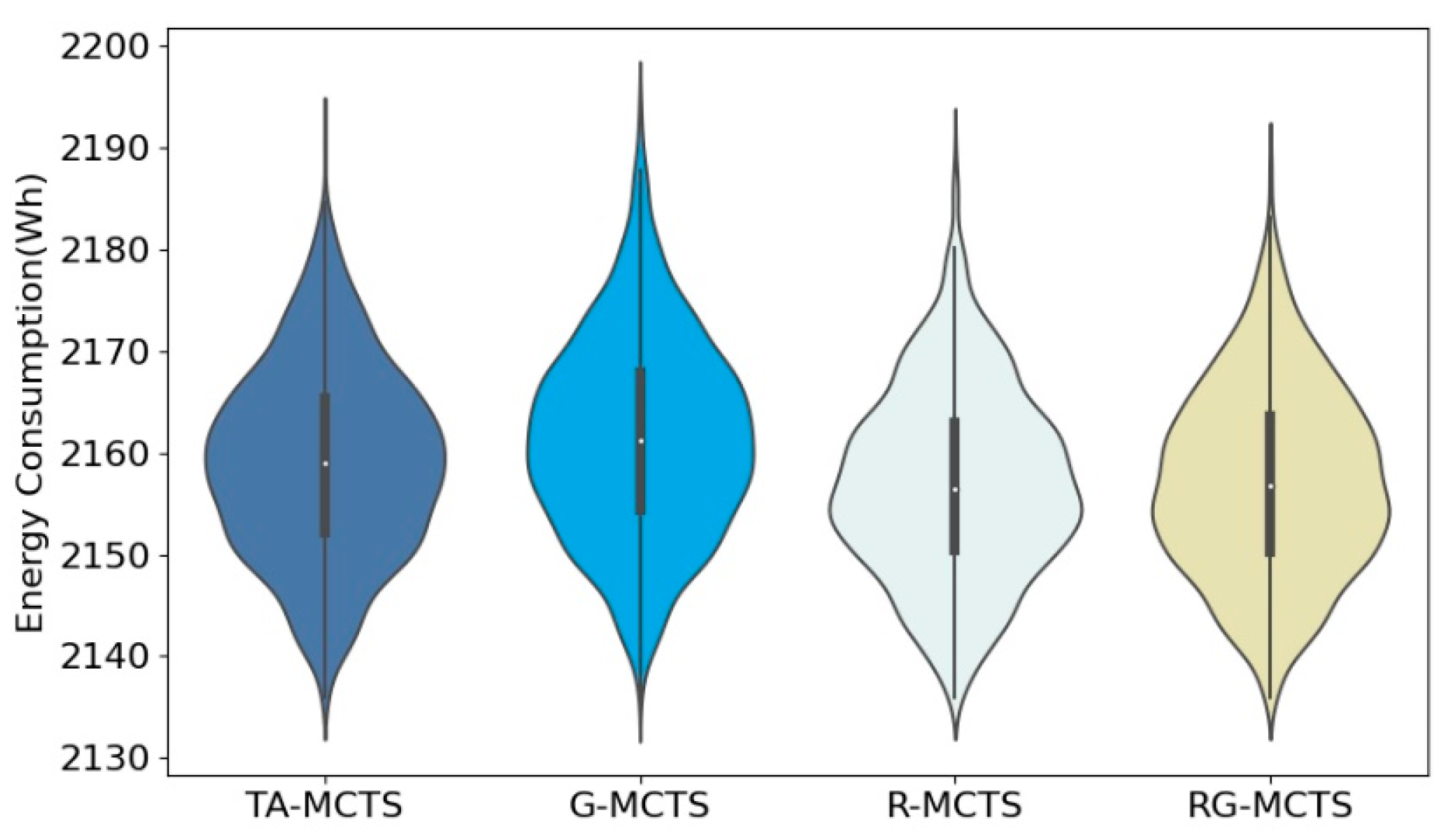
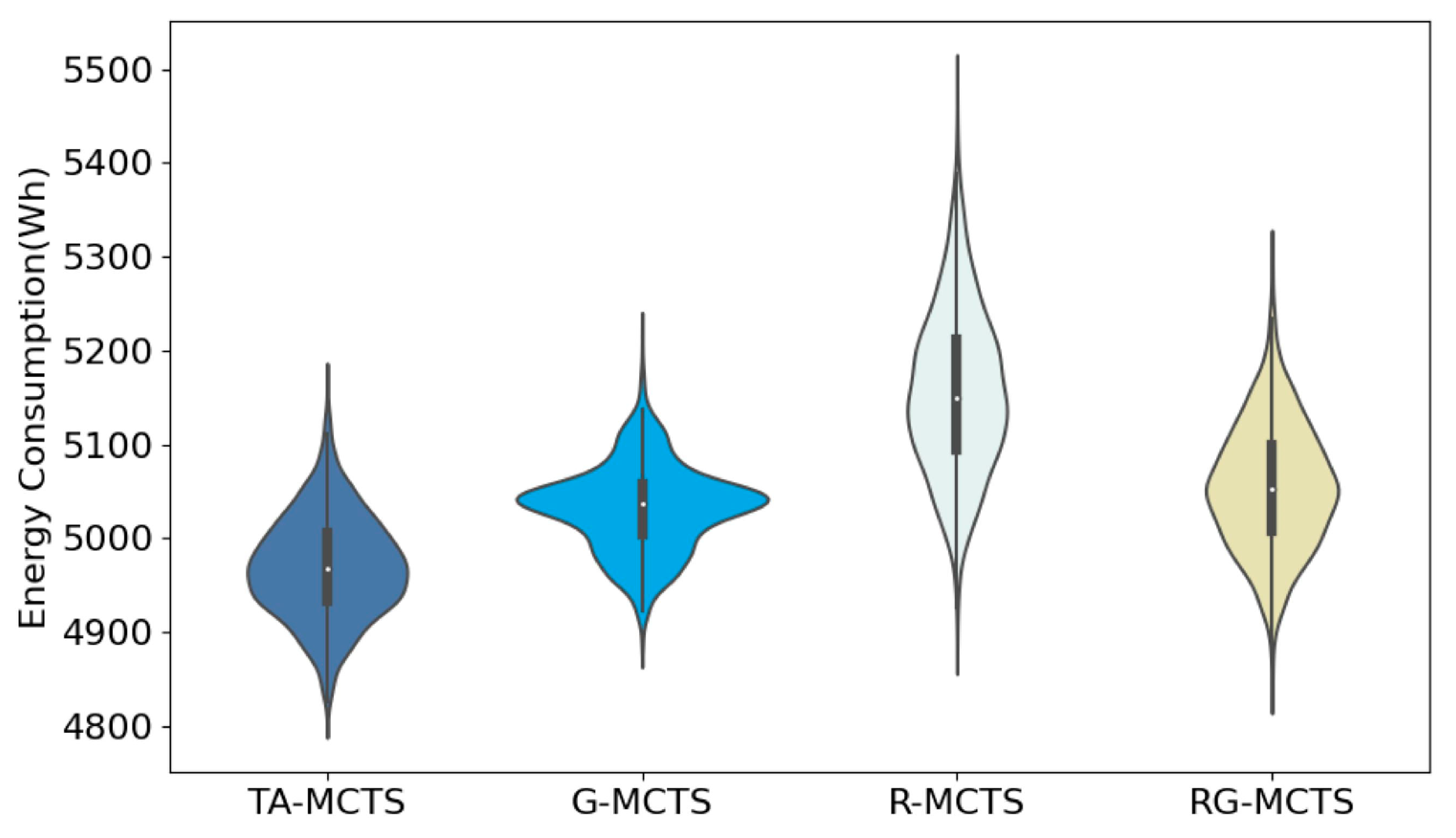
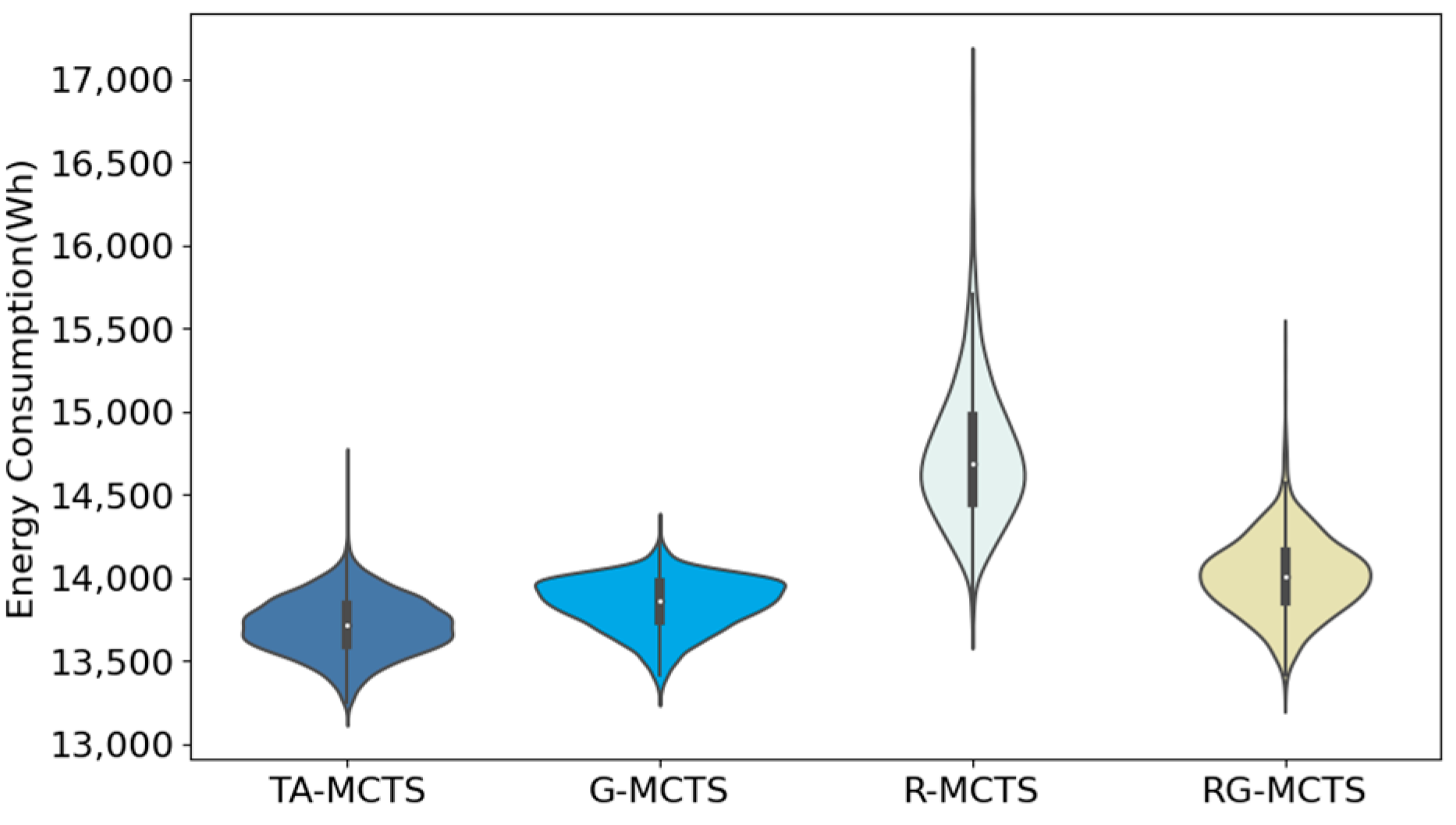
In order to show the effect of each method more clearly, this paper used violin plots to show the characteristics of the data distribution of energy consumption for 2000 experiments; the results are shown in Figure 10, Figure 11 and Figure 12. As seen in Figure 10, due to the small area of Scenario A, the UAVs carrying energy could cover almost the whole area, so the difference in the data distribution obtained by the four methods was small. Figure 11 and Figure 12 show that in Scenarios B and C, the difference in the distribution of energy consumption among the four methods was more evident due to the expansion of the area. In Scenario B, the data concentration of TA-MCTS is better than the remaining three methods. The optimal and worst energy consumption of TA-MCTS was also better than the other three methods. In Scenario C, TA-MCTS indicated significantly lower energy consumption in the concentrated area than RG-MCTS and G-MCTS. R-MCTS performed less well than the other algorithms, and the distribution of results was relatively scattered due to its intrinsic randomness.
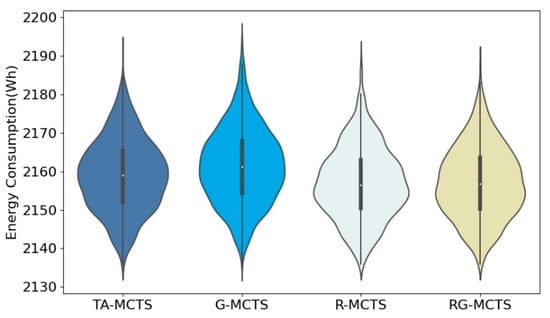
Figure 10.
Violin plot presenting the distribution of energy consumption in Scenario A.
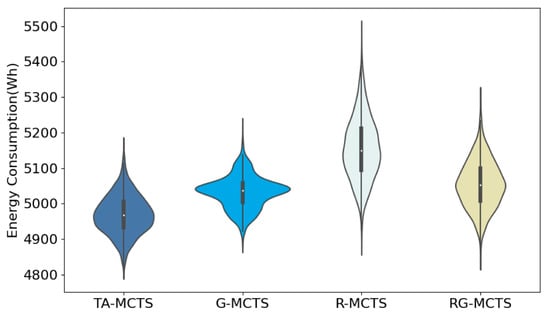
Figure 11.
Violin plot presenting the distribution of energy consumption in Scenario B.
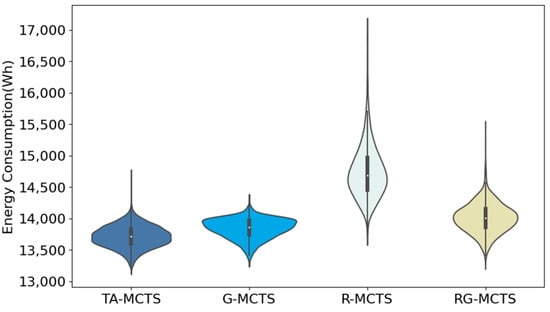
Figure 12.
Violin plot presenting the distribution of energy consumption in Scenario C.
Figure 13a–c show the iterative process for a sub-task group in scenarios A, B, and C, respectively. In the three scenarios, the number of iterations required to converge was approximately the same for all four methods. However, the TA-MCTS method proposed in this paper obtained better results after a similar number of iterations, proving the superiority of the TA-MCTS method.
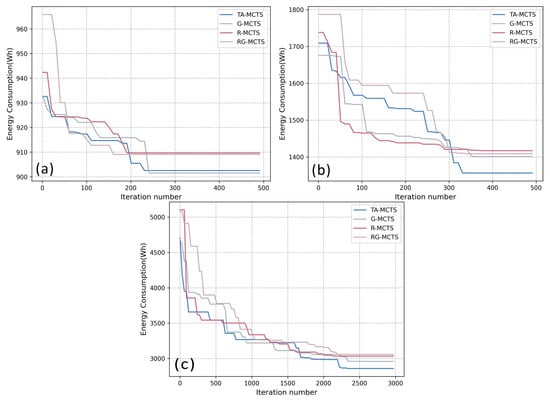
Figure 13.
Comparison of iteration numbers. (a) The iterative process for a sub-task group in scenario A. (b) The iterative process for a sub-task group in scenario B. (c) The iterative process for a sub-task group in scenario C.
To further illustrate the impact of different data in Table 2 and Table 3 on the results, the average number of visits to UAV docks in different scenarios was counted in this paper, as shown in Table 5, Table 6 and Table 7. In the descriptions in Table 2 and Table 3, Scenarios A and B, the smaller area and the small number of missions undertaken by the UAVs resulted in the UAVs not needing to visit the UAV dock as frequently to change batteries. Therefore, the four methods show fewer passes through the docks, but overall, the TA-MCTS led to fewer passes through the UAV docks than other methods. Combining the descriptions of Scenario C in Table 2 and Table 3, the increase in the number of missions and the size of the area resulted in the UAVs needing to visit the UAV docks more times to replenish their energy to complete the missions. Therefore, the data in Table 7 show that the average number of times the TA-MCTS method passes through the docks was better than the other algorithms.

Table 5.
Average number of passes through the UAV docks in scenario A.

Table 6.
Average number of passes through the UAV docks in scenario B.

Table 7.
Average number of passes through the UAV docks in scenario C.
Figure 14 illustrates the task allocation of TA-MCTS in three scenarios. Figure 14a–c represent the results under scenarios A, B, and C, respectively. The dotted lines of different colors represent different task groups, and the green dots represent the task locations.
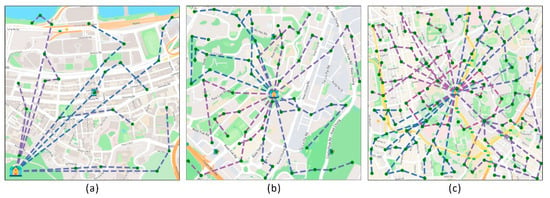
Figure 14.
The result of task allocation in different scenarios. (a) The result of task distribution in scenario A. (b) The result of task distribution in scenario B. (c) The result of task distribution in scenario C.
After the above comparative analysis, the TA-MCTS proposed in this paper was shown to have significant advantages, and it can reasonably accomplish multi-UAV task allocation. TA-MCTS ensured the UAVs minimized energy consumption in accomplishing all the tasks, regardless of the scenario. These experiments highlight the innovation and effectiveness of the TA-MCTS method and provide a powerful solution for multi-UAV task allocation in urban logistics with practical applications.
5. Conclusions
This paper investigated the multi-task assignment method for UAV logistics in urban low-altitude environments. Based on the traditional K-means, this paper proposes UD-Kmeans to realize multi-task grouping and reduce the scope of multi-task allocation. On this basis, we proposed TA-MCTS by improving the selection and simulation strategies of MCTS. We utilized multiple collaborative trees for decision evaluation to effectively accomplish multi-task allocation. From Table 4 and Figure 8, UD-Kmeans exhibited stability in task grouping, ensuring the number of tasks within each grouping was consistent. The advantages of TA-MCTS were illustrated through comprehensive comparisons with other related MCTS methods. Table 5, Table 6 and Table 7 and Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 showed that TA-MCTS efficiently performs in solution optimality. The main findings are as follows:
(1) UD-Kmeans ensures that the number of tasks in each group is balanced while performing clustering, effectively avoiding uneven task allocation.
(2) In the TA-MCTS method, using SEOS, conflict-free node selection is achieved in the selection phase. In the expansion phase, selective expansion is performed according to the UAV’s energy situation to reduce the number of possible subsequent ineffective searches.
(3) TA-MCTS optimizes the simulation strategy by collecting the simulation results of multiple UAVs and constructing a historical information repository. The historical information is used to guide the subsequent simulation, thus improving the effectiveness of the simulation.
In subsequent research, we plan to optimize these methods further and explore the implementation of task allocation among multiple scenarios. Moreover, with the development of UAV technology, we plan to conduct more extensive research in the real world with real UAV performance situations.
Author Contributions
Conceptualization, Z.M. and J.C.; methodology, Z.M.; software, Z.M.; validation, Z.M. and J.C.; formal analysis, Z.M.; investigation, Z.M.; resources, Z.M.; data curation, Z.M.; writing—original draft preparation, Z.M.; writing—review and editing, Z.M. and J.C.; visualization, Z.M.; supervision, Z.M. and J.C.; project administration, J.C.; funding acquisition, J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the financial support of the Fundamental Research Funds for the Central Universities, China (Grant No. 2042022dx0001).
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ahmed, F.; Mohanta, J.C.; Keshari, A.; Yadav, P.S. Recent Advances in Unmanned Aerial Vehicles: A Review. Arab. J. Sci. Eng. 2022, 47, 7963–7984. [Google Scholar] [CrossRef] [PubMed]
- Siebert, S.; Teizer, J. Mobile 3D Mapping for Surveying Earthwork Projects Using an Unmanned Aerial Vehicle (UAV) System. Autom. Constr. 2014, 41, 1–14. [Google Scholar] [CrossRef]
- Kim, J.; Kim, S.; Ju, C.; Son, H.I. Unmanned Aerial Vehicles in Agriculture: A Review of Perspective of Platform, Control, and Applications. IEEE Access 2019, 7, 105100–105115. [Google Scholar] [CrossRef]
- Yeong, S.P.; King, L.M.; Dol, S.S. A Review on Marine Search and Rescue Operations Using Unmanned Aerial Vehicles. Int. J. Mar. Environ. Sci. 2015, 9, 396–399. [Google Scholar] [CrossRef]
- Coifman, B.; McCord, M.; Mishalani, R.G.; Redmill, K. Surface Transportation Surveillance from Unmanned Aerial Vehicles. In Proceedings of the 83rd Annual Meeting of the Transportation Research Board, Washington, DC, USA, 11–15 January 2004; Volume 28. [Google Scholar]
- Eichleay, M.; Evens, E.; Stankevitz, K.; Parker, C. Using the Unmanned Aerial Vehicle Delivery Decision Tool to Consider Transporting Medical Supplies via Drone. Glob. Health Sci. Pract. 2019, 7, 500–506. [Google Scholar] [CrossRef]
- Hossein Motlagh, N.; Taleb, T.; Arouk, O. Low-Altitude Unmanned Aerial Vehicles-Based Internet of Things Services: Comprehensive Survey and Future Perspectives. IEEE Internet Things J. 2016, 3, 899–922. [Google Scholar] [CrossRef]
- Mehmood, Y.; Ahmad, F.; Yaqoob, I.; Adnane, A.; Imran, M.; Guizani, S. Internet-of-Things-Based Smart Cities: Recent Advances and Challenges. IEEE Commun. Mag. 2017, 55, 16–24. [Google Scholar] [CrossRef]
- Elloumi, M.; Dhaou, R.; Escrig, B.; Idoudi, H.; Saidane, L.A. Monitoring Road Traffic with a UAV-Based System. In Proceedings of the 2018 IEEE Wireless Communications and Networking Conference (WCNC), Barcelona, Spain, 15–18 April 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Carlsson, J.G.; Song, S. Coordinated Logistics with a Truck and a Drone. Manag. Sci. 2018, 64, 4052–4069. [Google Scholar] [CrossRef]
- Pan, J.S.; Song, P.C.; Chu, S.C.; Peng, Y.J. Improved Compact Cuckoo Search Algorithm Applied to Location of Drone Logistics Hub. Mathematics 2020, 8, 333. [Google Scholar] [CrossRef]
- Pollet, B.G.; Staffell, I.; Shang, J.L. Current Status of Hybrid, Battery and Fuel Cell Electric Vehicles: From Electrochemistry to Market Prospects. Electrochim. Acta 2012, 84, 235–249. [Google Scholar] [CrossRef]
- Mitchell, S.; Steinbach, J.; Flanagan, T.; Ghabezi, P.; Harrison, N.; O’Reilly, S.; Killian, S.; Finnegan, W. Evaluating the Sustainability of Lightweight Drones for Delivery: Towards a Suitable Methodology for Assessment. Funct. Compos. Mater 2023, 4, 4. [Google Scholar] [CrossRef]
- Stolaroff, J.K.; Samaras, C.; O’Neill, E.R.; Lubers, A.; Mitchell, A.S.; Ceperley, D. Energy Use and Life Cycle Greenhouse Gas Emissions of Drones for Commercial Package Delivery. Nat. Commun. 2018, 9, 409. [Google Scholar] [CrossRef] [PubMed]
- Kang, P.; Song, G.; Xu, M.; Miller, T.R.; Wang, H.; Zhang, H.; Liu, G.; Zhou, Y.; Ren, J.; Zhong, R.; et al. Low-Carbon Pathways for the Booming Express Delivery Sector in China. Nat. Commun. 2021, 12, 450. [Google Scholar] [CrossRef] [PubMed]
- Goodchild, A.; Toy, J. Delivery by Drone: An Evaluation of Unmanned Aerial Vehicle Technology in Reducing CO2 Emissions in the Delivery Service Industry. Transp. Res. Part D Transp. Environ. 2018, 61, 58–67. [Google Scholar] [CrossRef]
- Djimantoro, M.I.; Suhardjanto, G. The Advantage by Using Low-Altitude UAV for Sustainable Urban Development Control. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2018; Volume 109. [Google Scholar] [CrossRef]
- Singireddy, S.R.R.; Daim, T.U. Technology Roadmap: Drone Delivery—Amazon Prime Air. Innov. Technol. Knowl. Manag. 2018, 387–412. [Google Scholar] [CrossRef]
- Hwang, J.; Choe, J.Y. (Jacey). Exploring Perceived Risk in Building Successful Drone Food Delivery Services. Int. J. Contemp. Hosp. Manag. 2019, 31, 3249–3269. [Google Scholar] [CrossRef]
- Scott, J.; Scott, C. Drone Delivery Models for Healthcare. In Proceedings of the 50th Hawaii International Conference on System Sciences, Hilton Waikoloa Village, HI, USA, 4–7 January 2017. [Google Scholar]
- Yoo, W.; Yu, E.; Jung, J. Drone Delivery: Factors Affecting the Public’s Attitude and Intention to Adopt. Telemat. Inform. 2018, 35, 1687–1700. [Google Scholar] [CrossRef]
- De Silva, S.C.; Phlernjai, M.; Rianmora, S.; Ratsamee, P. Inverted Docking Station: A Conceptual Design for a Battery-Swapping Platform for Quadrotor UAVs. Drones 2022, 6, 56. [Google Scholar] [CrossRef]
- Grlj, C.G.; Krznar, N.; Pranjić, M. A Decade of UAV Docking Stations: A Brief Overview of Mobile and Fixed Landing Platforms. Drones 2022, 6, 17. [Google Scholar] [CrossRef]
- Bláha, L.; Severa, O.; Goubej, M.; Myslivec, T.; Reitinger, J. Automated Drone Battery Management System—Droneport: Technical Overview. Drones 2023, 7, 234. [Google Scholar] [CrossRef]
- Oh, G.; Kim, Y.; Ahn, J.; Choi, H.-L. Task Allocation of Multiple UAVs for Cooperative Parcel Delivery. In Advances in Aerospace Guidance, Navigation and Control; Springer: Berlin/Heidelberg, Germany, 2018; pp. 443–454. [Google Scholar] [CrossRef]
- Kuhn, H.W. The Hungarian Method for the Assignment Problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef]
- Madridano, Á.; Al-Kaff, A.; Martín, D.; de la Escalera, A. 3D Trajectory Planning Method for UAVs Swarm in Building Emergencies. Sensors 2020, 20, 642. [Google Scholar] [CrossRef] [PubMed]
- Bellingham, J.; Tillerson, M.; Richards, A.; How, J.P. Multi-Task Allocation and Path Planning for Cooperating UAVs. In Cooperative Control: Models, Applications and Algorithms; Springer: Berlin/Heidelberg, Germany, 2003; pp. 23–41. [Google Scholar] [CrossRef]
- Driess, D.; Oguz, O.; Ha, J.S.; Toussaint, M. Deep Visual Heuristics: Learning Feasibility of Mixed-Integer Programs for Manipulation Planning. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 9563–9569. [Google Scholar] [CrossRef]
- Weckenborg, C.; Kieckhäfer, K.; Müller, C.; Grunewald, M.; Spengler, T.S. Balancing of Assembly Lines with Collaborative Robots. Bus. Res. 2020, 13, 93–132. [Google Scholar] [CrossRef]
- Seenu, N.; Kuppan Chetty, R.M.; Ramya, M.M.; Janardhanan, M.N. Review on State-of-the-Art Dynamic Task Allocation Strategies for Multiple-Robot Systems. Ind. Rob. 2020, 47, 929–942. [Google Scholar] [CrossRef]
- Liu, C.; Kroll, A. A Centralized Multi-Robot Task Allocation for Industrial Plant Inspection by Using A* and Genetic Algorithms. In International Conference on Artificial Intelligence and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7268, pp. 466–474. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992; ISBN 0262581116. [Google Scholar]
- Martin, J.G.; Frejo, J.R.D.; García, R.A.; Camacho, E.F. Multi-Robot Task Allocation Problem with Multiple Nonlinear Criteria Using Branch and Bound and Genetic Algorithms. Intell. Serv. Robot. 2021, 14, 707–727. [Google Scholar] [CrossRef]
- Wei, C.; Ji, Z.; Cai, B. Particle Swarm Optimization for Cooperative Multi-Robot Task Allocation: A Multi-Objective Approach. IEEE Robot. Autom. Lett. 2020, 5, 2530–2537. [Google Scholar] [CrossRef]
- Mouradian, C.; Sahoo, J.; Glitho, R.H.; Morrow, M.J.; Polakos, P.A. A Coalition Formation Algorithm for Multi-Robot Task Allocation in Large-Scale Natural Disasters. In Proceedings of the 2017 13th International Wireless Communications and Mobile Computing Conference (IWCMC), Valencia, Spain, 26–30 June 2017; pp. 1909–1914. [Google Scholar] [CrossRef]
- Puttewar, A.S.; Chatpalliwar, A.S. An Overview of Ant Colony Optimization (ACO) for Multiple-Robot Task Allocation (MRTA). Res. J. Eng. Technol. 2013, 4, 107–112. [Google Scholar]
- Bertsekas, D.P. Auction Algorithms. Encycl. Optim. 2009, 1, 73–77. [Google Scholar]
- Choi, H.L.; Brunet, L.; How, J.P. Consensus-Based Decentralized Auctions for Robust Task Allocation. IEEE Trans. Robot. 2009, 25, 912–926. [Google Scholar] [CrossRef]
- Cheng, Q.; Yin, D.; Yang, J.; Shen, L. An Auction-Based Multiple Constraints Task Allocation Algorithm for Multi-UAV System. In Proceedings of the 2016 International Conference on Cybernetics, Robotics and Control (CRC), Hong Kong, China, 19–21 August 2016; IEEE: New York, NY, USA, 2016; pp. 1–5. [Google Scholar]
- Otte, M.; Kuhlman, M.J.; Sofge, D. Auctions for Multi-Robot Task Allocation in Communication Limited Environments. Auton. Robots 2020, 44, 547–584. [Google Scholar] [CrossRef]
- Bai, X.; Fielbaum, A.; Kronmuller, M.; Knoedler, L.; Alonso-Mora, J. Group-Based Distributed Auction Algorithms for Multi-Robot Task Assignment. IEEE Trans. Autom. Sci. Eng. 2023, 20, 1292–1303. [Google Scholar] [CrossRef]
- Coulom, R. Efficient Selectivity and Backup Operators in Monte-Carlo Tree Search. In International Conference on Computers and Games; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4630, pp. 72–83. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the Game of Go with Deep Neural Networks and Tree Search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Senington, R.; Schmidt, B.; Syberfeldt, A. Monte Carlo Tree Search for Online Decision Making in Smart Industrial Production. Comput. Ind. 2021, 128, 103433. [Google Scholar] [CrossRef]
- Qi, H.; Hu, X. Monte Carlo Tree Search-Based Intersection Signal Optimization Model with Channelized Section Spillover. Transp. Res. Part C Emerg. Technol. 2019, 106, 281–302. [Google Scholar] [CrossRef]
- Mo, S.; Pei, X.; Wu, C. Safe Reinforcement Learning for Autonomous Vehicle Using Monte Carlo Tree Search. IEEE Trans. Intell. Transp. Syst. 2022, 23, 6766–6773. [Google Scholar] [CrossRef]
- Qian, Y.; Sheng, K.; Ma, C.; Li, J.; Ding, M.; Hassan, M. Path Planning for the Dynamic UAV-Aided Wireless Systems Using Monte Carlo Tree Search. IEEE Trans. Veh. Technol. 2022, 71, 6716–6721. [Google Scholar] [CrossRef]
- Grelier, C.; Goudet, O.; Hao, J.K. On Monte Carlo Tree Search for Weighted Vertex Coloring. In European Conference on Evolutionary Computation in Combinatorial Optimization (Part of EvoStar); Springer: Berlin/Heidelberg, Germany, 2022; Volume 13222, pp. 1–16. [Google Scholar] [CrossRef]
- Browne, C.B.; Powley, E.; Whitehouse, D.; Lucas, S.M.; Cowling, P.I.; Rohlfshagen, P.; Tavener, S.; Perez, D.; Samothrakis, S.; Colton, S. A Survey of Monte Carlo Tree Search Methods. IEEE Trans. Comput. Intell. AI Games 2012, 4, 1–43. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).