Optimal Model-Free Finite-Time Control Based on Terminal Sliding Mode for a Coaxial Rotor
Abstract
:1. Introduction

- An innovative model-free control strategy aimed at achieving precise tracking of both position and attitude for a coaxial rotor is proposed. By removing the requirement for an intricate dynamic model, our approach bolsters the robustness and flexibility of the control strategy.
- A hybrid controller configuration combining terminal sliding mode estimation with a model-free controller is proposed for ensuring robustness to external disturbances, uncertainty in parameters, and unmodeled dynamics. The proposed controller relies on local measurements and reduces the complexity of implementation.
- Global closed-loop stability of the estimator–controller pair is rigorously established to show finite-time convergence and path tracking of the system.
- The primary challenges associated with sliding mode control lie in the convergence time and chattering phenomena induced by the discontinuous function sgn(.). In this study, we have tackled these issues by introducing new controller schemes enhanced with finite-time convergence.
- The controller parameters are optimized using an accelerated particle swarm optimization (APSO) algorithm, striking a balance between optimal tracking performance and satisfying the design conditions for closed-loop stability.
- The prevailing model-based control strategies advocated for multirotor UAVs in [4,31], hinging on the presumption of either partial or complete knowledge of the aerial vehicle model for control design. However, this inherent reliance renders them highly susceptible to unmodeled dynamics and the impact of parameter variations, severely curtailing their practical applicability. In stark contrast, our proposed approach is boldly model-free, eliminating the need for any a priori knowledge of system parameters or dynamic functions. This groundbreaking feature empowers the approach to attain exceptional performance, successfully surmounting challenges posed by nonlinearity and uncertainty in control problems.
- While the existing model-free control (MFC) strategies for UAVs [18,20] showcase good path tracking performance, they often utilize ultra-local models for robust controllers, limiting their effectiveness to local stability validation. In contrast, our approach ensures stability and proves asymptotic convergence of tracking errors to zero for both individual subsystems and the whole coaxial rotor system, backed by a rigorous Lyapunov theory proof.
- In [26,32], the authors proposed advanced model-free control (MFC) using adaptive intelligent networks for quadrotor UAVs. These controllers employ neural networks or fuzzy systems to approximate uncertainties due to unmodeled dynamics, parameter variations, and disturbances. However, their design parameters are randomly selected and require expert knowledge. In contrast, this paper introduces a simple structure for nonlinear estimator and utilizes the SMC technique to develop a robust and straightforward model-free controller.
- In the realm of UAV control design, exemplified by works like [15,24,25,26,27,28,29], crucial design parameters surface, demanding meticulous selection. Indeed, these parameters have been chosen through a laborious trial-and-error process, targeting stabilization requirements. However, this conventional approach falters in achieving optimal performance, imposing substantial constraints on proposed methodologies. Hence, we suppose the selection of design parameters for the proposed controller, framing it as an optimization challenge with the goal of improving the performance. Harnessing the metaheuristic APSO, we employ an optimization approach to pinpoint the optimal values for control parameters.
2. Coaxial Rotor Helicopter Modelling
Control Oriented Model Development
3. Robust Nonlinear Controller
- Develop a direct control structure based on local measurements, eliminating the need for prior knowledge of the system’s dynamic model.
- Ensure that the proposed control strategy drives the tracking error to finite-time convergence in the closed-loop system in the presence of disturbances.
- Enhance the performance of the controller by incorporating a metaheuristic algorithm to optimize the control parameters and improve robustness.
3.1. Model-Free Control Based on Terminal Sliding Mode
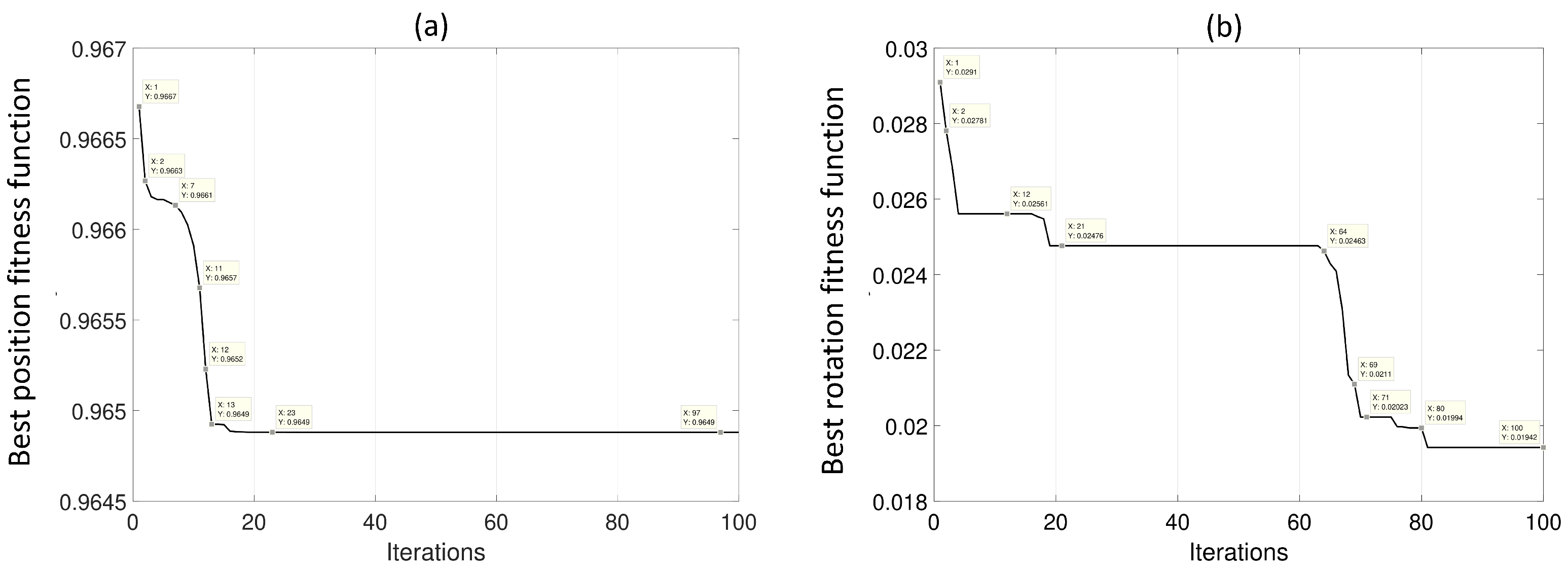
3.2. Optimization of Control Parameters
- Step 1: Initialize the following parameters:
- Population size: The number of swarms in the population.
- Number of iterations: The maximum number of iterations the algorithm will perform.
- Step size t: The step size is used for generating new parameter values during pollination operations.
- Step 2: Generate the initial feasible solutions according to the search space set from experience, with the same size as the dimensional problem. For each initial solution, compute mean absolute error (MAE), which is used as the fitness function and denoted by , as follows:
- Step 3: Update the velocity and position of each particle using the APSO algorithm. This involves adjusting the control parameters based on the particle’s previous position, velocity, and its best-known position and the best-known position in the entire swarm.
- Step 4: Repeat steps 2 and 3 for a predefined number of iterations or until a convergence criterion is met. Once the optimization process is complete, the control parameters of the particle with the best fitness are considered as the tuned proposed parameters.
4. Results and Discussion
4.1. APSO-Based Parameter Tuning
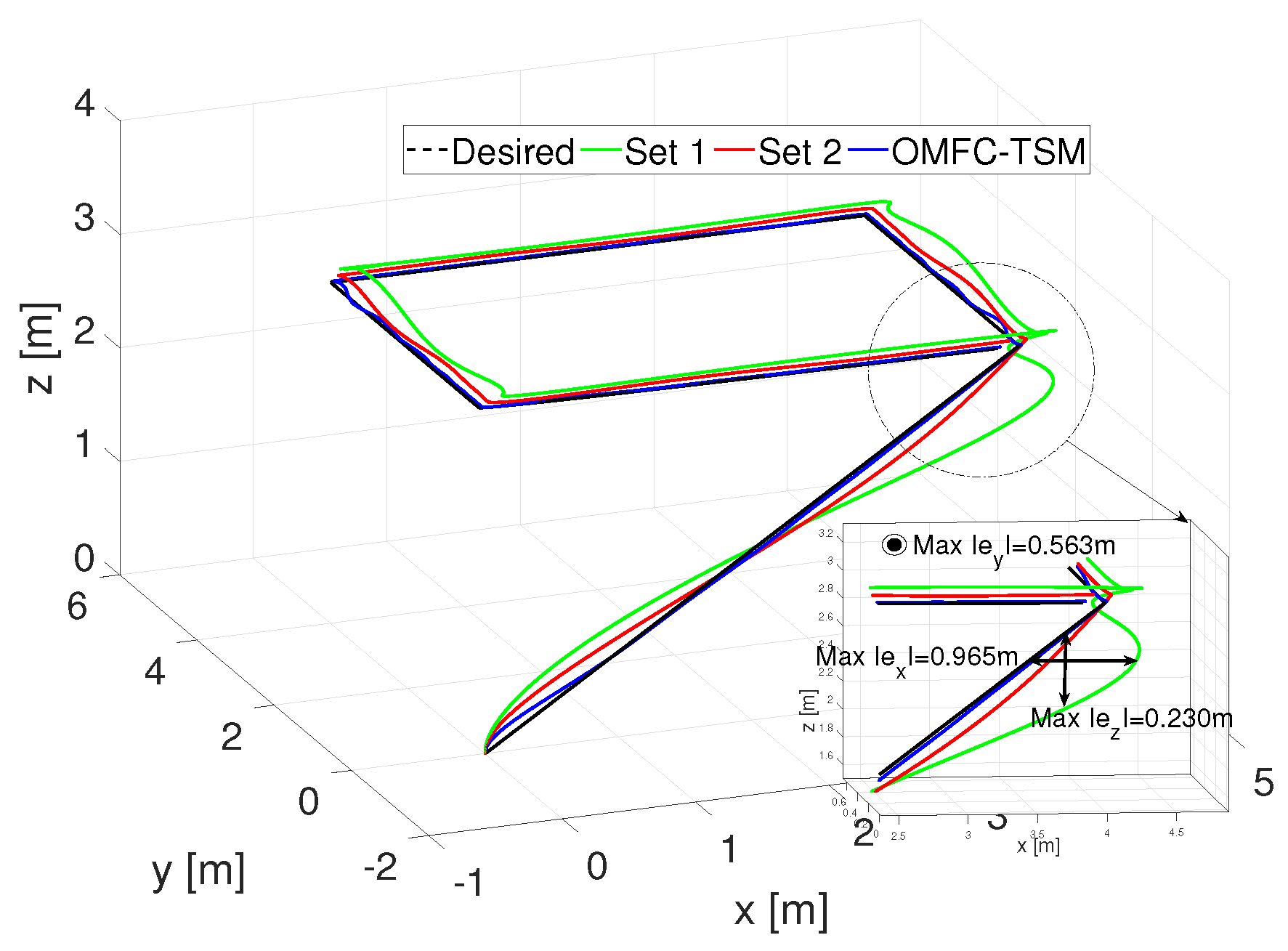
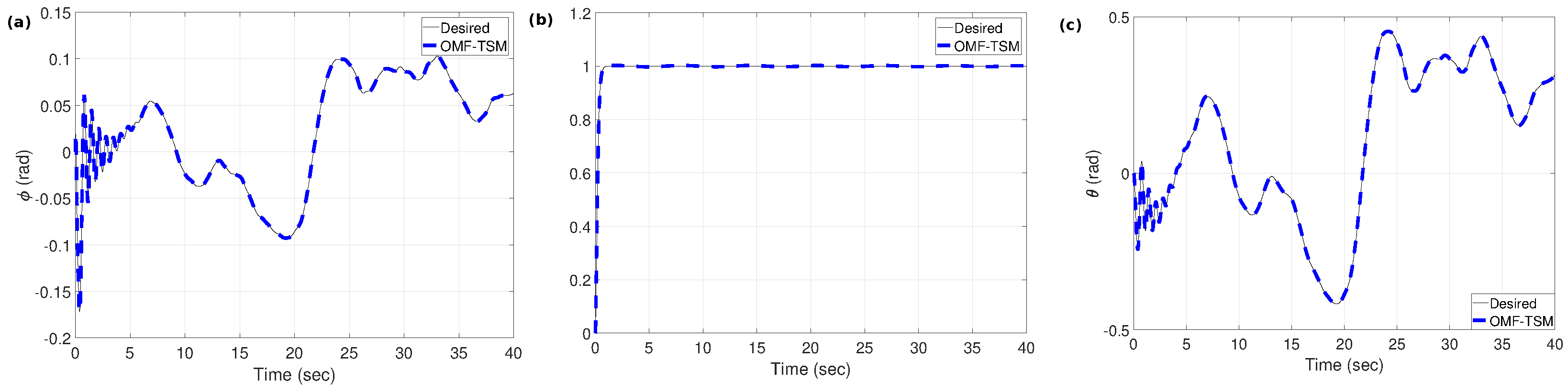
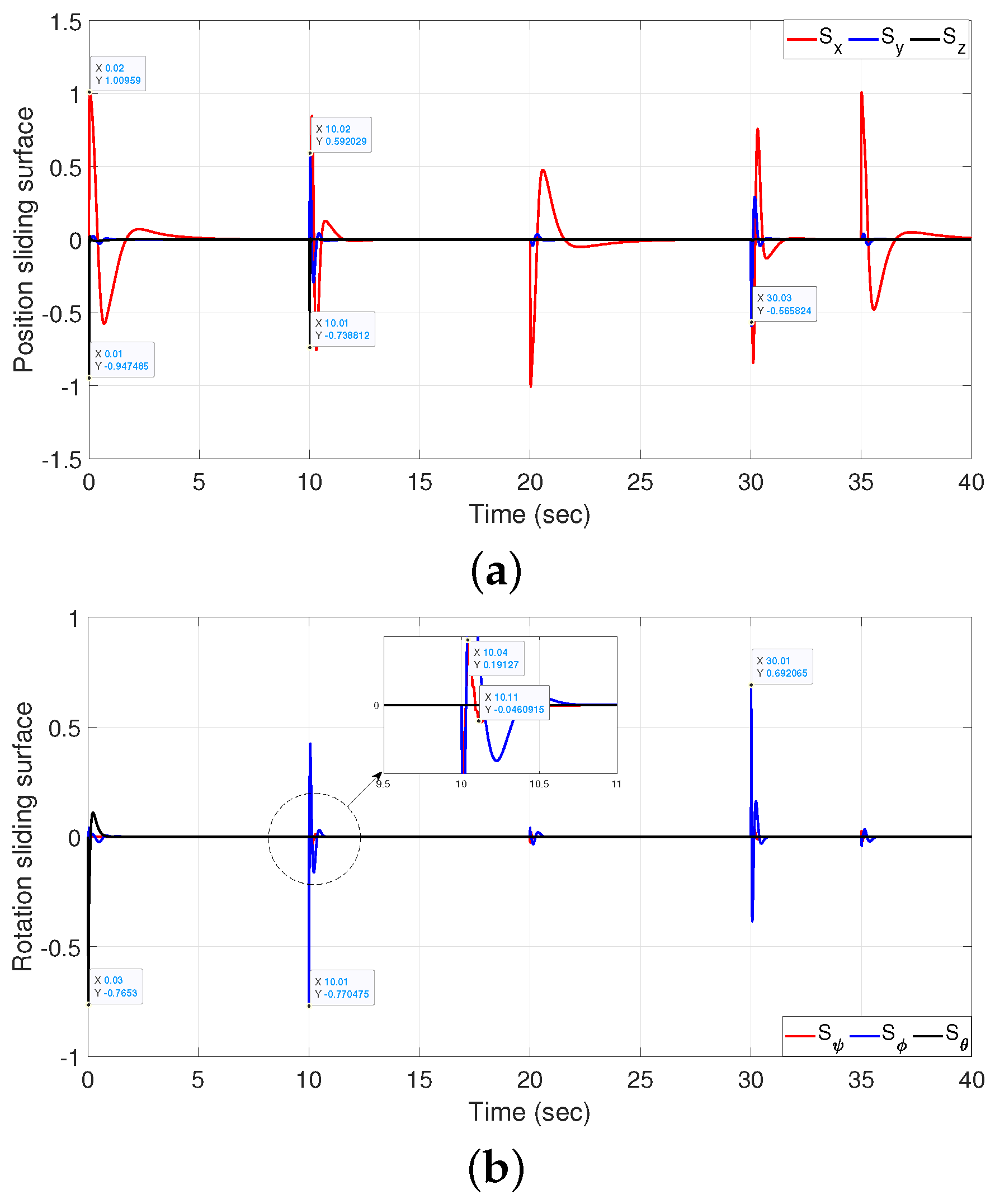
4.2. Performance Evaluation of APSO-Tuned OMFC-TSM Controller
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kumar, V.; Michael, N. Opportunities and challenges with autonomous micro aerial vehicles. Int. J. Robot. Res. 2012, 31, 1279–1291. [Google Scholar] [CrossRef]
- Ouyang, F.; Cheng, H.; Lan, Y.; Zhang, Y.; Yin, X.; Hu, J.; Peng, X.; Wang, G.; Chen, S. Automatic delivery and recovery system of Wireless Sensor Networks (WSN) nodes based on UAV for agricultural applications. Comput. Electron. Agric. 2019, 162, 31–43. [Google Scholar] [CrossRef]
- Lippiello, V.; Fontanelli, G.A.; Ruggiero, F. Image-Based Visual-Impedance Control of a Dual-Arm Aerial Manipulator. IEEE Robot. Autom. Lett. 2018, 3, 1856–1863. [Google Scholar] [CrossRef]
- Mokhtari, M.R.; Cherki, B.; Braham, A.C. Disturbance observer based hierarchical control of coaxial-rotor UAV. ISA Trans. 2017, 67, 466–475. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.J.; Shim, D.H. A flight control system for aerial robots: Algorithms and experiments. Control Eng. Pract. 2003, 11, 1389–1400. [Google Scholar] [CrossRef]
- Mettler, B. Identification Modeling and Characteristics of Miniature Rotorcraft; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Artale, V.; Milazzo, C.L.; Orlando, C.; Ricciardello, A. Comparison of GA and PSO approaches for the direct and LQR tuning of a multirotor PD controller. J. Ind. Manag. Optim. 2017, 13, 2067. [Google Scholar] [CrossRef]
- Drouot, A.; Zasadzinski, M.; Souley-Ali, H.; Richard, E.; Boutayeb, M. Two robust static output feedback Hinf control architectures for a Gun Launched Micro Aerial Vehicle. In Proceedings of the 21st Mediterranean Conference on Control and Automation, Chania, Crete, 25–28 June 2013; pp. 185–190. [Google Scholar]
- Joel, N.C.; Djalo, H.; Aurelien, K. Robust control of UAV coaxial rotor by using exact feedback linearization and PI-observer. Int. J. Dyn. Control 2019, 7, 201–208. [Google Scholar] [CrossRef]
- Espinoza, E.S.; Garcia, O.; Lugo, I.; Ordaz, P.; Malo, A.; Lozano, R. Modeling and sliding mode control of a micro helicopter-airplane system. J. Intell. Robot. Syst. 2014, 73, 469–486. [Google Scholar] [CrossRef]
- Drouot, A.; Richard, E.; Boutayeb, M. An approximate backstepping based trajectory tracking control of a gun launched micro aerial vehicle in crosswind. J. Intell. Robot. Syst. 2013, 70, 133–150. [Google Scholar] [CrossRef]
- Drouot, A.; Richard, E.; Boutayeb, M. Hierarchical backstepping-based control of a Gun Launched MAV in crosswinds: Theory and experiment. Control Eng. Pract. 2014, 25, 16–25. [Google Scholar] [CrossRef]
- Zhang, J.; Ren, Z.; Deng, C.; Wen, B. Adaptive fuzzy global sliding mode control for trajectory tracking of quadrotor UAVs. Nonlinear Dyn. 2019, 97, 609–627. [Google Scholar] [CrossRef]
- Zhang, H.; Zeng, Z.; Yu, C.; Jiang, Z.; Han, B.; Lian, L. Predictive and sliding mode cascade control for cross-domain locomotion of a coaxial aerial underwater vehicle with disturbances. Appl. Ocean Res. 2020, 100, 102183. [Google Scholar] [CrossRef]
- Zeghlache, S.; Mekki, H.; Bouguerra, A.; Djerioui, A. Actuator fault tolerant control using adaptive RBFNN fuzzy sliding mode controller for coaxial octorotor UAV. ISA Trans. 2018, 80, 267–278. [Google Scholar] [CrossRef] [PubMed]
- Lv, Z.; Wu, Y.; Zhao, Q.; Sun, X.M. Design and Control of a Novel Coaxial Tilt-Rotor UAV. IEEE Trans. Ind. Electron. 2021, 69, 3810–3821. [Google Scholar] [CrossRef]
- Fliess, M.; Join, C. Model-free control. Int. J. Control 2013, 86, 2228–2252. [Google Scholar] [CrossRef]
- Al Younes, Y.; Drak, A.; Noura, H.; Rabhi, A.; El Hajjaji, A. Robust model-free control applied to a quadrotor UAV. J. Intell. Robot. Syst. 2016, 84, 37–52. [Google Scholar] [CrossRef]
- Barth, J.M.; Condomines, J.P.; Moschetta, J.M.; Cabarbaye, A.; Join, C.; Fliess, M. Full model-free control architecture for hybrid UAVs. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 71–78. [Google Scholar]
- Wang, H.; Ye, X.; Tian, Y.; Zheng, G.; Christov, N. Model-free–based terminal SMC of quadrotor attitude and position. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2519–2528. [Google Scholar] [CrossRef]
- Li, Z.; Ma, X.; Li, Y. Model-free control of a quadrotor using adaptive proportional derivative-sliding mode control and robust integral of the signum of the error. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418800885. [Google Scholar] [CrossRef]
- Bouzid, Y.; Siguerdidjane, H.; Bestaoui, Y. Generic dynamic modeling for multirotor VTOL UAVs and robust Sliding Mode based Model-Free Control for 3D navigation. In Proceedings of the 2018 International Conference on Unmanned Aircraft Systems (ICUAS), Dallas, TX, USA, 12–15 June 2018; pp. 970–979. [Google Scholar] [CrossRef]
- Glida, H.E.; Abdou, L.; Chelihi, A.; Sentouh, C.; Hasseni, S.E.I. Optimal model-free backstepping control for a quadrotor helicopter. Nonlinear Dyn. 2020, 100, 3449–3468. [Google Scholar] [CrossRef]
- Fu, C.; Hong, W.; Lu, H.; Zhang, L.; Guo, X.; Tian, Y. Adaptive robust backstepping attitude control for a multi-rotor unmanned aerial vehicle with time-varying output constraints. Aerosp. Sci. Technol. 2018, 78, 593–603. [Google Scholar] [CrossRef]
- Wang, G.; Yang, W.; Zhao, N.; Shen, Y.; Wang, C. An approximation-free simple controller for uncertain quadrotor systems in the presence of thrust saturation. Mechatronics 2020, 72, 102450. [Google Scholar] [CrossRef]
- Bounemeur, A.; Chemachema, M.; Essounbouli, N. Indirect adaptive fuzzy fault-tolerant tracking control for MIMO nonlinear systems with actuator and sensor failures. ISA Trans. 2018, 79, 45–61. [Google Scholar] [CrossRef]
- Zeghlache, S.; Djerioui, A.; Benyettou, L.; Benslimane, T.; Mekki, H.; Bouguerra, A. Fault tolerant control for modified quadrotor via adaptive type-2 fuzzy backstepping subject to actuator faults. ISA Trans. 2019, 95, 330–345. [Google Scholar] [CrossRef] [PubMed]
- Chekakta, Z.; Zerikat, M.; Bouzid, Y.; Koubaa, A. Adaptive fuzzy model-free control for 3D trajectory tracking of quadrotor. Int. J. Mechatron. Autom. 2020, 7, 134–146. [Google Scholar] [CrossRef]
- Camci, E.; Kripalani, D.R.; Ma, L.; Kayacan, E.; Khanesar, M.A. An aerial robot for rice farm quality inspection with type-2 fuzzy neural networks tuned by particle swarm optimization-sliding mode control hybrid algorithm. Swarm Evol. Comput. 2018, 41, 1–8. [Google Scholar] [CrossRef]
- Glida, H.E.; Abdou, L.; Chelihi, A.; Sentouh, C.; Perozzi, G. Optimal model-free fuzzy logic control for autonomous unmanned aerial vehicle. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2022, 236, 952–967. [Google Scholar] [CrossRef]
- Wei, Y.R.; Deng, H.B.; Pan, Z.H.; Li, K.W.; Chen, H. Research on a combinatorial control method for coaxial rotor aircraft based on sliding mode. Def. Technol. 2022, 18, 280–292. [Google Scholar] [CrossRef]
- Yan, K.; Chen, M.; Wu, Q. Neural network-based adaptive fault tolerant tracking control for unmanned autonomous helicopters with prescribed performance. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 4350–4362. [Google Scholar] [CrossRef]
- Koehl, A.; Rafaralahy, H.; Boutayeb, M.; Martinez, B. Aerodynamic modelling and experimental identification of a coaxial-rotor UAV. J. Intell. Robot. Syst. 2012, 68, 53–68. [Google Scholar] [CrossRef]
- Glida, H.E.; Chelihi, A.; Abdou, L.; Sentouh, C.; Perozzi, G. Trajectory tracking control of a coaxial rotor drone: Time-delay estimation-based optimal model-free fuzzy logic approach. ISA Trans. 2022, 137, 236–247. [Google Scholar] [CrossRef] [PubMed]
- Nonami, K.; Kendoul, F.; Suzuki, S.; Wang, W.; Nakazawa, D. Autonomous Flying Robots: Unmanned Aerial Vehicles and Micro Aerial Vehicles; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Huang, X.; Lin, W.; Yang, B. Global finite-time stabilization of a class of uncertain nonlinear systems. Automatica 2005, 41, 881–888. [Google Scholar] [CrossRef]
- Yu, S.; Yu, X.; Shirinzadeh, B.; Man, Z. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Zhihong, M.; Yu, X.H. Terminal sliding mode control of MIMO linear systems. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 1997, 44, 1065–1070. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Sari, N.N.; Pham, V.T.; Alsaadi, F.E.; Hayat, T. Optimal adaptive higher order controllers subject to sliding modes for a carrier system. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418782097. [Google Scholar] [CrossRef]
- Yousefpour, A.; Jahanshahi, H.; Gan, D. Fuzzy integral sliding mode technique for synchronization of memristive neural networks. In Mem-Elements for Neuromorphic Circuits with Artificial Intelligence Applications; Elsevier: Amsterdam, The Netherlands, 2021; pp. 485–500. [Google Scholar]
- Zhou, S.S.; Jahanshahi, H.; Din, Q.; Bekiros, S.; Alcaraz, R.; Alassafi, M.O.; Alsaadi, F.E.; Chu, Y.M. Discrete-time macroeconomic system: Bifurcation analysis and synchronization using fuzzy-based activation feedback control. Chaos Solitons Fract. 2021, 142, 110378. [Google Scholar] [CrossRef]
- Yang, X.S. Nature-Inspired Optimization Algorithms; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Hsia, T.S.; Lasky, T.; Guo, Z. Robust independent joint controller design for industrial robot manipulators. IEEE Trans. Ind. Electron. 1991, 38, 21–25. [Google Scholar] [CrossRef]
- Hasseni, S.E.I.; Abdou, L.; Glida, H.E. Parameters tuning of a quadrotor PID controllers by using nature-inspired algorithms. Evol. Intell. 2021, 14, 61–73. [Google Scholar] [CrossRef]






| Parameters | Value |
|---|---|
| g | 9.81 m/s2 |
| d | 0.0676 m |
| m | 0.41 kg |
| 1.383 × 10 kg.m2 | |
| 1.383 × 10 kg.m2 | |
| 2.72 × 10 kg.m2 | |
| 3.683 × 10 N/rad2 s2 | |
| 3.776 × 10 N/rad2 s2 | |
| 1.476 × 10 N.m/rad2 s2 | |
| 1.326 × 10 N.m/rad2 s2 |
| ith Controller | Parameter Value | ||||
|---|---|---|---|---|---|
| x | 9.451 | 3.183 | 3.968 | 1.159 | 2.174 |
| y | 10.135 | 2.642 | 2.154 | 0.947 | 2.691 |
| z | 13.267 | 4.548 | 4.957 | 2.153 | 1.983 |
| 5.642 | 1.846 | 1.679 | 0.187 | 1.872 | |
| 3.946 | 1.751 | 1.781 | 0.924 | 1.781 | |
| 4.873 | 1.976 | 2.115 | 1.542 | 1.1371 | |
| Criterion | Controller | |||
|---|---|---|---|---|
| PID | TDEC | OMFC-TSM | ||
| MAE | Position System | 0.2589 | 0.1062 | 0.0351 |
| Rotation System | 0.0012 | 6.35 | 5 | |
| RMSE | Position System | 0.5075 | 0.2921 | 0.1740 |
| Rotation System | 0.0199 | 0.0129 | 0.0129 | |
| MaxAE | Position System | 1.4115 | 1.0207 | 0.0788 |
| Rotation System | 0.0048 | 0.0028 | 0.0030 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Glida, H.E.; Sentouh, C.; Rath, J.J. Optimal Model-Free Finite-Time Control Based on Terminal Sliding Mode for a Coaxial Rotor. Drones 2023, 7, 706. https://doi.org/10.3390/drones7120706
Glida HE, Sentouh C, Rath JJ. Optimal Model-Free Finite-Time Control Based on Terminal Sliding Mode for a Coaxial Rotor. Drones. 2023; 7(12):706. https://doi.org/10.3390/drones7120706
Chicago/Turabian StyleGlida, Hossam Eddine, Chouki Sentouh, and Jagat Jyoti Rath. 2023. "Optimal Model-Free Finite-Time Control Based on Terminal Sliding Mode for a Coaxial Rotor" Drones 7, no. 12: 706. https://doi.org/10.3390/drones7120706
APA StyleGlida, H. E., Sentouh, C., & Rath, J. J. (2023). Optimal Model-Free Finite-Time Control Based on Terminal Sliding Mode for a Coaxial Rotor. Drones, 7(12), 706. https://doi.org/10.3390/drones7120706






