Performance Analysis of the Thermal Automatic Tracking Method Based on the Model of the UAV Dynamic Model in a Thermal and Cubature Kalman Filter
Abstract
:1. Introduction
2. Pitching Dynamics Modeling of SUAV
2.1. Review of Prior Models
2.2. UAVs Roll Moment Model in Thermal
2.3. UAVs Pitching Moment Model in the Thermal
3. State Estimation Algorithms
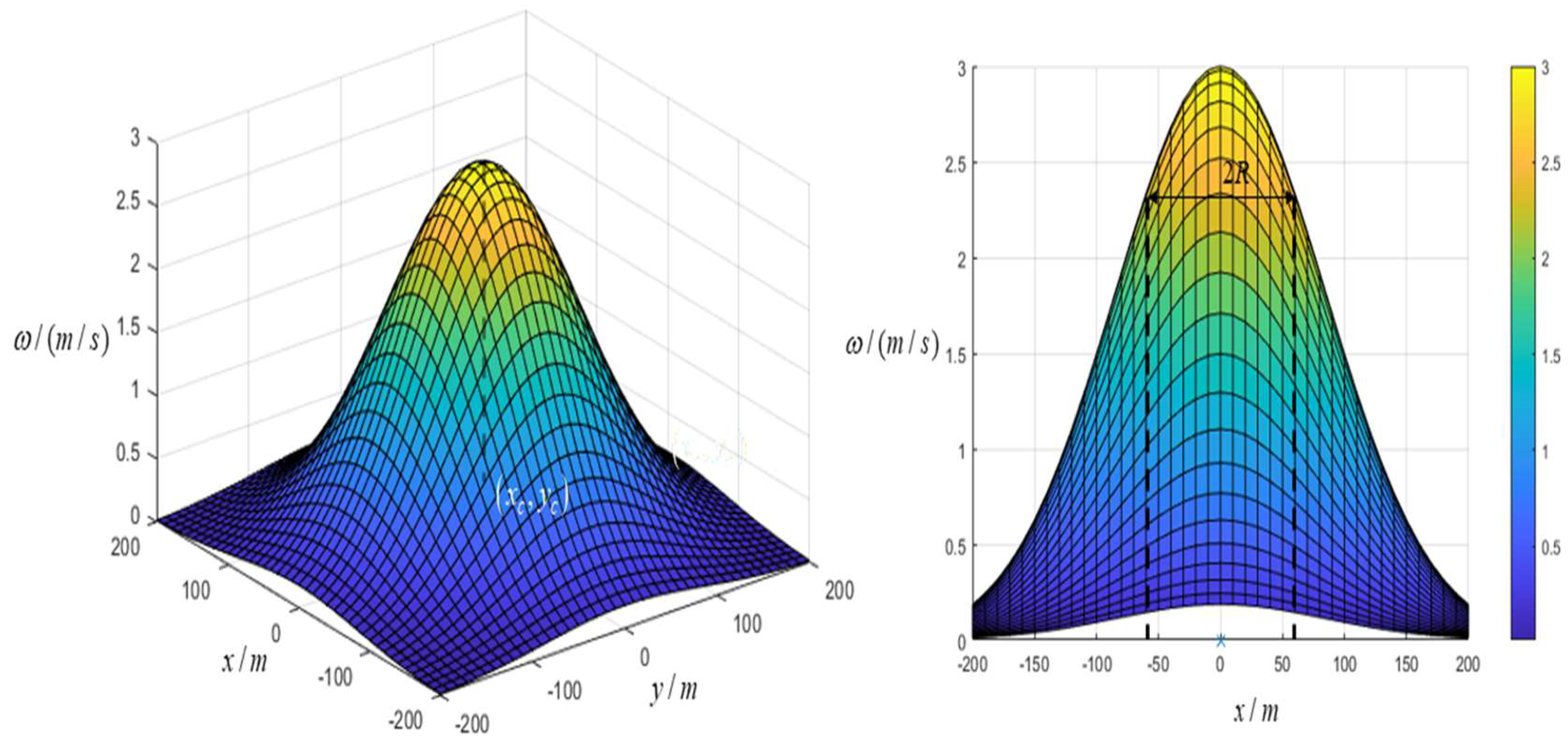
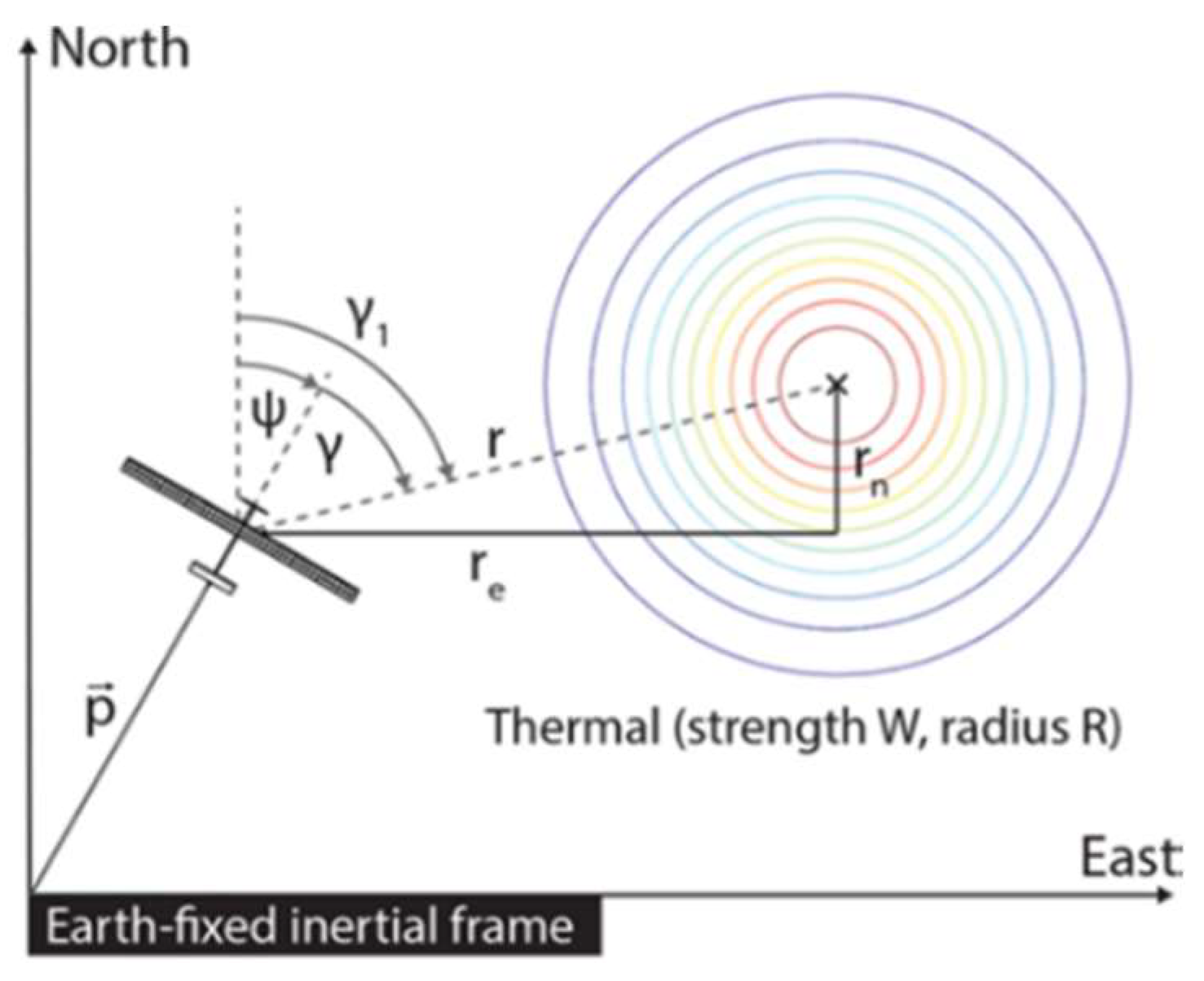
3.1. Thermal State Estimation and Measurement Models
3.2. Unscented Kalman Filter
- 1.
- Calculating sigma points:
- 2.
- Time update:
- Calculating sigma points:
- Measurement update:
- State Estimation:
3.3. Cubature Kalman Filter
- Calculating sigma point:
- Time update:
- Calculating sigma point:
- Measurement update:
- State Estimation:
4. Simulation Results Analysis
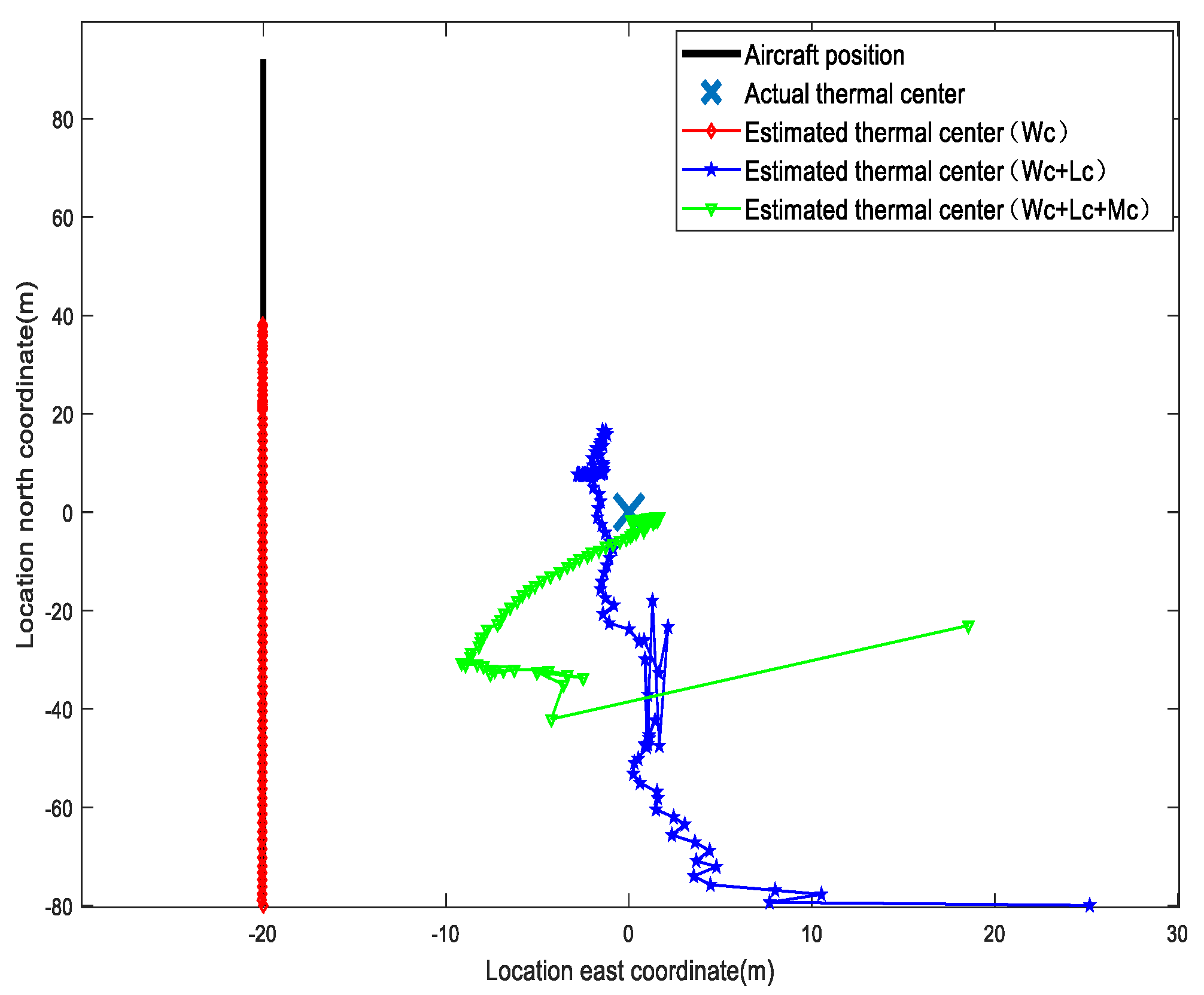
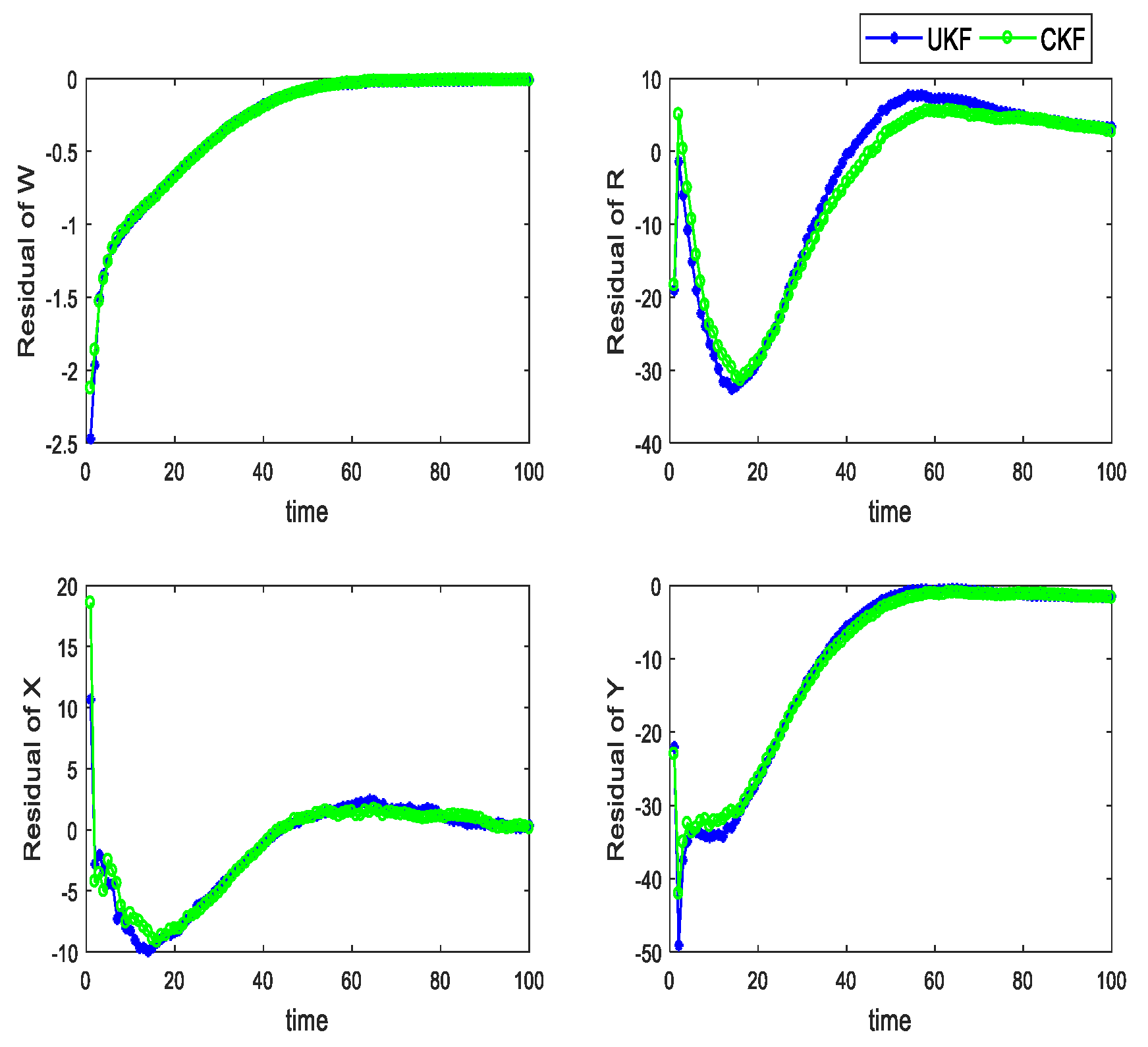
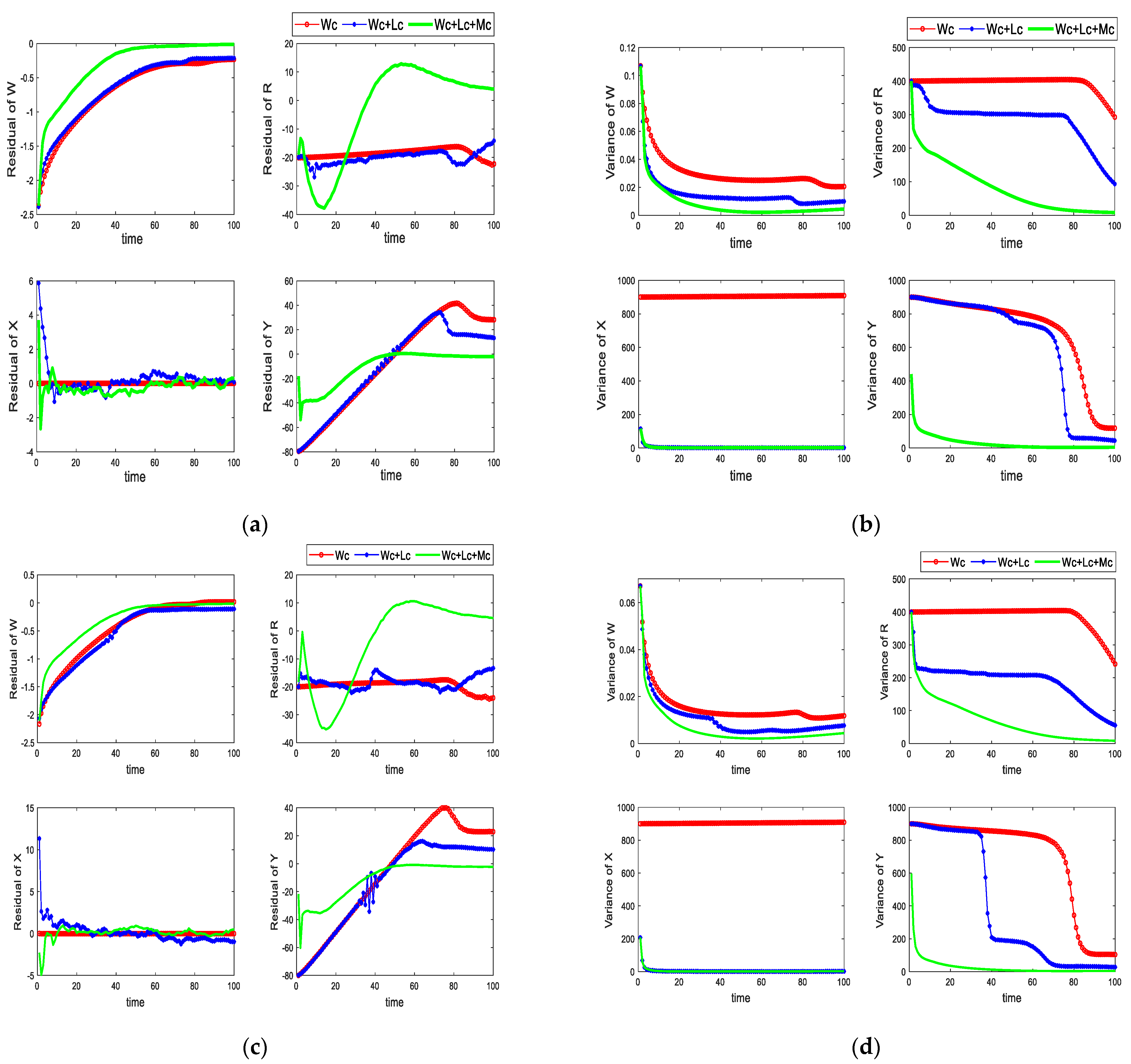
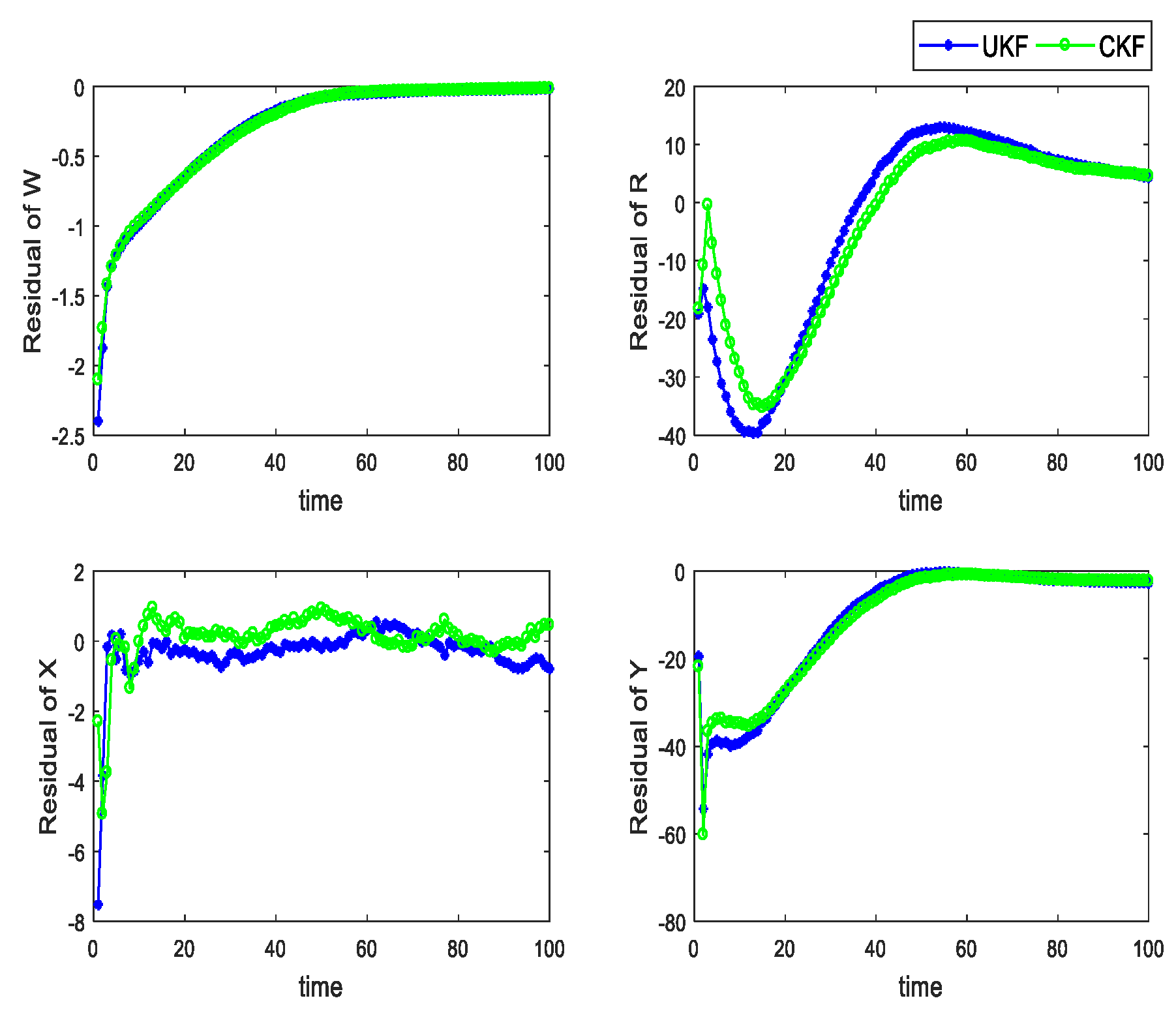
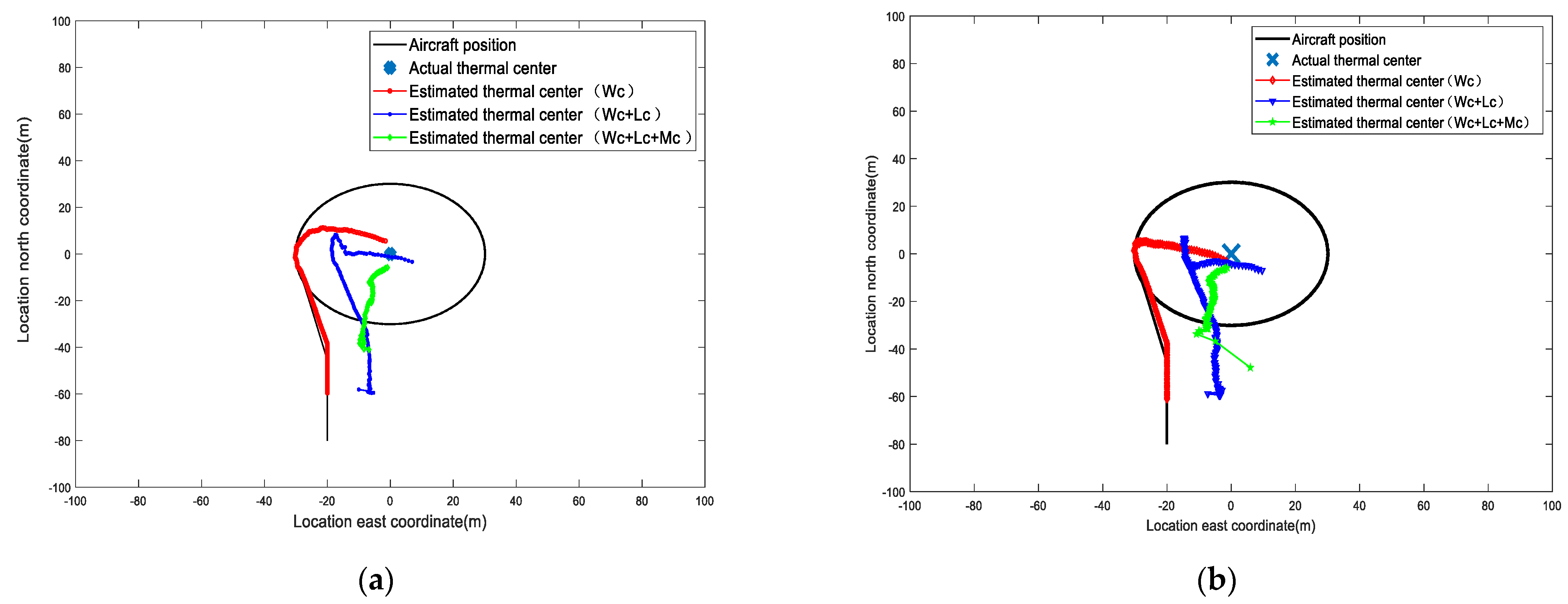
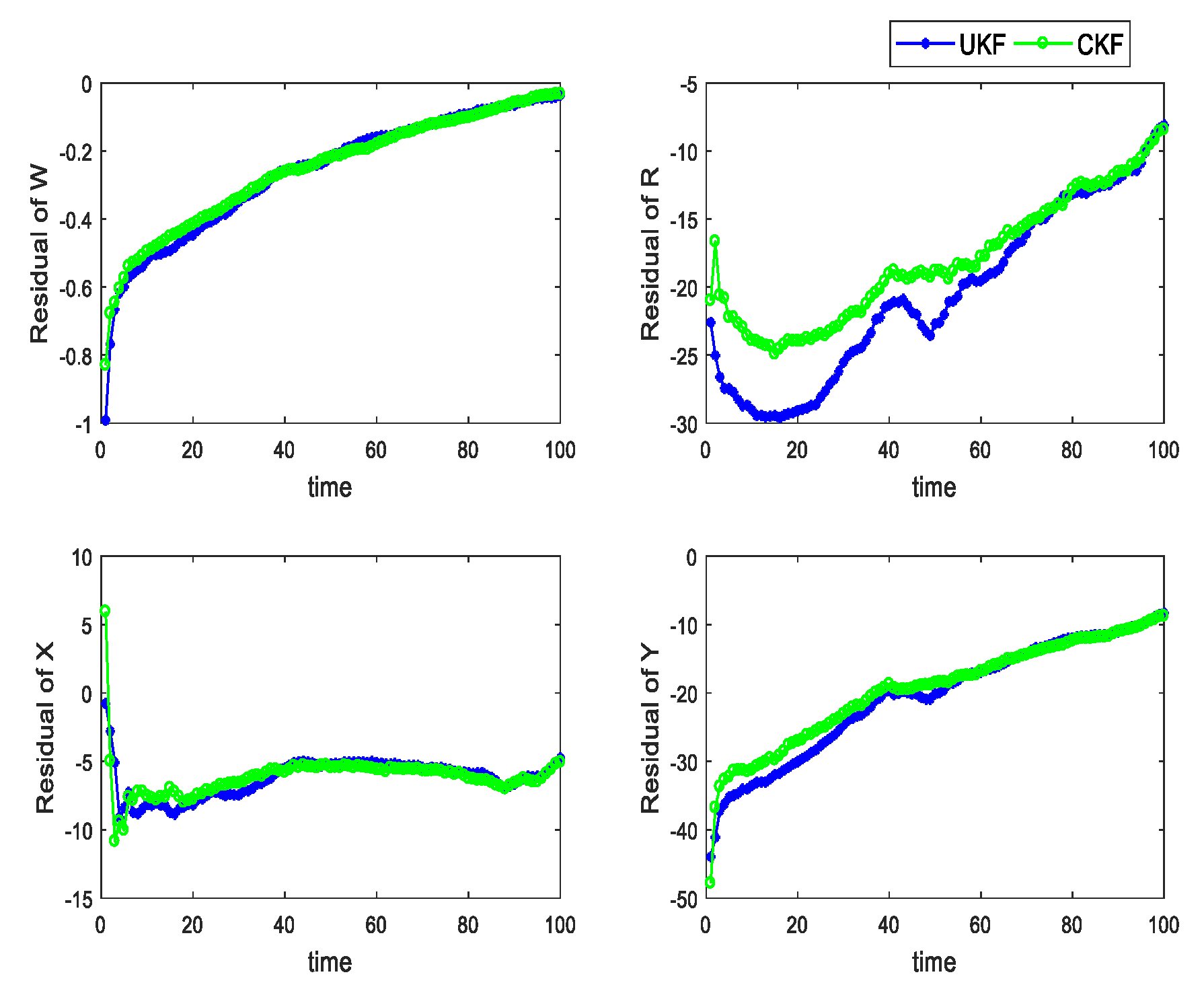
4.1. The Algorithm Efficiency
4.2. The Algorithm Efficiency under Different Flight Paths
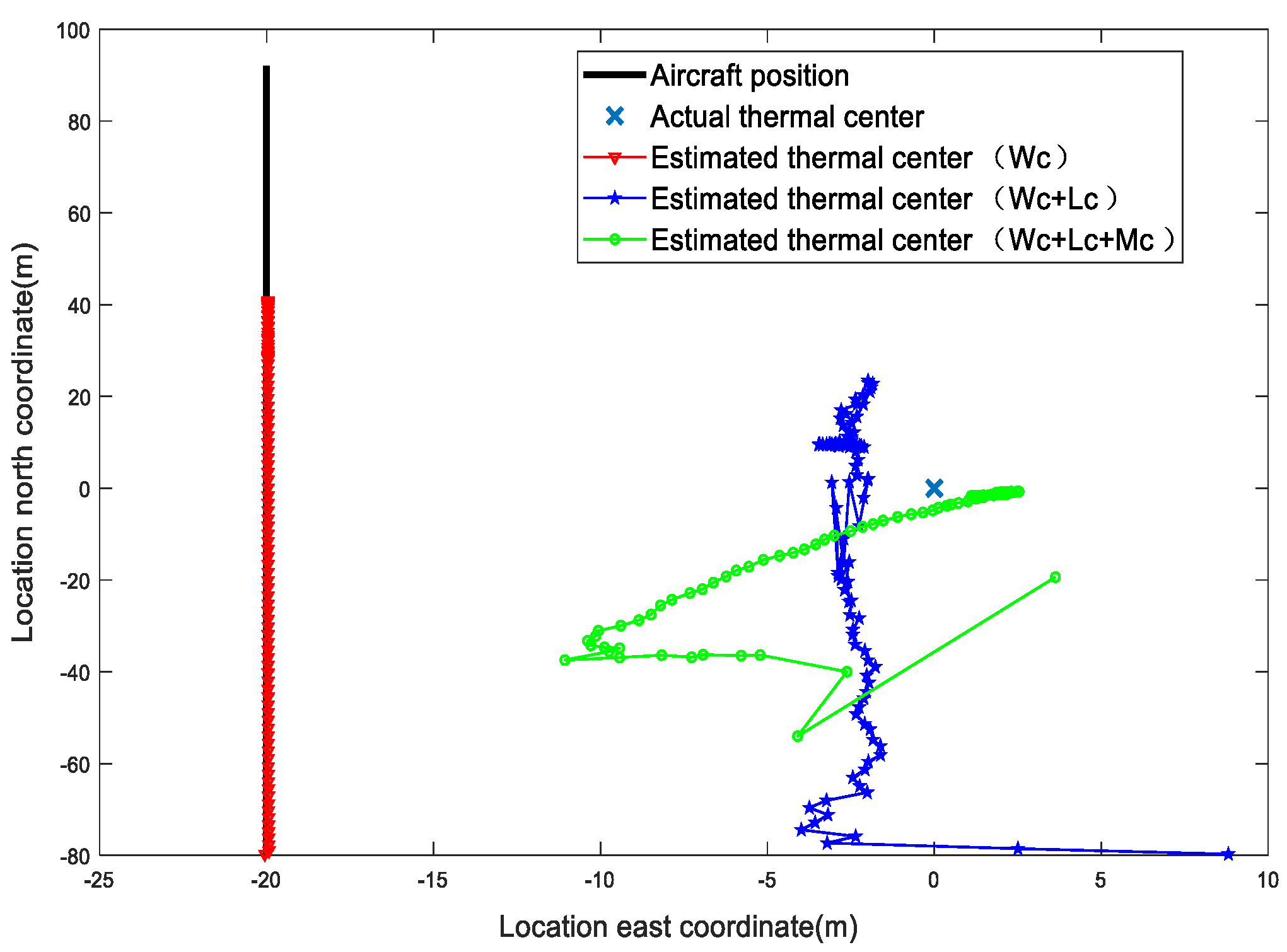
4.3. The Algorithm Efficiency While Hovering around the Thermal
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gupta, S.G.; Ghonge MM, P.M.; Jawandhiya, P. Review of Unmanned Aircraft System (UAS). Int. J. Adv. Res. Comput. Eng. Technol. 2013. [Google Scholar] [CrossRef]
- Lun, Y.; Wang, H.; Wu, J.; Liu, Y.; Wang, Y. Target Search in Dynamic Environments With Multiple Solar-Powered UAVs. IEEE Trans. Veh. Technol. 2022, 71, 9309–9321. [Google Scholar] [CrossRef]
- Tian, Z.; Haas, Z.J.; Shinde, S. Routing in Solar-Powered UAV Delivery System. Drones 2022, 6, 282. [Google Scholar] [CrossRef]
- Chu, Y.; Ho, C.; Lee, Y.; Li, B. Development of a Solar-Powered Unmanned Aerial Vehicle for Extended Flight Endurance. Drones 2021, 5, 44. [Google Scholar] [CrossRef]
- El-Atab, N.; Mishra, R.B.; Alshanbari, R.; Hussain, M.M. Solar Powered Small Unmanned Aerial Vehicles: A Review. Energy Technology 2021, 9, 2170121. [Google Scholar] [CrossRef]
- Kim, E.J.; Perez, R.E. Neuroevolutionary Control for Autonomous Soaring. Aerospace 2021, 8, 267. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, J.; Wang, H.; Su, G. A method of 3D path planning for solar-powered UAV with fixed target and solar tracking. Aerosp. Sci. Technol. 2019, 92, 831–838. [Google Scholar] [CrossRef]
- Reddy, G.; Celani, A.; Sejnowski, T.J.; Vergassola, M. Learning to soar in turbulent environments. Proc. Natl. Acad. Sci. USA 2016, 113, E4877–E4884. [Google Scholar] [CrossRef]
- Mohamed, A.; Taylor, G.K.; Watkins, S.; Windsor, S.P. Opportunistic soaring by birds suggests new opportunities for atmospheric energy harvesting by flying robots. J. R. Soc. Interface 2022, 19, 20220671. [Google Scholar] [CrossRef]
- Notter, S.; Groß, P.; Schrapel, P.; Fichter, W. Multiple Thermal Updraft Estimation and Observability Analysis. J. Guid. Control Dyn. 2020, 43, 490–503. [Google Scholar] [CrossRef]
- Allen, M.J. Autonomous Soaring for Small Unmanned Aerial Vehicles (UAVs). 2006. Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=1y2w0xb0w44q0my0652j00d0rw780327 (accessed on 17 January 2023).
- Guilliard, I.; Rogahn, R.; Piavis, J.; Kolobov, A. Autonomous Thermalling as a Partially Observable Markov Decision Process. In Proceedings of the 14th Conference on Robotics—Science and Systems, Pittsburgh, PA, USA, 26–30 June 2018. [Google Scholar]
- Notter, S.; Zürn, M.; Groß, P.; Fichter, W. Reinforced Learning to Cross-Country Soar in the Vertical Plane of Motion. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Cheng, K.; Langelaan, J.W. Guided Exploration for Coordinated Autonomous Soaring Flight. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar]
- Lawrance NR, J.; Sukkarieh, S. Path Planning for Autonomous Soaring Flightin Dynamic Wind Fields. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011. [Google Scholar]
- Kahn, A.D. Atmospheric Thermal Location Estimation. J. Guid. Control Dyn. 2017, 40, 2359–2365. [Google Scholar] [CrossRef]
- Hazard, M. Unscented Kalman Filter for Thermal Parameter Identification. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010. [Google Scholar]
- Tabor, S.; Guilliard, I.; Kolobov, A. ArduSoar: An Open-Source Thermalling Controller for Resource-Constrained Autopilots. In Proceedings of the 25th IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018. [Google Scholar]
- Oettershagen, P.; Stastny, T.; Hinzmann, T.; Rudin, K.; Mantel, T.; Melzer, A.; Wawrzacz, B.; Hitz, G.; Siegwart, R. Robotic technologies for solar-powered UAVs: Fully autonomous updraft-aware aerial sensing for multiday search-and-rescue missions. J. Field Robot. 2018, 35, 612–640. [Google Scholar] [CrossRef]
- Meng, Y.; Wang, W.; Han, H.; Ban, J. A visual/inertial integrated landing guidance method for UAV landing on the ship. Aerosp. Sci. Technol. 2019, 85, 474–480. [Google Scholar] [CrossRef]
- Song, H.-L.; Ko, Y.-C. Robust and Low Complexity Beam Tracking With Monopulse Signal for UAV Communications. Ieee Trans. Veh. Technol. 2021, 70, 3505–3513. [Google Scholar] [CrossRef]
- Guo, K.; Ye, Z.; Liu, D.; Peng, X. UAV flight control sensing enhancement with a data-driven adaptive fusion model. Reliab. Eng. Syst. Saf. 2021, 213, 107654. [Google Scholar] [CrossRef]
- Julier, S.; Uhlmann, J.; Durrant-Whyte, H.F. A new method for the nonlinear transformation of means and covariances in filters and estimators. IEEE Trans. Autom. Control 2000, 45, 477–482. [Google Scholar] [CrossRef]
- Djuric, P.M.; Kotecha, J.H.; Zhang, J.; Huang, Y.; Ghirmai, T.; Bugallo, M.F.; Miguez, J. Particle filtering. IEEE Signal Process. Mag. 2003, 20, 19–38. [Google Scholar] [CrossRef]
- Santos, N.P.; Lobo, V.; Bernardino, A. Unscented Particle Filters with Refinement Steps for UAV Pose Tracking. J. Intell. Robot. Syst. 2021, 102, 52. [Google Scholar] [CrossRef]
- Fu, R.; Al-Absi, M.A.; Lee, Y.S.; Al-Absi, A.A.; Lee, H.J. Modified Uncertainty Error Aware Estimation Model for Tracking the Path of Unmanned Aerial Vehicles. Appl. Sci. 2022, 12, 11313. [Google Scholar] [CrossRef]
- Lefebvre, T.; Bruyninckx, H.; De Schutter, J. Kalman filters for non-linear systems: A comparison of performance. Int J Control 2004, 77, 639–653. [Google Scholar] [CrossRef]
- Edwards, D. Implementation Details and Flight Test Results of an Autonomous Soaring Controller; In Proceedings of the 46 th AIAA Guidance, Navigation and Control Conference and Exhibit, Reno, Nevada, 7–10 January 2008.
- Arasaratnam, I.; Haykin, S. Cubature Kalman Filters. IEEE Trans Autom Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef] [Green Version]
- Allen, M. Updraft Model for Development of Autonomous Soaring Uninhabited Air Vehicles. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 9–12 January 2006. [Google Scholar]




| Quantity | Default Parameters |
|---|---|
| time step | 8.6 m/s 0.2 s |
| thermal parameter | |
| initial thermal estimation | [5, 120, 0, 0] |
| initial UAVs position | [1.5, 100, 0, 0] |
| initial UAVs flight direction | 0 deg |
| 1D | 2D | 3D | ||
|---|---|---|---|---|
| ARMSE | ||||
| UKF | 0.9792 | 0.8373 | 0.5402 0.5406 | |
| CKF | 0.7467 | 0.7547 | ||
| UKF | 17.4332 | 8.6705 | 12.3160 | |
| CKF | 19.3272 | 11.1973 | 13.1580 | |
| UKF | 20 | 3.6578 | 4.4521 | |
| CKF | 20 | 4.2449 | 4.6538 | |
| UKF | 39.1139 | 34.9439 | 14.5073 | |
| CKF | 36.6828 | 33.4117 | 15.5878 | |
| 1D | 2D | 3D | |
|---|---|---|---|
| Run Times (s) | |||
| UKF | 0.0035 | 0.0043 | 0.0044 0.0062 |
| CKF | 0.0036 | 0.0061 | |
| 1D | 2D | 3D | ||
|---|---|---|---|---|
| ARMSE | ||||
| UKF | 0.9039 | 0.8352 | 0.5184 0.5105 | |
| CKF | 0.6843 | 0.7377 | ||
| UKF | 17.4645 | 10.3216 | 13.4091 | |
| CKF | 19.3414 | 11.8441 | 13.8194 | |
| UKF | 0 | 1.5783 | 1.9192 | |
| CKF | 0 | 1.5367 | 1.9006 | |
| UKF | 39.1920 | 35.2057 | 14.9090 | |
| CKF | 36.7658 | 33.5224 | 15.6311 | |
| 1D | 2D | 3D | |
|---|---|---|---|
| Run Times (s) | |||
| UKF | 0.0192 | 0.0243 | 0.0245 0.0387 |
| CKF | 0.0195 | 0.0368 | |
| 1D | 2D | 3D | ||
|---|---|---|---|---|
| ARMSE | ||||
| UKF | 0.1450 | 0.1468 | 0.1135 0.1076 | |
| CKF | 0.1497 | 0.1460 | ||
| UKF | 19.9011 | 32.1705 | 12.6546 | |
| CKF | 19.7294 | 31.6387 | 11.0360 | |
| UKF | 20.1486 | 10.1971 | 4.3759 | |
| CKF | 19.5357 | 10.4851 | 4.2104 | |
| UKF | 14.6715 | 13.3180 | 11.6022 | |
| CKF | 14.2345 | 12.9013 | 11.1126 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Chen, X.; Liu, H.; Wang, S.; Li, K.; Li, B. Performance Analysis of the Thermal Automatic Tracking Method Based on the Model of the UAV Dynamic Model in a Thermal and Cubature Kalman Filter. Drones 2023, 7, 102. https://doi.org/10.3390/drones7020102
Li K, Chen X, Liu H, Wang S, Li K, Li B. Performance Analysis of the Thermal Automatic Tracking Method Based on the Model of the UAV Dynamic Model in a Thermal and Cubature Kalman Filter. Drones. 2023; 7(2):102. https://doi.org/10.3390/drones7020102
Chicago/Turabian StyleLi, Ke, Xiaodan Chen, Haobo Liu, Shaofan Wang, Ke Li, and Bo Li. 2023. "Performance Analysis of the Thermal Automatic Tracking Method Based on the Model of the UAV Dynamic Model in a Thermal and Cubature Kalman Filter" Drones 7, no. 2: 102. https://doi.org/10.3390/drones7020102
APA StyleLi, K., Chen, X., Liu, H., Wang, S., Li, K., & Li, B. (2023). Performance Analysis of the Thermal Automatic Tracking Method Based on the Model of the UAV Dynamic Model in a Thermal and Cubature Kalman Filter. Drones, 7(2), 102. https://doi.org/10.3390/drones7020102






