Distributed Bearing-Only Formation Control for UAV-UWSV Heterogeneous System
Abstract
:1. Introduction
- We extend the LFF graph for the homogeneous multiagent systems to the HLFF graph for the heterogeneous system. The HLFF graph is verified to have distinct properties from LFF graphs as a single-leader bearing-only graph since both the translation and scale of the formation can be uniquely determined by the position of the leader other than the position of the leader and its distance between the leader and the first follower. Thus the distance measurements between the leader and the first follower are not required as [26,27,28].
- Compared with the existing control methods for UAV-UWSV systems [13,14,15,16,17,18], which heavily rely on global positioning, our proposed control scheme only requires relative bearing vectors between neighboring vehicles, which can be obtained via onboard sensors such as vision cameras and sensing arrays.
- Different from the bearing-only formation control for a homogeneous system [22,23,24,25] and a heterogeneous system with identical system order [29], our proposed formation protocol can be applied to heterogeneous mixed-order systems, which is more challenging and complex as some agents have spatial constraints.
2. Preliminaries and Problem Formulation
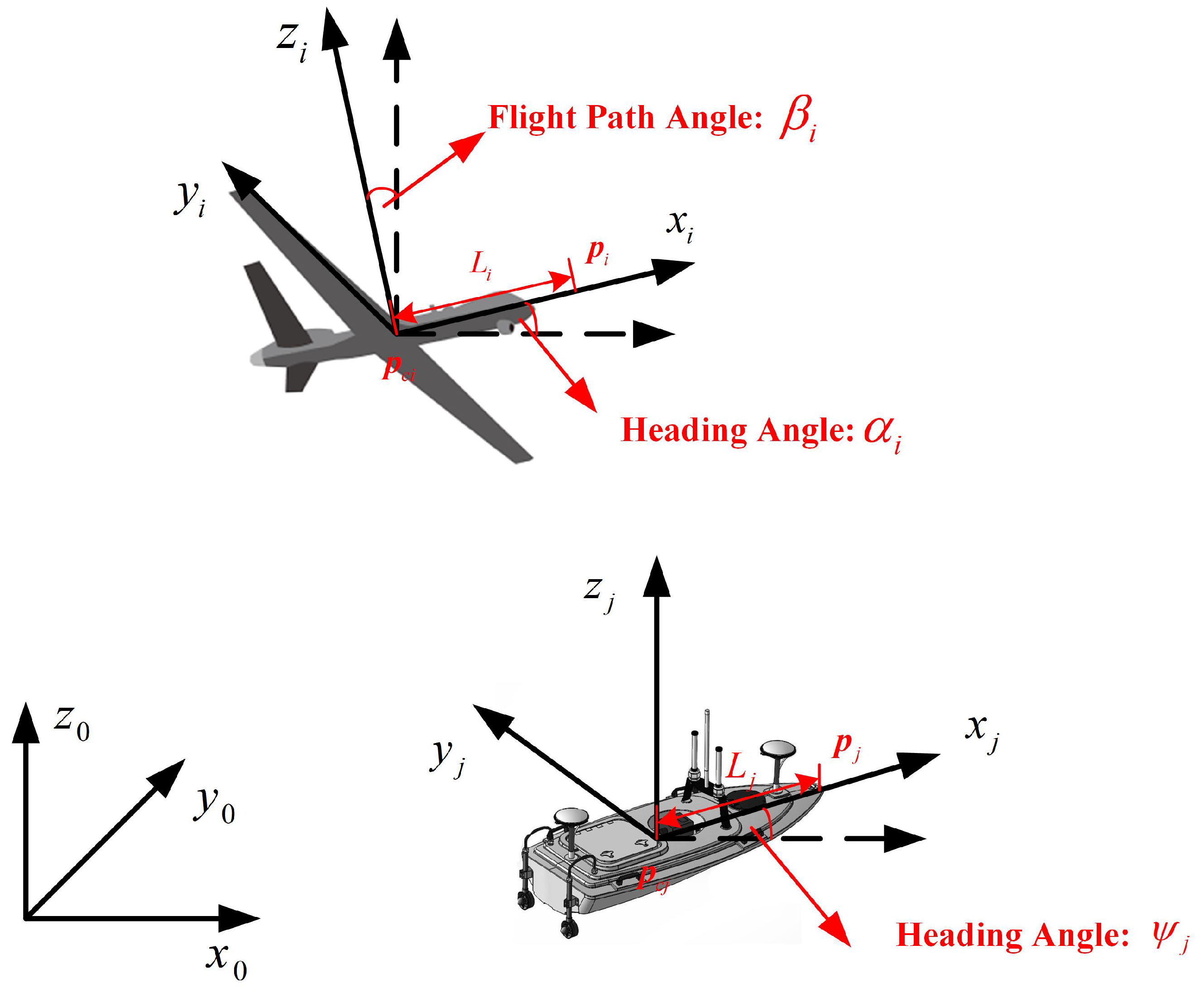
2.1. Model of UAV and UWSV
2.1.1. UAV Model
2.1.2. UWSV Model
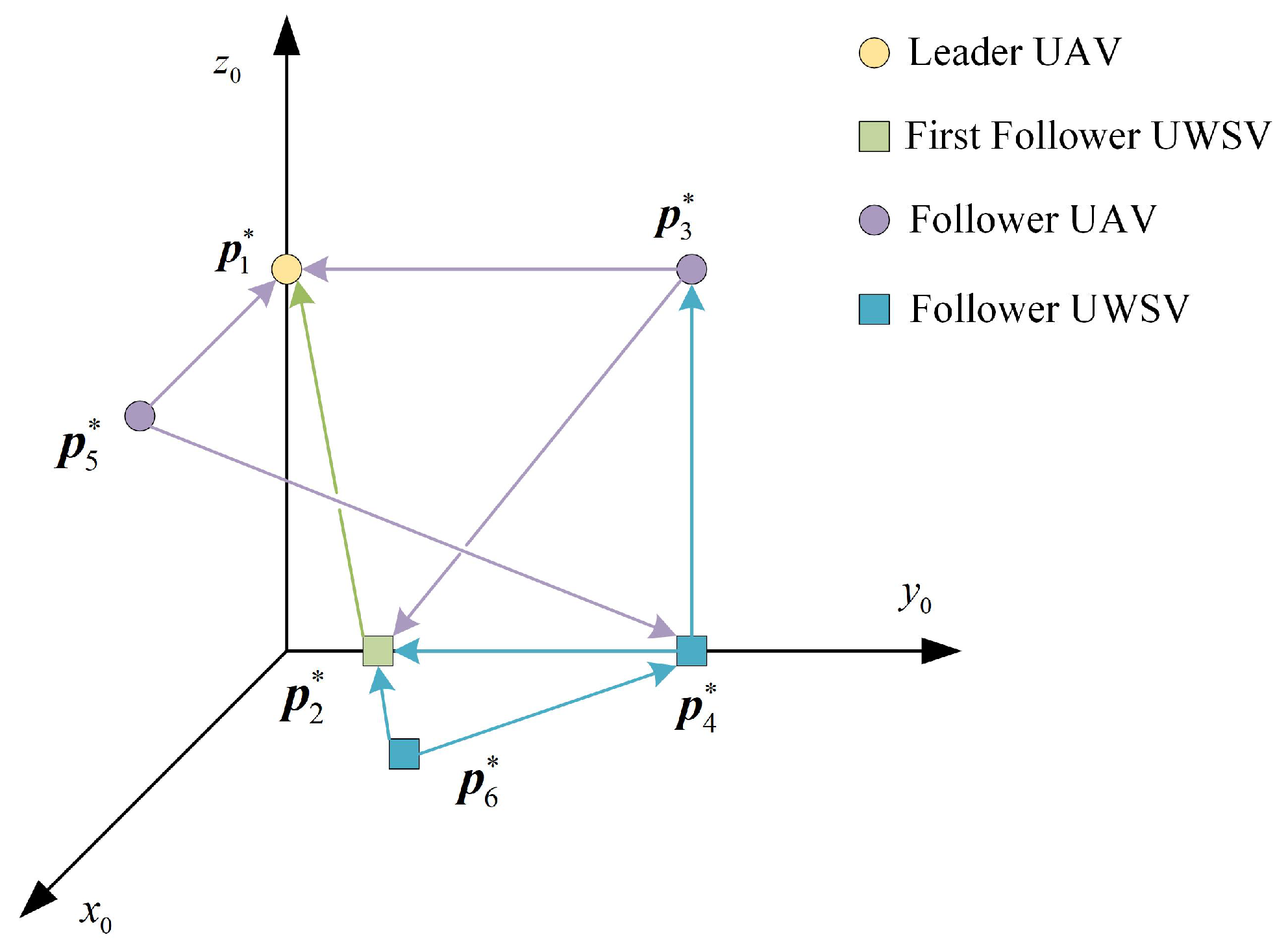
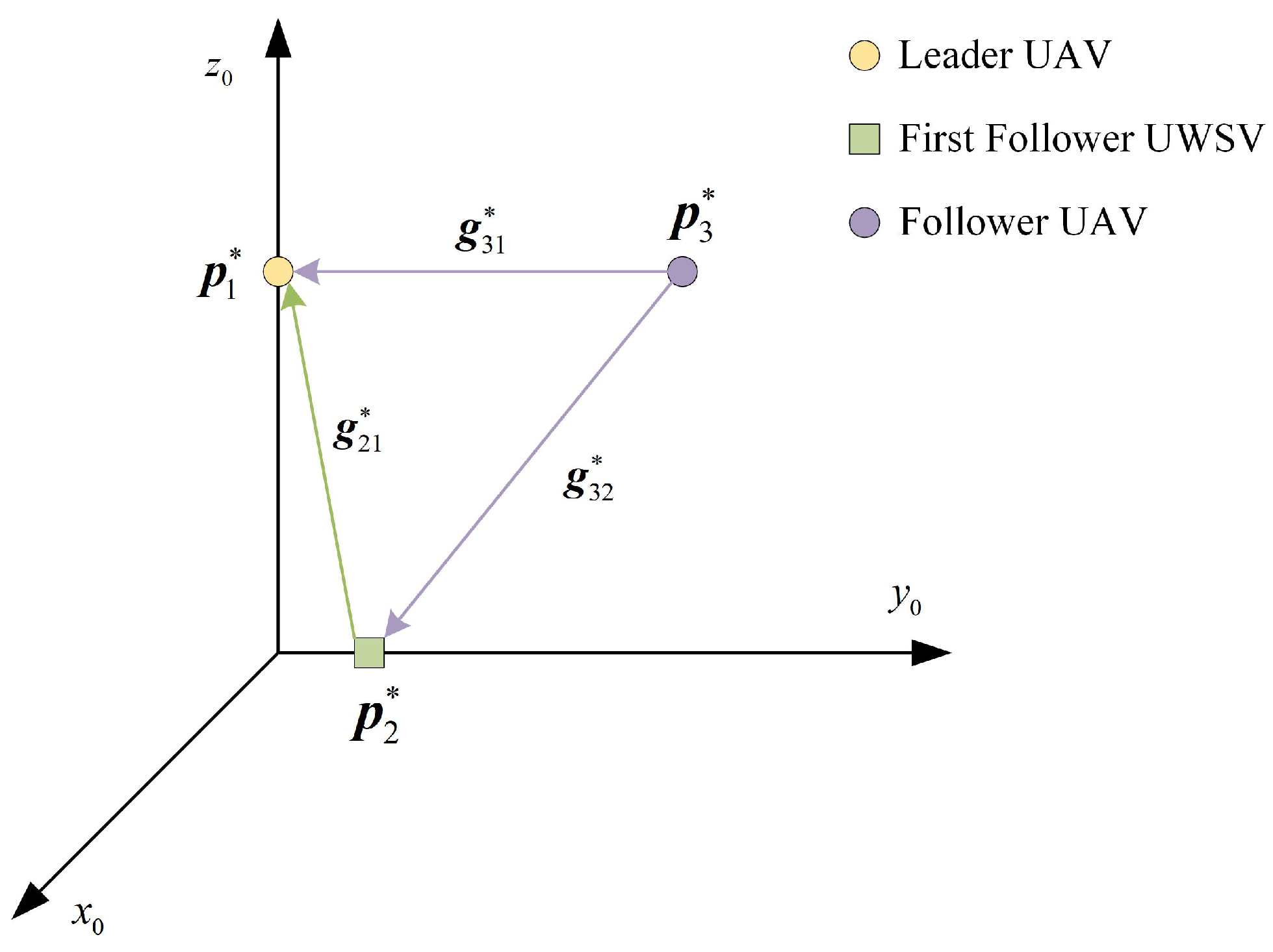
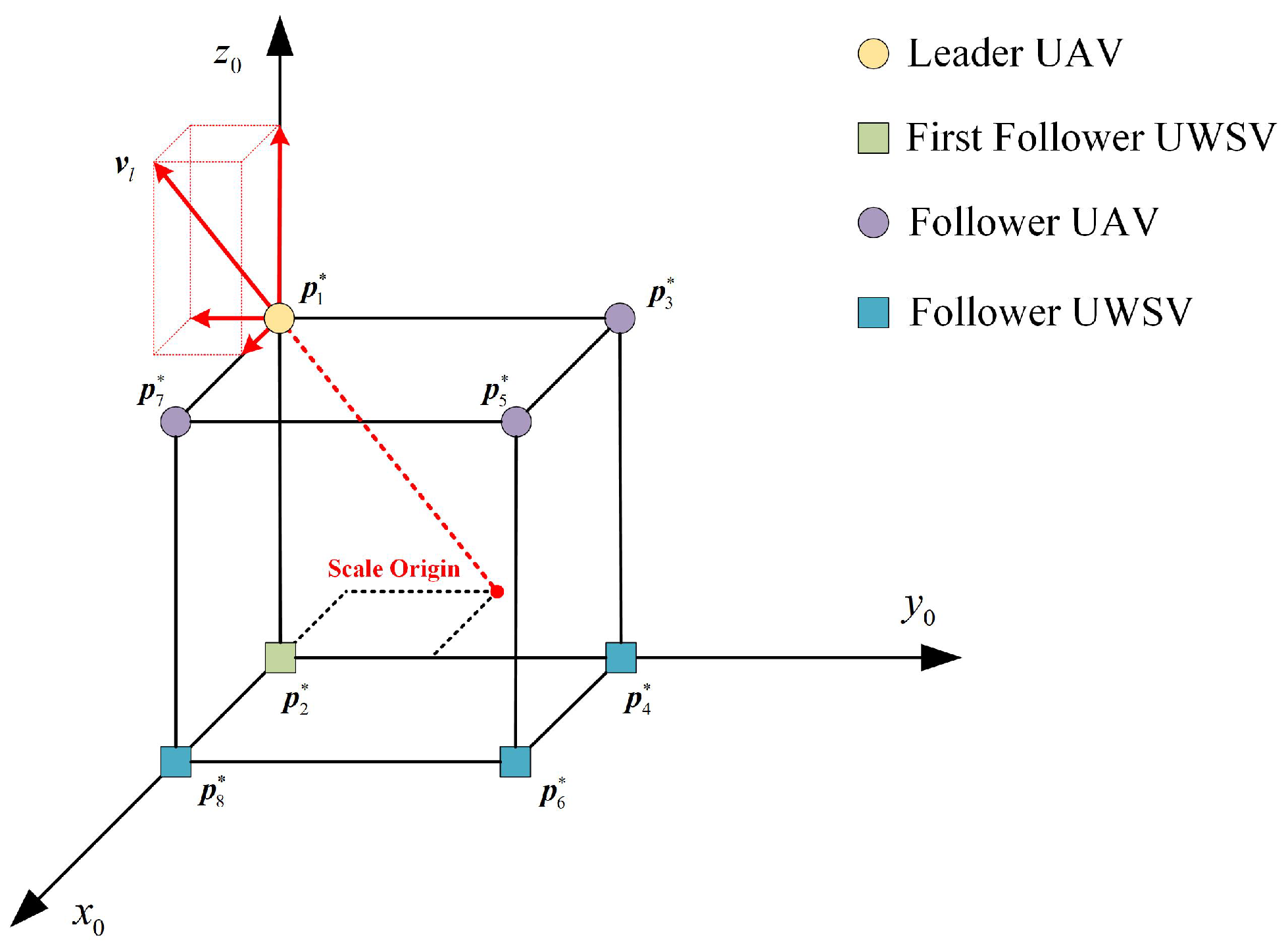
2.2. Heterogeneous Leader-First Follower Formation
2.3. Properties of HLFF Graph
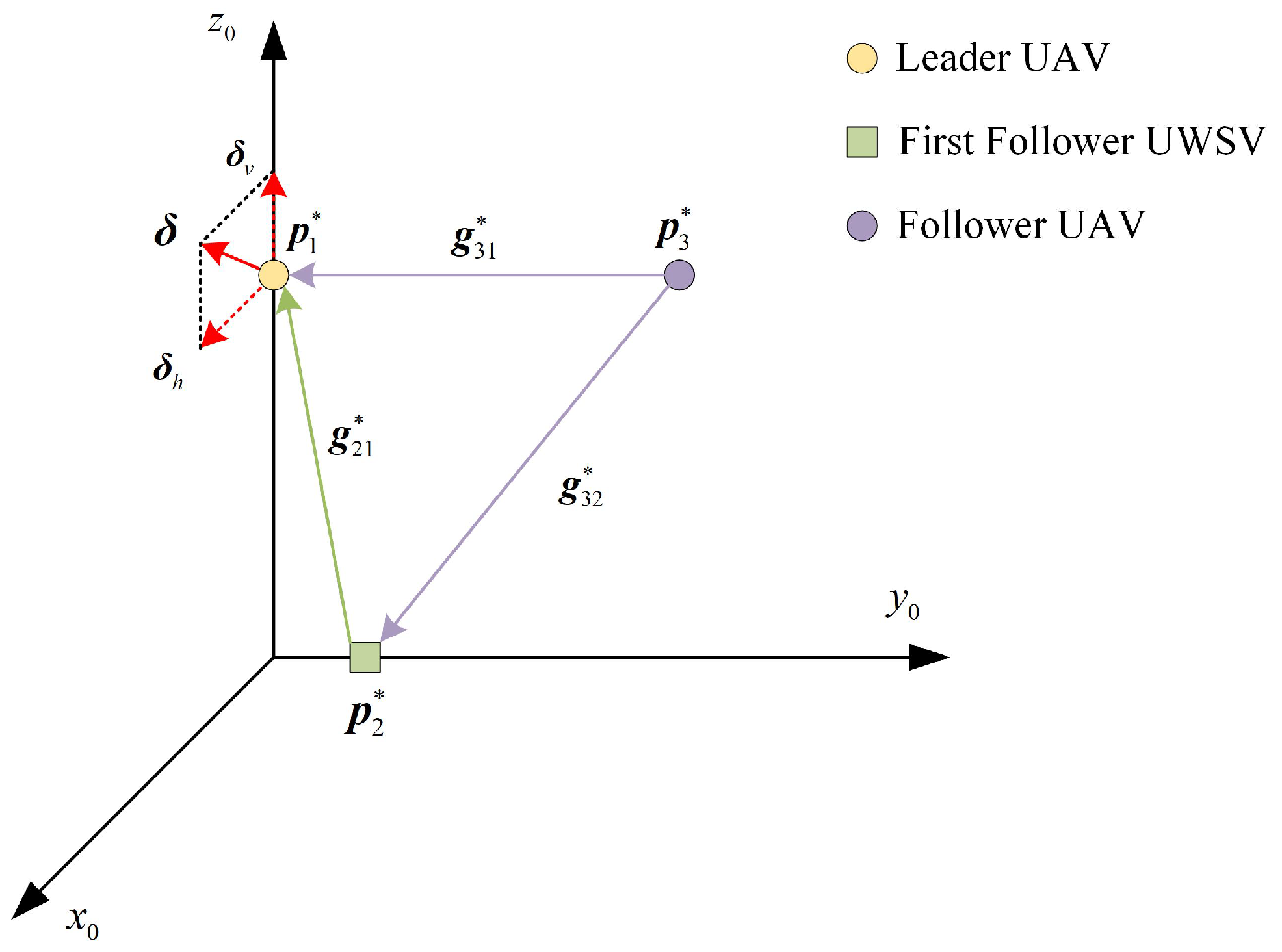
2.4. Problem Formulation
3. Bearing-Only Formation Control Scheme
3.1. Finite-time Distributed Observer Design
3.2. Bearing-Only Formation Control Law Design
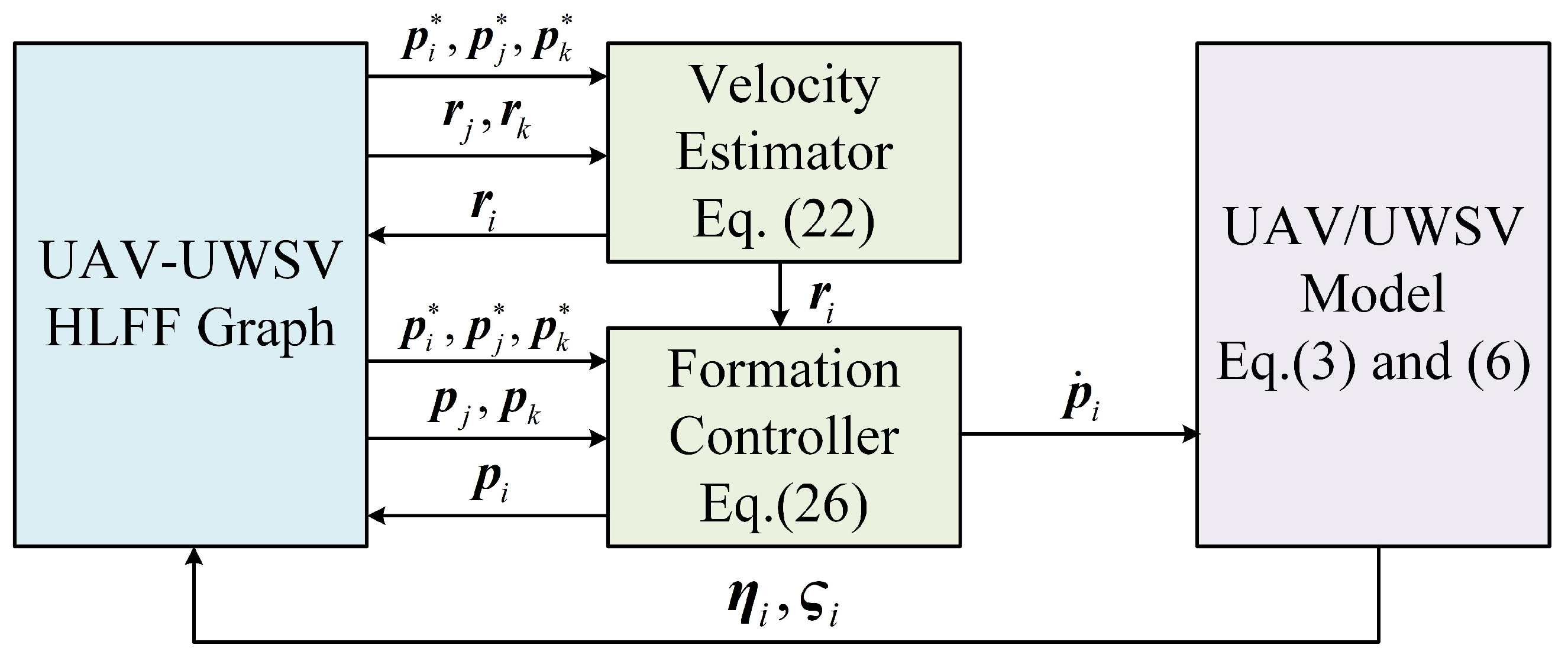
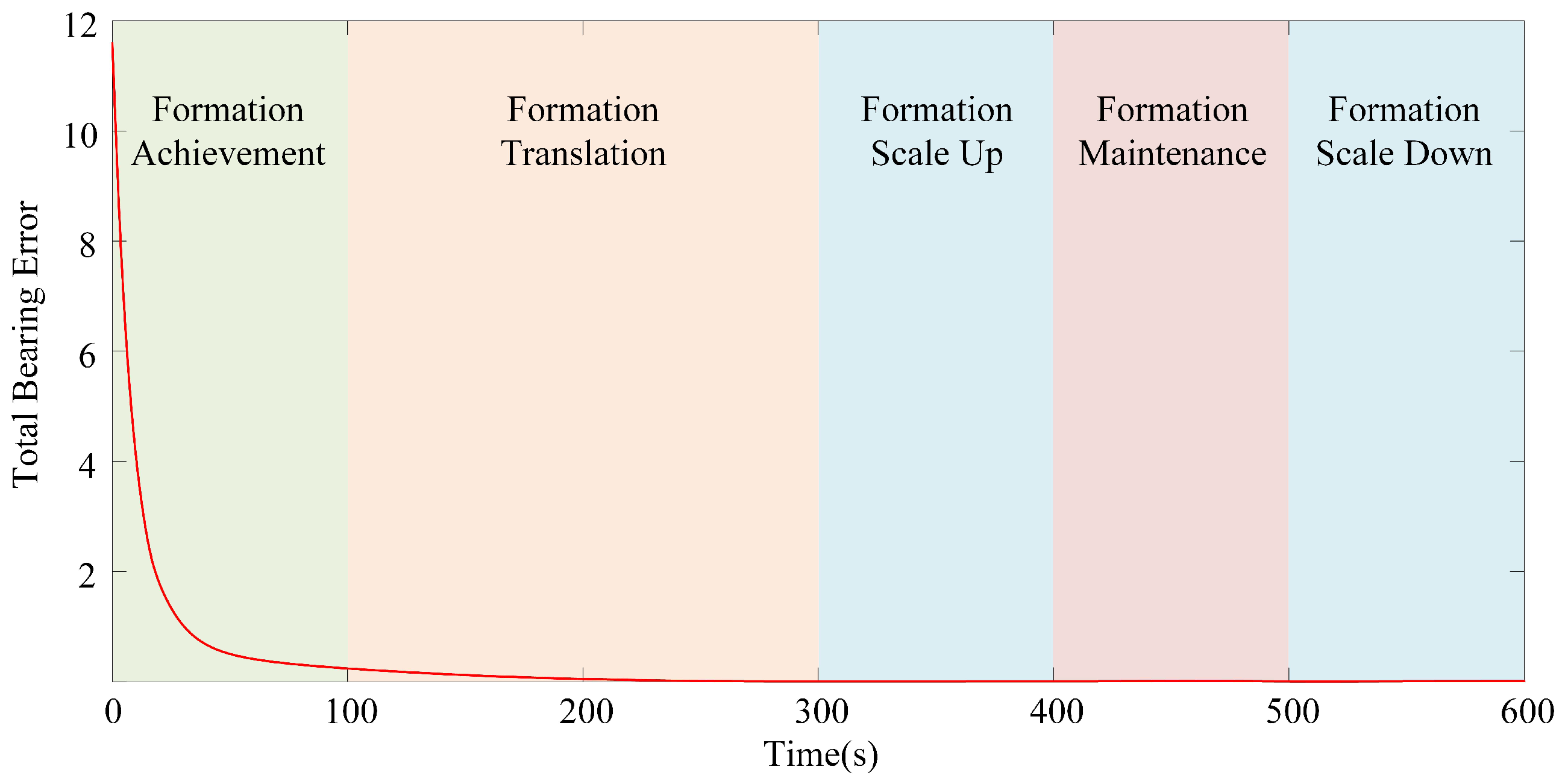
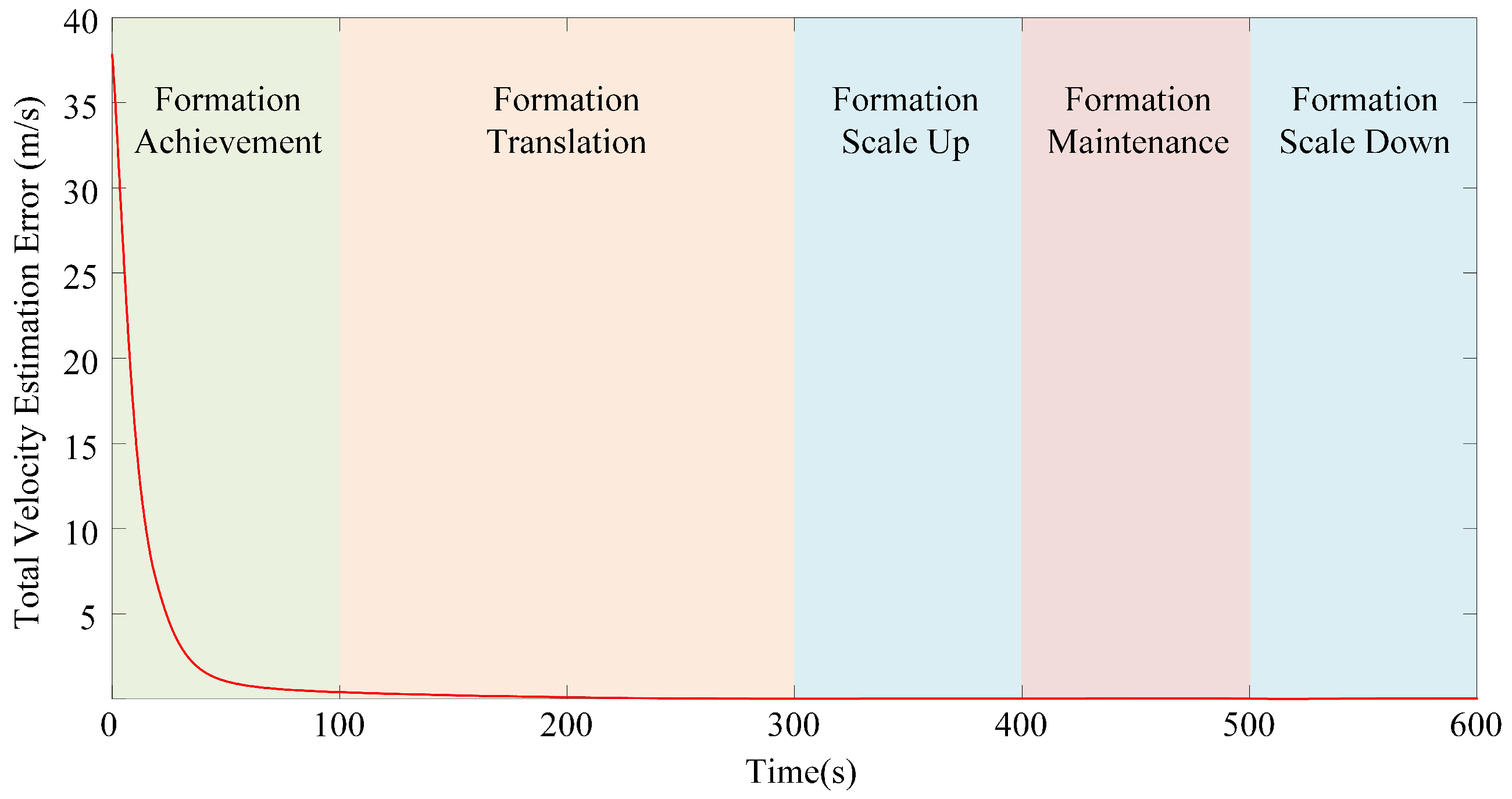
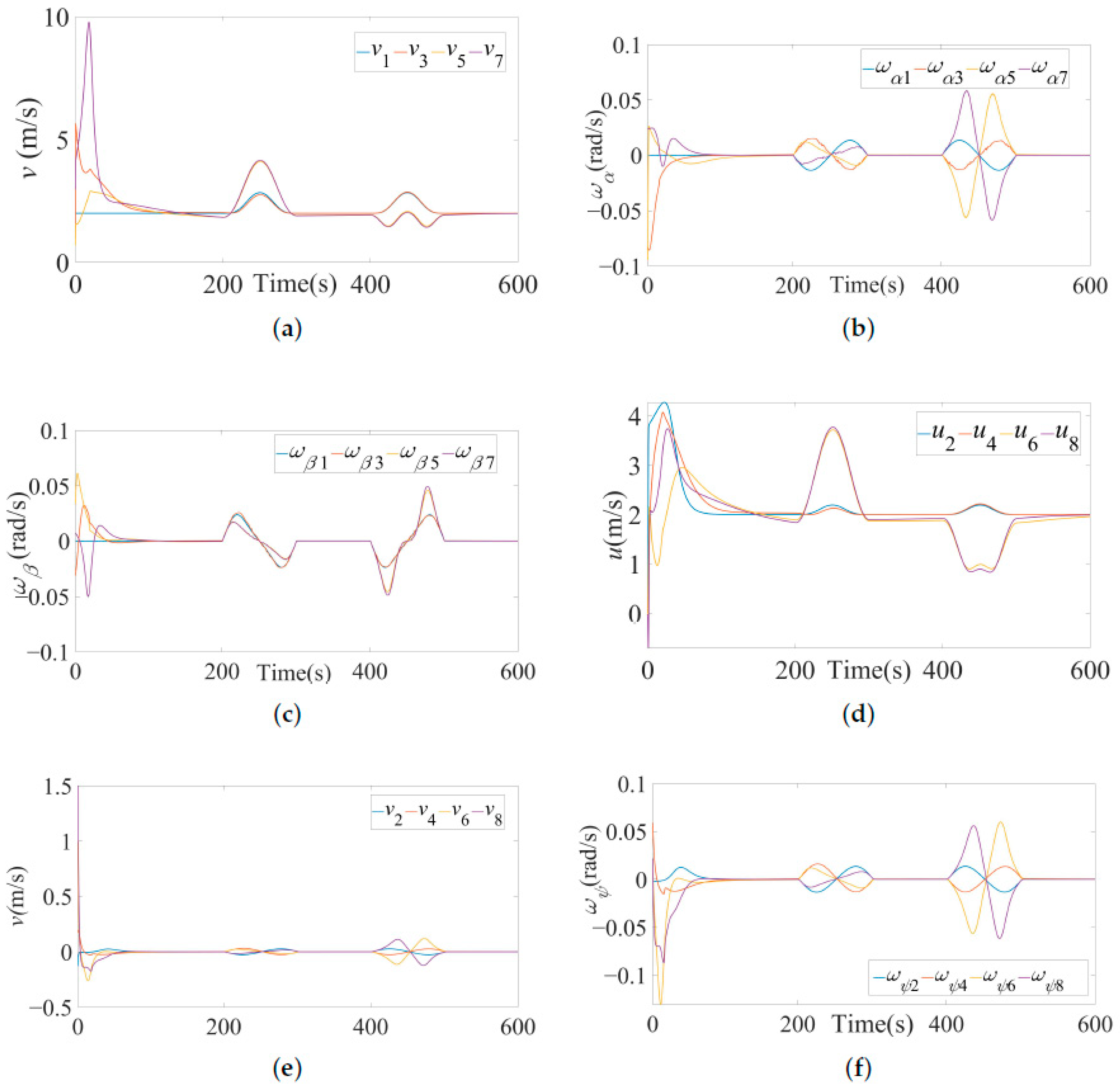
4. Simulations
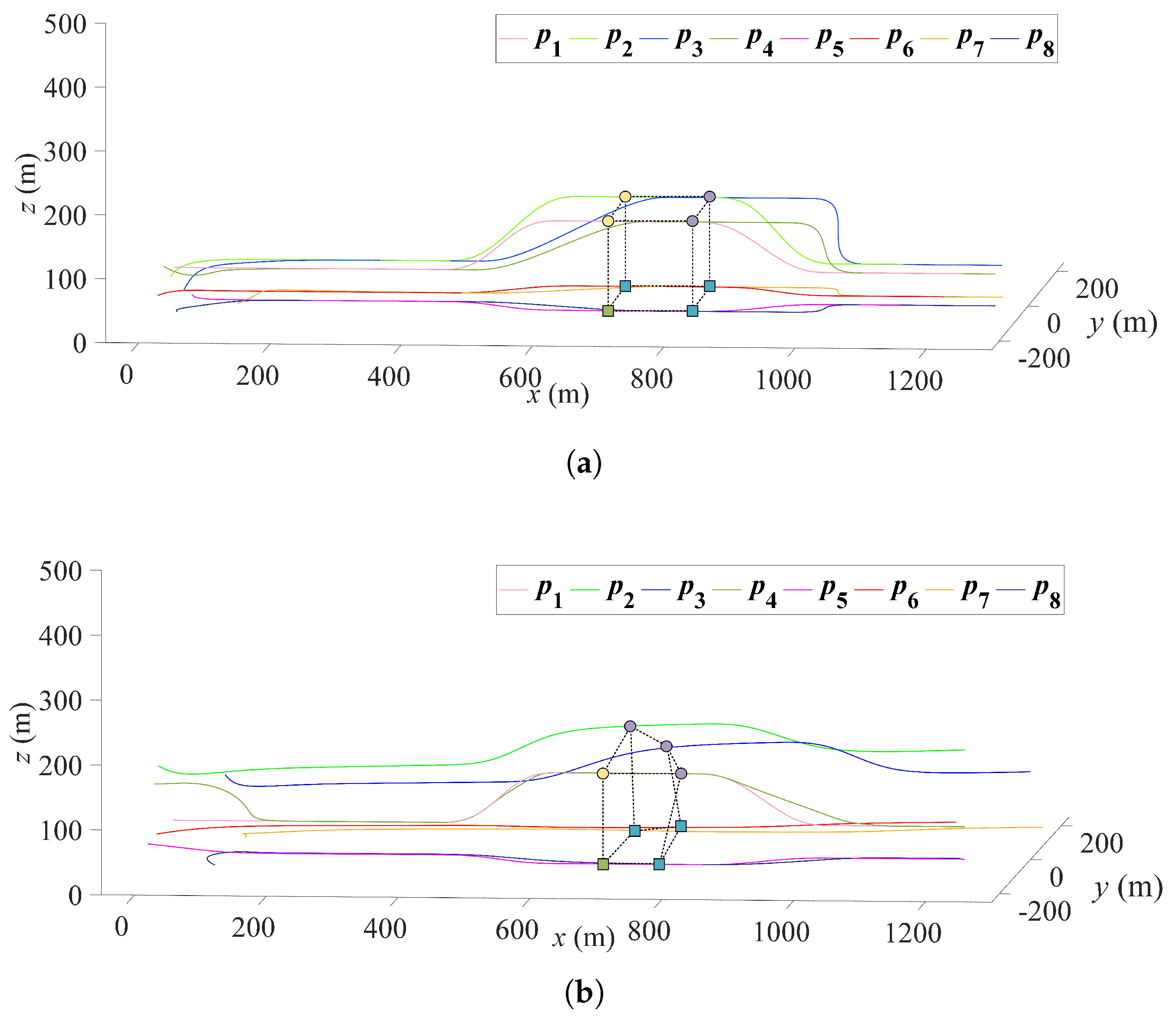
4.1. Tracking the Target Formation with Time-Varying Velocity
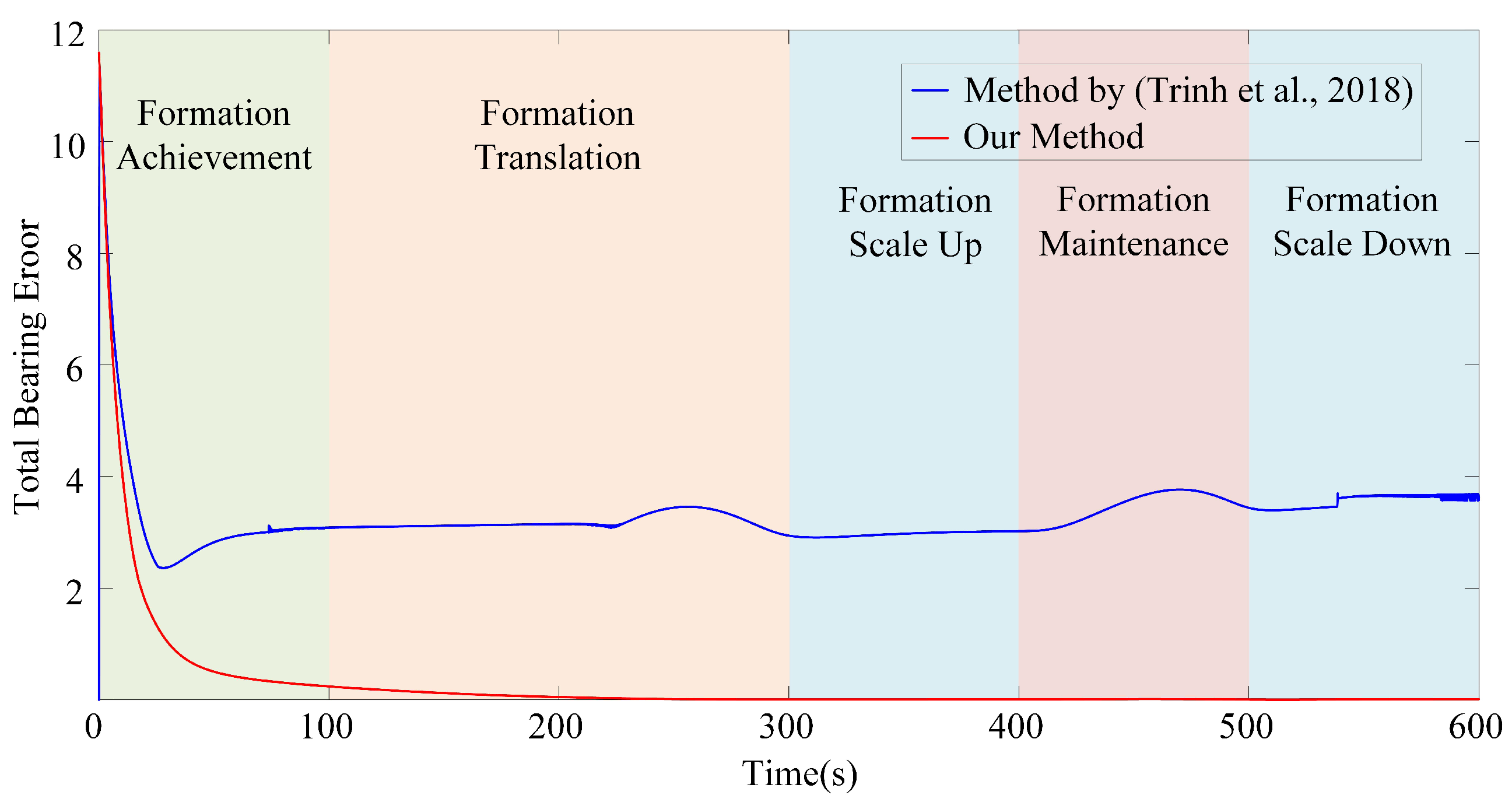
4.2. Comparisons with Existing Works
5. Conclusions and Future Research
5.1. Conclusions
5.2. Future Research
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, J.; Jiahao, X. Cooperative task assignment of multi-UAV system. Chin. J. Aeronaut. 2020, 33, 2825–2827. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, Z.; Cai, Z.; Zhao, J.; Wu, K. Multi-UAV coordination control by chaotic grey wolf optimization based distributed MPC with event-triggered strategy. Chin. J. Aeronaut. 2020, 33, 2877–2897. [Google Scholar] [CrossRef]
- Zhen, z.; Zhu, P.; Xue, Y.; Ji, Y. Distributed intelligent self-organized mission planning of multi-UAV for dynamic targets cooperative search-attack. Chin. J. Aeronaut. 2019, 32, 2706–2716. [Google Scholar] [CrossRef]
- Sial, M.B.; Zhang, Y.; Wang, S.; Ali, S.; Wang, X.; Yang, X.; Liao, Z.; Yang, Z. Bearing-Based Distributed Formation Control of Unmanned Aerial Vehicle Swarm by Quaternion-Based Attitude Synchronization in Three-Dimensional Space. Drones 2022, 6, 227. [Google Scholar] [CrossRef]
- Huo, M.; Duan, H.; Fan, Y. Pigeon-inspired circular formation control for multi-UAV system with limited target information. Guid. Navig. Control 2021, 1, 2150004. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Park, D.; Ngoc, D.N.; Xuan-Mung, N.; Huynh, T.T.; Nguyen, T.N.; Hong, S.K. Quadrotor formation control via terminal sliding mode approach: Theory and experiment results. Drones 2022, 6, 172. [Google Scholar] [CrossRef]
- Yan, J.; Yu, Y.; Wang, X. Distance-based formation control for fixed-wing UAVs with input constraints: A low gain method. Drones 2022, 6, 159. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Wang, S.; Tian, X. Three-dimensional formation–containment control of underactuated AUVs with heterogeneous uncertain dynamics and system constraints. Ocean Eng. 2021, 238, 109661. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Heinrich, M.K.; Wang, X.; Dorigo, M. 3D hybrid formation control of an underwater robot swarm: Switching topologies, unmeasurable velocities, and system constraints. ISA Trans. 2022, in press. [Google Scholar] [CrossRef]
- Wu, Y.; Low, K.H.; Lv, C. Cooperative path planning for heterogeneous unmanned vehicles in a search-and-track mission aiming at an underwater target. IEEE Trans. Veh. Technol. 2020, 69, 6782–6787. [Google Scholar] [CrossRef]
- Wei, W.; Wang, J.; Fang, Z.; Chen, J.; Ren, Y.; Dong, Y. 3U: Joint Design of UAV-USV-UUV Networks for Cooperative Target Hunting. IEEE Trans. Veh. Technol. 2022, in press. [Google Scholar] [CrossRef]
- De Campos, G.R.; Brinón-Arranz, L.; Seuret, A.; Niculescu, S.I. On the consensus of heterogeneous multi-agent systems: A decoupling approach. IFAC Proc. Vol. 2012, 45, 246–251. [Google Scholar] [CrossRef]
- Li, J.; Zhang, G.; Li, B. Robust adaptive neural cooperative control for the USV-UAV based on the LVS-LVA guidance principle. J. Mar. Sci. Eng. 2022, 10, 51. [Google Scholar] [CrossRef]
- Li, J.; Zhang, G.; Shan, Q.; Zhang, W. A Novel Cooperative Design for USV-UAV Systems: 3D Mapping Guidance and Adaptive Fuzzy Control. IEEE Trans. Control. Netw. Syst. 2022, in press. [Google Scholar] [CrossRef]
- Shao, G.; Ma, Y.; Malekian, R.; Yan, X.; Li, Z. A novel cooperative platform design for coupled USV–UAV systems. IEEE Trans. Ind. Inform. 2019, 15, 4913–4922. [Google Scholar] [CrossRef]
- Li, H.; Li, X. Distributed consensus of heterogeneous linear time-varying systems on UAVs–USVs coordination. IEEE Trans. Circuits Syst. II Express Briefs 2019, 67, 1264–1268. [Google Scholar] [CrossRef]
- Liu, H.; Weng, P.; Tian, X.; Mai, Q. Distributed adaptive fixed-time formation control for UAV-USV heterogeneous multi-agent systems. Ocean Eng. 2023, 267, 113240. [Google Scholar] [CrossRef]
- Xue, K.; Wu, T. Distributed consensus of USVs under heterogeneous uav-usv multi-agent systems cooperative control scheme. J. Mar. Sci. Eng. 2021, 9, 1314. [Google Scholar] [CrossRef]
- Basiri, M.; Bishop, A.N.; Jensfelt, P. Distributed control of triangular formations with angle-only constraints. Syst. Control Lett. 2010, 59, 147–154. [Google Scholar] [CrossRef]
- Zhao, S.; Lin, F.; Peng, K.; Chen, B.M.; Lee, T.H. Distributed control of angle-constrained cyclic formations using bearing-only measurements. Syst. Control Lett. 2014, 63, 12–24. [Google Scholar] [CrossRef]
- Zhao, S.; Zelazo, D. Bearing rigidity theory and its applications for control and estimation of network systems: Life beyond distance rigidity. IEEE Control Syst. Mag. 2019, 39, 66–83. [Google Scholar] [CrossRef]
- Zhao, S.; Li, Z.; Ding, Z. Bearing-only formation tracking control of multiagent systems. IEEE Trans. Autom. Control 2019, 64, 4541–4554. [Google Scholar] [CrossRef]
- Su, H.; Chen, C.; Yang, Z.; Zhu, S.; Guan, X. Bearing-Based Formation Tracking Control With Time-Varying Velocity Estimation. IEEE Trans. Cybern. 2022, in press. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wen, C.; Chen, C. Adaptive formation control of networked robotic systems with bearing-only measurements. IEEE Trans. Cybern. 2020, 51, 199–209. [Google Scholar] [CrossRef]
- Van Tran, Q.; Trinh, M.H.; Zelazo, D.; Mukherjee, D.; Ahn, H.S. Finite-time bearing-only formation control via distributed global orientation estimation. IEEE Trans. Control Netw. Syst. 2018, 6, 702–712. [Google Scholar] [CrossRef]
- Trinh, M.H.; Zhao, S.; Sun, Z.; Zelazo, D.; Anderson, B.D.; Ahn, H.S. Bearing-based formation control of a group of agents with leader-first follower structure. IEEE Trans. Autom. Control 2018, 64, 598–613. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Wang, S.; Tian, X. Distributed bearing-based formation control of unmanned aerial vehicle swarm via global orientation estimation. Chin. J. Aeronaut. 2022, 35, 44–58. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Wang, X.; Tian, X. Bearing-based formation control for multiple underactuated autonomous surface vehicles with flexible size scaling. Ocean Eng. 2023, 267, 113242. [Google Scholar] [CrossRef]
- Wu, K.; Hu, J.; Lennox, B.; Arvin, F. Finite-time bearing-only formation tracking of heterogeneous mobile robots with collision avoidance. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 3316–3320. [Google Scholar] [CrossRef]
- Moshtagh, N.; Jadbabaie, A. Distributed geodesic control laws for flocking of nonholonomic agents. IEEE Trans. Autom. Control 2007, 52, 681–686. [Google Scholar] [CrossRef] [Green Version]
- Cai, X.; De Queiroz, M. Adaptive rigidity-based formation control for multirobotic vehicles with dynamics. IEEE Trans. Control Syst. Technol. 2014, 23, 389–396. [Google Scholar] [CrossRef]
- Khoo, S.; Xie, L.; Man, Z. Robust finite-time consensus tracking algorithm for multirobot systems. IEEE/ASME Trans. Mechatron. 2009, 14, 219–228. [Google Scholar] [CrossRef]
- Anderson, B.D.; Yu, C.; Fidan, B.; Hendrickx, J.M. Rigid graph control architectures for autonomous formations. IEEE Control Syst. Mag. 2008, 28, 48–63. [Google Scholar]
- Zhao, S.; Zelazo, D. Translational and scaling formation maneuver control via a bearing-based approach. IEEE Trans. Control Netw. Syst. 2015, 4, 429–438. [Google Scholar] [CrossRef]
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Zhao, S.; Dimarogonas, D.V.; Sun, Z.; Bauso, D. A general approach to coordination control of mobile agents with motion constraints. IEEE Trans. Autom. Control 2017, 63, 1509–1516. [Google Scholar] [CrossRef]
- Jafari, M.; Xu, H. A biologically-inspired distributed fault tolerant flocking control for multi-agent system in presence of uncertain dynamics and unknown disturbance. Eng. Appl. Artif. Intell. 2019, 79, 1–12. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Wang, X.; Wang, S.; Zhang, Y. Distributed Bearing-Only Formation Control for UAV-UWSV Heterogeneous System. Drones 2023, 7, 124. https://doi.org/10.3390/drones7020124
Li S, Wang X, Wang S, Zhang Y. Distributed Bearing-Only Formation Control for UAV-UWSV Heterogeneous System. Drones. 2023; 7(2):124. https://doi.org/10.3390/drones7020124
Chicago/Turabian StyleLi, Shaoshi, Xingjian Wang, Shaoping Wang, and Yuwei Zhang. 2023. "Distributed Bearing-Only Formation Control for UAV-UWSV Heterogeneous System" Drones 7, no. 2: 124. https://doi.org/10.3390/drones7020124
APA StyleLi, S., Wang, X., Wang, S., & Zhang, Y. (2023). Distributed Bearing-Only Formation Control for UAV-UWSV Heterogeneous System. Drones, 7(2), 124. https://doi.org/10.3390/drones7020124






