Two-Step Approach toward Alignment of Spatiotemporal Wide-Area Unmanned Aerial Vehicle Imageries
Abstract
:1. Introduction
2. Materials and Methods
2.1. Problem Definition and Method Overview
2.2. Global Alignment
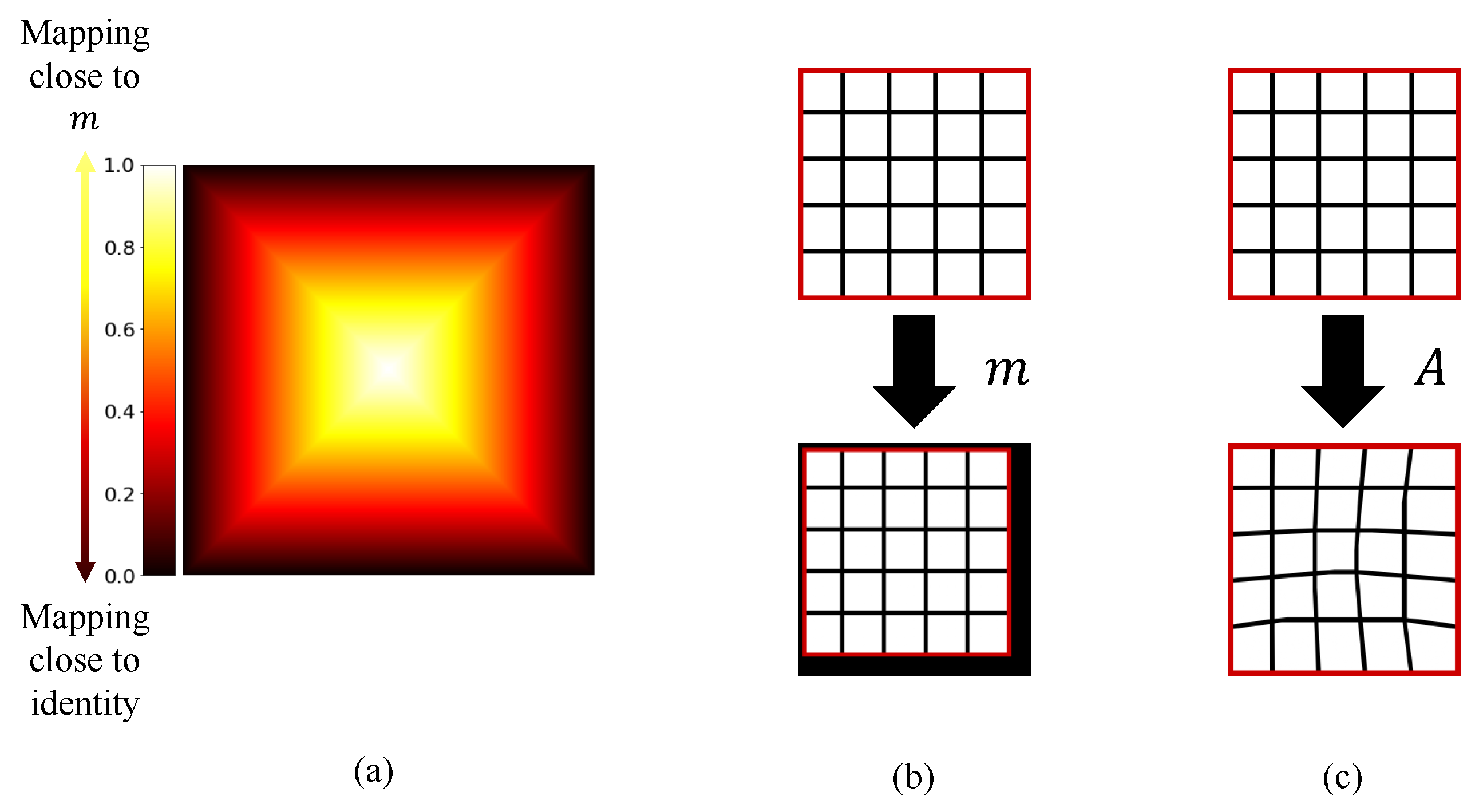
2.3. Local Alignment
3. Experimental Setups
3.1. UAV Image Acquisition
3.2. Preprocessing Dataset
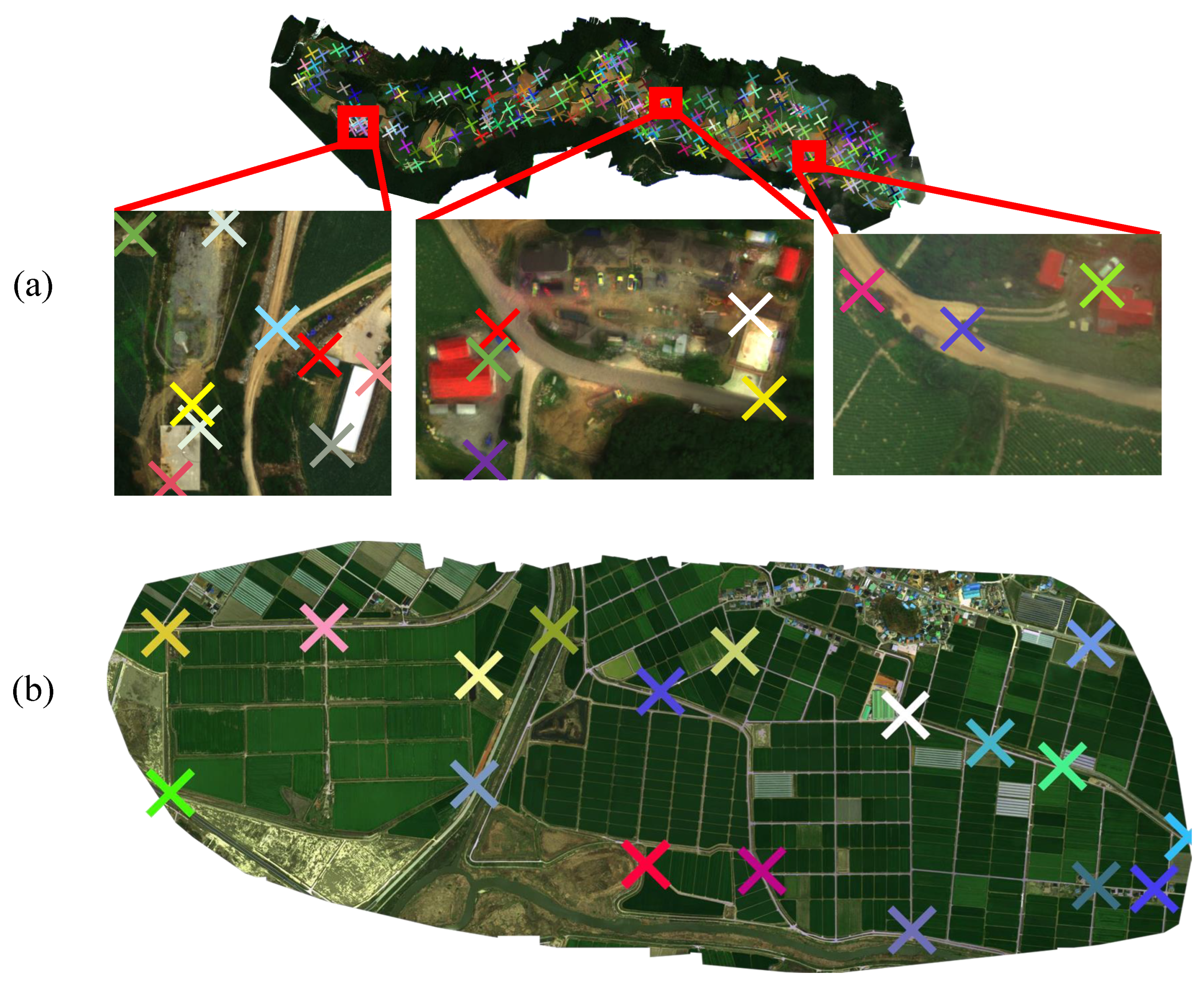
3.3. Case Studies on Local Alignment
3.4. Evaluation Metric
3.5. Method Implementations
4. Results and Discussions
4.1. Performance Comparisons
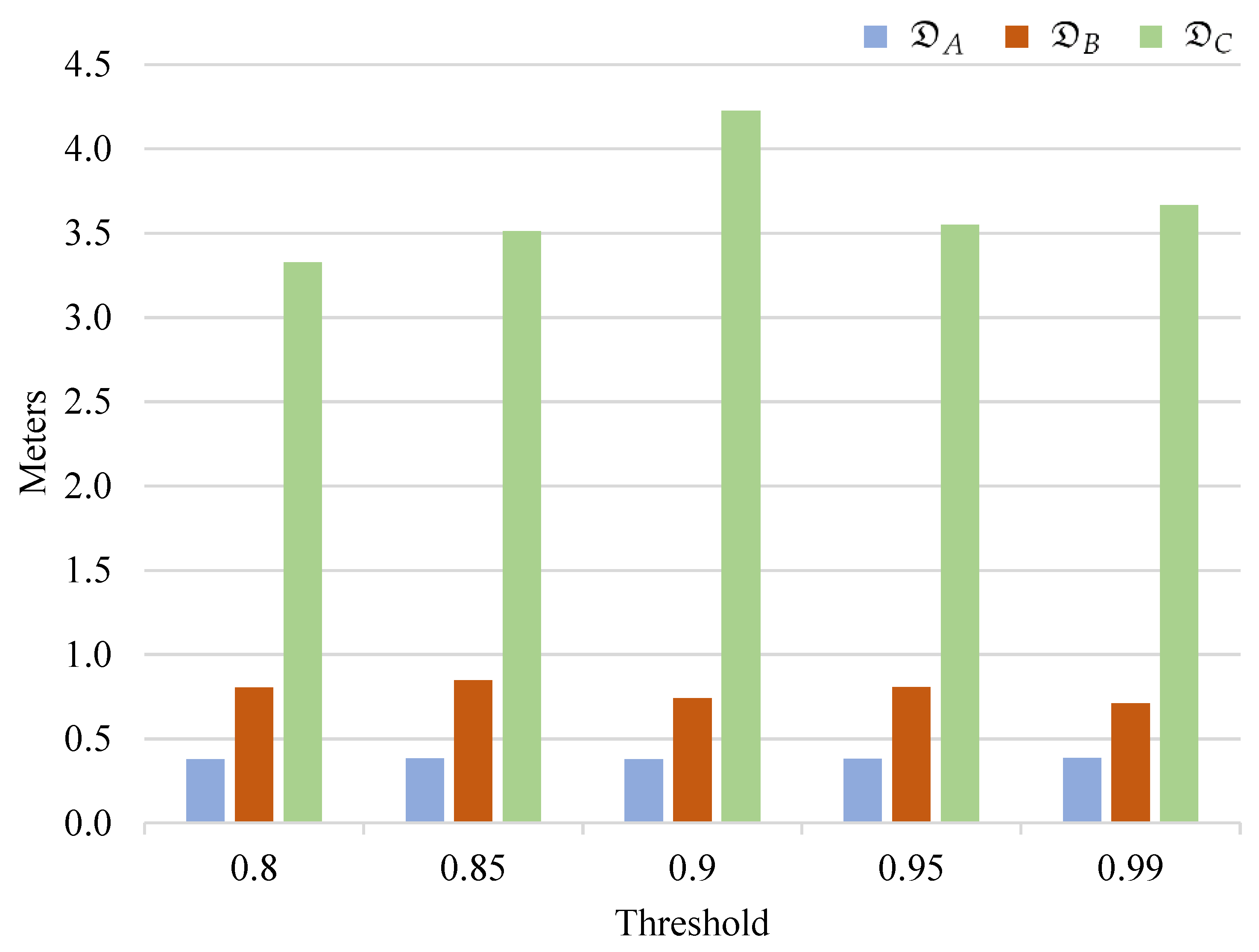
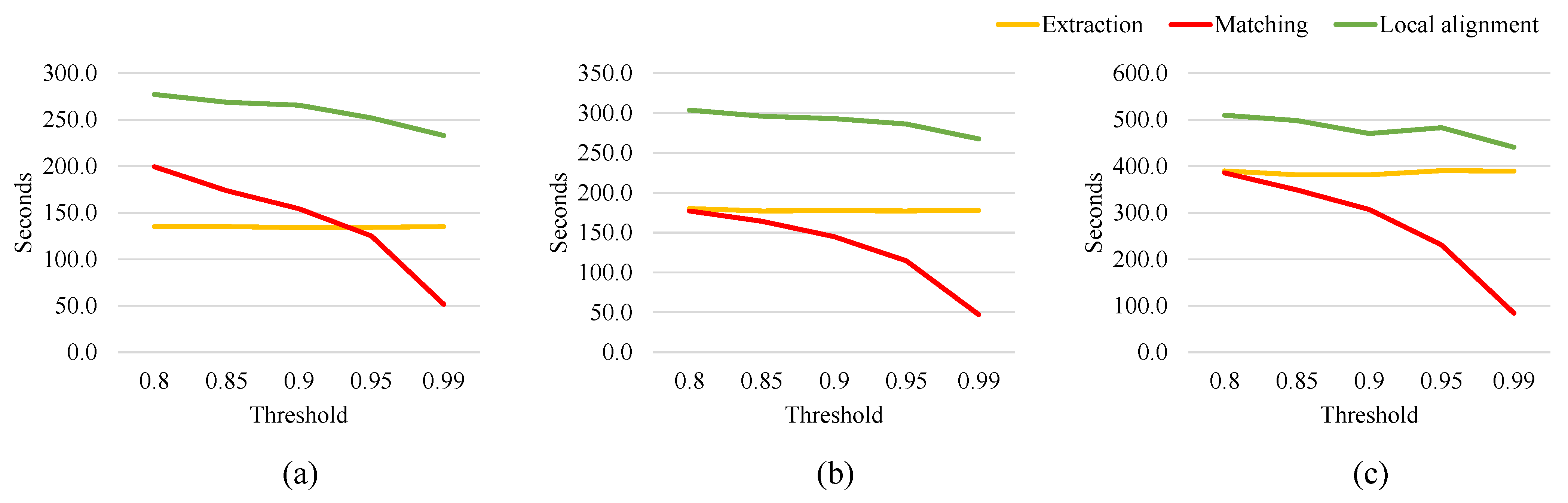
4.2. Effects of the Number of Keypoints on Accuracy and Speed
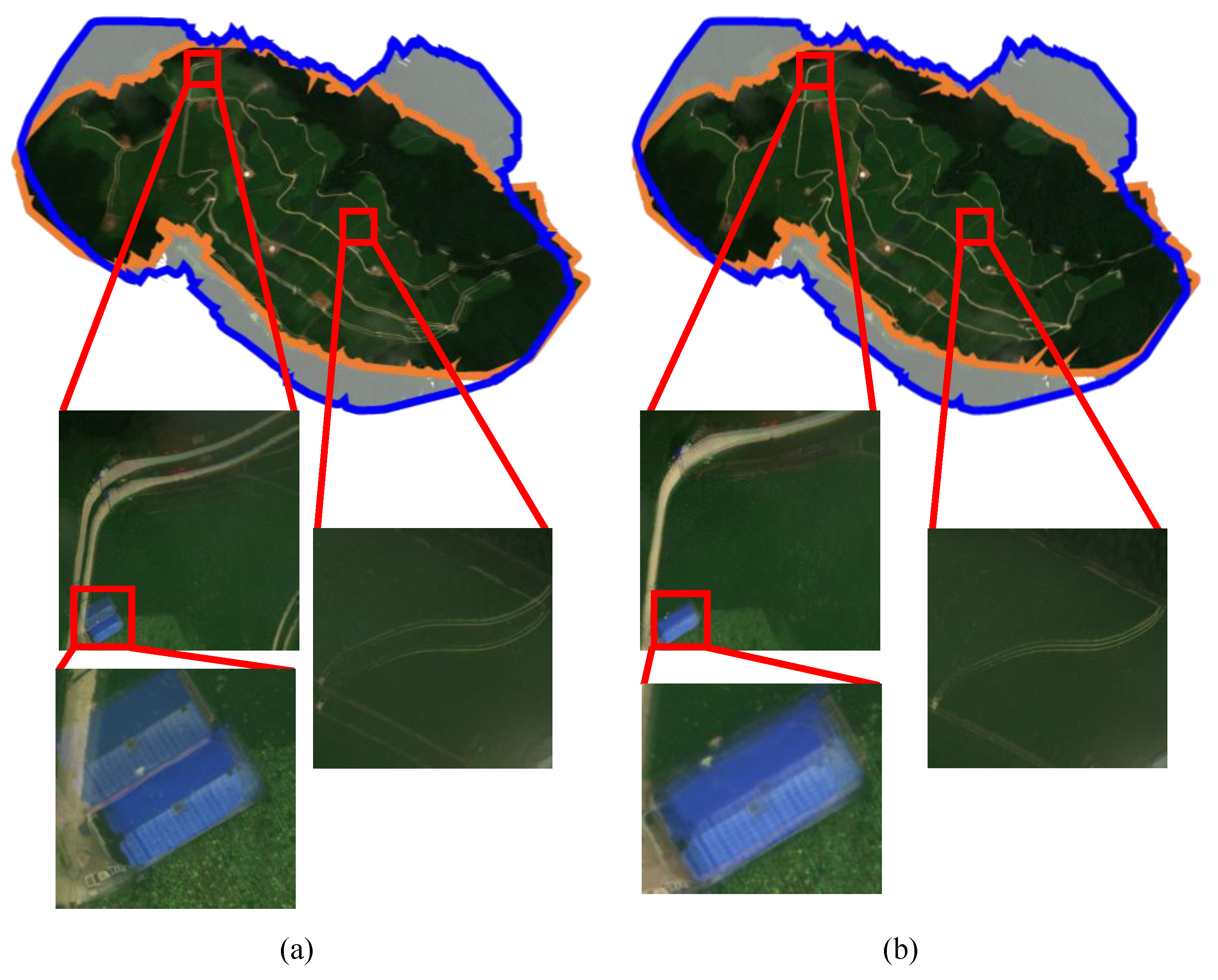
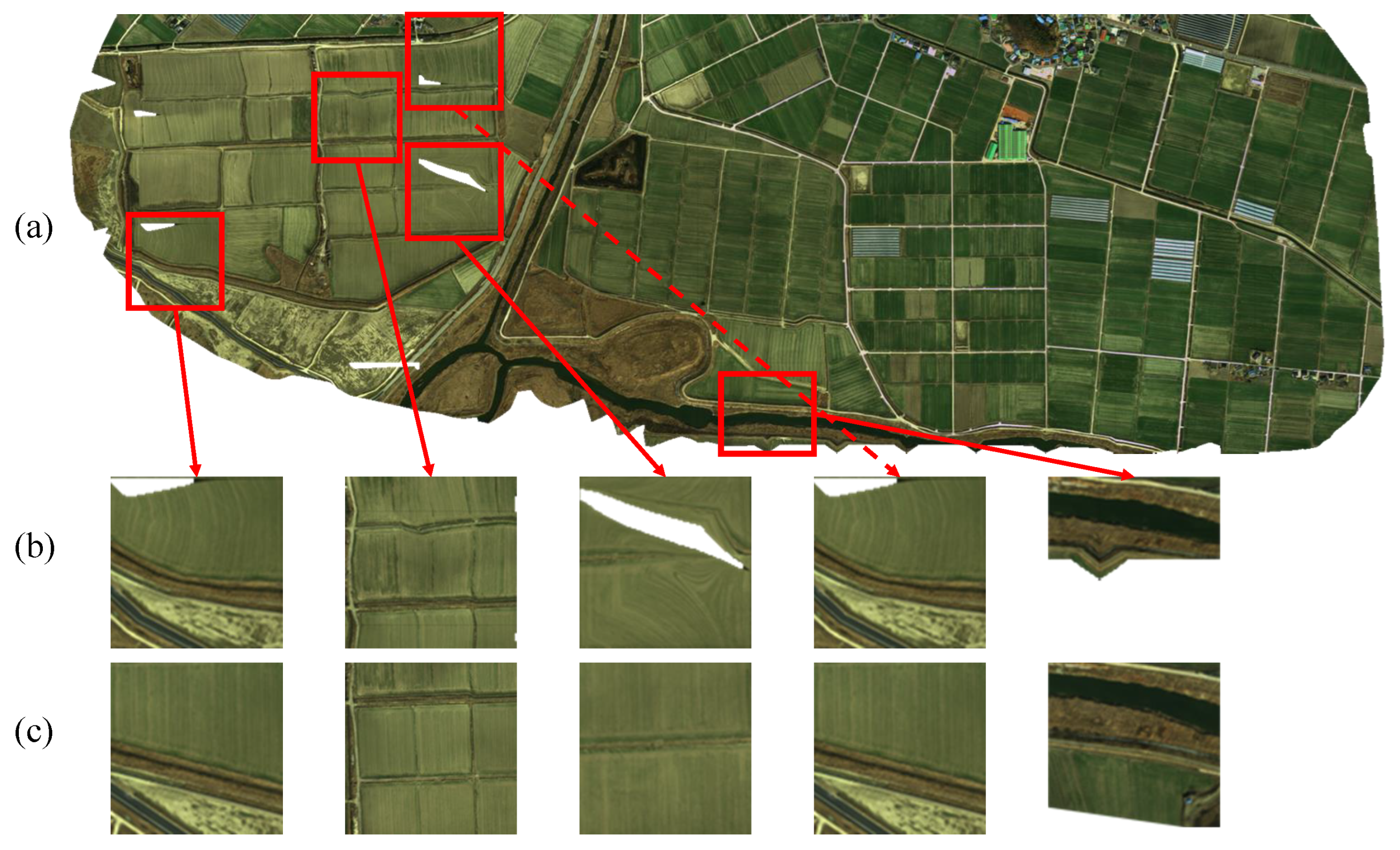
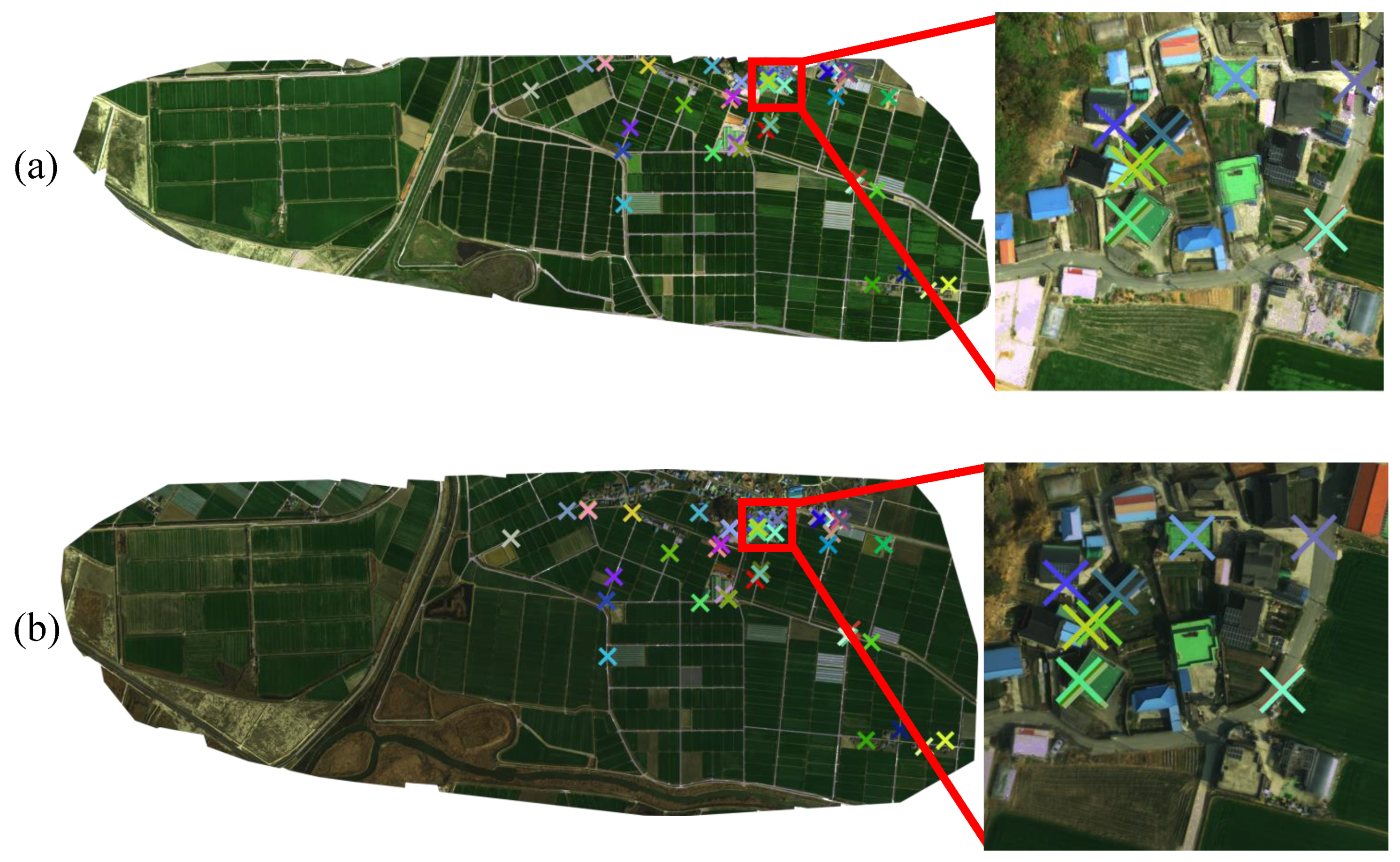
4.3. Qualitative Evaluations
4.4. Discussions for Improving the Proposed Method
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Dataset | ||||
|---|---|---|---|---|
| Study site | Anbanduck | Gwinemi | Maebongsan | Nampo-ri |
| Provincial location | Gangwon | Gangwon | Gangwon | Jeollabuk |
| Geographic longitude | N 37°13′05″ | N 37°20′21″ | N 37°37′31″ | N 35°48′20″ |
| Geographic latitude | E 128°57′58″ | E 129°00′20″ | E 128°44′21″ | E 126°46′55″ |
| Area of study site (km2) | 8.55 | 2.18 | 3.85 | 3.77 |
| Crops | Kimchi cabbage | Kimchi cabbage | Kimchi cabbage | Barley |
| Dates of acquisition (yymmdd) | 190725, 190809, 190828, 190909 | 190807, 190809, 190902, 190909 | 190724, 190729, 190805, 190808 | 210223, 210323, 210415, 210420, 210427, 210506, 210518, 210525, 210609 |
| UAV model used | DJI M210 (rotary wing) | DJI M210 | DJI M210 | Xeno FX (fixed wing) |
| Image sensor used | RedEdge-MX (MicaSense) | RedEdge-MX | RedEdge-MX | Double 4K (Sentera) |
| Flight altitude | 1235 | 1075 | 1235 | 300 |
| UAV Image resolution (width × height) | 1280 × 960 | 1280 × 960 | 1280 × 960 | 4000 × 3000 |
| Ground sampling distance | 13.58 | 11.97 | 13.81 | 8.14 |
| Acquisition frequency (frames/s) | 2 | 2 | 2 | Variable |
| Average mosaic resolution (width × height × channel) | 11,973 × 38,023 × 3 (RGB) | 11,075 × 13,941 × 3 | 17,037 × 11,982 × 3 | 39,817 × 14,431 × 3 |
| # images for mosaicking | 197,666 | 9325 | 11,227 | 623 |
| # reference points (Annotation method) | 268 (Manually) | 338 (Manually) | 260 (Manually) | 100 (Manually + GCP) |
| Dataset | Source | # KPs in Global Alignment () | # Patches | # KPs/Patch in Local Alignment | # GCPs |
|---|---|---|---|---|---|
| 190725 | 2.09 | 120 | - | - | |
| 190809 | 3.04 | 120 | 142.51 | - | |
| 190828 | 2.93 | 133 | 276.95 | - | |
| 190909 | 2.26 | 133 | 197.92 | - | |
| 190807 | 1.30 | 42 | - | - | |
| 190809 | 1.56 | 48 | 22,048 | - | |
| 190902 | 1.70 | 42 | 434.02 | - | |
| 190909 | 1.72 | 48 | 371.96 | - | |
| 190729 | 1.26 | 54 | - | - | |
| 190724 | 0.97 | 54 | 2189.13 | - | |
| 190805 | 0.97 | 63 | 105.16 | - | |
| 190808 | 1.91 | 63 | 115.16 | - | |
| 210506 | 1.13 | 70 | - | - | |
| 210223 | 1.23 | 78 | 0.54 | 20 | |
| 210323 | 1.13 | 65 | 0.906 | - | |
| 210415 | 1.29 | 84 | 14.41 | 20 | |
| 210420 | 1.40 | 84 | 22.45 | - | |
| 210427 | 1.40 | 84 | 81.6 | - | |
| 210518 | 1.13 | 70 | 3.48 | - | |
| 210525 | 1.32 | 70 | 1.02 | - | |
| 210609 | 1.02 | 70 | 3.26 | 20 |
| Dataset | Source | Global (G) | G + Ref. | G + RANSAC (LR) | G + LR + BA |
|---|---|---|---|---|---|
| 190828 | 2.35 | 2.49 | 1.83 | 2.26 | |
| 190909 | 2.58 | 2.61 | 2.10 | 2.58 | |
| avg. error | 2.54 | 2.54 | 2.02 | 2.46 | |
| avg. error (pixels) | 18.72 | 18.71 | 14.85 | 18.12 | |
| 190902 | 0.72 | 0.71 | 0.56 | 0.48 | |
| 190909 | 0.35 | 0.35 | 0.32 | 0.35 | |
| avg. error | 0.62 | 0.61 | 0.42 | 0.46 | |
| avg. error (pixels) | 5.14 | 5.11 | 3.49 | 3.88 | |
| 190805 | 0.92 | 1.00 | 0.65 | 0.88 | |
| 190808 | 0.85 | 0.90 | 0.64 | 0.84 | |
| avg. error | 0.87 | 0.91 | 0.62 | 0.79 | |
| avg. error (pixels) | 6.28 | 6.59 | 4.46 | 5.69 | |
| 210223 | 2.82 | 1.02 | 2.82 | 2.82 | |
| 210323 | 0.73 | 1.06 | 0.75 | 0.73 | |
| 210415 | 1.02 | 1.33 | 0.76 | 0.84 | |
| 210420 | 0.74 | 0.91 | 0.61 | 0.64 | |
| 210427 | 0.78 | 0.79 | 0.56 | 0.69 | |
| 210518 | 1.33 | 0.93 | 1.27 | 1.25 | |
| 210525 | 1.01 | 0.90 | 1.01 | 1.01 | |
| 210609 | 0.99 | 1.34 | 0.94 | 0.94 | |
| avg. error | 1.18 | 1.04 | 1.09 | 1.12 | |
| avg. error (pixels) | 14.46 | 12.73 | 13.36 | 13.73 |
References
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef]
- Zhou, X.; Zheng, H.; Xu, X.; He, J.; Ge, X.; Yao, X.; Cheng, T.; Zhu, Y.; Cao, W.; Tian, Y. Predicting grain yield in rice using multi-temporal vegetation indices from UAV-based multispectral and digital imagery. ISPRS J. Photogramm. Remote Sens. 2017, 130, 246–255. [Google Scholar] [CrossRef]
- Kim, J.I.; Kim, H.C.; Kim, T. Robust Mosaicking of Lightweight UAV Images Using Hybrid Image Transformation Modeling. Remote Sens. 2020, 12, 1002. [Google Scholar] [CrossRef]
- Jannoura, R.; Brinkmann, K.; Uteau, D.; Bruns, C.; Joergensen, R.G. Monitoring of crop biomass using true colour aerial photographs taken from a remote controlled hexacopter. Biosyst. Eng. 2015, 129, 341–351. [Google Scholar] [CrossRef]
- Jay, S.; Baret, F.; Dutartre, D.; Malatesta, G.; Héno, S.; Comar, A.; Weiss, M.; Maupas, F. Exploiting the centimeter resolution of UAV multispectral imagery to improve remote-sensing estimates of canopy structure and biochemistry in sugar beet crops. Remote Sens. Environ. 2019, 231, 110898. [Google Scholar] [CrossRef]
- Feng, A.; Zhou, J.; Vories, E.D.; Sudduth, K.A.; Zhang, M. Yield estimation in cotton using UAV-based multi-sensor imagery. Biosyst. Eng. 2020, 193, 101–114. [Google Scholar] [CrossRef]
- Fernandez-Gallego, J.A.; Kefauver, S.C.; Vatter, T.; Gutiérrez, N.A.; Nieto-Taladriz, M.T.; Araus, J.L. Low-cost assessment of grain yield in durum wheat using RGB images. Eur. J. Agron. 2019, 105, 146–156. [Google Scholar] [CrossRef]
- Walter, J.; Edwards, J.; McDonald, G.; Kuchel, H. Photogrammetry for the estimation of wheat biomass and harvest index. Field Crops Res. 2018, 216, 165–174. [Google Scholar] [CrossRef]
- Sofonia, J.; Shendryk, Y.; Phinn, S.; Roelfsema, C.; Kendoul, F.; Skocaj, D. Monitoring sugarcane growth response to varying nitrogen application rates: A comparison of UAV SLAM LiDAR and photogrammetry. Int. J. Appl. Earth Obs. Geoinf. 2019, 82, 101878. [Google Scholar] [CrossRef]
- Jensen, A.M.; Baumann, M.; Chen, Y. Low-cost multispectral aerial imaging using autonomous runway-free small flying wing vehicles. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 6–11 July 2008; IEEE: New York, NY, USA, 2008; Volume 5, p. V-506. [Google Scholar]
- Zhang, C.; Kovacs, J.M. The application of small unmanned aerial systems for precision agriculture: A review. Precis. Agric. 2012, 13, 693–712. [Google Scholar] [CrossRef]
- Khaki, S.; Wang, L. Crop yield prediction using deep neural networks. Front. Plant Sci. 2019, 10, 621. [Google Scholar] [CrossRef]
- Gil-Yepes, J.L.; Ruiz, L.A.; Recio, J.A.; Balaguer-Beser, Á.; Hermosilla, T. Description and validation of a new set of object-based temporal geostatistical features for land-use/land-cover change detection. ISPRS J. Photogramm. Remote Sens. 2016, 121, 77–91. [Google Scholar] [CrossRef]
- van Deventer, H.; Cho, M.A.; Mutanga, O. Multi-season RapidEye imagery improves the classification of wetland and dryland communities in a subtropical coastal region. ISPRS J. Photogramm. Remote Sens. 2019, 157, 171–187. [Google Scholar] [CrossRef]
- Alibabaei, K.; Gaspar, P.D.; Lima, T.M. Crop Yield Estimation Using Deep Learning Based on Climate Big Data and Irrigation Scheduling. Energies 2021, 14, 3004. [Google Scholar] [CrossRef]
- Khaki, S.; Wang, L.; Archontoulis, S.V. A cnn-rnn framework for crop yield prediction. Front. Plant Sci. 2020, 10, 1750. [Google Scholar] [CrossRef] [PubMed]
- Xingjian, S.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 802–810. [Google Scholar]
- Ji, S.; Zhang, C.; Xu, A.; Shi, Y.; Duan, Y. 3D convolutional neural networks for crop classification with multi-temporal remote sensing images. Remote Sens. 2018, 10, 75. [Google Scholar] [CrossRef]
- Pelletier, C.; Webb, G.I.; Petitjean, F. Temporal convolutional neural network for the classification of satellite image time series. Remote Sens. 2019, 11, 523. [Google Scholar] [CrossRef]
- Lai, Y.; Pringle, M.; Kopittke, P.M.; Menzies, N.W.; Orton, T.G.; Dang, Y.P. An empirical model for prediction of wheat yield, using time-integrated Landsat NDVI. Int. J. Appl. Earth Obs. Geoinf. 2018, 72, 99–108. [Google Scholar]
- Xu, Z.; Guan, K.; Casler, N.; Peng, B.; Wang, S. A 3D convolutional neural network method for land cover classification using LiDAR and multi-temporal Landsat imagery. ISPRS J. Photogramm. Remote Sens. 2018, 144, 423–434. [Google Scholar] [CrossRef]
- Fernandez-Manso, A.; Quintano, C.; Roberts, D.A. Burn severity analysis in Mediterranean forests using maximum entropy model trained with EO-1 Hyperion and LiDAR data. ISPRS J. Photogramm. Remote Sens. 2019, 155, 102–118. [Google Scholar] [CrossRef]
- Galin, E.; Guérin, E.; Peytavie, A.; Cordonnier, G.; Cani, M.P.; Benes, B.; Gain, J. A review of digital terrain modeling. In Proceedings of the Computer Graphics Forum, Genoa, Italy, 6–10 May 2019; Volume 38, pp. 553–577. [Google Scholar]
- Habib, A.F.; Kim, E.M.; Kim, C.J. New methodologies for true orthophoto generation. Photogramm. Eng. Remote Sens. 2007, 73, 25–36. [Google Scholar] [CrossRef]
- Demiray, B.Z.; Sit, M.; Demir, I. D-SRGAN: DEM super-resolution with generative adversarial networks. SN Comput. Sci. 2021, 2, 48. [Google Scholar] [CrossRef]
- Panagiotou, E.; Chochlakis, G.; Grammatikopoulos, L.; Charou, E. Generating Elevation Surface from a Single RGB Remotely Sensed Image Using Deep Learning. Remote Sens. 2020, 12, 2002. [Google Scholar] [CrossRef]
- Väänänen, P. Removing 3D Point Cloud Occlusion Artifacts with Generative Adversarial Networks. Ph.D. Thesis, Department of Computer Science, University of Helsinki, Helsinki, Findland, 2019. [Google Scholar]
- Huang, H.; Deng, J.; Lan, Y.; Yang, A.; Zhang, L.; Wen, S.; Zhang, H.; Zhang, Y.; Deng, Y. Detection of helminthosporium leaf blotch disease based on UAV imagery. Appl. Sci. 2019, 9, 558. [Google Scholar] [CrossRef]
- de Souza, C.H.W.; Mercante, E.; Johann, J.A.; Lamparelli, R.A.C.; Uribe-Opazo, M.A. Mapping and discrimination of soya bean and corn crops using spectro-temporal profiles of vegetation indices. Int. J. Remote Sens. 2015, 36, 1809–1824. [Google Scholar] [CrossRef]
- Nevavuori, P.; Narra, N.; Linna, P.; Lipping, T. Crop yield prediction using multitemporal UAV data and spatio-temporal deep learning models. Remote Sens. 2020, 12, 4000. [Google Scholar] [CrossRef]
- Malambo, L.; Popescu, S.C.; Murray, S.C.; Putman, E.; Pugh, N.A.; Horne, D.W.; Richardson, G.; Sheridan, R.; Rooney, W.L.; Avant, R.; et al. Multitemporal field-based plant height estimation using 3D point clouds generated from small unmanned aerial systems high-resolution imagery. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 31–42. [Google Scholar] [CrossRef]
- Varela, S.; Varela, S.; Leakey, A.D.; Leakey, A.D. Implementing spatio-temporal 3D-convolution neural networks and UAV time series imagery to better predict lodging damage in sorghum. AgriRxiv 2022, 20220024994. [Google Scholar] [CrossRef]
- Yu, M.; Wu, B.; Yan, N.; Xing, Q.; Zhu, W. A method for estimating the aerodynamic roughness length with NDVI and BRDF signatures using multi-temporal Proba-V data. Remote Sens. 2016, 9, 6. [Google Scholar] [CrossRef]
- Kim, D.H.; Yoon, Y.I.; Choi, J.S. An efficient method to build panoramic image mosaics. Pattern Recognit. Lett. 2003, 24, 2421–2429. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Moussa, A.; El-Sheimy, N. A Fast Approach for Stitching of Aerial Images. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 769–774. [Google Scholar] [CrossRef]
- Faraji, M.R.; Qi, X.; Jensen, A. Computer vision–based orthorectification and georeferencing of aerial image sets. J. Appl. Remote Sens. 2016, 10, 036027. [Google Scholar] [CrossRef]
- Zhang, W.; Guo, B.; Li, M.; Liao, X.; Li, W. Improved seam-line searching algorithm for UAV image mosaic with optical flow. Sensors 2018, 18, 1214. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Yao, J.; Xie, R.; Li, J. Edge-enhanced optimal seamline detection for orthoimage mosaicking. IEEE Geosci. Remote Sens. Lett. 2018, 15, 764–768. [Google Scholar] [CrossRef]
- Fang, F.; Wang, T.; Fang, Y.; Zhang, G. Fast color blending for seamless image stitching. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1115–1119. [Google Scholar] [CrossRef]
- Jaderberg, M.; Simonyan, K.; Zisserman, A.; Kavukcuoglu, K. Spatial transformer networks. arXiv 2015, arXiv:1506.02025. [Google Scholar]
- Revaud, J.; Weinzaepfel, P.; De Souza, C.; Pion, N.; Csurka, G.; Cabon, Y.; Humenberger, M. R2D2: Repeatable and reliable detector and descriptor. arXiv 2019, arXiv:1906.06195. [Google Scholar]
- DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superpoint: Self-supervised interest point detection and description. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 224–236. [Google Scholar]
- Christiansen, P.H.; Kragh, M.F.; Brodskiy, Y.; Karstoft, H. Unsuperpoint: End-to-end unsupervised interest point detector and descriptor. arXiv 2019, arXiv:1907.04011. [Google Scholar]
- Sarlin, P.E.; DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superglue: Learning feature matching with graph neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Online, 14–19 June 2020; pp. 4938–4947. [Google Scholar]
- Yuan, Y.; Fang, F.; Zhang, G. Superpixel-Based Seamless Image Stitching for UAV Images. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1565–1576. [Google Scholar] [CrossRef]
- Li, L.; Xia, M.; Liu, C.; Li, L.; Wang, H.; Yao, J. Jointly optimizing global and local color consistency for multiple image mosaicking. ISPRS J. Photogramm. Remote Sens. 2020, 170, 45–56. [Google Scholar] [CrossRef]
- Shen, X.; Darmon, F.; Efros, A.A.; Aubry, M. Ransac-flow: Generic two-stage image alignment. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Part IV 16. Springer: Online, 2020; pp. 618–637. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E. Use of the Hough transformation to detect lines and curves in pictures. Commun. ACM 1972, 15, 11–15. [Google Scholar] [CrossRef]
- Rosenfeld, A.; Pfaltz, J.L. Distance functions on digital pictures. Pattern Recognit. 1968, 1, 33–61. [Google Scholar] [CrossRef]
- National Geographic Information Institute. Available online: http://map.ngii.go.kr/ (accessed on 23 December 2022).
- Korea Rural Economic Institute. Available online: https://aglook.krei.re.kr/ (accessed on 23 December 2022).
- SZ DJI Technology Company, Limited. Available online: https://www.dji.com/ (accessed on 23 December 2022).
- MicaSense, Incorporated. Available online: https://micasense.com/ (accessed on 23 December 2022).
- PIX4Dmapper. Available online: https://www.pix4d.com/product/pix4dmapper-photogrammetry-software/ (accessed on 23 December 2022).
- Zaragoza, J.; Chin, T.J.; Brown, M.S.; Suter, D. As-projective-as-possible image stitching with moving DLT. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2339–2346. [Google Scholar]






| Notations | Definitions |
|---|---|
| (Section 2.1) | Source mosaic image |
| (Section 2.2) | Source mosaic image that has been transformed by the global alignment |
| (Section 2.1) | Target mosaic image |
| (Section 2.1) | A set of referent points annotated in |
| (Section 2.1) | A set of referent points annotated in |
| (Section 2.1) | A global mapping to map to their counterparts in |
| (Section 2.1) | A set of local mappings applied to each patch of |
| (Section 2.1) | A distance measure between two point sets A and B |
| (Section 2.1) | A set of transformed keypoints A using global alignment G and a set of patch-wise local alignments L |
| h (Section 2.2) | A 3 × 3 matrix to represent a homography |
| (Section 2.2) | A set of keypoints in |
| (Section 2.2) | A set of keypoints in |
| (Section 2.2) | Multidimensional descriptor for a keypoint k |
| (Section 2.3) | A set of nonoverlapped patches for |
| (Section 2.3) | A set of patches for |
| (Section 2.3) | A refined set of keypoints for |
| (Section 2.3) | A refined set of keypoints for |
| Method | Average Alignment Error | |||
|---|---|---|---|---|
| Global (G) | 2.54 | 0.62 | 0.87 | 1.18 |
| G + reference points | 2.54 | 0.62 | 0.91 | 1.04 |
| MDLT | 2.54 | 0.53 | 0.85 | 1.16 |
| G + RANSAC | 2.02 | 0.42 | 0.62 | 1.09 |
| G + RANSAC-flow | 1.64 | 0.40 | 0.62 | 0.76 |
| G + RANSAC + BA (proposed) | 2.46 | 0.46 | 0.79 | 1.12 |
| G + RANSAC-flow + BA (proposed) | 2.36 | 0.44 | 0.72 | 0.82 |
| Dataset | Threshold | |||||
|---|---|---|---|---|---|---|
| 0.80 | 0.85 | 0.90 | 0.95 | 0.99 | ||
| # KPs in global alignment | 3.77 | 3.58 | 3.26 | 2.74 | 1.38 | |
| # KPs/patch in local alignment | 257.12 | 250.22 | 235.59 | 192.76 | 121.55 | |
| # KPs in global alignment | 2.19 | 2.09 | 1.93 | 1.66 | 0.89 | |
| # KPs/patch in local alignment | 399.20 | 386.62 | 370.75 | 338.16 | 213.76 | |
| # KPs in global alignment | 2.17 | 2.07 | 1.91 | 1.64 | 0.88 | |
| # KPs/patch in local alignment | 873.12 | 850.43 | 805.98 | 733.85 | 438.72 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.; Kim, S.; Lim, D.; Bae, S.-H.; Kang, L.-H.; Kim, S. Two-Step Approach toward Alignment of Spatiotemporal Wide-Area Unmanned Aerial Vehicle Imageries. Drones 2023, 7, 131. https://doi.org/10.3390/drones7020131
Lee H, Kim S, Lim D, Bae S-H, Kang L-H, Kim S. Two-Step Approach toward Alignment of Spatiotemporal Wide-Area Unmanned Aerial Vehicle Imageries. Drones. 2023; 7(2):131. https://doi.org/10.3390/drones7020131
Chicago/Turabian StyleLee, Hyeonseok, Semo Kim, Dohun Lim, Seoung-Hun Bae, Lae-Hyong Kang, and Sungchan Kim. 2023. "Two-Step Approach toward Alignment of Spatiotemporal Wide-Area Unmanned Aerial Vehicle Imageries" Drones 7, no. 2: 131. https://doi.org/10.3390/drones7020131
APA StyleLee, H., Kim, S., Lim, D., Bae, S.-H., Kang, L.-H., & Kim, S. (2023). Two-Step Approach toward Alignment of Spatiotemporal Wide-Area Unmanned Aerial Vehicle Imageries. Drones, 7(2), 131. https://doi.org/10.3390/drones7020131







