Optimal Energy and Delay Tradeoff in UAV-Enabled Wireless Sensor Networks
Abstract
1. Introduction
- We propose the optimization framework called MOACO-ACM for designing the flight speed as well as the flight trajectory of each UAV, which achieves different Pareto-optimal tradeoffs between the maximum single-UAV energy consumption among all UAVs and the task completion time.
- We validate the effectiveness of the proposed algorithm through extensive simulations. We also reveal the impact of UAV’s different flight speed scheduling on the tradeoff between the task completion time and the energy consumption across UAVs.
2. Related Works and Motivation
3. System Model and Problem Formulation
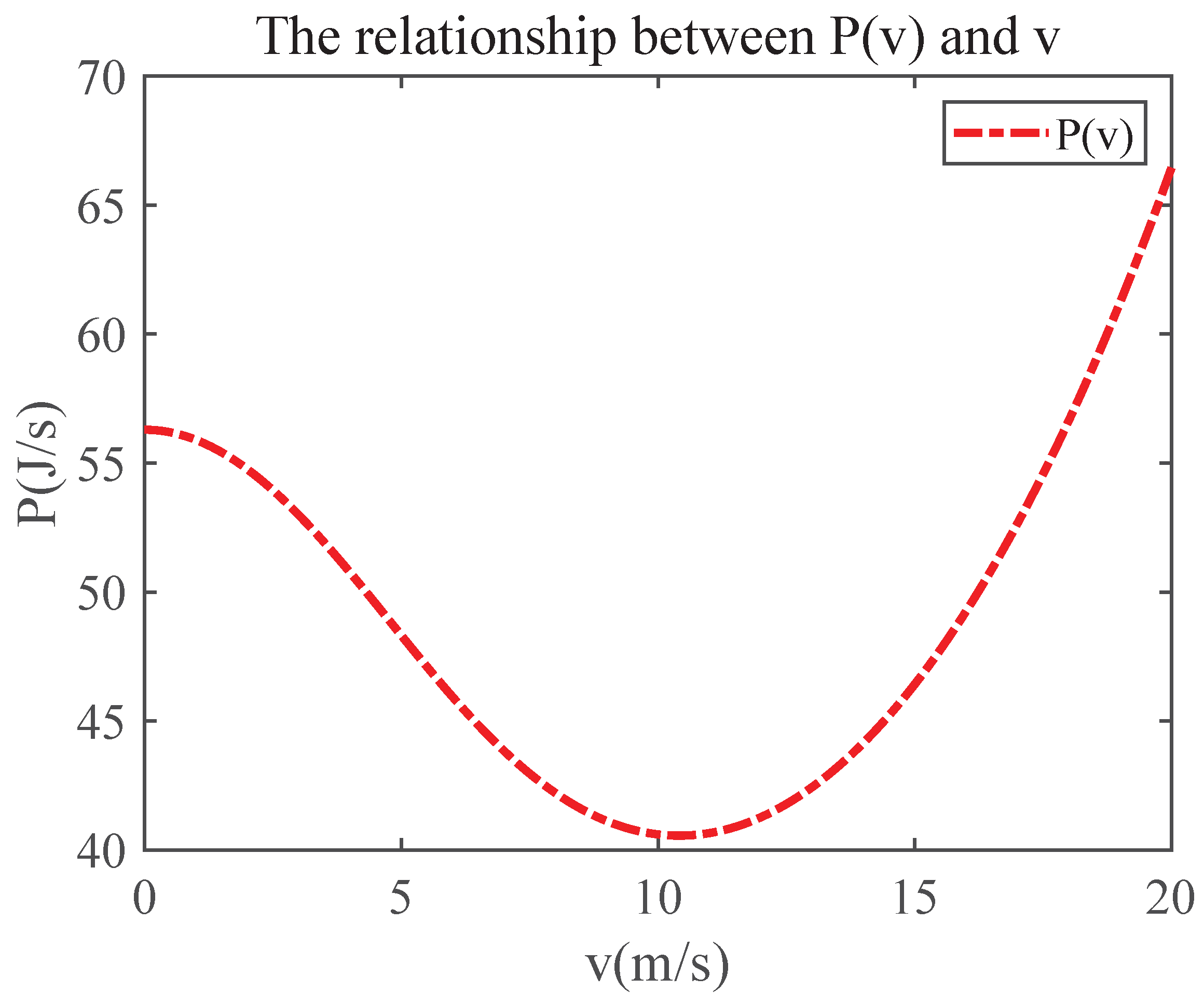
3.1. The Relationship between the Flight Power Consumption and Flight Speed
3.2. Flight Energy Consumption Model
3.3. Hovering Energy Consumption Model
3.4. Communication Energy Consumption Model
3.5. Total Energy Consumption Model
3.6. Problem Formulation
4. Multi-UAV Trajectory Design and Speed Control
- (1)
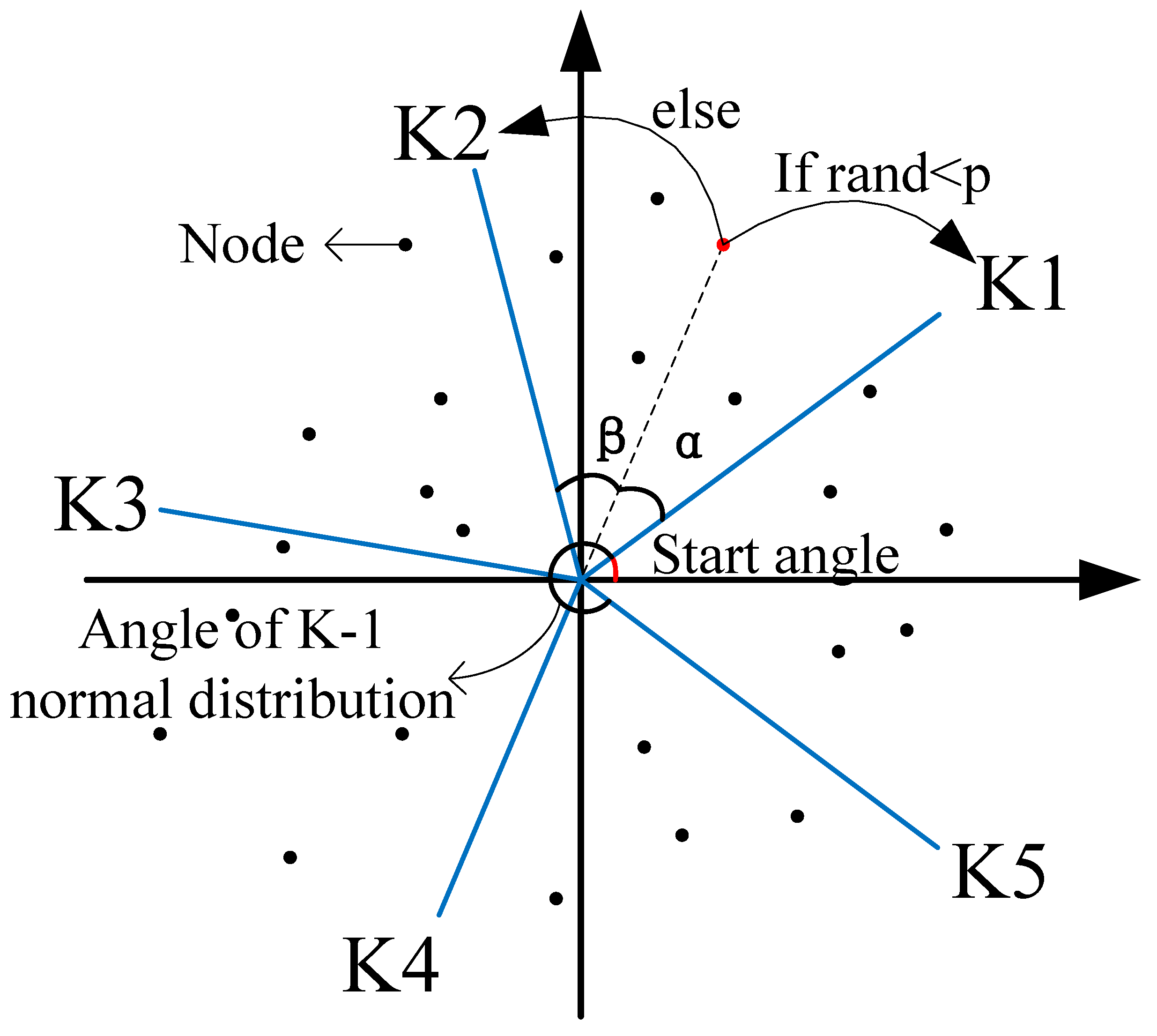
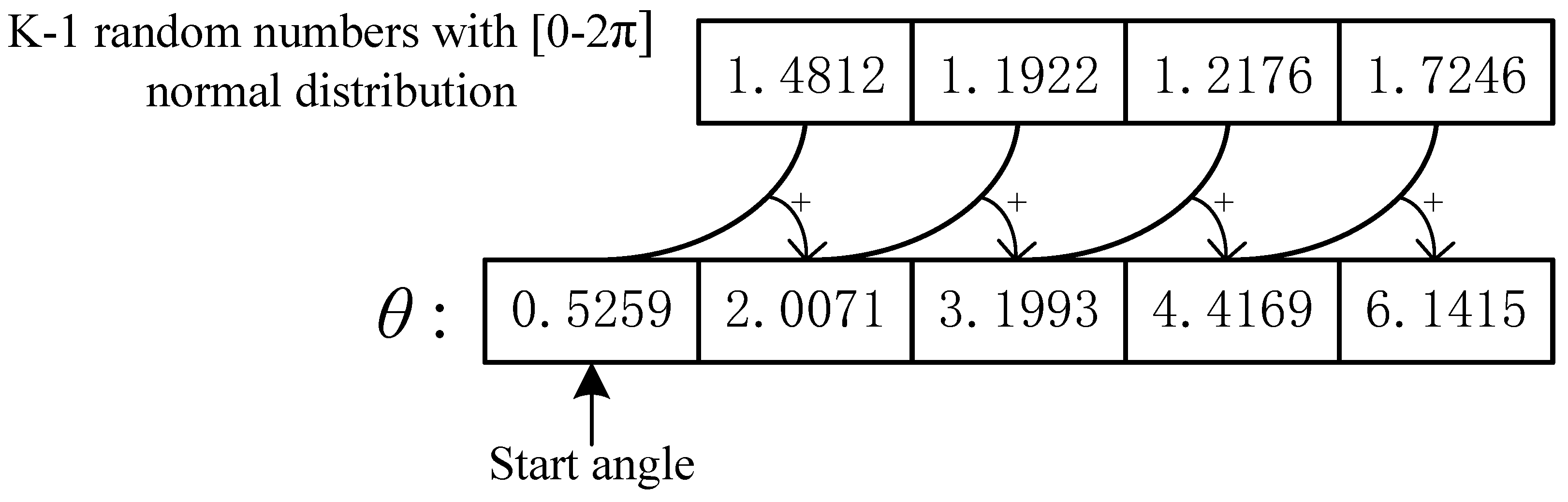
- The adaptive coordinate method is used to determine orbital nodes for each UAV. Initially, N task nodes are mapped to a two-dimensional plane coordinate system denoted as , where . Assuming the central hangar is at (0, 0), K rays are generated from this node, dividing the two-dimensional plane into K regions, each containing a certain number of task nodes. To ensure that each task node falls between two adjacent rays, a node capture mechanism is designed. This mechanism assigns a node to a task node based on the angle and distance between the node and its adjacent rays. The generation of K rays follows these steps: a random generation strategy is used during the first period of the iteration to explore the entire area and avoid local optima. After this period, local exploration is performed by adjusting the angles of the K rays using Equations (18)–(20).
- (2)
- Once the first stage is completed, the matching between the flying UAVs and the N task nodes is established. Then, the ACO is applied to find the shortest TSP path for each UAV based on the assigned task nodes.
- (3)
- The UAV’s speed interval is discretized into several speed values. Each speed value is sequentially substituted to solve for the candidate optimum between the task completion time of the largest single UAV and the energy consumption of the largest single UAV, resulting in a Pareto front.
| Algorithm 1 MOACO-ACM. |
Input: The coordinate of each node, the number of UAVs K and the maximum number of iterations . Output: Pareto-optimal solution to the proposed problem.
|
| Algorithm 2 Ant colony optimization algorithm for optimizing the flight trajectory of the UAV. |
Input: The city number visited by the UAV; (Maximum number of iterations of ant colony optimization algorithm); (Ant colony numbers). Output: trajectory of the UAV.
|
4.1. Adaptive Coordinate Method
4.2. The Discussion of the Impact of Flight Speed
5. Comparison Algorithm Design
5.1. Comparison Algorithms and Parameter Setting
- (1)
- UAV trajectory optimization algorithms: Our algorithm was compared with three popular trajectory optimization algorithms (variation of the ant colony algorithm named ACO-NODE [38], a genetic trajectory planning algorithm with variable population size naemd GTPA-VP [39], a novel reinforcement learning based grey wolf optimizer algorithm called RLGWO [40]). In this section of the experiment, the UAV speed is set to 10. The parameters of all the algorithms being compared are based on the settings described in the paper. The maximum number of iterations is set to 1000. However, this section does not discuss the communication traffic of task nodes.
- (2)
- Multi-objective algorithms: Our algorithm was compared with two advanced multi-objective methods (multi-objective particle swarm optimization (MOPSO), multi-objective ant colony optimization-Kmeans (MOACO-Kmeans)). PlatEMO or Github uploaded the source code of the corresponding algorithms. The common parameters of these algorithms are shown in Table 2, and some unique parameters are defined as follows.
5.2. Experimental Setting
5.3. Evaluation Index
6. Simulation Experiment and Result Analysis
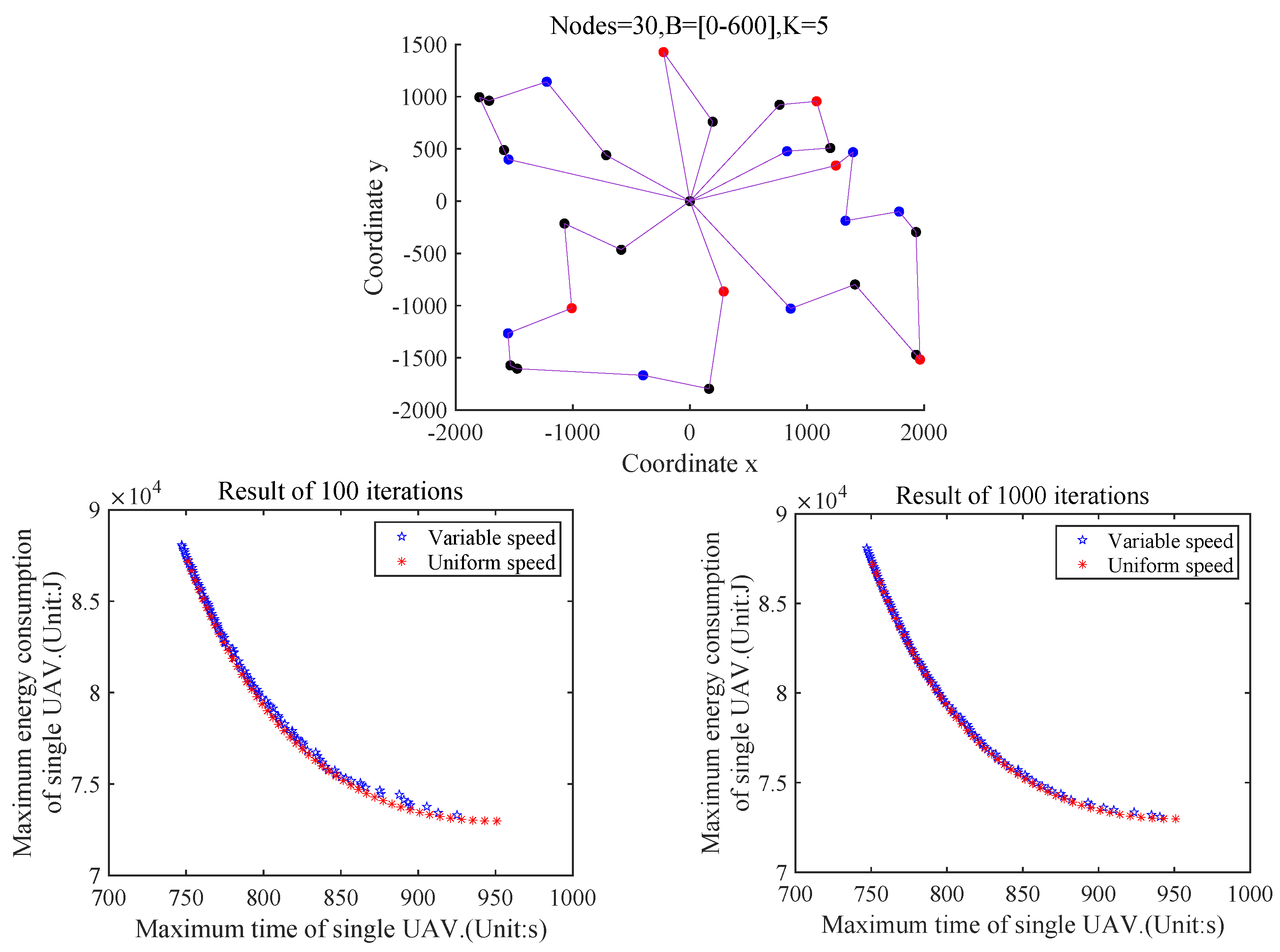
6.1. Comparison of the Speed in the Same Trajectory
6.2. Comparison Algorithms
6.2.1. UAV Trajectory Comparison Optimization Algorithms
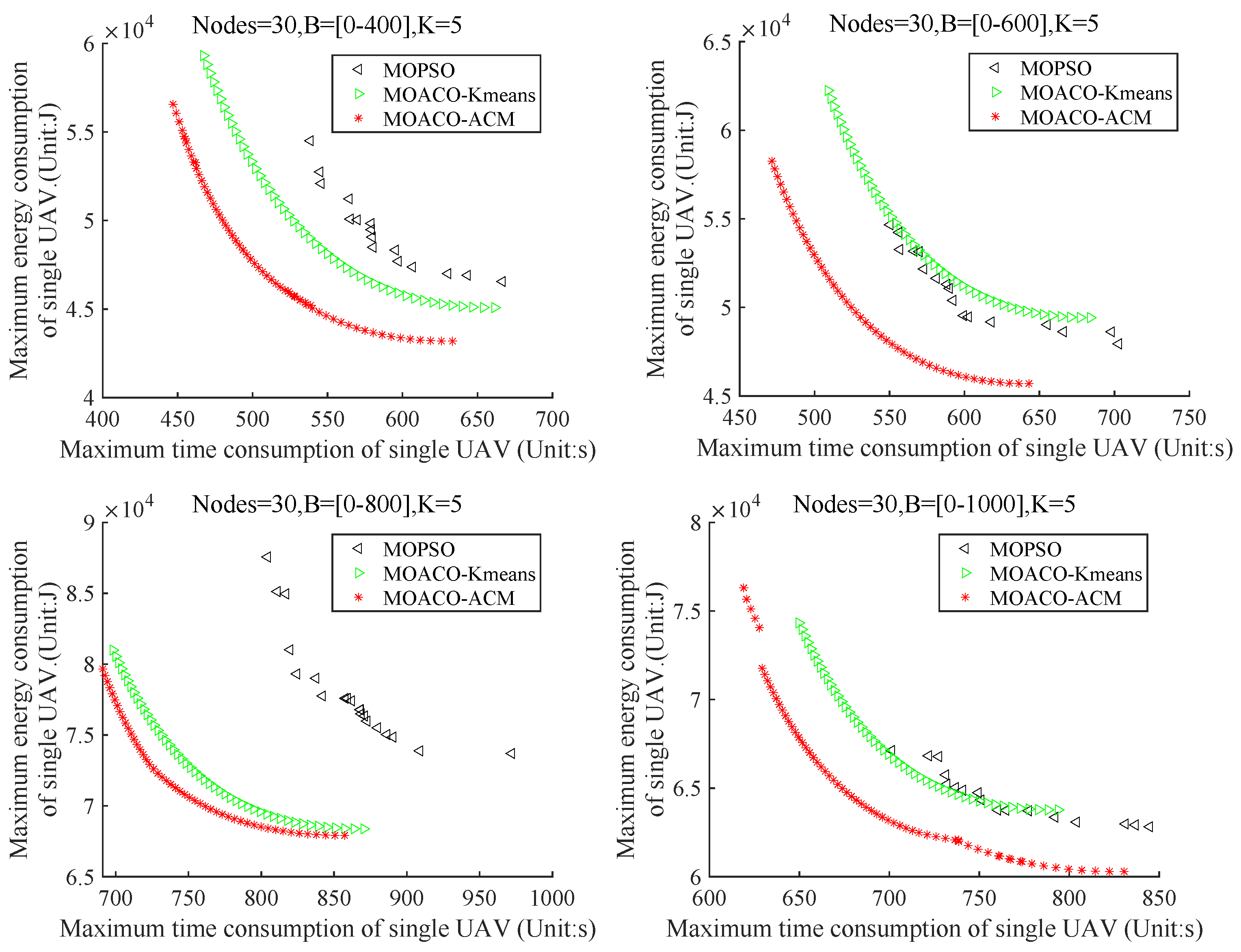
6.2.2. Multi-Objective Comparison Algorithms
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zeng, Y.; Wu, Q.; Zhang, R. Accessing from the sky: A tutorial on UAV communications for 5G and beyond. Proc. IEEE 2019, 107, 2327–2375. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, R.; Lim, T.J. Wireless communications with unmanned aerial vehicles: Opportunities and challenges. IEEE Commun. Mag. 2016, 54, 36–42. [Google Scholar] [CrossRef]
- Li, X.; Wang, Q.; Liu, Y.; Tsiftsis, T.A.; Ding, Z.; Nallanathan, A. UAV-aided multi-way NOMA networks with residual hardware impairments. IEEE Wirel. Commun. Lett. 2020, 9, 1538–1542. [Google Scholar] [CrossRef]
- Do, D.T.; Nguyen, T.T.T.; Le, C.B.; Voznak, M.; Kaleem, Z.; Rabie, K.M. UAV relaying enabled NOMA network with hybrid duplexing and multiple antennas. IEEE Access 2020, 8, 186993–187007. [Google Scholar] [CrossRef]
- Hayat, S.; Yanmaz, E.; Muzaffar, R. Survey on unmanned aerial vehicle networks for civil applications: A communications viewpoint. IEEE Commun. Surv. Tutorials 2016, 18, 2624–2661. [Google Scholar] [CrossRef]
- Erdelj, M.; Natalizio, E.; Chowdhury, K.R.; Akyildiz, I.F. Help from the sky: Leveraging UAVs for disaster management. IEEE Pervasive Comput. 2017, 16, 24–32. [Google Scholar] [CrossRef]
- Li, S.; Duo, B.; Yuan, X.; Liang, Y.C.; Di Renzo, M. Reconfigurable intelligent surface assisted UAV communication: Joint trajectory design and passive beamforming. IEEE Wirel. Commun. Lett. 2020, 9, 716–720. [Google Scholar] [CrossRef]
- Li, S.; Duo, B.; Di Renzo, M.; Tao, M.; Yuan, X. Robust secure UAV communications with the aid of reconfigurable intelligent surfaces. IEEE Trans. Wirel. Commun. 2021, 20, 6402–6417. [Google Scholar] [CrossRef]
- Gupta, L.; Jain, R.; Vaszkun, G. Survey of important issues in UAV communication networks. IEEE Commun. Surv. Tutorials 2015, 18, 1123–1152. [Google Scholar] [CrossRef]
- Ngu, A.H.; Gutierrez, M.; Metsis, V.; Nepal, S.; Sheng, Q.Z. IoT middleware: A survey on issues and enabling technologies. IEEE Int. Things J. 2016, 4, 1–20. [Google Scholar] [CrossRef]
- Yan, H.; Chen, Y.; Yang, S.H. UAV-enabled wireless power transfer with base station charging and UAV power consumption. IEEE Trans. Veh. Technol. 2020, 69, 12883–12896. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Debbah, M. Mobile Internet of Things: Can UAVs provide an energy-efficient mobile architecture? In Proceedings of the 2016 IEEE Global Communications Conference (GLOBECOM), IEEE, Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar]
- Zhan, C.; Zeng, Y.; Zhang, R. Energy-efficient data collection in UAV enabled wireless sensor network. IEEE Wirel. Commun. Lett. 2017, 7, 328–331. [Google Scholar] [CrossRef]
- Lyu, J.; Zeng, Y.; Zhang, R. Cyclical multiple access in UAV-aided communications: A throughput-delay tradeoff. IEEE Wirel. Commun. Lett. 2016, 5, 600–603. [Google Scholar] [CrossRef]
- Zhan, C.; Zeng, Y.; Zhang, R. Trajectory design for distributed estimation in UAV-enabled wireless sensor network. IEEE Trans. Veh. Technol. 2018, 67, 10155–10159. [Google Scholar] [CrossRef]
- Xu, J.; Zeng, Y.; Zhang, R. UAV-enabled wireless power transfer: Trajectory design and energy optimization. IEEE Trans. Wirel. Commun. 2018, 17, 5092–5106. [Google Scholar] [CrossRef]
- Zeng, Y.; Xu, J.; Zhang, R. Energy minimization for wireless communication with rotary-wing UAV. IEEE Trans. Wirel. Commun. 2019, 18, 2329–2345. [Google Scholar] [CrossRef]
- Ren, H.; Zhang, Z.; Peng, Z.; Li, L.; Pan, C. Energy minimization in RIS-assisted UAV-enabled wireless power transfer systems. IEEE Int. Things J. 2022, 10, 5794–5809. [Google Scholar] [CrossRef]
- Zeng, Y.; Xu, X.; Zhang, R. Trajectory design for completion time minimization in UAV-enabled multicasting. IEEE Trans. Wirel. Commun. 2018, 17, 2233–2246. [Google Scholar] [CrossRef]
- Li, J.; Zhao, H.; Wang, H.; Gu, F.; Wei, J.; Yin, H.; Ren, B. Joint optimization on trajectory, altitude, velocity, and link scheduling for minimum mission time in UAV-aided data collection. IEEE Int. Things J. 2019, 7, 1464–1475. [Google Scholar] [CrossRef]
- Zhan, C.; Zeng, Y. Completion time minimization for multi-UAV-enabled data collection. IEEE Trans. Wirel. Commun. 2019, 18, 4859–4872. [Google Scholar] [CrossRef]
- Shan, F.; Luo, J.; Xiong, R.; Wu, W.; Li, J. Looking before crossing: An optimal algorithm to minimize UAV energy by speed scheduling with a practical flight energy model. In Proceedings of the IEEE INFOCOM 2020-IEEE Conference on Computer Communications, IEEE, Toronto, ON, Canada, 6–9 July 2020; pp. 1758–1767. [Google Scholar]
- Zhang, S.; Cao, R.; Jiang, Z. Energy-Efficient Data Collection and Trajectory Design for UAV-Enabled Wireless Sensor Network. In Proceedings of the 2022 IEEE 5th International Conference on Electronics Technology (ICET), IEEE, Chengdu, China, 13–16 May 2022; pp. 933–938. [Google Scholar]
- Dai, X.; Duo, B.; Yuan, X.; Tang, W. Energy-Efficient UAV Communications: A Generalized Propulsion Energy Consumption Model. IEEE Wirel. Commun. Lett. 2022, 11, 2150–2154. [Google Scholar] [CrossRef]
- Yang, D.; Wu, Q.; Zeng, Y.; Zhang, R. Energy tradeoff in ground-to-UAV communication via trajectory design. IEEE Trans. Veh. Technol. 2018, 67, 6721–6726. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, R. Energy-efficient UAV communication with trajectory optimization. IEEE Trans. Wirel. Commun. 2017, 16, 3747–3760. [Google Scholar] [CrossRef]
- Zhu, K.; Xu, X.; Han, S. Energy-efficient UAV trajectory planning for data collection and computation in mMTC networks. In Proceedings of the 2018 IEEE Globecom Workshops (GC Wkshps), IEEE, Abu Dhabi, UAE, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Tao, Q.; Su, G.; Chen, B.; Dai, M.; Lin, X.; Wang, H. Secrecy Energy Efficiency Maximization for UAV Enabled Communication Systems. In Proceedings of the 2021 30th Wireless and Optical Communications Conference (WOCC), IEEE, Taipei, Taiwan, 7–8 October 2021; pp. 240–244. [Google Scholar]
- Sun, C.; Xiong, X.; Ni, W.; Wang, X. Three-Dimensional Trajectory Design for Energy-Efficient UAV-Assisted Data Collection. In Proceedings of the ICC 2022-IEEE International Conference on Communications, IEEE, Rome, Italy, 28 May–1 June 2022; pp. 3580–3585. [Google Scholar]
- Zhan, C.; Hu, H.; Sui, X.; Liu, Z.; Niyato, D. Completion time and energy optimization in the UAV-enabled mobile-edge computing system. IEEE Int. Things J. 2020, 7, 7808–7822. [Google Scholar] [CrossRef]
- Jin, C.; Wang, J.; Tang, Q.; Li, F. Wireless Powered Collaborative UAV-Enabled Mobile Edge Computing for the weighted time and energy minimization. In Proceedings of the 2021 IEEE Region 10 Symposium (TENSYMP), IEEE, Jeju, Republic of Korea, 23–25 August 2021; pp. 1–5. [Google Scholar]
- Luo, Y.; Xu, Y.; Zhang, T. Completion Time Minimization for Content Delivery in Cache-Enabled UAV Networks. In Proceedings of the 2021 Computing, Communications and IoT Applications (ComComAp), IEEE, Shenzhen, China, 26–28 November 2021; pp. 268–273. [Google Scholar]
- Wang, H.; Wang, J.; Ding, G.; Chen, J.; Yang, J. Completion time minimization for turning angle-constrained UAV-to-UAV communications. IEEE Trans. Veh. Technol. 2020, 69, 4569–4574. [Google Scholar] [CrossRef]
- Zhu, G.; Guo, L.; Dong, C.; Mu, X. Mission time minimization for multi-UAV-enabled data collection with interference. In Proceedings of the 2021 IEEE Wireless Communications and Networking Conference (WCNC), IEEE, Nanjing, China, 29 March–1 April 2021; pp. 1–6. [Google Scholar]
- Gong, J.; Chang, T.H.; Shen, C.; Chen, X. Flight time minimization of UAV for data collection over wireless sensor networks. IEEE J. Sel. Areas Commun. 2018, 36, 1942–1954. [Google Scholar] [CrossRef]
- Zong, J.; Shen, C.; Cheng, J.; Gong, J.; Chang, T.H.; Chen, L.; Ai, B. Flight time minimization via UAV’s trajectory design for ground sensor data collection. In Proceedings of the 2019 16th International Symposium on Wireless Communication Systems (ISWCS), IEEE, Oulu, Finland, 27–30 August 2019; pp. 255–259. [Google Scholar]
- Hellaoui, H.; Bagaa, M.; Chelli, A.; Taleb, T.; Yang, B. On Supporting Multi-Services in UAV-Enabled Aerial Communication for the Internet of Things. IEEE Int. Things J. 2023; Early Access. [Google Scholar] [CrossRef]
- Perez-Carabaza, S.; Besada-Portas, E.; Lopez-Orozco, J.A.; de la Cruz, J.M. Ant colony optimization for multi-UAV minimum time search in uncertain domains. Appl. Soft Comput. 2018, 62, 789–806. [Google Scholar] [CrossRef]
- Asim, M.; Mashwani, W.K.; Belhaouari, S.B.; Hassan, S. A novel genetic trajectory planning algorithm with variable population size for multi-UAV-assisted mobile edge computing system. IEEE Access 2021, 9, 125569–125579. [Google Scholar] [CrossRef]
- Qu, C.; Gai, W.; Zhong, M.; Zhang, J. A novel reinforcement learning based grey wolf optimizer algorithm for unmanned aerial vehicles (UAVs) path planning. Appl. Soft Comput. 2020, 89, 106099. [Google Scholar] [CrossRef]
- Bertran, E.; Sànchez-Cerdà, A. On the tradeoff between electrical power consumption and flight performance in fixed-wing UAV autopilots. IEEE Trans. Veh. Technol. 2016, 65, 8832–8840. [Google Scholar] [CrossRef]
- Thibbotuwawa, A.; Nielsen, P.; Zbigniew, B.; Bocewicz, G. Factors affecting energy consumption of unmanned aerial vehicles: An analysis of how energy consumption changes in relation to UAV routing. In Proceedings of 39th International Conference on Information Systems Architecture and Technology–ISAT 2018: Part II; Springer: Berlin/Heidelberg, Germany, 2019; pp. 228–238. [Google Scholar]
- Yang, X.S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the 2009 World congress on nature & biologically inspired computing (NaBIC), IEEE, Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- MarcoDorigoaLuc, M. Ant colonies for the traveling salesman problem. Biosystems 1997, 43, 73–81. [Google Scholar]
- Golberg, D.E. Genetic algorithms in search, optimization, and machine learning. Addion Wesley 1989, 1989, 36. [Google Scholar]
- Storn, R.; Price, K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, IEEE, Perth, WA, USA, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Laporte, G. The traveling salesman problem: An overview of exact and approximate algorithms. Eur. J. Oper. Res. 1992, 59, 231–247. [Google Scholar] [CrossRef]
- Kolo, T.; Fanggidae, A. Analisis Metode Cycle Crossover (Cx) Dan Metode Partial Mapped Crossover (Pmx) Pada Penyelesaian Kasus Traveling Salesman Problem (Tsp). J-ICON J. Komput. Dan Inform. 2019, 7, 61–66. [Google Scholar]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Nouri-Moghaddam, B.; Ghazanfari, M.; Fathian, M. A novel multi-objective forest optimization algorithm for wrapper feature selection. Expert Syst. Appl. 2021, 175, 114737. [Google Scholar] [CrossRef]











| Symbol | Physical Meaning | Numerical Value |
|---|---|---|
| Communication energy consumption in J/s | ||
| Hover energy consumption in J/s | 100 | |
| / | Search space size in m2 | 1000 × 1000 |
| b | Data transmission speed in mbit/s | 50 |
| Blade power, | ||
| Induced power, | ||
| Tip speed of the rotor blade, | 80 | |
| Mean rotor induced speed | ||
| Fuselage drag ratio | ||
| Air density in kg/m3 | ||
| s | Rotor solidity, | |
| A | Rotor disc area in | |
| R | Rotor radius in meter m | |
| W | Aircraft weight in Newton, g = 9.8 m/s2 | |
| k | Incremental correction factor to induced power | |
| Blade angular speed in r/s | 400 | |
| Fuselage equivalent flat plate area in m2 | ||
| b | Number of blades | 4 |
| c | Blade or aerofoil chord length | |
| m | Airframe mass in kg | |
| Profile drag coefficient |
| Algorithm | Fixed Parameters |
|---|---|
| MOPSO | Inertia Weight w = 0.5; Intertia Weight Damping Rate = 0.99; Personal Learning Coefficient = 1; Global Learning Coefficient = 2; Mutation Rate = 0.1; |
| MOACO | Route selection probability parameter = 0.3; Heuristic weight parameter = 1; Initial pheromone concentration Q = 1; The pheromone evaporation rate = 0.5; Number of ants = 50; Maximum number of iterations of ant colony optimization algorithm = 100; |
| HV (Nodes = 30, K = 3) | MOPSO | MOACO-Kmeans | MOACO-ACM | Reference Point Z* | |
|---|---|---|---|---|---|
| B = [0–400] | Mean | 1.02 × | 1.53 × | [1.23 × , 1.06 ] | |
| Std | 2.42 × | 3.89 × | 1.40 × | ||
| B = [0–600] | Mean | 8.37 × | 1.56 × | [1.27 × , 1.10 × ] | |
| Std | 2.08 × | 8.33 × | 8.87 × | ||
| B = [0–800] | Mean | 7.42 × | 7.93 × | [1.67 × , 1.39 × ] | |
| Std | 2.18 × | 9.28 × | 1.28 × | ||
| B = [0–1000] | Mean | 1.05 × | 1.16 × | [1.59 × , 1.29 × ] | |
| Std | 3.00 × | 4.12 × | 1.26 × | ||
| HV (Nodes = 30, K = 5) | MOPSO | MOACO-Kmeans | MOACO-ACM | Reference Point Z* | |
|---|---|---|---|---|---|
| B = [0–400] | Mean | 6.04 × | 1.10 × | [8.95 ×, 7.28 ×] | |
| Std | 1.31 × | 2.01 × | 5.10 × | ||
| B = [0–600] | Mean | 4.65 × | 8.04 × | [9.29 ×, 7.01 ×] | |
| Std | 1.45 × | 9.25 × | 7.91 × | ||
| B = [0–800] | Mean | 3.66 × | 8.42 × | [1.13 × , 9.09 ×] | |
| Std | 8.52 × | 5.15 × | 5.79 × | ||
| B = [0–1000] | Mean | 4.39 × | 6.34 × | [1.05 × , 8.52 ×] | |
| Std | 1.22 × | 5.56 × | 5.53 × | ||
| HV (Nodes = 50, K = 5) | MOPSO | MOACO-Kmeans | MOACO-ACM | Reference Point Z* | |
|---|---|---|---|---|---|
| B = [0–400] | Mean | 1.25 × | 4.08 × | [1.49 ×, 1.30 ×] | |
| Std | 1.10 × | 3.37 × | 3.37 × | ||
| B = [0–600] | Mean | 5.19 × | 2.18 × | [1.66 ×, 1.20 ×] | |
| Std | 4.88 × | 1.80 × | 2.05 × | ||
| B = [0–800] | Mean | 6.59 × | 2.56 × | [1.73 ×, 1.45 ×] | |
| Std | 6.11 × | 2.13 × | 2.29 × | ||
| B = [0–1000] | Mean | 5.73 × | 1.84 × | [1.89 ×, 1.43 ×] | |
| Std | 5.28 × | 1.57 × | 2.27 × | ||
| HV (Nodes = 50, K = 8) | MOPSO | MOACO-Kmeans | MOACO-ACM | Reference Point Z* | |
|---|---|---|---|---|---|
| B = [0–400] | Mean | 4.17 × | 1.29 × | [1.14 ×, 7.61 ×] | |
| Std | 3.74 × | 1.07 × | 1.19 × | ||
| B = [0–600] | Mean | 5.68 × | 1.47 × | [1.20 ×, 1.01 ×] | |
| Std | 4.94 × | 1.21 × | 1.43 × | ||
| B = [0–800] | Mean | 3.40 × | 1.01 × | [1.35 ×, 9.58 ×] | |
| Std | 3.21 × | 8.49 × | 1.04 × | ||
| B = [0–1000] | Mean | 5.71 × | 1.22 × | [1.45 ×, 1.04 ×] | |
| Std | 5.06 × | 1.02 × | 1.24 × | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, J.; Fu, Q.; Jia, R.; Lin, F.; Li, M.; Zheng, Z. Optimal Energy and Delay Tradeoff in UAV-Enabled Wireless Sensor Networks. Drones 2023, 7, 368. https://doi.org/10.3390/drones7060368
Xie J, Fu Q, Jia R, Lin F, Li M, Zheng Z. Optimal Energy and Delay Tradeoff in UAV-Enabled Wireless Sensor Networks. Drones. 2023; 7(6):368. https://doi.org/10.3390/drones7060368
Chicago/Turabian StyleXie, Jiapin, Qiyong Fu, Riheng Jia, Feilong Lin, Ming Li, and Zhonglong Zheng. 2023. "Optimal Energy and Delay Tradeoff in UAV-Enabled Wireless Sensor Networks" Drones 7, no. 6: 368. https://doi.org/10.3390/drones7060368
APA StyleXie, J., Fu, Q., Jia, R., Lin, F., Li, M., & Zheng, Z. (2023). Optimal Energy and Delay Tradeoff in UAV-Enabled Wireless Sensor Networks. Drones, 7(6), 368. https://doi.org/10.3390/drones7060368






