A Deep-Learning-Based GPS Signal Spoofing Detection Method for Small UAVs
Abstract
1. Introduction
- (1)
- We propose a GPS signal spoofing detection model based on PCA-CNN-LSTM, which mainly consists of three parts: principal component analysis (PCA), a convolutional neural network (CNN), and a long short-term memory (LSTM) network. We chose the PCA method to downgrade the input GPS signal data, the CNN was used to extract the features of the GPS signal data, and the role of the LSTM network was to model the output of the CNN as a sequence.
- (2)
- To address the problem of the small amount of real GPS signal data, we propose an approach based on the SVM-SMOTE model to expand the GPS signal data.
- (3)
- In the simulation experimental environment, we verified that the PCA-CNN-LSTM model obtained an accuracy of 0.9943, precision of 0.9798, recall of 0.965, and an F1_Score of 0.9722 on the GPS signal dataset.
2. Related Works
2.1. Traditional Machine-Learning-Based Methods
2.2. Deep-Learning-Based Methods
3. Data Acquisition and Preprocessing
3.1. Hardware System
3.2. Data Acquisition
3.3. Data Preprocessing
3.4. Data Augmentation
- The boundary information between samples is considered, and the generated synthetic samples are closer to the real minority class samples.
- Combining the advantages of SVM classifier, it can handle high-dimensional feature space and nonlinear problems.
- By increasing the number of minority category samples, the classifier’s ability to recognize minority categories is improved.
- The formula for SVM-SMOTE can be expressed as follows:
4. Methods
4.1. PCA
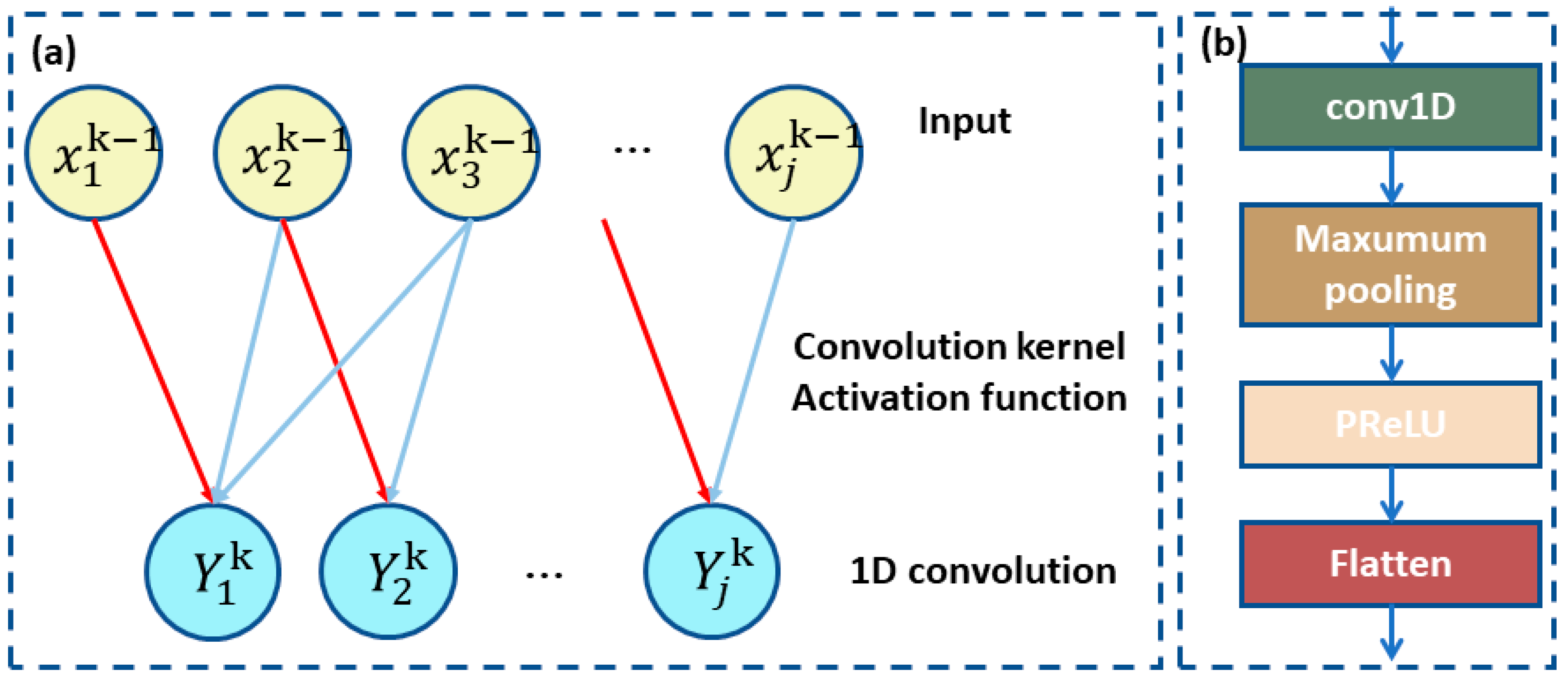
4.2. CNN
4.3. LSTM
4.4. PCA-CNN-LSTM Model Training
5. Results
5.1. Evaluation Method
- True positive (TP): The number of cases in the model where the true and predicted labels are both positive.
- False negative (FN): The number of cases in the model where the true label is positive but the predicted label is negative.
- False positive (FP): The number of cases in the model where the true label is negative but the predicted label is positive.
- False negative (TN): The number of cases in the model where the true and predicted labels are both negative.
5.2. Ten-Fold Cross-Verification
5.3. Model Evaluation Results
5.4. Comparison with Traditional Machine Learning Models
5.5. Comparison with Other Deep Learning Models
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bao, L.; Wu, R.; Wang, W.; Lu, D. Spoofing mitigation in Global Positioning System based on C/A code self-coherence with array signal processing. J. Commun. Technol. Electron. 2017, 62, 66–73. [Google Scholar] [CrossRef]
- Hartmann, K.; Giles, K. UAV exploitation: A new domain for cyber power. In Proceedings of the 2016 8th International Conference on Cyber Conflict (CyCon), Tallinn, Estonia, 31 May–3 June 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Hartmann, K.; Steup, C. The vulnerability of UAVs to cyber attacks—An approach to the risk assessment. In Proceedings of the 2013 5th International Conference on Cyber Conflict (CYCON 2013), Tallinn, Estonia, 4–7 June 2013; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar]
- Liu, Y.; Li, S.; Fu, Q.; Liu, Z. Impact assessment of GNSS spoofing attacks on INS/GNSS integrated navigation system. Sensors 2018, 18, 1433. [Google Scholar] [CrossRef] [PubMed]
- Psiaki, M.L.; Humphreys, T.E.; Stauffer, B. Attackers can spoof navigation signals without our knowledge. Here’s how to fight back GPS lies. IEEE Spectr. 2016, 53, 26–53. [Google Scholar] [CrossRef]
- Psiaki, M.L.; Powell, S.P.; O’Hanlon, B.W. GNSS spoofing detection using high-frequency antenna motion and carrier-phase data. In Proceedings of the 26th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2013), Nashville, TN, USA, 16–20 September 2013. [Google Scholar]
- Ruckle, L.J. The Dragon Lady and the Beast of Kandahar: Bush and Obama-era US Aerial Drone Surveillance Policy Based on a Case Study Comparison of the 1960 U-2 Crash with the 2011 RQ-170 Crash. In Technology and the Intelligence Community: Challenges and Advances for the 21st Century; Springer: Cham, Switzerland, 2018; pp. 83–113. [Google Scholar]
- Liang, C.; Miao, M.; Ma, J.; Yan, H.; Zhang, Q.; Li, X.; Li, T. Detection of GPS spoofing attack on unmanned aerial vehicle system. In Proceedings of the Machine Learning for Cyber Security: Second International Conference, ML4CS 2019, Xi’an, China, 19–21 September 2019; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Zhang, B.; Teunissen, P.J.G.; Yuan, Y.; Zhang, H.; Li, M. Joint estimation of vertical total electron content (VTEC) and satellite differential code biases (SDCBs) using low-cost receivers. J. Geod. 2018, 92, 401–413. [Google Scholar] [CrossRef]
- Nasser, A.; Hassan, H.A.H.; Chaaya, J.A.; Mansour, A.; Yao, K.-C. Spectrum sensing for cognitive radio: Recent advances and future challenge. Sensors 2021, 21, 2408. [Google Scholar] [CrossRef] [PubMed]
- Mohanti, S.; Soltani, N.; Sankhe, K.; Jaisinghani, D.; Di Felice, M.; Chowdhury, K. AirID: Injecting a custom RF fingerprint for enhanced UAV identification using deep learning. In Proceedings of the GLOBECOM 2020—2020 IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar]
- Meng, L.; Yang, L.; Ren, S.; Tang, G.; Zhang, L.; Yang, F.; Yang, W. An approach of linear regression-based UAV GPS spoofing detection. Wirel. Commun. Mobile Comput. 2021, 2021, 5517500. [Google Scholar] [CrossRef]
- Shafique, A.; Mehmood, A.; Elhadef, M. Detecting signal spoofing attack in uavs using machine learning models. IEEE Access 2021, 9, 93803–93815. [Google Scholar] [CrossRef]
- Talaei Khoei, T.; Ismail, S.; Kaabouch, N. Dynamic selection techniques for detecting GPS spoofing attacks on UAVs. Sensors 2022, 22, 662. [Google Scholar] [CrossRef]
- Wei, X.; Sun, C.; Lyu, M.; Song, Q.; Li, Y. ConstDet: Control Semantics-Based Detection for GPS Spoofing Attacks on UAVs. Remote Sens. 2022, 14, 5587. [Google Scholar] [CrossRef]
- Nayfeh, M.; Li, Y.; Al Shamaileh, K.; Devabhaktuni, V.; Kaabouch, N. Machine Learning Modeling of GPS Features with Applications to UAV Location Spoofing Detection and Classification. Comput. Secur. 2023, 126, 103085. [Google Scholar] [CrossRef]
- Feng, Z.; Guan, N.; Lv, M.; Liu, W.; Deng, Q.; Liu, X.; Yi, W. Efficient drone hijacking detection using two-step GA-XGBoost. J. Syst. Arch. 2020, 103, 101694. [Google Scholar] [CrossRef]
- Wang, S.; Wang, J.; Su, C.; Ma, X. Intelligent detection algorithm against uavs’ gps spoofing attack. In Proceedings of the 2020 IEEE 26th International Conference on Parallel and Distributed Systems (ICPADS), Hong Kong, China, 2–4 December 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar]
- Shafiee, E.; Mosavi, M.R.; Moazedi, M. Detection of spoofing attack using machine learning based on multi-layer neural network in single-frequency GPS receivers. J. Navig. 2018, 71, 169–188. [Google Scholar] [CrossRef]
- Jullian, O.; Otero, B.; Stojilović, M.; Costa, J.J.; Verdú, J.; Pajuelo, M.A. Deep Learning Detection of GPS Spoofing. In Proceedings of the Machine Learning, Optimization, and Data Science: 7th International Conference, LOD 2021, Grasmere, UK, 4–8 October 2021; Revised Selected Papers, Part. Springer: Cham, Switzerland, 2022. [Google Scholar]
- Dang, Y.; Benzaid, C.; Yang, B.; Taleb, T.; Shen, Y. Deep-Ensemble-Learning-Based GPS Spoofing Detection for Cellular-Connected UAVs. IEEE Internet Things J. 2022, 9, 25068–25085. [Google Scholar] [CrossRef]
- Sung, Y.-H.; Park, S.-J.; Kim, D.-Y.; Kim, S. GPS Spoofing Detection Method for Small UAVs Using 1D Convolution Neural Network. Sensors 2022, 22, 9412. [Google Scholar] [CrossRef]
- Wu, S.; Li, Y.; Wang, Z.; Tan, Z.; Pan, Q. A Highly Interpretable Framework for Generic Low-Cost UAV Attack Detection. IEEE Sens. J. 2023, 23, 7288–7300. [Google Scholar] [CrossRef]
- Kang, Q.; Shi, L.; Zhou, M.; Wang, X.; Wu, Q.; Wei, Z. A distance-based weighted undersampling scheme for support vector machines and its application to imbalanced classification. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 4152–4165. [Google Scholar] [CrossRef] [PubMed]
- Napierala, K.; Stefanowski, J. Types of minority class examples and their influence on learning classifiers from imbalanced data. J. Intell. Inf. Syst. 2016, 46, 563–597. [Google Scholar] [CrossRef]
- Kovács, G. An empirical comparison and evaluation of minority oversampling techniques on a large number of imbalanced datasets. Appl. Soft Comput. 2019, 83, 105662. [Google Scholar] [CrossRef]
- Tao, X.; Li, Q.; Ren, C.; Guo, W.; Li, C.; He, Q.; Liu, R.; Zou, J. Real-value negative selection over-sampling for imbalanced data set learning. Expert Syst. Appl. 2019, 129, 118–134. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Washington, DC, USA, 7–13 December 2015. [Google Scholar]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
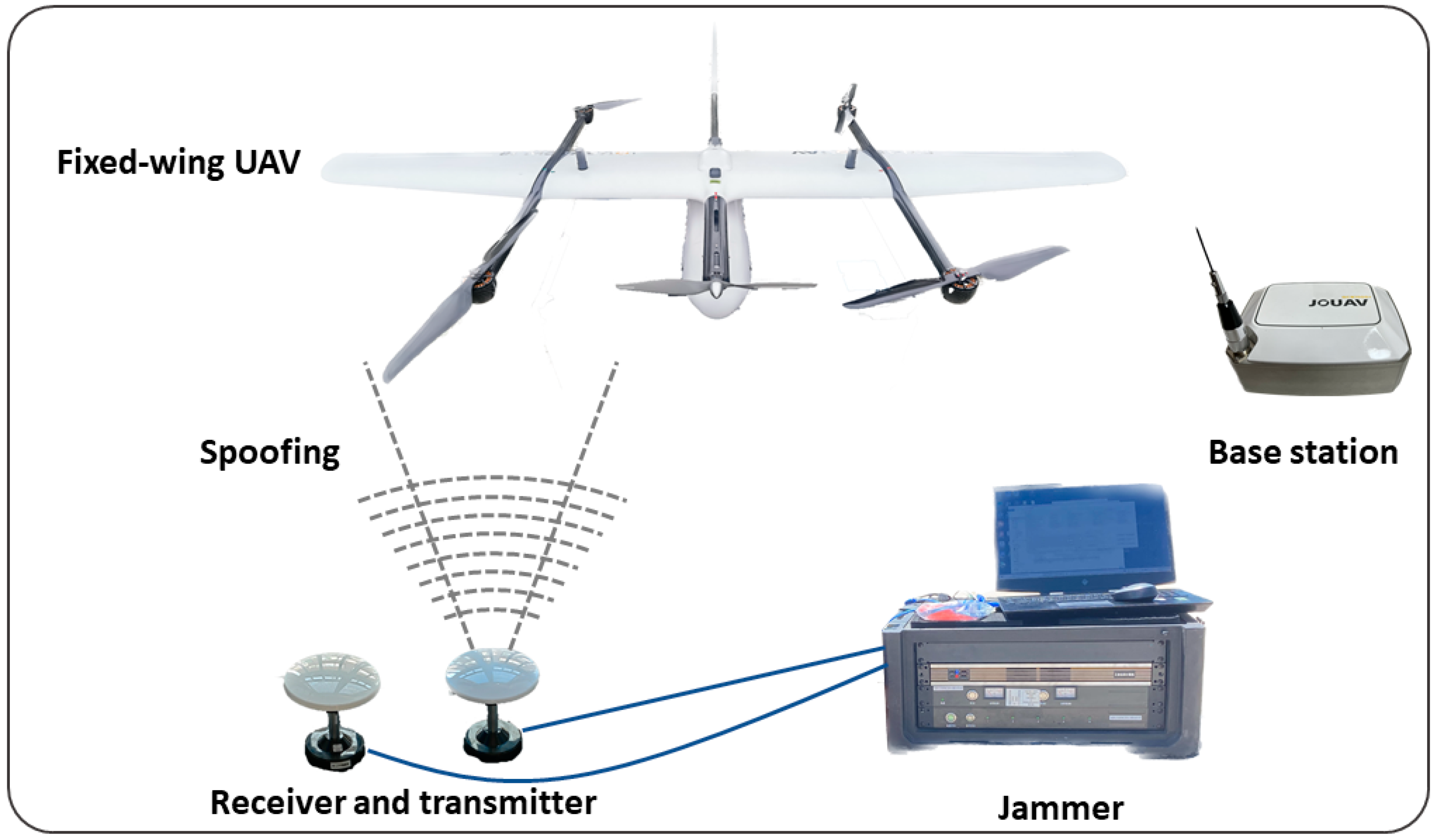















| Projects | Main Technical Indicators |
|---|---|
| Maximum takeoff weight | 12 kg |
| Optimal cruising airspeed | 20 m/s |
| Maximum airspeed | 30 m/s |
| Battery life | 90 min |
| Wind resistance | Level 5 |
| Takeoff and landing approach | Vertical takeoff and landing |
| Projects | Main Technical Indicators |
|---|---|
| Spoofing signal output frequency | GPS: L1 |
| Spoofing signal modulation mode | BPSK |
| Spoofing signal size | GPS: L1 16 channels |
| Spoofing signal power | ≤10 dBm |
| Range | 500 m |
| Machine power consumption | ≤80 W |
| Data | Weather Types | Temperature | Direction of Wind |
|---|---|---|---|
| 27 December 2021 | Sunny | −7 °C to 7 °C | South wind < Force 3 |
| 28 December 2021 | Sunny | −6 °C to 5 °C | Southwest wind < Force 3 |
| 29 December 2021 | Sunny | −13 °C to −5 °C | Northwest wind: Force 4–5 to 3–4 |
| 30 December 2021 | Sunny | −7 °C to 6 °C | Northwest wind: Force 3–4 to < 3 |
| Flight Mode | Time of Flight | With Spoofing |
|---|---|---|
| Rectilinear flight | 10:00:00 | NO |
| Rectilinear flight | 10:30:00 | YES |
| Rectilinear flight | 11:00:00 | YES |
| Rectilinear flight | 11:30:00 | YES |
| Rectilinear flight | 13:30:00 | YES |
| Arc flight | 14:30:00 | NO |
| Arc flight | 15:30:00 | YES |
| Arc flight | 16:30:00 | YES |
| No. | Name | Unit | No. | Name | Unit |
|---|---|---|---|---|---|
| 1 | GPS position accuracy | / | 19 | Northward ground velocity | m/s |
| 2 | GPS satellite count | / | 20 | Eastward ground velocity | m/s |
| 3 | GPS walk second | / | 21 | Downward ground velocity | m/s |
| 4 | GPS navigation solution status | / | 22 | Dynamic pressure | Pa |
| 5 | Avionics temperature | / | 23 | X magnetic field strength | milligauss |
| 6 | Latitude | deg | 24 | Y magnetic field strength | milligauss |
| 7 | Longitude | deg | 25 | Z magnetic field strength | milligauss |
| 8 | Height | meter | 26 | Compass | / |
| 9 | Airspeed command | / | 27 | Port aileron command | / |
| 10 | Euler angle of roll | deg | 28 | Elevator command | / |
| 11 | Euler angle of pitch | deg | 29 | Rudder command | / |
| 12 | Euler angle of yaw | deg | 30 | Longitudinal control command | / |
| 13 | X-axis acceleration | m/s2 | 31 | X-axis acceleration deviation | m/s2 |
| 14 | Y-axis acceleration | m/s2 | 32 | Y-axis acceleration deviation | m/s2 |
| 15 | Z-axis acceleration | m/s2 | 33 | Z-axis acceleration deviation | m/s2 |
| 16 | X angular velocity | deg/s | 34 | Pressure–height | / |
| 17 | Y angular velocity | deg/s | 35 | South wind | m/s |
| 18 | Z angular velocity | deg/s | 36 | West wind | m/s |
| Proposed Model | Value | |
|---|---|---|
| Convolution | Filters | 8 |
| Kernel_size | 1 | |
| Activation function | PReLU | |
| Maxpooling | Pool_size | 1 |
| Activation function | PReLU | |
| LSTM | Hidden nodes | 50 |
| Activation function | Tanh | |
| TimeDistributed | Dense | 64 |
| Activation function | PReLU | |
| Output | — | 2 |
| Confusion Matrix | Predicted Label | ||
|---|---|---|---|
| Negative | Positive | ||
| True label | Negative | TN | FN |
| Positive | FP | TP | |
| Accuracy | Precision | Recall | F1_Score | |
|---|---|---|---|---|
| 1 | 0.9987 | 1 | 0.9889 | 0.9944 |
| 2 | 0.9935 | 1 | 0.939 | 0.9686 |
| 3 | 0.9948 | 0.974 | 0.974 | 0.974 |
| 4 | 0.9961 | 0.9863 | 0.973 | 0.9796 |
| 5 | 0.9974 | 1 | 0.9661 | 0.9828 |
| 6 | 0.9922 | 0.9659 | 0.9659 | 0.9659 |
| 7 | 0.9896 | 0.9306 | 0.9571 | 0.9437 |
| 8 | 0.9896 | 0.9659 | 0.9444 | 0.9551 |
| 9 | 0.9961 | 0.9756 | 0.9877 | 0.9816 |
| 10 | 0.9948 | 1 | 0.9535 | 0.9762 |
| Means | 0.9943 | 0.9798 | 0.965 | 0.9722 |
| Model | Hyperparameter | ||
|---|---|---|---|
| PCA-Decision Tree | Max_depth = 5 | min_samples_leaf = 5 | |
| Max_leaf_node = 30 | Criterion = entropy | ||
| PCA-KNN | N-neighbor = 9 | P = 5 | Weights = Uniform |
| PCA-LR | C = 10 | Penalty: L2 | |
| PCA-NB | / | ||
| PCA-SVM | C = 10 | Kernel = rbf | Gamma = 0.01 |
| PCA-Random Forest | C = 10 | Kernel = rbf | Gamma = 0.01 |
| PCA-AdaBoost | Criterion = entropy | Learning_rate = 0.001 | N_estimators = 50 |
| Max_leaf_nodes = 25 | Max_depth = 20 | ||
| PCA-GBDT | Learning_rate = 0.05 | Max_depth = 10 | min_samples_leaf =70 |
| Min_sample_split = 100 | N_estimators = 50 | Subsample = 0.75 | |
| PCA-LightGBM | Learning_rate = 0.005 | Max_depth = 5 | min_samples_leaf = 60 |
| Min_sample_split = 300 | N_estimators = 800 | Subsample = 0.6 | |
| PCA-XGBoost | Max_depth = 5 | Min_child_weight = 5 | Min_sample_split = 100 |
| N_estimators = 200 | Subsample = 0.85 | Reg_alpha = 0 | |
| Learning_rate = 0.025 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Yu, M.; Wang, L.; Li, T.; Dong, M. A Deep-Learning-Based GPS Signal Spoofing Detection Method for Small UAVs. Drones 2023, 7, 370. https://doi.org/10.3390/drones7060370
Sun Y, Yu M, Wang L, Li T, Dong M. A Deep-Learning-Based GPS Signal Spoofing Detection Method for Small UAVs. Drones. 2023; 7(6):370. https://doi.org/10.3390/drones7060370
Chicago/Turabian StyleSun, Yichen, Mingxin Yu, Luyang Wang, Tianfang Li, and Mingli Dong. 2023. "A Deep-Learning-Based GPS Signal Spoofing Detection Method for Small UAVs" Drones 7, no. 6: 370. https://doi.org/10.3390/drones7060370
APA StyleSun, Y., Yu, M., Wang, L., Li, T., & Dong, M. (2023). A Deep-Learning-Based GPS Signal Spoofing Detection Method for Small UAVs. Drones, 7(6), 370. https://doi.org/10.3390/drones7060370






