Hysteresis Modeling and Compensation for a Fast Piezo-Driven Scanner in the UAV Image Stabilization System
Abstract
1. Introduction
2. Hysteresis Modeling of an FPDS
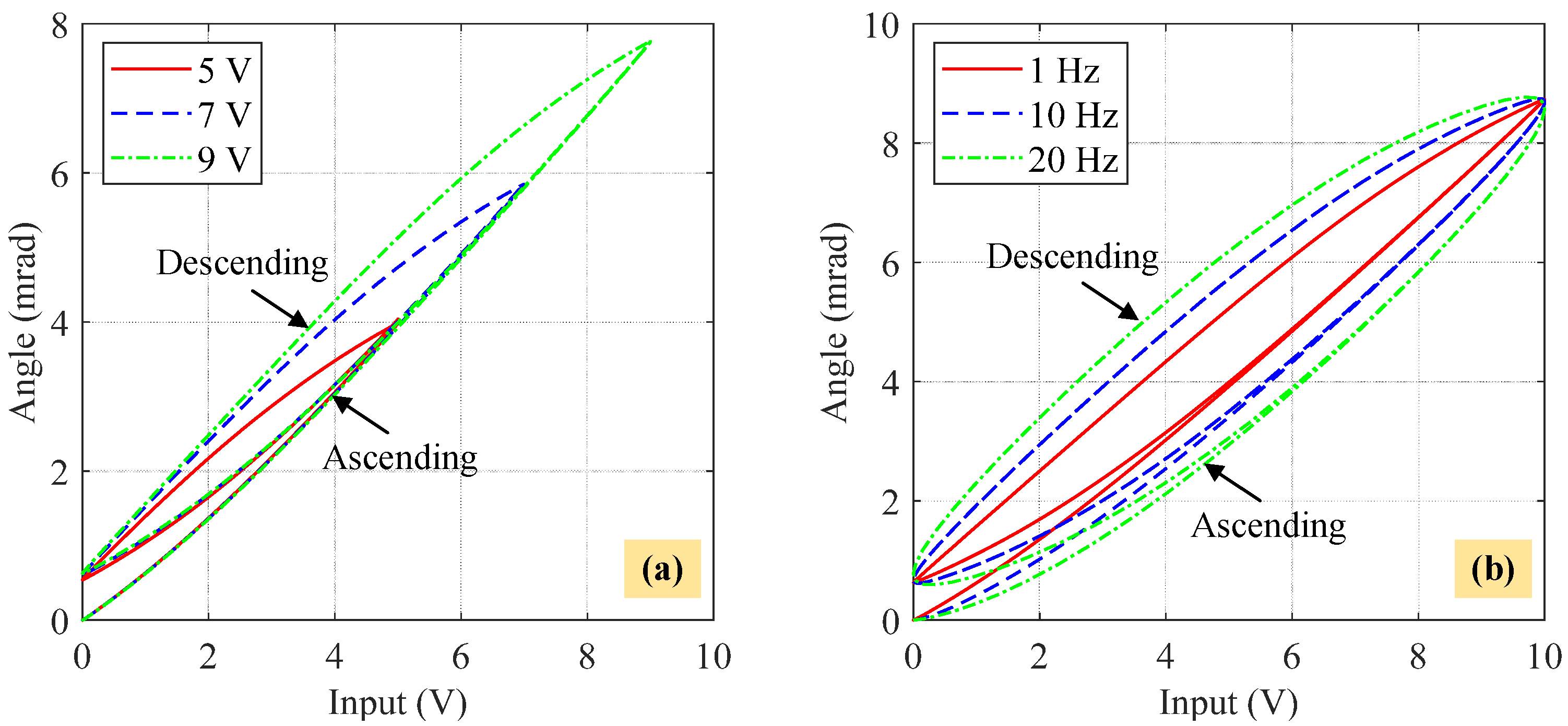
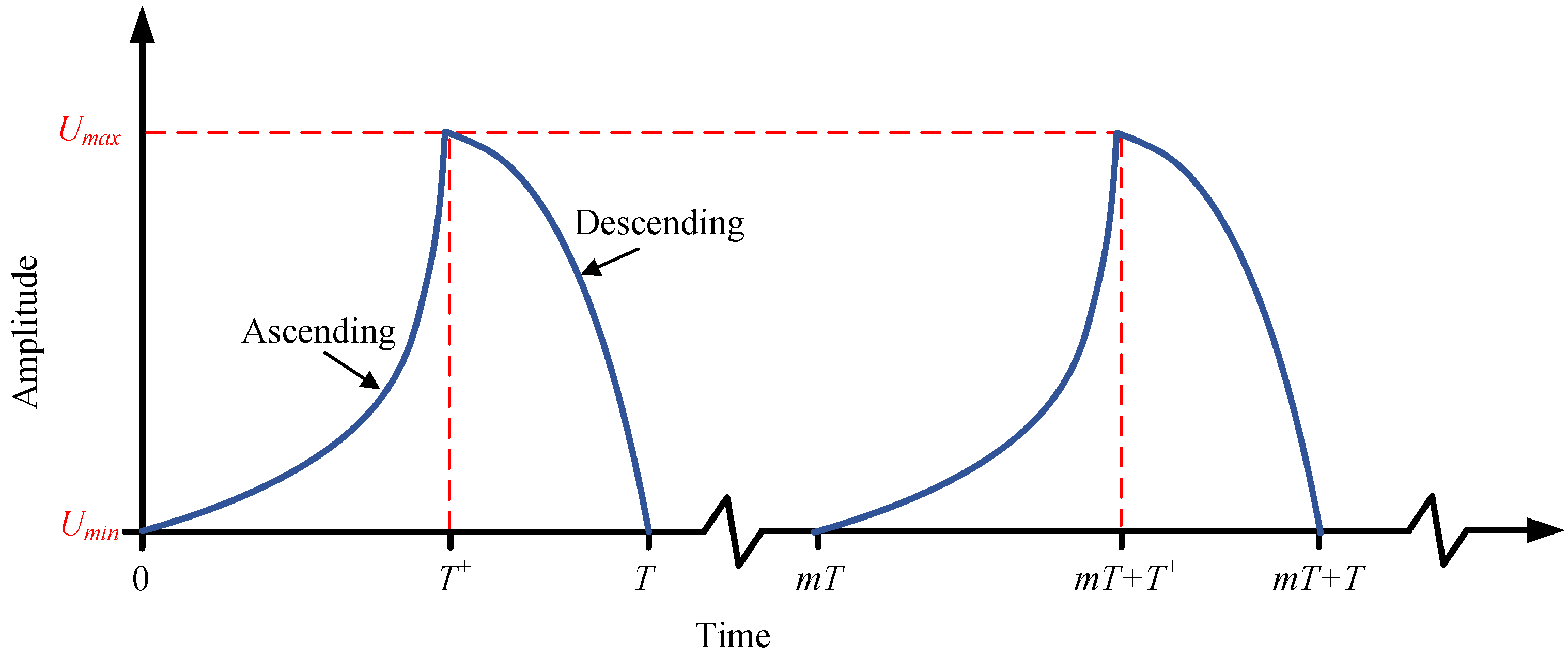
2.1. Hysteresis Characterization
2.2. The CBW Model
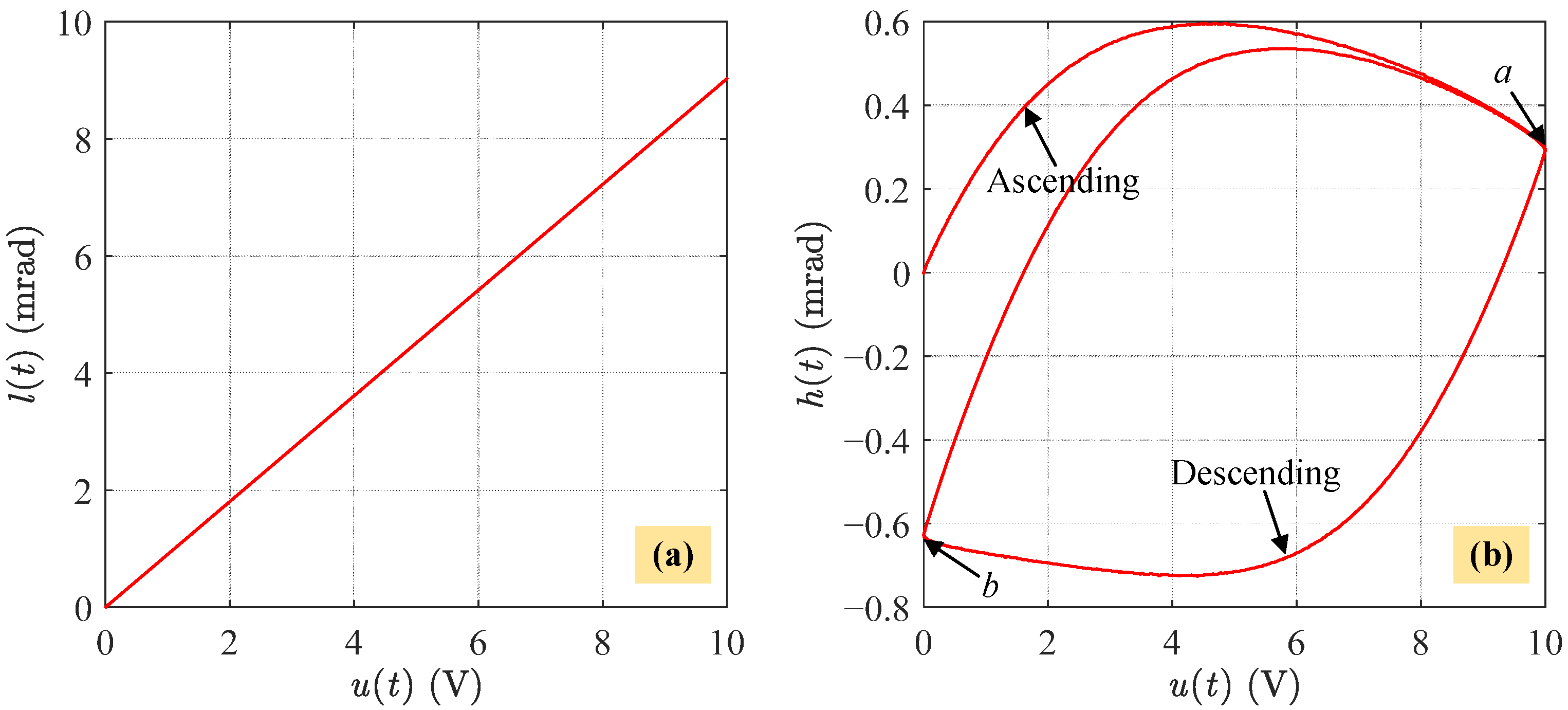
2.3. Proposed MBW Model
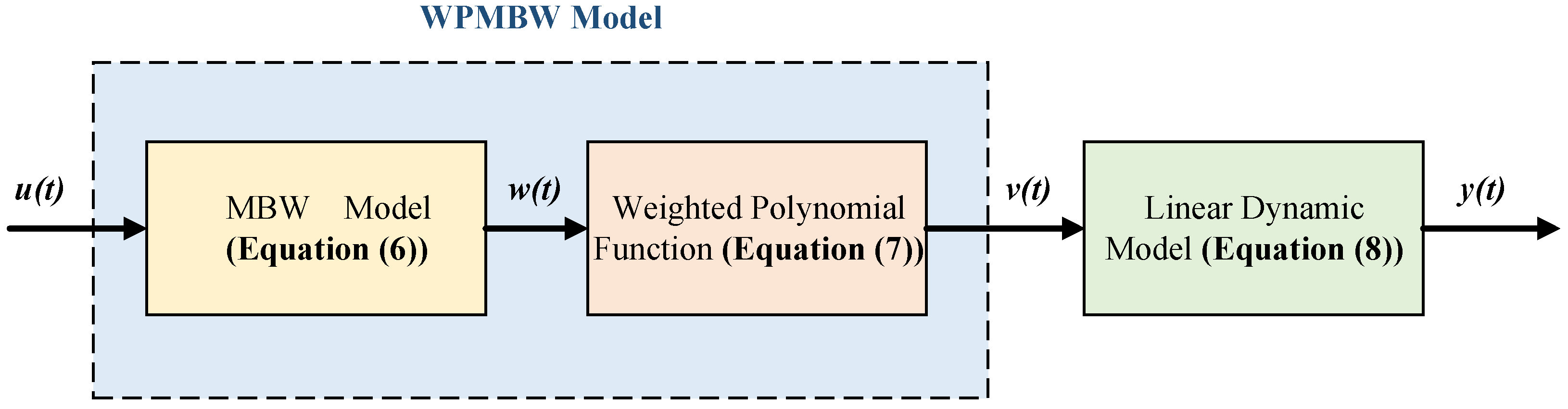
2.4. Proposed WPMBW Model Cascaded with a Linear Dynamic Model
3. Characteristics of the WPMBW Model
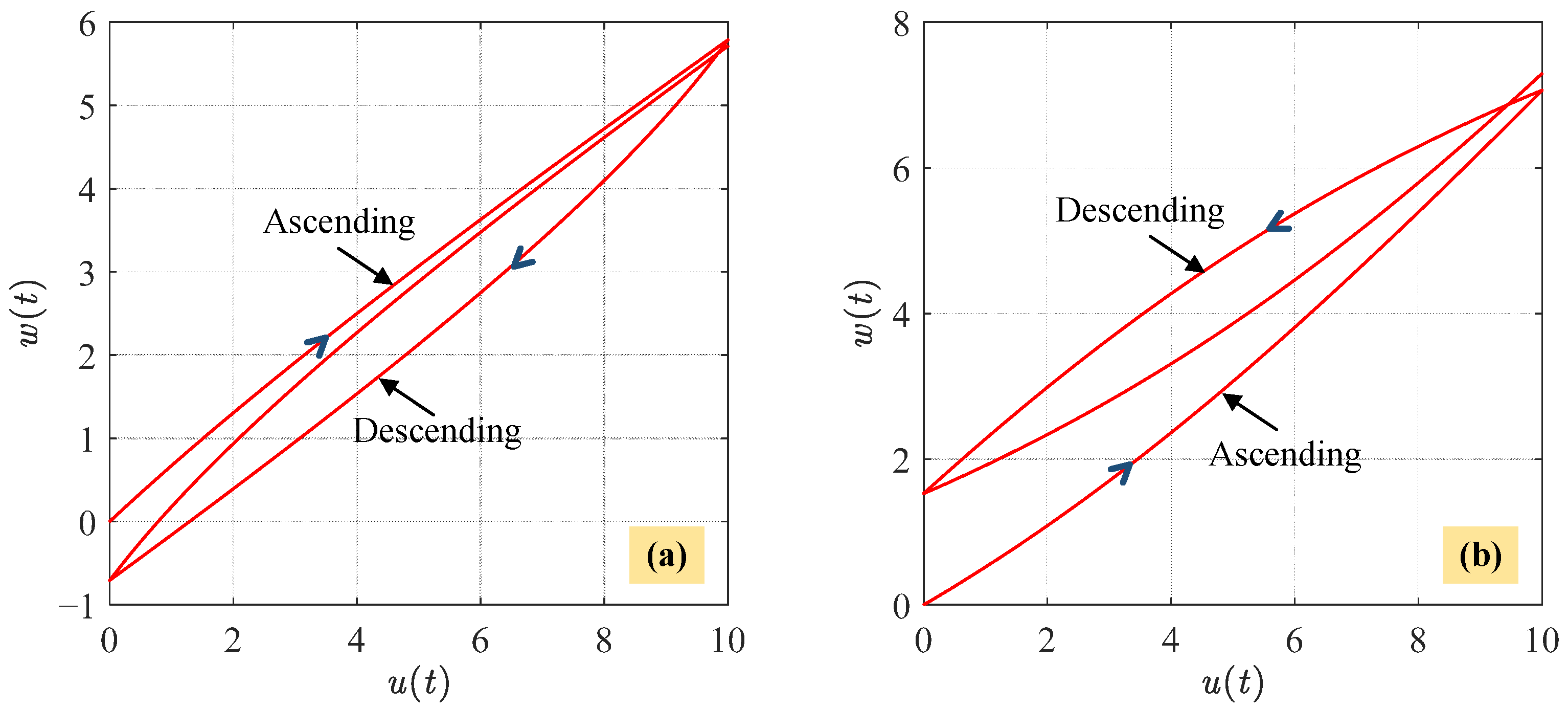
3.1. Counterclockwise Characteristics
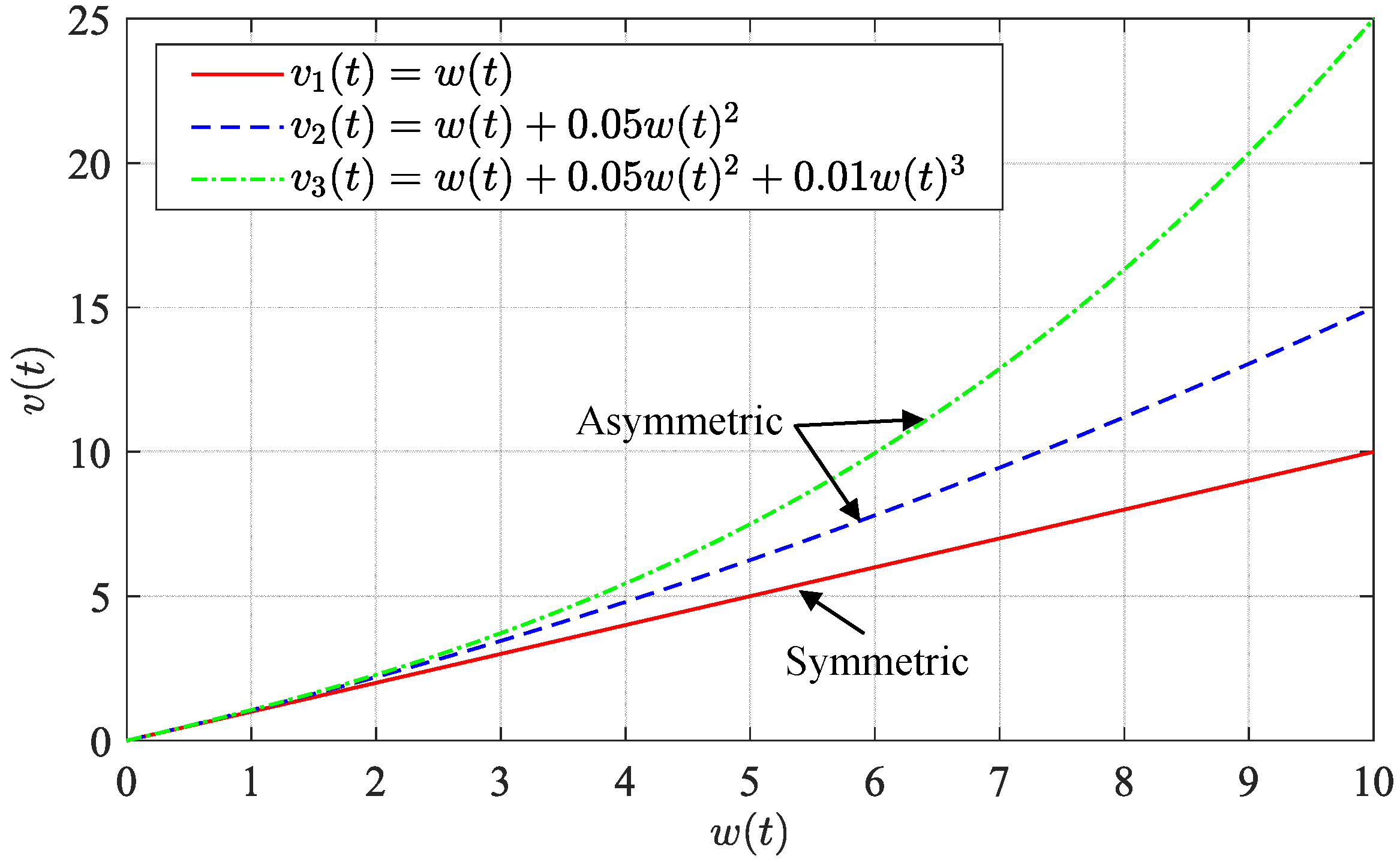
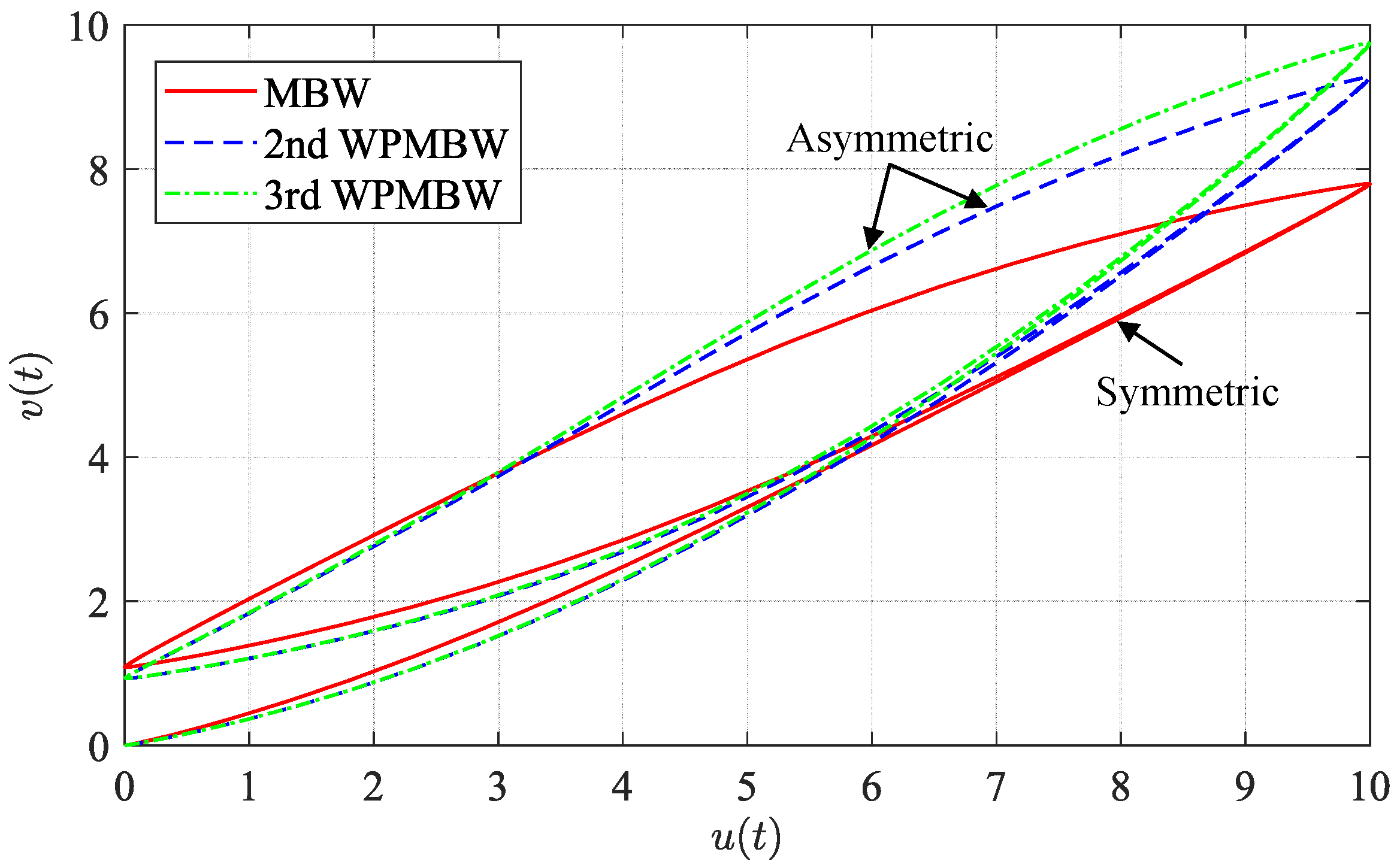
3.2. Asymmetric Characteristics
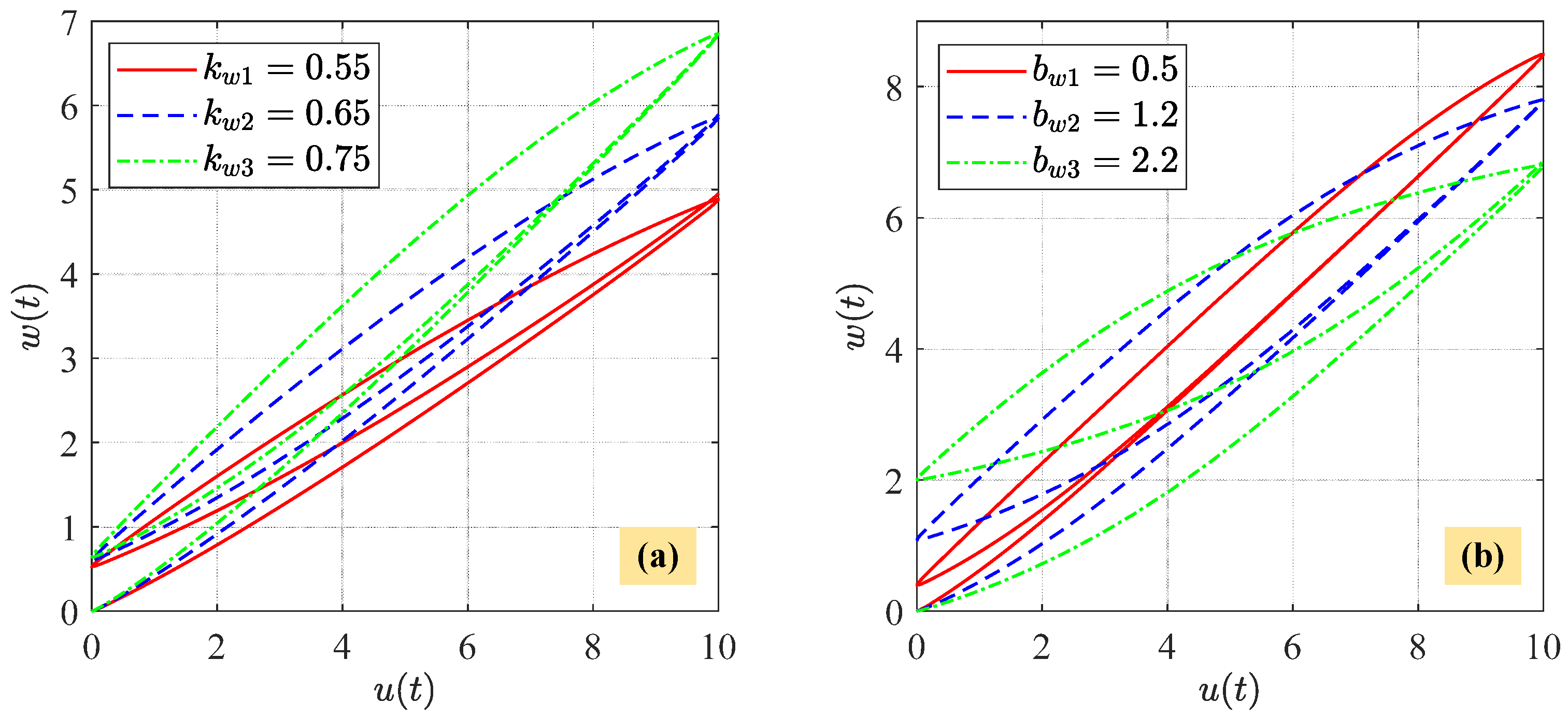
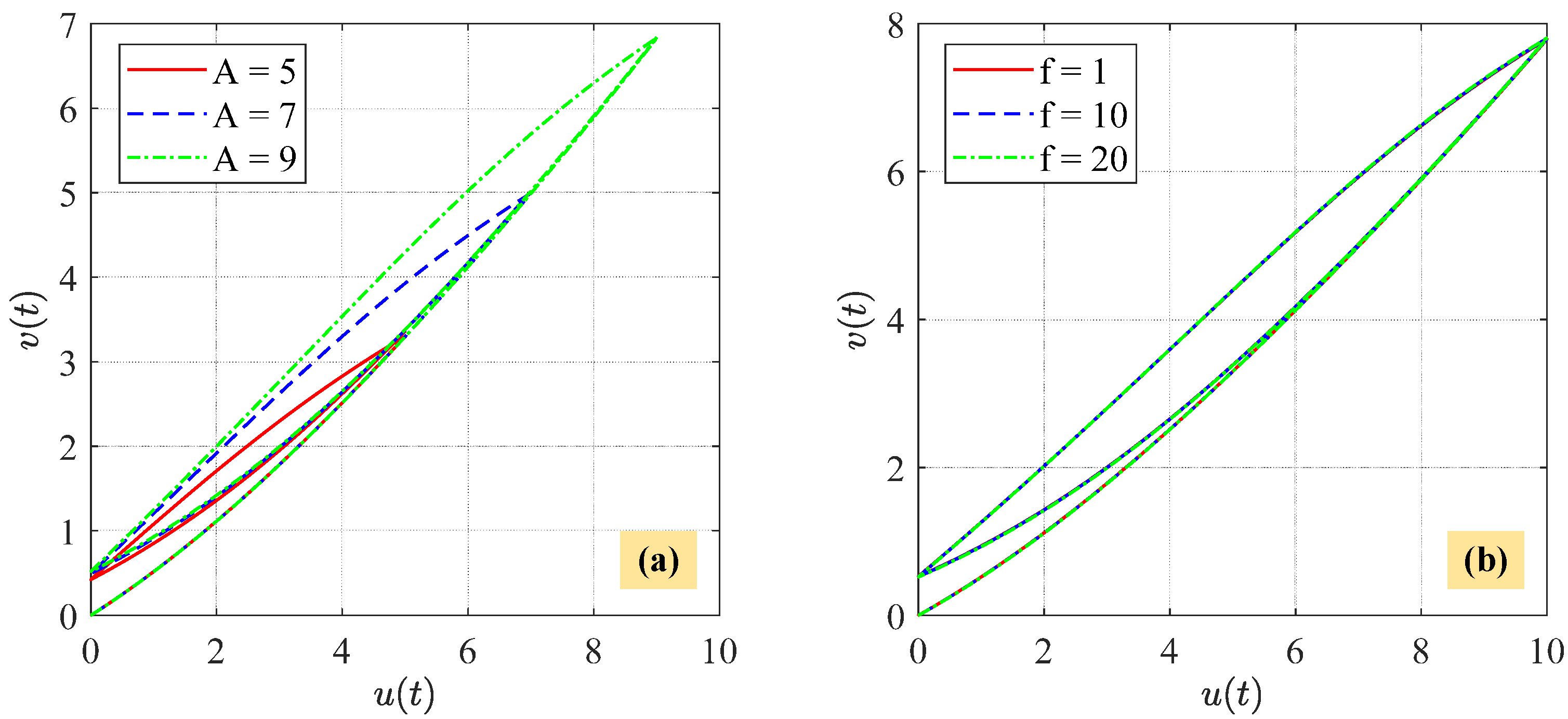
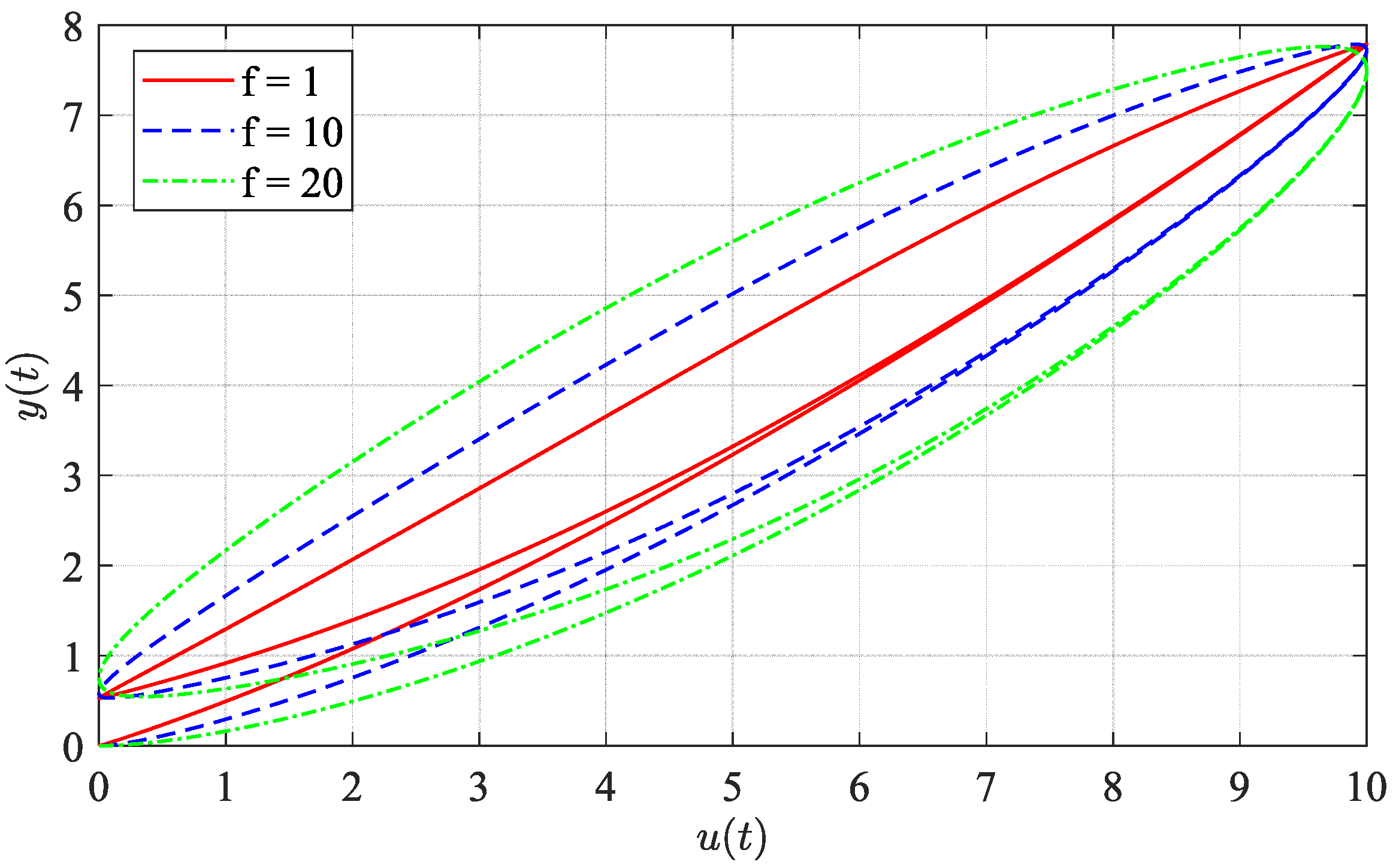
3.3. Amplitude-Dependent and Rate-Dependent Characteristics
3.4. Inverse WPMBW Model
4. Hysteresis Identification, Verification, and Compensation
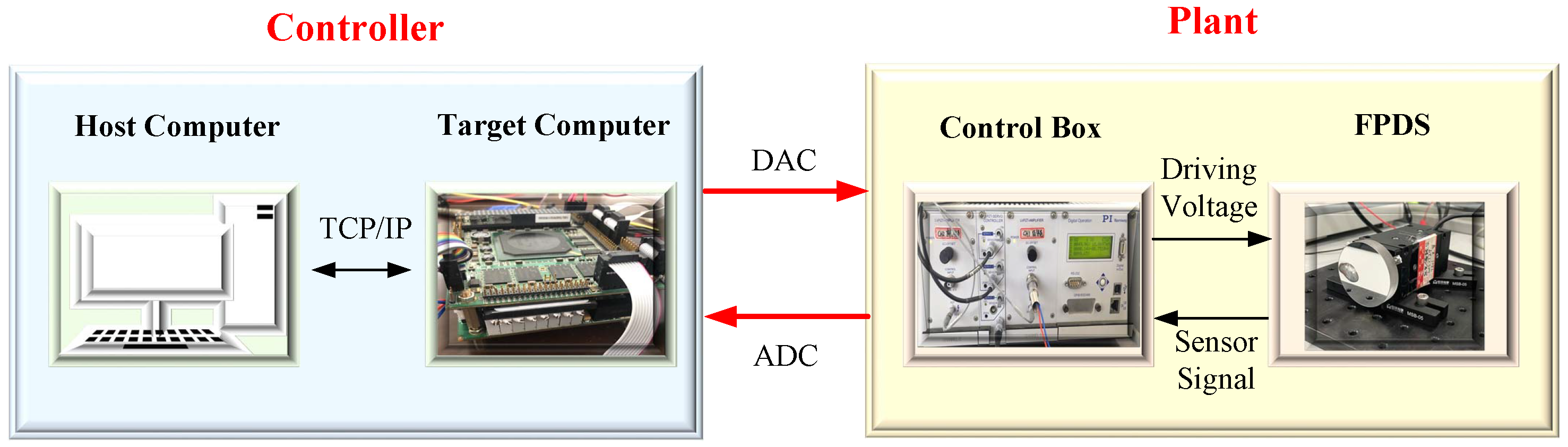
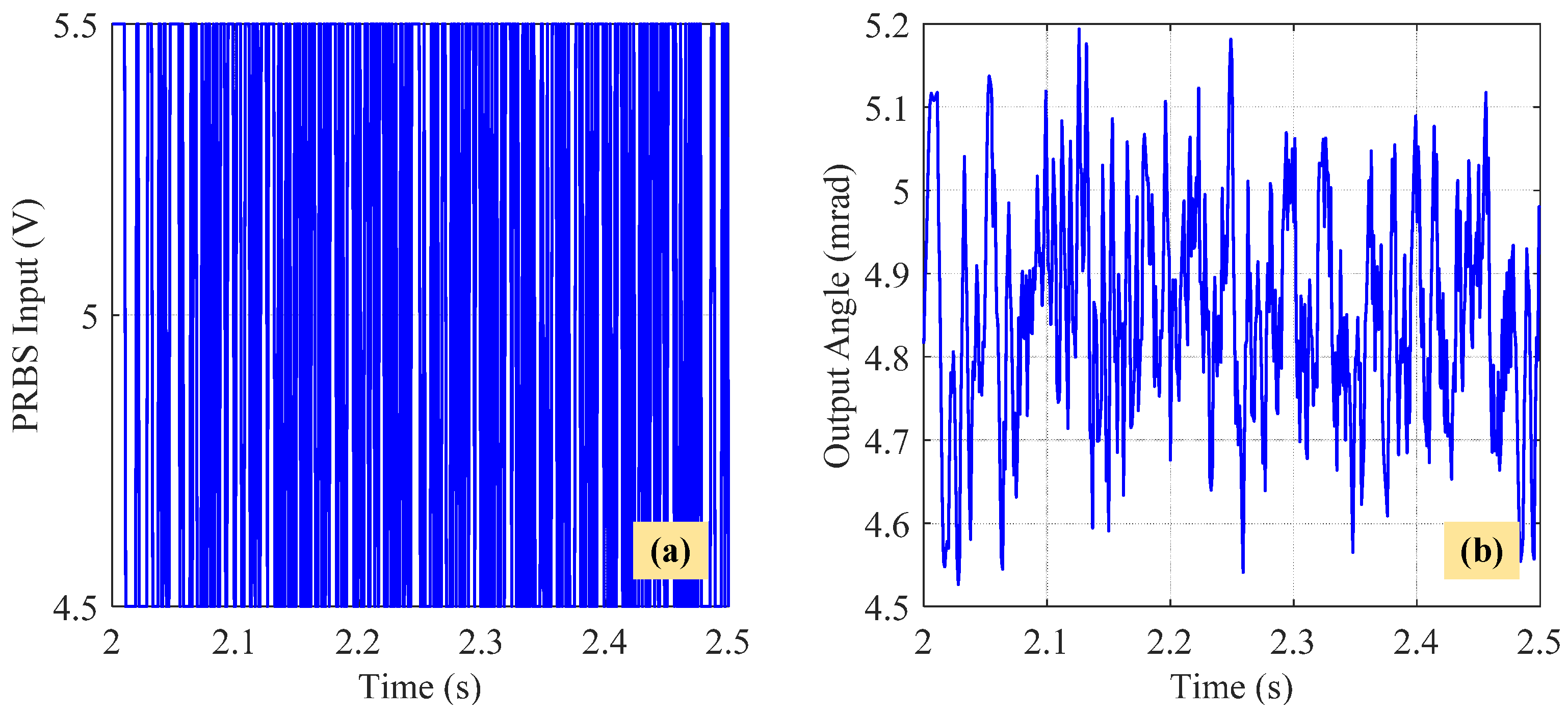
4.1. Experimental Setup
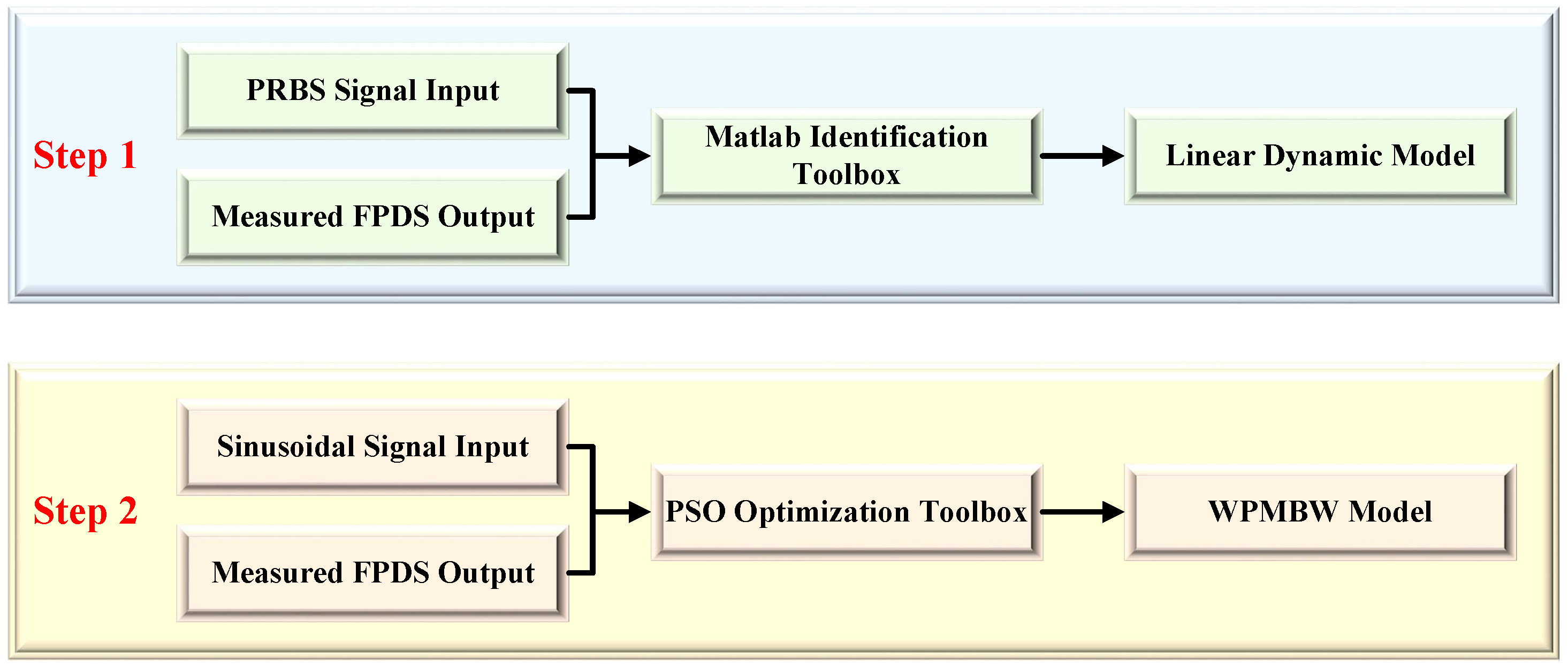
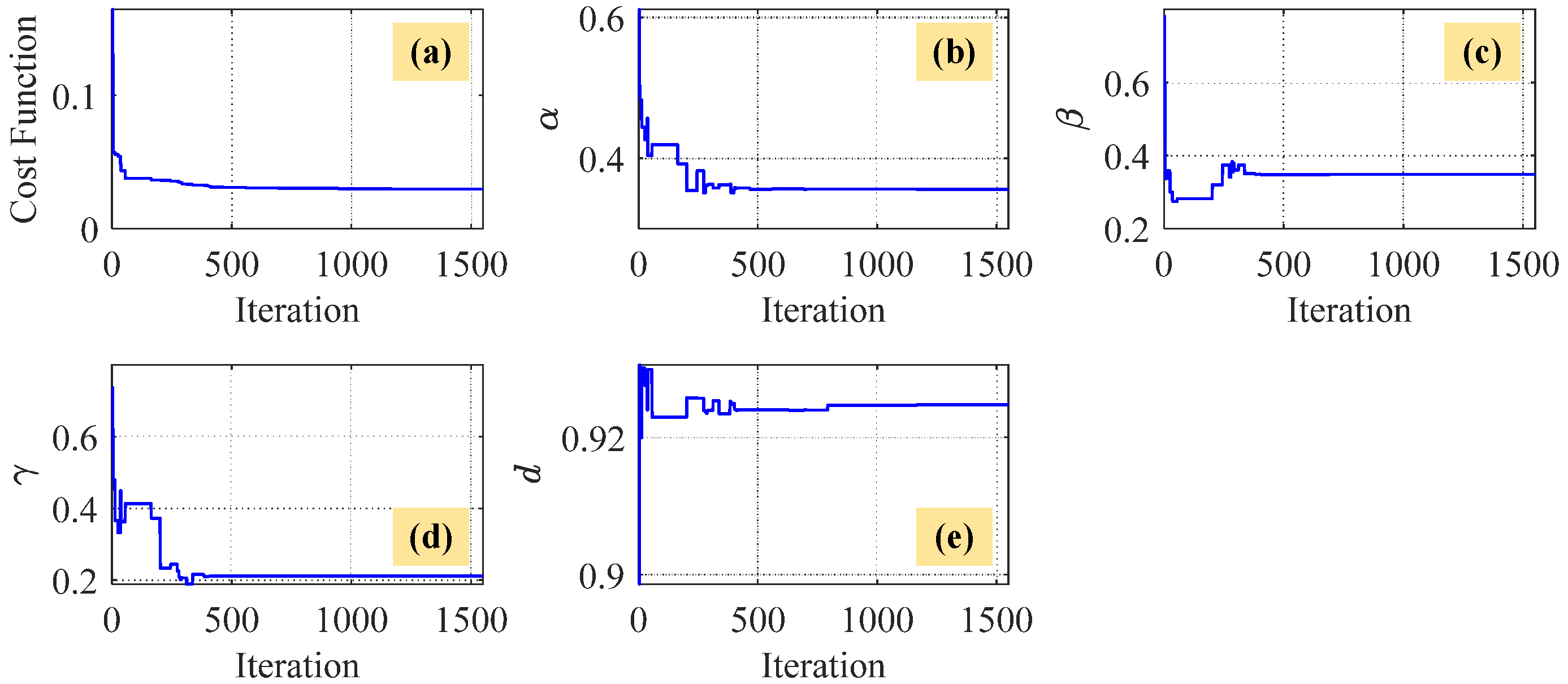
4.2. Parameter Identification
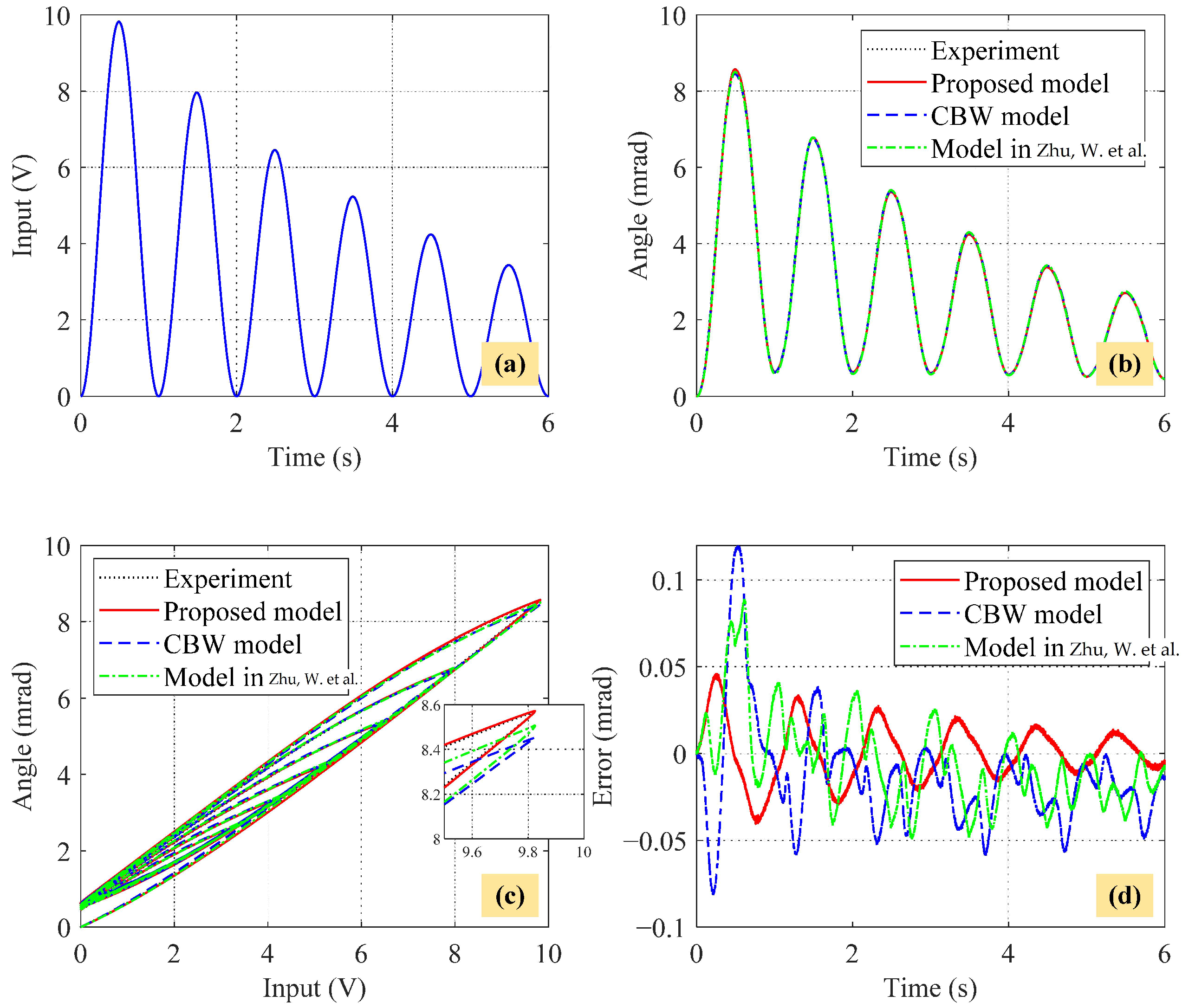
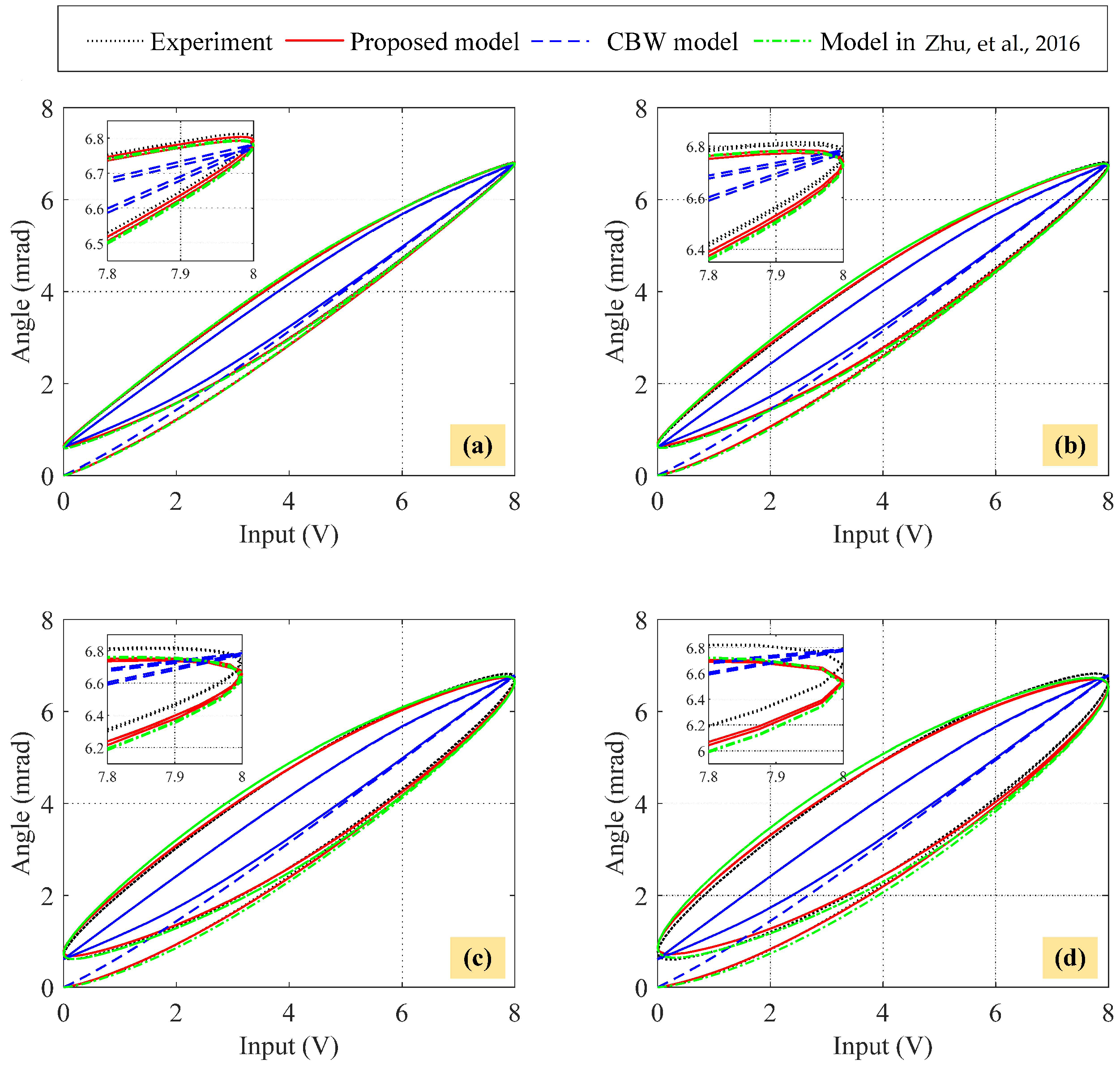
4.3. Model Verification
- (1)
- (2)
- The traditional asymmetric BW model is introduced here as follows:where m, b, and k represent the mass, damping, and stiffness coefficients of the FPDS, respectively; denotes the piezoelectric coefficient; and parameters , , , and are used to regulate the shape of hysteresis loops. In particular, the term accounts for the asymmetric feature of hysteresis loops. It should be mentioned that the original term in [36] has been replaced by since the piezoelectric coefficient is a constant [53]. Similar to the identification procedure of the CBW model, the parameters of the traditional asymmetric BW model are acquired as follows: , , , , , , , , and , as shown in Figure 19.
4.4. Hysteresis Compensation
4.5. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bollas, N.; Kokinou, E.; Polychronos, V. Comparison of sentinel-2 and UAV multispectral data for use in precision agriculture: An application from northern Greece. Drones 2021, 5, 35. [Google Scholar] [CrossRef]
- Zeng, Y.; Xu, J.; Zhang, R. Energy minimization for wireless communication with rotary-wing UAV. IEEE Trans. Wirel. Commun. 2019, 18, 2329–2345. [Google Scholar] [CrossRef]
- Shahmoradi, J.; Talebi, E.; Roghanchi, P.; Hassanalian, M. A comprehensive review of applications of drone technology in the mining industry. Drones 2020, 4, 34. [Google Scholar] [CrossRef]
- Masroor, R.; Naeem, M.; Ejaz, W. Efficient deployment of UAVs for disaster management: A multi-criterion optimization approach. Comput. Commun. 2021, 177, 185–194. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Khan, M.A.; Noor, F.; Ullah, I.; Alsharif, M.H. Towards the unmanned aerial vehicles (UAVs): A comprehensive review. Drones 2022, 6, 147. [Google Scholar] [CrossRef]
- Stuckel, K.J.; Semke, W.H.; Baer, N.; Schultz, R.R. A high frequency stabilization system for UAS imaging payloads. In Structural Dynamics, Proceedings of the 28th IMAC, A Conference on Structural Dynamics, Jacksonville, FL, USA, 1–4 February 2010; Springer: New York, NY, USA, 2011; Volume 3, pp. 1411–1419. [Google Scholar]
- Oshiki, M.; Fukada, E. Inverse piezoelectric effect and electrostrictive effect in polarized poly (vinylidene fluoride) films. J. Mater. Sci. 1975, 10, 1–6. [Google Scholar] [CrossRef]
- Louis, A.; Valérie, P.B.; Joël, B.G. Comparison of control strategies for hysteresis attenuation in electromechanical actuators subject to dispersion. Control. Eng. Pract. 2023, 130, 105348. [Google Scholar] [CrossRef]
- Saikumar, N.; Sinha, R.K.; HosseinNia, S.H. Resetting disturbance observers with application in compensation of bounded nonlinearities like hysteresis in piezo-actuators. Control. Eng. Pract. 2019, 82, 36–49. [Google Scholar] [CrossRef]
- Xu, Q.; Li, Y. Micro-/nanopositioning using model predictive output integral discrete sliding mode control. IEEE Trans. Ind. Electron. 2011, 59, 1161–1170. [Google Scholar] [CrossRef]
- Ahmed, S.; Wang, H.; Tian, Y. Adaptive high-order terminal sliding mode control based on time delay estimation for the robotic manipulators with backlash hysteresis. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 1128–1137. [Google Scholar] [CrossRef]
- Chen, X.; Feng, Y.; Su, C.Y. Adaptive control for continuous-time systems with actuator and sensor hysteresis. Automatica 2016, 64, 196–207. [Google Scholar] [CrossRef]
- Nie, L.; Luo, Y.; Gao, W.; Zhou, M. Rate-dependent asymmetric hysteresis modeling and robust adaptive trajectory tracking for piezoelectric micropositioning stages. Nonlinear Dyn. 2022, 108, 2023–2043. [Google Scholar] [CrossRef]
- Wang, C.H.; Huang, D.Y. A new intelligent fuzzy controller for nonlinear hysteretic electronic throttle in modern intelligent automobiles. IEEE Trans. Ind. Electron. 2012, 60, 2332–2345. [Google Scholar] [CrossRef]
- Wang, F.; Liu, Z.; Zhang, Y.; Chen, C.P. Adaptive fuzzy control for a class of stochastic pure-feedback nonlinear systems with unknown hysteresis. IEEE Trans. Fuzzy Syst. 2015, 24, 140–152. [Google Scholar] [CrossRef]
- Xu, Y.; Li, X.; Yang, X.; Yang, Z.; Wu, L.; Chen, Q. A two-stage model for rate-dependent inverse hysteresis in reluctance actuators. Mech. Syst. Signal Process. 2020, 135, 106427. [Google Scholar] [CrossRef]
- Qin, Y.; Duan, H.; Han, J. Direct inverse hysteresis compensation of piezoelectric actuators using adaptive Kalman filter. IEEE Trans. Ind. Electron. 2021, 69, 9385–9395. [Google Scholar] [CrossRef]
- Zhou, D.; Kamlah, M.; Munz, D. Rate dependence of soft PZT ceramics under electric field loading. In Proceedings of the Smart Structures and Materials 2001: Active Materials: Behavior and Mechanics, Newport Beach, CA, USA, 5–8 March 2001; Volume 4333, pp. 64–70. [Google Scholar]
- Delibas, B.; Arockiarajan, A.; Seemann, W. Rate dependent properties of perovskite type tetragonal piezoelectric materials using micromechanical model. Int. J. Solids Struct. 2006, 43, 697–712. [Google Scholar] [CrossRef]
- Arockiarajan, A.; Menzel, A.; Delibas, B.; Seemann, W. Computational modeling of rate-dependent domain switching in piezoelectric materials. Eur. J. Mech.-A/Solids 2006, 25, 950–964. [Google Scholar] [CrossRef]
- Arockiarajan, A.; Delibas, B.; Menzel, A.; Seemann, W. Studies on rate-dependent switching effects of piezoelectric materials using a finite element model. Comput. Mater. Sci. 2006, 37, 306–317. [Google Scholar] [CrossRef]
- Tao, Y.D.; Li, H.X.; Zhu, L.M. Rate-dependent hysteresis modeling and compensation of piezoelectric actuators using Gaussian process. Sensors Actuators A Phys. 2019, 295, 357–365. [Google Scholar] [CrossRef]
- Hassani, V.; Tjahjowidodo, T.; Do, T.N. A survey on hysteresis modeling, identification and control. Mech. Syst. Signal Process. 2014, 49, 209–233. [Google Scholar] [CrossRef]
- Ge, P.; Jouaneh, M. Generalized Preisach model for hysteresis nonlinearity of piezoceramic actuators. Precis. Eng. 1997, 20, 99–111. [Google Scholar] [CrossRef]
- Al Janaideh, M.; Rakheja, S.; Su, C.Y. An analytical generalized Prandtl–Ishlinskii model inversion for hysteresis compensation in micropositioning control. IEEE/ASME Trans. Mechatron. 2010, 16, 734–744. [Google Scholar] [CrossRef]
- Xu, R.; Zhou, M. Elman neural network-based identification of Krasnosel’skii-Pokrovskii model for magnetic shape memory alloys actuator. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar]
- Ikhouane, F. A survey of the hysteretic duhem model. Arch. Comput. Methods Eng. 2018, 25, 965–1002. [Google Scholar] [CrossRef]
- Su, C.Y.; Stepanenko, Y.; Svoboda, J.; Leung, T.P. Robust adaptive control of a class of nonlinear systems with unknown backlash-like hysteresis. IEEE Trans. Autom. Control 2000, 45, 2427–2432. [Google Scholar] [CrossRef]
- Rakotondrabe, M. Bouc-Wen modeling and inverse multiplicative structure to compensate hysteresis nonlinearity in piezoelectric actuators. IEEE Trans. Autom. Sci. Eng. 2010, 8, 428–431. [Google Scholar] [CrossRef]
- Mao, X.; Wang, Y.; Liu, X.; Guo, Y. A hybrid feedforward-feedback hysteresis compensator in piezoelectric actuators based on least-squares support vector machine. IEEE Trans. Ind. Electron. 2017, 65, 5704–5711. [Google Scholar] [CrossRef]
- Chen, G.; Lou, Y. Recurrent-neural-network-based rate-dependent hysteresis modeling and feedforward torque control of the magnetorheological clutch. IEEE/ASME Trans. Mechatron. 2021, 27, 2875–2886. [Google Scholar] [CrossRef]
- Ismail, M.; Ikhouane, F.; Rodellar, J. The hysteresis Bouc-Wen model, a survey. Arch. Comput. Methods Eng. 2009, 16, 161–188. [Google Scholar] [CrossRef]
- Li, C.X.; Li, L.L.; Gu, G.Y.; Zhu, L.M. Modeling of rate-dependent hysteresis in piezoelectric actuators using a Hammerstein-like structure with a modified Bouc-Wen model. In Proceedings of the Intelligent Robotics and Applications: 9th International Conference, ICIRA 2016, Tokyo, Japan, 22–24 August 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 672–684. [Google Scholar]
- Zhu, W.; Wang, D.h. Non-symmetrical Bouc–Wen model for piezoelectric ceramic actuators. Sensors Actuators A Phys. 2012, 181, 51–60. [Google Scholar] [CrossRef]
- Wang, G.; Chen, G.; Bai, F. Modeling and identification of asymmetric Bouc–Wen hysteresis for piezoelectric actuator via a novel differential evolution algorithm. Sensors Actuators A Phys. 2015, 235, 105–118. [Google Scholar] [CrossRef]
- Zhu, W.; Rui, X.T. Hysteresis modeling and displacement control of piezoelectric actuators with the frequency-dependent behavior using a generalized Bouc–Wen model. Precis. Eng. 2016, 43, 299–307. [Google Scholar] [CrossRef]
- Kang, S.; Wu, H.; Li, Y.; Yang, X.; Yao, J. A fractional-order normalized Bouc–Wen model for piezoelectric hysteresis nonlinearity. IEEE/ASME Trans. Mechatron. 2021, 27, 126–136. [Google Scholar] [CrossRef]
- Gu, G.Y.; Li, C.X.; Zhu, L.M.; Su, C.Y. Modeling and identification of piezoelectric-actuated stages cascading hysteresis nonlinearity with linear dynamics. IEEE/ASME Trans. Mechatron. 2015, 21, 1792–1797. [Google Scholar] [CrossRef]
- Zhang, H.T.; Hu, B.; Li, L.; Chen, Z.; Wu, D.; Xu, B.; Huang, X.; Gu, G.; Yuan, Y. Distributed Hammerstein modeling for cross-coupling effect of multiaxis piezoelectric micropositioning stages. IEEE/ASME Trans. Mechatron. 2018, 23, 2794–2804. [Google Scholar] [CrossRef]
- Wen, Z.; Ding, Y.; Liu, P.; Ding, H. An efficient identification method for dynamic systems with coupled hysteresis and linear dynamics: Application to piezoelectric-actuated nanopositioning stages. IEEE/ASME Trans. Mechatron. 2019, 24, 326–337. [Google Scholar] [CrossRef]
- Li, Z.; Shan, J.; Gabbert, U. A direct inverse model for hysteresis compensation. IEEE Trans. Ind. Electron. 2020, 68, 4173–4181. [Google Scholar] [CrossRef]
- Bai, E.W. Decoupling the linear and nonlinear parts in Hammerstein model identification. Automatica 2004, 40, 671–676. [Google Scholar] [CrossRef]
- Birge, B. PSOt-a particle swarm optimization toolbox for use with Matlab. In Proceedings of the 2003 IEEE Swarm Intelligence Symposium, SIS’03 (Cat. No. 03EX706), Indianapolis, IN, USA, 26 April 2003; pp. 182–186. [Google Scholar]
- Verma, M.; Lafarga, V.; Baron, M.; Collette, C. Active stabilization of unmanned aerial vehicle imaging platform. J. Vib. Control 2020, 26, 1791–1803. [Google Scholar] [CrossRef]
- Ikhouane, F.; Rodellar, J. On the hysteretic Bouc-Wen model. Nonlinear Dyn. 2005, 42, 63–78. [Google Scholar] [CrossRef]
- Ikhouane, F.; Mañosa, V.; Rodellar, J. Dynamic properties of the hysteretic Bouc-Wen model. Syst. Control Lett. 2007, 56, 197–205. [Google Scholar] [CrossRef]
- Yi, S.; Zhang, Q.; Xu, L.; Wang, T.; Li, L. Experimental characterization and modular modeling of hystereses for smart material actuators. Smart Mater. Struct. 2021, 30, 125025. [Google Scholar] [CrossRef]
- Ikhouane, F.; Rodellar, J. On the Hysteretic Bouc-Wen Model, Part II: Robust Parametric Identification. Nonlinear Dyn. 2005, 42, 79–95. [Google Scholar] [CrossRef]
- Nie, Z.Y.; Liu, R.J.; Wang, Q.G.; Guo, D.S.; Ma, Y.J.; Lan, Y.H. Novel identification approach for nonlinear systems with hysteresis. Nonlinear Dyn. 2019, 95, 1053–1066. [Google Scholar] [CrossRef]
- Giri, F.; Rochdi, Y.; Chaoui, F.Z.; Brouri, A. Identification of Hammerstein systems in presence of hysteresis-backlash and hysteresis-relay nonlinearities. Automatica 2008, 44, 767–775. [Google Scholar] [CrossRef]
- Giri, F.; Rochdi, Y.; Brouri, A.; Chaoui, F.Z. Parameter identification of Hammerstein systems containing backlash operators with arbitrary-shape parametric borders. Automatica 2011, 47, 1827–1833. [Google Scholar] [CrossRef]
- Butcher, M.; Giustiniani, A.; Masi, A. On the identification of Hammerstein systems in the presence of an input hysteretic nonlinearity with nonlocal memory: Piezoelectric actuators—An experimental case study. Phys. B Condens. Matter 2016, 486, 101–105. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Q. Adaptive sliding mode control with perturbation estimation and PID sliding surface for motion tracking of a piezo-driven micromanipulator. IEEE Trans. Control Syst. Technol. 2009, 18, 798–810. [Google Scholar] [CrossRef]





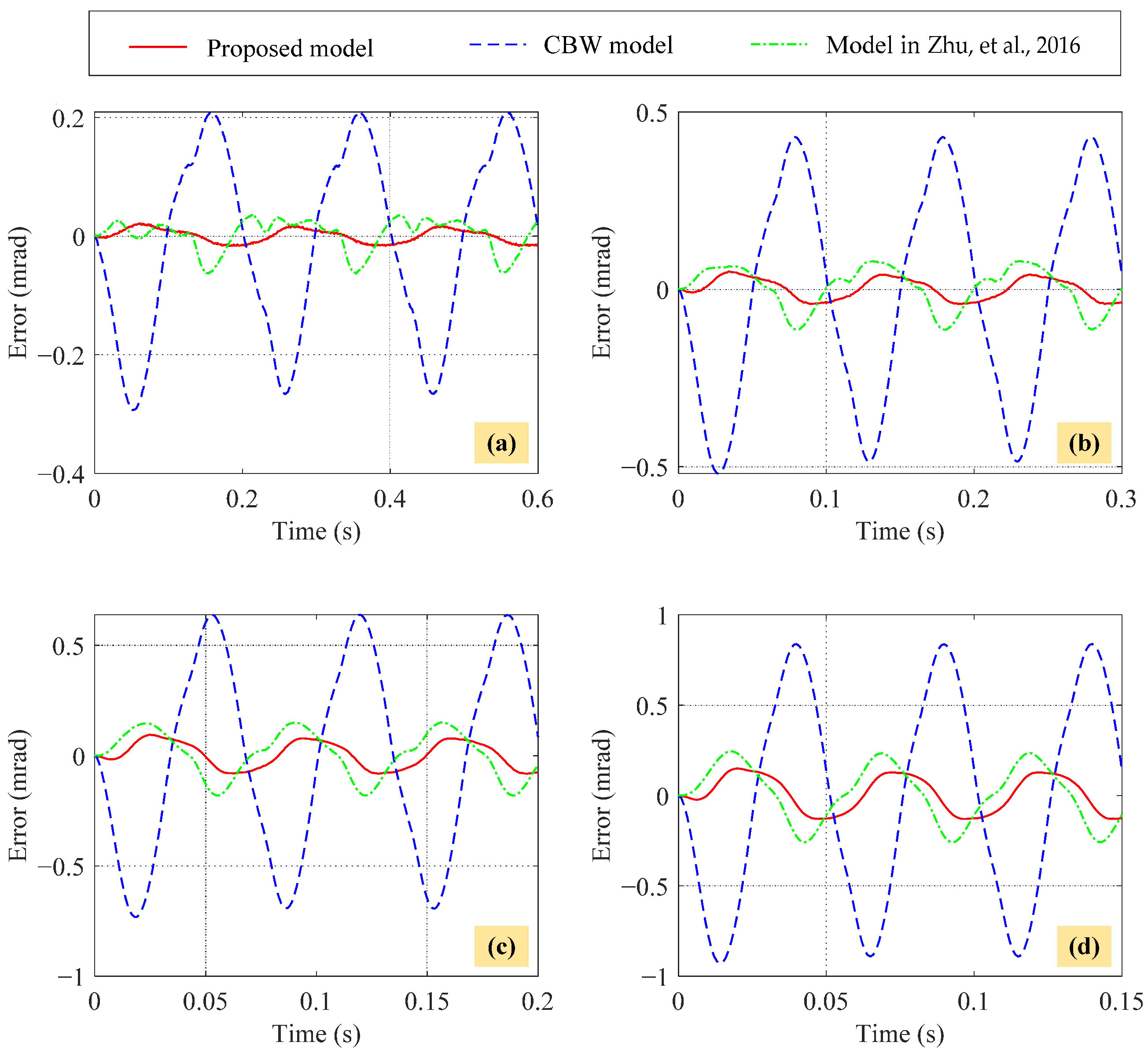

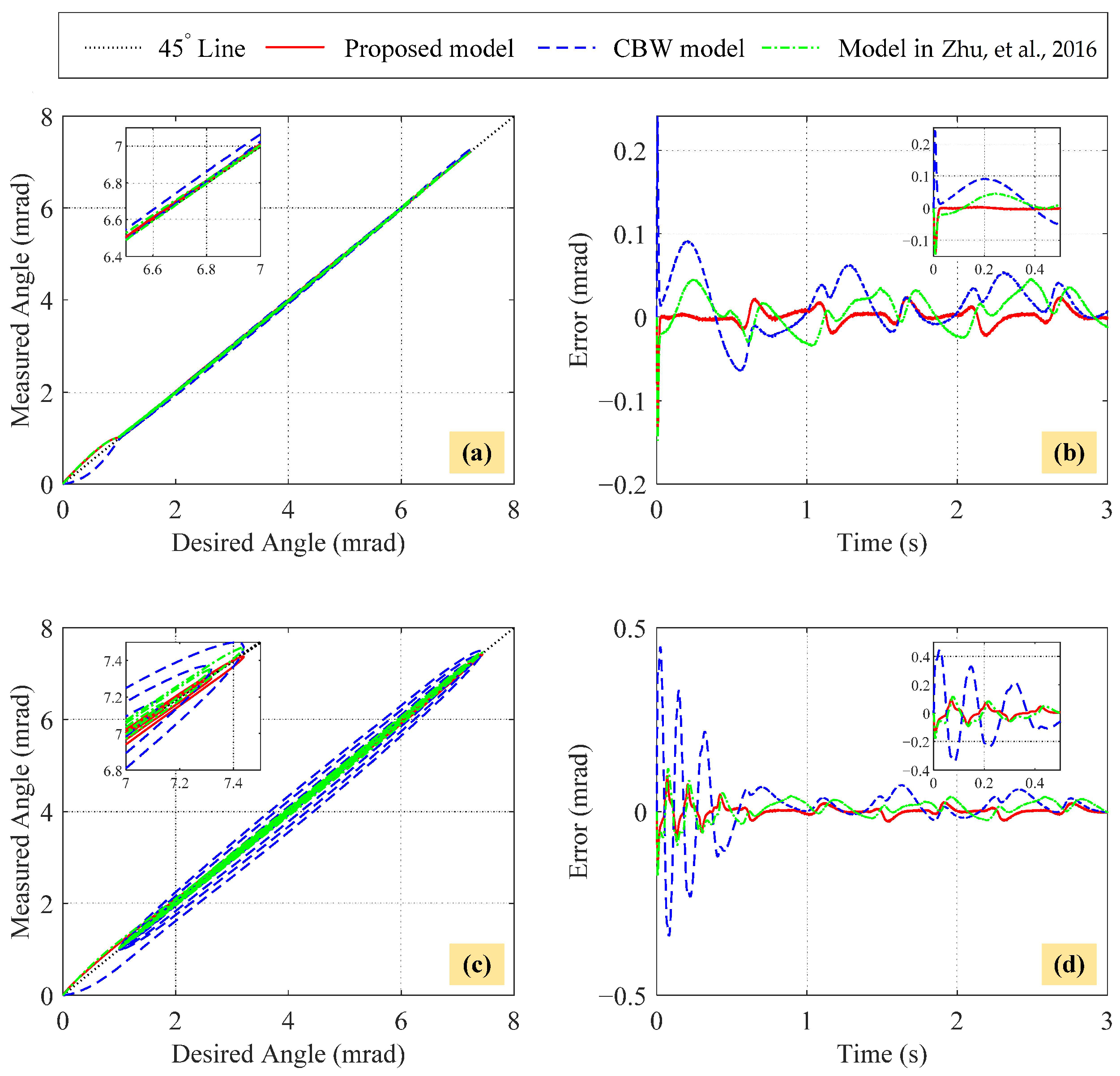
| Errors | CBW Model | Model in [36] | Proposed Model |
|---|---|---|---|
| MPME (22) | 11.99% | 8.90% | 4.58% |
| RMSE (23) | 0.0345 | 0.0268 | 0.0165 |
| Frequency | Errors | CBW Model | Model in [36] | Proposed Model |
|---|---|---|---|---|
| 5 Hz | MPME | 29.37% | 6.36% | 2.17% |
| RMSE | 0.1578 | 0.0273 | 0.0113 | |
| 10 Hz | MPME | 51.91% | 11.39% | 5.03% |
| RMSE | 0.3073 | 0.0595 | 0.0295 | |
| 15 Hz | MPME | 73.14% | 18.07% | 9.56% |
| RMSE | 0.4506 | 0.1037 | 0.0592 | |
| 20 Hz | MPME | 92.96% | 25.85% | 15.01% |
| RMSE | 0.5886 | 0.1576 | 0.0983 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, J.; Wang, J.; Bo, Y.; Zhang, X. Hysteresis Modeling and Compensation for a Fast Piezo-Driven Scanner in the UAV Image Stabilization System. Drones 2023, 7, 392. https://doi.org/10.3390/drones7060392
Lu J, Wang J, Bo Y, Zhang X. Hysteresis Modeling and Compensation for a Fast Piezo-Driven Scanner in the UAV Image Stabilization System. Drones. 2023; 7(6):392. https://doi.org/10.3390/drones7060392
Chicago/Turabian StyleLu, Jinlei, Jun Wang, Yuming Bo, and Xianchun Zhang. 2023. "Hysteresis Modeling and Compensation for a Fast Piezo-Driven Scanner in the UAV Image Stabilization System" Drones 7, no. 6: 392. https://doi.org/10.3390/drones7060392
APA StyleLu, J., Wang, J., Bo, Y., & Zhang, X. (2023). Hysteresis Modeling and Compensation for a Fast Piezo-Driven Scanner in the UAV Image Stabilization System. Drones, 7(6), 392. https://doi.org/10.3390/drones7060392






