High-Resolution Profiling of Atmospheric Turbulence Using UAV Autopilot Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Models of Atmospheric Turbulence
2.1.1. Von Karman Model
2.1.2. Dryden Model
2.2. General Information about the Experiment
3. Results and Discussion
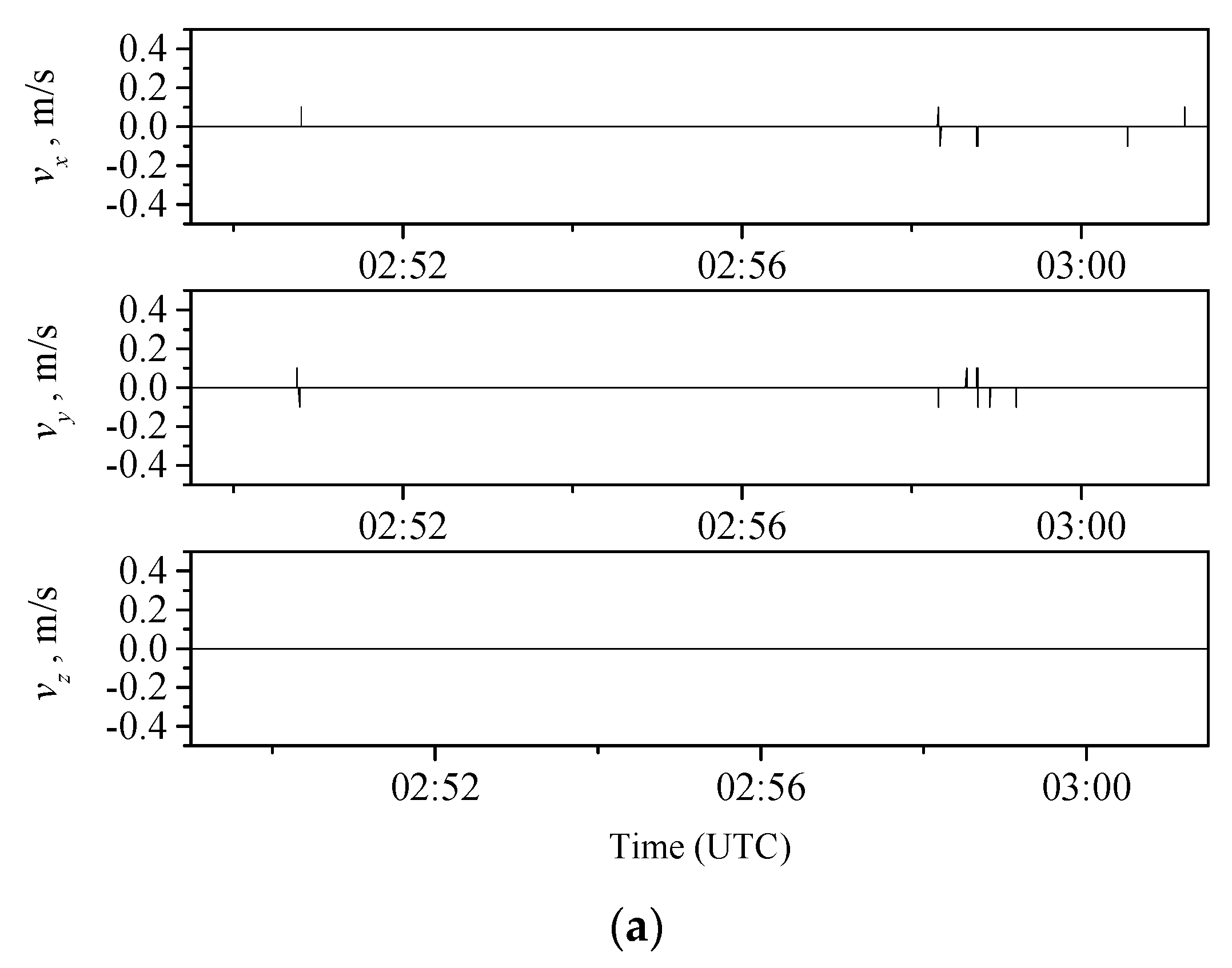
3.1. Quadcopter Velocity
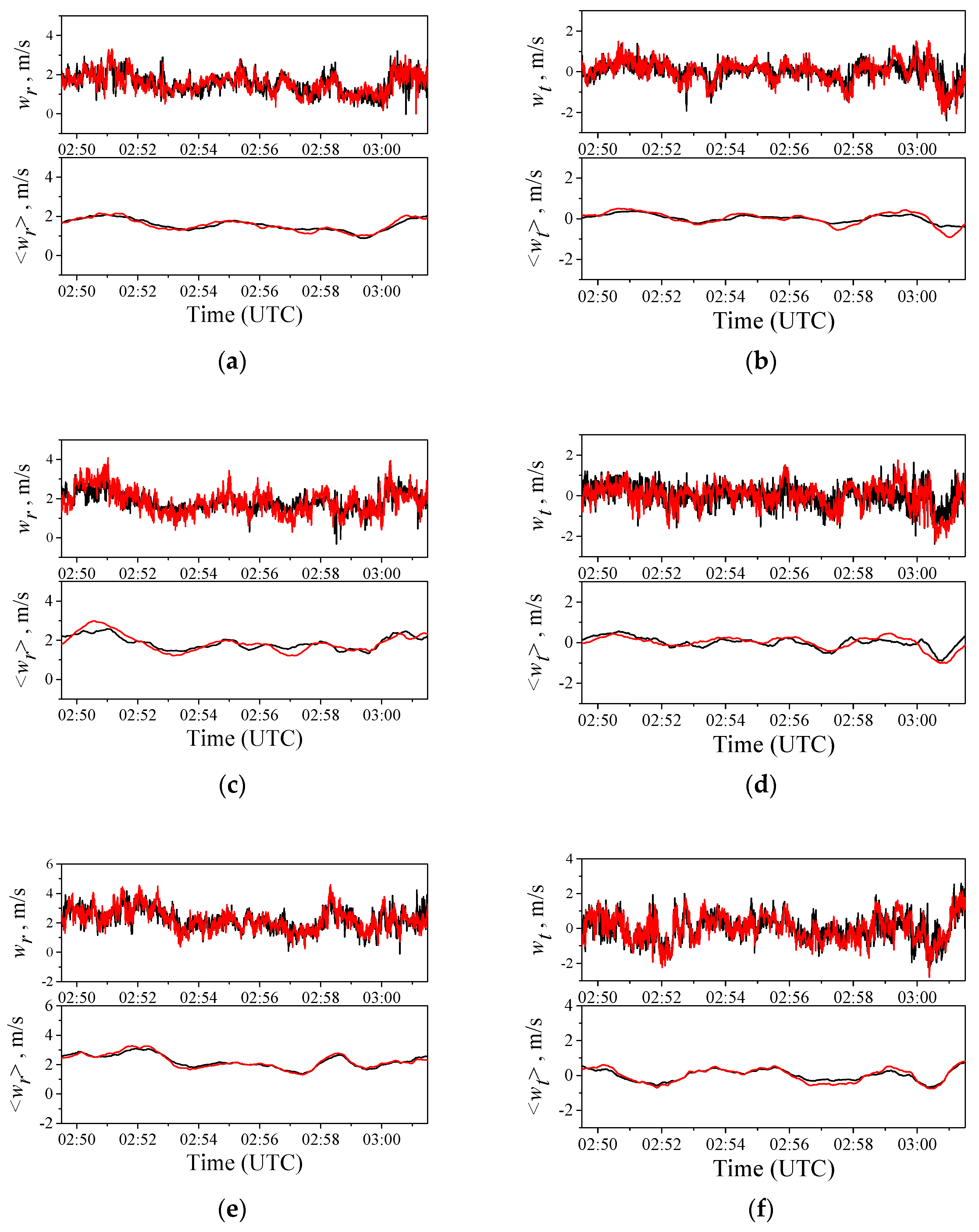
3.2. Longitudinal and Lateral Wind Velocity Components
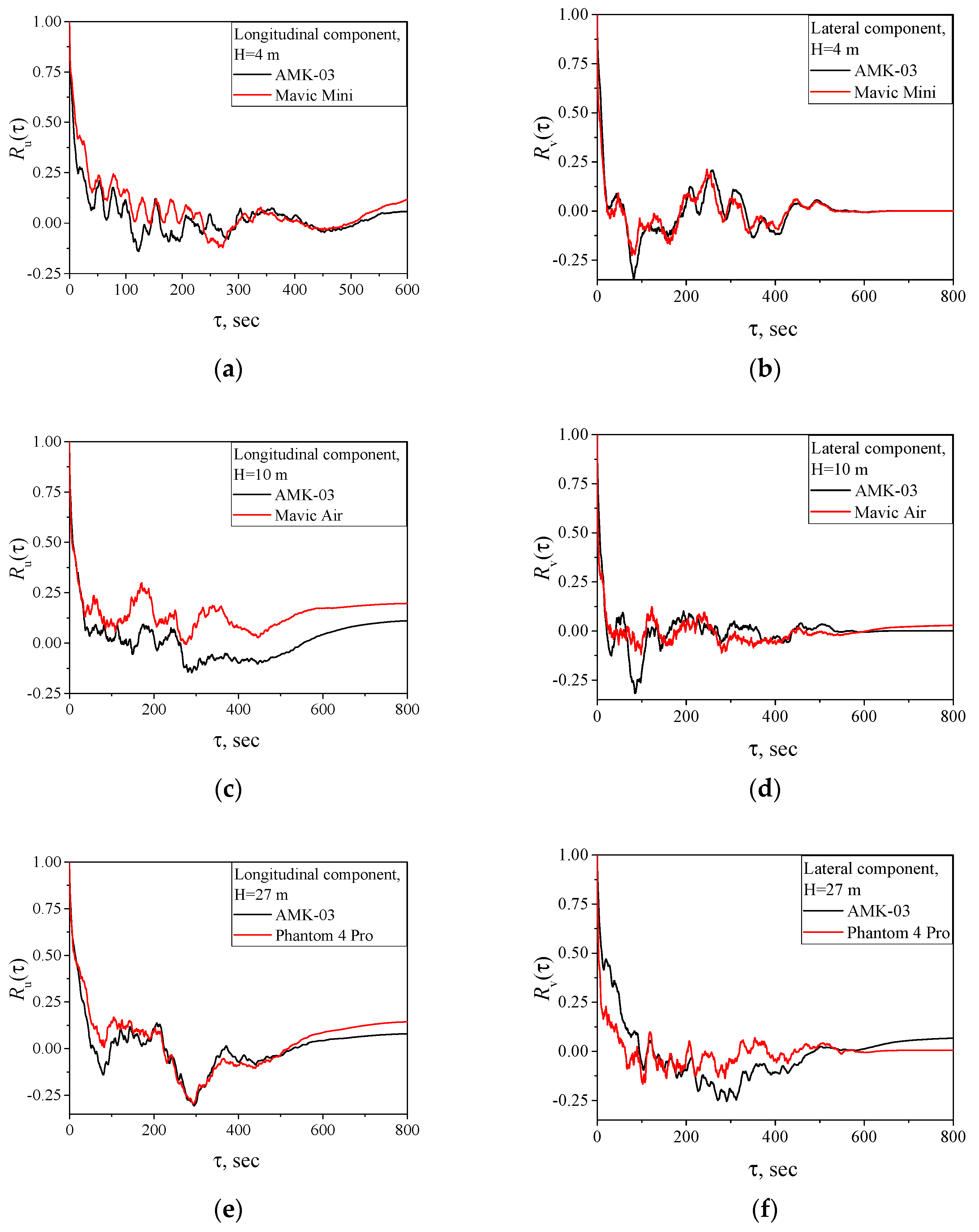
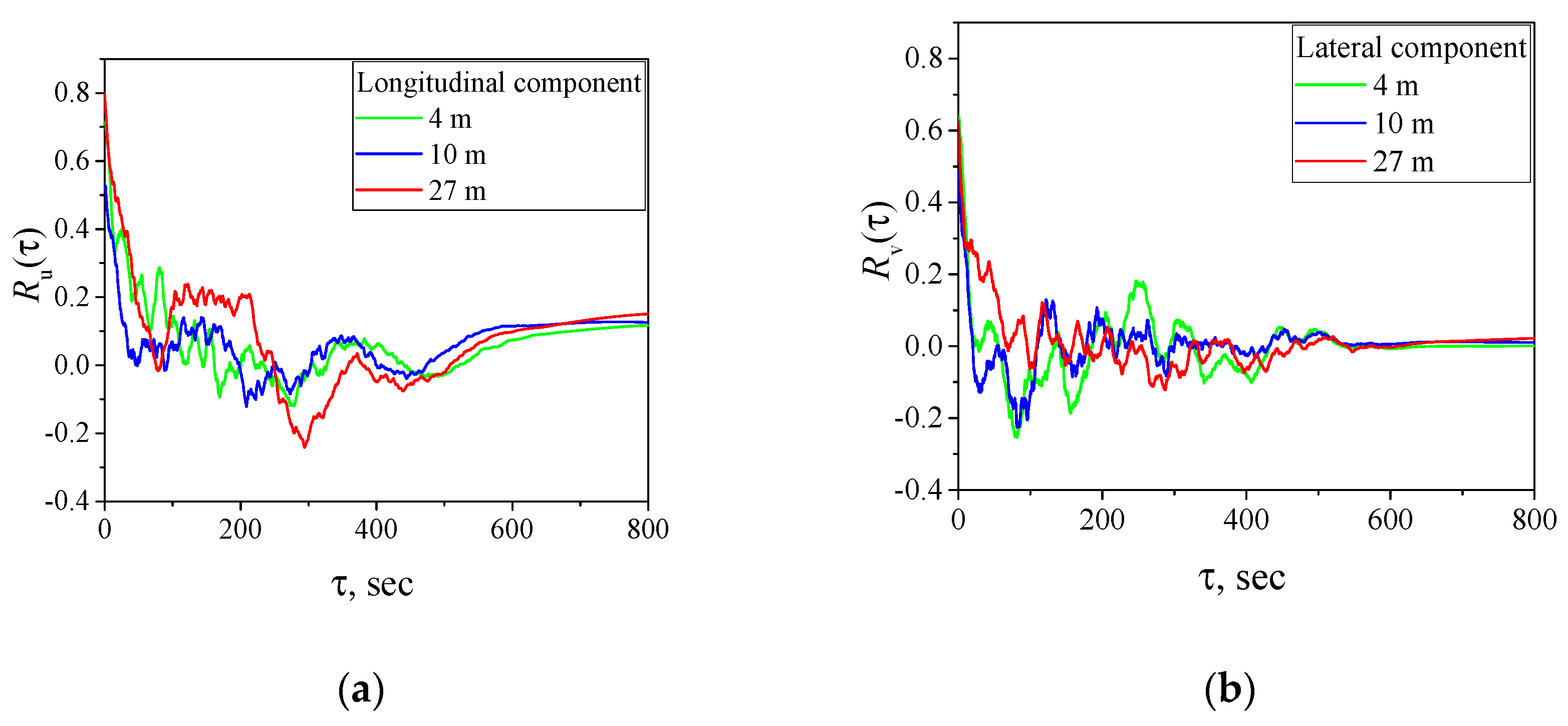
3.3. Correlation Analysis
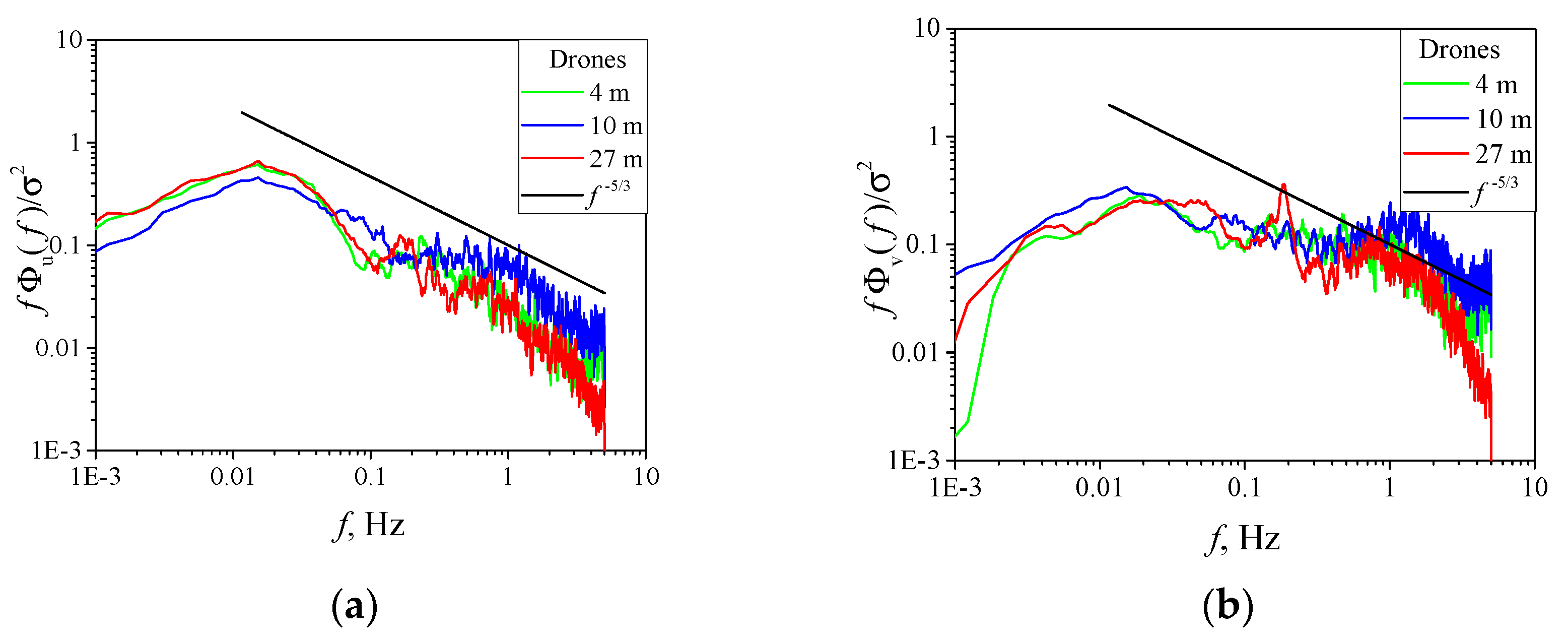
3.4. Spectral Analysis
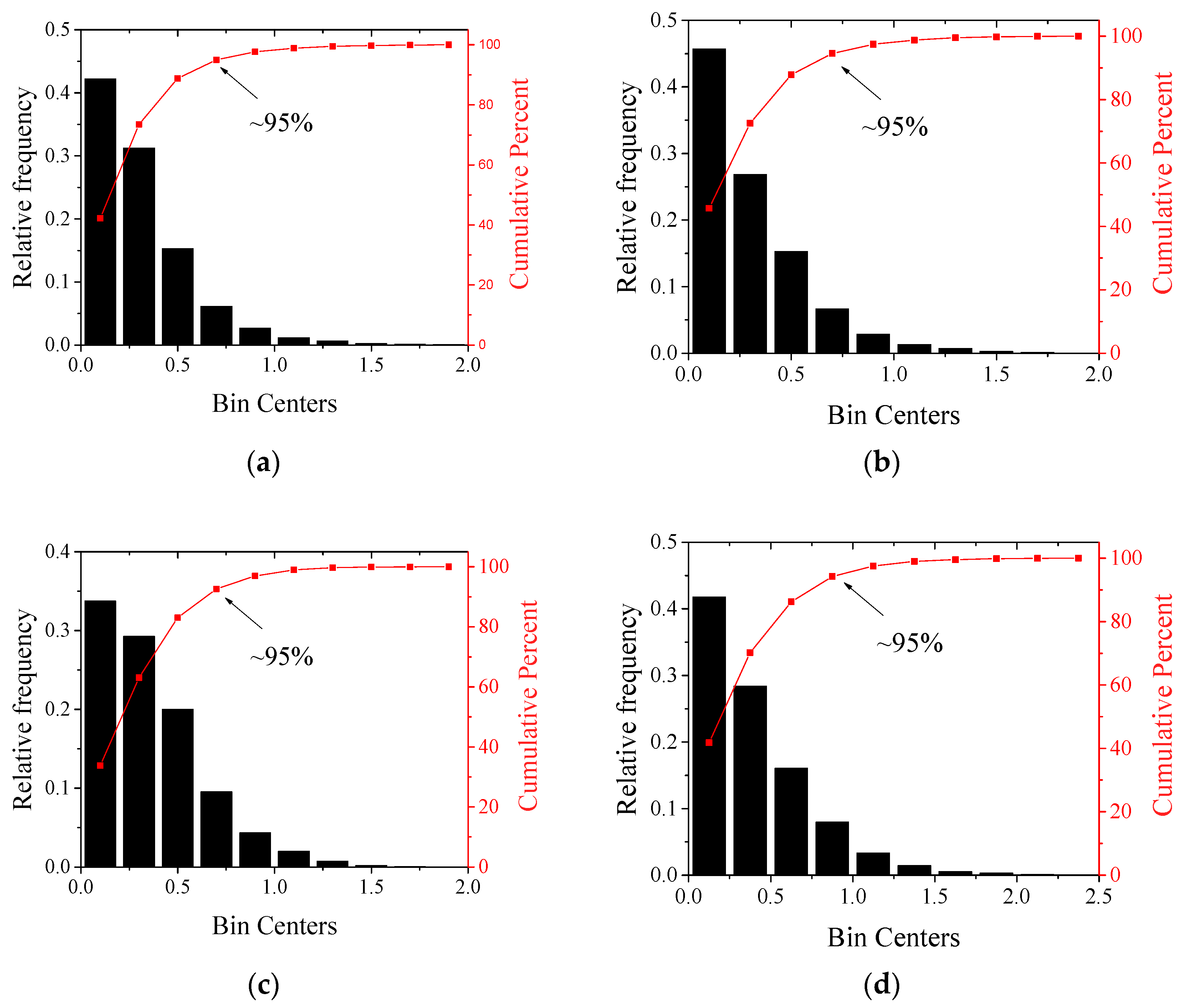
3.5. Longitudinal and Lateral Scales of Turbulence
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cornman, L.B.; Chan, W.N. Summary of a workshop on integrating weather into unmanned aerial system traffic management. Bull. Am. Meteorol. Soc. 2017, 98, ES257–ES259. [Google Scholar] [CrossRef]
- Beard, R.; McLain, T. Small Unmanned Aircraft: Theory and Practice; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Shelekhov, A.; Afanasiev, A.; Shelekhova, E.; Kobzev, A.; Tel’minov, A.; Molchunov, A.; Poplevina, O. Low-Altitude Sensing of Urban Atmospheric Turbulence with UAV. Drones 2022, 6, 61. [Google Scholar] [CrossRef]
- Kral, S.T.; Reuder, J.; Vihma, T.; Suomi, I.; O’Connor, E.; Kouznetsov, R.; Wrenger, B.; Rautenberg, A.; Urbancic, G.; Jonassen, M.O.; et al. Innovative strategies for observations in the arctic atmospheric boundary layer (ISOBAR)—The Hailuoto 2017 campaign. Atmosphere 2018, 9, 268. [Google Scholar] [CrossRef] [Green Version]
- Stith, J.L.; Baumgardner, D.; Haggerty, J.; Hardesty, M.; Lee, W.; Lenschow, D.; Pilewskie, P.; Smith, P.L.; Steiner, M.; Vömel, H. 100 Years of progress in atmospheric observing systems. Meteorol. Monogr. 2018, 59, 2.1–2.55. [Google Scholar] [CrossRef]
- Hocking, W.K.; Röttger, J.; Palmer, R.D.; Sato, T.; Chilson, P.B. Atmospheric Radar; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Leosphere, Windcube, Vaisala. Available online: https://www.vaisala.com/en/wind-lidars/wind-energy/windcube/ (accessed on 30 April 2023).
- METEK Meteorologische Messtechnik GmbH. Available online: https://metek.de/product-group/doppler-sodar/ (accessed on 30 April 2023).
- Scintec. Available online: https://www.scintec.com/ (accessed on 30 April 2023).
- Zhu, B.; Qunbo, L.; Tan, Z. Adaptive Multi-Scale Fusion Blind Deblurred Generative Adversarial Network Method for Sharpening Image Data. Drones 2023, 7, 96. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhang, J.; Chen, W.; Wang, Y.; You, J.; Wang, Q. SR-DeblurUGAN: An End-to-End Super-Resolution and Deblurring Model with High Performance. Drones 2022, 6, 162. [Google Scholar] [CrossRef]
- Tajima, Y.; Hiraguri, T.; Matsuda, T.; Imai, T.; Hirokawa, J.; Shimizu, H.; Kimura, T.; Maruta, K. Analysis of Wind Effect on Drone Relay Communications. Drones 2023, 7, 182. [Google Scholar] [CrossRef]
- Commission for Basic Systems and Commission for Instruments and Methods of Observation: Workshop on Use of Unmanned Aerial Vehicles (UAV) for Operational Meteorology WMO. 2019. Available online: https://library.wmo.int/doc_num.php?explnum_id=9951 (accessed on 30 April 2023).
- AMDAR Reference Manual: Aircraft Meteorological Data Relay WMO-No. 958, WMO. 2003. Available online: https://library.wmo.int/doc_num.php?explnum_id=9026 (accessed on 30 April 2023).
- Stoffelen, A.; Benedetti, A.; Borde, R.; Dabas, A.; Flamant, P.; Forsythe, M.; Hardesty, M.; Isaksen, L.; Källén, E.; Körnich, H.; et al. Wind Profile Satellite Observation Requirements and Capabilities. Bull. Amer. Meteor. Soc. 2020, 101, E2005–E2021. [Google Scholar] [CrossRef]
- Liao, X.; Xu, C.; Ye, H.; Tan, X.; Fang, S.; Huang, Y.; Lin, J. Critical Infrastructures for Developing UAVs’ Applications and Low-altitude Public Air-Route Network Planning. Bull. Chin. Acad. Sci. (Chin. Version) 2022, 37, 977–988. [Google Scholar]
- González-Rocha, J.; Bilyeu, L.; Ross, S.D.; Foroutan, H.; Jacquemin, S.J.; Ault, A.P.; Schmale, D.G., III. Sensing atmospheric flows in aquatic environments using a multirotor small unscrewed aircraft system (sUAS). Environ. Sci. Atmos. 2023, 3, 305–315. [Google Scholar] [CrossRef]
- Lepikhin, A.P.; Lyakhin, Y.S.; Lucnikov, A.I. The Experience in Drone Use to Evaluate the Coefficients of Turbulent Diffusion in Small Water Bodies. Water Resour. 2023, 50, 242–251. [Google Scholar] [CrossRef]
- McConville, A.; Richardson, T. High-altitude vertical wind profile estimation using multirotor vehicles. Front. Robot. AI 2023, 10, 1112889. [Google Scholar] [CrossRef] [PubMed]
- Villa, T.F.; Gonzalez, F.; Miljievic, B.; Ristovski, Z.D.; Morawska, L. An Overview of Small Unmanned Aerial Vehicles for Air Quality Measurements: Present Applications and Future Prospectives. Sensors 2016, 16, 1072. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Loubimov, G.; Kinzel, M.P.; Bhattacharya, S. Measuring Atmospheric Boundary Layer Profiles Using UAV Control Data. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; American Institute of Aeronautics and Astronautics: Orlando, FL, USA, 2020. [Google Scholar] [CrossRef]
- Li, Z.; Pu, O.; Pan, Y.; Huang, B.; Zhao, Z.; Wu, H. A Study on Measuring the Wind Field in the Air Using a Multi-rotor UAV Mounted with an Anemometer. Bound.-Layer Meteorol. 2023, 188, 1–27. [Google Scholar] [CrossRef]
- González-Rocha, J.; De Wekker, S.F.J.; Ross, S.D.; Woolsey, C.A. Wind Profiling in the Lower Atmosphere from Wind-Induced Perturbations to Multirotor UAS. Sensors 2020, 20, 1341. [Google Scholar] [CrossRef] [Green Version]
- González-Rocha, J.; Woolsey, C.A.; Sultan, C.; De Wekker, S.F.J. Sensing wind from quadrotor motion. J. Guid. Control Dyn. 2019, 42, 836–852. [Google Scholar] [CrossRef]
- González-Rocha, J.; Woolsey, C.A.; Sultan, C.; De Wekker, S.F. Model-based wind profiling in the lower atmosphere with multirotor UAS. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 1598. [Google Scholar]
- Neumann, P.; Bartholmai, M. Real-time wind estimation on a micro unmanned aerial vehicle using its inertial measurement unit. Sens. Actuators A Phys. 2015, 235, 300–310. [Google Scholar] [CrossRef]
- Palomaki, R.T.; Rose, N.T.; van den Bossche, M.; Sherman, T.J.; De Wekker, S.F.J. Wind estimation in the lower atmosphere using multirotor aircraft. J. Atmos. Ocean. Technol. 2017, 34, 1183–1190. [Google Scholar] [CrossRef]
- Meier, K.; Hann, R.; Skaloud, J.; Garreau, A. Wind Estimation with Multirotor UAVs. Atmosphere 2022, 13, 551. [Google Scholar] [CrossRef]
- Cheng, X.; Wang, Y.; Cai, Z.; Liu, N.; Zhao, J. Wind Estimation of a Quadrotor Unmanned Aerial Vehicle. In Advances in Guidance, Navigation and Control; ICGNC 2022 Lecture Notes in Electrical Engineering; Yan, L., Duan, H., Deng, Y., Eds.; Springer: Singapore, 2023; Volume 845. [Google Scholar] [CrossRef]
- Shelekhov, A.P.; Afanasiev, A.L.; Kobzev, A.A.; Shelekhova, E.A. Opportunities to monitor the urban atmospheric turbulence using unmanned aerial system. In Remote Sensing Technologies and Applications in Urban Environments V; SPIE: Washington, DC, USA, 2020; Volume 11535, p. 1153506. [Google Scholar] [CrossRef]
- Shelekhov, A.P.; Afanasiev, A.L.; Shelekhova, E.A.; Kobzev, A.A.; Tel’minov, A.E.; Molchunov, A.N.; Poplevina, O.N. Profiling the turbulence from spectral measurements in the urban atmosphere using UAVs. In Remote Sensing Technologies and Applications in Urban Environments VI; SPIE: Washington, DC, USA, 2021; Volume 11864, p. 118640B. [Google Scholar] [CrossRef]
- Shelekhov, A.; Afanasiev, A.; Shelekhova, E.; Kobzev, A.; Tel’minov, A.; Molchunov, A.; Poplevina, O. Using small unmanned aerial vehicles for turbulence measurements in the atmosphere. Izv. Atmos. Ocean. Phys. 2021, 57, 533–545. [Google Scholar] [CrossRef]
- Monin, A.S.; Yaglom, A.M. Statistical Hydromechanics. Part 2. In Turbulent Mechanics; Nauka: Moscow, Russia, 1967. [Google Scholar]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1989. [Google Scholar]
- Kaimal, J.C.; Finnigan, J.J. Atmospheric Boundary Layer Flows: Their Structure and Measurement; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Wildmann, N.; Wetz, T. Towards vertical wind and turbulent flux estimation with multicopter uncrewed aircraft systems. Atmos. Meas. Tech. 2022, 15, 5465–5477. [Google Scholar] [CrossRef]
- Wetz, T.; Wildmann, N. Spatially distributed and simultaneous wind measurements with a fleet of small quadrotor UAS. J. Phys. Conf. Ser. 2022, 2265, 022086. [Google Scholar] [CrossRef]
- Shishov, E.A.; Solenaya, O.A.; Chkhetiani, O.G.; Azizyan, G.V.; Koprov, V.M. Multipoint measurements of temperature and wind in the surface layer. Izv. Atmos. Ocean. Phys. 2021, 57, 254–263. [Google Scholar] [CrossRef]
- Shishov, E.A.; Solyonaya, O.A.; Koprov, B.M.; Koprov, V.M. Investigation into variations of wind directions near the surface. Izv. Atmos. Ocean. Phys. 2018, 54, 515–523. [Google Scholar] [CrossRef]
- Azbukin, A.A.; Bogushevich, A.Y.; Korolkov, V.A.; Tikhomirov, A.A.; Shelevoi, V.D. A field version of the AMK-03 automated ultrasonic meteorological complex. Russ. Meteorol. Hydrol. 2009, 34, 133–136. [Google Scholar] [CrossRef]
- Azbukin, A.A.; Bogushevich, A.Y.; Kobzev, A.A.; Korolkov, V.A.; Tikhomirov, A.A.; Shelevoy, V.D. AMK-03 Automatic weather stations, their modifications and applications. Sens. Syst. 2012, 3, 47–52. [Google Scholar]
- McCombs, A.G.; Hiscox, A.L. Always in flux: The nature of turbulence. In Conceptual Boundary Layer Meteorology; Hiscox, A.L., Ed.; Academic Press: Cambridge, MA, USA, 2023; pp. 19–35. [Google Scholar] [CrossRef]
- Tieleman, H.W. Universality of velocity spectra. J. Wind Eng. Ind. Aerodyn. 1995, 56, 55–69. [Google Scholar] [CrossRef]
- Flay, R.G.J.; Stevenson, D.C. Integral length scales in an atmospheric boundary-layer near the Ground. In Proceedings of the 9th Australasian Fluid Mechanics Conference, Auckland, New Zealand, 8–12 December 1986. [Google Scholar]
- Guide to Instruments and Methods of Observation Volume I—Measurement of Meteorological Variables (WMO-No. 8) WMO; WMO: Geneva, Switzerland, 2021.
- O’Neill, P.L.; Nicolaides, D.; Honnery, D.; Soria, J. Autocorrelation Functions and the Determination of Integral Length with Reference to Experimental and Numerical Data. In Proceedings of the 15th Australasian Fluid Mechanics Conference, Sydney, Australia, 13–17 December 2004. [Google Scholar]
- Emes, M.J.; Arjomandi, M.; Kelso, R.M.; Ghanadi, F. Integral length scales in a low-roughness atmospheric boundary layer. In Proceedings of the 18th Australasian Wind Engineering Society Workshop, McLaren Vale, Australia, 6–8 July 2016; pp. 1–4. [Google Scholar]
- Yaglom, A.M. Correlation Theory of Stationary and Related Random Functions, Volume 1: Basic Results; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
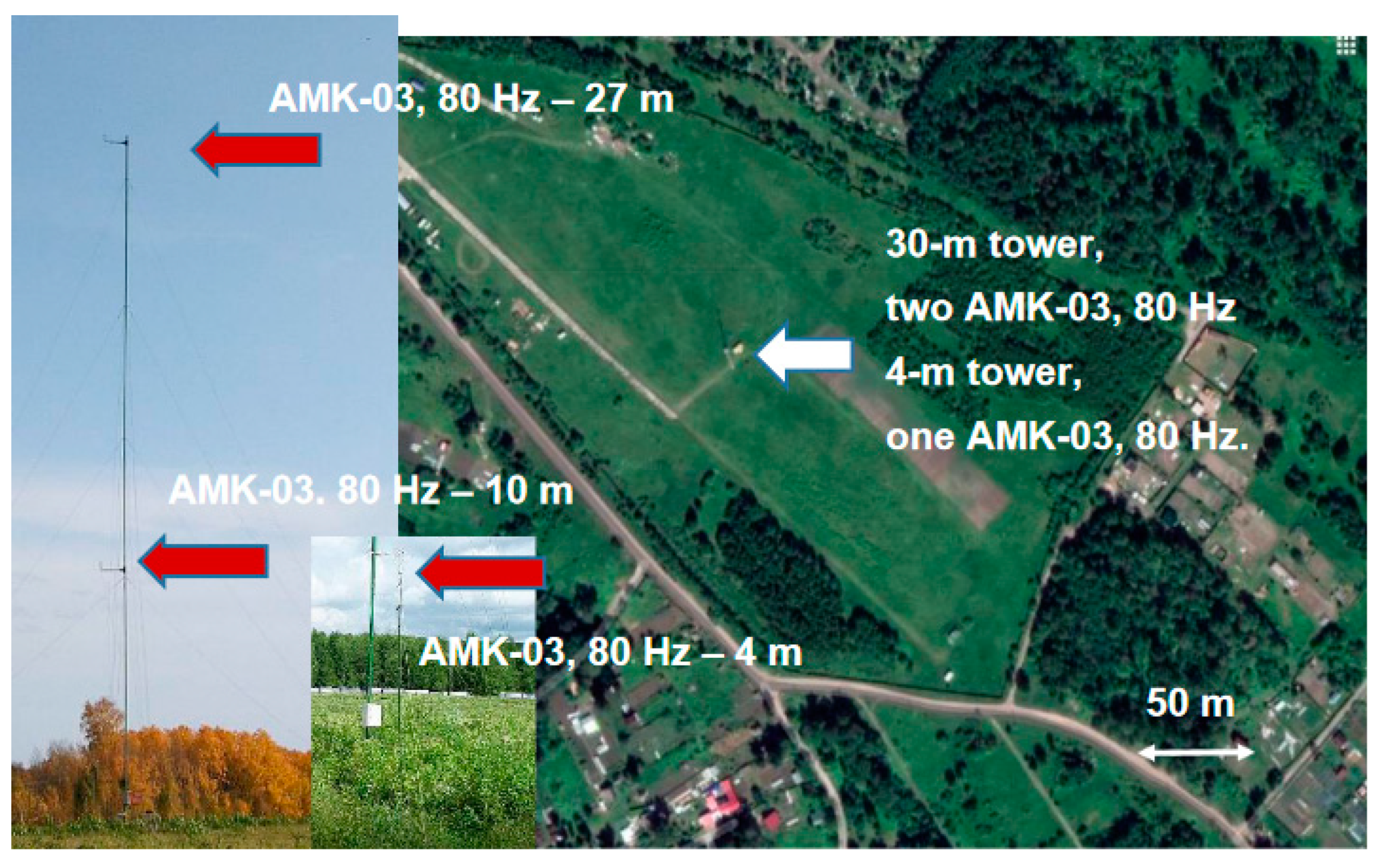

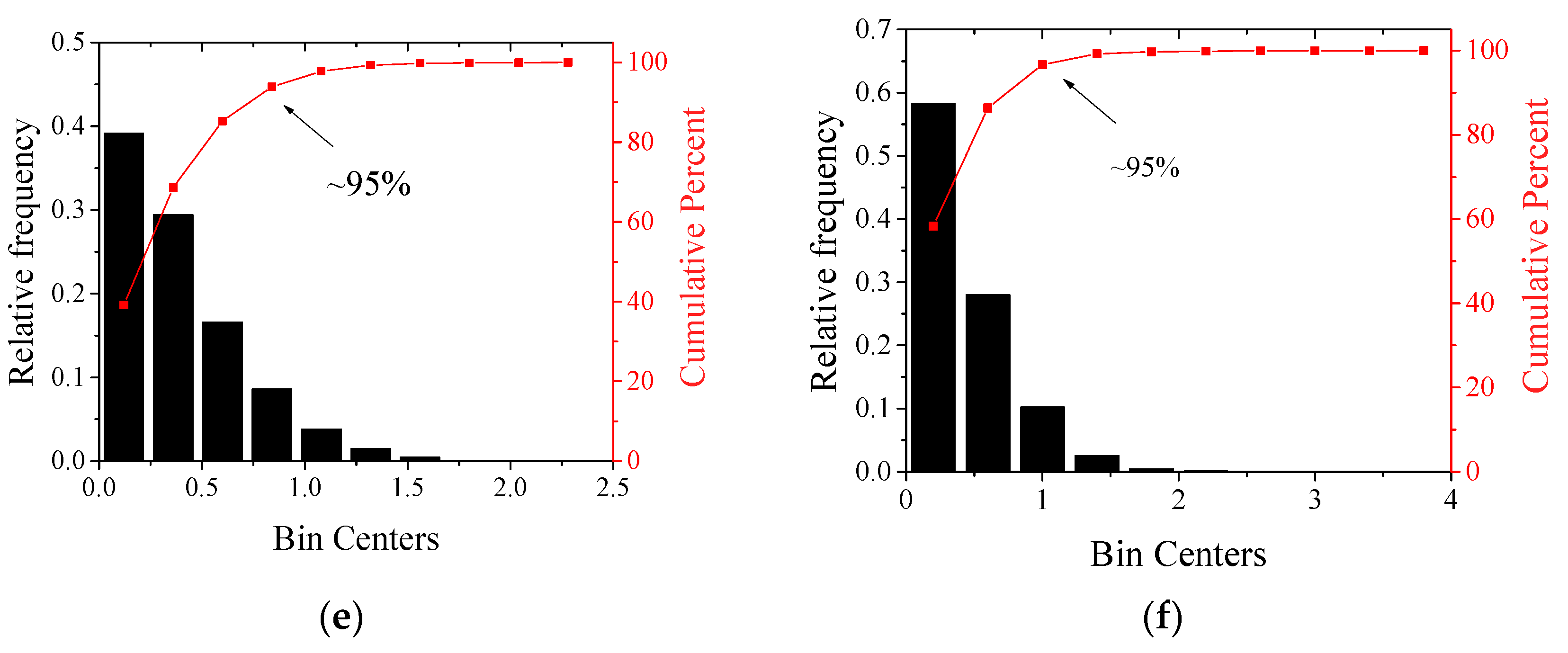



| UAV | Start, UTC | End, UTC | Hover Height, m | Wind Speed, m/s |
|---|---|---|---|---|
| DJI Mini | 02:48:30 | 03:01:30 | 4 | 1.6 |
| DJI Air | 10 | 1.9 | ||
| DJI Phantom 4 Pro | 27 | 2.2 |
| Height, m | , m2/s2 | , m2/s2 | ||||||
|---|---|---|---|---|---|---|---|---|
| 4 | 0.43 | −0.10 | 0.48 | 0.00 | 1.56/1.56 * | 0.00/0.00 | 0.48/0.51 | 0.54/0.44 |
| 10 | 0.38 | 0.92 | 0.41 | 0.00 | 1.86/1.86 * | 0.00/0.00 | 0.63/0.44 | 0.59/0.48 |
| 27 | 0.65 | 0.27 | 0.61 | 0.00 | 2.23/2.23 * | 0.00/0.00 | 0.73/0.68 | 0.76/0.70 |
| Height | Longitudinal Component | Lateral Component | ||
|---|---|---|---|---|
| 4 m | 0.40 | 0.11 | 0.40 | 0.15 |
| 10 m | 0.45 | 0.21 | 0.52 | 0.21 |
| 30 m | 0.50 | 0.12 | 0.54 | 0.14 |
| Average | 0.45 | 0.15 | 0.49 | 0.17 |
| Height | Longitudinal Component | Lateral Component | ||
|---|---|---|---|---|
| No Smoothing | Smoothing | No Smoothing | Smoothing | |
| 4 m | 0.68 | 0.94 | 0.68 | 0.93 |
| 10 m | 0.69 | 0.89 | 0.56 | 0.77 |
| 30 m | 0.75 | 0.97 | 0.72 | 0.96 |
| Average | 0.71 | 0.93 | 0.66 | 0.89 |
| 4 m | |||
| AMK-03 | 14.9/16.3 * | 9.0/10.0 | 0.61/0.61 |
| DJI Mavic Mini | 14.9/16.3 | 8.7/9.7 | 0.59/0.59 |
| 10 m | |||
| AMK-03 | 17.8/19.4 | 11.6/12.8 | 0.65/0.66 |
| DJI Mavic Air | 17.8/19.4 | 12.9/14.3 | 0.73/0.74 |
| 27 m | |||
| AMK-03 | 21.4/23.3 | 15.5/17.1 | 0.73/0.74 |
| DJI Phantom 4 Pro | 21.4/23.3 | 12.5/13.8 | 0.59/0.59 |
| 4 m | |||
| AMK-03 | 15 | 11 | 0.7 |
| DJI Mavic Mini | 17 | 9 | 0.5 |
| 10 m | |||
| AMK-03 | 21 | 12 | 0.6 |
| DJI Mavic Air | 20 | 10 | 0.5 |
| 27 m | |||
| AMK-03 | 25 | 17 | 0.7 |
| DJI Phantom 4 Pro | 24 | 12 | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shelekhov, A.; Afanasiev, A.; Shelekhova, E.; Kobzev, A.; Tel’minov, A.; Molchunov, A.; Poplevina, O. High-Resolution Profiling of Atmospheric Turbulence Using UAV Autopilot Data. Drones 2023, 7, 412. https://doi.org/10.3390/drones7070412
Shelekhov A, Afanasiev A, Shelekhova E, Kobzev A, Tel’minov A, Molchunov A, Poplevina O. High-Resolution Profiling of Atmospheric Turbulence Using UAV Autopilot Data. Drones. 2023; 7(7):412. https://doi.org/10.3390/drones7070412
Chicago/Turabian StyleShelekhov, Alexander, Alexey Afanasiev, Evgeniya Shelekhova, Alexey Kobzev, Alexey Tel’minov, Alexander Molchunov, and Olga Poplevina. 2023. "High-Resolution Profiling of Atmospheric Turbulence Using UAV Autopilot Data" Drones 7, no. 7: 412. https://doi.org/10.3390/drones7070412
APA StyleShelekhov, A., Afanasiev, A., Shelekhova, E., Kobzev, A., Tel’minov, A., Molchunov, A., & Poplevina, O. (2023). High-Resolution Profiling of Atmospheric Turbulence Using UAV Autopilot Data. Drones, 7(7), 412. https://doi.org/10.3390/drones7070412






