SmrtSwarm: A Novel Swarming Model for Real-World Environments
Abstract
:1. Introduction
- We develop an enhanced Reynolds model that incorporates leader–follower behavior. The control is still distributed; however, the leader is a distinguished drone that knows the final destination.
- We propose new Reynolds-like flocking rules that enable a swarm to navigate through GPS-aided environments containing physical obstacles while maintaining swarm behavior. The total processing time of our model is less than 1 ms on a popular embedded board.
- We propose new flocking rules for GPS-denied environments as well. We develop a method to process depth maps quickly and process frames in around 13 ms (≈75 fps) on a popular embedded board.
2. Background and Related Work
2.1. Swarming Models in an Environment with GPS Signals
2.1.1. Self-Organized Swarming
- (i)
- Cohesion: Each swarm member must try to travel towards the group’s center. This behavior is achieved by applying an attractive force between each flock member and the group’s center of mass, which pulls the member towards the center (refer to Figure 2a).
- (ii)
- Separation: Every member must keep a safe distance from its neighbors to prevent collisions. This is achieved by exerting a repulsive force between each flock member and its nearest neighbors (refer to Figure 2b).
- (iii)
- Alignment: Every member in the swarm should try to match its neighbors’ speed and direction. This behavior is achieved by exerting an attractive force between each flock member and its neighbors. This pushes the member’s velocity closer to the group’s average velocity (refer to Figure 2c).
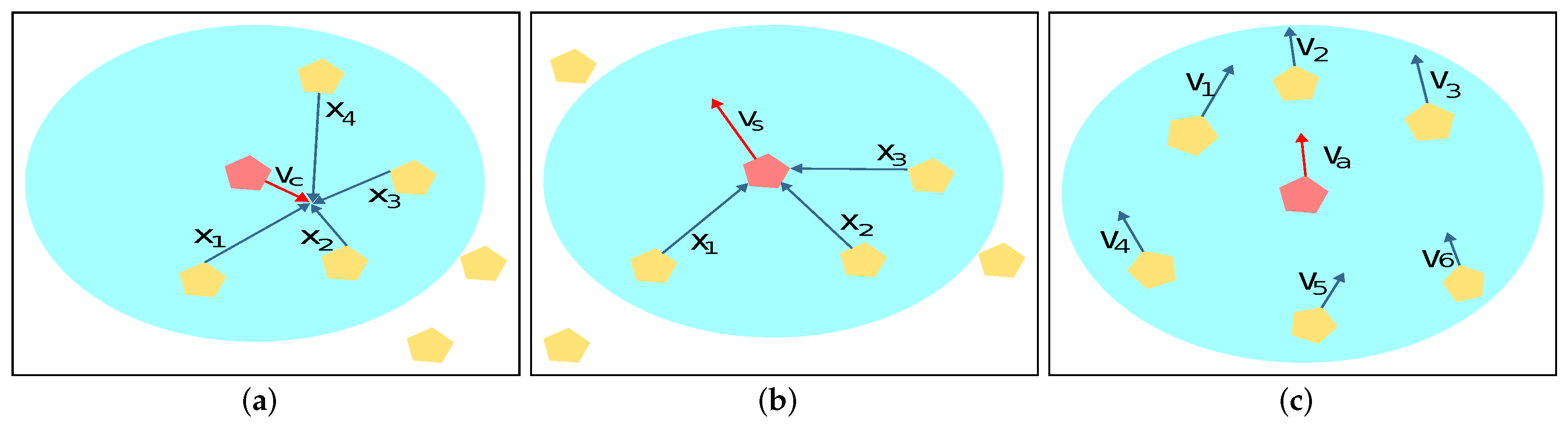
2.1.2. Leader–Follower Swarming
2.2. Swarming in a GPS-Denied Environment
3. Materials and Methods
3.1. in GPS-Aided Environments
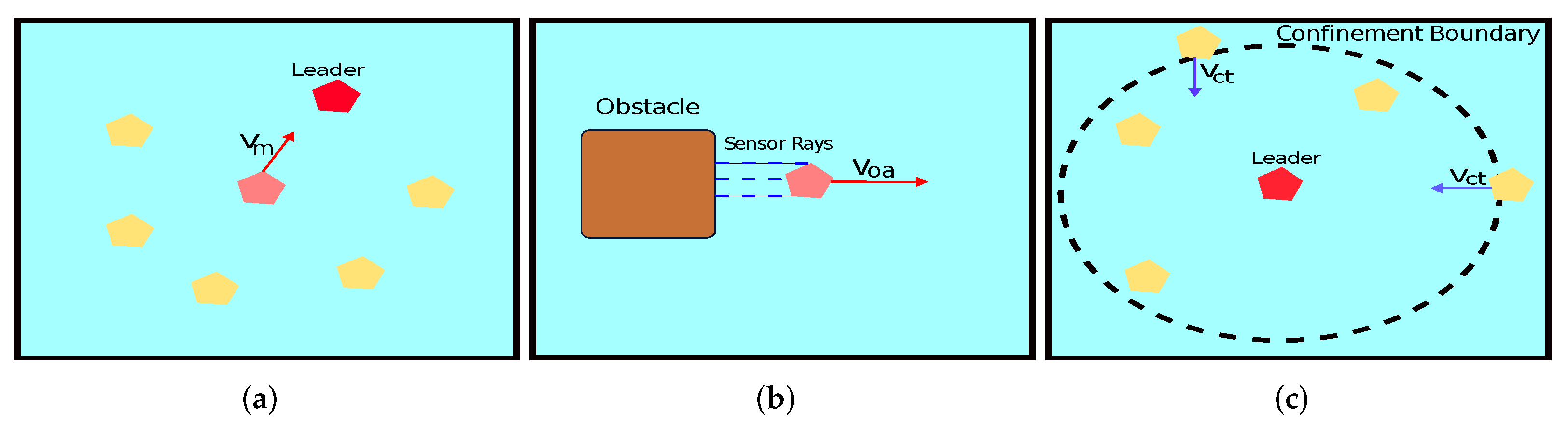
3.1.1. New Rule: Migration Rule
3.1.2. New Rule: Obstacle Avoidance Rule
3.1.3. New Rule: Confinement Rule
3.1.4. Old Rule: Cohesion Rule
3.1.5. Old Rule: Separation Rule
3.1.6. Old Rule: Alignment Rule
3.1.7. The Final Velocity
3.2. in GPS-Denied Environments
3.2.1. Object Detection in the Depth Map
- ❶
- A depth map is a 2D matrix, where the value in each cell represents the depth of the relevant part of the object corresponding to it.
- ❷
- The objects seen on the depth map form a cluster of pixels with similar pixel values. On the boundaries of these clusters, we can find a sudden change in pixel values.
- ❸
- The values of the pixels belonging to objects far away from the reference point are very high.
3.2.2. Object Tracking
- ❶
- A pair of positions in the list for the previous and current frames exists such that the difference between them is less than the threshold. Then we conclude that these are the positions of the same drone, and the drone is given the same tag in the current frame as it was in the previous frame.
- ❷
- If a position in the list for the previous frame exists for which we are not able to find such a match (described in point 1) in the list for the current frame, then that position refers to a drone that recently left the FoV, and we do not issue a tag. In other words, if a tag found in the previous frame is not present in the current frame, then that drone has left the FoV of the reference drone.
- ❸
- If a position in the list of the current frame exists for which we cannot find such a match in the list of the previous frame, then that position refers to a newly appeared drone in the FoV. It needs to be assigned a new tag.
3.2.3. Flocking Rules in GPS-Denied Environments
Alignment Rule for GPS-Denied Environments
| Algorithm 1: Alignment. |
| 1 Function Alignment(): 2 3 4 /* Initialize the count of valid neighbors */ 5 while do /* Get the current position and tag of the drone */ 6 7 8 /* Initialize the inner loop counter */ 9 while i < prevTags.size do 10 if currTag == prevTags[i] then 11 /* Get the previous position of the corresponding drone */ 12 /* Add the difference of positions, i.e., their velocity in a unit time frame to the alignment vector */ 13 14 break 15 end 16 /* Move to the next tag in prevTags list */ 17 end 18 /* Move to the next drone */ 19 end 20 /* Normalize the alignment vector */ 21 return |
Confinement Rule for GPS-Denied Environments
| Algorithm 2: Confinement. |
| 1 Function Confinement (): 2 // If there are neighboring drones in the FoV 3 if then 4 5 6 end 7 else /* Set the confinement vector opposite to the previous velocity */ 8 9 /* If the confinement counter exceeds the limit */ 10 if then 11 /* update the limit */ 12 end 13 end 14 return |
3.3. Workflow of the Proposed Model
4. Results and Analysis
4.1. Simulation Setup
4.2. Setting the Hyperparameters (Coefficients in the Equations)
- ❶
- Experiments 5 and 9 (highlighted in bold) show the base set of values of the weights for the GPS-aided and GPS-denied environments, respectively. We set these values as the default for the subsequent experiments.
- ❷
- For the best case, the rule contributing the most to the final velocity is cohesion. Even though the values of , , and are much lower than , the overall performance is quite sensitive to these values—this is also observed in Section 4.4.1.
4.3. Performance Analysis
4.3.1. Swarming in a GPS-Aided Environment
4.3.2. Swarming in a GPS-Denied Environment
- ❶
- The pixels within an object have similar depth values.
- ❷
- We observe that clusters corresponding to obstacles are much larger than those of drones and have at least 2000 pixels. This defines a threshold for us—we use this to designate a cluster as an obstacle. Furthermore, obstacles, being static objects, often start from the bottom of the FoV.
- ❸
- Also, there are a few clusters that correspond to random noise (far-away objects), which can be discarded if the total number of pixels forming a cluster is fewer than 8.
- ❹
- As clear from Figure 11, some of the objects in the depth map may be occluded. Due to the fact that all the drones follow the flocking principles, there must be some distance between them and, as a result, a significant difference will be present in their depth values. This allows us to readily filter out each cluster even in the presence of occlusion.
4.4. Sensitivity Analysis
- ❶
- The weights are almost the same for all the environments.
- ❷
- The model works well for almost all the environments if the value of the six-tuple , , , , , = 〈80, 1, 1, 1, 25, 5〉 for a GPS-aided environment.
- ❸
- For a GPS-denied environment, the optimal value of the weight tuple is 〈750, 6, 1, 1, 1〉.
4.4.1. Effect of the Proposed Rules
- ❶
- As per the migration rule, the drones migrated in the direction of the leader; after disabling this, the drones did not even move, and the significance of the migration force became abundantly clear.
- ❷
- Without the obstacle avoidance force, drones collided with the obstacles.
- ❸
- In the absence of the confinement force, all of the follower drones moved far ahead of the leader. However, when there was a confinement force, they remained confined within a boundary.
4.5. Scalability Analysis
- ❶
- The weights were almost the same for all swarm sizes.
- ❷
- For the GPS-aided environment, the model worked well with all the swarm sizes if the weight values , , , , , = 〈80, 1, 1, 1, 25, 5〉. The results are in line with the observations made in Section 4.4.
- ❸
- Similarly, for the GPS-denied environment, the optimal values of weights are the same as given in Section 4.4.
4.6. Real-Time Performance of
- ❶
- For a GPS-aided environment, all the steps have an extremely low latency (<0.3 ms). Additionally, the variance in execution times is very low (<).
- ❷
- The previously mentioned observation (point (1)) holds true in a GPS-denied environment as well, except for two steps: object detection and obstacle avoidance. The maximum and average latencies for these steps vary significantly across frames because these values are directly proportional to the number of objects in the depth map.
- ❸
- The step that takes the longest (with a maximum value of ≈12 ms) is object detection in the depth map using our algorithm.
- ❹
- The total latency for the GPS-aided environment is very low (<0.5 ms). The FPS (frames processed per second) can be as high as 2000 frames per second, which is orders of magnitude more than what is required (we typically need 10–20 FPS; 75 FPS is considered to be high given that traditional displays operate at 30 FPS) for drones, which are relatively slow-moving. Even for a GPS-denied environment, the maximum frame rate that can be achieved is 75 FPS (total execution time < 14 ms).
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Masehian, E.; Royan, M. Characteristics of and approaches to flocking in swarm robotics. In Applied Mechanics and Materials; Trans Tech Publications: Zurich, Switzerland, 2016; Volume 841, pp. 240–249. [Google Scholar]
- Schilling, F.; Soria, E.; Floreano, D. On the scalability of vision-based drone swarms in the presence of occlusions. IEEE Access 2022, 10, 28133–28146. [Google Scholar] [CrossRef]
- Schilling, F.; Schiano, F.; Floreano, D. Vision-based drone flocking in outdoor environments. IEEE Robot. Autom. Lett. 2021, 6, 2954–2961. [Google Scholar] [CrossRef]
- Research, G.V. Commercial Drone Market Size, Share and Trends Analysis Report by Product, by Application, by End-Use, by Propulsion Type, by Range, by Operating Mode, by Endurance, by Region, and Segment Forecasts, 2023–2030. Available online: https://www.grandviewresearch.com/industry-analysis/global-commercial-drones-market (accessed on 2 August 2023).
- Ling, H.; Luo, H.; Chen, H.; Bai, L.; Zhu, T.; Wang, Y. Modelling and simulation of distributed UAV swarm cooperative planning and perception. Int. J. Aerosp. Eng. 2021, 2021, 9977262. [Google Scholar] [CrossRef]
- Braga, R.G.; da Silva, R.X.; Ramos, A.C. Development of a Swarming Algorithm Based on Reynolds Rules to Control a Group of Multi-Rotor UAVs Using ROS. 2016. Available online: https://api.semanticscholar.org/CorpusID:221093766 (accessed on 7 August 2023).
- Braga, R.G.; Da Silva, R.C.; Ramos, A.C.; Mora-Camino, F. Collision avoidance based on reynolds rules: A case study using quadrotors. In Proceedings of the Information Technology-New Generations: 14th International Conference on Information Technology, Las Vegas, NV, USA, 10–12 April 2017; Springer: Berlin/Heidelberg, Germany, 2018; pp. 773–780. [Google Scholar]
- Eversham, J.D.; Ruiz, V.F. Experimental analysis of the Reynolds flocking model. Paladyn 2011, 2, 145–155. [Google Scholar] [CrossRef]
- Reynolds, C.W. Flocks, herds and schools: A distributed behavioral model. In Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques, Anaheim, CA, USA, 27–31 July 1987; pp. 25–34. [Google Scholar]
- Blomqvist, O.; Bremberg, S.; Zauer, R. Mathematical Modeling of Flocking Behavior; Degree Project in Mathematics, Optimization and Systems Theory, First Level; Royal Institute of Technology: Stockholm, Sweden, 2012. [Google Scholar]
- Rizk, Y.; Awad, M.; Tunstel, E.W. Cooperative heterogeneous multi-robot systems: A survey. ACM Comput. Surv. CSUR 2019, 52, 1–31. [Google Scholar] [CrossRef]
- Gunnarsson, H.; Åsbrink, A. Intelligent Drone Swarms: Motion Planning and Safe Collision Avoidance Control of Autonomous Drone Swarms. 2022. Available online: https://www.diva-portal.org/smash/record.jsf?pid=diva2%3A1677350&dswid=7935 (accessed on 7 August 2023).
- Olfati-Saber, R. Flocking for multi-agent dynamic systems: Algorithms and theory. IEEE Trans. Autom. Control 2006, 51, 401–420. [Google Scholar] [CrossRef]
- Wang, T.; Wang, C.; Liang, J.; Chen, Y.; Zhang, Y. Vision-aided inertial navigation for small unmanned aerial vehicles in GPS-denied environments. Int. J. Adv. Robot. Syst. 2013, 10, 276. [Google Scholar] [CrossRef]
- Lu, Z.; Liu, F.; Lin, X. Vision-based localization methods under GPS-denied conditions. arXiv 2022, arXiv:2211.11988. [Google Scholar]
- Balamurugan, G.; Valarmathi, J.; Naidu, V. Survey on UAV navigation in GPS denied environments. In Proceedings of the 2016 International Conference on Signal Processing, Communication, Power and Embedded System (SCOPES), Paralakhernundi, India, 3–5 October 2016; pp. 198–204. [Google Scholar]
- Morihiro, K.; Isokawa, T.; Nishimura, H.; Matsui, N. Characteristics of flocking behavior model by reinforcement learning scheme. In Proceedings of the 2006 SICE-ICASE International Joint Conference, Busan, Republic of Korea, 18–21 October 2006; pp. 4551–4556. [Google Scholar]
- Fine, B.T.; Shell, D.A. Unifying microscopic flocking motion models for virtual, robotic, and biological flock members. Auton. Robot. 2013, 35, 195–219. [Google Scholar] [CrossRef]
- Turgut, A.E.; Çelikkanat, H.; Gökçe, F.; Şahin, E. Self-organized flocking in mobile robot swarms. Swarm Intell. 2008, 2, 97–120. [Google Scholar] [CrossRef]
- Gu, D.; Wang, Z. Leader–Follower Flocking: Algorithms and Experiments. IEEE Trans. Control Syst. Technol. 2009, 17, 1211–1219. [Google Scholar] [CrossRef]
- Bhowmick, C.; Behera, L.; Shukla, A.; Karki, H. Flocking control of multi-agent system with leader-follower architecture using consensus based estimated flocking center. In Proceedings of the IECON 2016-42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 24–27 October 2016; pp. 166–171. [Google Scholar]
- Walker, P.; Amraii, S.A.; Lewis, M.; Chakraborty, N.; Sycara, K. Control of swarms with multiple leader agents. In Proceedings of the 2014 IEEE International Conference on Systems, Man, and Cybernetics (SMC), San Diego, CA, USA, 5–8 October 2014; pp. 3567–3572. [Google Scholar]
- Zheng, H.; Panerati, J.; Beltrame, G.; Prorok, A. An adversarial approach to private flocking in mobile robot teams. IEEE Robot. Autom. Lett. 2020, 5, 1009–1016. [Google Scholar] [CrossRef]
- Chen, S.; Yin, D.; Niu, Y. A survey of robot swarms’ relative localization method. Sensors 2022, 22, 4424. [Google Scholar] [CrossRef]
- Haller, N.K.; Lind, O.; Steinlechner, S.; Kelber, A. Stimulus motion improves spatial contrast sensitivity in budgerigars (Melopsittacus undulatus). Vis. Res. 2014, 102, 19–25. [Google Scholar] [CrossRef] [PubMed]
- Schilling, F.; Lecoeur, J.; Schiano, F.; Floreano, D. Learning vision-based flight in drone swarms by imitation. IEEE Robot. Autom. Lett. 2019, 4, 4523–4530. [Google Scholar] [CrossRef]
- Zhou, X.; Zhu, J.; Zhou, H.; Xu, C.; Gao, F. Ego-swarm: A fully autonomous and decentralized quadrotor swarm system in cluttered environments. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 4101–4107. [Google Scholar]
- Zanol, R.; Chiariotti, F.; Zanella, A. Drone mapping through multi-agent reinforcement learning. In Proceedings of the 2019 IEEE Wireless Communications and Networking Conference (WCNC), Marrakesh, Morocco, 15–18 April 2019; pp. 1–7. [Google Scholar]
- Baldazo, D.; Parras, J.; Zazo, S. Decentralized multi-agent deep reinforcement learning in swarms of drones for flood monitoring. In Proceedings of the 2019 27th European Signal Processing Conference (EUSIPCO), Coruna, Spain, 2–6 September 2019; pp. 1–5. [Google Scholar]
- Barksten, M.; Rydberg, D. Extending Reynolds’ Flocking Model to a Simulation of Sheep in the Presence of a Predator; Degree Project in Computer Science, First Level; Royal Institute of Technology: Stockholm, Sweden, 2013. [Google Scholar]
- Virágh, C.; Vásárhelyi, G.; Tarcai, N.; Szörényi, T.; Somorjai, G.; Nepusz, T.; Vicsek, T. Flocking algorithm for autonomous flying robots. Bioinspirat. Biomimet. 2014, 9, 025012. [Google Scholar] [CrossRef]
- Reynolds, C. Boids Background and Update. 2001. Available online: http://www.red3d.com/cwr/boids/ (accessed on 7 August 2023).
- Müller, H.; Niculescu, V.; Polonelli, T.; Magno, M.; Benini, L. Robust and efficient depth-based obstacle avoidance for autonomous miniaturized uavs. arXiv 2022, arXiv:2208.12624. [Google Scholar]
- Lin, J.; Zhu, H.; Alonso-Mora, J. Robust vision-based obstacle avoidance for micro aerial vehicles in dynamic environments. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 2682–2688. [Google Scholar]
- Siegwart, R.; Scaramuzza, D. Range Sensors. Available online: http://www.cs.columbia.edu/~allen/F15/NOTES/rangesensing.pdf (accessed on 10 October 2022).
- University of Tsukuba, C. Vision Image. Available online: https://home.cvlab.cs.tsukuba.ac.jp/dataset (accessed on 20 September 2022).
- Unity. Unity Scene. Available online: https://docs.unity3d.com/Manual/index.html (accessed on 2 March 2022).
- Unity Technologies. Unity. Available online: https://unity.com/frontpage (accessed on 7 August 2023).
- Unreal Engine. Available online: https://www.unrealengine.com/en-US (accessed on 7 August 2023).
- C#. Available online: https://learn.microsoft.com/en-us/dotnet/csharp/ (accessed on 4 February 2022).
- Unity Asset 2. Available online: https://assetstore.unity.com/packages/3d/environments/urban/city-low-poly-2455 (accessed on 6 August 2022).
- Unity Asset 1. Available online: https://assetstore.unity.com/packages/3d/environments/urban/polygon-city-low-poly-3d-art-by-synty-95214 (accessed on 10 August 2022).
- RealCamera. Available online: https://robu.in/product/high-definition-1200tvl-coms-camera-2-8mm-lens-fpv-camera-fpv-rc-drone-quadcopter/ (accessed on 4 February 2023).
- Verma, H.; Bhamu, N. Simulation Results. Available online: https://drive.google.com/drive/folders/1T_Gk5irVTQTxdUJGYH93ccMLhA5MEUYi?usp=sharing (accessed on 23 June 2023).
- Shaders. Available online: https://docs.unity3d.com/Manual/SL-ShaderPrograms.html (accessed on 4 January 2023).
- Viscido, S.V.; Wethey, D.S. Quantitative analysis of fiddler crab flock movement: Evidence for ‘selfish herd’behaviour. Anim. Behav. 2002, 63, 735–741. [Google Scholar] [CrossRef]
- Conradt, L.; Krause, J.; Couzin, I.D.; Roper, T.J. “Leading according to need” in self-organizing groups. Am. Nat. 2009, 173, 304–312. [Google Scholar] [CrossRef]
- Couzin, I.D.; Krause, J.; Franks, N.R.; Levin, S.A. Effective leadership and decision-making in animal groups on the move. Nature 2005, 433, 513–516. [Google Scholar] [CrossRef]
- Lopez, U.; Gautrais, J.; Couzin, I.D.; Theraulaz, G. From behavioural analyses to models of collective motion in fish schools. Interface Focus 2012, 2, 693–707. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.; Martin, A. Comparison of hard-core and soft-core potentials for modelling flocking in free space. arXiv 2009, arXiv:0905.2260. [Google Scholar]
- Szabó, P.; Nagy, M.; Vicsek, T. Turning with the others: Novel transitions in an SPP model with coupling of accelerations. In Proceedings of the 2008 Second IEEE International Conference on Self-Adaptive and Self-Organizing Systems, Venice, Italy, 20–24 October 2008; pp. 463–464. [Google Scholar]
- Levine, H.; Rappel, W.J.; Cohen, I. Self-organization in systems of self-propelled particles. Phys. Rev. E 2000, 63, 017101. [Google Scholar] [CrossRef] [PubMed]
- BeagleBone. BeagleBone Black. Available online: https://beagleboard.org/black (accessed on 20 June 2023).
- Drone Swarm Simulator. Available online: https://github.com/srsarangi/droneswarm (accessed on 8 August 2023).








| Work | Year | Flock’s Characteristics | Environment | Sensor Used | Algorithm | ||
|---|---|---|---|---|---|---|---|
| Leader-Follower | Self-Organized | GPS-Denied | Existence of Obstacles | ||||
| Eversham et al. [8] | 2011 | × | ✓ | × | × | GPS | - |
| Blomqvist et al. [10] | 2012 | × | ✓ | × | ✓ | GPS | - |
| Barksten et al. [30] | 2013 | × | ✓ | × | × | GPS | - |
| Walker et al. [22] | 2014 | ✓ | × | ✓ | ✓ | Distance-based | - |
| Virágh et al. [31] | 2014 | × | ✓ | × | × | GPS | - |
| Bhowmick et al. [21] | 2016 | ✓ | × | × | × | GPS | - |
| Braga et al. [6] | 2016 | × | ✓ | × | × | GPS | - |
| Schilling et al. [26] | 2019 | × | ✓ | ✓ | × | Vision-based | ML-based |
| Zheng et al. [23] | 2020 | ✓ | ✓ | × | × | GPS | - |
| Schilling et al. [3] | 2021 | × | ✓ | ✓ | × | Vision-based | ML-based |
| Chen et al. [24] | 2022 | × | ✓ | ✓ | × | Distance-based | - |
| Schilling et al. [2] | 2022 | × | ✓ | ✓ | × | Vision-based | ML-based |
| 2023 | ✓ | ✓ | ✓ | ✓ | Vision-based | Traditional CV | |
| Symbol | Meaning |
|---|---|
| , | Velocity and position of the drone, respectively. |
| , | Position of the leader drone and of the obstacle, respectively. |
| Radius of the confined area around the leader. | |
| , , , | Weights of the cohesion, separation, alignment, migration, confinement, |
| , , | and obstacle avoidance rules, respectively, in the final velocity of the drone. |
| , , , | Cohesion, separation, alignment, migration, |
| , , | confinement, and obstacle avoidance vector, respectively. |
| Parameter | Value |
|---|---|
| Simulator | Unity 2020.3.40f1 |
| Operating system | Windows 10 |
| Main memory | 1 TB |
| RAM | 32 GB |
| CPU | Intel(R) Core(TM) i7-8700 CPU @ 3.20 GHz |
| GPU | NVIDIA Ge-Force GT 710 |
| Video memory | 2 GB |
| Experiment | Weights | Performance | ||||||
|---|---|---|---|---|---|---|---|---|
| No. | #Collisions | Confined | ||||||
| 1 | 10 | 1.0 | 1.0 | 1.0 | 2 | 1.0 | 3 | × |
| 2 | 60 | 1.1 | 1.5 | 1.0 | 15 | 5.0 | 5 | ✓ |
| 3 | 75 | 1.2 | 1.0 | 1.1 | 25 | 5.0 | 3 | ✓ |
| 4 | 77 | 1.2 | 1.0 | 1.1 | 21 | 5.0 | 1 | × |
| 5 | 77 | 1.2 | 1.0 | 1.1 | 21 | 5.0 | 0 | ✓ |
| 6 | 78 | 1.0 | 1.2 | 1.0 | 24 | 4.9 | 1 | ✓ |
| 7 | 80 | 1.1 | 1.0 | 1.2 | 23 | 5.1 | 2 | ✓ |
| 8 | 80 | 11.0 | 1.0 | 1.2 | 23 | 5.1 | 2 | ✓ |
| 9 | 81 | 1.0 | 5.5 | 1.0 | 25 | 4.8 | 3 | ✓ |
| 10 | 81 | 1.0 | 1.5 | 4.0 | 25 | 4.8 | 1 | ✓ |
| 11 | 82 | 1.0 | 1.2 | 1.0 | 10 | 4.9 | 4 | × |
| 12 | 100 | 1.1 | 1.0 | 1.0 | 10 | 10.0 | 5 | ✓ |
| Experiment | Weights | Performance | |||||
|---|---|---|---|---|---|---|---|
| No. | #Collisions | Confined | |||||
| 1 | 10 | 1.0 | 1.0 | 1 | 1 | 3 | × |
| 2 | 100 | 5.0 | 1.5 | 5 | 1 | 4 | ✓ |
| 3 | 300 | 8.0 | 1.0 | 1 | 1 | 4 | ✓ |
| 4 | 500 | 6.0 | 1.0 | 1 | 1 | 5 | ✓ |
| 5 | 800 | 6.5 | 1.2 | 1 | 1 | 2 | ✓ |
| 6 | 750 | 5.5 | 1.0 | 1 | 1 | 1 | ✓ |
| 7 | 820 | 6.1 | 1.0 | 1 | 1 | 3 | × |
| 8 | 800 | 6.2 | 1.5 | 1 | 1 | 1 | ✓ |
| 9 | 750 | 6.0 | 1.1 | 1 | 1 | 0 | ✓ |
| 10 | 800 | 6.0 | 0.9 | 1 | 1 | 1 | ✓ |
| 11 | 810 | 6.2 | 1.2 | 1 | 5 | 0 | × |
| 12 | 800 | 6.2 | 1.0 | 3 | 1 | 1 | × |
| Scene | Weights | Performance | ||||||
|---|---|---|---|---|---|---|---|---|
| #Collisions | Confined | |||||||
| 1 | 78 | 1.0 | 1.0 | 1.0 | 21 | 5.0 | 0 | ✓ |
| 2 | 77 | 1.2 | 1.0 | 1.1 | 21 | 5.0 | 0 | ✓ |
| 3 | 77 | 1.1 | 1.5 | 1.0 | 25 | 5.0 | 0 | ✓ |
| 4 | 80 | 1.2 | 1.0 | 1.1 | 25 | 5.1 | 0 | ✓ |
| Scene | Weights | Performance | |||||
|---|---|---|---|---|---|---|---|
| #Collisions | Confined | ||||||
| 1 | 750 | 6.1 | 1.0 | 1 | 1 | 0 | ✓ |
| 2 | 750 | 6.0 | 1.1 | 1 | 1 | 0 | ✓ |
| 3 | 700 | 6.2 | 1.5 | 1 | 1 | 0 | ✓ |
| 4 | 800 | 6.0 | 1.0 | 1 | 1 | 0 | ✓ |
| Experiment | Swarm | Radius | Weights | Performance | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| No. | Size | () | #Collisions | Confined | ||||||
| 1 | 5 | 30 | 81.0 | 1.0 | 1.2 | 1.0 | 25 | 4.8 | 0 | ✓ |
| 2 | 7 | 35 | 79.0 | 1.1 | 1.5 | 1.1 | 25 | 4.7 | 0 | ✓ |
| 3 | 8 | 35 | 80.0 | 1.0 | 1.3 | 1.0 | 22 | 5.0 | 0 | ✓ |
| 4 | 10 | 40 | 79.5 | 1.0 | 1.4 | 1.1 | 24 | 4.8 | 0 | ✓ |
| 5 | 12 | 45 | 80.0 | 1.2 | 1.4 | 1.0 | 23 | 5.0 | 0 | ✓ |
| 6 | 15 | 50 | 79.0 | 1.1 | 1.4 | 1.0 | 24 | 5.0 | 0 | ✓ |
| Experiment | Swarm | Weights | Performance | |||||
|---|---|---|---|---|---|---|---|---|
| No. | Size | #Collisions | Confined | |||||
| 1 | 5 | 790 | 6.0 | 1 | 1.0 | 1.0 | 0 | ✓ |
| 2 | 7 | 808 | 6.2 | 1.2 | 1.0 | 1.0 | 0 | ✓ |
| 3 | 8 | 810 | 6.0 | 0.9 | 1.0 | 1.0 | 0 | ✓ |
| 4 | 10 | 800 | 6.5 | 1.0 | 1.0 | 1.0 | 0 | ✓ |
| 5 | 12 | 795 | 6.0 | 1.0 | 1.0 | 1.0 | 0 | ✓ |
| 6 | 15 | 800 | 6.0 | 1.0 | 1.0 | 1.0 | 0 | ✓ |
| Steps | Environment | |||||
|---|---|---|---|---|---|---|
| GPS-Aided | GPS-Denied | |||||
| Max | Min | Avg | Max | Min | Avg | |
| Object detection | - | - | - | 11.87 | 8.17 | 9.95 |
| Cohesion | 0.04 | 0.01 | 0.02 | 0.02 | 0.01 | 0.01 |
| Separation | 0.28 | 0.21 | 0.24 | 0.27 | 0.23 | 0.25 |
| Alignment | 0.01 | 0.01 | 0.01 | 0.02 | 0.01 | 0.01 |
| Migration | 0.01 | 0.01 | 0.01 | - | - | - |
| Confinement | 0.05 | 0.03 | 0.04 | 0.01 | 0.01 | 0.01 |
| Obstacle avoidance | 0.02 | 0.02 | 0.02 | 1.23 | 0.84 | 1.03 |
| Total time | 0.44 | 0.39 | 0.42 | 13.55 | 09.32 | 11.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhamu, N.; Verma, H.; Dixit, A.; Bollard, B.; Sarangi, S.R. SmrtSwarm: A Novel Swarming Model for Real-World Environments. Drones 2023, 7, 573. https://doi.org/10.3390/drones7090573
Bhamu N, Verma H, Dixit A, Bollard B, Sarangi SR. SmrtSwarm: A Novel Swarming Model for Real-World Environments. Drones. 2023; 7(9):573. https://doi.org/10.3390/drones7090573
Chicago/Turabian StyleBhamu, Nikita, Harshit Verma, Akanksha Dixit, Barbara Bollard, and Smruti R. Sarangi. 2023. "SmrtSwarm: A Novel Swarming Model for Real-World Environments" Drones 7, no. 9: 573. https://doi.org/10.3390/drones7090573
APA StyleBhamu, N., Verma, H., Dixit, A., Bollard, B., & Sarangi, S. R. (2023). SmrtSwarm: A Novel Swarming Model for Real-World Environments. Drones, 7(9), 573. https://doi.org/10.3390/drones7090573







