Predictive State Observer-Based Aircraft Distributed Formation Tracking Considering Input Delay and Saturations
Abstract
:1. Introduction
2. Preliminaries and Problem Statement
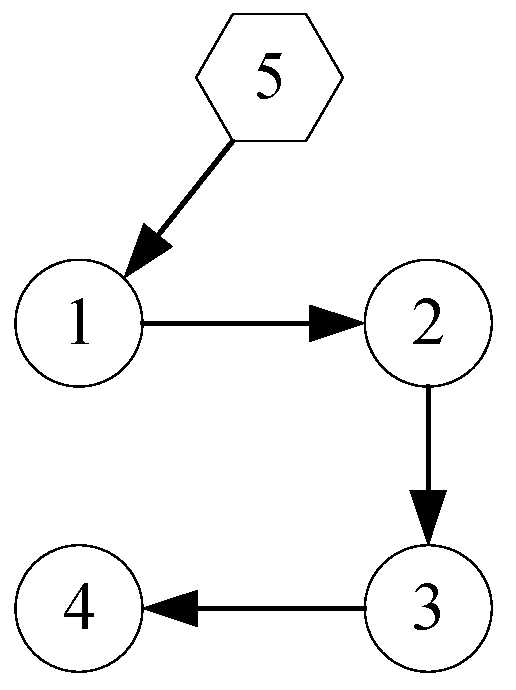
2.1. Basic Concepts on Graph Theory
2.2. Definitions and Lemmas
3. Mathematical Model of Fixed-Wing Aircraft
Problem Formulation
4. PESO-TVFTC Protocol Design and Analysis
4.1. PESO-TVFTC Protocol Design
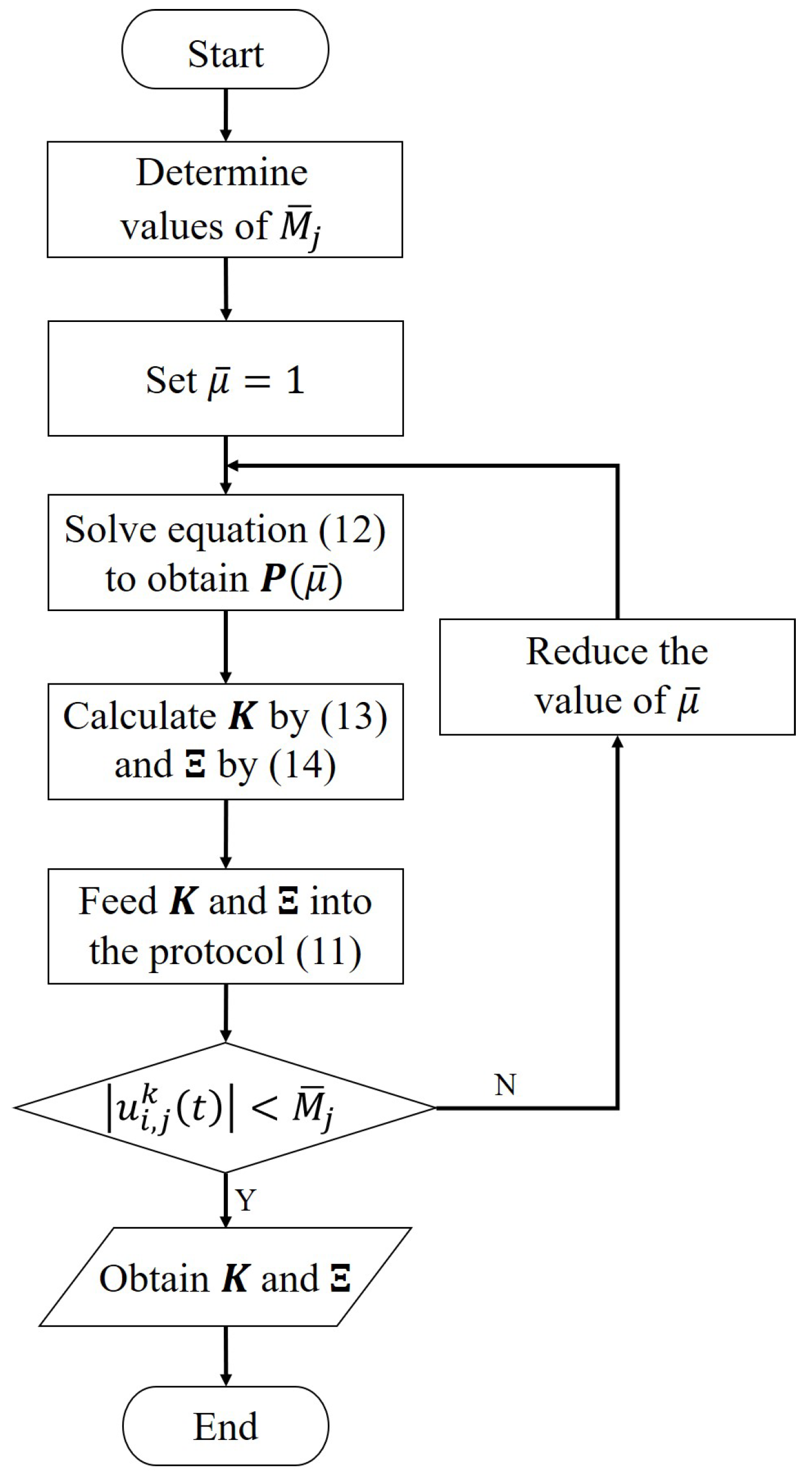
4.2. Low Gain Feedback Design Algorithm for Formation Tracking Control
| Algorithm 1 The parameters of protocol (11) can be specified in 4 steps: |
| Step 1. For systems (7) satisfying ANCBC, there exist a tuning parameter and a unique positive definite matrix satisfying the following algebraic Riccati equation: Step 2. The low gain feedback matrix can be specified by: Step 3. The gain matrix can be specified by: Step 4. The monotonically increasing function can be designed as |
4.3. Stability Analysis
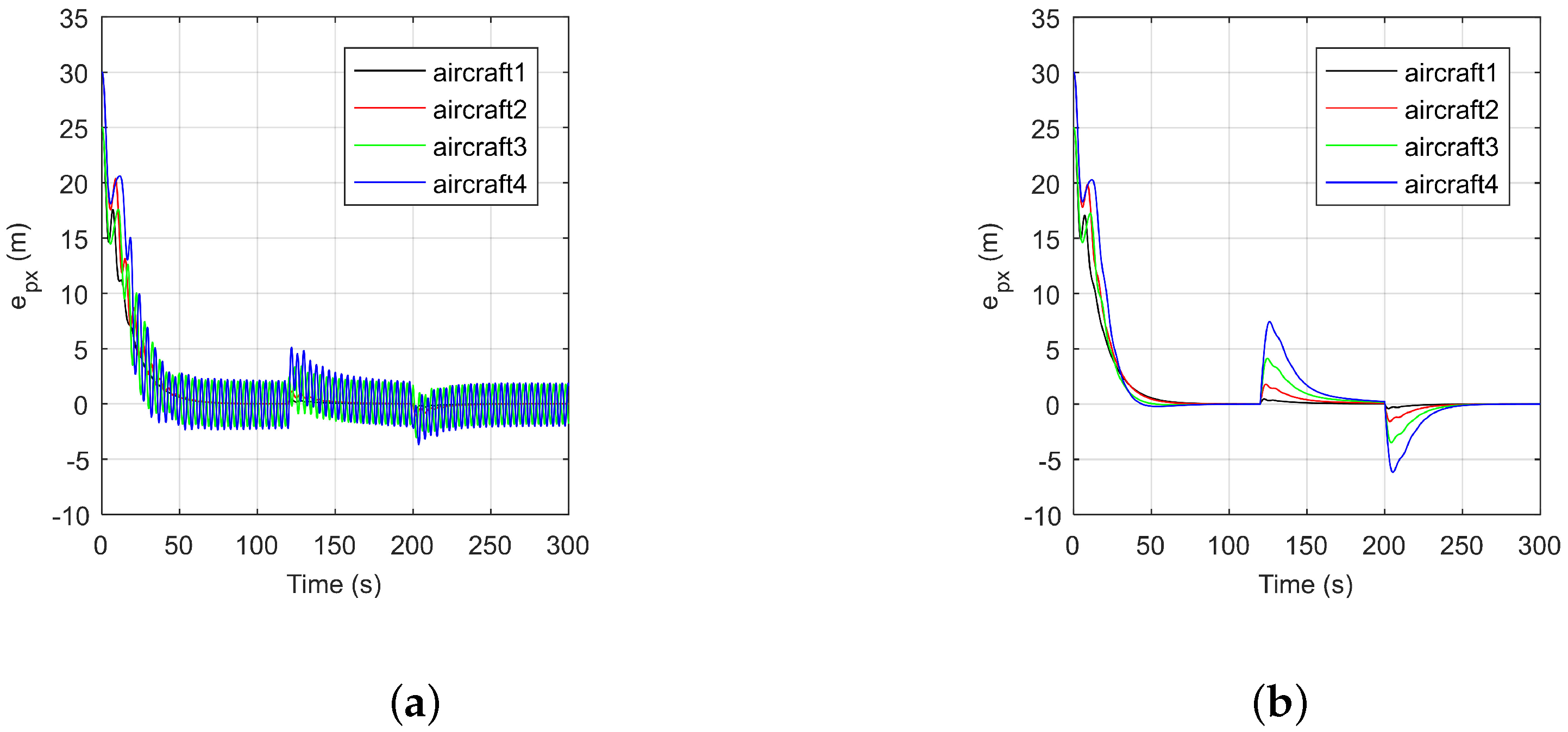
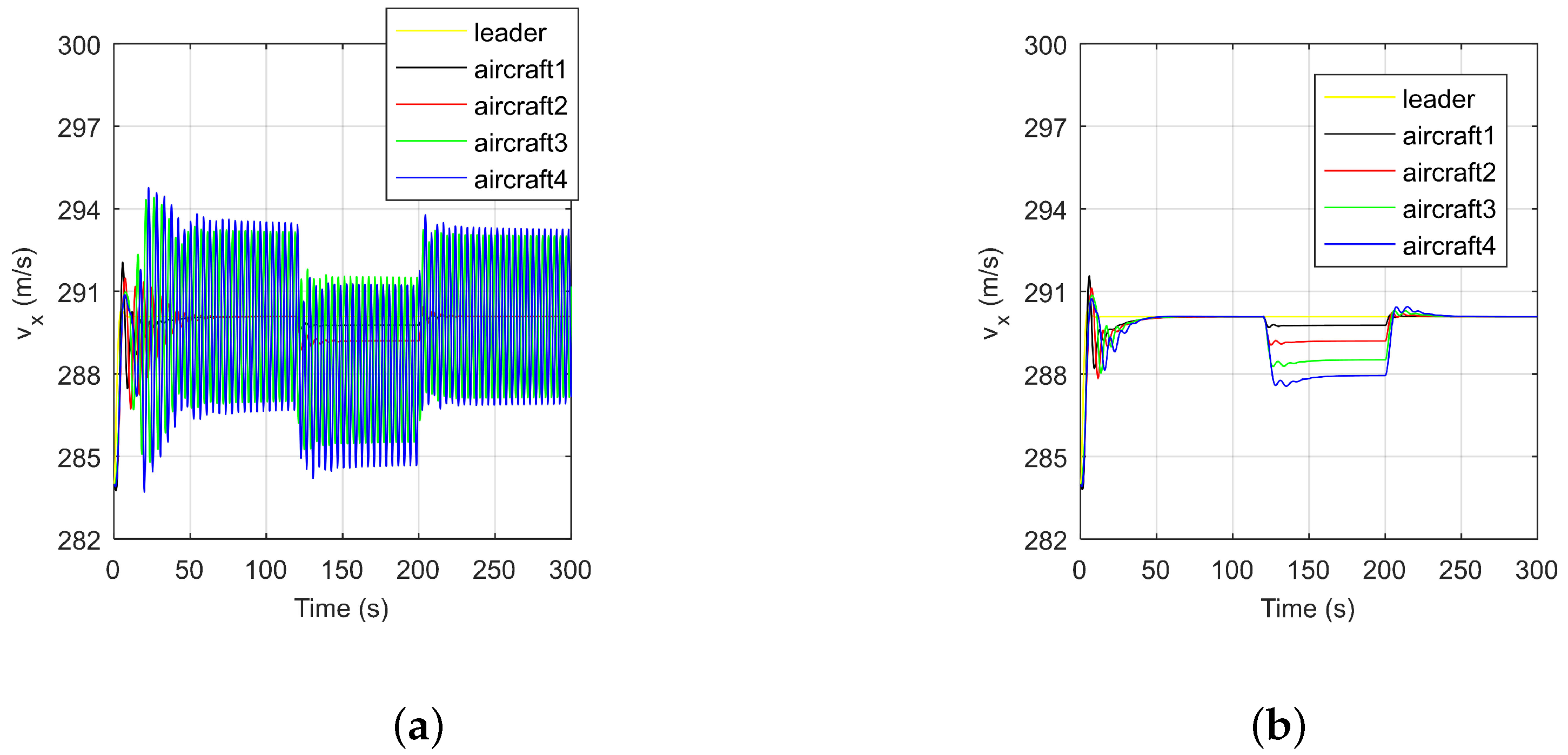
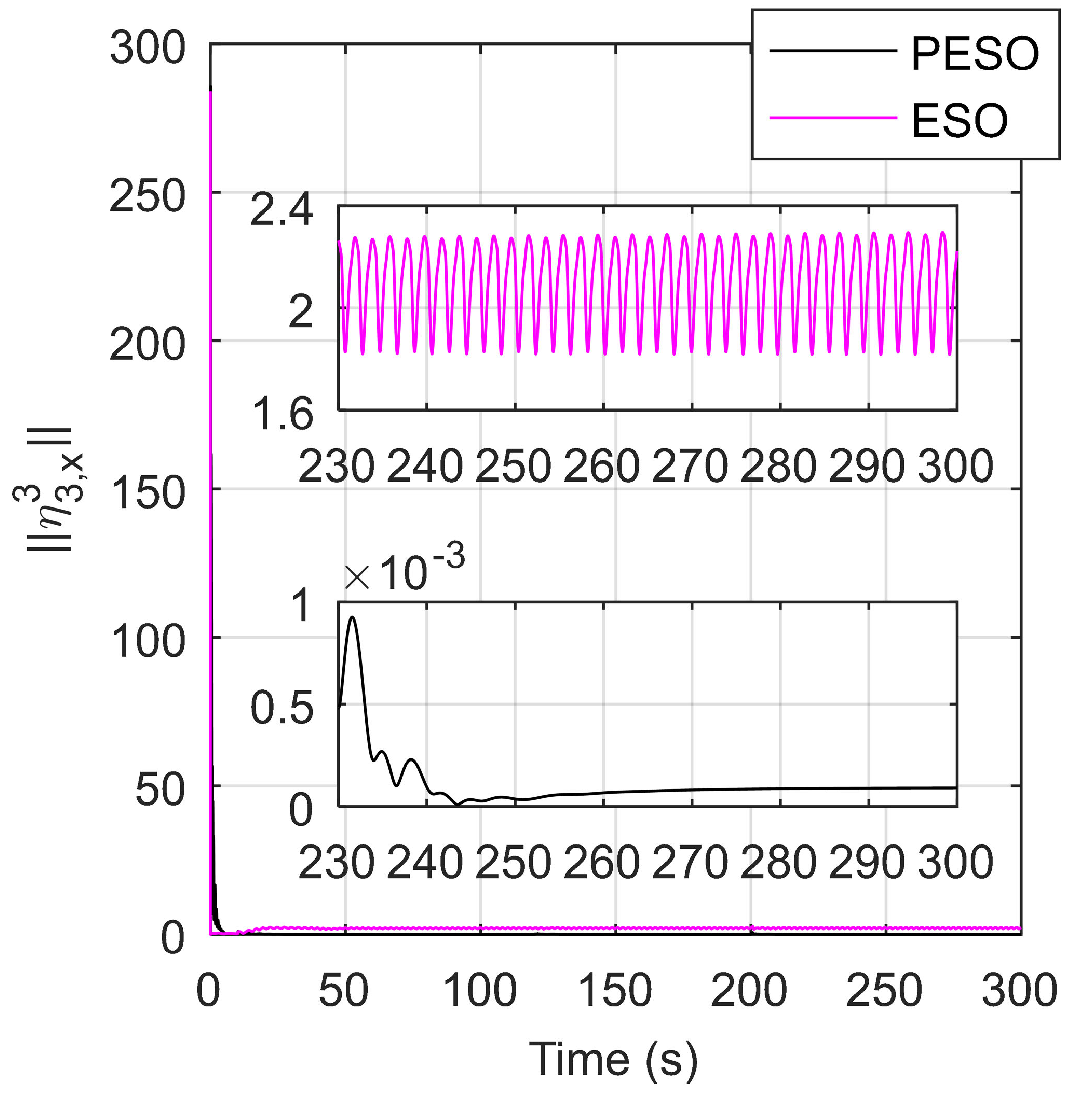
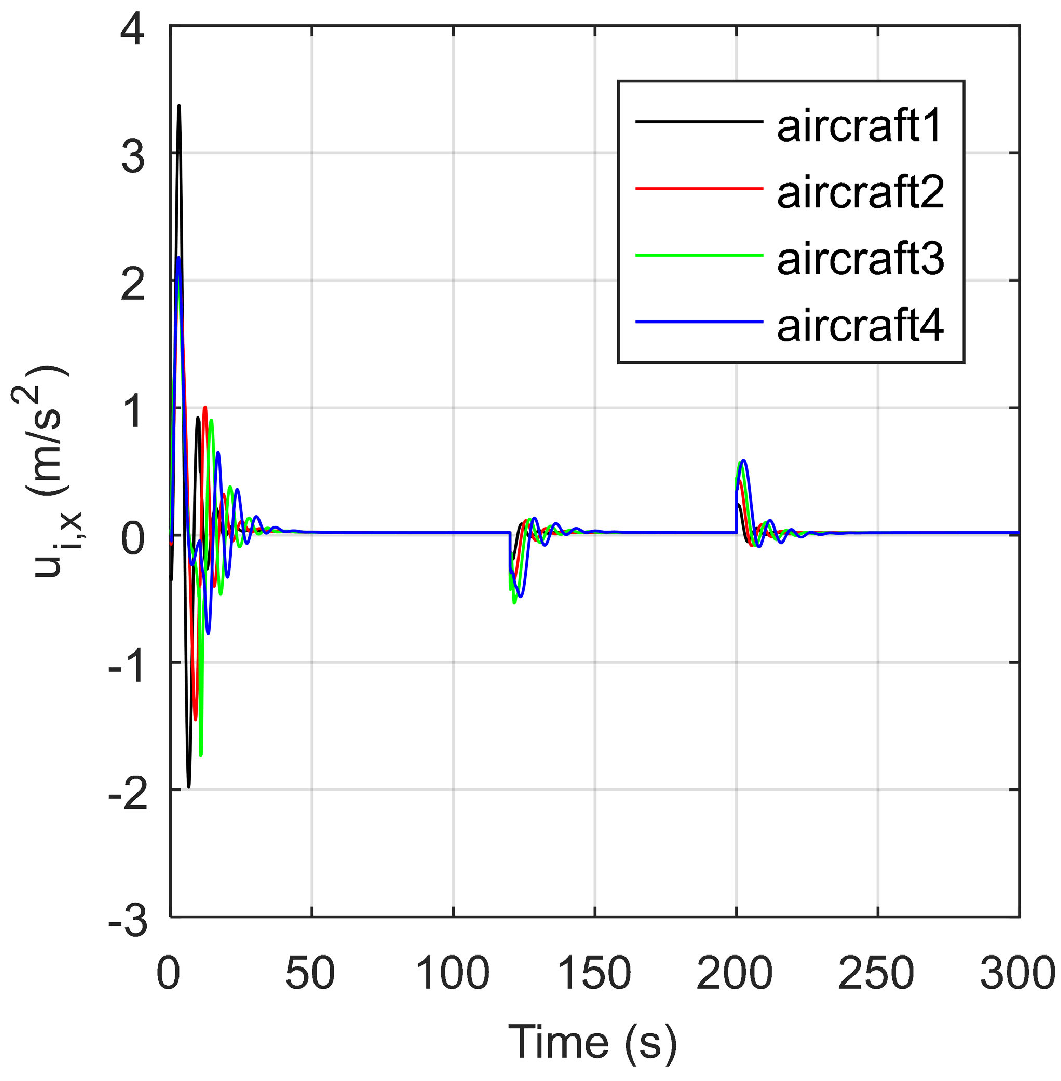
5. Simulation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Lemma 6
References
- Challa, V.R.; Ratnoo, A. On maneuverability of fixed-Wing unmanned aerial vehicle formations. J. Guid. Control Dyn. 2021, 44, 142–149. [Google Scholar] [CrossRef]
- Monje, C.A.; Garrido, S.; Moreno, L.; Balaguer, C. UAVs formation approach using fast marching square methods. IEEE Aerosp. Electron. Syst. Mag. 2020, 35, 36–46. [Google Scholar] [CrossRef]
- Yasin, J.N.; Mohamed, S.A.S.; Haghbayan, M.; Heikkonen, J.; Tenhunen, H.; Plosila, J. Unmanned Aerial Vehicles (UAVs): Collision Avoidance Systems and Approaches. IEEE Access 2020, 8, 105139–105155. [Google Scholar] [CrossRef]
- Huang, S.; Teo, R.S.H.; Tan, K.K. Collision avoidance of multi unmanned aerial vehicles: A review. Annu. Rev. Control 2019, 48, 147–164. [Google Scholar] [CrossRef]
- Bolandi, H.; Pari, H.M.; Izadi, M.R. Multiple spacecraft formation and station-keeping control in presence of static attitude constraint via decentralized virtual structure approach. J. Aerosp. Eng. 2022, 35, 04021104. [Google Scholar] [CrossRef]
- Wu, Y.; Cao, X.; Zheng, P.; Zeng, Z. Variable structure-based decentralized relative attitude-coordinated control for satellite formation. IEEE Aerosp. Electron. Syst. Mag. 2012, 27, 18–25. [Google Scholar] [CrossRef]
- Balch, T.; Arkin, R.C. Behavior-based formation control for multirobot teams. IEEE Trans. Robot. Autom. 1998, 14, 926–939. [Google Scholar] [CrossRef]
- Monteiro, S.; Bicho, E. A dynamical systems approach to behavior-based formation control. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation, Washington DC, USA, 11–15 May 2002; Volume 14, pp. 2606–2611. [Google Scholar]
- Ren, W.; Beard, R.W. Consensus seeking in multiagent systems under dynamically changing interaction topologies. IEEE Trans. Autom. Control. 2005, 50, 655–661. [Google Scholar] [CrossRef]
- Ren, W. Consensus strategies for cooperative control of vehicle formations. IET Contr. Theory Appl. 2007, 1, 505–512. [Google Scholar] [CrossRef]
- Dong, X.; Zhou, Y.; Ren, Z.; Zhong, Y. Time-varying formation control for unmanned aerial vehicles with switching interaction topologies. Control Eng. Pract. 2016, 46, 26–36. [Google Scholar] [CrossRef]
- Dong, X.; Zhou, Y.; Ren, Z.; Zhong, Y. Time-varying formation tracking for second-order multi-agent systems subjected to switching topologies With application to quadrotor formation flying. IEEE Trans. Ind. Electron. 2017, 64, 5014–5024. [Google Scholar] [CrossRef]
- Dong, X.; Hu, G. Time-varying formation tracking for linear multiagent systems with multiple leaders. IEEE Trans. Autom. Control 2017, 62, 3658–3664. [Google Scholar] [CrossRef]
- Wu, Y.; Gou, J.; Hu, X.; Huang, Y. A new consensus theory-based method for formation control and obstacle avoidance of UAVs. Aerosp. Sci. Technol. 2020, 107, 106332. [Google Scholar] [CrossRef]
- Li, Z.; Ren, W.; Liu, X.; Fu, M. Consensus of multi-agent systems with general linear and lipschitz nonlinear dynamics using distributed adaptive protocols. IEEE Trans. Autom. Control 2013, 58, 1786–1791. [Google Scholar] [CrossRef]
- Li, Z.; Wen, G.; Duan, Z.; Ren, W. Designing fully distributed consensus protocols for linear multi-agent systems with directed graphs. IEEE Trans. Autom. Control 2015, 60, 1152–1157. [Google Scholar] [CrossRef]
- Chen, C.; Xie, K.; Lewis, F.L.; Xie, S.; Davoudi, A. Fully distributed resilience for adaptive exponential synchronization of heterogeneous multiagent systems against actuator faults. IEEE Trans. Autom. Control 2019, 64, 3347–3354. [Google Scholar] [CrossRef]
- Jiang, W.; Wen, G.; Peng, Z.; Huang, T.; Rahmani, A. Fully distributed formation-containment control of heterogeneous linear multiagent systems. IEEE Trans. Autom. Control 2019, 64, 3889–3896. [Google Scholar] [CrossRef]
- Zhang, W.; Dong, C.; Ran, M.; Liu, Y. Fully distributed time-varying formation tracking control for multiple quadrotor vehicles via finite-time convergent extended state observer. Chin. J. Aeronaut. 2020, 33, 2907–2920. [Google Scholar] [CrossRef]
- Cheng, B.; Wu, Z.; Li, Z. Distributed edge-based event-triggered formation control. IEEE T. Cybern. 2021, 51, 1241–1252. [Google Scholar] [CrossRef]
- Nandiganahalli, J.S.; Kwon, C.; Huang, I. Delay-tolerant Adaptive Robust Control for Unmanned Aerial System. In Proceedings of the 2018 AIAA Information Systems-AIAA Infotech @ Aerospace, Kissimmee, FL, USA, 8–12 January 2018; p. 78. [Google Scholar]
- Muskardin, T.; Coelho, A.; Della-Noce, E.R.; Ollero, A.; Kondak, K. Energy-based cooperative control for landing fixed-wing uavs on mobile platforms under communication delays. IEEE Robot. Autom. Lett. 2020, 5, 5081–5088. [Google Scholar] [CrossRef]
- Muslimov, T.Z.; Munasypov, R.A. Consensus-based cooperative control of parallel fixed-wing UAV formations via adaptive backstepping. Aerosp. Sci. Technol. 2021, 109, 106416. [Google Scholar] [CrossRef]
- Zhen, Z.; Tao, G.; Xu, Y.; Song, G. Multivariable adaptive control based consensus flight control system for UAVs formation. Aerosp. Sci. Technol. 2019, 93, 105336. [Google Scholar] [CrossRef]
- Wang, X.; Saberi, A.; Stoorvogel, A.A.; Grip, F.H.; Yang, T. Consensus in the network with uniform constant communication delay. In Proceedings of the IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 3252–3257. [Google Scholar]
- Zong, X.; Li, T.; Zhang, J.F. Consensus conditions of continuous-time multi-agent systems with time-delays and measurement noises. Automatica 2019, 99, 412–419. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, R.; Chen, G. Consensus control of second-order time-delayed multiagent systems in noisy environments using absolute velocity and relative position measurements. IEEE T. Cybern. 2021, 51, 5364–5374. [Google Scholar] [CrossRef] [PubMed]
- Huang, R.; Ding, Z.; Cao, Z. Distributed output feedback consensus control of networked homogeneous systems with large unknown actuator and sensor delays. Automatica 2020, 122, 109249. [Google Scholar] [CrossRef]
- Artstein, Z. Linear systems with delayed controls: A reduction. IEEE Trans. Autom. Control 1982, 27, 869–879. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, C.; Meng, Y. Fully distributed time-varying formation tracking control of linear multi-agent systems with input delay and disturbances. Syst. Control Lett. 2020, 146, 104814. [Google Scholar] [CrossRef]
- Zhou, B.; Lin, Z. Consensus of high-order multi-agent systems with large input and communication delays. Automatica 2014, 50, 452–464. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, Z.; Wang, C.; Ding, Z. Cascade structure predictive observer design for consensus control with applications to UAVs formation flying. Automatica 2020, 121, 109200. [Google Scholar] [CrossRef]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Wang, C.; Zuo, Z.; Qi, Z.; Ding, Z. Predictor-based extended-state-observer design for consensus of mass with delays and disturbances. IEEE Trans. Cybern. 2019, 49, 1259–1269. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Peng, Z.; Rahmani, A.; Hu, W.; Wen, G. Distributed consensus of linear MASs with an unknown leader via a predictive extended state observer considering input delay and disturbances. Neurocomputing 2018, 315, 465–475. [Google Scholar] [CrossRef]
- Liu, L.; Cui, Y.; Liu, Y.; Tong, S. Observer-based adaptive neural output feedback constraint controller design for switched systems under average dwell time. IEEE Trans. Circuits Syst. I-Regul. Pap. 2021, 68, 3901–3912. [Google Scholar] [CrossRef]
- Kong, L.; He, W.; Liu, Z.; Yu, X.; Silvestre, C. Adaptive tracking control with global performance for output-constrained MIMO nonlinear systems. IEEE Trans. Autom. Control 2023, 68, 3760–3767. [Google Scholar] [CrossRef]
- Lin, Z. Low Gain Feedback, 1st ed.; Springer: London, UK, 1999; pp. 43–64. [Google Scholar]
- Su, H.; Chen, M.Z.; Lam, J.; Lin, Z. Semi-global leader-following consensus of linear multi-agent systems with input saturation via low gain feedback. IEEE Trans. Circuits Syst. I-Regul. Pap. 2013, 60, 1881–1889. [Google Scholar] [CrossRef]
- Chu, H.; Yuan, J.; Zhang, W. Observer-based adaptive consensus tracking for linear multi-agent systems with input saturation. IET Contr. Theory Appl. 2015, 9, 2124–2131. [Google Scholar] [CrossRef]
- Yang, T.; Stoorvogel, A.A.; Grip, H.F.; Saberi, A. Semi-global regulation of output synchronization for heterogeneous network of non-introspective, invertible agents subject to actuator saturation. Int. J. Robust Nonlinear Control 2014, 24, 548–566. [Google Scholar] [CrossRef]
- Su, H.; Ye, Y.; Qiu, Y.; Gao, Y.; Chen, M.Z. Semi-global output consensus for discrete-time switching networked systems subject to input saturation and external disturbances. IEEE Trans. Cybern. 2019, 49, 3934–3945. [Google Scholar] [CrossRef]
- Wang, B.; Chen, W.; Zhang, B. Semi-global robust tracking consensus for multi-agent uncertain systems with input saturation via metamorphic low-gain feedback. Automatica 2019, 103, 363–373. [Google Scholar] [CrossRef]
- Wang, B.; Chen, W.; Wang, J.; Zhang, B.; Shi, P. Semiglobal tracking cooperative control for multiagent systems with input saturation: A multiple saturation levels framework. IEEE Trans. Autom. Control 2021, 66, 1215–1222. [Google Scholar] [CrossRef]
- Ran, M.; Wang, Q.; Dong, C.; Xie, L. Active disturbance rejection control for uncertain time-delay nonlinear systems. Automatica 2020, 112, 108692. [Google Scholar] [CrossRef]
- Yu, J.; Dong, X.; Li, Q.; Ren, Z. Cooperative integrated practical time-varying formation tracking and control for multiple missiles system. Aerosp. Sci. Technol. 2019, 93, 105300. [Google Scholar] [CrossRef]
- Obuz, S.; Klotz, J.R.; Kamalapurkar, R.; Dixon, W. Unknown time-varying input delay compensation for uncertain nonlinear systems. Automatica 2017, 76, 222–229. [Google Scholar] [CrossRef]
- Ran, M.; Wang, Q.; Dong, C. Active disturbance rejection control for uncertain nonaffine-in-control nonlinear systems. IEEE Trans. Autom. Control 2017, 62, 5830–5836. [Google Scholar] [CrossRef]
- Chakraborty, A.; Seiler, P.; Balas, G. Applications of linear and nonlinear robustness analysis techniques to the F/A-18 flight control laws. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10–13 August 2009; p. 5675. [Google Scholar]
- Acquatella, P.; van Kampen, E.J.; Chu, Q.P. Incremental backstepping for robust nonlinear flight control. In Proceedings of the 2nd CEAS Specialist Conference on Guidance, Navigation and Control, Delft, The Netherlands, 12–14 April 2013; pp. 1444–1463. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Liu, X.; Tan, W.; Deng, Y.; Jiao, J.; Zhao, M. Predictive State Observer-Based Aircraft Distributed Formation Tracking Considering Input Delay and Saturations. Drones 2024, 8, 23. https://doi.org/10.3390/drones8010023
Sun L, Liu X, Tan W, Deng Y, Jiao J, Zhao M. Predictive State Observer-Based Aircraft Distributed Formation Tracking Considering Input Delay and Saturations. Drones. 2024; 8(1):23. https://doi.org/10.3390/drones8010023
Chicago/Turabian StyleSun, Liguo, Xiaoyu Liu, Wenqian Tan, Yi Deng, Junkai Jiao, and Mengjie Zhao. 2024. "Predictive State Observer-Based Aircraft Distributed Formation Tracking Considering Input Delay and Saturations" Drones 8, no. 1: 23. https://doi.org/10.3390/drones8010023
APA StyleSun, L., Liu, X., Tan, W., Deng, Y., Jiao, J., & Zhao, M. (2024). Predictive State Observer-Based Aircraft Distributed Formation Tracking Considering Input Delay and Saturations. Drones, 8(1), 23. https://doi.org/10.3390/drones8010023





