MPC-Based Dynamic Trajectory Spoofing for UAVs
Abstract
:1. Introduction
- (1)
- A novel non-cooperative UAV dynamic trajectory spoofing method is proposed, which significantly reduces the errors between the actual trajectory of the UAV and the desired trajectory of the spoofer.
- (2)
- An MPC algorithm has been employed to optimize the spoofing operation. Control input of the spoofing model is optimized using predictive information, enabling the UAV to follow the intended trajectory of the spoofer more precisely.
- (3)
- Extensive simulation experiments have been conducted in various scenarios, demonstrating that the proposed method significantly enhances the spoofing effect, leading to a considerable reduction in cumulative errors and a marked improvement in spoofing accuracy.
2. UAV Trajectory Control Model
3. UAV Dynamic Trajectory Spoofing
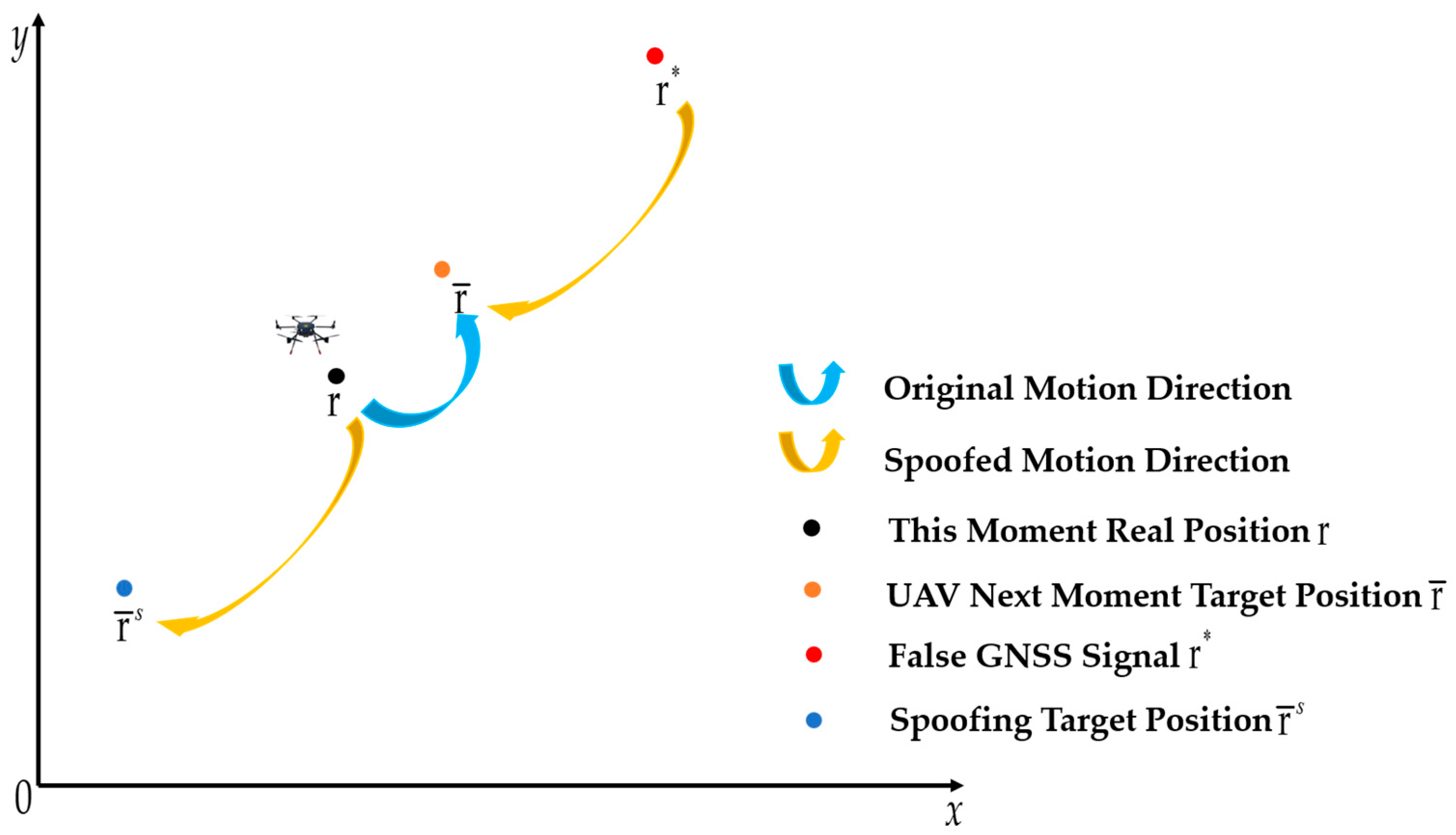
3.1. The Methodology of Dynamic Trajectory Spoofing
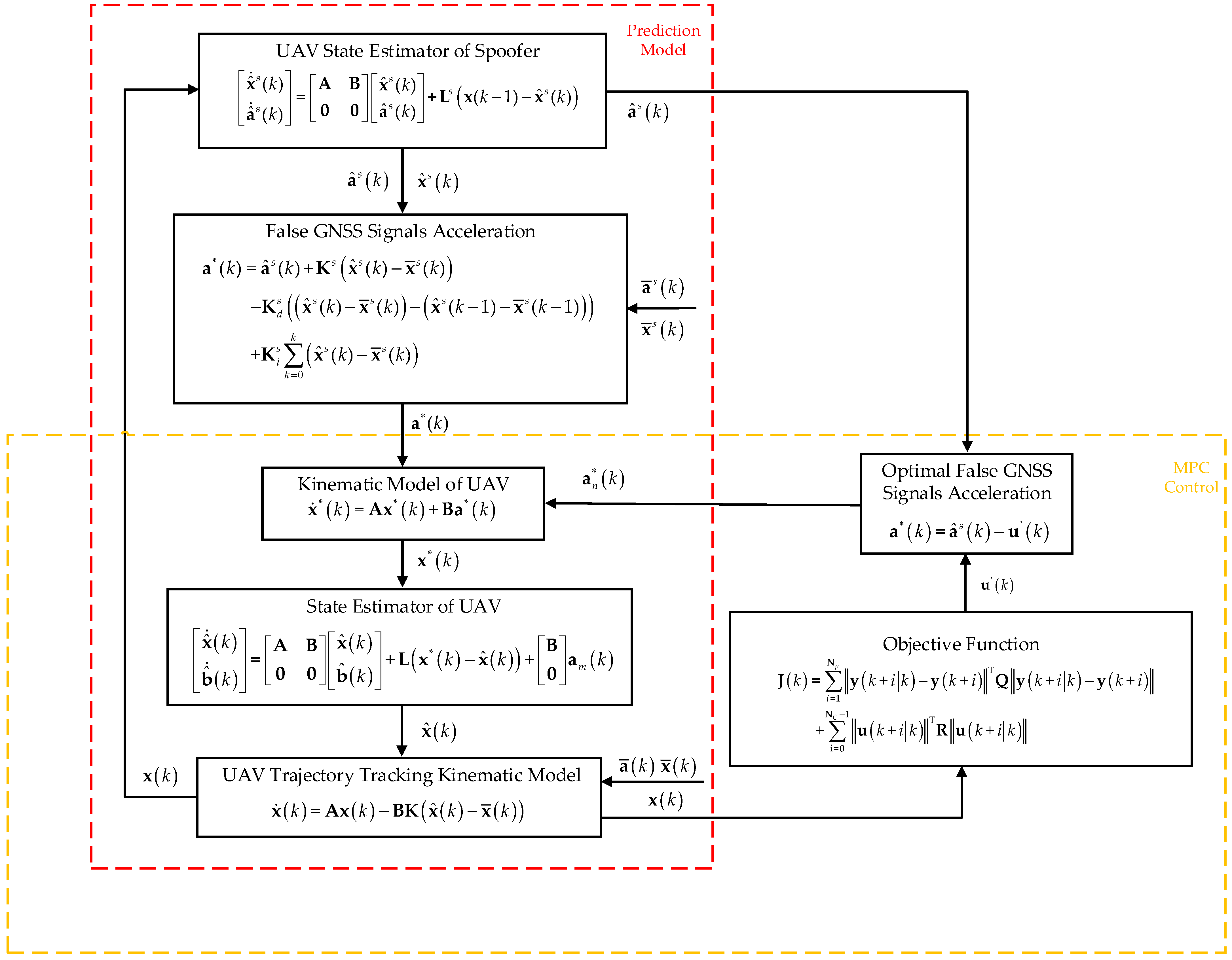
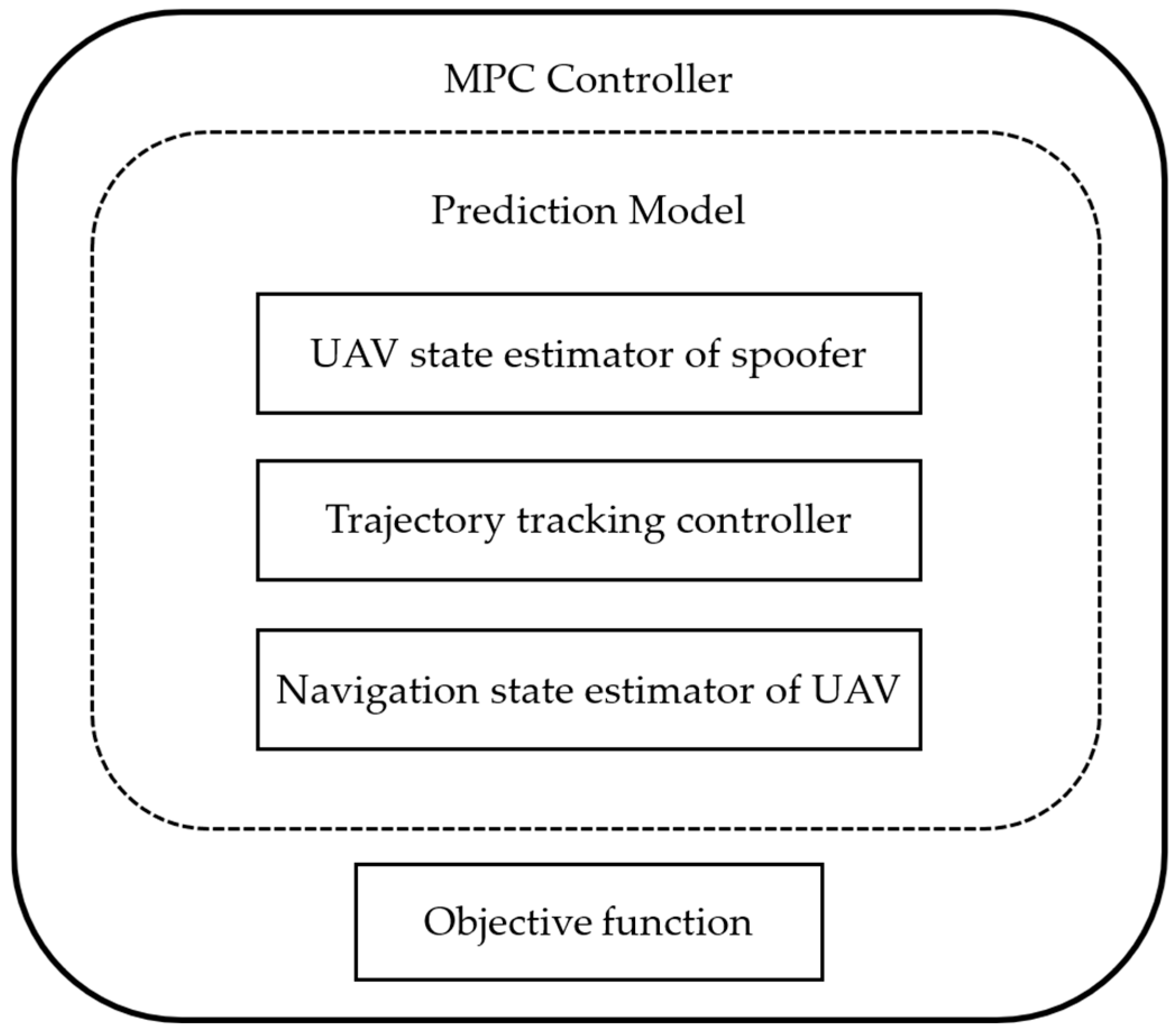
3.2. MPC-Based Dynamic Trajectory Spoofing Method
- (1)
- Estimate the system state at time instance ;
- (2)
- Use the input to calculate the system output based on the spoofing model and the objective function (16). Here is the control horizon and is the prediction horizon;
- (3)
- Substitute the input and output into the objective function to determine the optimal input, and use the optimal input as the current time instance input in the spoofing model;
- (4)
- Return to step (2) and continue the calculations from the subsequent time instance, and apply the aforementioned steps repeatedly until the end of the spoofing operation.
| Algorithm 1. MPC-based UAV dynamic trajectory spoofing algorithm procedure |
| Input: Reference trajectory, spoofing trajectory |
| 1: Initialization: x = 0 |
| 2: for k = 1 until meeting terminal condition |
| 3: Use state estimator of spoofer to get UAV state |
| 4: Acquire with and spoofing trajectory |
| 5: Calculate with Equation (19) |
| 6: Substitute into the double-integrator kinematic model to get |
| 7: Use state estimator of UAV to get |
| 8: Calculate UAV actual state with Equations (1) and (11) |
| 9: Calculate the output with |
| 10: Substitute input and output to objective function |
| 11: if minimizes objective function |
| 12: Update input with |
| 13: Substitute to step 5 to 9 |
| 14: end if |
| 15: Update: Set k = k + 1 |
| 16: end for |
| Output: |
4. Simulation Verification and Discussion
- Experiment 1: Triangular Reference Trajectory (see Figure 4).

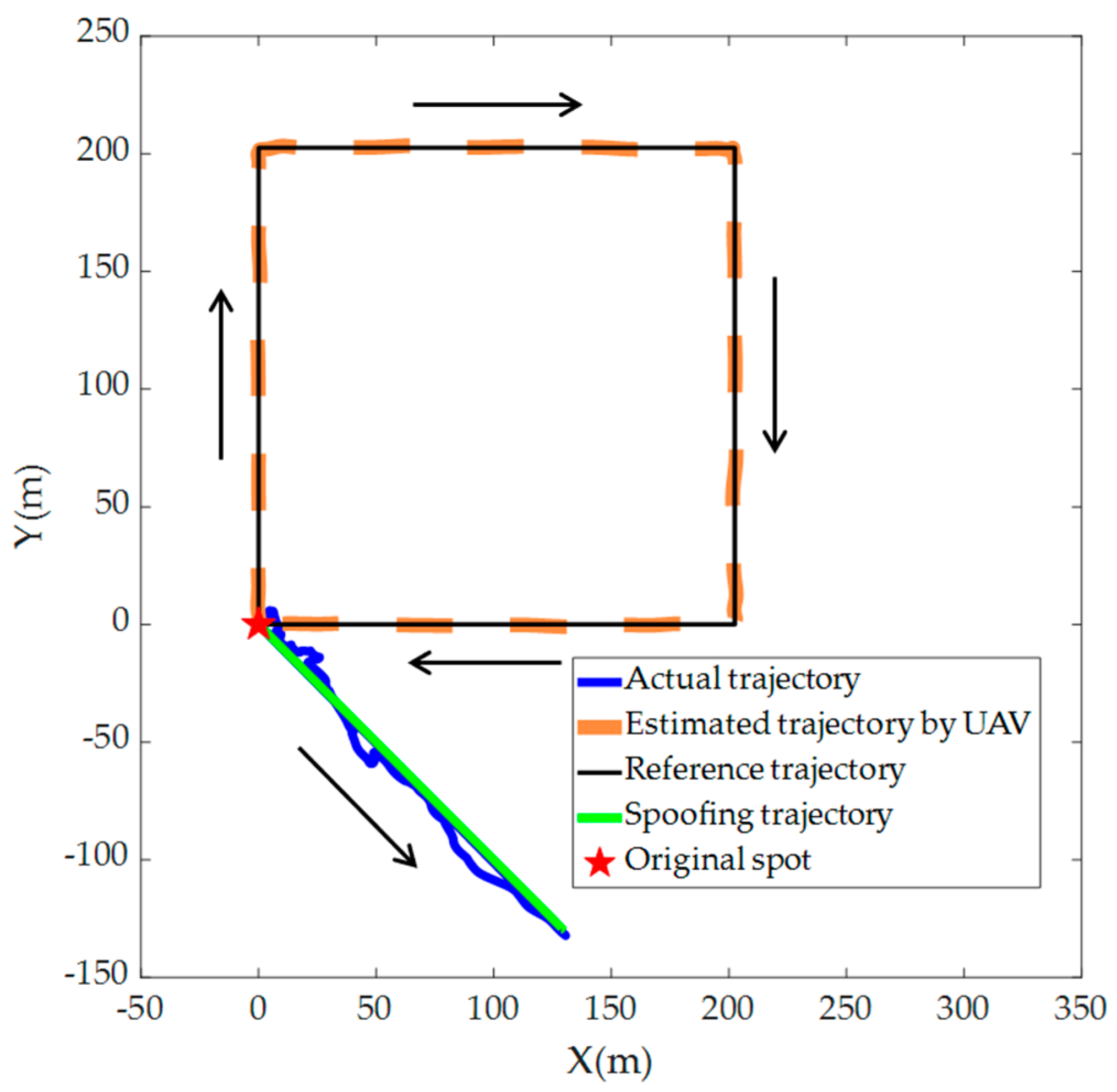
- Experiment 2: Square Reference Trajectory (see Figure 7).
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAV | Unmanned aircraft vehicle |
| MPC | Model predictive control |
| GNSS | Global navigation satellite system |
| INS | Inertial navigation system |
| IMU | Inertial measurement unit |
| SDR | Software-defined radio |
References
- Muchiri, G.; Kimathi, S. A review of applications and potential applications of UAV. In Proceedings of the Sustainable Research and Innovation Conference, Riyadh, Saudi Arabia, 19–22 February 2022; pp. 280–283. [Google Scholar]
- Tsouros, D.; Bibi, S.; Sarigiannidis, P. A review on UAV-based applications for precision agriculture. Information 2019, 11, 349. [Google Scholar] [CrossRef]
- Fan, B.; Li, Y.; Zhang, R. Review on the technological development and application of UAV systems. Chin. J. Electron. 2020, 29, 199–207. [Google Scholar] [CrossRef]
- Perikleous, D.; Koustas, G.; Velanas, S.; Margariti, K.; Velanas, P.; Gonzalez-Aguilera, D. A novel drone design based on a reconfigurable unmanned aerial vehicle for wildfire management. Drones 2024, 8, 203. [Google Scholar] [CrossRef]
- Kovács, B.; Vörös, F.; Vas, T.; Károly, K.; Gajdos, M.; Varga, Z. Safety and security-specific application of multiple drone sensors at movement areas of an aerodrome. Drones 2024, 8, 231. [Google Scholar] [CrossRef]
- Novák, A.; Kováčiková, K.; Kandera, B.; Sedláčková, A.N. Global navigation satellite systems signal vulnerabilities in unmanned aerial vehicle operations: Impact of affordable software-defined radio. Drones 2024, 8, 109. [Google Scholar] [CrossRef]
- Mugnai, M.; Teppati Losé, M.; Herrera-Alarcón, E.; Baris, G.; Satler, M.; Avizzano, C. An efficient framework for autonomous UAV missions in partially-unknown GNSS-denied environments. Drones 2023, 7, 471. [Google Scholar] [CrossRef]
- Lemieszewski, Ł.; Prochacki, S. Decision support for autonomous drone flight based on satellite navigation signal. Procedia Comput. Sci. 2023, 225, 1691–1698. [Google Scholar] [CrossRef]
- Zhang, R.; Hao, G.; Zhang, K. Unmanned aerial vehicle navigation in underground structure inspection: A review. Geol. J. 2023, 58, 2454–2472. [Google Scholar] [CrossRef]
- Lemieszewski, Ł.; Borkowski, P.; Radomska-Zalas, A.; Dobryakova, L.; Ochin, E. Cybersecurity of the Unmanned Marine Vehicles in the Conditions of Partial or Complete Interruption Multi-GNSS Signals by Jamming and/or Spoofing. In Emerging Challenges in Intelligent Management Information Systems; Springer: Cham, Switzerland, 2024; pp. 83–94. [Google Scholar]
- Ochin, E.; Lemieszewski, A. Chapter 3—Security of GNSS. In GPS and GNSS Technology in Geosciences; Petropoulos, G.P., Srivastava, P.K., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 51–74. [Google Scholar]
- Warner, J.; Johnston, R. A simple demonstration that the global positioning system (GPS) is vulnerable to spoofing. J. Secur. Adm. 2002, 25, 19–27. [Google Scholar]
- Warner, J.; Johnston, R. GPS spoofing countermeasures. Homel. Secur. J. 2003, 25, 19–27. [Google Scholar]
- Humphreys, T.; Ledvina, B.; Psiaki, M. Assessing the spoofing threat: Development of a portable GPS civilian spoofer. In Proceedings of the ION GNSS Conference, Savannah, GA, USA, 16–19 September 2008; pp. 2314–2325. [Google Scholar]
- Shepard, D.; Bhatti, J.; Humphreys, T. Evaluation of smart grid and civilian UAV vulnerability to GPS spoofing attacks. In Proceedings of the ION GNSS Conference, Nashville, TN, USA, 17–21 September 2012; pp. 3591–3605. [Google Scholar]
- Seo, S.; Lee, B.; Im, S.; Jee, G. Effect of spoofing on unmanned aerial vehicle using counterfeited GPS signal. J. Position. Navig. Timing 2015, 4, 57–65. [Google Scholar] [CrossRef]
- Norhashim, N.; Kamal, N.; Sahwee, Z.; Shah, S.; Sathyamoorthy, D.; Alfian, N. Effect of Global Navigation Satellite Signal (GNSS) spoofing on unmanned aerial vehicles (UAVs) via field measurement. In Proceedings of the IEEE 16th Malaysia International Conference on Communication (MICC), Kuala Lumpur, Malaysia, 10–12 December 2023; pp. 41–45. [Google Scholar]
- Feng, W.; Friedt, J.; Goavec-Merou, G.; Meyer, F. Software-defined radio implemented GPS spoofing and its computationally efficient detection and suppression. IEEE Aerosp. Electron. Syst. Mag. 2021, 36, 36–52. [Google Scholar] [CrossRef]
- Ferreira, R.; Gaspar, J.; Sebasti, A.; Souto, N. A software defined radio based anti-UAV mobile system with jamming and spoofing capabilities. Sensors 2022, 22, 1487. [Google Scholar] [CrossRef] [PubMed]
- He, D.; Qiao, Y.; Chen, S. A friendly and low-cost technique for capturing non-cooperative civilian unmanned aerial vehicles. IEEE Netw. 2019, 33, 146–151. [Google Scholar] [CrossRef]
- Chae, M.; Park, S.; Choi, S.; Choi, C. Commercial fixed-wing drone redirection system using GNSS deception. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 5699–5713. [Google Scholar] [CrossRef]
- Alharasees, O.; Abdalla, M.; Kale, U. Analysis of human factors analysis and classification system (HFACS) of UAV operators. In Proceedings of the New Trends in Aviation Development (NTAD), Novy Smokovec, Slovakia, 24–25 November 2022; pp. 10–14. [Google Scholar]
- Alharasees, O.; Adali, O.; Kale, U. Human factors in the age of autonomous UAVs: Impact of artificial intelligence on operator performance and safety. In Proceedings of the International Conference on Unmanned Aircraft Systems, Warsaw, Poland, 6–9 June 2023; pp. 798–805. [Google Scholar]
- Alharasees, O.; Adali, O.; Kale, U. UAV operators’ cognition and automation: Comprehensive measurements. In Proceedings of the New Trends in Aviation Development (NTAD), Stary Smokovec, Slovakia, 23–24 November 2023; pp. 15–20. [Google Scholar]
- Lee, Y.; Yeom, J.; Jung, B. A novel array antenna-based GNSS spoofing detection and mitigation technique. In Proceedings of the IEEE 20th Consumer Communications & Networking Conference, Las Vegas, NV, USA, 8–11 January 2023; pp. 489–492. [Google Scholar]
- Burbank, J.; Greene, T.; Kaabouch, N. Detecting and mitigating attacks on GPS devices. Sensors 2024, 24, 5529. [Google Scholar] [CrossRef]
- Nayfeh, M.; Li, Y.; Shamaileh, K.A.; Devabhaktuni, V.; Kaabouch, N. Machine learning modeling of GPS features with applications to UAV location spoofing detection and classification. Comput. Secur. 2023, 126, 103085. [Google Scholar] [CrossRef]
- Aissou, G.; Slimane, H.O.; Benouadah, S.; Kaabouch, N. Tree-based supervisedmachine learningmodels for detecting GPS spoofing attacks on UAS. In Proceedings of the IEEE 12th Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON), New York, NY, USA, 1–4 December 2021; pp. 0649–0653. [Google Scholar]
- Jiang, P.; Wu, H.; Xin, C. DeepPOSE: Detecting GPS spoofing attack via deep recurrent neural network. Digit. Commun. Netw. 2022, 8, 791–803. [Google Scholar] [CrossRef]
- Talaei Khoei, T.; Ismail, S.; Kaabouch, N. Dynamic selection techniques for detecting GPS spoofing attacks on UAVs. Sensors 2022, 22, 662. [Google Scholar] [CrossRef]
- Jayaweera, M. A novel deep learning GPS anti-spoofing system with DOA time-series estimation. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar]
- Varshosaz, M.; Afary, A.; Mojaradi, B.; Saadatseresht, M.; Ghanbari Parmehr, E. Spoofing detection of civilian UAVs using visual odometry. ISPRS Int. J. Geo-Inf. 2020, 9, 6. [Google Scholar] [CrossRef]
- Finn, A.; Jia, M.; Li, Y.; Yuan, J. Detecting Stealthy GPS spoofing attack against uavs using onboard sensors. In Proceedings of the IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Vancouver, BC, Canada, 20–23 May 2024; pp. 1–6. [Google Scholar]
- Kerns, A.; Shepard, D.; Bhatti, J. Unmanned aircraft capture and control via GPS spoofing. J. Field Robot. 2014, 31, 617–636. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, M.; Tang, K. Position deceptive tracking controller and parameters analysis via error characteristics for unmanned aerial vehicle. Int. J. Adv. Robot. Syst. 2018, 16, 172988141882540. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, M.; Tang, K. Covert spoofing algorithm of UAV based on GPS/INS-integrated navigation. IEEE Trans. Veh. Technol. 2019, 68, 6557–6564. [Google Scholar] [CrossRef]
- Gao, Y.; LI, G. A GNSS instrumentation covert directional spoofing algorithm for UAV equipped with tightly-coupled GNSS/IMU. IEEE Trans. Instrum. Meas. 2023, 72, 99. [Google Scholar] [CrossRef]
- Geng, X.; Guo, Y.; Tang, K.; Wu, W.; Ren, Y. Research on covert directional spoofing method for INS/GNSS loosely integrated navigation. IEEE Trans. Veh. Technol 2023, 72, 5654–5663. [Google Scholar] [CrossRef]
- Dong, P.; Xiang, X.; Liang, Y. The research on channel estimation and signal-noise ratio estimation based on minimum error entropy Kalman filter for single carrier frequency domain equalization system. Int. J. Commun. Syst. 2023, 36, e5403. [Google Scholar] [CrossRef]
- Hu, G.; Xu, L.; Gao, B. Robust unscented Kalman filter-based decentralized multi sensor information fusion for INS/GNSS/CNS integration in hypersonic vehicle navigation. IEEE Trans. Instrum. Meas. 2023, 72, 1–11. [Google Scholar]
- Kiswanto, G.; Baskoro, A.; Hasymi, Z.; Ko, T. Tool wear monitoring in micro-milling based on digital twin technology with an extended Kalman filter. J. Manuf. Mater. Process 2024, 8, 108. [Google Scholar]
- Li, D.; Felix, J.; Chin, Y.; Jusuf, L.; Susanto, L. Integrated extended Kalman filter and deep learning platform for electric vehicle battery health prediction. Appl. Sci. 2024, 14, 4354. [Google Scholar] [CrossRef]
- Richalet, J.; Rault, A.; Testud, J. Model predictive heuristic control: Applications to industrial processes. Automatica 1978, 14, 413–428. [Google Scholar] [CrossRef]
- Yang, L.; Wang, X.; Zhou, Y.; Liu, Z.; Shen, L. Online predictive visual servo control for constrained target tracking of fixed-wing unmanned aerial vehicles. Drones 2024, 8, 136. [Google Scholar] [CrossRef]
- Wang, S.; Guo, J.; Mao, Y.; Wang, H.; Fan, J. Research on the model predictive trajectory tracking control of unmanned ground tracked vehicles. Drones 2023, 7, 496. [Google Scholar] [CrossRef]
- Li, B.; Song, C.; Bai, S.; Huang, J.; Ma, R.; Wan, K.; Neretin, E. Multi-UAV trajectory planning during cooperative tracking based on a fusion algorithm integrating MPC and standoff. Drones 2023, 7, 196. [Google Scholar] [CrossRef]
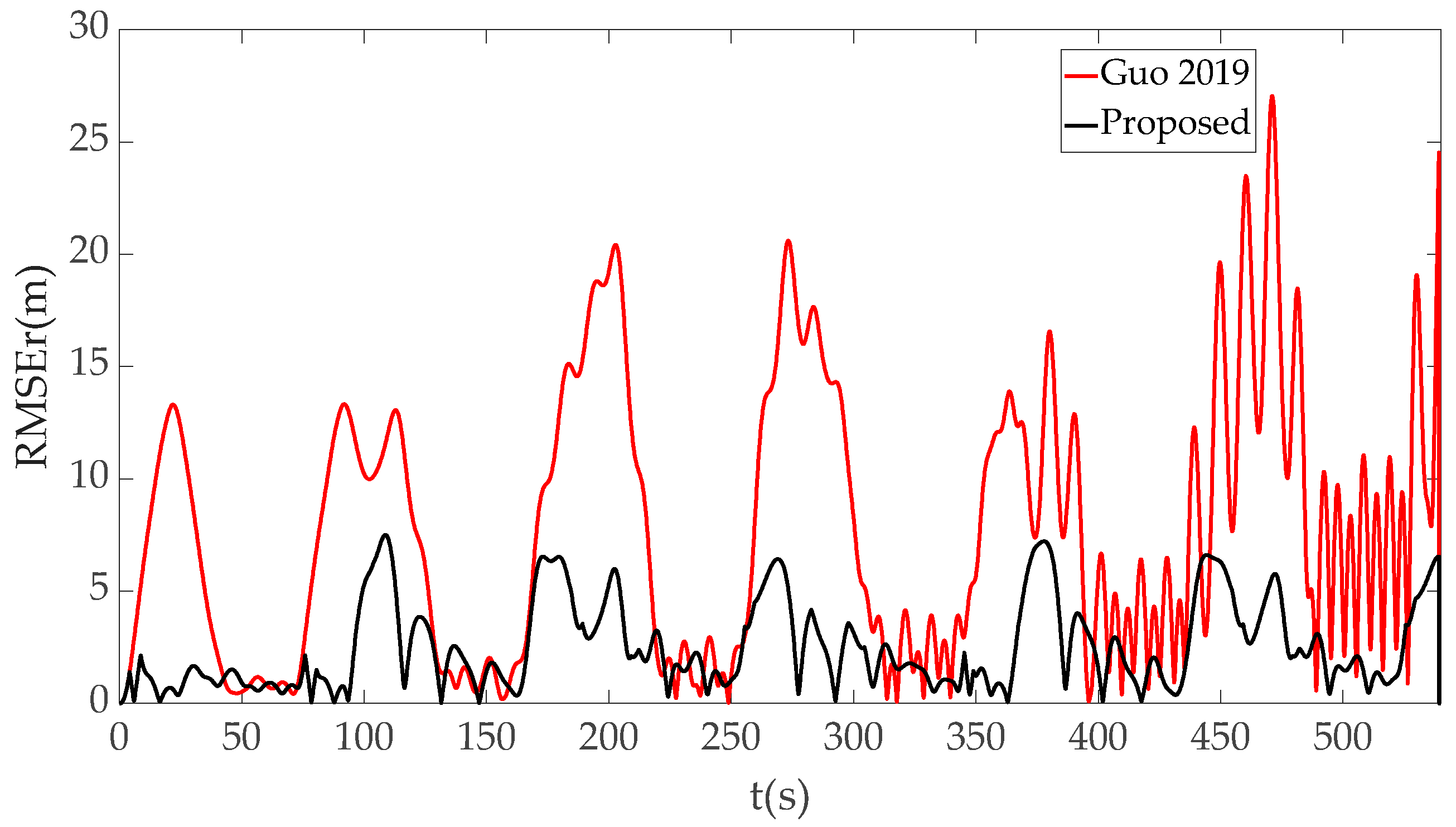

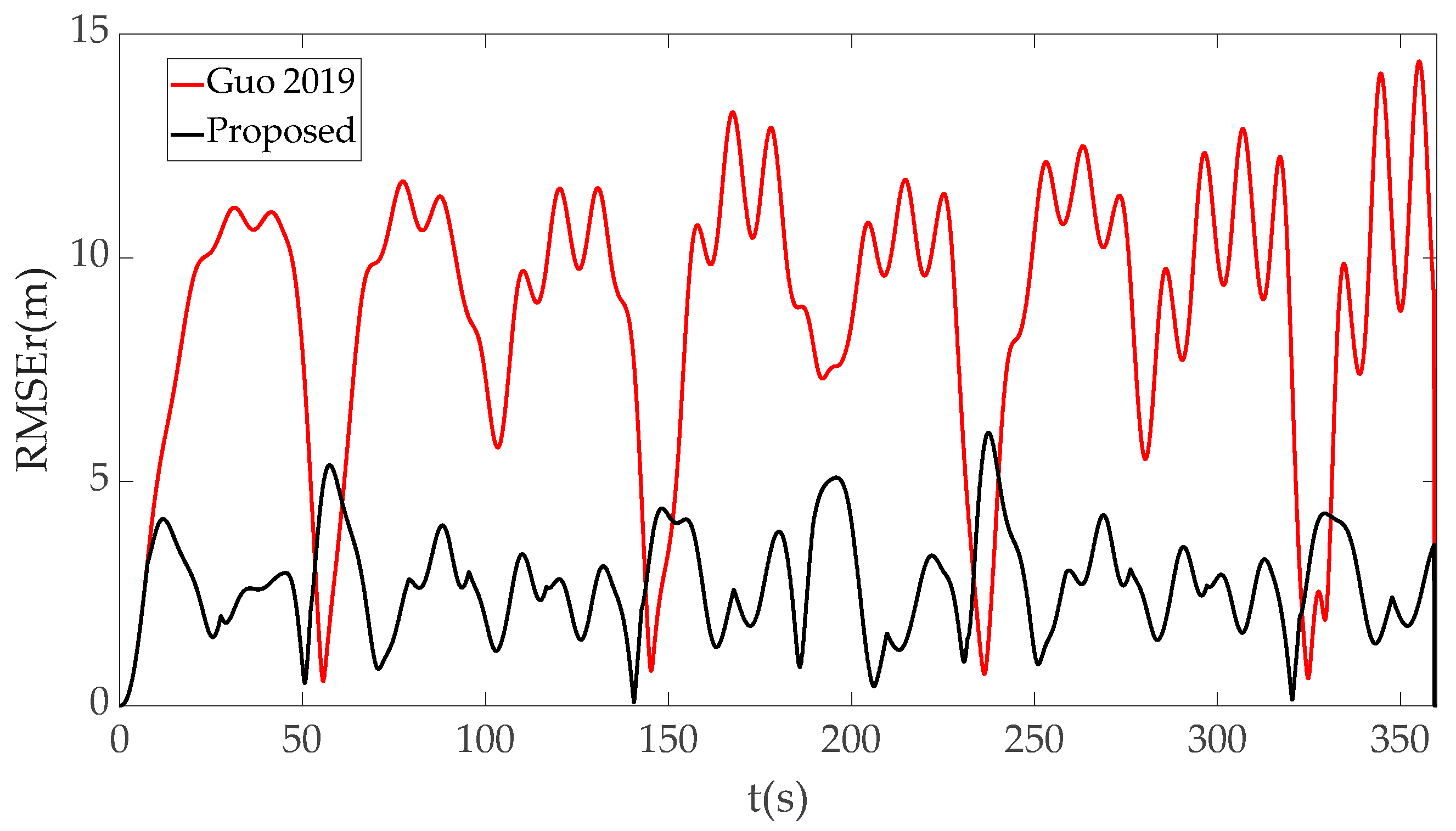
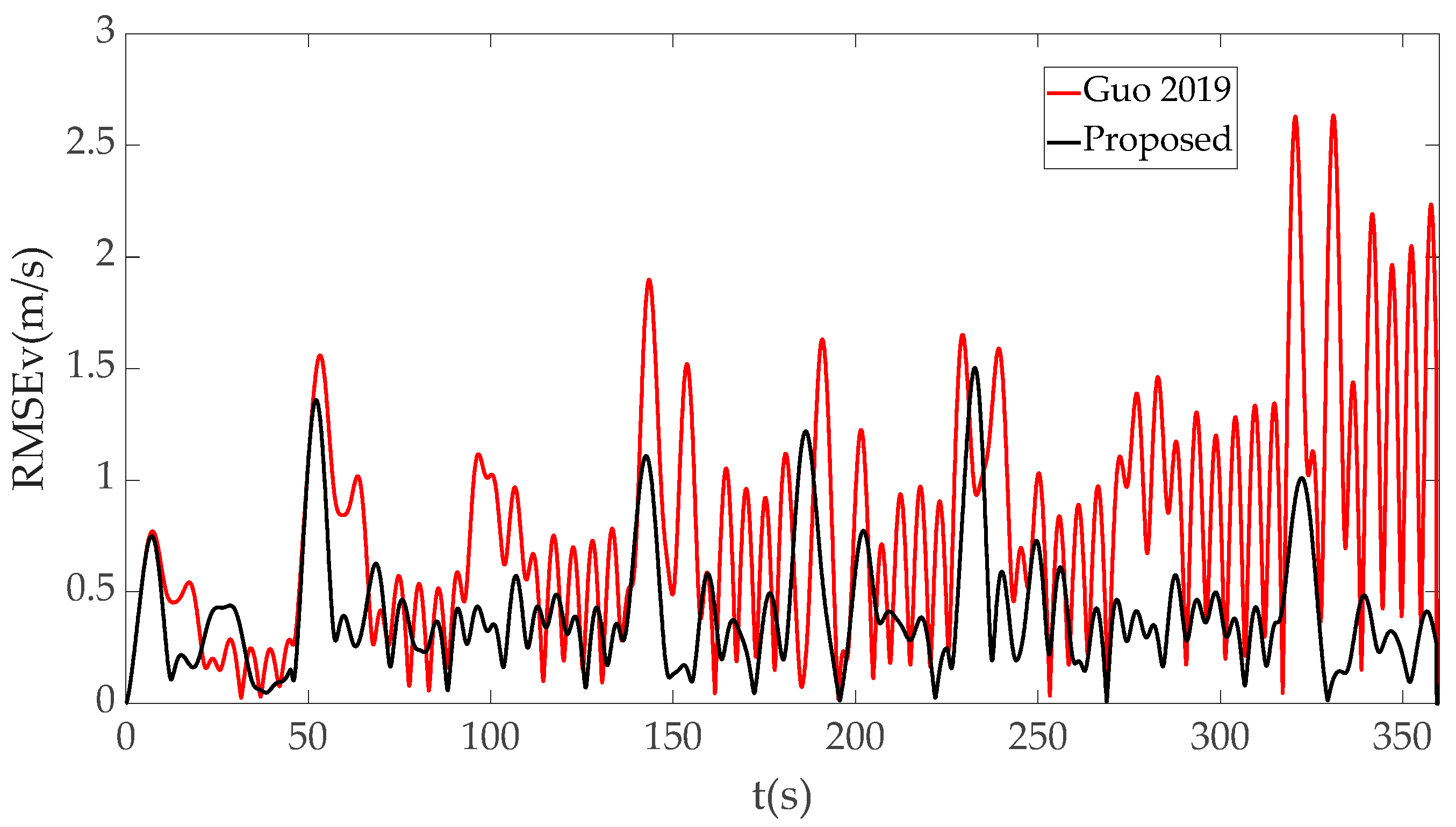
| Spoofing Method | RMSEr Max | RMSEr Mean | RMSEv Max | RMSEv Mean |
|---|---|---|---|---|
| Literature [36] | 27.0491 | 7.7619 | 7.8816 | 1.4832 |
| Proposed | 7.5043 | 2.5241 | 1.5687 | 0.4481 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, B.; Yin, Z.; Jin, X.; Fan, Z.; Wang, H. MPC-Based Dynamic Trajectory Spoofing for UAVs. Drones 2024, 8, 602. https://doi.org/10.3390/drones8100602
Hou B, Yin Z, Jin X, Fan Z, Wang H. MPC-Based Dynamic Trajectory Spoofing for UAVs. Drones. 2024; 8(10):602. https://doi.org/10.3390/drones8100602
Chicago/Turabian StyleHou, Bo, Zhongjie Yin, Xiaolong Jin, Zhiliang Fan, and Haiyang Wang. 2024. "MPC-Based Dynamic Trajectory Spoofing for UAVs" Drones 8, no. 10: 602. https://doi.org/10.3390/drones8100602
APA StyleHou, B., Yin, Z., Jin, X., Fan, Z., & Wang, H. (2024). MPC-Based Dynamic Trajectory Spoofing for UAVs. Drones, 8(10), 602. https://doi.org/10.3390/drones8100602










