Adaptive Sliding Mode Control for Trajectory Tracking of Quadrotor Unmanned Aerial Vehicles Under Input Saturation and Disturbances
Abstract
:1. Introduction
- An adaptive sliding mode trajectory tracking controller is proposed for the uncertain QUAV, ensuring globally uniformly ultimate boundedness (UUB) despite disturbances, input saturation, and parameter uncertainties.
- To address parameter uncertainties, adaptive laws are developed to estimate the quadrotor’s mass and unknown constants related to the moment of inertia. These adaptive laws are integrated into the control scheme, allowing the controller to compensate for external disturbances and input saturation without requiring prior knowledge of the quadrotor’s physical properties.
- The method also incorporates disturbance observers and auxiliary systems, designed to function without prior knowledge of the quadrotor’s mass and moments of inertia. This enables the system to effectively handle unknown disturbances and input saturation, ensuring robust adaptive path tracking performance under uncertain conditions.
2. Mathematical Model of the Quadrotor
3. Control Design
3.1. Position Subsystem Adaptive Control
3.2. Attitude Subsystem Adaptive Control
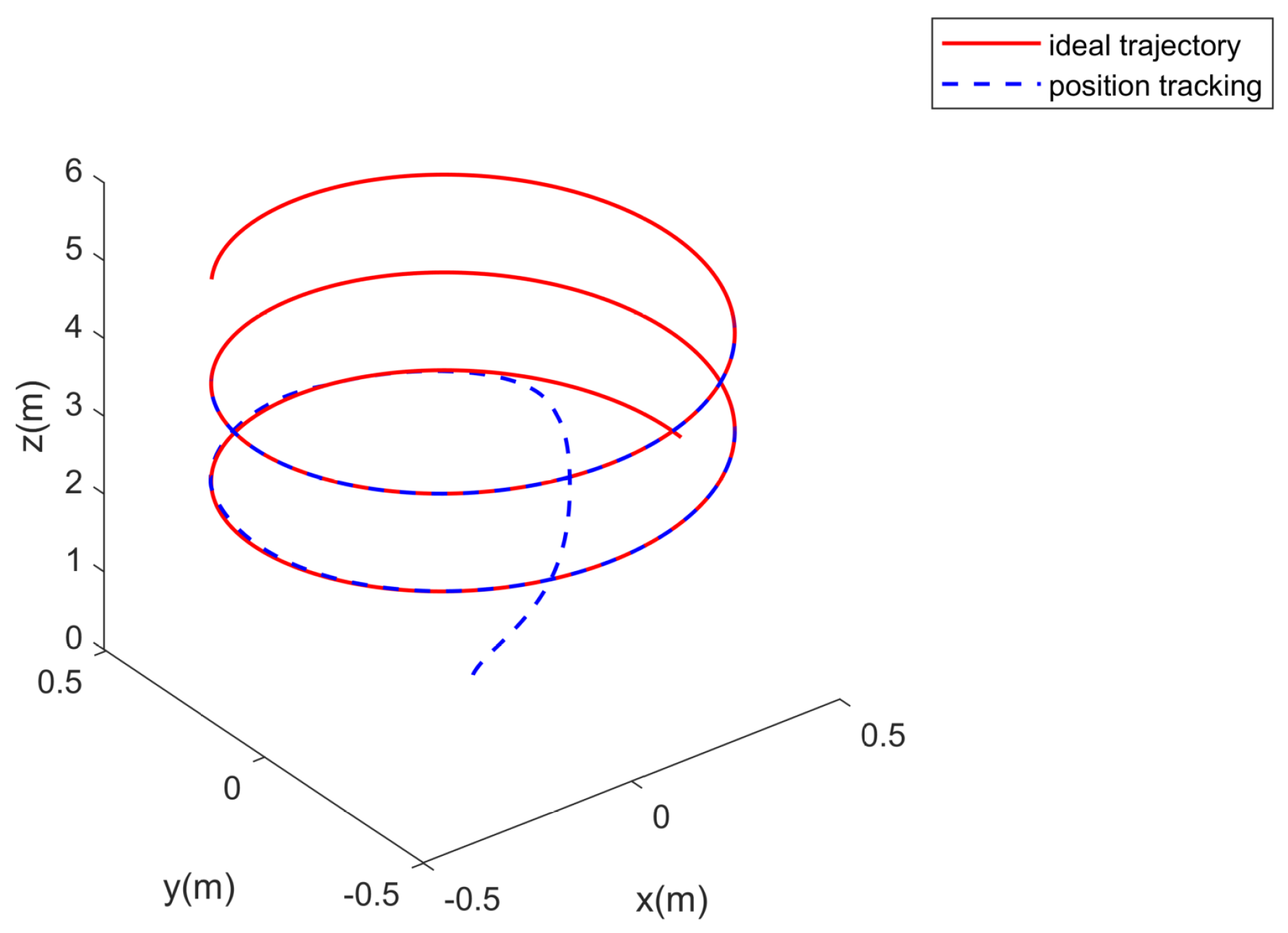
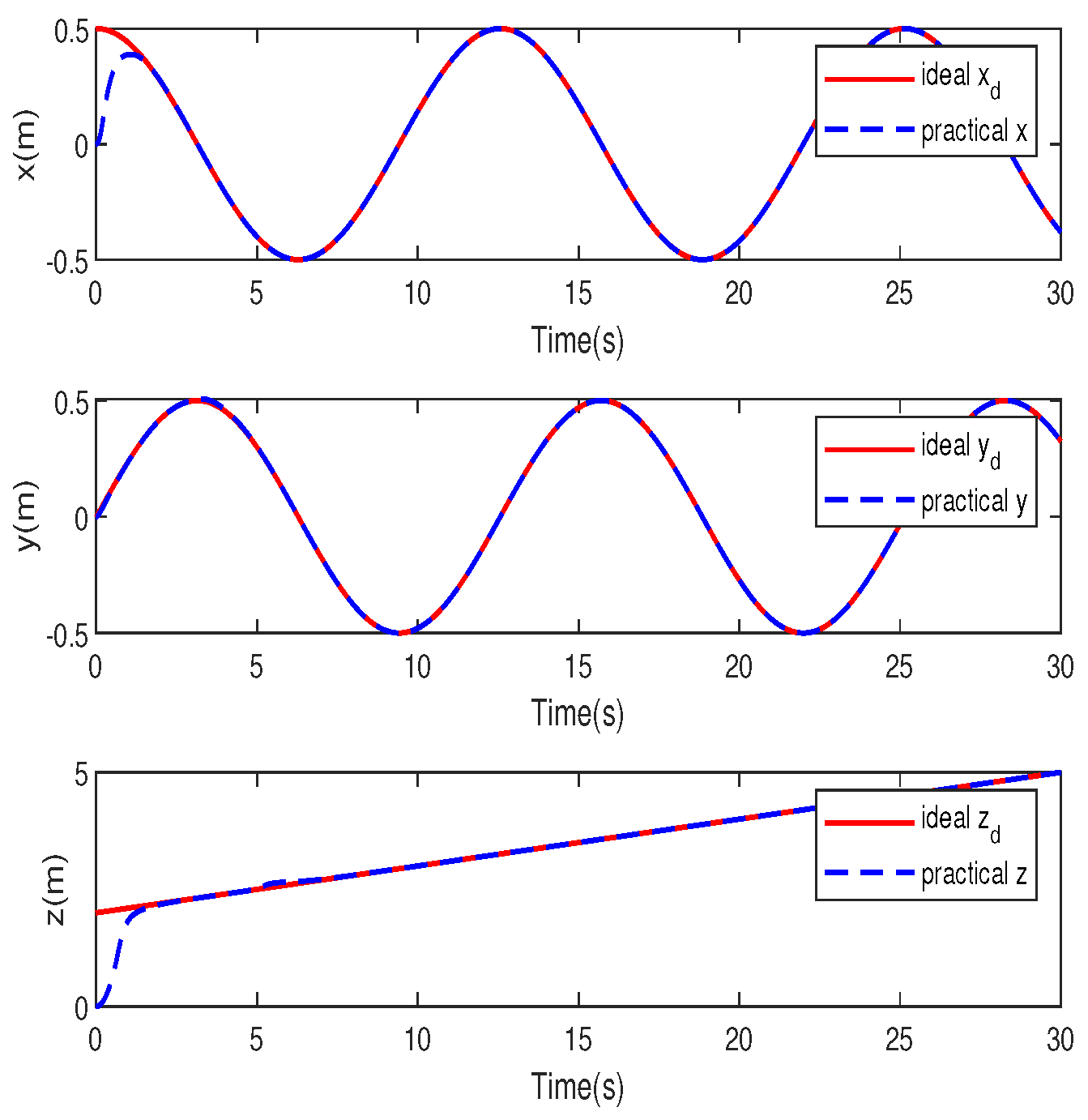
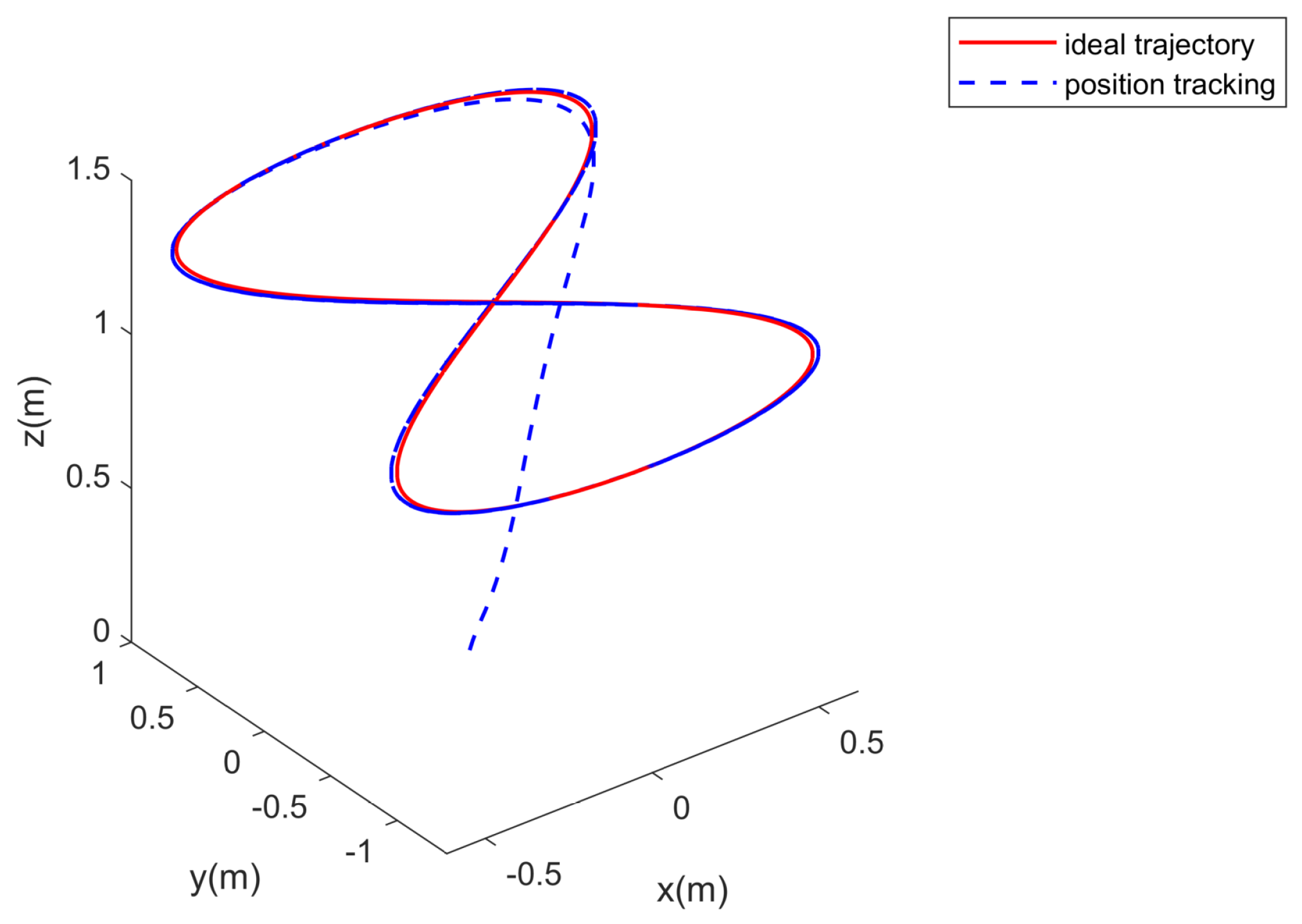
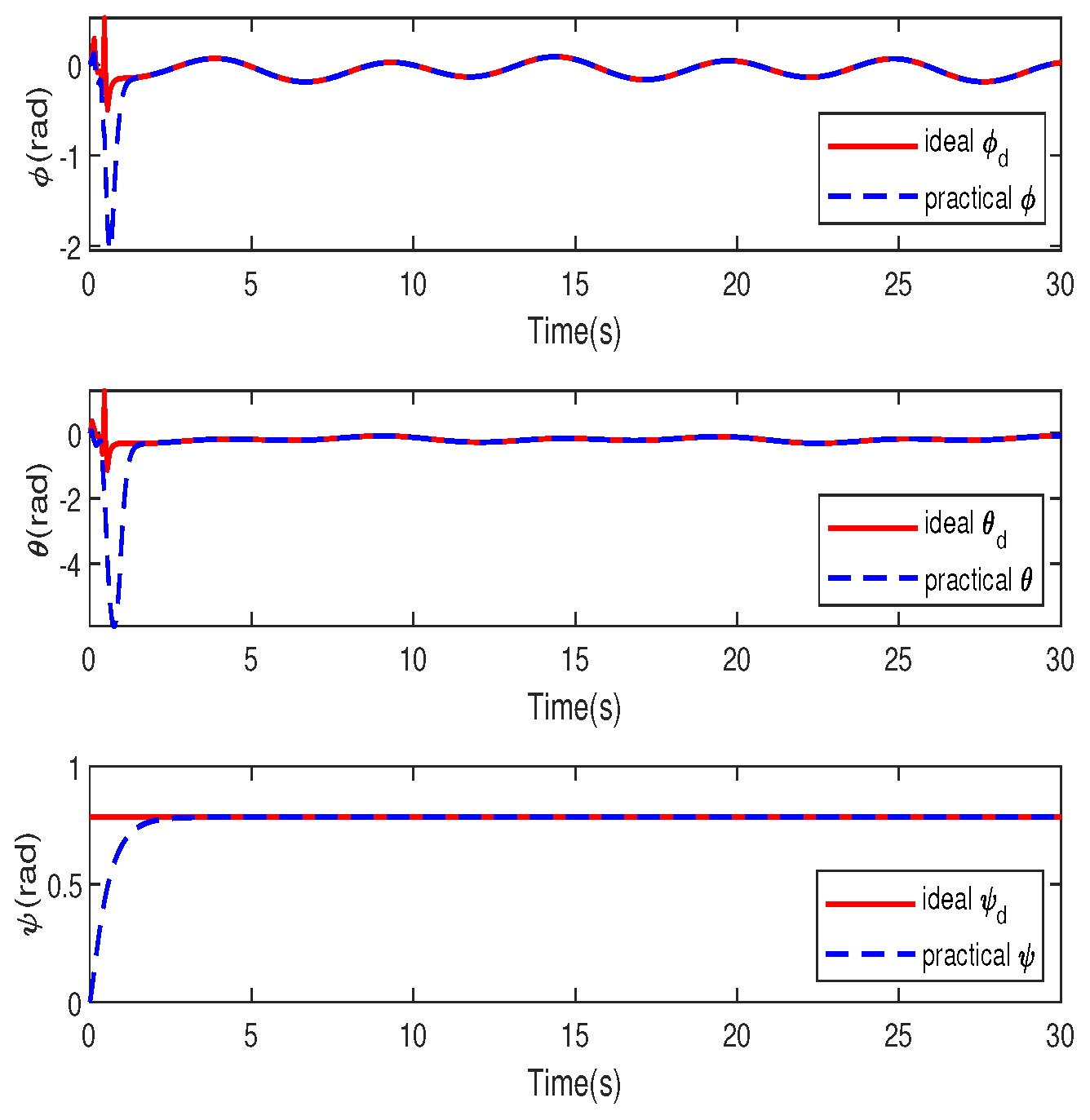
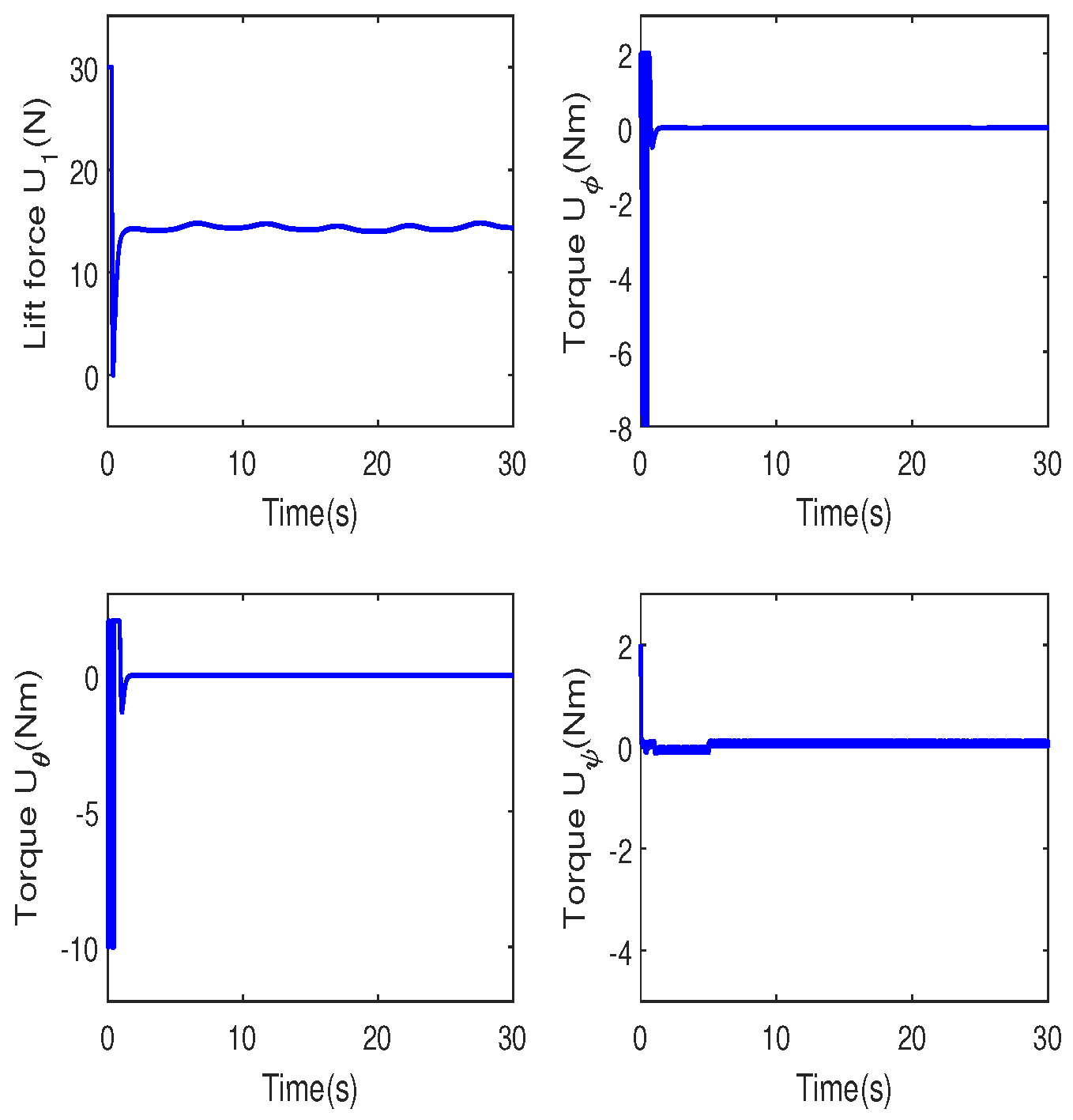
4. Simulation Study
- A. Robustness to constant disturbances.
- B. Robustness to time-varying disturbances.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kendoul, F.; Yu, Z.; Nonami, K. Guidance and nonlinear control system for autonomous flight of minirotorcraft unmanned aerial vehicles. J. Field Robot. 2010, 27, 311–334. [Google Scholar] [CrossRef]
- Nagaty, A.; Saeedi, S.; Thibault, C.; Seto, M.; Li, H. Control and navigation framework for quadrotor helicopters. J. Intell. Robot. Syst. 2013, 70, 1–12. [Google Scholar] [CrossRef]
- Gupte, S.; Mohandas, P.I.T.; Conrad, J.M. A survey of quadrotor unmanned aerial vehicles. In Proceedings of the 2012 Proceedings of IEEE Southeastcon, Orlando, FL, USA, 15–18 March 2012; pp. 1–6. [Google Scholar]
- Antonio-Toledo, M.E.; Sanchez, E.N.; Alanis, A.Y.; Flórez, J.; Perez-Cisneros, M.A. Real-time integral backstepping with sliding mode control for a quadrotor UAV. IFAC-PapersOnLine 2018, 51, 549–554. [Google Scholar] [CrossRef]
- Jia, Z.; Yu, J.; Mei, Y.; Chen, Y.; Shen, Y.; Ai, X. Integral backstepping sliding mode control for quadrotor helicopter under external uncertain disturbances. Aerosp. Sci. Technol. 2017, 68, 299–307. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, J.; Dou, J.; Wen, B. A fuzzy adaptive backstepping control based on mass observer for trajectory tracking of a quadrotor UAV. Int. Adapt. Control. Signal Process. 2018, 32, 1675–1693. [Google Scholar] [CrossRef]
- Labbadi, M.; Cherkaoui, M. Robust adaptive backstepping fast terminal sliding mode controller for uncertain quadrotor UAV. Aerosp. Sci. Technol. 2019, 93, 105306. [Google Scholar] [CrossRef]
- Zhang, J.; Ren, Z.; Deng, C.; Wen, B. Adaptive fuzzy global sliding mode control for trajectory tracking of quadrotor UAVs. Nonlinear Dyn. 2019, 97, 609–627. [Google Scholar] [CrossRef]
- Razmi, H.; Afshinfar, S. Neural network-based adaptive sliding mode control design for position and attitude control of a quadrotor UAV. Aerosp. Sci. Technol. 2019, 91, 12–27. [Google Scholar] [CrossRef]
- Xiong, J.J.; Zheng, E.H. Position and attitude tracking control for a quadrotor UAV. ISA Trans. 2014, 53, 725–731. [Google Scholar] [CrossRef]
- Labbadi, M.; Cherkaoui, M. Adaptive fractional-order nonsingular fast terminal sliding mode based robust tracking control of quadrotor UAV with Gaussian random disturbances and uncertainties. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2265–2277. [Google Scholar] [CrossRef]
- Nguyen, L.V.; Phung, M.D.; Ha, Q.P. Iterative learning sliding mode control for UAV trajectory tracking. Electronics 2021, 10, 2474. [Google Scholar] [CrossRef]
- Ohnishi, K. A new servo method in mechatronics. Trans. Jpn. Soc. Electr. Eng. D 1987, 177, 83–86. [Google Scholar]
- Chen, W.H. Disturbance observer based control for nonlinear systems. IEEE/ASME Trans. Mechatronics 2004, 9, 706–710. [Google Scholar] [CrossRef]
- Chen, M.; Xiong, S.; Wu, Q. Tracking flight control of quadrotor based on disturbance observer. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 1414–1423. [Google Scholar] [CrossRef]
- Wang, H.; Chen, M. Trajectory tracking control for an indoor quadrotor UAV based on the disturbance observer. Trans. Inst. Meas. Control 2016, 38, 675–692. [Google Scholar] [CrossRef]
- Sun, N.; Yang, T.; Fang, Y.; Wu, Y.; Chen, H. Transportation control of double-pendulum cranes with a nonlinear quasi-PID scheme: Design and experiments. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 1408–1418. [Google Scholar] [CrossRef]
- Wang, R.; Liu, J. Trajectory tracking control of a 6-DOF quadrotor UAV with input saturation via backstepping. J. Frankl. Inst. 2018, 355, 3288–3309. [Google Scholar] [CrossRef]
- Liu, K.; Wang, X.; Wang, R.; Sun, G.; Wang, X. Antisaturation finite-time attitude tracking control based observer for a quadrotor. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 2047–2051. [Google Scholar] [CrossRef]
- Castañeda, H.; Rodriguez, J.; Gordillo, J.L. Continuous and smooth differentiator based on adaptive sliding mode control for a quad-rotor MAV. Asian J. Control 2021, 23, 661–672. [Google Scholar] [CrossRef]
- Simoud, L.; Kadri, B.; Bousserhane, I.K. Adaptive fuzzy-sliding mode controller for trajectory tracking control of quad-rotor. J. Autom. Mob. Robot. Intell. Syst. 2020, 14, 15–24. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, M.; Tang, K.; Wang, X. Integral back-stepping algorithm for designing the quadrotor aircraft controller. Chin. J. Intell. Sci. Technol 2019, 1, 133–139. [Google Scholar]
- Chen, M.; Yan, K.; Wu, Q. Multiapproximator-based fault-tolerant tracking control for unmanned autonomous helicopter with input saturation. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 5710–5722. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; Chen, W.H.; Chen, X. Disturbance Observer-Based Control: Methods and Applications; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Yu, J.; Shi, P.; Dong, W.; Yu, H. Observer and command-filter-based adaptive fuzzy output feedback control of uncertain nonlinear systems. IEEE Trans. Ind. Electron. 2015, 62, 5962–5970. [Google Scholar] [CrossRef]
- Chen, M.; Ma, H.; Kang, Y.; Wu, Q. Adaptive neural safe tracking control design for a class of uncertain nonlinear systems with output constraints and disturbances. IEEE Trans. Cybern. 2021, 52, 12571–12582. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Ji, H. Robust Adaptive Trajectory Tracking Control for Uncertain Quadrotor Unmanned Aerial Vechicles in the Presence of Actuator Saturation. In Proceedings of the 2020 5th International Conference on Control and Robotics Engineering (ICCRE), Osaka, Japan, 24–26 April 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 104–108. [Google Scholar]
- Yang, Q.; Chen, M. Adaptive neural prescribed performance tracking control for near space vehicles with input nonlinearity. Neurocomputing 2016, 174, 780–789. [Google Scholar] [CrossRef]
- Boskovic, J.D.; Chen, L.; Mehra, R.K. Adaptive control design for nonaffine models arising in flight control. J. Guid. Control Dyn. 2004, 27, 209–217. [Google Scholar] [CrossRef]
- Yoo, J.; Jang, D.; Kim, H.J.; Johansson, K.H. Hybrid reinforcement learning control for a micro quadrotor flight. IEEE Control Syst. Lett. 2020, 5, 505–510. [Google Scholar] [CrossRef]
- Phadke, A.; Medrano, F.A.; Chu, T.; Sekharan, C.N.; Starek, M.J. Modeling Wind and Obstacle Disturbances for Effective Performance Observations and Analysis of Resilience in UAV Swarms. Aerospace 2024, 11, 237. [Google Scholar] [CrossRef]





| Parameter | Symbol | Magnitude | Unit |
|---|---|---|---|
| Mass | m | 2 | |
| Airframe inertia of roll | Jx | 0.02 | |
| Airframe inertia of pitch | Jy | 0.02 | |
| Airframe inertia of yaw | Jz | 0.04 | |
| Distance | l | 0.2 | |
| Gravity | g | 9.8 |
| Parameter | Magnitude |
|---|---|
| diag([2 2 2]) | |
| diag([20 20 20]) | |
| diag([2 2 2]) | |
| diag([10 10 10]) | |
| diag([15 15 15]) | |
| [0.2 0.2 0.2 0.2] | |
| [0.5 0.5 0.5 0.5] | |
| diag([18 18 18]) | |
| diag([30 30 30]) | |
| diag([5 5 5]) | |
| diag([10 10 10]) | |
| diag([15 15 15]) |
| Channel | Magnitude | Unit |
|---|---|---|
| x | 0.074 | |
| y | 0.003 | |
| z | 2.034 | |
| 0.327 | ||
| 0.292 | ||
| 0.186 |
| Channel | Magnitude | Unit |
|---|---|---|
| x | 0.005 | |
| y | 0.007 | |
| z | 0.476 | |
| 0.818 | ||
| 0.924 | ||
| 0.184 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuang, J.; Chen, M. Adaptive Sliding Mode Control for Trajectory Tracking of Quadrotor Unmanned Aerial Vehicles Under Input Saturation and Disturbances. Drones 2024, 8, 614. https://doi.org/10.3390/drones8110614
Kuang J, Chen M. Adaptive Sliding Mode Control for Trajectory Tracking of Quadrotor Unmanned Aerial Vehicles Under Input Saturation and Disturbances. Drones. 2024; 8(11):614. https://doi.org/10.3390/drones8110614
Chicago/Turabian StyleKuang, Jingyang, and Mou Chen. 2024. "Adaptive Sliding Mode Control for Trajectory Tracking of Quadrotor Unmanned Aerial Vehicles Under Input Saturation and Disturbances" Drones 8, no. 11: 614. https://doi.org/10.3390/drones8110614
APA StyleKuang, J., & Chen, M. (2024). Adaptive Sliding Mode Control for Trajectory Tracking of Quadrotor Unmanned Aerial Vehicles Under Input Saturation and Disturbances. Drones, 8(11), 614. https://doi.org/10.3390/drones8110614







