Safety-Critical Fixed-Time Formation Control of Quadrotor UAVs with Disturbance Based on Robust Control Barrier Functions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dynamic Model
2.2. Graph Theory
2.3. Control Objectives
2.4. Necessary Lemmas and Assumptions
3. Nominal Formation Control Law
3.1. Fixed-Time Disturbance Observer
3.2. Nominal Control Law
4. Safety-Critical Control via CBF
4.1. Control Barrier Functions
4.2. Robust ECBF Design
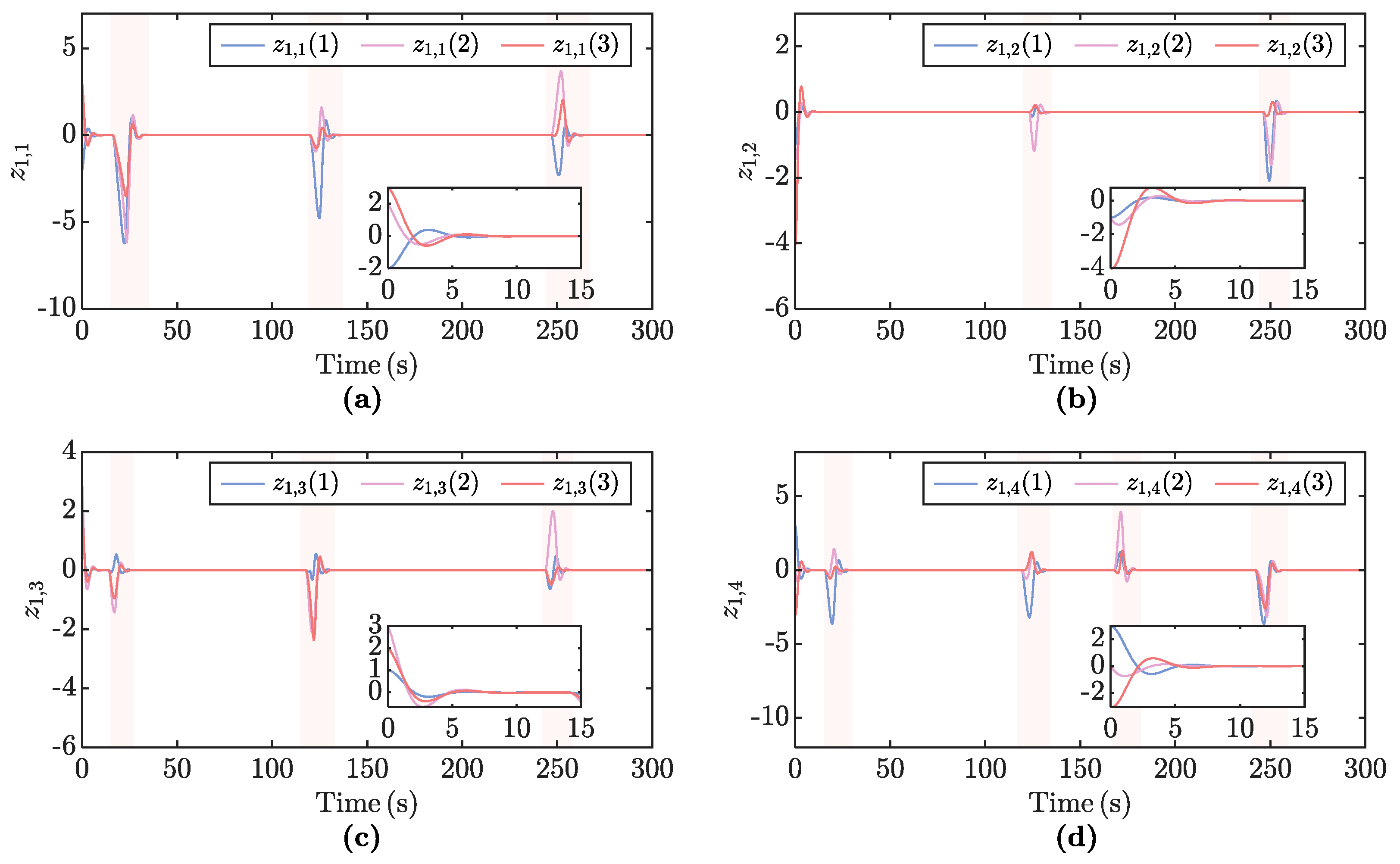
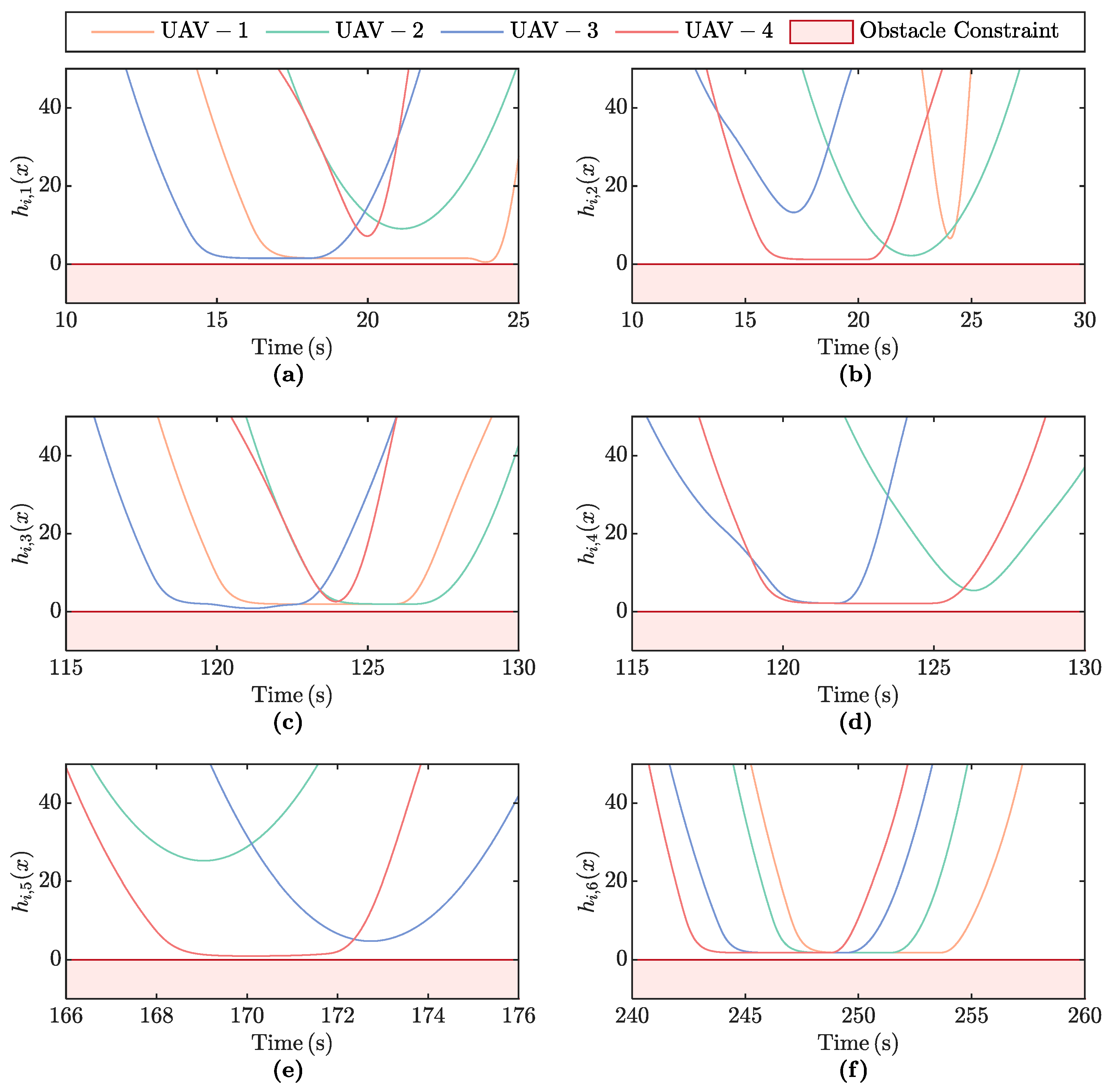
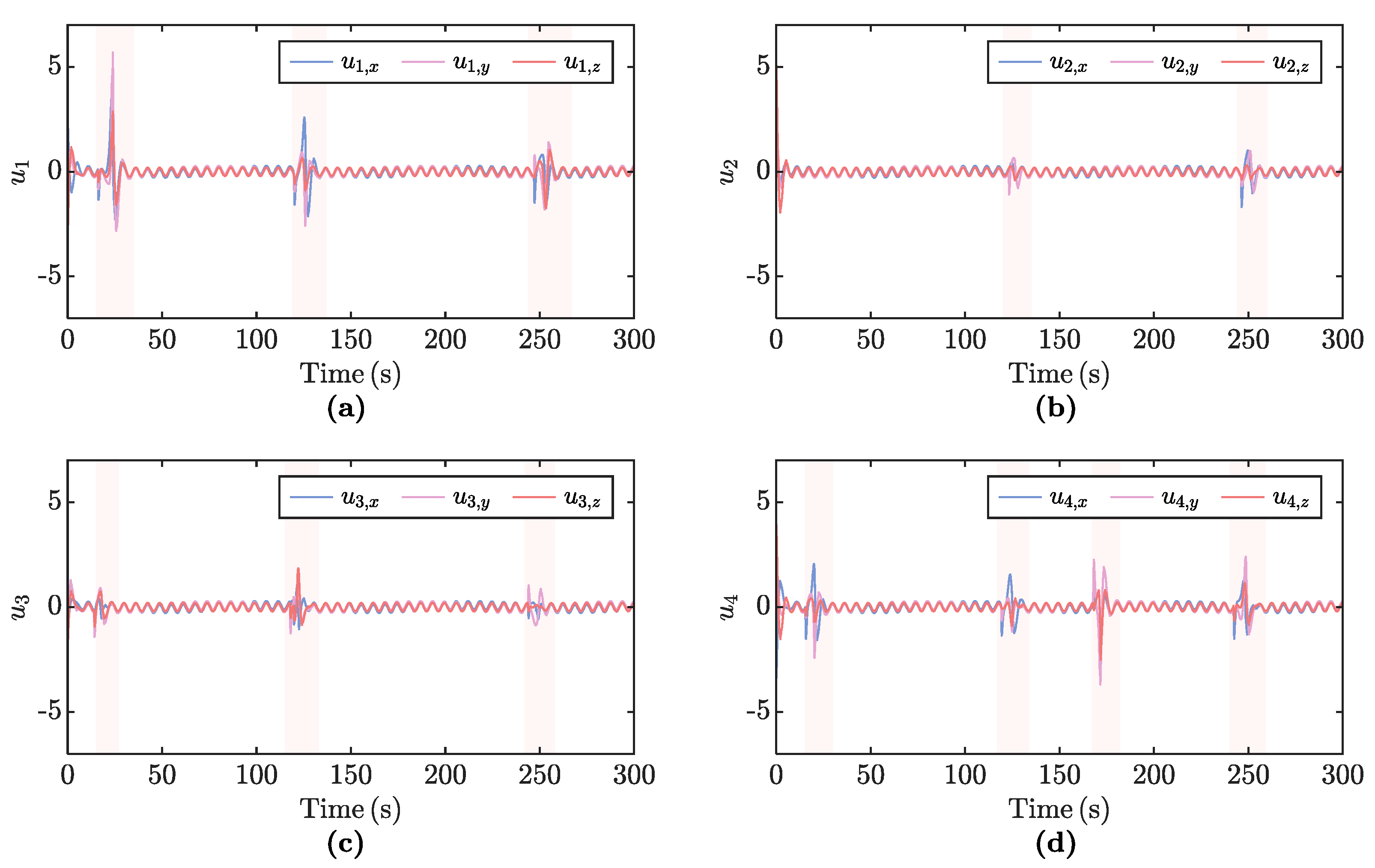
5. Simulation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sarkar, N.I.; Gul, S. Artificial Intelligence-Based Autonomous UAV Networks: A Survey. Drones 2023, 7, 322. [Google Scholar] [CrossRef]
- Muslimov, T.Z.; Munasypov, R.A. Consensus-based cooperative control of parallel fixed-wing UAV formations via adaptive backstepping. Aerosp. Sci. Technol. 2021, 109, 106416. [Google Scholar] [CrossRef]
- Yang, Y.; Xiong, X.; Yan, Y. UAV Formation Trajectory Planning Algorithms: A Review. Drones 2023, 7, 62. [Google Scholar] [CrossRef]
- Han, W.; Wang, J.; Wang, Y.; Xu, B. Multi-UAV Flocking Control with a Hierarchical Collective Behavior Pattern Inspired by Sheep. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 2267–2276. [Google Scholar] [CrossRef]
- Wu, Y.; Gou, J.; Hu, X.; Huang, Y. A new consensus theory-based method for formation control and obstacle avoidance of UAVs. Aerosp. Sci. Technol. 2020, 107, 106332. [Google Scholar] [CrossRef]
- Tang, J.; Duan, H.; Lao, S. Swarm intelligence algorithms for multiple unmanned aerial vehicles collaboration: A comprehensive review. Artif. Intell. Rev. 2023, 56, 4295–4327. [Google Scholar] [CrossRef]
- Yue, J.; Qin, K.; Shi, M.; Jiang, B.; Li, W.; Shi, L. Event-Trigger-Based Finite-Time Privacy-Preserving Formation Control for Multi-UAV System. Drones 2023, 7, 235. [Google Scholar] [CrossRef]
- Feng, Z.; Hu, G.; Dong, X.; Lu, J. Discrete-time adaptive distributed output observer for time-varying formation tracking of heterogeneous multi-agent systems. Automatica 2024, 160, 111400. [Google Scholar] [CrossRef]
- Wang, B.; Chen, W.; Zhang, B.; Shi, P.; Zhang, H. A Nonlinear Observer-Based Approach to Robust Cooperative Tracking for Heterogeneous Spacecraft Attitude Control and Formation Applications. IEEE Trans. Autom. Control 2023, 68, 400–407. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, J.; Zheng, Z.; Yuan, J. Distributed Finite-Time ESO-Based Consensus Control for Multiple Fixed-Wing UAVs Subjected to External Disturbances. Drones 2024, 8, 260. [Google Scholar] [CrossRef]
- Song, Z.; Wu, Z.; Huang, H. Safety-critical containment control for multi-agent systems with communication delays. IEEE Trans. Netw. Sci. Eng. 2024, 11, 4911–4922. [Google Scholar] [CrossRef]
- Li, L.; Li, Y.; Zhang, Y.; Xu, G.; Zeng, J.; Feng, X. Formation Control of Multiple Autonomous Underwater Vehicles under Communication Delay, Packet Discreteness and Dropout. J. Mar. Sci. Eng. 2022, 10, 920. [Google Scholar] [CrossRef]
- Zhao, W.; Xia, Y.; Zhai, D.-H.; Cui, B. Adaptive event-triggered coordination control of unknown autonomous underwater vehicles under communication link faults. Automatica 2023, 158, 111277. [Google Scholar] [CrossRef]
- Chen, L.; Duan, H. Collision-free formation-containment control for a group of UAVs with unknown disturbances. Aerosp. Sci. Technol. 2022, 126, 107618. [Google Scholar] [CrossRef]
- Li, S.; Wang, X. Finite-time consensus and collision avoidance control algorithms for multiple AUVs. Automatica 2013, 49, 3359–3367. [Google Scholar] [CrossRef]
- Yang, P.; Zhang, A.; Zhou, D. Event-triggered Finite-time Formation Control for Multiple Unmanned Aerial Vehicles with Input Saturation. Int. J. Control Autom. Syst. 2021, 19, 1760–1773. [Google Scholar] [CrossRef]
- Qi, W.-N.; Wu, A.-G.; Huang, J.; Dong, R.-Q. Finite-time attitude consensus control for multiple rigid spacecraft based on distributed observers. IET Control Theory Appl. 2023, 17, 341–356. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, K.; Li, W.; Shi, M.; Lin, B.; Cao, L. Prescribed Performance Rotating Formation Control of Multi-Spacecraft Systems with Uncertainties. Drones 2022, 6, 348. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.-h.; Chang, B.; Wu, W.-h. Adaptive constrained backstepping controller with prescribed performance methodology for carrier-based UAV. Aerosp. Sci. Technol. 2019, 92, 55–65. [Google Scholar] [CrossRef]
- Wu, Q.; Zhu, Q. Prescribed Performance Fault-Tolerant Attitude Tracking Control for UAV with Actuator Faults. Drones 2024, 8, 204. [Google Scholar] [CrossRef]
- Sun, P.; Li, S.; Zhu, B.; Zheng, Z.; Zuo, Z. Vision-based finite-time prescribed performance control for uncooperative UAV target-tracking subject to field of view constraints. ISA Trans. 2024, 149, 168–177. [Google Scholar] [CrossRef] [PubMed]
- Meng, Q.; Ma, Q.; Shi, Y. Adaptive Fixed-Time Stabilization for a Class of Uncertain Nonlinear Systems. IEEE Trans. Autom. Control 2023, 68, 6929–6936. [Google Scholar] [CrossRef]
- Miao, Q.; Zhang, K.; Jiang, B. Fixed-Time Collision-Free Fault-Tolerant Formation Control of Multi-UAVs Under Actuator Faults. IEEE Trans. Cybern. 2024, 54, 3679–3691. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Li, M.; Yu, Z.; Cheng, Y.; Xu, G.; Zhang, Y. Fault Detection and Fault-Tolerant Cooperative Control of Multi-UAVs under Actuator Faults, Sensor Faults, and Wind Disturbances. Drones 2023, 7, 503. [Google Scholar] [CrossRef]
- Jiang, H.; Ma, Q.; Guo, J. Fuzzy-Based Fixed-Time Attitude Control of Quadrotor Unmanned Aerial Vehicle with Full-State Constraints: Theory and Experiments. IEEE Trans. Fuzzy Syst. 2024, 32, 1108–1115. [Google Scholar] [CrossRef]
- Khodaverdian, M.; Hajshirmohamadi, S.; Hakobyan, A.; Ijaz, S. Predictor-based constrained fixed-time sliding mode control of multi-UAV formation flight. Aerosp. Sci. Technol. 2024, 148, 109113. [Google Scholar] [CrossRef]
- Jia, J.; Chen, X.; Wang, W.; Liao, H.; Xie, M. Collision avoidance in target encirclement and tracking of unmanned aerial vehicles under a dynamic event-triggered formation control. Control Eng. Pract. 2024, 142, 105781. [Google Scholar] [CrossRef]
- Cui, G.; Xu, H.; Chen, X.; Yu, J. Fixed-Time Distributed Adaptive Formation Control for Multiple QUAVs with Full-State Constraints. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4192–4206. [Google Scholar] [CrossRef]
- Zheng, R.; Zhu, Q.; Huang, S.; Du, Z.; Shi, J.; Lyu, Y. Extended State Observer-Based Sliding-Mode Control for Aircraft in Tight Formation Considering Wake Vortices and Uncertainty. Drones 2024, 8, 165. [Google Scholar] [CrossRef]
- Lei, Y.; Fu, R. Disturbance-Observer-based Fast Terminal Sliding Mode Control for Quadrotor UAVs. In Proceedings of the Chinese Control and Decision Conference (CCDC), Yichang, China, 20–22 May 2023; pp. 953–958. [Google Scholar]
- Ma, Z.; Gong, H.; Wang, X. Fault-Tolerant Event-Triggrred Control for Multiple UAVs with Predefined Tracking Performance. Drones 2024, 8, 25. [Google Scholar] [CrossRef]
- Cao, L.; Li, H.; Wang, N.; Zhou, Q. Observer-Based Event-Triggered Adaptive Decentralized Fuzzy Control for Nonlinear Large-Scale Systems. IEEE Trans. Fuzzy Syst. 2019, 27, 1201–1214. [Google Scholar] [CrossRef]
- Song, Z.; Xie, M.; Huang, H. Bearing-Only Formation Tracking Control for Multi-Agent Systems with Time-Varying Velocity Leaders. IEEE Control Syst. Lett. 2024, 8, 2027–2032. [Google Scholar] [CrossRef]
- Wang, J.; Bi, C.; Wang, D.; Kuang, Q.; Wang, C. Finite-time distributed event-triggered formation control for quadrotor UAVs with experimentation. ISA Trans. 2022, 126, 585–596. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Wang, H.; Hu, Z.; Wang, Y.; Wang, H. A Multi-Time-Scale Finite Time Controller for the Quadrotor UAVs with Uncertainties. J. Intell. Robot. Syst. 2019, 94, 521–533. [Google Scholar] [CrossRef]
- Sun, L.; Sun, G.; Jiang, J. Disturbance observer-based saturated fixed-time pose tracking for feature points of two rigid bodies. Automatica 2022, 144, 110475. [Google Scholar] [CrossRef]
- Rezaei, E.; Bolandi, H.; Fathi, M. Designing a fixed-time observer-based adaptive non-singular sliding mode controller for flexible spacecraft. ISA Trans. 2024, 148, 32–44. [Google Scholar] [CrossRef]
- Sui, B.; Zhang, J.; Liu, Z.; Wei, J. Fixed-Time Trajectory Tracking Control of Fully Actuated Unmanned Surface Vessels with Error Constraints. J. Mar. Sci. Eng. 2024, 12, 584. [Google Scholar] [CrossRef]
- Zhang, P.; He, Y.; Wang, Z.; Li, S.; Liang, Q. Research on Multi-UAV Obstacle Avoidance with Optimal Consensus Control and Improved APF. Drones 2024, 8, 248. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, C.; Wang, Y.; Zhang, T.; Gong, Y. A fast formation obstacle avoidance algorithm for clustered UAVs based on artificial potential field. Aerosp. Sci. Technol. 2024, 147, 108974. [Google Scholar] [CrossRef]
- Qian, M.; Wu, Z.; Jiang, B. Cerebellar Model Articulation Neural Network-Based Distributed Fault Tolerant Tracking Control with Obstacle Avoidance for Fixed-Wing UAVs. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 6841–6852. [Google Scholar] [CrossRef]
- Singletary, A.; Klingebiel, K.; Bourne, J.; Browning, A.; Tokumaru, P.; Ames, A. Comparative Analysis of Control Barrier Functions and Artificial Potential Fields for Obstacle Avoidance. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–01 October 2021; pp. 8129–8136. [Google Scholar]
- Ames, A.D.; Xu, X.; Grizzle, J.W.; Tabuada, P. Control Barrier Function Based Quadratic Programs for Safety Critical Systems. IEEE Trans. Autom. Control 2017, 62, 3861–3876. [Google Scholar] [CrossRef]
- Li, B.; Wen, S.; Yan, Z.; Wen, G.; Huang, T. A Survey on the Control Lyapunov Function and Control Barrier Function for Nonlinear-Affine Control Systems. IEEE/CAA J. Automat. Sin. 2023, 10, 584–602. [Google Scholar] [CrossRef]
- Hegde, A.; Ghose, D. Collaborative Guidance of UAV-Transported Semi-Flexible Payloads in Environments with Obstacles. In Proceedings of the IEEE Conference on Decision and Control (CDC), Austin, TX, USA, 13–17 December 2021; pp. 490–495. [Google Scholar]
- Lin, J.; Miao, Z.; Wang, Y.; Wang, H.; Wang, X.; Fierro, R. Vision-Based Safety-Critical Landing Control of Quadrotors with External Uncertainties and Collision Avoidance. IEEE Trans. Control. Syst. Technol. 2024, 32, 1310–1322. [Google Scholar] [CrossRef]
- Wu, G.; Sreenath, K. Safety-Critical Control of a Planar Quadrotor. In Proceedings of the American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 2252–2258. [Google Scholar]
- Xiao, W.; Belta, C. Control Barrier Functions for Systems with High Relative Degree. In Proceedings of the IEEE Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019; pp. 474–479. [Google Scholar]
- Kim, S.-J.; Suh, J.-H. Model-Free RBF Neural Network Intelligent-PID Control Applying Adaptive Robust Term for Quadrotor System. Drones 2024, 8, 179. [Google Scholar] [CrossRef]
- Jagtap, P.; Pappas, G.J.; Zamani, M. Control Barrier Functions for Unknown Nonlinear Systems using Gaussian Processes. In Proceedings of the IEEE Conference on Decision and Control (CDC), 14–18 December 2020; pp. 3699–3704. [Google Scholar]
- Zhao, P.; Mao, Y.; Tao, C.; Hovakimyan, N.; Wang, X. Adaptive Robust Quadratic Programs using Control Lyapunov and Barrier Functions. In Proceedings of the IEEE Conference on Decision and Control (CDC), 14–18 December 2020; pp. 3353–3358. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; Volume 2. [Google Scholar]
- Kolathaya, S.; Ames, A.D. Input-to-State Safety with Control Barrier Functions. IEEE Control Syst. Lett. 2019, 3, 108–113. [Google Scholar] [CrossRef]
- Alan, A.; Taylor, A.J.; He, C.R.R.; Ames, A.D.; Orosz, G. Control Barrier Functions and Input-to-State Safety with Application to Automated Vehicles. IEEE Trans. Control Syst. Technol. 2023, 31, 2744–2759. [Google Scholar] [CrossRef]
- Buch, J.; Liao, S.-C.; Seiler, P. Robust Control Barrier Functions with Sector-Bounded Uncertainties. IEEE Control Syst. Lett. 2022, 6, 1994–1999. [Google Scholar] [CrossRef]
- Shao, S.; Xu, S.; Zhao, Y.; Wu, X. Unknown Input Observer-Based Fixed-Time Trajectory Tracking Control for QUAV with Actuator Saturation and Faults. Drones 2023, 7, 344. [Google Scholar] [CrossRef]
- Xie, T.; Xian, B.; Gu, X.; Hu, J.; Liu, M. Disturbance Observer-Based Fixed-Time Tracking Control for a Tilt Trirotor Unmanned Aerial Vehicle. IEEE Trans. Ind. Electron. 2024, 71, 3894–3903. [Google Scholar] [CrossRef]
- Ai, X.; Yu, J. Fixed-time trajectory tracking for a quadrotor with external disturbances: A flatness-based sliding mode control approach. Aerosp. Sci. Technol. 2019, 89, 58–76. [Google Scholar] [CrossRef]
- Gao, S.; Peng, Z.; Wang, H.; Liu, L.; Wang, D. Safety-Critical Model-Free Control for Multi-Target Tracking of USVs with Collision Avoidance. IEEE/CAA J. Automat. Sin. 2022, 9, 1323–1326. [Google Scholar] [CrossRef]
- Du, H.; Zhu, W.; Wen, G.; Wu, D. Finite-time formation control for a group of quadrotor aircraft. Aerosp. Sci. Technol. 2017, 69, 609–616. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear Feedback Design for Fixed-Time Stabilization of Linear Control Systems. IEEE Trans. Autom. Control 2012, 57, 2106–2110. [Google Scholar] [CrossRef]
- Hardy, G.H.; Littlewood, J.E. ; Pólya., G. Inequalities; Cambridge University Press: Cambridge, UK, 1952. [Google Scholar]
- Liu, Z.; Liu, J.; Zhang, O.; Zhao, Y.; Chen, W.; Gao, Y. Adaptive Disturbance Observer-Based Fixed-Time Tracking Control for Uncertain Robotic Systems. IEEE Trans. Ind. Electron. 2024, 71, 14823–14831. [Google Scholar] [CrossRef]
- Ames, A.D.; Coogan, S.; Egerstedt, M.; Notomista, G.; Sreenath, K.; Tabuada, P. Control Barrier Functions: Theory and Applications. In Proceedings of the European Control Conference (ECC), Naples, Italy, 25–28 June 2019; pp. 3420–3431. [Google Scholar]
- Wang, H.; Shan, J. Fully Distributed Event-Triggered Formation Control for Multiple Quadrotors. IEEE Trans. Ind. Electron. 2023, 70, 12566–12575. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Z.; Huang, H. Safety-Critical Fixed-Time Formation Control of Quadrotor UAVs with Disturbance Based on Robust Control Barrier Functions. Drones 2024, 8, 618. https://doi.org/10.3390/drones8110618
Song Z, Huang H. Safety-Critical Fixed-Time Formation Control of Quadrotor UAVs with Disturbance Based on Robust Control Barrier Functions. Drones. 2024; 8(11):618. https://doi.org/10.3390/drones8110618
Chicago/Turabian StyleSong, Zilong, and Haocai Huang. 2024. "Safety-Critical Fixed-Time Formation Control of Quadrotor UAVs with Disturbance Based on Robust Control Barrier Functions" Drones 8, no. 11: 618. https://doi.org/10.3390/drones8110618
APA StyleSong, Z., & Huang, H. (2024). Safety-Critical Fixed-Time Formation Control of Quadrotor UAVs with Disturbance Based on Robust Control Barrier Functions. Drones, 8(11), 618. https://doi.org/10.3390/drones8110618






