A Hierarchical Deep Reinforcement Learning Approach for Throughput Maximization in Reconfigurable Intelligent Surface-Aided Unmanned Aerial Vehicle–Integrated Sensing and Communication Network
Abstract
:1. Introduction
- We investigate a RIS-aided UAV-ISAC system, where the UAV is equipped with the ISAC devices and sends ISAC signals, and an RIS is deployed to improve the link quality for better system performance. Subject to constraints on the maximum transmission power, maximum flight speed, and minimum sensing beampattern gain requirements, we jointly optimize the trajectory of the UAV, the beamforming matrix of the UAV, and the passive beamforming matrix of the RIS to maximize the sum-rate throughput of the system.
- We transform the non-convex problem into a semi-Markov decision process (SMDP); the orignal problem is first decomposed into two subproblems, which are trajectory optimization and sum-rate throughput optimization. We then propose an HDRL framework with a hierarchical twin-delayed deep deterministic policy gradient (HTD3) structure for the joint optimization of the trajectory and beamforming matrix of the UAV as well as the passive beamforming matrix of the RIS.
- We simulate the proposed algorithm and other benchmarks for comparison. Extensive results represent the effectiveness and superiority of the proposed HTD3. Specifically, we verify the convergence of the proposed algorithm via different environment parameters based on numerous experiments, and the experimental results demonstrate that HTD3 achieves a higher sum-rate throughput compared to other benchmarks.
2. System Model
2.1. System Overview
2.2. Transmission Model
2.3. Sensing Model
2.4. Problem Formulation
3. The Proposed Algorithm
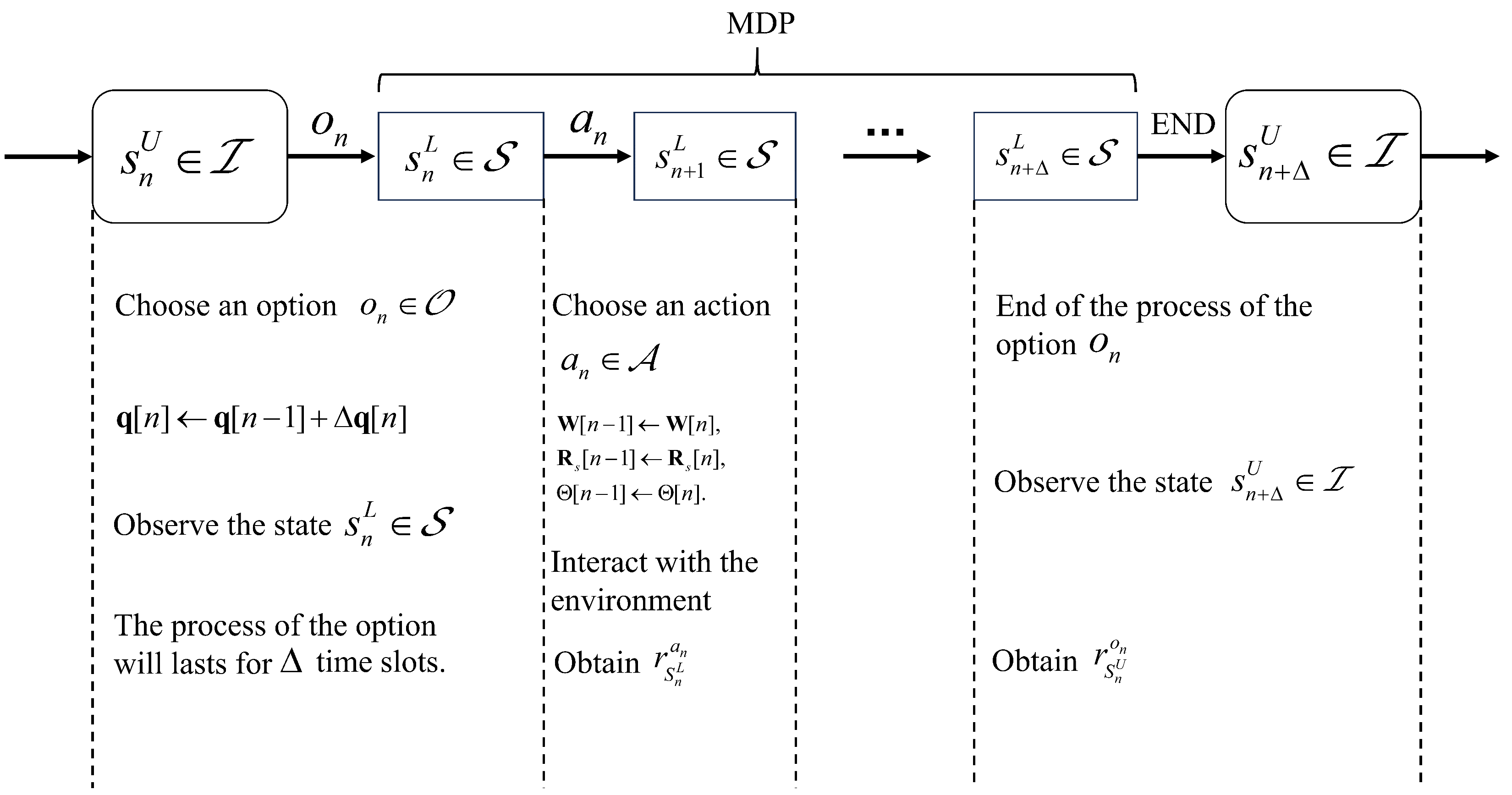
3.1. SMDP
- (1)
- State space : CSI is the most influential factor, which includes the estimated CSI between the UAV and the RIS, and between the UAV and the UEs. To evaluate the sensing performance, the distance between the UAV and the targets is also considered, and thus the state set of the options can be described as:
- (2)
- Policy set : denotes the policy set under an option ; since our option is the adjustment of locations of the UAV and we choose proper options to maximize (), the policy function can be described as the adjustment of the beamforming matrix, the sensing signal of the UAV, and the passive beamforming matrix of the RIS under the option , which are actions required to complete an option and can be described as:
- (3)
- Termination probability : denotes the termination probability at state . Each option denotes the location adjustment of the UAV in time slot n, and the UAV performs the sensing and communication tasks for the later time slots; hence, means the termination probability of the option in the time slot is 1, where denotes the state in time slot .
- (1)
- State space : The observed state consists of the location of the UAV, which is determined by the option , the estimated CSI between the UAV and the RIS, and between the UAV and the UEs, and the distance between the UAV and the targets; thus, the state space can be expressed as
- (2)
- Action space : The action space contains the actions to perform the sensing and communication during the time slots, which is consistent with the policy set , (i.e., Equation (22)).
- (3)
- Reward : Since our object is to maximize the sum-rate throughput during the whole N process, the sum-rate throughput within time slot n can be directly used as the reward, which can be expressed aswhere denotes the reward obtained by executing action at the state , and denotes the penalty coefficient, which is set to 0 (i.e., no data transmission).
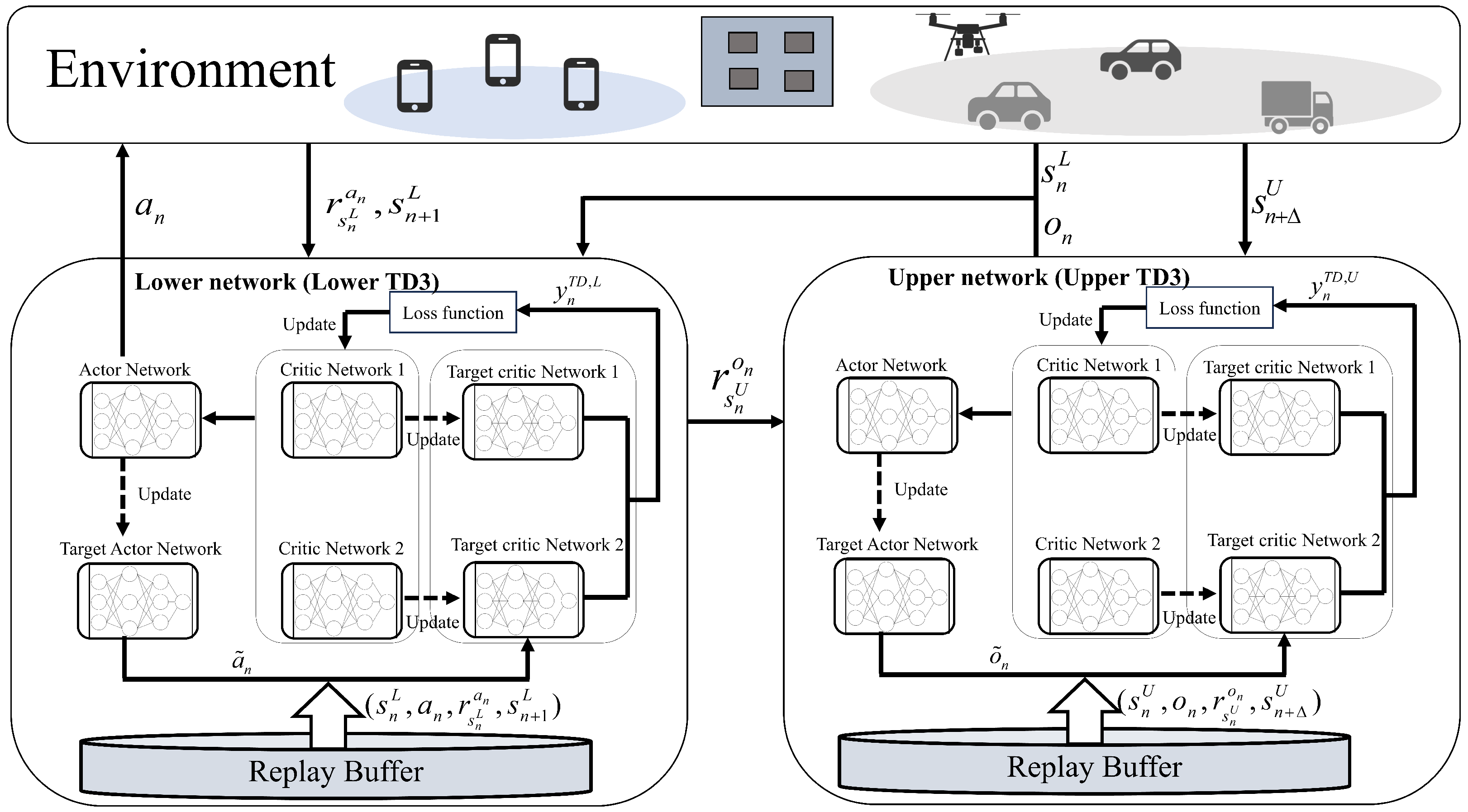
3.2. HDRL Framework
| Algorithm 1 The HDRL Algorithm |
|
4. Simulations
4.1. Simulation Settings
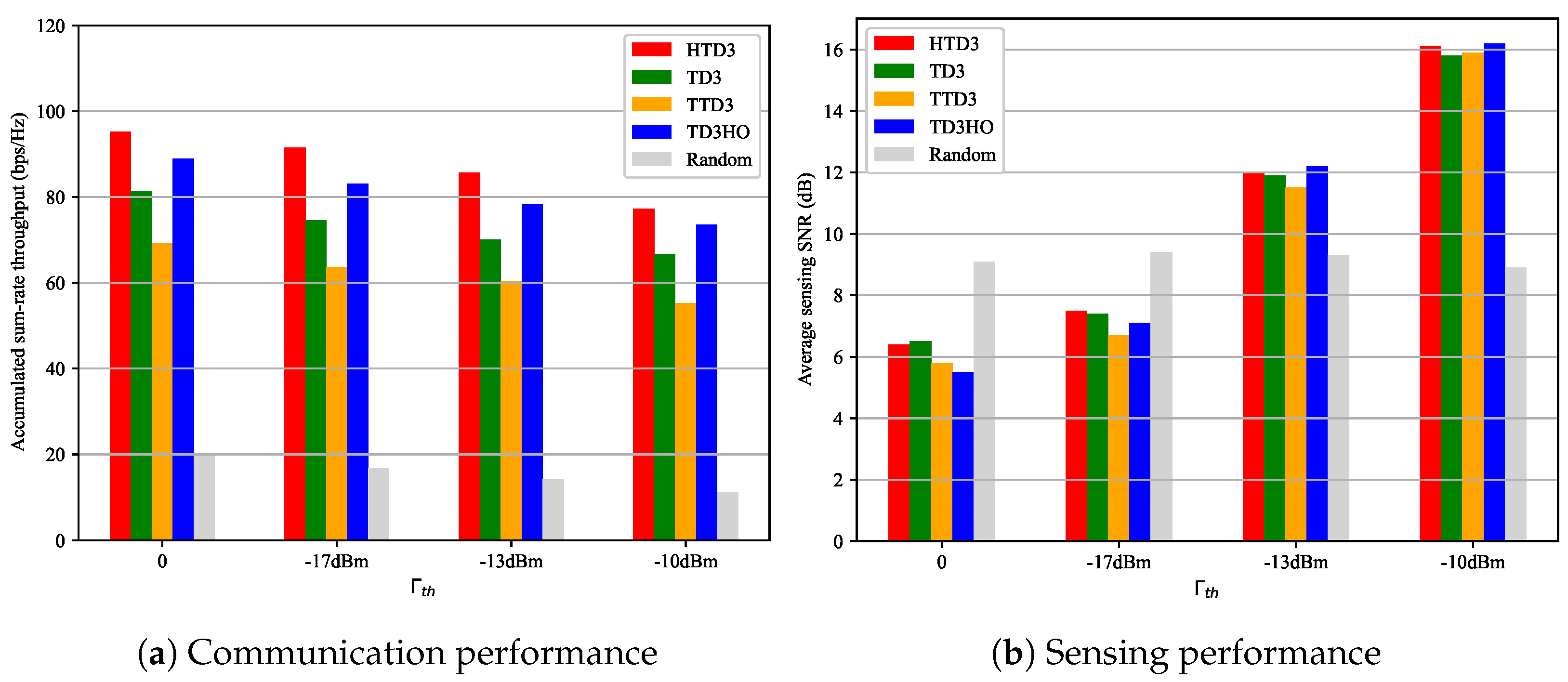
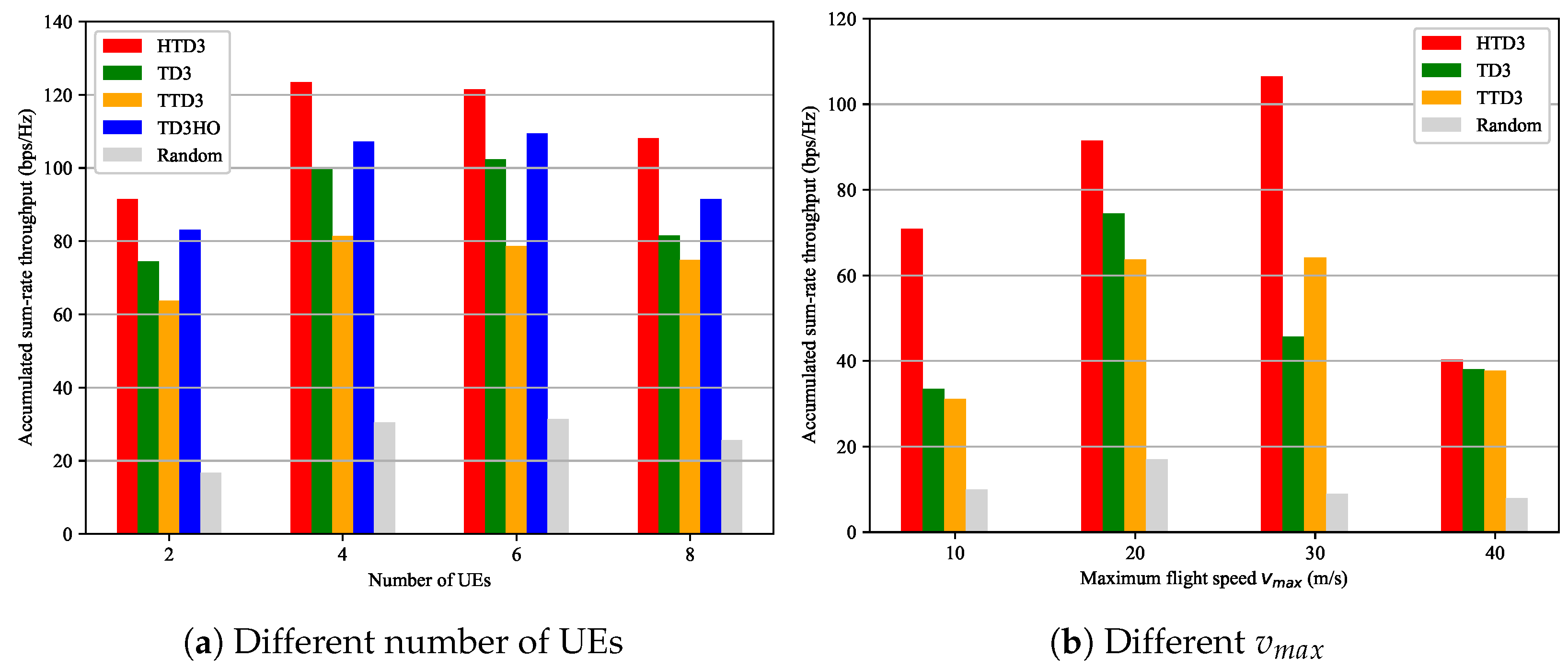
4.2. The Impact of Environmental Parameters on HTD3
4.3. Benchmark Schemes
- (1)
- TD3: We use TD3 to jointly control the trajectory of the UAV, the beamforming matrix of the UAV, and the passive beamforming matrix of the RIS. Differently from HTD3, all actions are output by one actor network. We use this benchmark to verify the effectiveness of decomposing the original problems.
- (2)
- TTD3: TTD3 was proposed in [25] and uses two agents to output two different sets of actions. In this article, in the TTD3 case, two agents are adopted to adjust the location of the UAV and handle the sensing and communication tasks. Differently from HTD3, which is a hierarchical structure, although both TTD3 and HTD3 contain two agents, TTD3 adopts a parallel structure, which outputs all actions simultaneously. We use this benchmark to verify the effectiveness of our hierarchical structure design.
- (3)
- TD3 with Hovering Only (TD3-HO): We use TD3 to jointly control the beamforming matrix of the UAV and the passive beamforming matrix of the RIS, while the UAV hovers at a fixed position. We use this benchmark to verify the effectiveness of the optimization of the trajectory.
- (4)
- Random action: The UAV randomly executes actions. We use this benchmark to verify the effectiveness of DRL.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lu, S.; Liu, F.; Li, Y.; Zhang, K.; Huang, H.; Zou, J.; Li, X.; Dong, Y.; Dong, F.; Zhu, J.; et al. Integrated Sensing and Communications: Recent Advances and Ten Open Challenges. IEEE Internet Things J. 2024, 11, 19094–19120. [Google Scholar] [CrossRef]
- Lyu, Z.; Zhu, G.; Xu, J. Joint Maneuver and Beamforming Design for UAV-Enabled Integrated Sensing and Communication. IEEE Trans. Wirel. Commun. 2023, 22, 2424–2440. [Google Scholar] [CrossRef]
- Deng, C.; Fang, X.; Wang, X. Beamforming Design and Trajectory Optimization for UAV-Empowered Adaptable Integrated Sensing and Communication. IEEE Trans. Wirel. Commun. 2023, 22, 8512–8526. [Google Scholar] [CrossRef]
- Luo, H.; Liu, R.; Li, M.; Liu, Q. RIS-Aided Integrated Sensing and Communication: Joint Beamforming and Reflection Design. IEEE Trans. Veh. Technol. 2023, 72, 9626–9630. [Google Scholar] [CrossRef]
- Sankar, R.S.P.; Chepuri, S.P.; Eldar, Y.C. Beamforming in Integrated Sensing and Communication Systems with Reconfigurable Intelligent Surfaces. IEEE Trans. Wirel. Commun. 2024, 23, 4017–4031. [Google Scholar] [CrossRef]
- Long, X.; Zhao, Y.; Wu, H.; Xu, C.Z. Deep Reinforcement Learning for Integrated Sensing and Communication in RIS-assisted 6G V2X System. IEEE Internet Things J. 2024. early access. [Google Scholar] [CrossRef]
- Saikia, P.; Singh, K.; Huang, W.J.; Duong, T.Q. Hybrid Deep Reinforcement Learning for Enhancing Localization and Communication Efficiency in RIS-Aided Cooperative ISAC Systems. IEEE Internet Things J. 2024, 11, 29494–29510. [Google Scholar] [CrossRef]
- Meng, K.; Wu, Q.; Xu, J.; Chen, W.; Feng, Z.; Schober, R.; Swindlehurst, A.L. UAV-Enabled Integrated Sensing and Communication: Opportunities and Challenges. IEEE Wirel. Commun. 2024, 31, 97–104. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, X.; Liu, Y.; Leung, V.C.M.; Durrani, T.S. UAV Assisted Integrated Sensing and Communications for Internet of Things: 3D Trajectory Optimization and Resource Allocation. IEEE Trans. Wirel. Commun. 2024, 23, 8654–8667. [Google Scholar] [CrossRef]
- Meng, K.; Wu, Q.; Ma, S.; Chen, W.; Wang, K.; Li, J. Throughput Maximization for UAV-Enabled Integrated Periodic Sensing and Communication. IEEE Trans. Wirel. Commun. 2023, 22, 671–687. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, Y.; Tang, R.; Zhao, H.; Xiao, Q.; Wang, C. A Joint UAV Trajectory, User Association, and Beamforming Design Strategy for Multi-UAV-Assisted ISAC Systems. IEEE Internet Things J. 2024, 11, 29360–29374. [Google Scholar] [CrossRef]
- Wu, J.; Yuan, W.; Hanzo, L. When UAVs Meet ISAC: Real-Time Trajectory Design for Secure Communications. IEEE Trans. Veh. Technol. 2023, 72, 16766–16771. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Liu, Z.; Yu, Y.; Jia, M.; Na, Z.; Durrani, T.S. Secure Rate Maximization for ISAC-UAV Assisted Communication Amidst Multiple Eavesdroppers. IEEE Trans. Veh. Technol. 2024, 73, 15843–15847. [Google Scholar] [CrossRef]
- Yu, X.; Xu, J.; Zhao, N.; Wang, X.; Niyato, D. Security Enhancement of ISAC via IRS-UAV. IEEE Trans. Wirel. Commun. 2024, 23, 15601–15612. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, J.; Lu, W.; Zhao, N.; Wang, X.; Niyato, D. Secure Transmission for IRS-Aided UAV-ISAC Networks. IEEE Trans. Wirel. Commun. 2024, 23, 12256–12269. [Google Scholar] [CrossRef]
- Wu, Z.; Li, X.; Cai, Y.; Yuan, W. Joint Trajectory and Resource Allocation Design for RIS-Assisted UAV-Enabled ISAC Systems. IEEE Wirel. Commun. Lett. 2024, 13, 1384–1388. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Q.; Miao, J.; Yu, F.R.; Fu, F.; Du, J.; Wu, T. Energy-Efficient Secure Video Streaming in UAV-Enabled Wireless Networks: A Safe-DQN Approach. IEEE Trans. Green Commun. Netw. 2021, 5, 1892–1905. [Google Scholar] [CrossRef]
- Miao, J.; Bai, S.; Mumtaz, S.; Zhang, Q.; Mu, J. Utility-Oriented Optimization for Video Streaming in UAV-Aided MEC Network: A DRL Approach. IEEE Trans. Green Commun. Netw. 2024, 8, 878–889. [Google Scholar] [CrossRef]
- Yan, M.; Xiong, R.; Wang, Y.; Li, C. Edge Computing Task Offloading Optimization for a UAV-Assisted Internet of Vehicles via Deep Reinforcement Learning. IEEE Trans. Veh. Technol. 2024, 73, 5647–5658. [Google Scholar] [CrossRef]
- Yao, Y.; Miao, J.; Zhang, T.; Tang, X.; Kang, J.; Niyato, D. Towards Secrecy Energy-Efficient RIS Aided UAV Network: A Lyapunov-Guided Reinforcement Learning Approach. In Proceedings of the 2024 IEEE Wireless Communications and Networking Conference (WCNC), Dubai, United Arab Emirates, 21–24 April 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, Z.; Zhang, J.; Cao, X.; Zheng, D.; Gao, Y.; Ng, D.W.K.; Renzo, M.D. Trajectory Design for UAV-Based Internet of Things Data Collection: A Deep Reinforcement Learning Approach. IEEE Internet Things J. 2022, 9, 3899–3912. [Google Scholar] [CrossRef]
- Liu, Q.; Zhu, Y.; Li, M.; Liu, R.; Liu, Y.; Lu, Z. DRL-Based Secrecy Rate Optimization for RIS-Assisted Secure ISAC Systems. IEEE Trans. Veh. Technol. 2023, 72, 16871–16875. [Google Scholar] [CrossRef]
- Qin, Y.; Zhang, Z.; Li, X.; Huangfu, W.; Zhang, H. Deep Reinforcement Learning Based Resource Allocation and Trajectory Planning in Integrated Sensing and Communications UAV Network. IEEE Trans. Wirel. Commun. 2023, 22, 8158–8169. [Google Scholar] [CrossRef]
- Lim, H.K.; Ullah, I.; Kim, J.B.; Han, Y.H. Virtual Network Embedding Based on Hierarchical Cooperative Multiagent Reinforcement Learning. IEEE Internet Things J. 2024, 11, 8552–8568. [Google Scholar] [CrossRef]
- Tham, M.L.; Wong, Y.J.; Iqbal, A.; Ramli, N.B.; Zhu, Y.; Dagiuklas, T. Deep Reinforcement Learning for Secrecy Energy- Efficient UAV Communication with Reconfigurable Intelligent Surface. In Proceedings of the 2023 IEEE Wireless Communications and Networking Conference (WCNC), Glasgow, UK, 26–29 March 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, Z.; Miao, J.; Zhang, T.; Tang, X.; Kang, J.; Niyato, D. QoE Maximization for Video Streaming in Cache-Enable Satellite-UAV-Terrestrial Network. In Proceedings of the ICC 2024—IEEE International Conference on Communications, Denver, CO, USA, 9–13 June 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Ren, T.; Niu, J.; Dai, B.; Liu, X.; Hu, Z.; Xu, M.; Guizani, M. Enabling Efficient Scheduling in Large-Scale UAV-Assisted Mobile-Edge Computing via Hierarchical Reinforcement Learning. IEEE Internet Things J. 2022, 9, 7095–7109. [Google Scholar] [CrossRef]
- Susarla, P.; Deng, Y.; Juntti, M.; Sílven, O. Hierarchial-DQN Position-Aided Beamforming for Uplink mmWave Cellular-Connected UAVs. In Proceedings of the GLOBECOM 2022—2022 IEEE Global Communications Conference, Rio de Janeiro, Brazil, 4–8 December 2022; pp. 1308–1313. [Google Scholar] [CrossRef]
- Khuwaja, A.A.; Chen, Y.; Zhao, N.; Alouini, M.S.; Dobbins, P. A Survey of Channel Modeling for UAV Communications. IEEE Commun. Surv. Tutor. 2018, 20, 2804–2821. [Google Scholar] [CrossRef]
- Khalili, A.; Rezaei, A.; Xu, D.; Schober, R. Energy-Aware Resource Allocation and Trajectory Design for UAV-Enabled ISAC. In Proceedings of the GLOBECOM 2023—2023 IEEE Global Communications Conference, Kuala Lumpur, Malaysia, 4–8 December 2023; pp. 4193–4198. [Google Scholar] [CrossRef]





| Notation | Definition | Value |
|---|---|---|
| H | The fixed altitude of the UAV | 40 m |
| The fixed altitude of the RIS | 15 m | |
| A | The number of antennas of the UAV | 4 |
| M | The number of antennas of the RIS | 4 |
| The flight time in each time slot | 0.1 s | |
| The channel power gain at reference distance m | −30 dB | |
| The NLOS coefficients | [2.3, 34] [29] | |
| The NLOS coefficients | [27.23, 0.097] [29] | |
| The carrier frequency | 2 GHz | |
| The speed of light | m/s | |
| The radar cross-section of targets | 1 m2 | |
| The noise power | −114 dBm | |
| The maximum transmission power of the UAV | 1 W | |
| The maximum speed of the UAV | 20 m/s | |
| The training rounds | 1000 | |
| N | The number of time slots of each round | 100 |
| The steps of the lower layer network | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Miao, J.; Wang, R.; Li, H.; Zhang, X. A Hierarchical Deep Reinforcement Learning Approach for Throughput Maximization in Reconfigurable Intelligent Surface-Aided Unmanned Aerial Vehicle–Integrated Sensing and Communication Network. Drones 2024, 8, 717. https://doi.org/10.3390/drones8120717
Chen H, Miao J, Wang R, Li H, Zhang X. A Hierarchical Deep Reinforcement Learning Approach for Throughput Maximization in Reconfigurable Intelligent Surface-Aided Unmanned Aerial Vehicle–Integrated Sensing and Communication Network. Drones. 2024; 8(12):717. https://doi.org/10.3390/drones8120717
Chicago/Turabian StyleChen, Haitao, Jiansong Miao, Ruisong Wang, Hao Li, and Xiaodan Zhang. 2024. "A Hierarchical Deep Reinforcement Learning Approach for Throughput Maximization in Reconfigurable Intelligent Surface-Aided Unmanned Aerial Vehicle–Integrated Sensing and Communication Network" Drones 8, no. 12: 717. https://doi.org/10.3390/drones8120717
APA StyleChen, H., Miao, J., Wang, R., Li, H., & Zhang, X. (2024). A Hierarchical Deep Reinforcement Learning Approach for Throughput Maximization in Reconfigurable Intelligent Surface-Aided Unmanned Aerial Vehicle–Integrated Sensing and Communication Network. Drones, 8(12), 717. https://doi.org/10.3390/drones8120717





