Review of Aerial Transportation of Suspended-Cable Payloads with Quadrotors
Abstract
1. Introduction
2. Methodology
3. Cable Modeling for Payload Transportation with UAVs
3.1. Individual Transport
- The quadrotor is modeled as a symmetric rigid body.
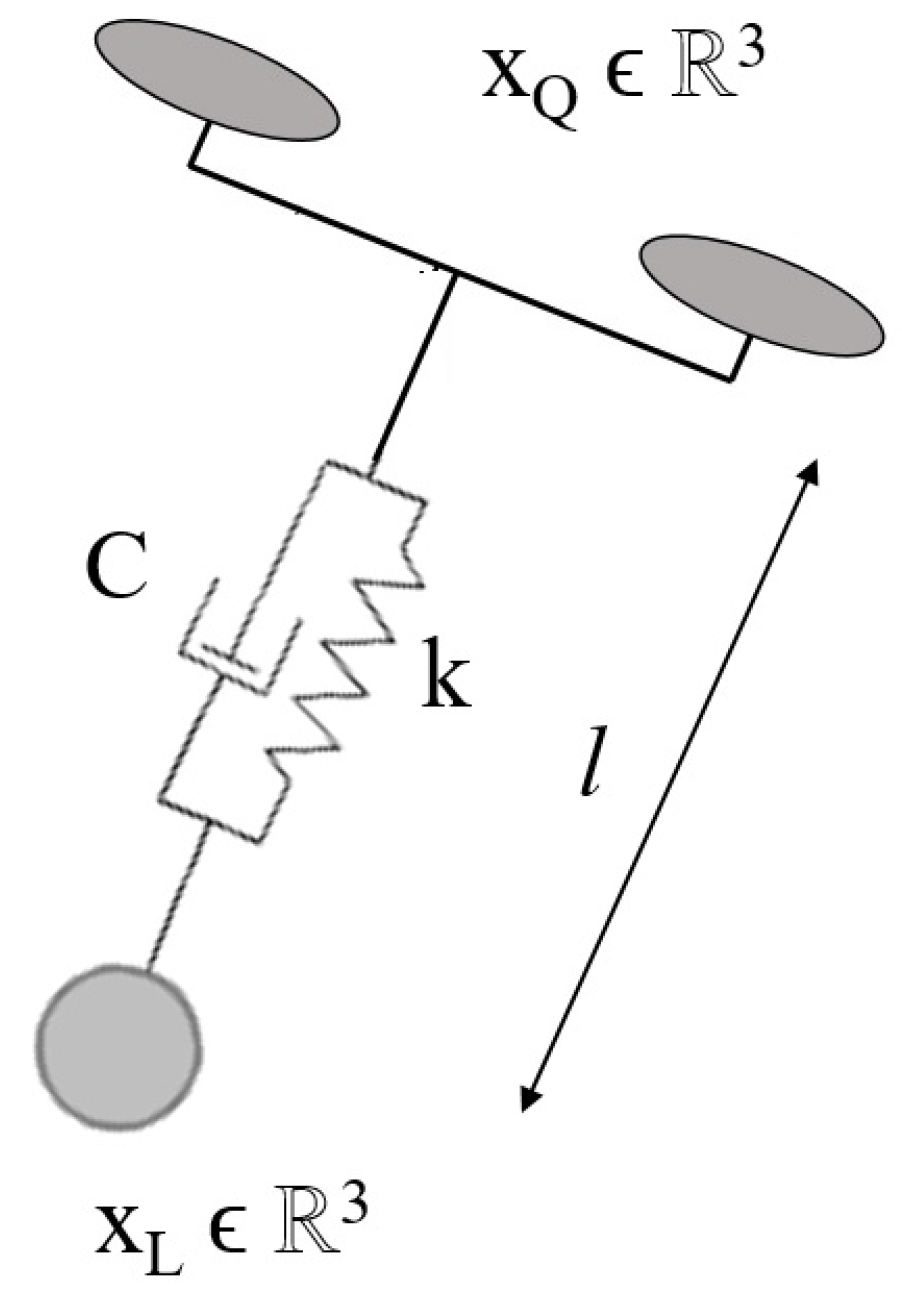
- The cable is modeled as inextensible, massless and attached to the center of the quadrotor, and the payload is modeled as a point mass attached to the cable.
- The mass of the payload is small compared to the mass of the quadrotor, which implies that its motion has little impact on the motion of the quadrotor.
- The effects of the payload and the cable are treated as an external force applied to the UAV.
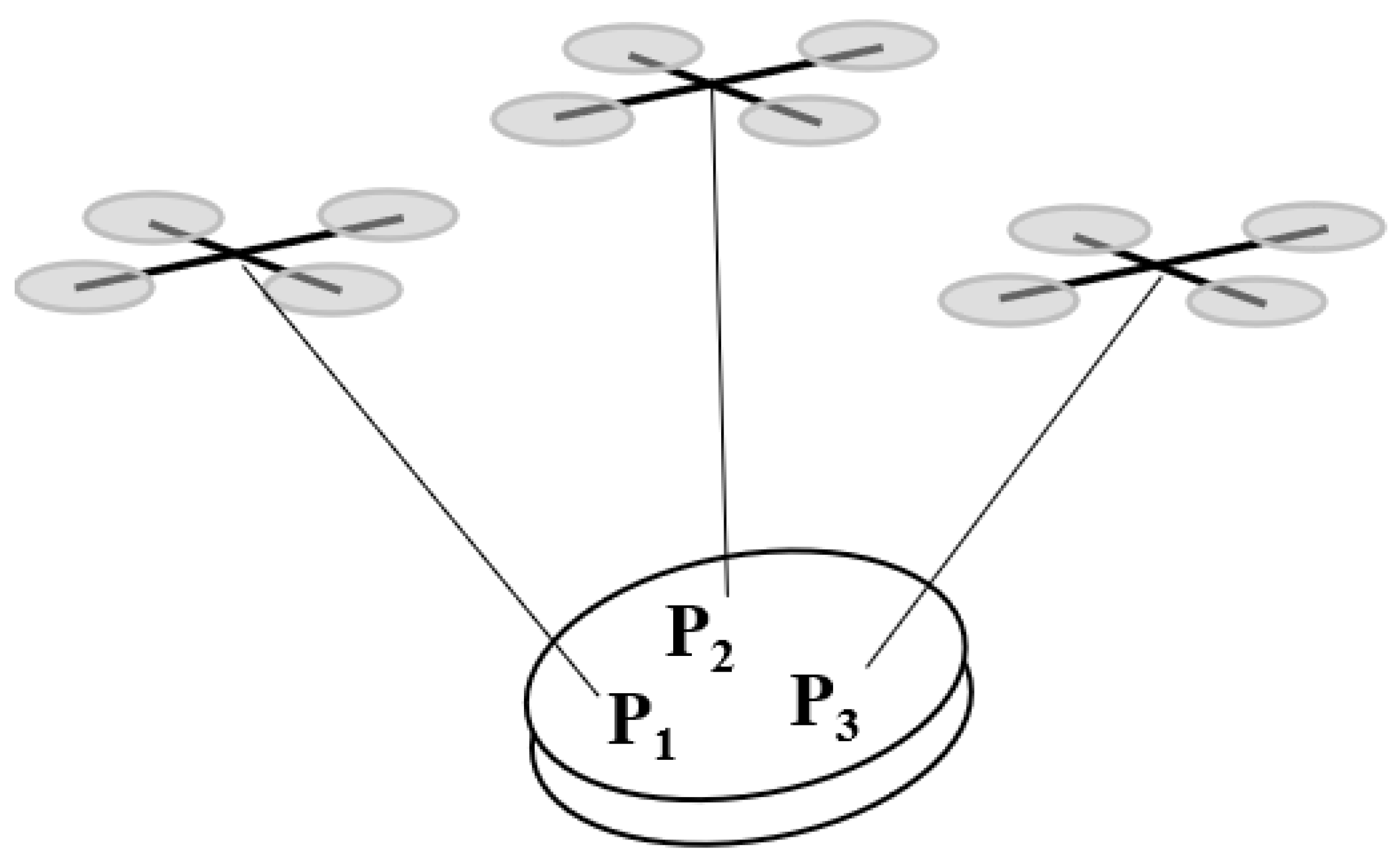
3.2. Collaborative Transport
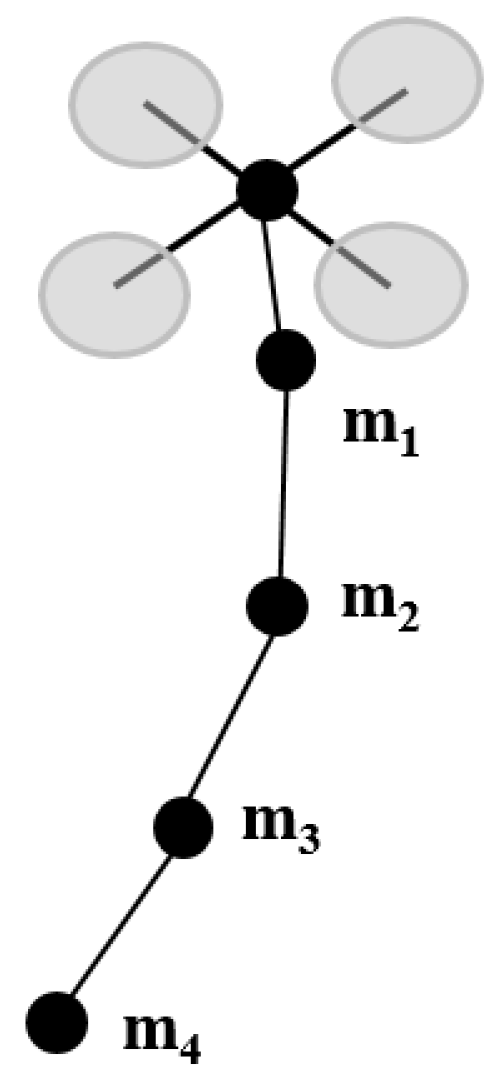
- The cable diameter is negligible compared to its length. Thus, the cable can be modeled as a 1D object.
- The mass per unit length of the cable is constant.
- The cable cannot elastically lengthen (Young’s modulus is large).
- There is no torsion in the cable.
4. Control Strategies
4.1. Individual Transport
4.1.1. Anti-Swing Control
4.1.2. Optimal Trajectory Following
4.1.3. Aggressive Maneuvers
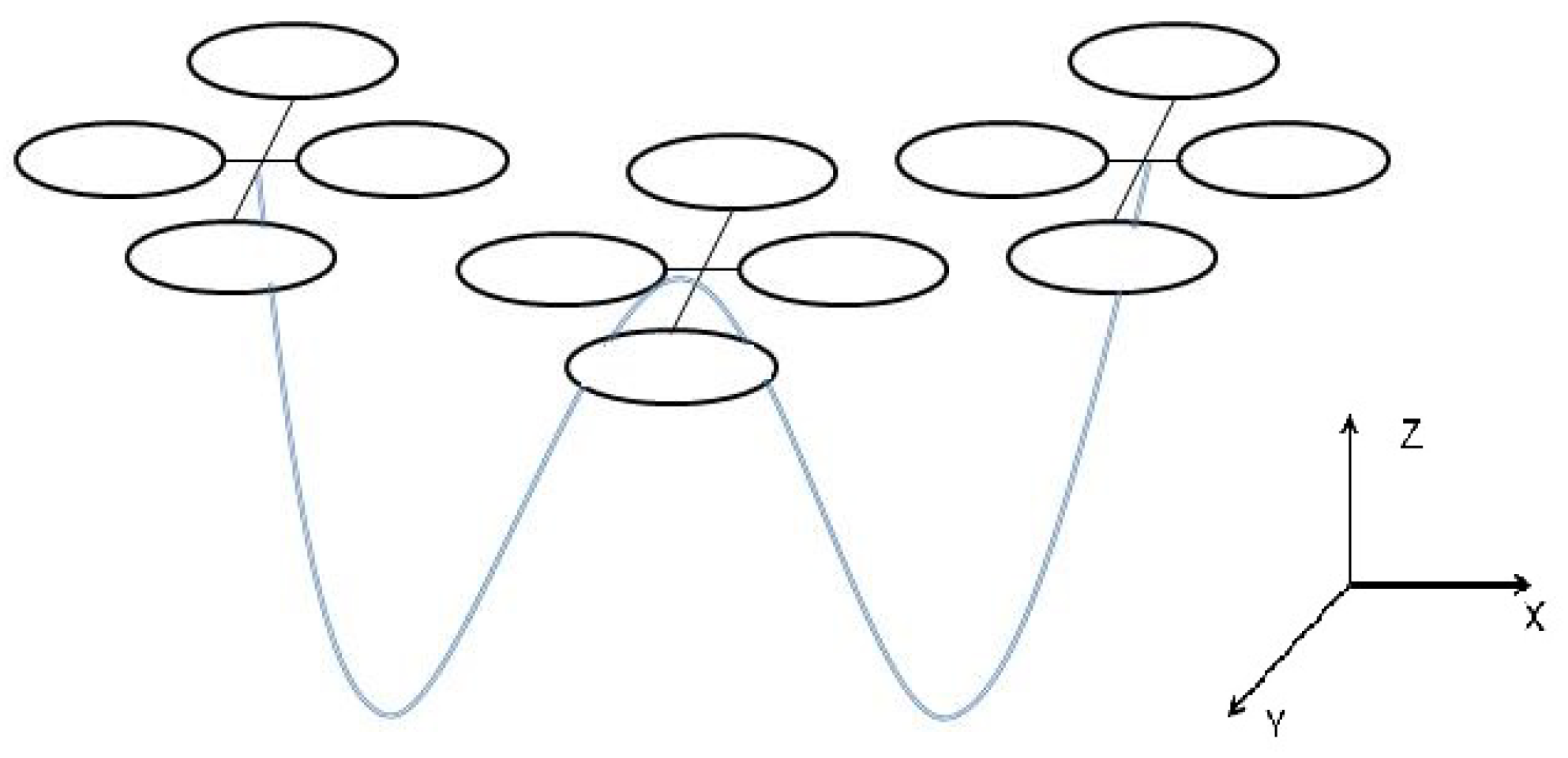
4.2. Collaborative Transport Control
5. Discussion
5.1. Trends in Technology
5.2. Future Challenges
6. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Abdel-Rahman, E.M.; Nayfeh, A.H.; Masoud, Z.N. Dynamics and control of cranes: A review. Modal Anal. 2003, 9, 863–908. [Google Scholar] [CrossRef]
- Kaya, U.C.; Subbarao, K. Momentum Preserving Simulation of Cooperative Multirotors with Flexible-Cable Suspended Payload. J. Dyn. Syst. Meas. Control 2022, 144, 041007. [Google Scholar] [CrossRef]
- Yurchenko, D.; Alevras, P.; Zhou, S.; Wang, J.; Litak, G.; Gaidai, O.; Ye, R. Nonlinear vibration mitigation of a crane’s payload using pendulum absorber. Mech. Syst. Signal Process. 2021, 156, 107558. [Google Scholar] [CrossRef]
- Strip, D. Swing-free transport of suspended objects: A general treatment. IEEE Trans. Robot. Autom. 1989, 5, 234–236. [Google Scholar] [CrossRef]
- D’Andrea-Novel, B.; Boustany, F.; Conrad, F. Control of an overhead crane: Stabilization of flexibilities. In Boundary Control and Boundary Variation; Springer: Berlin/Heidelberg, Germany, 1992; pp. 1–26. [Google Scholar]
- Choo, Y.I.; Casarella, M.J. A Survey of Analytical Methods for Dynamic Simulation of Cable-Body Systems. J. Hydronautics 1973, 7, 137–144. [Google Scholar] [CrossRef]
- Skop, R.A.; Choo, Y.I. The configuration of a cable towed in a circular path. J. Aircr. 1971, 8, 856–862. [Google Scholar] [CrossRef]
- Anderson, V. Method and Apparatus for Pickup and Delivery by Aircraft in Flight. U.S. Patent 2295537, 15 September 1942. [Google Scholar]
- De Laurier, J.D. A stability analysis for tethered aerodynamically shaped balloons. J. Aircr. 1972, 9, 646–651. [Google Scholar] [CrossRef]
- Kamman, J.W.; Huston, R.L. Modeling of variable length towed and tethered cable systems. J. Guid. Control. Dyn. 1999, 22, 602–608. [Google Scholar] [CrossRef]
- Etkin, B. Stability of a towed body. J. Aircr. 1998, 35, 197–205. [Google Scholar] [CrossRef]
- Ro, K.; Kamman, J.W. Modeling and simulation of hose-paradrogue aerial refueling systems. J. Guid. Control. Dyn. 2010, 33, 53–63. [Google Scholar] [CrossRef]
- Sun, L. Dynamic Modeling, Trajectory Generation and Tracking for Towed Cable Systems. Ph.D. Thesis, Brigham Young University, Provo, UT, USA, 2012. [Google Scholar]
- Yi, J.; Zhang, H.; Wang, F.; Ning, C.; Liu, H.; Zhong, G. An Operational Capacity Assessment Method for an Urban Low-Altitude Unmanned Aerial Vehicle Logistics Route Network. Drones 2023, 7, 582. [Google Scholar] [CrossRef]
- Hoffmann, G.M.; Huang, H.; Waslander, S.L.; Tomlin, C.J. Precision flight control for a multi-vehicle quadrotor helicopter testbed. Control Eng. Pract. 2011, 19, 1023–1036. [Google Scholar] [CrossRef]
- Pizetta, I.H.B.; Brandao, A.S.; Sarcinelli-Filho, M. Modelling and control of a PVTOL quadrotor carrying a suspended load. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 444–450. [Google Scholar]
- Kotaru, P.; Wu, G.; Sreenath, K. Dynamics and control of a quadrotor with a payload suspended through an elastic cable. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 3906–3913. [Google Scholar]
- Chen, T.; Shan, J.; Liu, H.H. Cooperative transportation of a flexible payload using two quadrotors. J. Guid. Control. Dyn. 2021, 44, 2099–2107. [Google Scholar] [CrossRef]
- Theobald, K.; Zhu, W.; Waters, T.; Cherrett, T.; Oakey, A.; Royall, P.G. Stability of Medicines Transported by Cargo Drones: Investigating the Effects of Vibration from Multi-Stage Flight. Drones 2023, 7, 658. [Google Scholar] [CrossRef]
- Godbole, A.R.; Subbarao, K. Nonlinear control of unmanned aerial vehicles with cable suspended payloads. Aerosp. Sci. Technol. 2019, 93, 105299. [Google Scholar] [CrossRef]
- Chen, T.; Shan, J. A novel cable-suspended quadrotor transportation system: From theory to experiment. Aerosp. Sci. Technol. 2020, 104, 105974. [Google Scholar] [CrossRef]
- Thomas, J.; Loianno, G.; Polin, J.; Sreenath, K.; Kumar, V. Toward autonomous avian-inspired grasping for micro aerial vehicles. Bioinspir. Biomimetics 2014, 9, 025010. [Google Scholar] [CrossRef]
- Guo, K.; Jia, J.; Yu, X.; Guo, L.; Xie, L. Multiple observers based anti-disturbance control for a quadrotor UAV against payload and wind disturbances. Control Eng. Pract. 2020, 102, 104560. [Google Scholar] [CrossRef]
- Goodarzi, F.A.; Lee, D.; Lee, T. Geometric control of a quadrotor UAV transporting a payload connected via flexible cable. Int. J. Control. Autom. Syst. 2015, 13, 1486–1498. [Google Scholar] [CrossRef]
- Guerrero, M.; Mercado, D.; Lozano, R.; García, C. Passivity based control for a quadrotor UAV transporting a cable-suspended payload with minimum swing. In Proceedings of the 2015 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 6718–6723. [Google Scholar]
- Villa, D.K.D.; Brandão, A.S.; Sarcinelli-Filho, M. A Survey on Load Transportation Using Multirotor UAVs. J. Intell. Robot. Syst. 2020, 98, 267–296. [Google Scholar] [CrossRef]
- Ding, X.; Guo, P.; Xu, K.; Yu, Y. A review of aerial manipulation of small-scale rotorcraft unmanned robotic systems. Chin. J. Aeronaut. 2019, 32, 200–214. [Google Scholar] [CrossRef]
- Bonyan Khamseh, H.; Janabi-Sharifi, F.; Abdessameud, A. Aerial manipulation—A literature survey. Robot. Auton. Syst. 2018, 107, 221–235. [Google Scholar] [CrossRef]
- Ruggiero, F.; Lippiello, V.; Ollero, A. Aerial Manipulation: A Literature Review. IEEE Robot. Autom. Lett. 2018, 3, 1957–1964. [Google Scholar] [CrossRef]
- Oshman, Y.; Isakow, M. Mini-UAV altitude estimation using an inertially stabilized payload. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 1191–1203. [Google Scholar] [CrossRef]
- Borky, J.M. Payload technologies and applications for uninhabited air vehicles (UAVs). In Proceedings of the 1997 IEEE Aerospace Conference, Snowmass, CO, USA, 13 February 1997; Volume 3, pp. 267–283. [Google Scholar]
- Qian, L.; Graham, S.; Liu, H.H.T. Guidance and control law design for a slung payload in autonomous landing: A drone delivery case study. IEEE/ASME Trans. Mechatron. 2020, 25, 1773–1782. [Google Scholar] [CrossRef]
- Guo, M.; Gu, D.; Zha, W.; Zhu, X.; Su, Y. Controlling a quadrotor carrying a cable-suspended load to pass through a window. J. Intell. Robot. Syst. 2020, 98, 387–401. [Google Scholar] [CrossRef]
- Tang, S.; Wüest, V.; Kumar, V. Aggressive flight with suspended payloads using vision-based control. IEEE Robot. Autom. Lett. 2018, 3, 1152–1159. [Google Scholar] [CrossRef]
- Sun, L.; Wang, K.; Mishamandani, A.H.A.; Zhao, G.; Huang, H.; Zhao, X.; Zhang, B. A novel tension-based controller design for the quadrotor–load system. Control Eng. Pract. 2021, 112, 104818. [Google Scholar] [CrossRef]
- Lv, Z.; Zhao, Q.; Li, S.; Wu, Y. Finite-time control design for a quadrotor transporting a slung load. Control Eng. Pract. 2022, 122, 105082. [Google Scholar] [CrossRef]
- Zameroski, D.; Starr, G.; Wood, J.; Lumia, R. Rapid swing-free transport of nonlinear payloads using dynamic programming. J. Dyn. Syst. Meas. Control 2008, 130, 041001. [Google Scholar] [CrossRef]
- Lupashin, S.; D’Andrea, R. Stabilization of a flying vehicle on a taut tether using inertial sensing. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 2432–2438. [Google Scholar]
- Sreenath, K.; Michael, N.; Kumar, V. Trajectory generation and control of a quadrotor with a cable-suspended load—A differentially-flat hybrid system. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 4888–4895. [Google Scholar]
- Akhtar, A.; Saleem, S.; Shan, J. Path following of a quadrotor with a cable-suspended payload. IEEE Trans. Ind. Electron. 2022, 70, 1646–1654. [Google Scholar] [CrossRef]
- Reis, J.; Yu, G.; Cabecinhas, D.; Silvestre, C. High-performance quadrotor slung load transportation with damped oscillations. Int. J. Robust Nonlinear Control 2022, 33, 10227–10256. [Google Scholar] [CrossRef]
- Belguith, M.; Samaali, S.; Bennaceur, S. Modeling and Control of Quadrotor Transporting Cable-Suspended Load in the Longitudinal & Lateral Planes. In Proceedings of the 2023 European Control Conference (ECC), Bucharest, Romania, 13–16 June 2023; pp. 1–6. [Google Scholar]
- de Angelis, E.L.; Giulietti, F. Stability and control issues of multirotor suspended load transportation: An analytical closed–form approach. Aerosp. Sci. Technol. 2023, 135, 108201. [Google Scholar] [CrossRef]
- Estevez, J.; Lopez-Guede, J.M.; Garate, G.; Graña, M. A hybrid control approach for the swing free transportation of a double pendulum with a quadrotor. Appl. Sci. 2021, 11, 5487. [Google Scholar] [CrossRef]
- Castillo, A.; Sanz, R.; Garcia, P.; Qiu, W.; Wang, H.; Xu, C. Disturbance observer-based quadrotor attitude tracking control for aggressive maneuvers. Control Eng. Pract. 2019, 82, 14–23. [Google Scholar] [CrossRef]
- Klausen, K.; Fossen, T.I.; Johansen, T.A. Nonlinear Control with Swing Damping of a Multirotor UAV with Suspended Load. J. Intell. Robot. Syst. 2017, 88, 379–394. [Google Scholar] [CrossRef]
- Cruz, P.J.; Oishi, M.; Fierro, R. Lift of a cable-suspended load by a quadrotor: A hybrid system approach. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 1887–1892. [Google Scholar]
- Cruz, P.J.; Fierro, R. Cable-suspended load lifting by a quadrotor UAV: Hybrid model, trajectory generation, and control. Auton. Robot. 2017, 41, 1629–1643. [Google Scholar] [CrossRef]
- Bisgaard, M.; Bendtsen, J.D.; la Cour-Harbo, A. Modeling of generic slung load system. J. Guid. Control. Dyn. 2009, 32, 573–585. [Google Scholar] [CrossRef]
- Alothman, Y.; Jasim, W.; Gu, D. Quad-rotor lifting-transporting cable-suspended payloads control. In Proceedings of the 2015 21st International Conference on Automation and Computing (ICAC), Glasgow, UK, 11–12 September 2015; pp. 1–6. [Google Scholar]
- Estévez, J.; Lopez-Guede, J.M. Control of transitory take-off regime in the transportation of a pendulum by a quadrotor. In From Bioinspired Systems and Biomedical Applications to Machine Learning, Proceedings of the 8th International Work-Conference on the Interplay between Natural and Artificial Computation, IWINAC 2019, Almería, Spain, 3–7 June 2019; Proceedings, Part II 8; Springer: Cham, Switzerland, 2019; pp. 117–126. [Google Scholar]
- Li, G.; Liu, X.; Loianno, G. RotorTM: A Flexible Simulator for Aerial Transportation and Manipulation. arXiv 2022, arXiv:2205.05140. [Google Scholar] [CrossRef]
- Brandão, A.S.; Smrcka, D.; Pairet, É.; Nascimento, T.; Saska, M. Side-pull maneuver: A novel control strategy for dragging a cable-tethered load of unknown weight using a UAV. IEEE Robot. Autom. Lett. 2022, 7, 9159–9166. [Google Scholar] [CrossRef]
- Yi, K.; Han, J.; Liang, X.; He, Y. Contact transition control with acceleration feedback enhancement for a quadrotor. ISA Trans. 2021, 109, 288–294. [Google Scholar] [CrossRef] [PubMed]
- Romero, J.G.; Rodríguez-Cortés, H. Asymptotic stability for a transformed nonlinear UAV model with a suspended load via energy shaping. Eur. J. Control 2020, 52, 87–96. [Google Scholar] [CrossRef]
- Bingöl, Ö.; Güzey, H.M. Fixed-time neuro-sliding mode controller design for quadrotor UAV transporting a suspended payload. Eur. J. Control 2023, 73, 100879. [Google Scholar] [CrossRef]
- Chang, P.; Yang, S.; Tong, J.; Zhang, F. A new adaptive control design for a quadrotor system with suspended load by an elastic rope. Nonlinear Dyn. 2023, 111, 19073–19092. [Google Scholar] [CrossRef]
- Luo, C.; Zhao, W.; Du, Z.; Yu, L. A neural network based landing method for an unmanned aerial vehicle with soft landing gears. Appl. Sci. 2019, 9, 2976. [Google Scholar] [CrossRef]
- Gautam, A.; Sujit, P.; Saripalli, S. Application of guidance laws to quadrotor landing. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 372–379. [Google Scholar]
- Goodarzi, F.A. Autonomous aerial payload delivery with quadrotor using varying length cable. In Proceedings of the 2016 International Conference on Advanced Mechatronic Systems (ICAMechS), Melbourne, VIC, Australia, 30 November–3 December 2016; pp. 394–399. [Google Scholar]
- Tan, Y.H.; Lai, S.; Wang, K.; Chen, B.M. Cooperative control of multiple unmanned aerial systems for heavy duty carrying. Annu. Rev. Control 2018, 46, 44–57. [Google Scholar] [CrossRef]
- Pizetta, I.H.B.; Brandão, A.S.; Sarcinelli-Filho, M. Avoiding obstacles in cooperative load transportation. ISA Trans. 2019, 91, 253–261. [Google Scholar] [CrossRef] [PubMed]
- Parra-Vega, V.; Sanchez, A.; Izaguirre, C.; Garcia, O.; Ruiz-Sanchez, F. Toward aerial grasping and manipulation with multiple UAVs. J. Intell. Robot. Syst. 2013, 70, 575–593. [Google Scholar] [CrossRef]
- Wu, P.X.; Yang, C.C.; Cheng, T.H. Cooperative Transportation of UAVs Without Inter-UAV Communication. IEEE/ASME Trans. Mechatron. 2023, 28, 2340–2351. [Google Scholar] [CrossRef]
- Loianno, G.; Kumar, V. Cooperative transportation using small quadrotors using monocular vision and inertial sensing. IEEE Robot. Autom. Lett. 2017, 3, 680–687. [Google Scholar] [CrossRef]
- Mellinger, D.; Shomin, M.; Michael, N.; Kumar, V. Cooperative grasping and transport using multiple quadrotors. In Distributed Autonomous Robotic Systems; Springer: Berlin/Heidelberg, Germany, 2013; pp. 545–558. [Google Scholar]
- Sanalitro, D.; Savino, H.J.; Tognon, M.; Cortés, J.; Franchi, A. Full-pose manipulation control of a cable-suspended load with multiple UAVs under uncertainties. IEEE Robot. Autom. Lett. 2020, 5, 2185–2191. [Google Scholar] [CrossRef]
- Nguyen, H.N.; Park, S.; Lee, D. Aerial tool operation system using quadrotors as rotating thrust generators. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1285–1291. [Google Scholar]
- Mohammadi, K.; Sirouspour, S.; Grivani, A. Passivity-Based Control of Multiple Quadrotors Carrying a Cable-Suspended Payload. IEEE/ASME Trans. Mechatron. 2021, 27, 2390–2400. [Google Scholar] [CrossRef]
- Tagliabue, A.; Kamel, M.; Siegwart, R.; Nieto, J. Robust collaborative object transportation using multiple MAVs. Int. J. Robot. Res. 2019, 38, 1020–1044. [Google Scholar] [CrossRef]
- Six, D.; Briot, S.; Chriette, A.; Martinet, P. Dynamic modelling and control of flying parallel robots. Control Eng. Pract. 2021, 117, 104953. [Google Scholar] [CrossRef]
- Arab, F.; Shirazi, F.A.; Yazdi, M.R.H. Planning and distributed control for cooperative transportation of a non-uniform slung-load by multiple quadrotors. Aerosp. Sci. Technol. 2021, 117, 106917. [Google Scholar] [CrossRef]
- Michael, N.; Fink, J.; Kumar, V. Cooperative manipulation and transportation with aerial robots. Auton. Robot. 2010, 30, 73–86. [Google Scholar] [CrossRef]
- Jiang, Q.; Kumar, V. Determination and Stability Analysis of Equilibrium Configurations of Objects Suspended From Multiple Aerial Robots. J. Mech. Robot. 2012, 4, 021005. [Google Scholar] [CrossRef]
- Goodarzi, F.A.; Lee, T. Stabilization of a rigid body payload with multiple cooperative quadrotors. J. Dyn. Syst. Meas. Control 2016, 138, 121001. [Google Scholar] [CrossRef]
- Lee, T. Geometric controls for a tethered quadrotor UAV. In Proceedings of the 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 2749–2754. [Google Scholar]
- Rastgoftar, H.; Atkins, E.M. Cooperative aerial lift and manipulation (CALM). Aerosp. Sci. Technol. 2018, 82, 105–118. [Google Scholar] [CrossRef]
- Chatjigeorgiou, I.K. A finite differences formulation for the linear and nonlinear dynamics of 2D catenary risers. Ocean Eng. 2008, 35, 616–636. [Google Scholar] [CrossRef]
- Gobat, J.I.; Grosenbaugh, M.A. Dynamics in the touchdown region of catenary moorings. Int. J. Offshore Polar Eng. 2001, 11, ISOPE-01-11-4-273. [Google Scholar]
- Suzuki, M.; Yokota, S.; Matsumoto, A.; Hashimoto, H.; Chugo, D. Position Estimation of the Drone Based on the Tensile Force of Cooperatively Towed Tube. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 4294–4299. [Google Scholar]
- Doroudgar, S. Static and Dynamic Modeling and Simulation of the Umbilical Cable in a Tethered Unmanned Aerial System. Ph.D. Thesis, Simon Fraser University, Burnaby, BC, Canada, 2016. [Google Scholar]
- Clifton, J.M.; Schmidt, L.V.; Stuart, T.D. Dynamic modeling of a trailing wire towed by an orbiting aircraft. J. Guid. Control. Dyn. 1995, 18, 875–881. [Google Scholar] [CrossRef]
- Estevez, J.; Graña, M.; Lopez-Guede, J.M. Online fuzzy modulated adaptive PD control for cooperative aerial transportation of deformable linear objects. Integr. Comput.-Aided Eng. 2017, 24, 41–55. [Google Scholar] [CrossRef]
- Estevez, J.; Lopez-Guede, J.M.; Garate, G.; Graña, M. Hybrid Modeling of Deformable Linear Objects for Their Cooperative Transportation by Teams of Quadrotors. Appl. Sci. 2022, 12, 5253. [Google Scholar] [CrossRef]
- D’antonio, D.S.; Cardona, G.A.; Saldana, D. The Catenary Robot: Design and Control of a Cable Propelled by Two Quadrotors. IEEE Robot. Autom. Lett. 2021, 6, 3857–3863. [Google Scholar] [CrossRef]
- Abhishek, V.; Srivastava, V.; Mukherjee, R. Towards a heterogeneous cable-connected team of UAVs for aerial manipulation. In Proceedings of the 2021 American Control Conference (ACC), New Orleans, LA, USA, 25–28 May 2021; pp. 54–59. [Google Scholar]
- Goodarzi, F.A.; Lee, T. Dynamics and control of quadrotor UAVs transporting a rigid body connected via flexible cables. In Proceedings of the American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 4677–4682. [Google Scholar]
- Shirani, B.; Najafi, M.; Izadi, I. Cooperative load transportation using multiple UAVs. Aerosp. Sci. Technol. 2019, 84, 158–169. [Google Scholar] [CrossRef]
- Bacelar, T.; Madeiras, J.; Melicio, R.; Cardeira, C.; Oliveira, P. On-board implementation and experimental validation of collaborative transportation of loads with multiple UAVs. Aerosp. Sci. Technol. 2020, 107, 106284. [Google Scholar] [CrossRef]
- Doakhan, M.; Kabganian, M.; Azimi, A. Cooperative payload transportation with real-time formation control of multi-quadrotors in the presence of uncertainty. J. Frankl. Inst. 2023, 360, 1284–1307. [Google Scholar] [CrossRef]
- Doakhan, M.; Kabganian, M.; Azimi, A. Robust adaptive control for formation-based cooperative transportation of a payload by multi quadrotors. Eur. J. Control 2023, 69, 100763. [Google Scholar] [CrossRef]
- Geng, J.; Langelaan, J.W. Cooperative transport of a slung load using load-leading control. J. Guid. Control. Dyn. 2020, 43, 1313–1331. [Google Scholar] [CrossRef]
- Goodman, J.R.; Beckers, T.; Colombo, L.J. Geometric control for load transportation with quadrotor UAVs by elastic cables. IEEE Trans. Control. Syst. Technol. 2023, 31, 2848–2862. [Google Scholar] [CrossRef]
- Goodman, J.; Colombo, L. Geometric control of two quadrotors carrying a rigid rod with elastic cables. J. Nonlinear Sci. 2022, 32, 65. [Google Scholar] [CrossRef]
- Gabellieri, C.; Tognon, M.; Sanalitro, D.; Franchi, A. Equilibria, Stability, and Sensitivity for the Aerial Suspended Beam Robotic System Subject to Parameter Uncertainty. IEEE Trans. Robot. 2023, 39, 3977–3993. [Google Scholar] [CrossRef]
- Arab, F.; Shirazi, F.A.; Yazdi, M.R.H. Cooperative parameter estimation of a nonuniform payload by multiple quadrotors. Robotica 2022, 40, 1587–1606. [Google Scholar] [CrossRef]
- Rao, N.; Sundaram, S. Integrated decision control approach for cooperative safety-critical payload transport in a cluttered environment. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 8800–8811. [Google Scholar] [CrossRef]
- Xian, B.; Wang, S.; Yang, S. An online trajectory planning approach for a quadrotor UAV with a slung payload. IEEE Trans. Ind. Electron. 2019, 67, 6669–6678. [Google Scholar] [CrossRef]
- Foehn, P.; Falanga, D.; Kuppuswamy, N.; Tedrake, R.; Scaramuzza, D. Fast Trajectory Optimization for Agile Quadrotor Maneuvers with a Cable-Suspended Payload. 2017. Available online: https://dspace.mit.edu/bitstream/handle/1721.1/124528/RSS17_Foehn.pdf?sequence=2&isAllowed=y (accessed on 24 January 2024).
- Villa, D.K.D.; Brandão, A.S.; Carelli, R.; Sarcinelli-Filho, M. Cooperative load transportation with two quadrotors using adaptive control. IEEE Access 2021, 9, 129148–129160. [Google Scholar] [CrossRef]
- Chen, T.; Shan, J. Distributed tracking of a class of underactuated Lagrangian systems with uncertain parameters and actuator faults. IEEE Trans. Ind. Electron. 2019, 67, 4244–4253. [Google Scholar] [CrossRef]
- Palunko, I.; Fierro, R.; Cruz, P. Trajectory generation for swing-free maneuvers of a quadrotor with suspended payload: A dynamic programming approach. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA), Saint Paul, MN, USA, 14–18 May 2012; pp. 2691–2697. [Google Scholar]
- de Angelis, E.L.; Giulietti, F.; Pipeleers, G. Two-time-scale control of a multirotor aircraft for suspended load transportation. Aerosp. Sci. Technol. 2019, 84, 193–203. [Google Scholar] [CrossRef]
- Nicotra, M.M.; Garone, E.; Naldi, R.; Marconi, L. Nested saturation control of an UAV carrying a suspended load. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 3585–3590. [Google Scholar]
- Zhou, X.; Liu, R.; Zhang, J.; Zhang, X. Stabilization of a quadrotor with uncertain suspended load using sliding mode control. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Charlotte, NC, USA, 21–24 August 2016; American Society of Mechanical Engineers: New York, NY, USA, 2016; Volume 50152. [Google Scholar]
- Yi, K.; Liang, X.; He, Y.; Yang, L.; Han, J. Active-model-based control for the quadrotor carrying a changed slung load. Electronics 2019, 8, 461. [Google Scholar] [CrossRef]
- Yu, G.; Xie, W.; Cabecinhas, D.; Cunha, R.; Silvestre, C. Adaptive control with unknown mass estimation for a quadrotor-slung-load system. ISA Trans. 2023, 133, 412–423. [Google Scholar] [CrossRef] [PubMed]
- Koksal, N.; An, H.; Fidan, B. Backstepping-based adaptive control of a quadrotor UAV with guaranteed tracking performance. ISA Trans. 2020, 105, 98–110. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Fang, Y.; Sun, N.; Lin, H. Dynamics analysis and time-optimal motion planning for unmanned quadrotor transportation systems. Mechatronics 2018, 50, 16–29. [Google Scholar] [CrossRef]
- Blackburn, D.; Singhose, W.; Kitchen, J.; Patrangenaru, V.; Lawrence, J.; Kamoi, T.; Taura, A. Command shaping for nonlinear crane dynamics. J. Vib. Control 2010, 16, 477–501. [Google Scholar] [CrossRef]
- Alkomy, H.; Shan, J. Vibration reduction of a quadrotor with a cable-suspended payload using polynomial trajectories. Nonlinear Dyn. 2021, 104, 3713–3735. [Google Scholar] [CrossRef]
- Huo, X.; Chen, J.; Liu, Q.; He, X. Vibration elimination for quadrotor slung system based on input shaping and double closed-loop control. In Proceedings of the 2019 12th Asian Control Conference (ASCC), Kitakyushu, Japan, 9–12 June 2019; pp. 492–497. [Google Scholar]
- Kusznir, T.; Smoczek, J. Sliding mode-based control of a UAV quadrotor for suppressing the cable-suspended payload vibration. J. Control Sci. Eng. 2020, 2020, 5058039. [Google Scholar] [CrossRef]
- Slabber, J.; Jordaan, H.W. Vision-Based Control of an Unknown Suspended Payload with a Multirotor. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 4875–4880. [Google Scholar]
- Lee, T. Collision avoidance for quadrotor UAVs transporting a payload via Voronoi tessellation. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 1842–1848. [Google Scholar]
- Lee, T. Geometric control of quadrotor UAVs transporting a cable-suspended rigid body. IEEE Trans. Control Syst. Technol. 2017, 26, 255–264. [Google Scholar] [CrossRef]
- Fliess, M.; Lévine, J.; Martin, P.; Rouchon, P. Flatness and defect of non-linear systems: Introductory theory and examples. Int. J. Control 1995, 61, 1327–1361. [Google Scholar] [CrossRef]
- Qian, L.; Liu, H.H.T. Path-Following Control of A Quadrotor UAV With A Cable-Suspended Payload Under Wind Disturbances. IEEE Trans. Ind. Electron. 2020, 67, 2021–2029. [Google Scholar] [CrossRef]
- Cabecinhas, D.; Cunha, R.; Silvestre, C. A trajectory tracking control law for a quadrotor with slung load. Automatica 2019, 106, 384–389. [Google Scholar] [CrossRef]
- Faust, A.; Palunko, I.; Cruz, P.; Fierro, R.; Tapia, L. Automated aerial suspended cargo delivery through reinforcement learning. Artif. Intell. 2017, 247, 381–398. [Google Scholar] [CrossRef]
- Li, R.; Yang, F.; Xu, Y.; Yuan, W.; Lu, Q. Deep Reinforcement Learning-based Swing-Free Trajectories Planning Algorithm for UAV with a Suspended Load. In Proceedings of the 2022 China Automation Congress (CAC), Xiamen, China, 25–27 November 2022; pp. 6149–6154. [Google Scholar]
- Urbina-Brito, N.; Guerrero-Sánchez, M.E.; Valencia-Palomo, G.; Hernández-González, O.; López-Estrada, F.R.; Hoyo-Montaño, J.A. A predictive control strategy for aerial payload transportation with an unmanned aerial vehicle. Mathematics 2021, 9, 1822. [Google Scholar] [CrossRef]
- Lee, B.Y.; Lee, H.I.; Yoo, D.W.; Moon, G.H.; Lee, D.Y.; young Kim, Y.; Tahk, M.J. Study on payload stabilization method with the slung-load transportation system using a quad-rotor. In Proceedings of the 2015 European Control Conference (ECC), Linz, Austria, 15–17 July 2015; pp. 2097–2102. [Google Scholar]
- Son, C.Y.; Seo, H.; Kim, T.; Kim, H.J. Model predictive control of a multi-rotor with a suspended load for avoiding obstacles. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 5233–5238. [Google Scholar]
- Hanover, D.; Foehn, P.; Sun, S.; Kaufmann, E.; Scaramuzza, D. Performance, precision, and payloads: Adaptive nonlinear MPC for quadrotors. IEEE Robot. Autom. Lett. 2021, 7, 690–697. [Google Scholar] [CrossRef]
- Faessler, M.; Fontana, F.; Forster, C.; Mueggler, E.; Pizzoli, M.; Scaramuzza, D. Autonomous, vision-based flight and live dense 3D mapping with a quadrotor micro aerial vehicle. J. Field Robot. 2016, 33, 431–450. [Google Scholar] [CrossRef]
- Tal, E.; Karaman, S. Accurate tracking of aggressive quadrotor trajectories using incremental nonlinear dynamic inversion and differential flatness. IEEE Trans. Control Syst. Technol. 2020, 29, 1203–1218. [Google Scholar] [CrossRef]
- Sreenath, K.; Lee, T.; Kumar, V. Geometric control and differential flatness of a quadrotor UAV with a cable-suspended load. In Proceedings of the 52nd IEEE Conference on Decision and Control, Philadelphia, PA, USA, 10–12 July 2013; pp. 2269–2274. [Google Scholar]
- Torrente, G.; Kaufmann, E.; Föhn, P.; Scaramuzza, D. Data-driven MPC for quadrotors. IEEE Robot. Autom. Lett. 2021, 6, 3769–3776. [Google Scholar] [CrossRef]
- Sun, S.; Romero, A.; Foehn, P.; Kaufmann, E.; Scaramuzza, D. A comparative study of nonlinear MPC and differential-flatness-based control for quadrotor agile flight. IEEE Trans. Robot. 2022, 38, 3357–3373. [Google Scholar] [CrossRef]
- Norouzi, A.; Shahpouri, S.; Gordon, D.; Winkler, A.; Nuss, E.; Abel, D.; Andert, J.; Shahbakhti, M.; Koch, C.R. Deep learning based model predictive control for compression ignition engines. Control Eng. Pract. 2022, 127, 105299. [Google Scholar] [CrossRef]
- Bangura, M.; Mahony, R. Real-time model predictive control for quadrotors. IFAC Proc. Vol. 2014, 47, 11773–11780. [Google Scholar] [CrossRef]
- Alexis, K.; Nikolakopoulos, G.; Tzes, A. On trajectory tracking model predictive control of an unmanned quadrotor helicopter subject to aerodynamic disturbances. Asian J. Control 2014, 16, 209–224. [Google Scholar] [CrossRef]
- Nguyen, H.; Kamel, M.; Alexis, K.; Siegwart, R. Model predictive control for micro aerial vehicles: A survey. In Proceedings of the 2021 European Control Conference (ECC), Rotterdam, The Netherlands, 29 June–2 July 2021; pp. 1556–1563. [Google Scholar]
- Maza, I.; Kondak, K.; Bernard, M.; Ollero, A. Multi-UAV Cooperation and Control for Load Transportation and Deployment. J. Intell. Robot. Syst. 2009, 57, 417–449. [Google Scholar] [CrossRef]
- Ariyibi, S.O.; Tekinalp, O. Quaternion-based nonlinear attitude control of quadrotor formations carrying a slung load. Aerosp. Sci. Technol. 2020, 105, 105995. [Google Scholar] [CrossRef]
- Klausen, K.; Meissen, C.; Fossen, T.I.; Arcak, M.; Johansen, T.A. Cooperative control for multirotors transporting an unknown suspended load under environmental disturbances. IEEE Trans. Control Syst. Technol. 2020, 28, 653–660. [Google Scholar] [CrossRef]
- Tognon, M.; Gabellieri, C.; Pallottino, L.; Franchi, A. Aerial co-manipulation with cables: The role of internal force for equilibria, stability, and passivity. IEEE Robot. Autom. Lett. 2018, 3, 2577–2583. [Google Scholar] [CrossRef]
- Wehbeh, J.; Rahman, S.; Sharf, I. Distributed model predictive control for UAVs collaborative payload transport. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 11666–11672. [Google Scholar]
- Gimenez, J.; Gandolfo, D.C.; Salinas, L.R.; Rosales, C.; Carelli, R. Multi-objective control for cooperative payload transport with rotorcraft UAVs. ISA Trans. 2018, 80, 491–502. [Google Scholar] [CrossRef] [PubMed]
- Gimenez, J.; Salinas, L.R.; Gandolfo, D.C.; Rosales, C.D.; Carelli, R. Control for cooperative transport of a bar-shaped payload with rotorcraft UAVs including a landing stage on mobile robots. Int. J. Syst. Sci. 2020, 51, 3378–3392. [Google Scholar] [CrossRef]
- Lee, T.; Sreenath, K.; Kumar, V. Geometric control of cooperating multiple quadrotor UAVs with a suspended payload. In Proceedings of the 52nd IEEE Conference on Decision and Control, Firenze, Italy, 10–13 December 2013; pp. 5510–5515. [Google Scholar]
- Sharma, M.; Sundaram, S. A geometric control approach for multi-UAV cooperative payload transfer. Nonlinear Dyn. 2023, 111, 10077–10096. [Google Scholar] [CrossRef]
- Outeiro, P.; Cardeira, C.; Oliveira, P. Control Architecture for a Quadrotor Transporting a Cable-Suspended Load of Uncertain Mass. Drones 2023, 7, 201. [Google Scholar] [CrossRef]
- Gabellieri, C.; Tognon, M.; Sanalitro, D.; Franchi, A. Force-based Pose Regulation of a Cable-Suspended Load Using UAVs with Force Bias. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, IROS 2023, Detroit, MI, USA, 1–5 October 2023. [Google Scholar]
- Estevez, J.; Lopez-Guede, J.M.; Graña, M. Quasi-stationary state transportation of a hose with quadrotors. Robot. Auton. Syst. 2015, 63 Pt 2, 187–194. [Google Scholar] [CrossRef]
- Tagliabue, A.; Kamel, M.; Verling, S.; Siegwart, R.; Nieto, J. Collaborative transportation using mavs via passive force control. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5766–5773. [Google Scholar]



| Criteria | Data |
|---|---|
| Scientific Database | IEEEXplore, Google Scholar, ISI Web of Knowledge, ScienceDirect |
| Publication Period | From 2007 to November 2023 |
| Keywords | (“quadrotor” OR “rotorcraft” OR “quadcopter” “UAV” OR “multi-rotor” OR “multiple quadrotor” OR “swarm robot” OR “collaborative robots” OR “team of quadrotors”) AND (“delivery” OR “transportation” OR “transport” OR “retrieval” OR “cargo” OR “cable” OR “payload” OR “suspended load”) |
| Single- and Multi-UAV Transportation Systems | |
|---|---|
| Model | Description |
| Taut cable | It is the most common and used model for both single and collaborative UAV systems. Mathematically simple, the payload is represented by a mass particle, and the cable is represented by a massless rigid bar that permanently maintains a constant distance between the payload and the quadrotor. It represents most of the cable dynamics with enough detail. It is al used for loose cables and for lifting payloads from the ground. Cable nonlinearities in aggressive maneuvers are not well represented. Particularly in multi-UAV systems, more real experimentation is required. References: [39,40,46,48,50,51,53,89,144] |
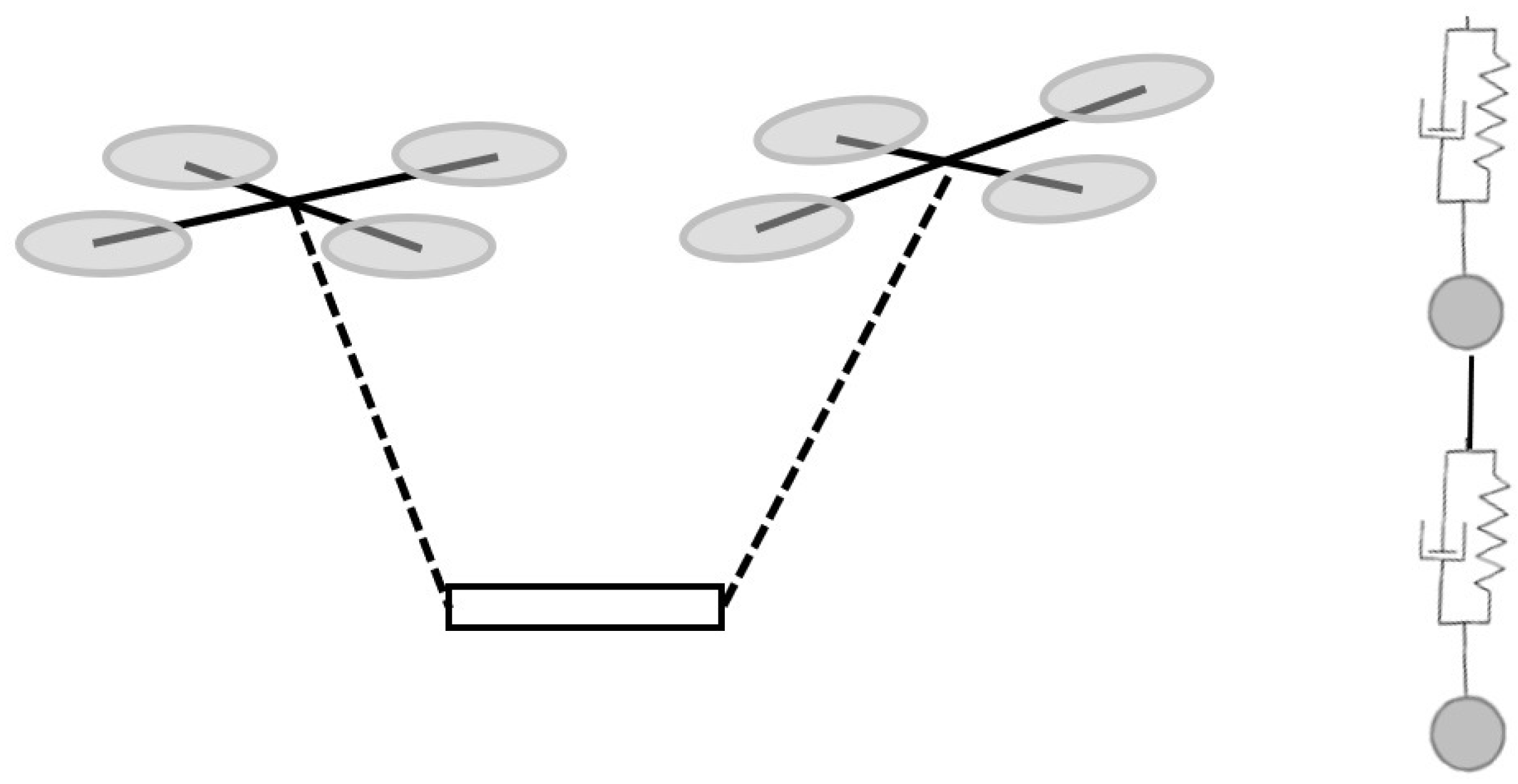
| Flexible cable | Flexible cables enhance some dynamic properties in simulations. The most used models are the spring-and-damping model and the cable formed by a series of weighted extensible segments of different sizes, connected with spherical joints. They are a better alternative for both performing aggressive maneuvers and lifting objects from the ground than taut cables. References: [17,24,60,93,94,141,145] |
| Catenaries and tensegrity muscles | There is scarce research in the literature on these models, and they are designed for very specific tasks. Catenaries are used as the dynamic model for cooperative cable transportation. Tensegrity muscles are modeled for representing tension and compression efforts with tethers and rigid bars in multi-UAV systems too. References: [77,83,146] |
| Single and Multi-UAV Transportation Systems | |
|---|---|
| Model | Description |
| PID and controller gains | Despite being traditional, it is one of the most used control systems in single- and multi-UAV transportation systems. It is usually based on a closed-loop cascade control circuit. Some authors even use PD controllers and apply it to both anti-swing and path-following strategies. In collaborative systems, there is no a clear trend between centralized and decentralized systems. However, according to some authors, this control system does not cope with aggressive maneuvers. Again, in collaborative UAV systems, more real experimentation is needed. References: [39,105,106,109,140,147] |
| MPC and geometric control | These nonlinear control systems are the most used methods for aggressive maneuvers and other transportation tasks, particularly in multi-UAV transportation systems. MPC can be NMPC, and it can be combined with other control systems, such as LQR or PID. Although simulation reflects the dynamic effects with enough detail, more real experimentation in collaborative UAV systems is needed. References: [44,124,125,129,132,139] |
| Deep learning | There is still scarce research based on these tools, but it might widen the spectrum of possibilities for the enhancing the autonomy and open-ended tasks in single- and multi-UAV transportation systems. References: [120,121] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Estevez, J.; Garate, G.; Lopez-Guede, J.M.; Larrea, M. Review of Aerial Transportation of Suspended-Cable Payloads with Quadrotors. Drones 2024, 8, 35. https://doi.org/10.3390/drones8020035
Estevez J, Garate G, Lopez-Guede JM, Larrea M. Review of Aerial Transportation of Suspended-Cable Payloads with Quadrotors. Drones. 2024; 8(2):35. https://doi.org/10.3390/drones8020035
Chicago/Turabian StyleEstevez, Julian, Gorka Garate, Jose Manuel Lopez-Guede, and Mikel Larrea. 2024. "Review of Aerial Transportation of Suspended-Cable Payloads with Quadrotors" Drones 8, no. 2: 35. https://doi.org/10.3390/drones8020035
APA StyleEstevez, J., Garate, G., Lopez-Guede, J. M., & Larrea, M. (2024). Review of Aerial Transportation of Suspended-Cable Payloads with Quadrotors. Drones, 8(2), 35. https://doi.org/10.3390/drones8020035







