Bifurcation Analysis and Sticking Phenomenon for Unmanned Rotor-Nacelle Systems with the Presence of Multi-Segmented Structural Nonlinearity
Abstract
1. Introduction
2. Aeroelastic Modeling of Multi-Segmented Freeplay System
3. Bifurcation Analysis and Characterization of Rotor-Nacelle Systems with Multi-Segmented Freeplay
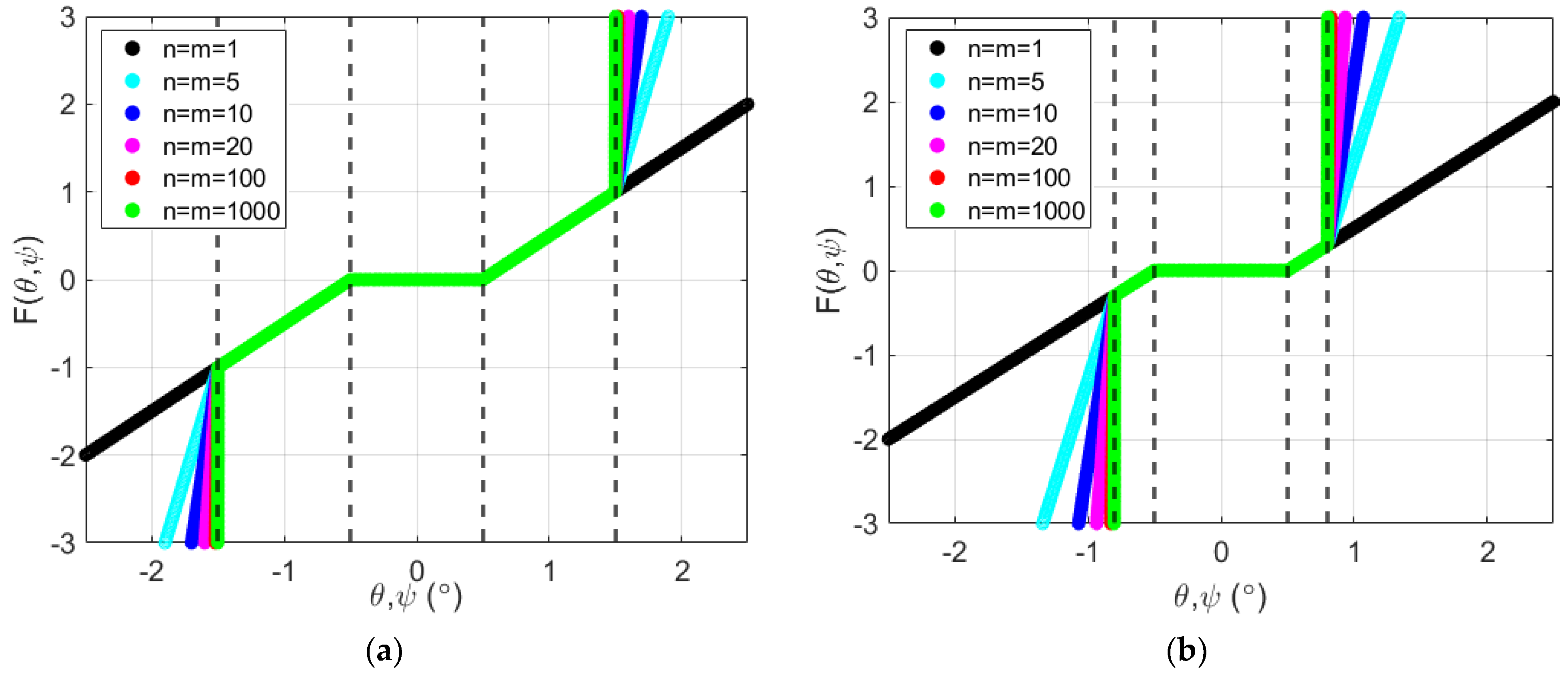
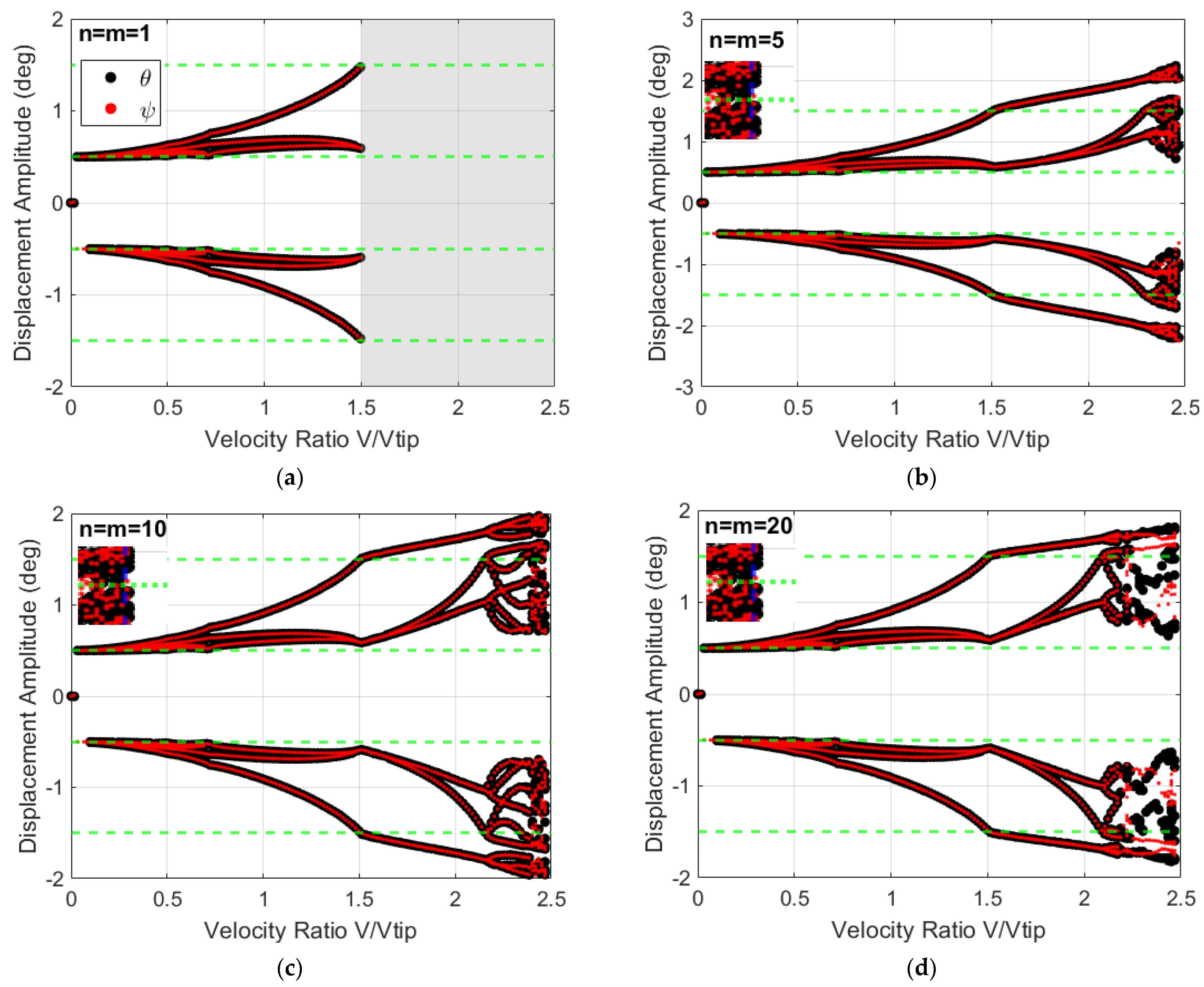
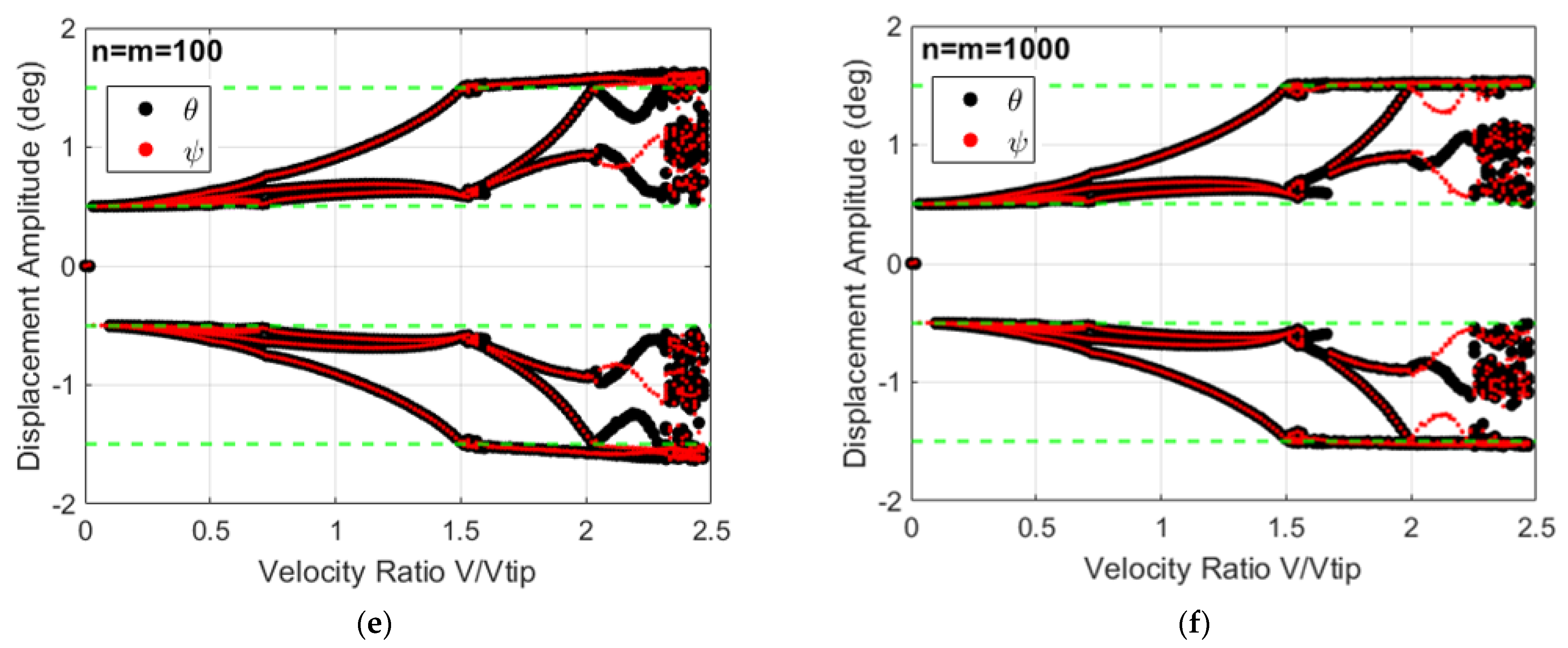
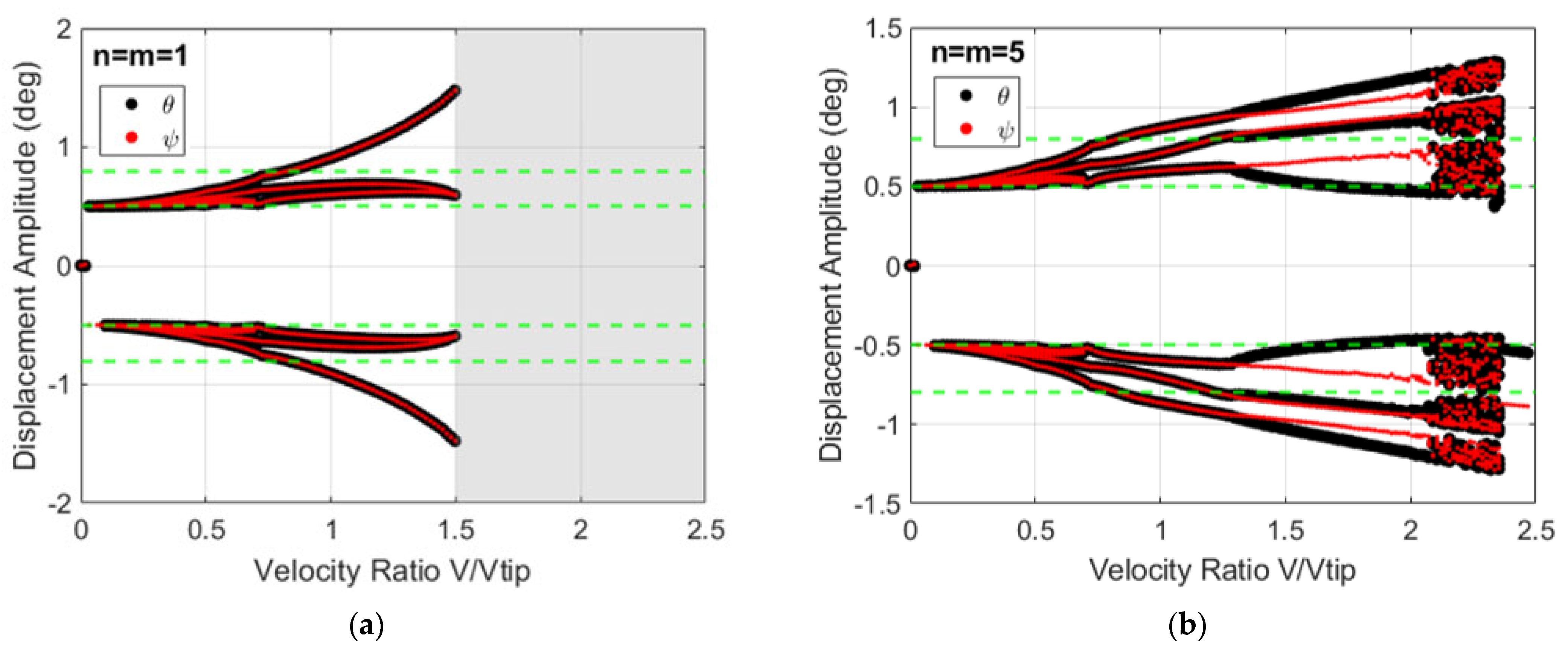
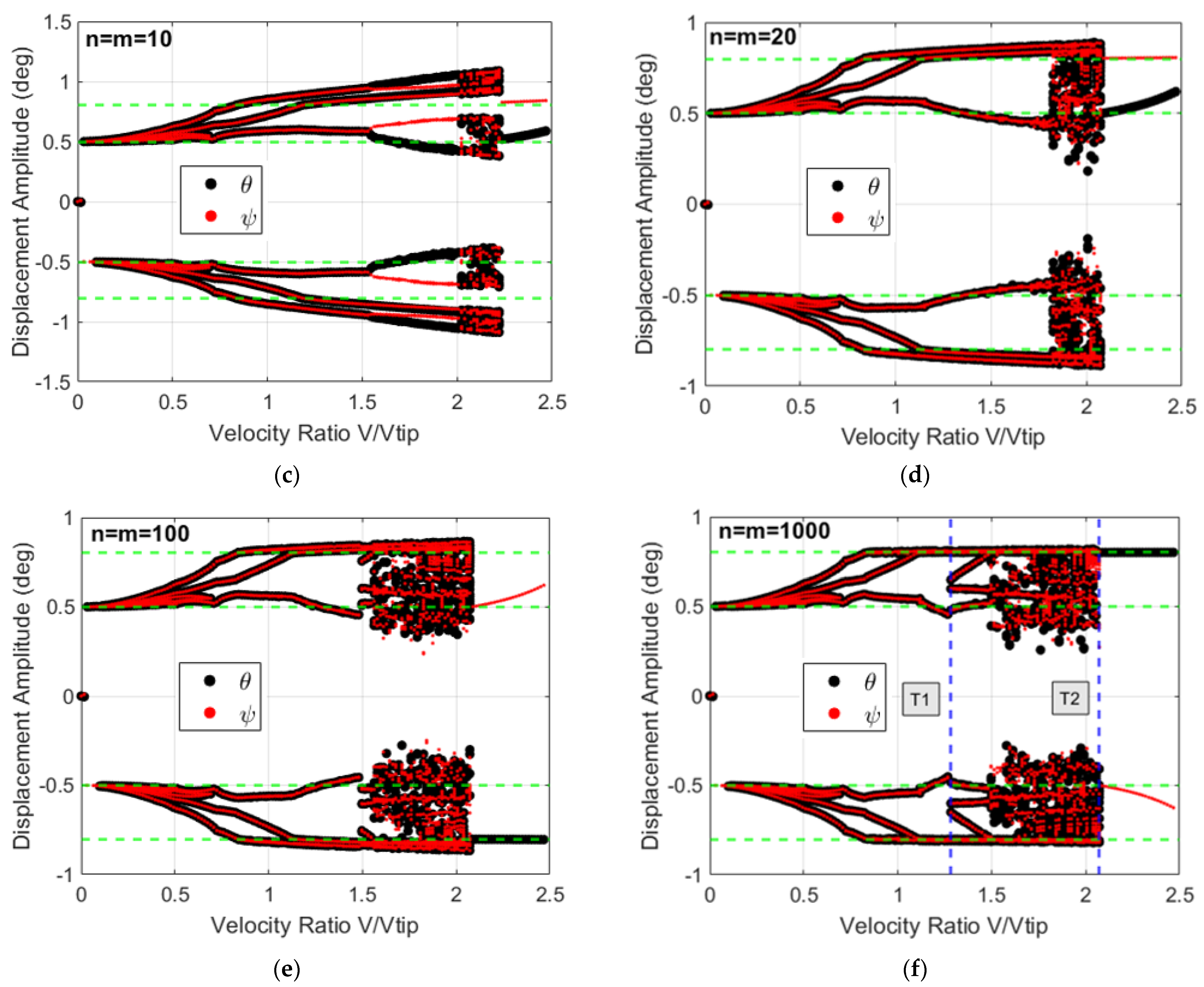
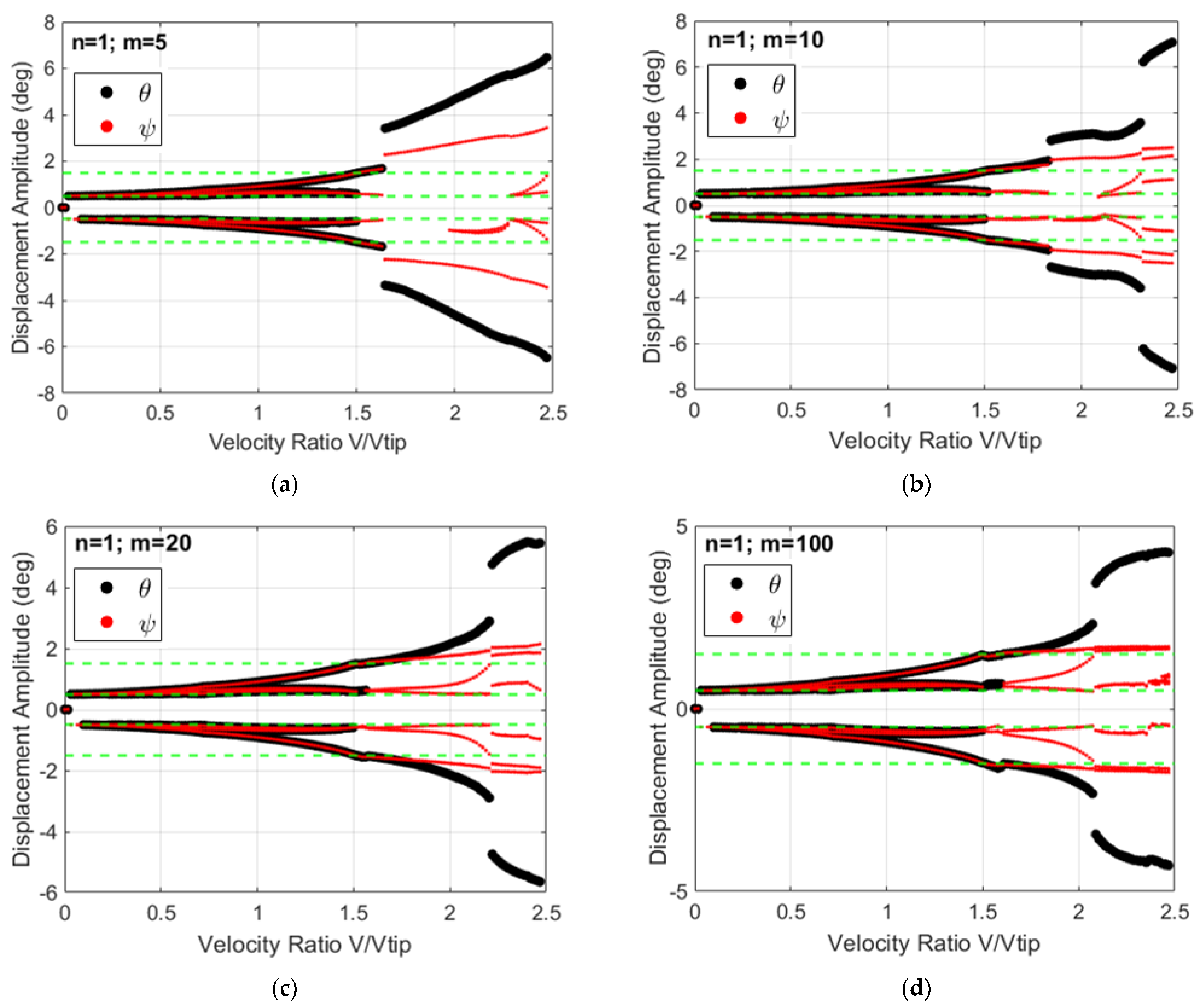
3.1. System Dynamics and Bifurcation Diagrams: Effects of Multi-Segmentation Properties
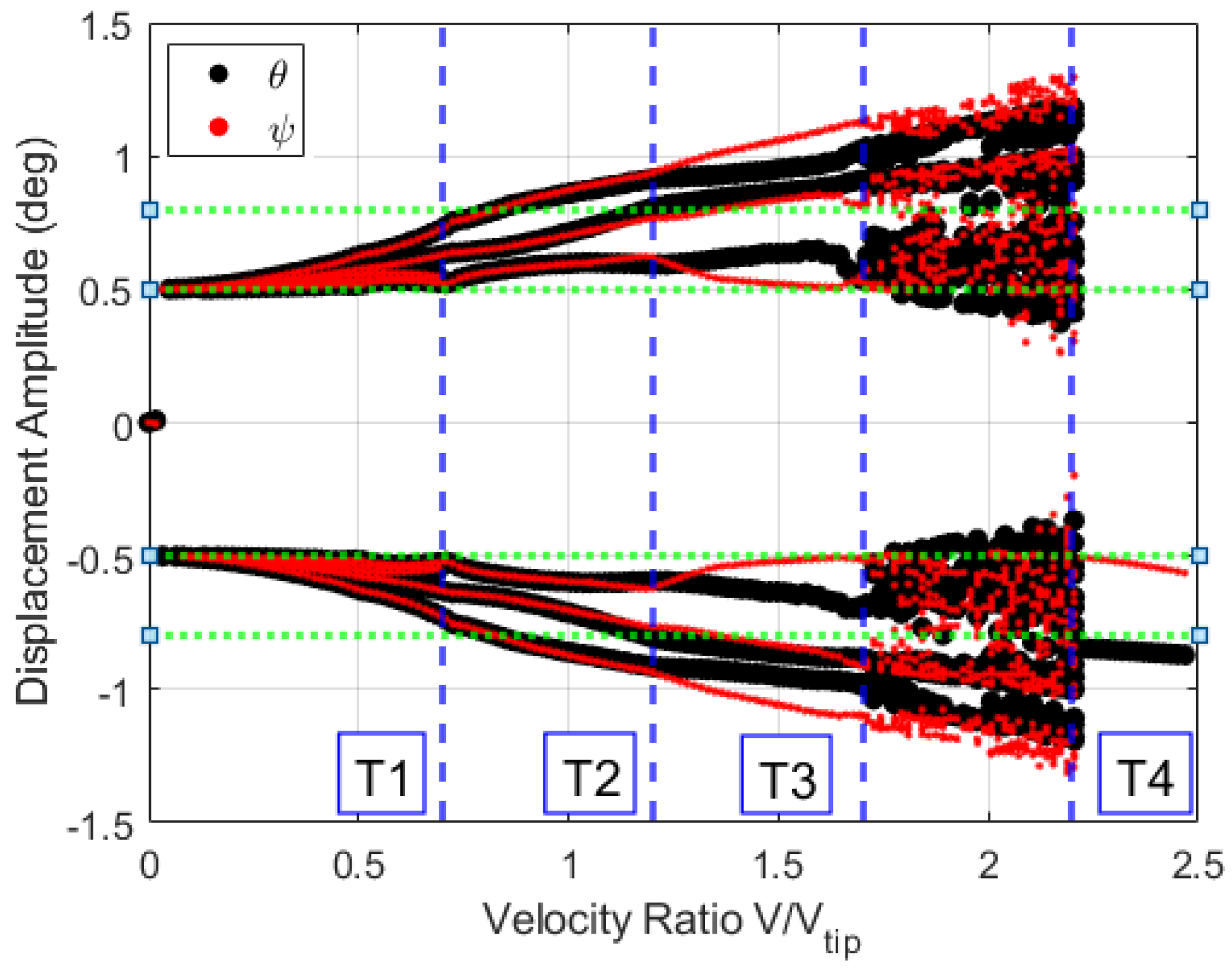
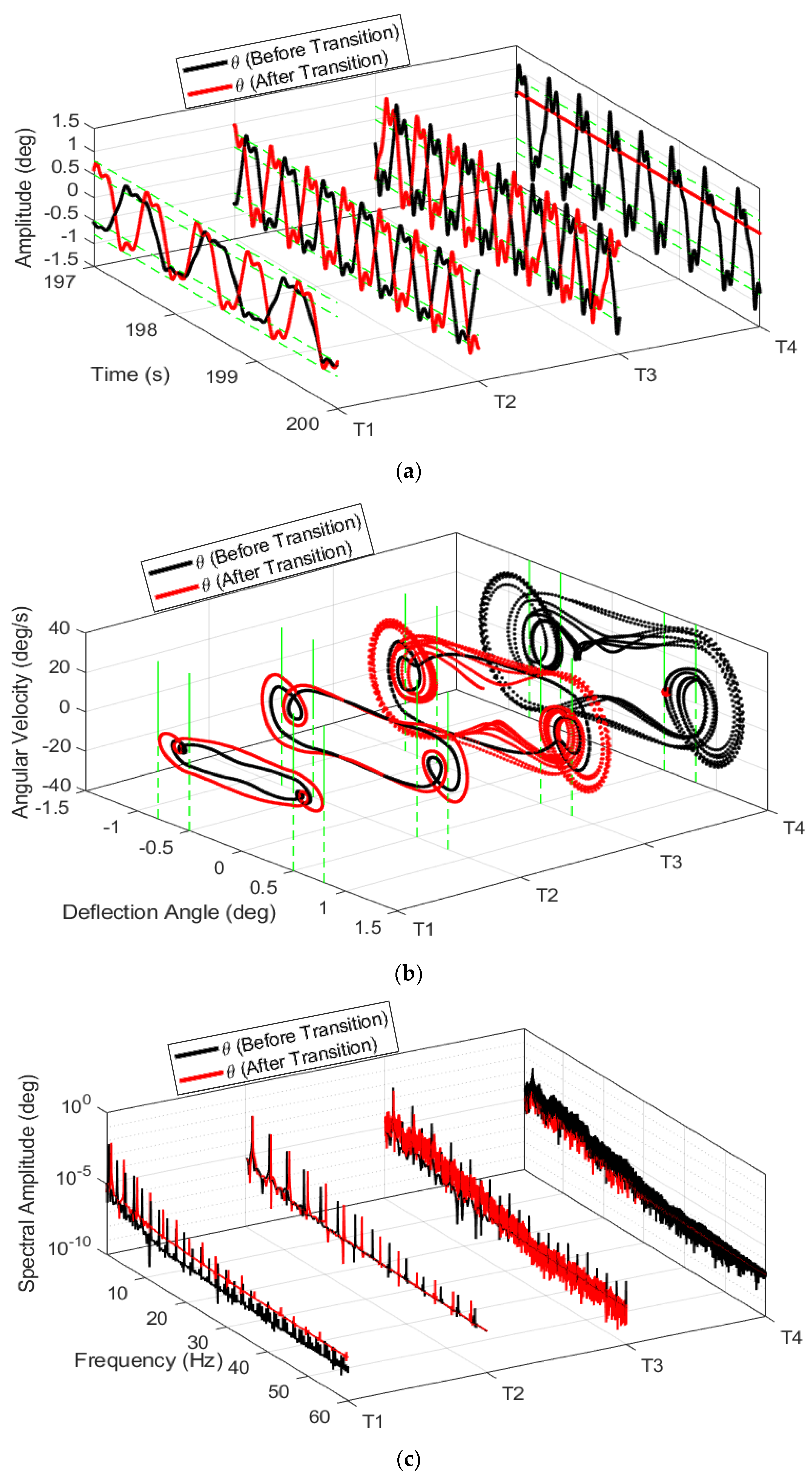
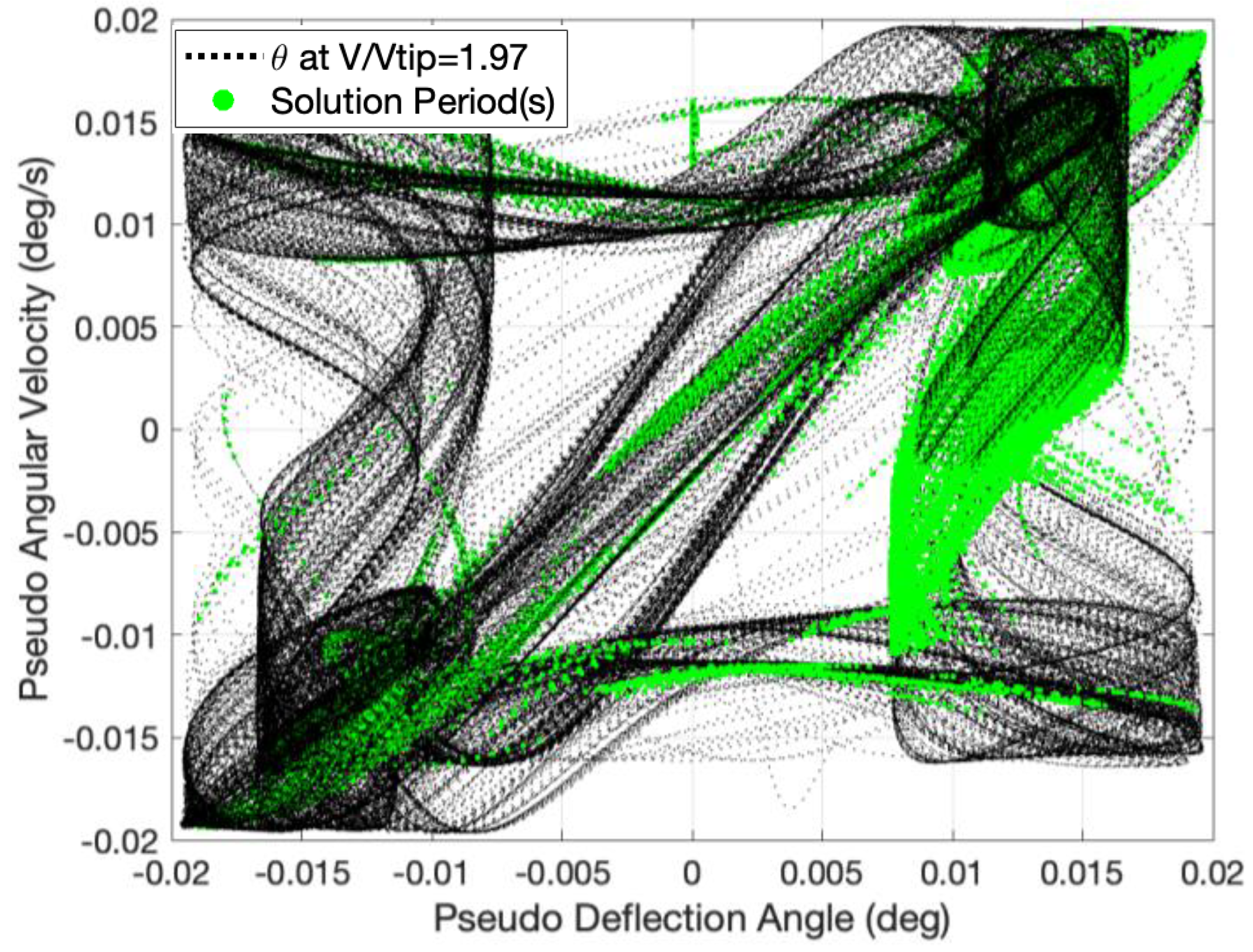
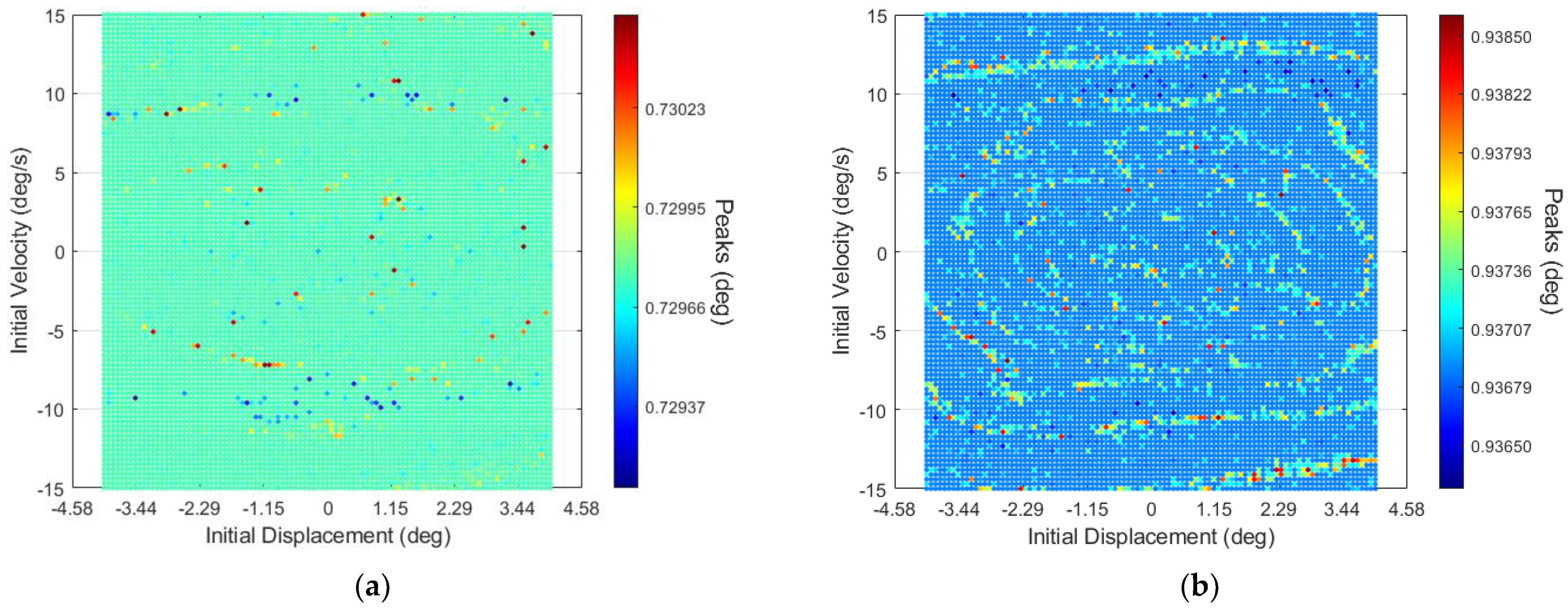
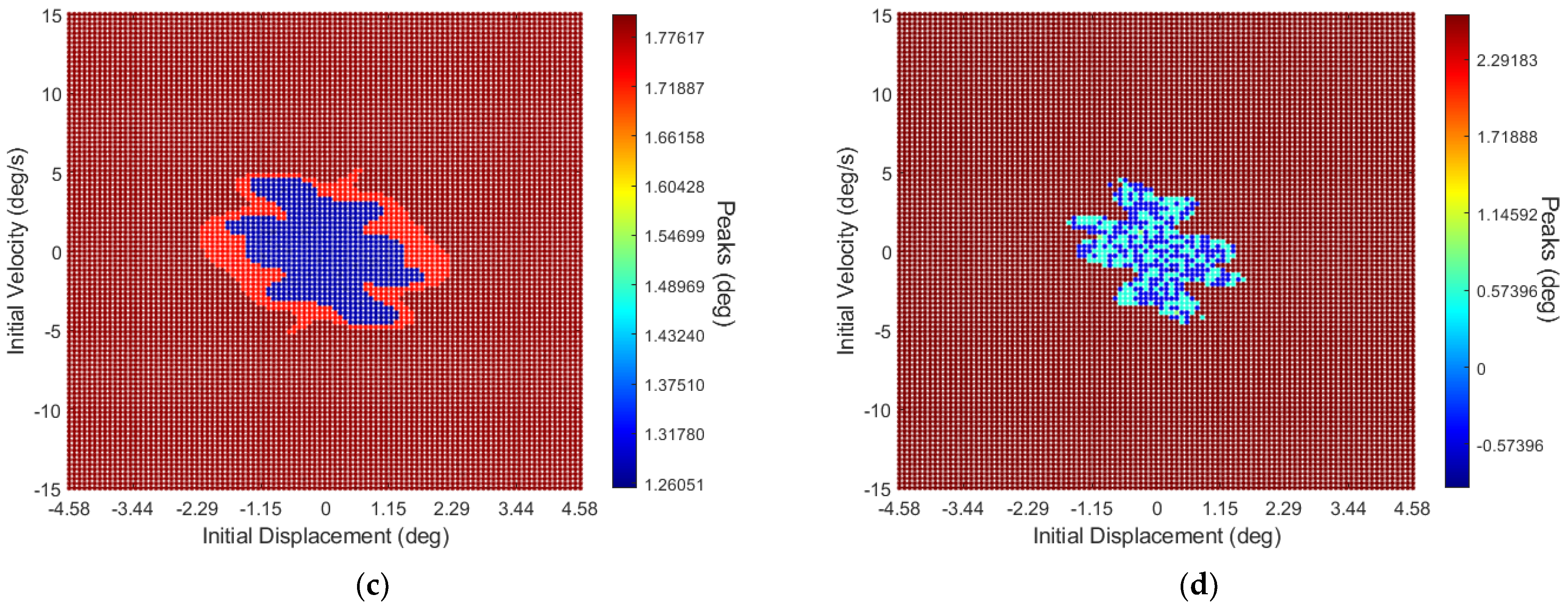
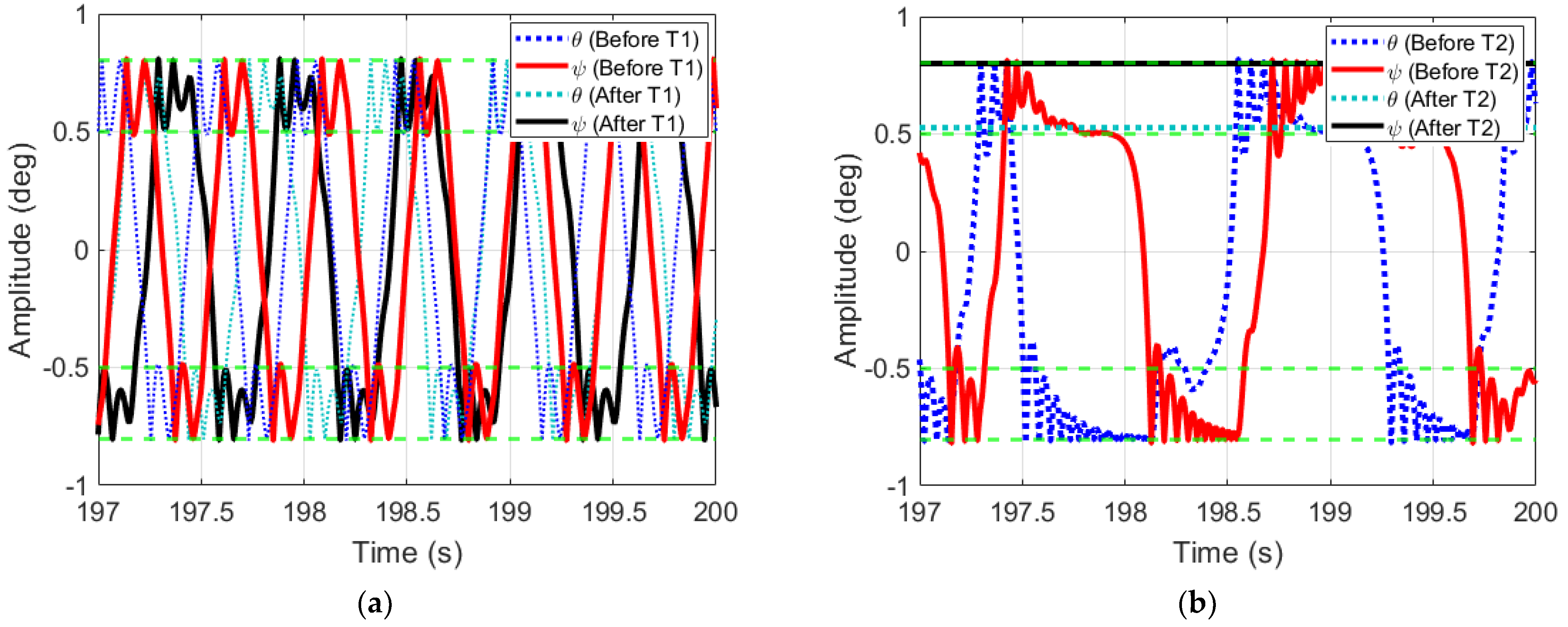
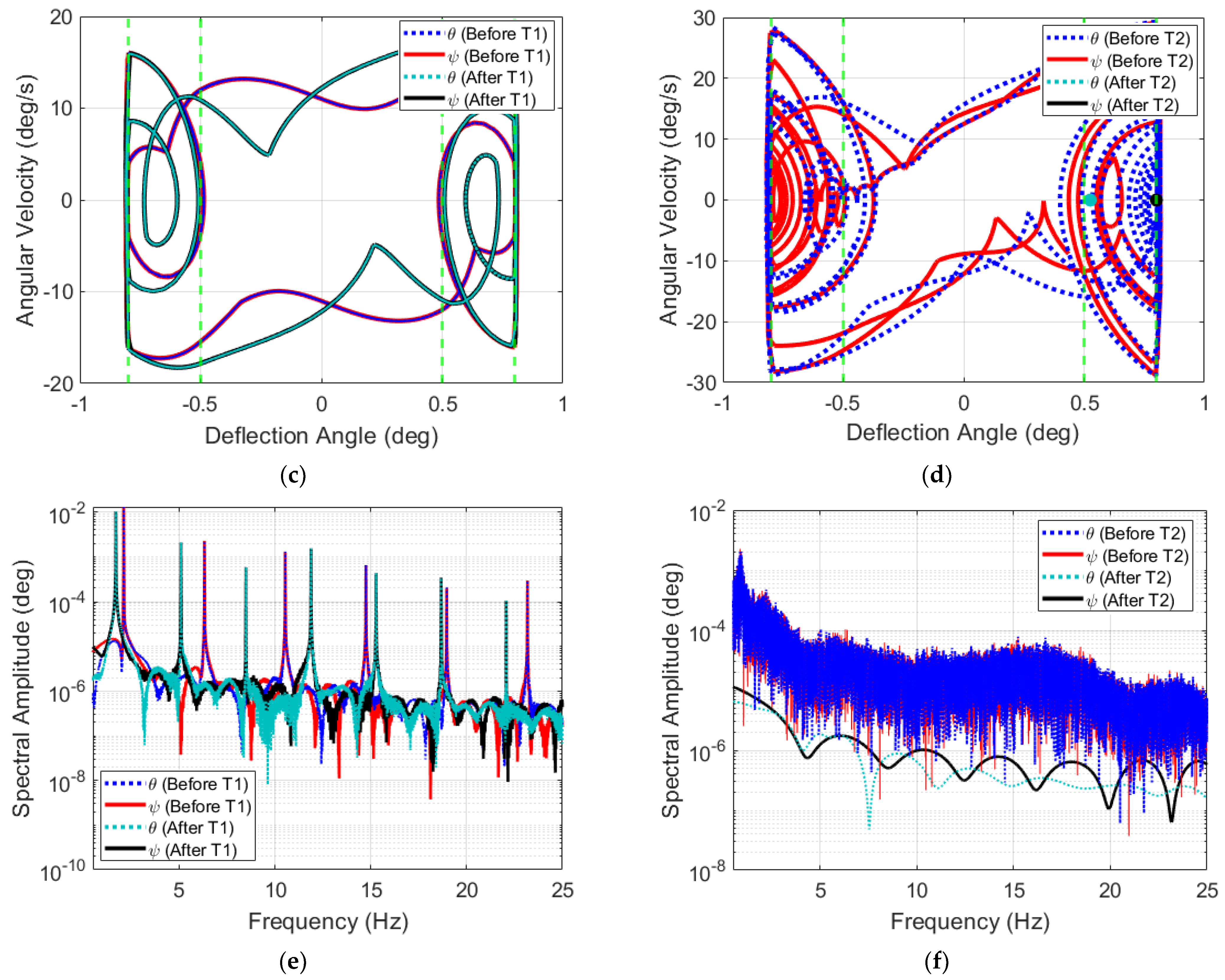
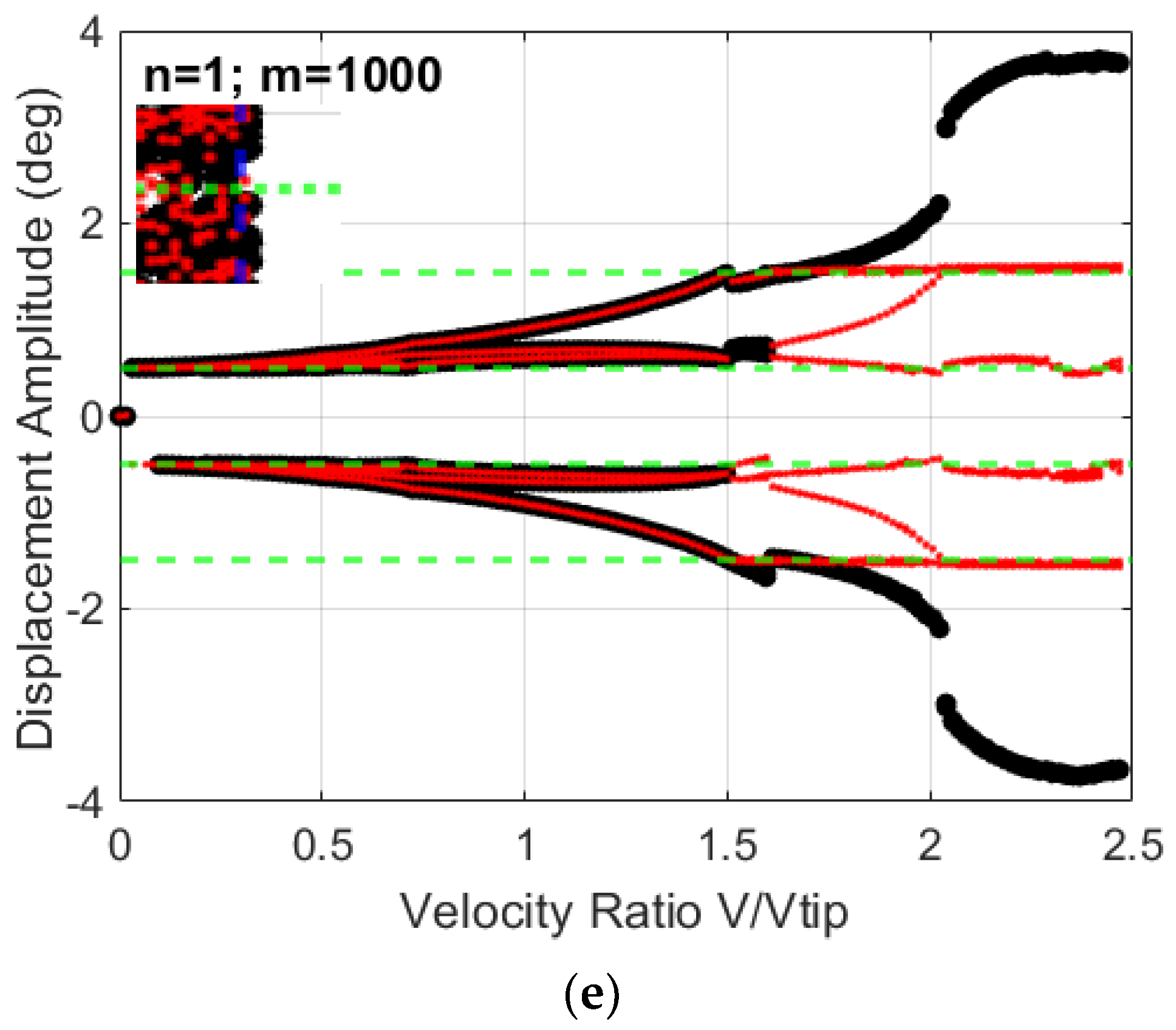
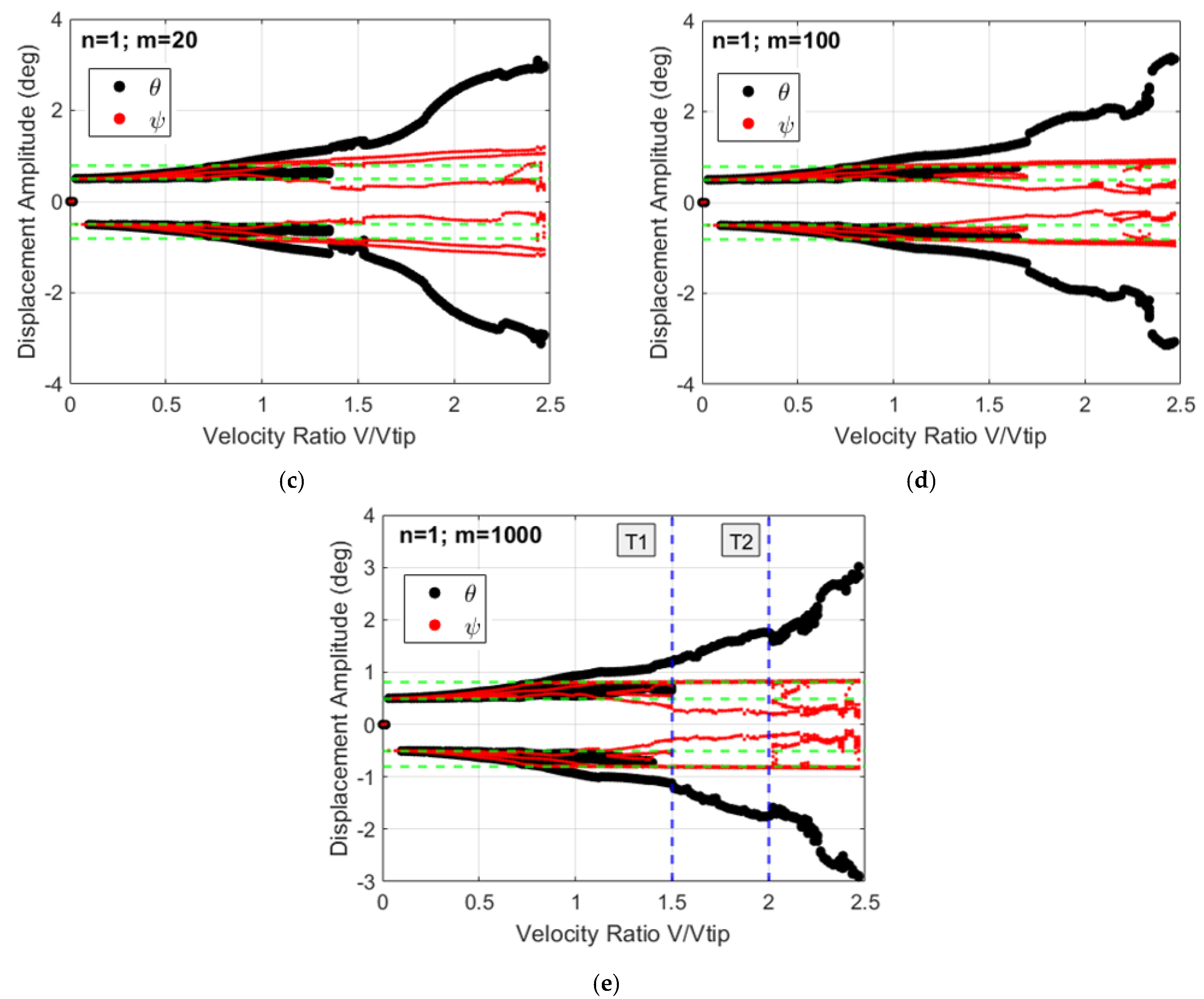
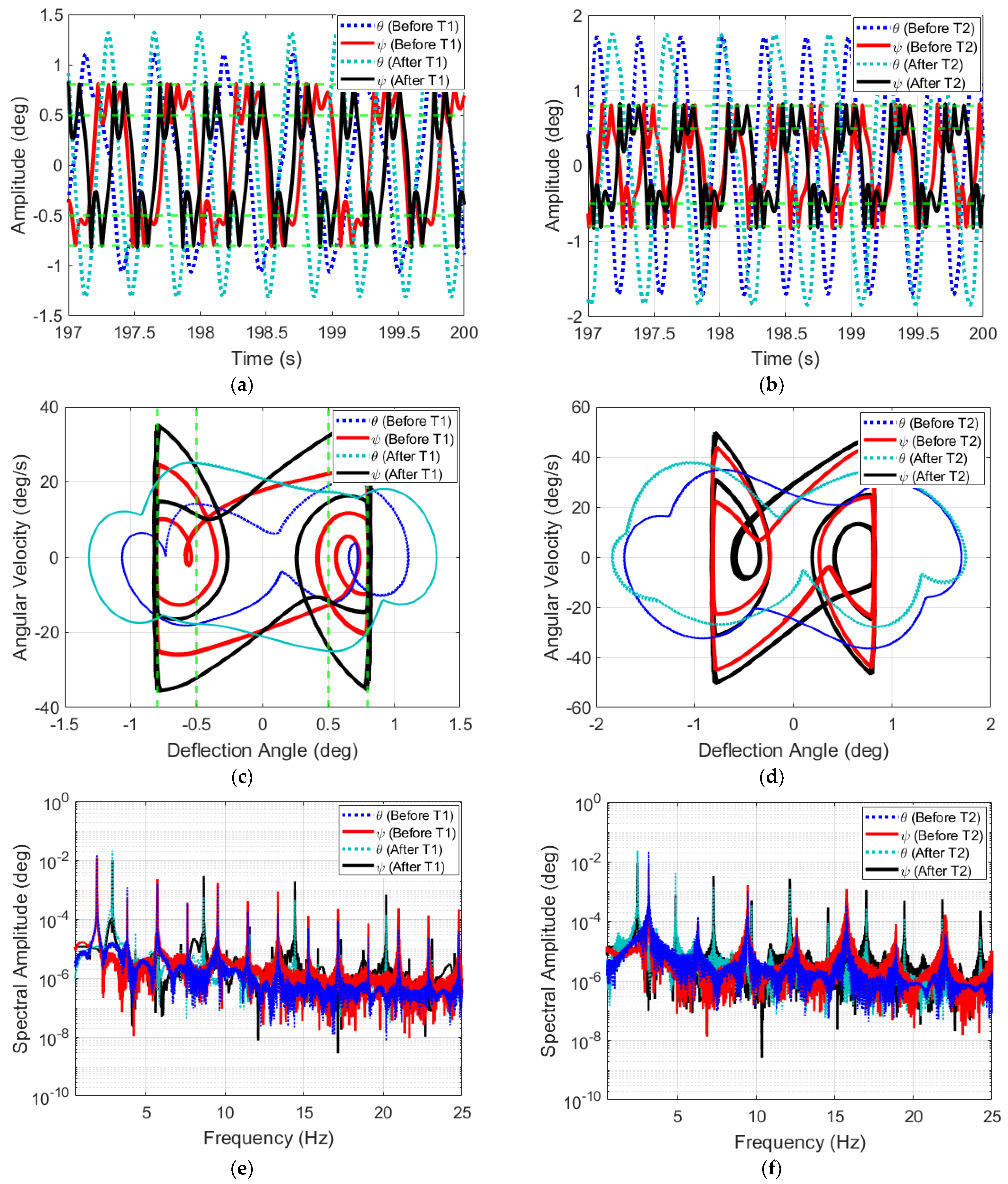
3.2. System’s Dynamics and Bifurcation Diagrams: Route to Impact
3.2.1. Symmetric Configuration for Multi-Segmented Rotor-Nacelle System
3.2.2. Asymmetric Configuration for Multi-Segmented Rotor-Nacelle System
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Ratio of pivot length to rotor radius | |
| Various aerodynamic integrals that arise from the total in-plane forces and moments | |
| Velocity ratio of freestream velocity to velocity at the blade | |
| c | Blade chord length |
| Damping matrix | |
| Consolidation of terms | |
| Sectional blade lift slope | |
| Structural yaw damping | |
| Structural pitch damping | |
| δ | Freeplay gap size |
| Moment about the pivot of yaw | |
| Moment about the pivot of pitch | |
| A local spanwise coordinate over the length of the element | |
| Nacelle moment of inertia | |
| Rotor moment of inertia | |
| Jacobian matrix | |
| K | Stiffness matrix |
| Structural yaw stiffness | |
| Structural pitch stiffness | |
| Number of blades | |
| Rotor angular velocity | |
| Air density | |
| R | Rotor radius |
| Angular deflection off of the y-z-plane | |
| Angular velocity off the y-z-plane | |
| Angular deflection off of the x-y-plane | |
| Angular velocity off the x-y-plane | |
| V | Freestream velocity |
| Velocity at the tip of the propeller blade |
References
- Caldwell, J.A. Fatigue in aviation. Travel Med. Infect. Dis. 2005, 3, 85–96. [Google Scholar] [CrossRef] [PubMed]
- Starke, E.A., Jr.; Staley, J.T. Application of modern aluminum alloys to aircraft. Prog. Aerosp. Sci. 1996, 32, 131–172. [Google Scholar] [CrossRef]
- Alcorn, C.W.; Croom, M.A.; Francis, M.S.; Ross, H. The X-31 aircraft: Advances in aircraft agility and performance. Prog. Aerosp. Sci. 1996, 32, 377–413. [Google Scholar] [CrossRef]
- Čečrdle, J. Whirl Flutter of Turboprop Aircraft Structures. Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Taylor, E.S.; Browne, K.A. Vibration isolation of aircraft power plants. J. Aeronaut. Sci. 1938, 6, 43–49. [Google Scholar] [CrossRef]
- Čečrdle, J.; Maleček, J.; Vích, O. Mechanical concept of whirl flutter aeroelastic demonstrator. In Proceedings of the 22nd International Conference Engineering Mechanics 2016, Svratka, Czech Republic, 9–12 May 2016. [Google Scholar]
- Reed, W.H., III. Propeller-rotor whirl flutter: A state-of-the-art review. J. Sound Vib. 1966, 4, 526–544. [Google Scholar] [CrossRef]
- Čečrdle, J. Aeroelastic stability of turboprop aircraft: Whirl flutter. Flight Phys. Models Tech. Technol. 2018, 139–158. [Google Scholar] [CrossRef]
- Janetzke, D.C.; Kaza, K.R. Whirl flutter analysis of a horizontal-axis wind turbine with a two-bladed teetering rotor. Solar Energy 1983, 31, 173–182. [Google Scholar] [CrossRef]
- Salles, L.; Staples, B.; Hoffmann, N.; Schwingshackl, C. Continuation techniques for analysis of whole aeroengine dynamics with imperfect bifurcations and isolated solutions. Nonlinear Dyn. 2016, 86, 1897–1911. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, M.; Liang, H.; Zhu, M. Structural and aeroelastic analyses of a wing with tip rotor. J. Fluids Struct. 2019, 86, 44–69. [Google Scholar] [CrossRef]
- Lockheed L-188 Electra—Price, Specs, Photo Gallery, History. Aero Corner. (n.d.). Retrieved 7 July 2022. Available online: https://aerocorner.com/aircraft/lockheed-l-188-electra/ (accessed on 20 December 2023).
- Kunz, D.L. Analysis of proprotor whirl flutter: Review and update. J. Aircr. 2005, 42, 172–178, “Crash of a Lockheed L-188C Electra in Chicago: 37 Killed” |Bureau of Aircraft Accidents Archives. 13 December 1962. Available online: https://www.baaa-acro.com/sites/default/files/import/uploads/2017/11/N137US.pdf (accessed on 20 December 2023). [CrossRef]
- Ivanov, I.; Myasnikov, V.; Blinnik, B. Study of dynamic loads dependence on aircraft engine mount variant after fan blade-out event. Vibroengineering Procedia 2019, 26, 1–6. [Google Scholar] [CrossRef]
- Ismail, M.A.; Bierig, A. Identifying Drone-Related Security Risks by a Laser Vibrometer-Based Payload Identification System. In Laser Radar Technology and Applications XXIII; International Society for Optics and Photonics: Bellingham, WA, USA, 2018; Volume 10636, p. 1063603. [Google Scholar]
- Heljeved, C. BAD: Black. Armored. Drone. Master’s Thesis, Jönköping University, Jönköping, Sweden, 2013. [Google Scholar]
- Hayward, J.; Gaurav, J. How Engines Are Attached to Aircraft. Simple Flying. 7 November 2022. Available online: https://simpleflying.com/how-engines-are-attached-to-aircraft/ (accessed on 20 December 2023).
- Bauchau, O.A.; Rodriguez, J.; Bottasso, C.L. Modeling of unilateral contact conditions with application to aerospace systems involving backlash, freeplay and friction. Mech. Res. Commun. 2001, 28, 571–599. [Google Scholar] [CrossRef]
- Mair, C.; Rezgui, D.; Titurus, B. Nonlinear stability analysis of whirl flutter in a rotor-nacelle system. Nonlinear Dyn. 2018, 94, 2013–2032. [Google Scholar] [CrossRef] [PubMed]
- Mair, C.; Titurus, B.; Rezgui, D. Stability analysis of whirl flutter in rotor-nacelle systems with freeplay nonlinearity. Nonlinear Dyn. 2021, 104, 65–89. [Google Scholar] [CrossRef]
- Quintana, A.; Vasconcellos, R.; Throneberry, G.; Abdelkefi, A. Nonlinear analysis and bifurcation characteristics of whirl flutter in unmanned aerial systems. Drones 2021, 5, 122. [Google Scholar] [CrossRef]
- Quintana, A.; Saunders, B.E.; Vasconcellos, R.; Abdelkefi, A. The influence of freeplay on the whirl flutter and nonlinear characteristics of rotor-nacelle systems. Meccanica 2023, 58, 659–686. [Google Scholar] [CrossRef]
- Vasconcellos, R.; Abdelkefi, A. Nonlinear dynamical analysis of an aeroelastic system with multi-segmented moment in the pitch degree-of-freedom. Commun. Nonlinear Sci. Numer. Simul. 2015, 20, 324–334. [Google Scholar] [CrossRef]
- Bouma, A.; Le, E.; Vasconcellos, R.; Abdelkefi, A. Effective design and characterization of flutter-based piezoelectric energy harvesters with discontinuous nonlinearities. Energy 2022, 238, 121662. [Google Scholar] [CrossRef]
- Bielawa, R.L. Rotary Wing Structural Dynamics and Aeroelasticity; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2006. [Google Scholar]
- Ribner, H.S. Propellers in Yaw; National Advisory Committee for Aeronautics: Washington, DC, USA, 1943. [Google Scholar]
- MATLAB; The MathWorks Inc.: Natick, MA, USA, 2019.
- Nayfeh, A.H.; Balachandran, B. Applied Nonlinear Dynamics: Analytical, Computational, and Experimental Methods; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
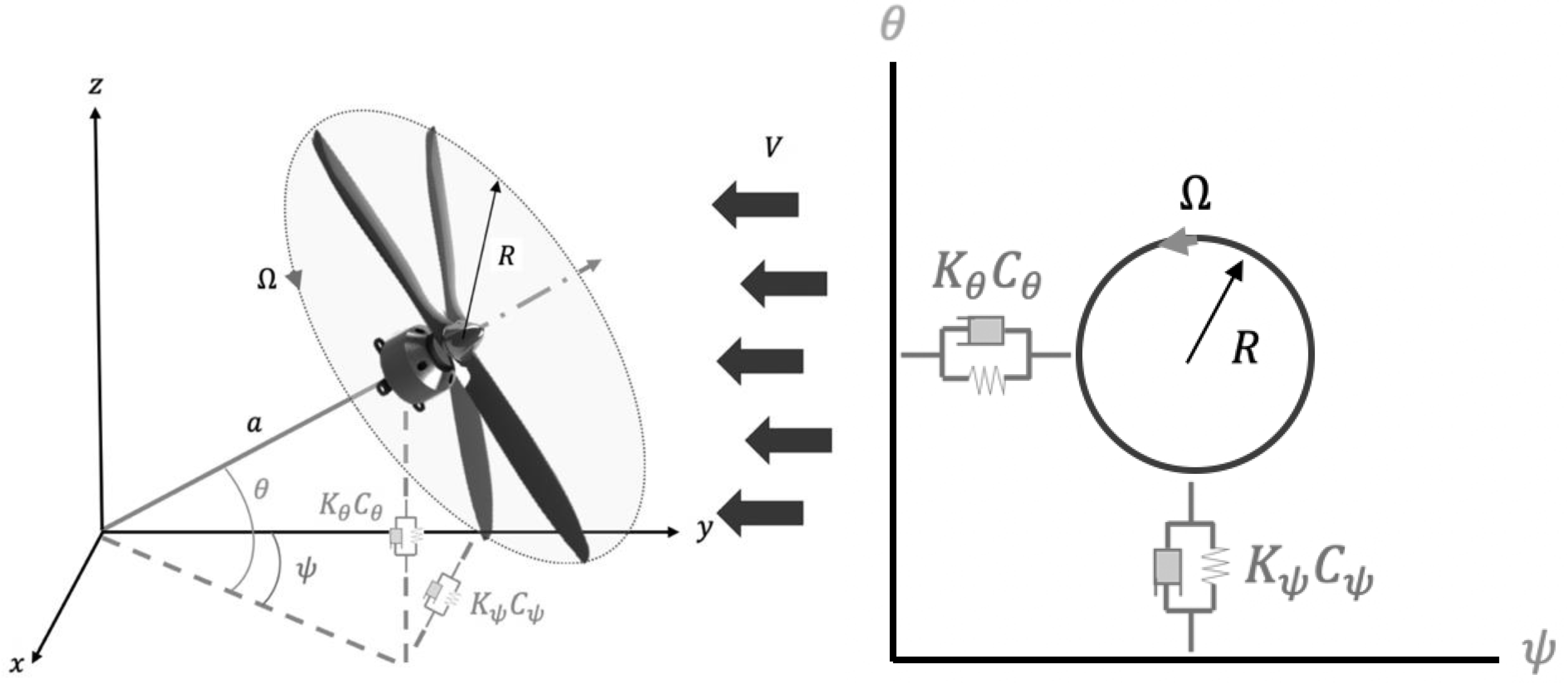
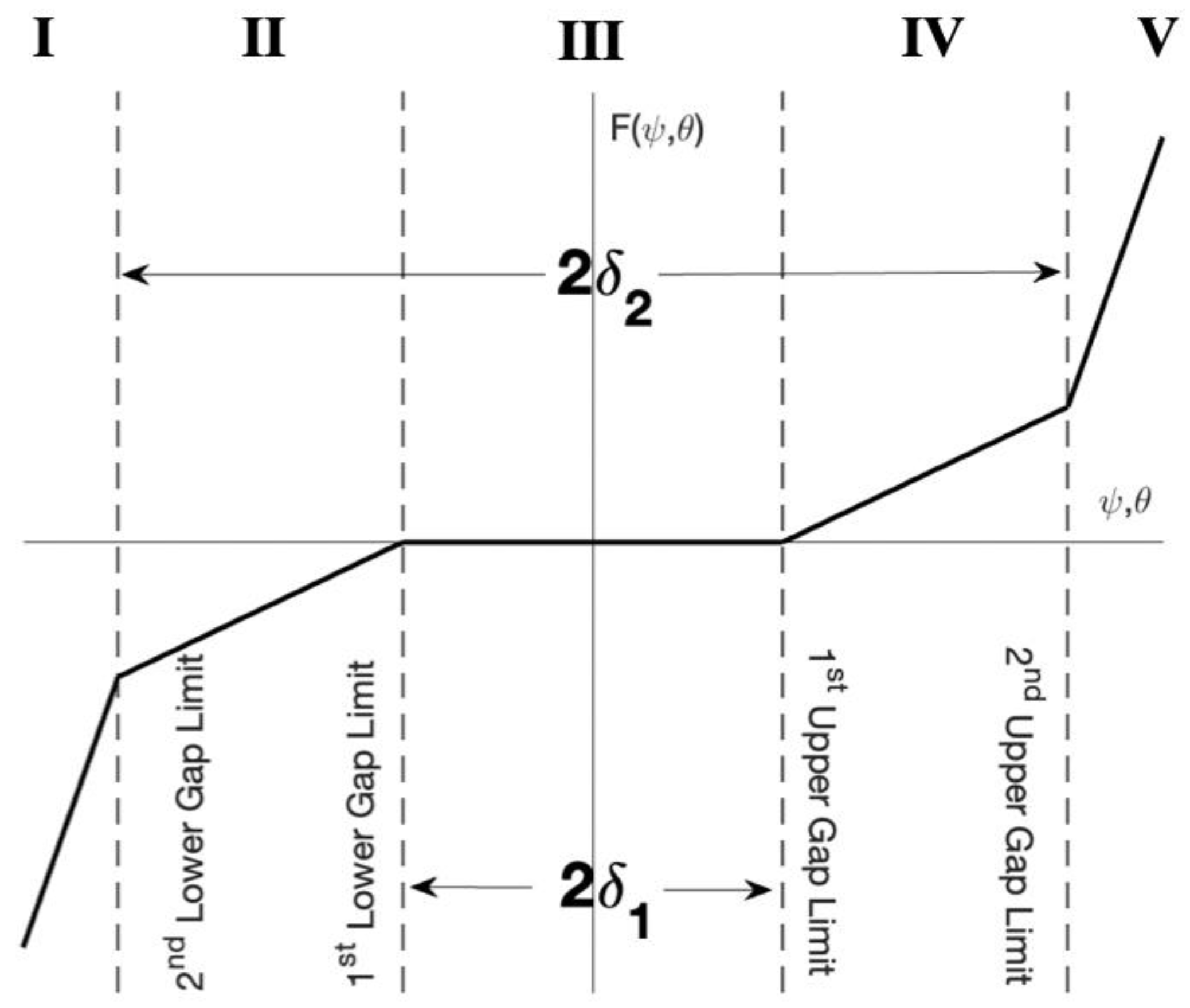
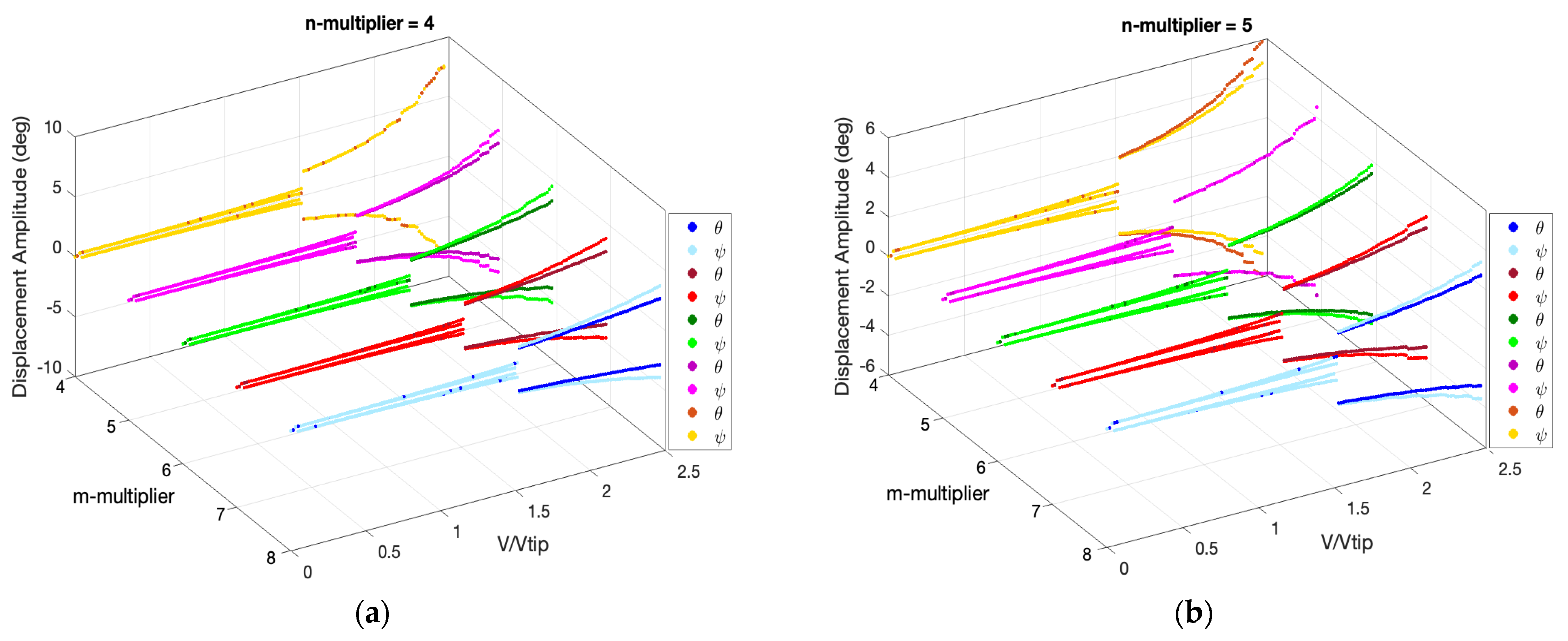


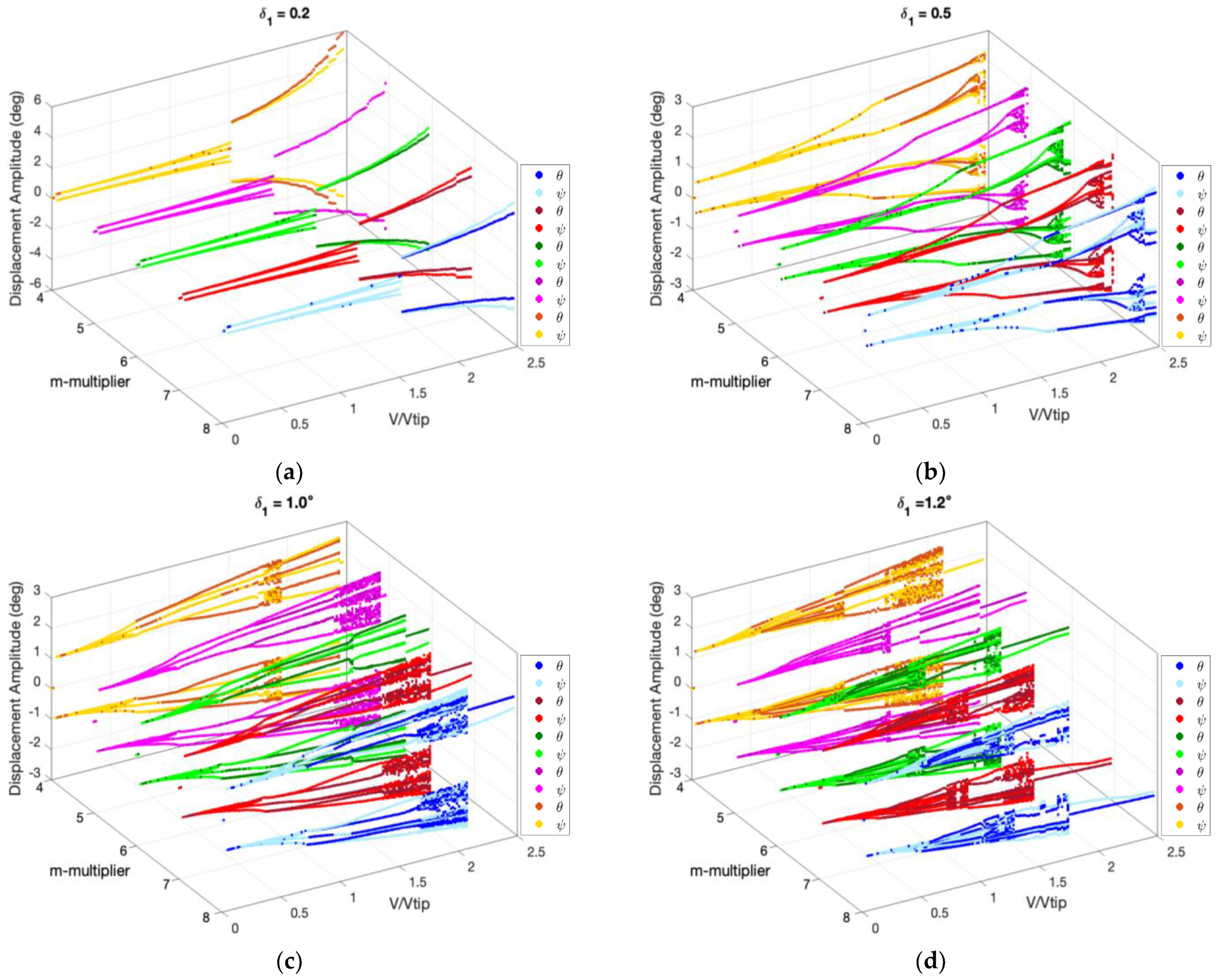

| Description | Symbol | Value | Description | Symbol | Value |
|---|---|---|---|---|---|
| Rotor radius | R | 0.152 m | Structural pitch damping | 0.001 Nm s rad−1 | |
| Rotor angular velocity | 40 rad s−1 | Structural pitch stiffness | 0.4 Nm rad−1 | ||
| Freestream velocity | V | 6.7 m s−1 | Structural yaw damping | 0.001 Nm s rad−1 | |
| Air density | 1.2 kg m−3 | Structural yaw stiffness | 0.4 Nm rad−1 | ||
| Pivot length to rotor radius ratio | 0.25 | Number of blades | 4 | ||
| Rotor moment of inertia | 0.000103 kg m2 | Blade chord | c | 0.026 m | |
| Nacelle moment of inertia | 0.000178 kg m2 | Blade lift slope | rad−1 |
| Strong Aperiodicity Range | Strong Aperiodicity Range | Sticking Phenomenon | |
|---|---|---|---|
| n= m = 1 | |||
| n= m = 5 | 2.31–2.47 (0.16) | 2.07–2.37 (0.30) | 2.37–2.47 (0.1) |
| n= m = 10 | 2.17–2.47 (0.3) | 2.02–2.22 (0.20) | 2.22–2.47 (0.25) |
| n= m = 20 | 2.08–2.47 (0.39) | 1.82–2.07 (0.25) | 2.07–2.47 (0.4) |
| n= m = 100 | 2.02–2.47 (0.45) | 1.49–2.07 (0.58) | 2.07–2.47 (0.4) |
| n= m = 1000 | 1.99–2.47(0.48) | 1.49–2.07 (0.58) | 2.07–2.47 (0.4) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quintana, A.; Saunders, B.E.; Vasconcellos, R.; Abdelkefi, A. Bifurcation Analysis and Sticking Phenomenon for Unmanned Rotor-Nacelle Systems with the Presence of Multi-Segmented Structural Nonlinearity. Drones 2024, 8, 59. https://doi.org/10.3390/drones8020059
Quintana A, Saunders BE, Vasconcellos R, Abdelkefi A. Bifurcation Analysis and Sticking Phenomenon for Unmanned Rotor-Nacelle Systems with the Presence of Multi-Segmented Structural Nonlinearity. Drones. 2024; 8(2):59. https://doi.org/10.3390/drones8020059
Chicago/Turabian StyleQuintana, Anthony, Brian Evan Saunders, Rui Vasconcellos, and Abdessattar Abdelkefi. 2024. "Bifurcation Analysis and Sticking Phenomenon for Unmanned Rotor-Nacelle Systems with the Presence of Multi-Segmented Structural Nonlinearity" Drones 8, no. 2: 59. https://doi.org/10.3390/drones8020059
APA StyleQuintana, A., Saunders, B. E., Vasconcellos, R., & Abdelkefi, A. (2024). Bifurcation Analysis and Sticking Phenomenon for Unmanned Rotor-Nacelle Systems with the Presence of Multi-Segmented Structural Nonlinearity. Drones, 8(2), 59. https://doi.org/10.3390/drones8020059







