Trajectory-Tracking Control for Quadrotors Using an Adaptive Integral Terminal Sliding Mode under External Disturbances

Abstract

In the face of external disturbances affecting the trajectory tracking of quadrotors, a control scheme targeted at accurate position and attitude trajectory tracking was designed. Initially, a quadrotor dynamic model, essential for control design, was derived. Adaptive integral backstepping control (AIBS) was then employed within the position loop, enabling the upper boundaries of disturbances to be estimated through adaptive estimation. Subsequently, a new adaptive backstepping fast nonsingular integral terminal sliding mode control (ABFNITSM) was proposed to enable adherence to the desired Euler angles. Rapid convergence and accurate tracking were facilitated by the incorporation of the nonsingular terminal sliding mode and an integral component. The dead zone technique was deployed to curtail estimation errors, while a saturation function was used to eradicate the phenomenon of chattering. Finally, to validate the proposed control scheme, simulation experiments were conducted in the Simulink environment, and the results were contrasted with those obtained from traditional integral terminal sliding mode control (ITSM) and integral backstepping control (IBS), providing evidence of the effectiveness of the proposed method.

1. Introduction

Recent years have seen the utilization of quadrotors in diverse domains, attributed to their compact size, economic efficiency, and Vertical Takeoff and Landing (VTOL) capabilities [1,2,3]. These considerable attributes coupled with their broad spectrum of applications have propelled a growing focus on quadrotors [4,5,6,7]. In practice, the inevitability of external disturbances and measurement inaccuracies is an acknowledged fact [8,9,10,11,12]. The successful execution of tasks such as power line inspection [13], logistics transportation [14], and pesticide spraying [15] is contingent on the proficiency of trajectory tracking. Consequently, enhancing the efficiency of trajectory-tracking control in the presence of external disturbances is of paramount theoretical relevance and practical value. Such a development ensures that quadrotors are equipped to meet flight requisites and avoid uncontrollable crashes.

Nair et al. achieved high-performance tracking for a satellite launch rocket system with time-varying uncertainties by designing an adaptive PID control [16]. In [17], the online identification of aerodynamic parameters using the Kalman filter was utilized, followed by compensation for rotor speed using an LQR strategy, resulting in improved control performance in terms of heading and altitude. Such works generally linearize the nonlinear dynamics of quadrotors, which leads to approximation errors and performance limitations. In [18], a fuzzy logic system was used to assess the unmodeled dynamics of a quadrotor. A nonlinear disturbance observer was employed to compensate for external disturbances and assessment error. In reference [19], the authors proposed a radical basis function neural network (RBFNN) to fix the unknown dynamic problem. To increase convergence speed and control precision, fractional-order backstepping control was introduced. Sliding mode control is widely applied in practical systems, e.g., robot manipulation [20], linear motor positioning [21], and underwater robots [22], because of its strong robustness, fast responsivity, and low sensitivity to uncertainties and disturbances. The conventional sliding mode (CSM) cannot guarantee the fast convergence of a control system [9,23,24]. The terminal sliding mode (TSM) was designed to deal with this situation [25]. Furthermore, the CSM may cause chattering. In [26], a modified second-order sliding mode control was introduced to address the chatting phenomenon. Omid Mofid et al. designed a super-twisting terminal sliding mode control scheme considering input-delay, model uncertainty, and wind disturbance for a fast response. In [27], the dynamic model was divided into an inner loop and an outer loop. Nonsingular terminal sliding mode control (NTSM) was utilized to allow convergence to the desired position and attitude in finite time. In [28], Hamid Ghadiri et al. proposed a novel adaptive nonsingular terminal sliding mode control (ANTSM). The input signal chattering was eliminated. Adaptive estimation was applied to compensate for unknown disturbances. In [29], the implementation of a neural network (NN) approximator was used to estimate model uncertainty. Adaptive algorithms were designed to compensate for the approximation error and update the NN weight matrix. Nonsingular fast terminal sliding mode control (NFTSMC) was used to guarantee the finite-time convergence of the quadrotor to its desired trajectory. An NN-NFTSMC algorithm was formulated to provide the system with robustness in the presence of model uncertainty and external disturbances. In [30], Mo H et al. conducted a comprehensive survey of control techniques for quadrotors. In this study, an adaptive terminal sliding mode was deemed the most appropriate method for quadrotor tracking control.

In order to develop a control scheme that ensures the complete trajectory tracking of a 6-DOF quadrotor’s position and attitude, an adaptive backstepping fast nonsingular integral terminal sliding mode (ABFNITSM) control was designed to track the desired attitude. The position loop is based on adaptive integral backstepping control. The main contributions of this article can be summarized as follows:

• A new control scheme is introduced for quadrotors under subjection to external disturbances.
• The proposed ABFNITSM control is characterized by strong robustness against nonlinearities and external disturbances, offering quicker responsivity and more precise tracking compared to traditional control methods.
• With the implementation of adaptive estimation, the controller parameters can be updated online, streamlining the tuning process. Furthermore, the dead zone technique was employed to compensate for disturbances.
• A new, differentiable saturation function was utilized to eradicate chattering efficiently.
• The stability of the quadrotor trajectory tracking control system was verified by the application of Lyapunov theory.

This article is organized as follows: The derivation of the quadrotor dynamic model is introduced in Section 2. The adaptive backstepping fast nonsingular integral terminal sliding mode for attitude control and the adaptive integral backstepping for position control are outlined in Section 3. Meanwhile, the stability of the control system is proven using Lyapunov theory. In Section 4, the simulation results are presented, followed by the conclusions.

2. Dynamic Model of the Quadrotor

A quadrotor is an underactuated system. The vector $\mathrm{P}={(\mathrm{x},\mathrm{y},\mathrm{z})}^{\mathrm{T}}$ represents translational motion, and the vector $\mathsf{\Theta }={(\mathsf{\varphi },\mathsf{\theta },\mathsf{\psi })}^{\mathrm{T}}$ denotes the Euler angle. Figure 1 shows a schematic diagram of a quadrotor.

This paper employs a body reference frame (BRF) $\mathbb{B}=\{{\mathrm{O}}_{\mathrm{B}},{\mathrm{x}}_{\mathrm{b}},{\mathrm{y}}_{\mathrm{b}},{\mathrm{z}}_{\mathrm{b}}\}$ and an inertial reference frame (IRF) $\mathbb{E}=\{{\mathrm{O}}_{\mathrm{E}},{\mathrm{x}}_{\mathrm{e}},{\mathrm{y}}_{\mathrm{e}},{\mathrm{z}}_{\mathrm{e}}\}$ to describe the 6DOF rigid-body motion of the quadrotor. x, y, and z represent longitudinal, lateral, and vertical translational motion, respectively. $\mathsf{\varphi }$, $\mathsf{\theta }$, and $\mathsf{\psi }$ are roll, pitch, and yaw angle, respectively.

According to the Newton–Euler principle, the system model can be written as follows:

$$\left\{\begin{array}{c}\mathrm{m}\ddot{\mathrm{P}}={\mathrm{F}}_{\mathrm{A}}+{\mathrm{F}}_{\mathrm{G}}+{\mathrm{F}}_{\mathrm{D}}\\ \mathrm{I}\dot{\mathsf{\Omega }}=-{\mathsf{\Omega }}_{\times }\mathrm{I}\mathsf{\Omega }+{\mathsf{\tau }}_{\mathrm{A}}+{\mathsf{\tau }}_{\mathrm{G}}+{\mathsf{\tau }}_{\mathrm{D}}\end{array}\right.,$$

(1)

${\mathrm{F}}_{\mathrm{A}}$ is the aerodynamic force in the inertial frame.

$${\mathrm{F}}_{\mathrm{A}}={\mathrm{R}}_{\mathrm{B}}^{\mathrm{E}}\left[\begin{array}{c}0\\ 0\\ {\mathrm{F}}_{\mathrm{T}}\end{array}\right],$$

(2)

${\mathrm{F}}_{\mathrm{i}}$ is the thrust produced by the i-th motor. ${\mathrm{R}}_{\mathrm{i}}$ describes the rotational speed of the motor. ${\mathrm{k}}_{\mathrm{L}}$ represents the lift coefficient of the motor.

$${\mathrm{F}}_{\mathrm{T}}={\sum }_{\mathrm{i}=1}^4{\mathrm{F}}_{\mathrm{i}}={\mathrm{k}}_{\mathrm{L}}{\sum }_{\mathrm{i}=1}^4{\mathrm{R}}_{\mathrm{i}}^2,$$

(3)

${\mathrm{R}}_{\mathrm{B}}^{\mathrm{E}}$ is the matrix for the transformation from the BRF to the IRF.

$$\begin{gathered} R_B^E= \\ \left[\begin{array}{ccc}\cos \theta \cos \psi & \sin \theta \sin \varphi \cos \psi -\cos \varphi \sin \psi & \cos \varphi \sin \theta \cos \psi +\sin \varphi \sin \psi \\ \cos \theta \sin \psi & \sin \theta \sin \varphi \sin \psi +\cos \varphi \cos \psi & \cos \varphi \sin \theta \sin \psi -\sin \varphi \cos \psi \\ -\sin \theta & \sin \varphi \cos \theta & \cos \varphi \cos \theta \end{array}\right], \end{gathered}$$

(4)

${\mathrm{F}}_{\mathrm{G}}$ is the gravitational force. ${\mathrm{F}}_{\mathrm{D}}$ represents the force due to air resistance.

$${\mathrm{F}}_{\mathrm{D}}={\mathrm{k}}_{\mathrm{F}}\left[\begin{array}{c}\dot{\mathrm{x}}\\ \dot{\mathrm{y}}\\ \dot{\mathrm{z}}\end{array}\right],$$

(5)

$\mathrm{I}$ is the inertia matrix of the quadrotor. Based on the assumptions in Appendix A, $\mathrm{I}$ is defined as follows:

$$\mathrm{I}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({\mathrm{I}}_{\mathrm{x}\mathrm{x}},{\mathrm{I}}_{\mathrm{y}\mathrm{y}},{\mathrm{I}}_{\mathrm{z}\mathrm{z}}\right),$$

(6)

${[]}_{\times }$ denotes the cross-product operator. Based on the vector $\mathsf{\Omega }$, it defines a skew-symmetric matrix.

$${\mathsf{\Omega }}_{\times }=\left[\begin{array}{ccc}0& -\mathrm{r}& \mathrm{q}\\ \mathrm{r}& 0& -\mathrm{p}\\ -\mathrm{q}& \mathrm{p}& 0\end{array}\right],$$

(7)

${\mathsf{\tau }}_{\mathrm{A}}$ denotes the aerodynamic torque produced by the motors. $\mathrm{d}$ is the distance between the rotation axis of one motor and the center of gravity. ${\mathrm{k}}_{\mathrm{M}}$ is the torque coefficient of one motor during rotation.

$${\mathsf{\tau }}_{\mathrm{A}}=\left[\begin{array}{c}\left({\mathrm{F}}_4-{\mathrm{F}}_2\right)\\ \left({\mathrm{F}}_1-{\mathrm{F}}_3\right)\\ {\mathrm{k}}_{\mathrm{M}}\left({\mathrm{R}}_1^2-{\mathrm{R}}_2^2+{\mathrm{R}}_3^2-{\mathrm{R}}_4^2\right)\end{array}\right]=\left[\begin{array}{c}{\mathrm{U}}_{\mathsf{\varphi }}\\ {\mathrm{U}}_{\mathsf{\theta }}\\ {\mathrm{U}}_{\mathsf{\psi }}\end{array}\right],$$

(8)

${\mathsf{\tau }}_{\mathrm{G}}$ stands for the torque caused by the gyroscopic effect. ${\mathsf{\tau }}_{\mathrm{D}}$ reflects the torque owing to air friction.

$${\mathsf{\tau }}_{\mathrm{D}}={\mathrm{k}}_{\mathrm{T}}\left[\begin{array}{c}{\mathrm{p}}^2\\ {\mathrm{q}}^2\\ {\mathrm{r}}^2\end{array}\right],$$

(9)

A quadrotor is subject to various problems, such as inaccurate parametric (mass and inertia) measurements, low control effectiveness, and external disturbances. These create obstacles in control scheme design. In order to formulate the control problem, Equation (2) is rewritten, incorporating matched and unmatched uncertainties:

$$\left\{\begin{array}{c}\left(\mathrm{m}+∆\mathrm{m}\right)\ddot{\mathrm{P}}={\mathrm{F}}_{\mathrm{A}}+∆{\mathrm{F}}_{\mathrm{A}}+{\mathrm{F}}_{\mathrm{G}}+∆{\mathrm{F}}_{\mathrm{G}}+{\mathrm{F}}_{\mathrm{D}}\\ \left(\mathrm{I}+∆\mathrm{I}\right)\dot{\mathsf{\Omega }}=-{\mathsf{\Omega }}_{\times }\left(\mathrm{I}+∆\mathrm{I}\right)\mathsf{\Omega }+{\mathsf{\tau }}_{\mathrm{A}}+∆{\mathsf{\tau }}_{\mathrm{A}}+{\mathsf{\tau }}_{\mathrm{G}}+{\mathsf{\tau }}_{\mathrm{D}}\end{array}\right.,$$

(10)

where $∆\mathrm{m}\in \mathcal{R}, ∆\mathrm{I}\in {\mathcal{R}}^{3\times 3}, ∆{\mathrm{F}}_{\mathrm{A}}\in {\mathcal{R}}^3,$ and $∆{\mathsf{\tau }}_{\mathrm{A}}\in {\mathcal{R}}^3$ represent uncertainty in terms of mass, inertia, and control effectiveness, respectively. According to Lemma 1, the above equation can be rewritten as

$$\left\{\begin{array}{c}m\ddot{\mathrm{P}}={\mathrm{F}}_{\mathrm{A}}+{\mathrm{F}}_{\mathrm{G}}+{\mathrm{F}}_{\mathrm{D}}+{\mathrm{D}}_{\mathrm{P}}\\ \dot{\mathsf{\Omega }}={\mathrm{I}}^{-1}\left(-{\mathsf{\Omega }}_{\times }\mathrm{I}\mathsf{\Omega }+{\mathsf{\tau }}_{\mathrm{A}}\right)+{\mathsf{\tau }}_{\mathrm{D}}+{\mathrm{D}}_{\mathrm{A}}\end{array}\right.,$$

(11)

where ${\mathrm{D}}_{\mathrm{P}}$ and ${\mathrm{D}}_{\mathrm{A}}$ are lumped uncertainties.

Lemma 1.

$${\left(\mathrm{A}+\mathrm{B}\mathrm{C}\mathrm{D}\right)}^{-1}={\mathrm{A}}^{-1}-{\left(\mathrm{E}+{\mathrm{A}}^{-1}\mathrm{B}\mathrm{C}\mathrm{D}\right)}^{-1}{\mathrm{A}}^{-1}\mathrm{B}\mathrm{C}\mathrm{D}{\mathrm{A}}^{-1},$$

(12)

where $\mathrm{A}\in {\mathcal{R}}^{\mathrm{m}\times \mathrm{m}}$, $\mathrm{B}\in {\mathcal{R}}^{\mathrm{m}\times \mathrm{n}}$, $\mathrm{C}\in {\mathcal{R}}^{\mathrm{n}\times \mathrm{p}}$, $\mathrm{D}\in {\mathcal{R}}^{\mathrm{p}\times \mathrm{m}}$, and $\mathrm{E}$is the unit diagonal matrix.

The relationships between the angular velocity of a quadrotor in the BRF and the angular velocity in the IRF are represented as follows:

$$\left[\begin{array}{c}\dot{\mathsf{\varphi }}\\ \dot{\mathsf{\theta }}\\ \dot{\mathsf{\psi }}\end{array}\right]=\left[\begin{array}{ccc}1& \sin \mathsf{\varphi }\tan \mathsf{\theta }& \cos \mathsf{\varphi }\tan \mathsf{\theta }\\ 0& \cos \mathsf{\varphi }& -\sin \mathsf{\varphi }\\ 0& \sin \mathsf{\varphi }\sec \mathsf{\theta }& \cos \mathsf{\varphi }\sec \mathsf{\theta }\end{array}\right]\left[\begin{array}{c}\mathrm{p}\\ \mathrm{q}\\ \mathrm{r}\end{array}\right],$$

(13)

According to the small-angle approximation principle, the transformation matrix can be approximated as an identity matrix.

$$\left[\begin{array}{c}\dot{\mathrm{p}}\\ \dot{\mathrm{q}}\\ \dot{\mathrm{r}}\end{array}\right]\approx \left[\begin{array}{c}\ddot{\mathsf{\varphi }}\\ \ddot{\mathsf{\theta }}\\ \ddot{\mathsf{\psi }}\end{array}\right],$$

(14)

The vector $\mathrm{X}=\left[\mathsf{\varphi },\dot{\mathsf{\varphi }},\mathsf{\theta },\dot{\mathsf{\theta }},\mathsf{\psi },\dot{\mathsf{\psi }},\mathrm{x},\dot{\mathrm{x}},\mathrm{y},\dot{\mathrm{y}},\mathrm{z},\dot{\mathrm{z}}\right]\in {\mathcal{R}}^{12}$ denotes the state variables.

The virtual position control inputs are defined as follows:

$$\left[\begin{array}{c}{\mathrm{U}}_{\mathrm{x}}\\ {\mathrm{U}}_{\mathrm{y}}\\ {\mathrm{U}}_{\mathrm{z}}\end{array}\right]=\left[\begin{array}{c}{\mathrm{F}}_{\mathrm{T}}{\mathrm{m}}^{-1}\left(\cos {\mathrm{x}}_1\sin {\mathrm{x}}_3\cos {\mathrm{x}}_5+\sin {\mathrm{x}}_1\sin {\mathrm{x}}_5\right)\\ {\mathrm{F}}_{\mathrm{T}}{\mathrm{m}}^{-1}\left(\cos {\mathrm{x}}_1\sin {\mathrm{x}}_3\sin {\mathrm{x}}_5-\sin {\mathrm{x}}_1\cos {\mathrm{x}}_5\right)\\ {\mathrm{F}}_{\mathrm{T}}{\mathrm{m}}^{-1}\cos {\mathrm{x}}_1\cos {\mathrm{x}}_3-\mathrm{g}\end{array}\right],$$

(15)

Equation (13) can be rewritten as follows:

$$\left[\begin{array}{c}{\dot{\mathrm{x}}}_1\\ {\dot{\mathrm{x}}}_2\\ \begin{array}{c}{\dot{\mathrm{x}}}_3\\ {\dot{\mathrm{x}}}_4\\ \begin{array}{c}{\dot{\mathrm{x}}}_5\\ \begin{array}{c}{\dot{\mathrm{x}}}_6\\ {\dot{\mathrm{x}}}_7\\ \begin{array}{c}{\dot{\mathrm{x}}}_8\\ {\dot{\mathrm{x}}}_9\\ \begin{array}{c}{\dot{\mathrm{x}}}_{10}\\ \begin{array}{c}{\dot{\mathrm{x}}}_{11}\\ {\dot{\mathrm{x}}}_{12}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right]=\left[\begin{array}{c}{\mathrm{x}}_2\\ {\mathrm{a}}_1{\mathrm{x}}_4{\mathrm{x}}_6+{\mathrm{a}}_2{\mathrm{x}}_2^2+{\mathrm{b}}_1{\mathrm{U}}_{\mathsf{\varphi }}+{\mathrm{d}}_{\mathsf{\varphi }}\\ \begin{array}{c}{\mathrm{x}}_4\\ {\mathrm{a}}_3{\mathrm{x}}_2{\mathrm{x}}_6+{\mathrm{a}}_4{\mathrm{x}}_4^2+{\mathrm{b}}_2{\mathrm{U}}_{\mathsf{\theta }}+{\mathrm{d}}_{\mathsf{\theta }}\\ \begin{array}{c}{\mathrm{x}}_6\\ \begin{array}{c}{\mathrm{a}}_5{\mathrm{x}}_2{\mathrm{x}}_4+{\mathrm{a}}_6{\mathrm{x}}_6^2+{\mathrm{b}}_3{\mathrm{U}}_{\mathsf{\psi }}+{\mathrm{d}}_{\mathsf{\psi }}\\ {\mathrm{x}}_8\\ \begin{array}{c}{\mathrm{a}}_7{\mathrm{x}}_8+{\mathrm{U}}_{\mathrm{x}}+{\mathrm{d}}_{\mathrm{x}}\\ {\mathrm{x}}_{10}\\ \begin{array}{c}{\mathrm{a}}_8{\mathrm{x}}_{10}+{\mathrm{U}}_{\mathrm{y}}+{\mathrm{d}}_{\mathrm{y}}\\ \begin{array}{c}{\mathrm{x}}_{12}\\ {\mathrm{a}}_9{\mathrm{x}}_{12}+{\mathrm{U}}_{\mathrm{z}}+{\mathrm{d}}_{\mathrm{z}}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right],$$

(16)

where

$$\left[\begin{array}{c}{\mathrm{a}}_1\\ {\mathrm{a}}_2\\ \begin{array}{c}{\mathrm{a}}_3\\ {\mathrm{a}}_4\\ \begin{array}{c}{\mathrm{a}}_5\\ \begin{array}{c}{\mathrm{a}}_6\\ {\mathrm{a}}_7\\ \begin{array}{c}{\mathrm{a}}_8\\ {\mathrm{a}}_9\\ \begin{array}{c}{\mathrm{b}}_1\\ \begin{array}{c}{\mathrm{b}}_2\\ {\mathrm{b}}_3\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right]=\left[\begin{array}{c}{\mathrm{I}}_{\mathrm{x}\mathrm{x}}^{-1}({\mathrm{I}}_{\mathrm{y}\mathrm{y}}-{\mathrm{I}}_{\mathrm{z}\mathrm{z}})\\ {\mathrm{I}}_{\mathrm{x}\mathrm{x}}^{-1}{\mathrm{k}}_{\mathrm{T}}\\ \begin{array}{c}{\mathrm{I}}_{\mathrm{y}\mathrm{y}}^{-1}({\mathrm{I}}_{\mathrm{z}\mathrm{z}}-{\mathrm{I}}_{\mathrm{x}\mathrm{x}})\\ {\mathrm{I}}_{\mathrm{y}\mathrm{y}}^{-1}{\mathrm{k}}_{\mathrm{T}}\\ \begin{array}{c}{\mathrm{I}}_{\mathrm{z}\mathrm{z}}^{-1}({\mathrm{I}}_{\mathrm{x}\mathrm{x}}-{\mathrm{I}}_{\mathrm{y}\mathrm{y}})\\ \begin{array}{c}{\mathrm{I}}_{\mathrm{z}\mathrm{z}}^{-1}{\mathrm{k}}_{\mathrm{T}}\\ {\mathrm{m}}^{-1}{\mathrm{k}}_{\mathrm{F}}\\ \begin{array}{c}{\mathrm{m}}^{-1}{\mathrm{k}}_{\mathrm{F}}\\ {\mathrm{m}}^{-1}{\mathrm{k}}_{\mathrm{F}}\\ \begin{array}{c}{\mathrm{I}}_{\mathrm{x}\mathrm{x}}^{-1}\mathrm{d}\\ \begin{array}{c}{\mathrm{I}}_{\mathrm{y}\mathrm{y}}^{-1}\mathrm{d}\\ {\mathrm{I}}_{\mathrm{z}\mathrm{z}}^{-1}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right],$$

(17)

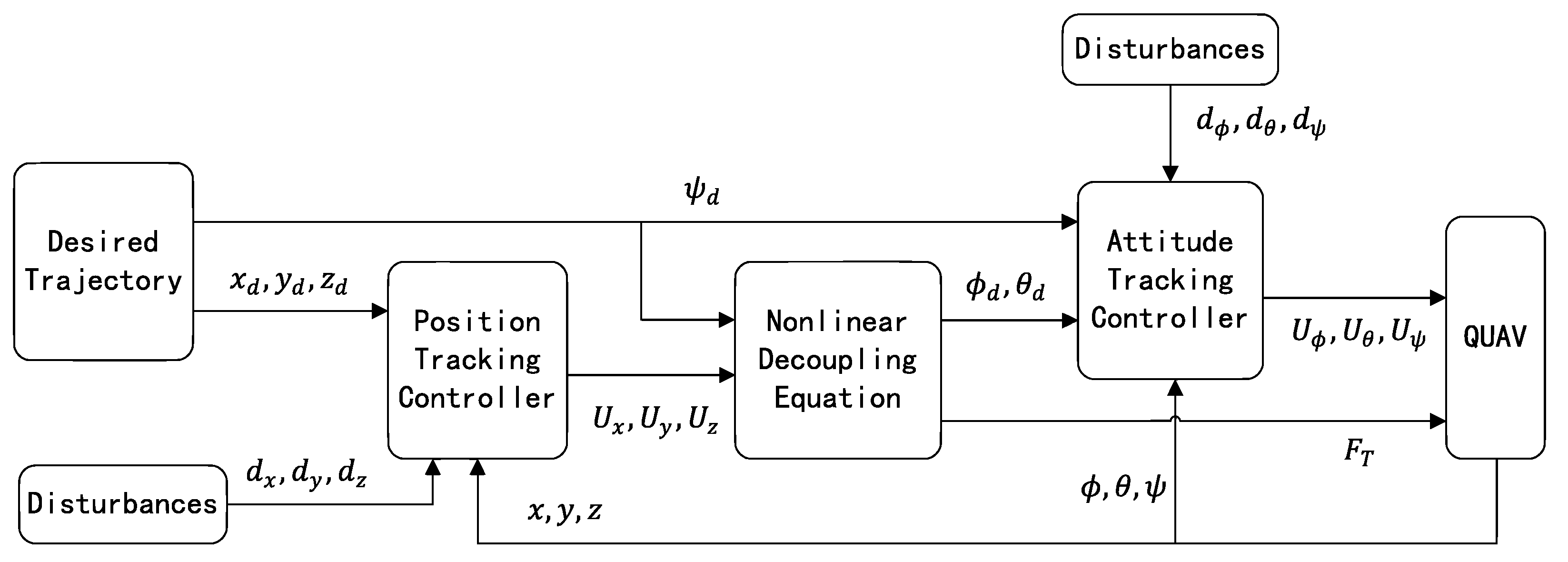
3. Control Scheme Design

This section is dedicated to the design of a trajectory-tracking control scheme and stability analysis. Taking parametric uncertainties and external disturbances into consideration, a trajectory-tracking control strategy is formulated to ensure the quick and accurate tracking of reference commands. To achieve this goal, a new control scheme is proposed, integrating a terminal sliding mode, an integral element, the backstepping technique, and the dead zone technique for attitude trajectory tracking. For the sake of chattering elimination, a new saturation function is designed. Additionally, an online adaptive estimation technique is introduced to compensate for parametric uncertainties and external disturbances. Adaptive integral backstepping control is introduced in a position loop. Figure 2 illustrates the entire control flow diagram.

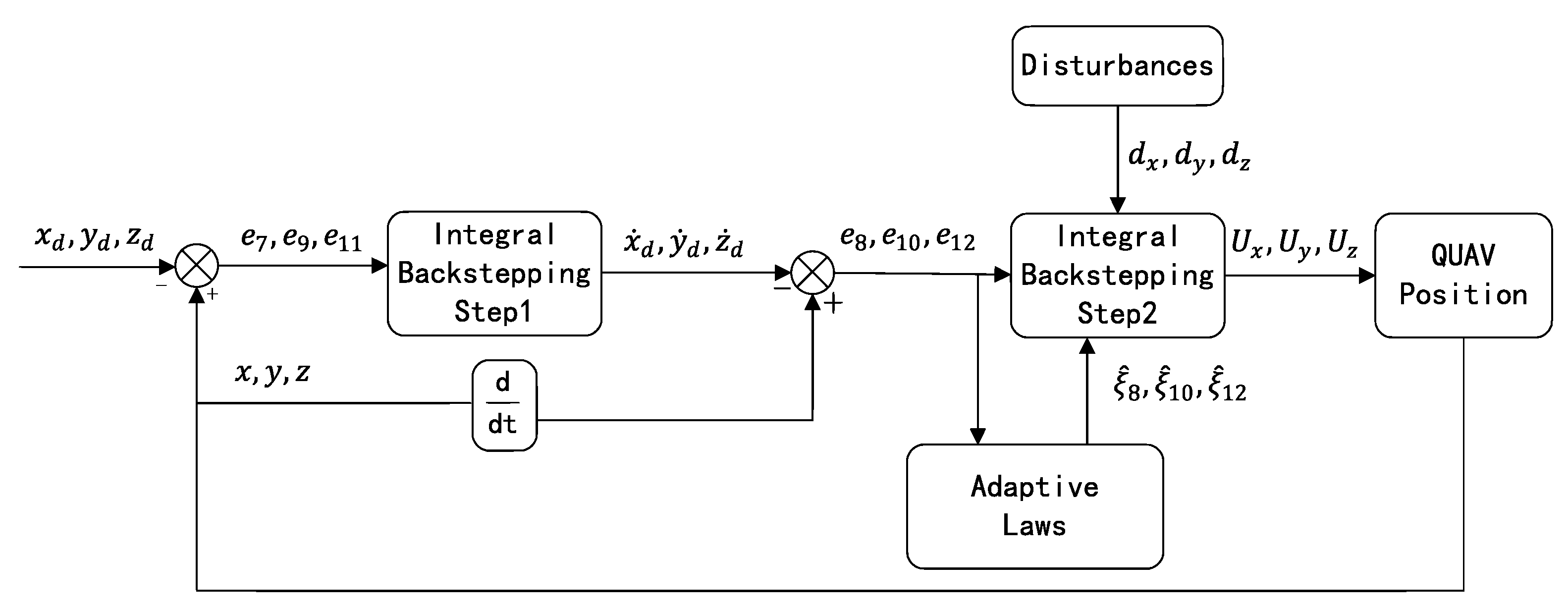
3.1. Position-Tracking Control Design

The adaptive integral backstepping (AIBS) control exhibits good robustness. It combines the characteristics of integral backstepping control and adaptive estimation to facilitate precise tracking and stable control. The basic idea of the backstepping method is to gradually introduce virtual control variables and recursively design control laws to guide the tracking errors from an initial state to zero. An adaptive law is used to compensate for modeling errors, external disturbances, and measurement noise. The design process of AIBS is depicted in Figure 3.

• AIBS control design step 1:

The position-tracking error is defined as follows:

$$\left[\begin{array}{c}{\mathrm{e}}_7\\ {\mathrm{e}}_9\\ {\mathrm{e}}_{11}\end{array}\right]=\left[\begin{array}{c}{\mathrm{x}}_7-{\mathrm{x}}_{7\mathrm{d}}\\ {\mathrm{x}}_9-{\mathrm{x}}_{9\mathrm{d}}\\ {\mathrm{x}}_{11}-{\mathrm{x}}_{11\mathrm{d}}\end{array}\right],$$

(18)

where ${\mathrm{x}}_{7\mathrm{d}}$, ${\mathrm{x}}_{9\mathrm{d}}$, and ${\mathrm{x}}_{11\mathrm{d}}$ denote the desired trajectory. The time derivative of Equation (18) is

$$\left[\begin{array}{c}{\dot{\mathrm{e}}}_7\\ {\dot{\mathrm{e}}}_9\\ {\dot{\mathrm{e}}}_{11}\end{array}\right]=\left[\begin{array}{c}{\dot{\mathrm{x}}}_7-{\dot{\mathrm{x}}}_{7\mathrm{d}}\\ {\dot{\mathrm{x}}}_9-{\dot{\mathrm{x}}}_{9\mathrm{d}}\\ {\dot{\mathrm{x}}}_{11}-{\dot{\mathrm{x}}}_{11\mathrm{d}}\end{array}\right]=\left[\begin{array}{c}{\mathrm{x}}_8-{\dot{\mathrm{x}}}_{7\mathrm{d}}\\ {\mathrm{x}}_{10}-{\dot{\mathrm{x}}}_{9\mathrm{d}}\\ {\mathrm{x}}_{12}-{\dot{\mathrm{x}}}_{11\mathrm{d}}\end{array}\right],$$

(19)

The Lyapunov function is defined as follows for a stable system:

$$\left[\begin{array}{c}{\mathrm{l}}_{\mathrm{x}1}\\ {\mathrm{l}}_{\mathrm{y}1}\\ {\mathrm{l}}_{\mathrm{z}1}\end{array}\right]=\frac{1}{2}\left[\begin{array}{c}{\mathrm{e}}_7^2+{\mathrm{k}}_7{\mathsf{\Gamma }}_7^2\\ {\mathrm{e}}_9^2+{\mathrm{k}}_9{\mathsf{\Gamma }}_9^2\\ {\mathrm{e}}_{11}^2+{\mathrm{k}}_{11}{\mathsf{\Gamma }}_{11}^2\end{array}\right],$$

(20)

where

$${\mathsf{\Gamma }}_{\ast }=\int {\mathrm{e}}_{\ast }\mathrm{d}\mathsf{\tau }\left(\ast \in 7,9,11\right),$$

(21)

The time derivative of Equation (20) is

$$\left[\begin{array}{c}{\dot{\mathrm{l}}}_{\mathrm{x}1}\\ {\dot{\mathrm{l}}}_{\mathrm{y}1}\\ {\dot{\mathrm{l}}}_{\mathrm{z}1}\end{array}\right]=\left[\begin{array}{c}{\mathrm{e}}_7{\dot{\mathrm{e}}}_7+{\mathrm{k}}_7{\mathsf{\Gamma }}_7{\dot{\mathsf{\Gamma }}}_7\\ {\mathrm{e}}_9{\dot{\mathrm{e}}}_9+{\mathrm{k}}_9{\mathsf{\Gamma }}_9{\dot{\mathsf{\Gamma }}}_9\\ {\mathrm{e}}_{11}{\dot{\mathrm{e}}}_{11}+{\mathrm{k}}_{11}{\mathsf{\Gamma }}_{11}{\dot{\mathsf{\Gamma }}}_{11}\end{array}\right]=\left[\begin{array}{c}{\mathrm{e}}_7\left({\mathrm{x}}_8-{\dot{\mathrm{x}}}_{7\mathrm{d}}\right)+{\mathrm{k}}_7{\mathsf{\Gamma }}_7{\dot{\mathsf{\Gamma }}}_7\\ {\mathrm{e}}_9\left({\mathrm{x}}_{10}-{\dot{\mathrm{x}}}_{9\mathrm{d}}\right)+{\mathrm{k}}_9{\mathsf{\Gamma }}_9{\dot{\mathsf{\Gamma }}}_9\\ {\mathrm{e}}_{11}\left({\mathrm{x}}_{12}-{\dot{\mathrm{x}}}_{11\mathrm{d}}\right)+{\mathrm{k}}_{11}{\mathsf{\Gamma }}_{11}{\dot{\mathsf{\Gamma }}}_{11}\end{array}\right],$$

(22)

The system virtual control input is selected as follows:

$$\left[\begin{array}{c}{\mathrm{x}}_{8\mathrm{d}}\\ {\mathrm{x}}_{10\mathrm{d}}\\ {\mathrm{x}}_{12\mathrm{d}}\end{array}\right]=\left[\begin{array}{c}-{\mathsf{\xi }}_7{\mathrm{e}}_7+{\dot{\mathrm{x}}}_{7\mathrm{d}}-{\mathrm{k}}_7{\mathsf{\Gamma }}_7\\ -{\mathsf{\xi }}_9{\mathrm{e}}_9+{\dot{\mathrm{x}}}_{9\mathrm{d}}-{\mathrm{k}}_9{\mathsf{\Gamma }}_9\\ -{\mathsf{\xi }}_{11}{\mathrm{e}}_{11}+{\dot{\mathrm{x}}}_{11\mathrm{d}}-{\mathrm{k}}_{11}{\mathsf{\Gamma }}_{11}\end{array}\right],$$

(23)

where ${\mathsf{\xi }}_7$, ${\mathsf{\xi }}_9$, and ${\mathsf{\xi }}_{11}$ are positive constants to be designed.

Substituting (23) into (22) yields

$$\left[\begin{array}{c}{\dot{\mathrm{l}}}_{\mathrm{x}1}\\ {\dot{\mathrm{l}}}_{\mathrm{y}1}\\ {\dot{\mathrm{l}}}_{\mathrm{z}1}\end{array}\right]=\left[\begin{array}{c}-{\mathsf{\xi }}_7{\mathrm{e}}_7^2\\ -{\mathsf{\xi }}_9{\mathrm{e}}_9^2\\ -{\mathsf{\xi }}_{11}{\mathrm{e}}_{11}^2\end{array}\right]\le 0,$$

(24)

• AIBS control design step 2:

The second tracking error is given by the following expression:

$$\left[\begin{array}{c}{\mathrm{e}}_8\\ {\mathrm{e}}_{10}\\ {\mathrm{e}}_{12}\end{array}\right]=\left[\begin{array}{c}{\mathrm{x}}_8-{\mathrm{x}}_{8\mathrm{d}}\\ {\mathrm{x}}_{10}-{\mathrm{x}}_{10\mathrm{d}}\\ {\mathrm{x}}_{12}-{\mathrm{x}}_{12\mathrm{d}}\end{array}\right],$$

(25)

The Lyapunov function can be defined as follows:

$$\left[\begin{array}{c}{\mathrm{l}}_{\mathrm{x}2}\\ {\mathrm{l}}_{\mathrm{y}2}\\ {\mathrm{l}}_{\mathrm{z}2}\end{array}\right]=\frac{1}{2}\left[\begin{array}{c}{\mathrm{e}}_7^2+{\mathrm{k}}_7{\mathsf{\Gamma }}_7^2+{\mathrm{e}}_8^2\\ {\mathrm{e}}_9^2+{\mathrm{k}}_9{\mathsf{\Gamma }}_9^2+{\mathrm{e}}_8^2\\ {\mathrm{e}}_{11}^2+{\mathrm{k}}_{11}{\mathsf{\Gamma }}_{11}^2+{\mathrm{e}}_{12}^2\end{array}\right],$$

(26)

The time derivative of Equation (26) is

$$\left[\begin{array}{c}{\dot{\mathrm{l}}}_{\mathrm{x}2}\\ {\dot{\mathrm{l}}}_{\mathrm{y}2}\\ {\dot{\mathrm{l}}}_{\mathrm{z}2}\end{array}\right]=\left[\begin{array}{c}{\mathrm{e}}_7{\dot{\mathrm{e}}}_7+{\mathrm{k}}_7{\mathsf{\Gamma }}_7{\dot{\mathsf{\Gamma }}}_7+{\mathrm{e}}_8{\dot{\mathrm{e}}}_8\\ {\mathrm{e}}_9{\dot{\mathrm{e}}}_9+{\mathrm{k}}_9{\mathsf{\Gamma }}_9{\dot{\mathsf{\Gamma }}}_9+{\mathrm{e}}_{10}{\dot{\mathrm{e}}}_{10}\\ {\mathrm{e}}_{11}{\dot{\mathrm{e}}}_{11}+{\mathrm{k}}_{11}{\mathsf{\Gamma }}_{11}{\dot{\mathsf{\Gamma }}}_{11}+{\mathrm{e}}_{12}{\dot{\mathrm{e}}}_{12}\end{array}\right],$$

(27)

Substituting (19), (23), and (25) into (27) yields

$$\left[\begin{array}{c}{\dot{\mathrm{l}}}_{\mathrm{x}2}\\ {\dot{\mathrm{l}}}_{\mathrm{y}2}\\ {\dot{\mathrm{l}}}_{\mathrm{z}2}\end{array}\right]=\left[\begin{array}{c}-{\mathsf{\xi }}_7{\mathrm{e}}_7^2+{\mathrm{e}}_8({\mathrm{e}}_7+{\dot{\mathrm{e}}}_8)\\ -{\mathsf{\xi }}_9{\mathrm{e}}_9^2+{\mathrm{e}}_{10}({\mathrm{e}}_9+{\dot{\mathrm{e}}}_{10})\\ -{\mathsf{\xi }}_{11}{\mathrm{e}}_{11}^2+{\mathrm{e}}_{12}({\mathrm{e}}_{11}+{\dot{\mathrm{e}}}_{12})\end{array}\right],$$

(28)

To ensure the stability of the position-tracking control system, we need to satisfy the following condition:

$$\left[\begin{array}{c}{\mathrm{e}}_7+{\dot{\mathrm{e}}}_8\\ {\mathrm{e}}_9+{\dot{\mathrm{e}}}_{10}\\ {\mathrm{e}}_{11}+{\dot{\mathrm{e}}}_{12}\end{array}\right]=\left[\begin{array}{c}-{\widehat{\mathsf{\xi }}}_8{\mathrm{e}}_8\\ -{\widehat{\mathsf{\xi }}}_{10}{\mathrm{e}}_{10}\\ -{\widehat{\mathsf{\xi }}}_{12}{\mathrm{e}}_{12}\end{array}\right],$$

(29)

where ${\widehat{\mathsf{\xi }}}_8$, ${\widehat{\mathsf{\xi }}}_{10}$, and ${\widehat{\mathsf{\xi }}}_{12}$ are the estimation of ${\mathsf{\xi }}_8$, ${\mathsf{\xi }}_{10}$, and ${\mathsf{\xi }}_{12}$, respectively.

Based on (29), the corresponding position control law can be derived as follows:

$$\left[\begin{array}{c}{\mathrm{U}}_{\mathrm{x}}\\ {\mathrm{U}}_{\mathrm{y}}\\ {\mathrm{U}}_{\mathrm{z}}\end{array}\right]=\left[\begin{array}{c}{\ddot{\mathrm{x}}}_{7\mathrm{d}}+\left({\mathsf{\xi }}_7^2-1-{\mathrm{k}}_7\right){\mathrm{e}}_7-\left({\mathsf{\xi }}_7+{\widehat{\mathsf{\xi }}}_8\right){\mathrm{e}}_8-{\mathrm{a}}_7{\mathrm{x}}_8+{\mathsf{\xi }}_7{\mathrm{k}}_7{\mathsf{\Gamma }}_7-{\mathrm{d}}_{\mathrm{x}}\\ {\ddot{\mathrm{x}}}_{9\mathrm{d}}+\left({\mathsf{\xi }}_9^2-1-{\mathrm{k}}_9\right){\mathrm{e}}_9-\left({\mathsf{\xi }}_9+{\widehat{\mathsf{\xi }}}_{10}\right){\mathrm{e}}_{10}-{\mathrm{a}}_8{\mathrm{x}}_{10}+{\mathsf{\xi }}_9{\mathrm{k}}_9{\mathsf{\Gamma }}_9-{\mathrm{d}}_{\mathrm{y}}\\ {\ddot{\mathrm{x}}}_{11\mathrm{d}}+\left({\mathsf{\xi }}_{11}^2-1-{\mathrm{k}}_{11}\right){\mathrm{e}}_{11}-\left({\mathsf{\xi }}_{11}+{\widehat{\mathsf{\xi }}}_{12}\right){\mathrm{e}}_{12}-{\mathrm{a}}_9{\mathrm{x}}_{12}+{\mathsf{\xi }}_{11}{\mathrm{k}}_{11}{\mathsf{\Gamma }}_{11}-{\mathrm{d}}_{\mathrm{z}}\end{array}\right],$$

(30)

• Proof of stability of position-tracking control:

To prove the stability of the system and determine the parametric values of ${\widehat{\mathsf{\xi }}}_8$, ${\widehat{\mathsf{\xi }}}_{10}$, and ${\widehat{\mathsf{\xi }}}_{12}$, ${\widehat{\mathsf{\xi }}}_8$ is taken as an illustration. The Lyapunov function is formulated as follows:

$${\mathrm{L}}_{\mathrm{P}\mathrm{x}}=\frac{1}{2}({\mathrm{e}}_7^2+{\mathrm{k}}_7{\mathsf{\Gamma }}_7^2+{\mathrm{e}}_8^2+\frac{1}{{\mathsf{\alpha }}_8}{\tilde{\mathrm{e}}}_{{\mathsf{\xi }}_8}^2),$$

(31)

where ${\alpha }_8$ is positive constant, and ${\tilde{\mathrm{e}}}_{{\mathsf{\xi }}_8}$ is the estimation error.

The time derivative of Equation (31) is

$${\dot{\mathrm{L}}}_{\mathrm{P}\mathrm{x}}=-{\mathsf{\xi }}_7{\mathrm{e}}_7^2-{\mathsf{\xi }}_8{\mathrm{e}}_8^2+{\tilde{\mathrm{e}}}_{{\mathsf{\xi }}_8}\left({\mathrm{e}}_8^2-\frac{1}{{\mathsf{\alpha }}_8}{\dot{\widehat{\mathsf{\xi }}}}_8\right),$$

(32)

If the third term on the right-hand side of (32) is set to 0, it can be deduced that

$${\dot{\widehat{\mathsf{\xi }}}}_8={\mathsf{\alpha }}_8{\mathrm{e}}_8^2,$$

(33)

Then,

$${\dot{\mathrm{L}}}_{\mathrm{P}\mathrm{x}}=-{\mathsf{\xi }}_7{\mathrm{e}}_7^2-{\mathsf{\xi }}_8{\mathrm{e}}_8^2\le 0,$$

(34)

Therefore, the subsystem is stable.

For the purpose of establishing a complete proof, the Lyapunov function is defined as follows:

$$\begin{gathered} {\mathrm{L}}_{\mathrm{P}}=\frac{1}{2}({\mathrm{e}}_7^2+{\mathrm{k}}_7{\mathsf{\Gamma }}_7^2+{\mathrm{e}}_8^2+\frac{1}{{\mathsf{\alpha }}_8}{\tilde{\mathrm{e}}}_{{\mathsf{\xi }}_8}^2+{\mathrm{e}}_9^2+{\mathrm{k}}_9{\mathsf{\Gamma }}_9^2+{\mathrm{e}}_{10}^2+\frac{1}{{\mathsf{\alpha }}_{10}}{\tilde{\mathrm{e}}}_{{\mathsf{\xi }}_{10}}^2+{\mathrm{e}}_{11}^2+{\mathrm{k}}_{11}{\mathsf{\Gamma }}_{11}^2+ \\ {\mathrm{e}}_{12}^2+\frac{1}{{\mathsf{\alpha }}_{12}}{\tilde{\mathrm{e}}}_{{\mathsf{\xi }}_{12}}^2), \end{gathered}$$

(35)

The time derivative of (36) is

$${\dot{\mathrm{L}}}_{\mathrm{P}}=-{\mathsf{\xi }}_7{\mathrm{e}}_7^2-{\mathsf{\xi }}_8{\mathrm{e}}_8^2-{\mathsf{\xi }}_9{\mathrm{e}}_9^2-{\mathsf{\xi }}_{10}{\mathrm{e}}_{10}^2-{\mathsf{\xi }}_{11}{\mathrm{e}}_{11}^2-{\mathsf{\xi }}_{12}{\mathrm{e}}_{12}^2\le 0,$$

(36)

where ${\mathsf{\xi }}_7$, ${\mathsf{\xi }}_8$, ${\mathsf{\xi }}_9$, ${\mathsf{\xi }}_{10}$, ${\mathsf{\xi }}_{11}$, and ${\mathsf{\xi }}_{12}$ are positive constants.

The stability proof of the position-tracking system is now complete.

• Adaptive laws:

$$\left[\begin{array}{c}{\dot{\widehat{\mathsf{\xi }}}}_8\\ {\dot{\widehat{\mathsf{\xi }}}}_{10}\\ {\dot{\widehat{\mathsf{\xi }}}}_{12}\end{array}\right]=\left[\begin{array}{c}{\mathsf{\alpha }}_8{\mathrm{e}}_8^2\\ {\mathsf{\alpha }}_{10}{\mathrm{e}}_{10}^2\\ {\mathsf{\alpha }}_{12}{\mathrm{e}}_{12}^2\end{array}\right],$$

(37)

where ${\alpha }_8$, ${\alpha }_{10}$, and ${\alpha }_{12}$ are the positive constants being designed.

Based on (15), thrust and the desired attitude angle can be calculated as follows:

$$\left\{\begin{array}{c}{\mathrm{F}}_{\mathrm{T}}=\mathrm{m}\sqrt{{\mathrm{U}}_{\mathrm{x}}^2+{\mathrm{U}}_{\mathrm{y}}^2+{\left({\mathrm{U}}_{\mathrm{z}}+\mathrm{g}\right)}^2}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\\ {\mathsf{\theta }}_{\mathrm{d}}={\tan }^{-1}\left(\frac{\cos {\mathsf{\psi }}_{\mathrm{d}}{\mathrm{U}}_{\mathrm{x}}+\sin {\mathsf{\psi }}_{\mathrm{d}}{\mathrm{U}}_{\mathrm{y}}}{{\mathrm{U}}_{\mathrm{z}}+\mathrm{g}}\right)\hspace{1em}\hspace{1em}\\ {\mathsf{\psi }}_{\mathrm{d}}={\tan }^{-1}\left(\cos {\mathsf{\theta }}_{\mathrm{d}}\frac{\sin {\mathsf{\psi }}_{\mathrm{d}}{\mathrm{U}}_{\mathrm{x}}-\cos {\mathsf{\psi }}_{\mathrm{d}}{\mathrm{U}}_{\mathrm{y}}}{{\mathrm{U}}_{\mathrm{z}}+\mathrm{g}}\right)\end{array}\right.,$$

(38)

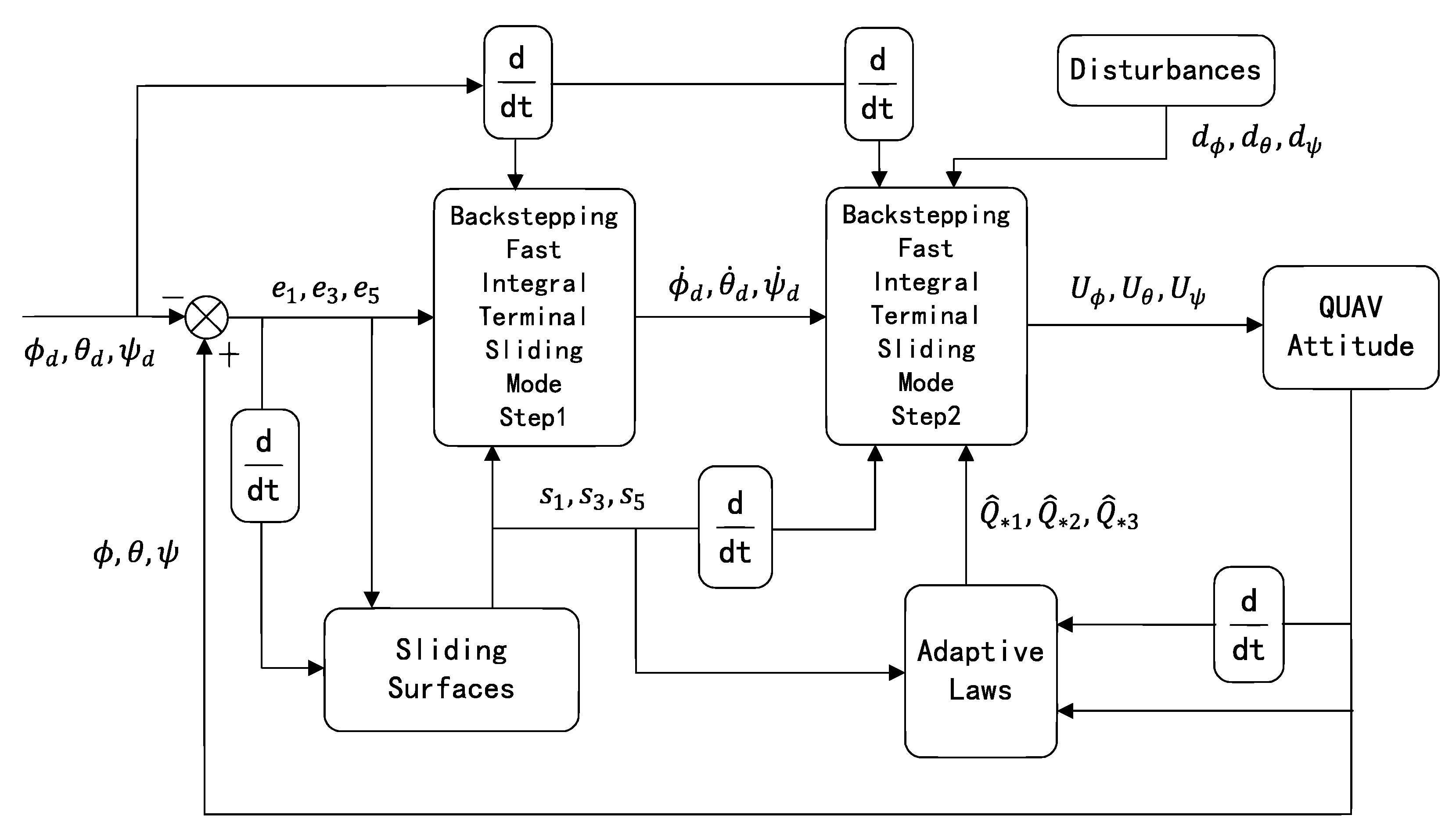
3.2. Attitude-Tracking Control Design

The previously proposed AIBS control has been effective in position tracking, ensuring the stability of the position subsystem. In this section, a robust adaptive backstepping fast nonsingular integral terminal sliding mode control (ABFNITSM) is proposed for attitude tracking. The design process of ABFNITSM is presented in Figure 4. A new saturation function is designed to eliminate chattering. The main objective of this control is to ensure system stability and achieve fast convergence of the Euler angle to the desired trajectory.

The saturation function is designed as follows:

$$\mathrm{s}\mathrm{a}\mathrm{t}\left(\mathrm{x}\right)=\frac{{\mathrm{e}}^{\mathrm{x}}-1}{{\mathrm{e}}^{\mathrm{x}}+1},$$

(39)

• ABFNITSM control design step 1:

The attitude-tracking error is defined as follows:

$$\left[\begin{array}{c}{\mathrm{e}}_1\\ {\mathrm{e}}_3\\ {\mathrm{e}}_5\end{array}\right]=\left[\begin{array}{c}{\mathrm{x}}_1-{\mathrm{x}}_{1\mathrm{d}}\\ {\mathrm{x}}_3-{\mathrm{x}}_{3\mathrm{d}}\\ {\mathrm{x}}_5-{\mathrm{x}}_{5\mathrm{d}}\end{array}\right],$$

(40)

where ${\mathrm{x}}_{1\mathrm{d}}$, ${\mathrm{x}}_{3\mathrm{d}}$, and ${\mathrm{x}}_{5\mathrm{d}}$ are the desired trajectory. The time derivative of Equation (40) is

$$\left[\begin{array}{c}{\dot{\mathrm{e}}}_1\\ {\dot{\mathrm{e}}}_3\\ {\dot{\mathrm{e}}}_5\end{array}\right]=\left[\begin{array}{c}{\dot{\mathrm{x}}}_1-{\dot{\mathrm{x}}}_{1\mathrm{d}}\\ {\dot{\mathrm{x}}}_3-{\dot{\mathrm{x}}}_{3\mathrm{d}}\\ {\dot{\mathrm{x}}}_5-{\dot{\mathrm{x}}}_{5\mathrm{d}}\end{array}\right]=\left[\begin{array}{c}{\mathrm{x}}_2-{\dot{\mathrm{x}}}_{1\mathrm{d}}\\ {\mathrm{x}}_4-{\dot{\mathrm{x}}}_{3\mathrm{d}}\\ {\mathrm{x}}_6-{\dot{\mathrm{x}}}_{5\mathrm{d}}\end{array}\right],$$

(41)

The Lyapunov function is defined as follows:

$$\left[\begin{array}{c}{\mathrm{l}}_{\mathsf{\varphi }1}\\ {\mathrm{l}}_{\mathsf{\theta }1}\\ {\mathrm{l}}_{\mathsf{\psi }1}\end{array}\right]=\frac{1}{2}\left[\begin{array}{c}{\mathrm{e}}_1^2\\ {\mathrm{e}}_3^2\\ {\mathrm{e}}_5^2\end{array}\right],$$

(42)

The time derivative of the (42) is

$$\left[\begin{array}{c}{\dot{\mathrm{l}}}_{\mathsf{\varphi }1}\\ {\dot{\mathrm{l}}}_{\mathsf{\theta }1}\\ {\dot{\mathrm{l}}}_{\mathsf{\psi }1}\end{array}\right]=\left[\begin{array}{c}{\mathrm{e}}_1{\dot{\mathrm{e}}}_1\\ {\mathrm{e}}_3{\dot{\mathrm{e}}}_3\\ {\mathrm{e}}_5{\dot{\mathrm{e}}}_5\end{array}\right]=\left[\begin{array}{c}{\mathrm{e}}_1\left({\mathrm{x}}_2-{\dot{\mathrm{x}}}_{1\mathrm{d}}\right)\\ {\mathrm{e}}_3\left({\mathrm{x}}_4-{\dot{\mathrm{x}}}_{3\mathrm{d}}\right)\\ {\mathrm{e}}_5\left({\mathrm{x}}_6-{\dot{\mathrm{x}}}_{5\mathrm{d}}\right)\end{array}\right],$$

(43)

The system virtual control input is selected as follows:

$$\left[\begin{array}{c}{\mathrm{x}}_{2\mathrm{d}}\\ {\mathrm{x}}_{4\mathrm{d}}\\ {\mathrm{x}}_{6\mathrm{d}}\end{array}\right]=\left[\begin{array}{c}{\mathrm{s}}_1+{\dot{\mathrm{x}}}_{1\mathrm{d}}-{\mathsf{\xi }}_1{\mathrm{e}}_1\\ {\mathrm{s}}_3+{\dot{\mathrm{x}}}_{3\mathrm{d}}-{\mathsf{\xi }}_3{\mathrm{e}}_3\\ {\mathrm{s}}_5+{\dot{\mathrm{x}}}_{5\mathrm{d}}-{\mathsf{\xi }}_5{\mathrm{e}}_5\end{array}\right],$$

(44)

• ABFNITSM control design step 2:

The sliding mode function is chosen as follows:

$$\left[\begin{array}{c}{\mathrm{s}}_1\\ {\mathrm{s}}_3\\ {\mathrm{s}}_5\end{array}\right]=\left[\begin{array}{c}{\dot{\mathrm{e}}}_1+{\int }_0^{\mathrm{t}}\left[{\mathsf{\delta }}_{\mathsf{\varphi }1}{\left|{\mathrm{e}}_1\right|}^{{\mathsf{\eta }}_{\mathsf{\varphi }1}}\mathrm{s}\mathrm{a}\mathrm{t}\left({\mathrm{e}}_1\right)+{\mathsf{\delta }}_{\mathsf{\varphi }2}{\left|{\dot{\mathrm{e}}}_1\right|}^{{\mathsf{\eta }}_{\mathsf{\varphi }2}}\mathrm{s}\mathrm{a}\mathrm{t}\left({\dot{\mathrm{e}}}_1\right)\right]\mathrm{d}\mathsf{\tau }\\ {\dot{\mathrm{e}}}_3+{\int }_0^{\mathrm{t}}\left[{\mathsf{\delta }}_{\mathsf{\theta }1}{\left|{\mathrm{e}}_3\right|}^{{\mathsf{\eta }}_{\mathsf{\theta }1}}\mathrm{s}\mathrm{a}\mathrm{t}\left({\mathrm{e}}_3\right)+{\mathsf{\delta }}_{\mathsf{\theta }2}{\left|{\dot{\mathrm{e}}}_3\right|}^{{\mathsf{\eta }}_{\mathsf{\theta }2}}\mathrm{s}\mathrm{a}\mathrm{t}\left({\dot{\mathrm{e}}}_3\right)\right]\mathrm{d}\mathsf{\tau }\\ {\dot{\mathrm{e}}}_5+{\int }_0^{\mathrm{t}}\left[{\mathsf{\delta }}_{\mathsf{\psi }1}{\left|{\mathrm{e}}_5\right|}^{{\mathsf{\eta }}_{\mathsf{\psi }1}}\mathrm{s}\mathrm{a}\mathrm{t}\left({\mathrm{e}}_5\right)+{\mathsf{\delta }}_{\mathsf{\psi }2}{\left|{\dot{\mathrm{e}}}_5\right|}^{{\mathsf{\eta }}_{\mathsf{\psi }2}}\mathrm{s}\mathrm{a}\mathrm{t}\left({\dot{\mathrm{e}}}_5\right)\right]\mathrm{d}\mathsf{\tau }\end{array}\right],$$

(45)

where ${\mathsf{\delta }}_{\ast \mathrm{i}}\left(\ast =\mathsf{\varphi },\mathsf{\theta },\mathsf{\psi };\mathrm{i}=\mathrm{1,2}\right)$ are positive constants to be designed.

With the sliding function ${\mathrm{s}}_{\mathrm{k}}$ designed to be differentiable and the system being designed to exhibit Hurwitz stability for ${\mathrm{s}}_{\mathrm{k}}=0(\mathrm{k}=\mathrm{1,3},5)$, the aforementioned controller parameters must satisfy the following condition:

$$\left[\begin{array}{c}{\mathsf{\eta }}_{\mathsf{\varphi }1}\\ {\mathsf{\eta }}_{\mathsf{\varphi }2}\\ \begin{array}{c}{\mathsf{\eta }}_{\mathsf{\theta }1}\\ {\mathsf{\eta }}_{\mathsf{\theta }2}\\ \begin{array}{c}{\mathsf{\eta }}_{\mathsf{\psi }1}\\ {\mathsf{\eta }}_{\mathsf{\psi }2}\end{array}\end{array}\end{array}\right]=\left[\begin{array}{c}\exp \left[-{\left(\left|{\mathrm{e}}_1\right|+0.25\right)}^{1.4}-{\left(\left|{\mathrm{e}}_1\right|+0.2\right)}^{0.7}\right]+0.5\\ 2{\mathsf{\eta }}_{\mathsf{\varphi }1}{(1+{\mathsf{\eta }}_{\mathsf{\varphi }1})}^{-1}\\ \begin{array}{c}\exp \left[-{\left(\left|{\mathrm{e}}_3\right|+0.25\right)}^{1.4}-{\left(\left|{\mathrm{e}}_3\right|+0.2\right)}^{0.7}\right]+0.5\\ 2{\mathsf{\eta }}_{\mathsf{\theta }1}{(1+{\mathsf{\eta }}_{\mathsf{\theta }1})}^{-1}\\ \begin{array}{c}\exp \left[-{\left(\left|{\mathrm{e}}_5\right|+0.25\right)}^{1.4}-{\left(\left|{\mathrm{e}}_5\right|+0.2\right)}^{0.7}\right]+0.5\\ {2{\mathsf{\eta }}_{\mathsf{\psi }1}(1+{\mathsf{\eta }}_{\mathsf{\psi }1})}^{-1}\end{array}\end{array}\end{array}\right],$$

(46)

The time derivative of Equation (45) is

$$\left[\begin{array}{c}{\dot{\mathrm{s}}}_1\\ {\dot{\mathrm{s}}}_3\\ {\dot{\mathrm{s}}}_5\end{array}\right]=\left[\begin{array}{c}{\ddot{\mathrm{e}}}_1+{\mathsf{\delta }}_{\mathsf{\varphi }1}{\left|{\mathrm{e}}_1\right|}^{{\mathsf{\eta }}_{\mathsf{\varphi }1}}\mathrm{s}\mathrm{a}\mathrm{t}\left({\mathrm{e}}_1\right)+{\mathsf{\delta }}_{\mathsf{\varphi }2}{\left|{\dot{\mathrm{e}}}_1\right|}^{{\mathsf{\eta }}_{\mathsf{\varphi }2}}\mathrm{s}\mathrm{a}\mathrm{t}\left({\dot{\mathrm{e}}}_1\right)\\ {\ddot{\mathrm{e}}}_3+{\mathsf{\delta }}_{\mathsf{\theta }1}{\left|{\mathrm{e}}_3\right|}^{{\mathsf{\eta }}_{\mathsf{\theta }1}}\mathrm{s}\mathrm{a}\mathrm{t}\left({\mathrm{e}}_3\right)+{\mathsf{\delta }}_{\mathsf{\theta }2}{\left|{\dot{\mathrm{e}}}_3\right|}^{{\mathsf{\eta }}_{\mathsf{\theta }2}}\mathrm{s}\mathrm{a}\mathrm{t}\left({\dot{\mathrm{e}}}_3\right)\\ {\ddot{\mathrm{e}}}_5+{\mathsf{\delta }}_{\mathsf{\psi }1}{\left|{\mathrm{e}}_5\right|}^{{\mathsf{\eta }}_{\mathsf{\psi }1}}\mathrm{s}\mathrm{a}\mathrm{t}\left({\mathrm{e}}_5\right)+{\mathsf{\delta }}_{\mathsf{\psi }2}{\left|{\dot{\mathrm{e}}}_5\right|}^{{\mathsf{\eta }}_{\mathsf{\psi }2}}\mathrm{s}\mathrm{a}\mathrm{t}\left({\dot{\mathrm{e}}}_5\right)\end{array}\right],$$

(47)

To ensure system stability, the following Lyapunov function is defined as follows:

$$\left[\begin{array}{c}{\mathrm{l}}_{\mathsf{\varphi }2}\\ {\mathrm{l}}_{\mathsf{\theta }2}\\ {\mathrm{l}}_{\mathsf{\psi }2}\end{array}\right]=\frac{1}{2}\left[\begin{array}{c}{\mathrm{e}}_1^2+{\mathrm{s}}_1^2\\ {\mathrm{e}}_3^2+{\mathrm{s}}_3^2\\ {\mathrm{e}}_5^2+{\mathrm{s}}_5^2\end{array}\right],$$

(48)

The time derivative of Equation (48) is

$$\left[\begin{array}{c}{\dot{\mathrm{l}}}_{\mathsf{\varphi }2}\\ {\dot{\mathrm{l}}}_{\mathsf{\theta }2}\\ {\dot{\mathrm{l}}}_{\mathsf{\psi }2}\end{array}\right]=\left[\begin{array}{c}{\mathrm{e}}_1{\dot{\mathrm{e}}}_1+{\mathrm{s}}_1{\dot{\mathrm{s}}}_1\\ {\mathrm{e}}_3{\dot{\mathrm{e}}}_3+{\mathrm{s}}_3{\dot{\mathrm{s}}}_3\\ {\mathrm{e}}_5{\dot{\mathrm{e}}}_5+{\mathrm{s}}_5{\dot{\mathrm{s}}}_5\end{array}\right],$$

(49)

Substituting (44) into (49) yields

$$\left[\begin{array}{c}{\dot{\mathrm{l}}}_{\mathsf{\varphi }2}\\ {\dot{\mathrm{l}}}_{\mathsf{\theta }2}\\ {\dot{\mathrm{l}}}_{\mathsf{\psi }2}\end{array}\right]=\left[\begin{array}{c}-{\mathsf{\xi }}_1{\mathrm{e}}_1^2+{\mathrm{s}}_1\left({\dot{\mathrm{s}}}_1+{\mathrm{e}}_1\right)\\ -{\mathsf{\xi }}_3{\mathrm{e}}_3^2+{\mathrm{s}}_3\left({\dot{\mathrm{s}}}_3+{\mathrm{e}}_3\right)\\ -{\mathsf{\xi }}_5{\mathrm{e}}_5^2+{\mathrm{s}}_5\left({\dot{\mathrm{s}}}_5+{\mathrm{e}}_5\right)\end{array}\right],$$

(50)

Designed to ensure system stability, the second term on the right-hand side of Equation (50) is expected to be equal to zero.

$$\left[\begin{array}{c}{\dot{\mathrm{s}}}_1+{\mathrm{e}}_1\\ {\dot{\mathrm{s}}}_3+{\mathrm{e}}_3\\ {\dot{\mathrm{s}}}_5+{\mathrm{e}}_5\end{array}\right]=0,$$

(51)

Neglecting the uncertainty term (i.e., ${\mathrm{D}}_{\mathrm{A}}=0$) and substituting (47) into (51), the equivalent control input is calculated as follows:

$$\begin{gathered} \left[\begin{array}{c}{\mathrm{U}}_{\mathsf{\varphi }0}\\ {\mathrm{U}}_{\mathsf{\theta }0}\\ {\mathrm{U}}_{\mathsf{\psi }0}\end{array}\right]= \\ \left[\begin{array}{c}{\mathrm{b}}_1^{-1}({\ddot{\mathrm{x}}}_{1\mathrm{d}}-{\mathrm{a}}_1{\mathrm{x}}_4{\mathrm{x}}_6-{\mathrm{a}}_2{\mathrm{x}}_2^2-d_{\varphi }-{\mathsf{\delta }}_{\mathsf{\varphi }1}{\left|{\mathrm{e}}_1\right|}^{{\mathsf{\eta }}_{\mathsf{\varphi }1}}\mathrm{s}\mathrm{a}\mathrm{t}\left({\mathrm{e}}_1\right)-{\mathsf{\delta }}_{\mathsf{\varphi }2}{\left|{\dot{\mathrm{e}}}_1\right|}^{{\mathsf{\eta }}_{\mathsf{\varphi }2}}\mathrm{s}\mathrm{a}\mathrm{t}\left({\dot{\mathrm{e}}}_1\right)-{\mathrm{e}}_1)\\ {\mathrm{b}}_2^{-1}({\ddot{\mathrm{x}}}_{3\mathrm{d}}-{\mathrm{a}}_2{\mathrm{x}}_2{\mathrm{x}}_6-{\mathrm{a}}_4{\mathrm{x}}_4^2-d_{\theta }-{\mathsf{\delta }}_{\mathsf{\theta }1}{\left|{\mathrm{e}}_3\right|}^{{\mathsf{\eta }}_{\mathsf{\theta }1}}\mathrm{s}\mathrm{a}\mathrm{t}\left({\mathrm{e}}_3\right)-{\mathsf{\delta }}_{\mathsf{\theta }2}{\left|{\dot{\mathrm{e}}}_3\right|}^{{\mathsf{\eta }}_{\mathsf{\theta }2}}\mathrm{s}\mathrm{a}\mathrm{t}\left({\dot{\mathrm{e}}}_3\right)-{\mathrm{e}}_3)\\ {\mathrm{b}}_3^{-1}({\ddot{\mathrm{x}}}_{5\mathrm{d}}-{\mathrm{a}}_3{\mathrm{x}}_2{\mathrm{x}}_4-{\mathrm{a}}_6{\mathrm{x}}_6^2-d_{\psi }-{\mathsf{\delta }}_{\mathsf{\psi }1}{\left|{\mathrm{e}}_5\right|}^{{\mathsf{\eta }}_{\mathsf{\psi }1}}\mathrm{s}\mathrm{a}\mathrm{t}\left({\mathrm{e}}_5\right)-{\mathsf{\delta }}_{\mathsf{\psi }2}{\left|{\dot{\mathrm{e}}}_5\right|}^{{\mathsf{\eta }}_{\mathsf{\psi }2}}\mathrm{s}\mathrm{a}\mathrm{t}\left({\dot{\mathrm{e}}}_5\right)-{\mathrm{e}}_5)\end{array}\right], \end{gathered}$$

(52)

Then, the reaching law is selected as follows:

$$\begin{gathered} \left[\begin{array}{c}{\mathrm{U}}_{\mathsf{\varphi }1}\\ {\mathrm{U}}_{\mathsf{\theta }1}\\ {\mathrm{U}}_{\mathsf{\psi }1}\end{array}\right]= \\ -\left[\begin{array}{c}{\mathrm{b}}_1^{-1}({\mathsf{\rho }}_{\mathsf{\varphi }1}{\mathrm{s}}_1+{\mathsf{\rho }}_{\mathsf{\varphi }2}{\left|{\mathrm{s}}_1\right|}^{{\mathsf{\sigma }}_{\mathsf{\varphi }}}\mathrm{s}\mathrm{a}\mathrm{t}\left({\mathrm{s}}_1\right)+\left({\widehat{\mathrm{Q}}}_{\mathsf{\varphi }1}+{\widehat{\mathrm{Q}}}_{\mathsf{\varphi }2}\left|{\mathrm{x}}_1\right|+{\widehat{\mathrm{Q}}}_{\mathsf{\varphi }3}\left|{\mathrm{x}}_2\right|\right)\mathrm{s}\mathrm{a}\mathrm{t}\left({\mathrm{s}}_1\right))\\ {\mathrm{b}}_2^{-1}({\mathsf{\rho }}_{\mathsf{\theta }1}{\mathrm{s}}_3+{\mathsf{\rho }}_{\mathsf{\theta }2}{\left|{\mathrm{s}}_3\right|}^{{\mathsf{\sigma }}_{\mathsf{\theta }}}\mathrm{s}\mathrm{a}\mathrm{t}\left({\mathrm{s}}_3\right)+\left({\widehat{\mathrm{Q}}}_{\mathsf{\theta }1}+{\widehat{\mathrm{Q}}}_{\mathsf{\theta }2}\left|{\mathrm{x}}_3\right|+{\widehat{\mathrm{Q}}}_{\mathsf{\theta }3}\left|{\mathrm{x}}_4\right|\right)\mathrm{s}\mathrm{a}\mathrm{t}\left({\mathrm{s}}_3\right))\\ {\mathrm{b}}_3^{-1}({\mathsf{\rho }}_{\mathsf{\psi }1}{\mathrm{s}}_5+{\mathsf{\rho }}_{\mathsf{\psi }2}{\left|{\mathrm{s}}_5\right|}^{{\mathsf{\sigma }}_{\mathsf{\psi }}}\mathrm{s}\mathrm{a}\mathrm{t}\left({\mathrm{s}}_5\right)+\left({\widehat{\mathrm{Q}}}_{\mathsf{\psi }1}+{\widehat{\mathrm{Q}}}_{\mathsf{\psi }2}\left|{\mathrm{x}}_5\right|+{\widehat{\mathrm{Q}}}_{\mathsf{\psi }3}\left|{\mathrm{x}}_6\right|\right)\mathrm{s}\mathrm{a}\mathrm{t}\left({\mathrm{s}}_5\right))\end{array}\right], \end{gathered}$$

(53)

where ${\mathsf{\rho }}_{\ast \mathrm{i}}$ and ${\mathsf{\sigma }}_{\ast }$ are controller parameters that need to be designed and are greater than zero. ${\widehat{\mathrm{Q}}}_{\ast \mathrm{j}}$ is the estimation of the parameters related to uncertainties, which is updated by the following adaptive estimation algorithm $(\ast \in \left\{\mathsf{\varphi },\mathsf{\theta },\mathsf{\psi }\right\},\mathrm{i}\in \left\{\mathrm{1,2}\right\},\mathrm{j}\in \{\mathrm{1,2},3\left\}\right)$:

• Adaptive estimation algorithm:

$$\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}{\dot{\widehat{\mathrm{Q}}}}_{\mathsf{\varphi }1}\\ {\dot{\widehat{\mathrm{Q}}}}_{\mathsf{\varphi }2}\end{array}\\ {\dot{\widehat{\mathrm{Q}}}}_{\mathsf{\varphi }3}\\ {\dot{\widehat{\mathrm{Q}}}}_{\mathsf{\theta }1}\end{array}\\ {\dot{\widehat{\mathrm{Q}}}}_{\mathsf{\theta }2}\\ \begin{array}{c}{\dot{\widehat{\mathrm{Q}}}}_{\mathsf{\theta }3}\\ {\dot{\widehat{\mathrm{Q}}}}_{\mathsf{\psi }1}\\ \begin{array}{c}{\dot{\widehat{\mathrm{Q}}}}_{\mathsf{\psi }2}\\ {\dot{\widehat{\mathrm{Q}}}}_{\mathsf{\psi }3}\end{array}\end{array}\end{array}\right]=\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}{\mathsf{\Delta }}_{\mathsf{\varphi }1}\left|{\mathrm{s}}_1\right|\\ {\mathsf{\Delta }}_{\mathsf{\varphi }2}\left|{\mathrm{s}}_1\right|\left|{\mathrm{x}}_1\right|\end{array}\\ {\mathsf{\Delta }}_{\mathsf{\varphi }3}\left|{\mathrm{s}}_1\right|\left|{\mathrm{x}}_2\right|\\ {\mathsf{\Delta }}_{\mathsf{\theta }1}\left|{\mathrm{s}}_3\right|\end{array}\\ {\mathsf{\Delta }}_{\mathsf{\theta }2}\left|{\mathrm{s}}_3\right|\left|{\mathrm{x}}_3\right|\\ \begin{array}{c}{\mathsf{\Delta }}_{\mathsf{\theta }3}\left|{\mathrm{s}}_3\right|\left|{\mathrm{x}}_4\right|\\ {\mathsf{\Delta }}_{\mathsf{\psi }1}\left|{\mathrm{s}}_5\right|\\ \begin{array}{c}{\mathsf{\Delta }}_{\mathsf{\psi }2}\left|{\mathrm{s}}_5\right|\left|{\mathrm{x}}_5\right|\\ {\mathsf{\Delta }}_{\mathsf{\psi }3}\left|{\mathrm{s}}_5\right|\left|{\mathrm{x}}_6\right|\end{array}\end{array}\end{array}\right],$$

(54)

where ${\mathsf{\Delta }}_{\ast \mathrm{i}}$ denotes positive constants that need to be confirmed. During the Lyapunov proof process, adaptive algorithm representations are derived. ${\mathrm{Q}}_{\ast 1}$ is connected with uncertain time-invariant disturbances, such as a shift in the center of gravity. ${\mathrm{Q}}_{\ast 2}$ pertains to torques resulting from the coupling of attitudes and mechanical stiffness. Lastly, ${\mathrm{Q}}_{\ast 3}$ is linked to unmodeled gyroscopic torque generated by the quadrotor’s four motors $(\ast \in \left\{\mathsf{\varphi },\mathsf{\theta },\mathsf{\psi }\right\},\mathrm{i}\in \{\mathrm{1,2},3\left\}\right)$.

• Dead zone technique:

In practical applications, the sliding variables ${\mathrm{s}}_1$, ${\mathrm{s}}_3$, and ${\mathrm{s}}_5$ often encounter chattering due to measurement noise, leading to an overestimation of $\mathrm{Q}$. To alleviate this issue, the dead-zone technique is used to adjust the adaptive law.

$$\left\{\begin{array}{c}{\dot{\widehat{\mathrm{Q}}}}_{\mathsf{\varphi }1}=\left\{\begin{array}{r}{\mathsf{\Delta }}_{\mathsf{\varphi }1}\left|{\mathrm{s}}_1\right|,\hspace{1em}\left|{\mathrm{s}}_1\right|\le \mathsf{\delta }\\ 0,\hspace{1em}\left|{\mathrm{s}}_1\right|>\mathsf{\delta }\end{array}\right.\\ {\dot{\widehat{\mathrm{Q}}}}_{\mathsf{\varphi }2}=\left\{\begin{array}{r}{\mathsf{\Delta }}_{\mathsf{\varphi }2}\left|{\mathrm{s}}_1\right|\left|{\mathrm{x}}_1\right|,\hspace{1em}\left|{\mathrm{s}}_1\right|\le \mathsf{\delta }\\ 0,\hspace{1em}\left|{\mathrm{s}}_1\right|>\mathsf{\delta }\end{array}\right.\\ \begin{array}{c}{\dot{\widehat{\mathrm{Q}}}}_{\mathsf{\varphi }3}=\left\{\begin{array}{r}{\mathsf{\Delta }}_{\mathsf{\varphi }3}\left|{\mathrm{s}}_1\right|\left|{\mathrm{x}}_2\right|,\hspace{1em}\left|{\mathrm{s}}_1\right|\le \mathsf{\delta }\\ 0,\hspace{1em}\left|{\mathrm{s}}_1\right|>\mathsf{\delta }\end{array}\right.\\ {\dot{\widehat{\mathrm{Q}}}}_{\mathsf{\theta }1}=\left\{\begin{array}{r}{\mathsf{\Delta }}_{\mathsf{\theta }1}\left|{\mathrm{s}}_3\right|,\hspace{1em}\left|{\mathrm{s}}_3\right|\le \mathsf{\delta }\\ 0,\hspace{1em}\left|{\mathrm{s}}_3\right|>\mathsf{\delta }\end{array}\right.\\ \begin{array}{c}{\dot{\widehat{\mathrm{Q}}}}_{\mathsf{\theta }2}=\left\{\begin{array}{r}{\mathsf{\Delta }}_{\mathsf{\theta }2}\left|{\mathrm{s}}_3\right|\left|{\mathrm{x}}_3\right|,\hspace{1em}\left|{\mathrm{s}}_3\right|\le \mathsf{\delta }\\ \mathrm{x},\hspace{1em}\left|{\mathrm{s}}_3\right|>\mathsf{\delta }\end{array}\right.\\ {\dot{\widehat{\mathrm{Q}}}}_{\mathsf{\theta }3}=\left\{\begin{array}{r}{\mathsf{\Delta }}_{\mathsf{\theta }3}\left|{\mathrm{s}}_3\right|\left|{\mathrm{x}}_4\right|,\hspace{1em}\left|{\mathrm{s}}_3\right|\le \mathsf{\delta }\\ 0,\hspace{1em}\left|{\mathrm{s}}_3\right|>\mathsf{\delta }\end{array}\right.\\ \begin{array}{c}{\dot{\widehat{\mathrm{Q}}}}_{\mathsf{\psi }1}=\left\{\begin{array}{r}{\mathsf{\Delta }}_{\mathsf{\psi }1}\left|{\mathrm{s}}_5\right|,\hspace{1em}\left|{\mathrm{s}}_5\right|\le \mathsf{\delta }\\ 0,\hspace{1em}\left|{\mathrm{s}}_5\right|>\mathsf{\delta }\end{array}\right.\\ {\dot{\widehat{\mathrm{Q}}}}_{\mathsf{\psi }2}=\left\{\begin{array}{r}{\mathsf{\Delta }}_{\mathsf{\psi }2}\left|{\mathrm{s}}_5\right|\left|{\mathrm{x}}_5\right|,\hspace{1em}\left|{\mathrm{s}}_5\right|\le \mathsf{\delta }\\ 0,\hspace{1em}\left|{\mathrm{s}}_5\right|>\mathsf{\delta }\end{array}\right.\\ {\dot{\widehat{\mathrm{Q}}}}_{\mathsf{\psi }3}=\left\{\begin{array}{r}{\mathsf{\Delta }}_{\mathsf{\psi }3}\left|{\mathrm{s}}_5\right|\left|{\mathrm{x}}_6\right|,\hspace{1em}\left|{\mathrm{s}}_5\right|\le \mathsf{\delta }\\ 0,\hspace{1em}\left|{\mathrm{s}}_5\right|>\mathsf{\delta }\end{array}\right.\end{array}\end{array}\end{array}\end{array}\right.,$$

(55)

Here, $\mathsf{\delta }>0$ represents the threshold for the deviation caused by influencing factors (such as sensor noise, uncertainty in estimation, and inertia delay of the motor). In this article, $\mathsf{\delta }$ is set to 0.3.

Adding the equivalent input and the convergence control input together yields the total control input:

$$\left[\begin{array}{c}{\mathrm{U}}_{\mathsf{\varphi }}\\ {\mathrm{U}}_{\mathsf{\theta }}\\ {\mathrm{U}}_{\mathsf{\psi }}\end{array}\right]=\left[\begin{array}{c}{\mathrm{U}}_{\mathsf{\varphi }0}+{\mathrm{U}}_{\mathsf{\varphi }1}\\ {\mathrm{U}}_{\mathsf{\theta }0}+{\mathrm{U}}_{\mathsf{\theta }1}\\ {\mathrm{U}}_{\mathsf{\psi }0}+{\mathrm{U}}_{\mathsf{\psi }1}\end{array}\right],$$

(56)

• Proof of the stability of attitude-tracking control:

The Lyapunov function is defined as follows:

$$\left[\begin{array}{c}{\mathrm{l}}_{\mathsf{\varphi }}\\ {\mathrm{l}}_{\mathsf{\theta }}\\ {\mathrm{l}}_{\mathsf{\psi }}\end{array}\right]=\frac{1}{2}\left[\begin{array}{c}{\mathrm{e}}_1^2+{\mathrm{s}}_1^2+\sum _{\mathrm{l}=1}^3\frac{1}{{∆}_{\mathsf{\varphi }\mathrm{l}}}{\tilde{\mathrm{Q}}}_{\mathsf{\varphi }\mathrm{l}}^2\\ {\mathrm{e}}_3^2+{\mathrm{s}}_3^2+\sum _{\mathrm{m}=1}^3\frac{1}{{∆}_{\mathsf{\theta }\mathrm{m}}}{\tilde{\mathrm{Q}}}_{\mathsf{\theta }\mathrm{m}}^2\\ {\mathrm{e}}_5^2+{\mathrm{s}}_5^2+\sum _{\mathrm{n}=1}^3\frac{1}{{∆}_{\mathsf{\psi }\mathrm{n}}}{\tilde{\mathrm{Q}}}_{\mathsf{\psi }\mathrm{n}}^2\end{array}\right],$$

(57)

$\tilde{\mathrm{Q}}$ represents the estimation error. The time derivative of Equation (57) is given as follows:

$$\left[\begin{array}{c}{\dot{\mathrm{l}}}_{\mathsf{\varphi }}\\ {\dot{\mathrm{l}}}_{\mathsf{\theta }}\\ {\dot{\mathrm{l}}}_{\mathsf{\psi }}\end{array}\right]=\left[\begin{array}{c}{\mathrm{e}}_1{\dot{\mathrm{e}}}_1+{\mathrm{s}}_1{\dot{\mathrm{s}}}_1+\sum _{\mathrm{l}=1}^3\frac{1}{{∆}_{\mathsf{\varphi }\mathrm{l}}}{\tilde{\mathrm{Q}}}_{\mathsf{\varphi }\mathrm{l}}{\dot{\tilde{\mathrm{Q}}}}_{\mathsf{\varphi }\mathrm{l}}\\ {\mathrm{e}}_3{\dot{\mathrm{e}}}_3+{\mathrm{s}}_3{\dot{\mathrm{s}}}_3+\sum _{\mathrm{m}=1}^3\frac{1}{{∆}_{\mathsf{\theta }\mathrm{m}}}{\tilde{\mathrm{Q}}}_{\mathsf{\theta }\mathrm{m}}{\dot{\tilde{\mathrm{Q}}}}_{\mathsf{\theta }\mathrm{m}}\\ {\mathrm{e}}_5{\dot{\mathrm{e}}}_5+{\mathrm{s}}_5{\dot{\mathrm{s}}}_5+\sum _{\mathrm{n}=1}^3\frac{1}{{∆}_{\mathsf{\psi }\mathrm{n}}}{\tilde{\mathrm{Q}}}_{\mathsf{\psi }\mathrm{n}}{\dot{\tilde{\mathrm{Q}}}}_{\mathsf{\psi }\mathrm{n}}\end{array}\right],$$

(58)

Substituting (44), (47), and (56) into (58) produces

$$\left[\begin{array}{c}{\dot{\mathrm{l}}}_{\mathsf{\varphi }}\\ {\dot{\mathrm{l}}}_{\mathsf{\theta }}\\ {\dot{\mathrm{l}}}_{\mathsf{\psi }}\end{array}\right]=\left[\begin{array}{c}-{\mathsf{\xi }}_1{\mathrm{e}}_1^2-{\mathsf{\rho }}_{\mathsf{\varphi }1}{\mathrm{s}}_1^2-{\mathsf{\rho }}_{\mathsf{\varphi }2}{\left|{\mathrm{s}}_1\right|}^{{\mathsf{\sigma }}_{\mathsf{\varphi }}+1}-{\mathsf{\Phi }}_{\mathsf{\varphi }}\left|{\mathrm{s}}_1\right|\\ -{\mathsf{\xi }}_3{\mathrm{e}}_3^2-{\mathsf{\rho }}_{\mathsf{\theta }1}{\mathrm{s}}_3^2-{\mathsf{\rho }}_{\mathsf{\theta }2}{\left|{\mathrm{s}}_3\right|}^{{\mathsf{\sigma }}_{\mathsf{\theta }}+1}-{\mathsf{\Phi }}_{\mathsf{\theta }}\left|{\mathrm{s}}_3\right|\\ -{\mathsf{\xi }}_5{\mathrm{e}}_5^2-{\mathsf{\rho }}_{\mathsf{\psi }1}{\mathrm{s}}_5^2-{\mathsf{\rho }}_{\mathsf{\psi }2}{\left|{\mathrm{s}}_5\right|}^{{\mathsf{\sigma }}_{\mathsf{\psi }}+1}-{\mathsf{\Phi }}_{\mathsf{\psi }}\left|{\mathrm{s}}_5\right|\end{array}\right]\le 0,$$

(59)

where

$$\left[\begin{array}{c}{\mathsf{\Phi }}_{\mathsf{\varphi }}\\ {\mathsf{\Phi }}_{\mathsf{\theta }}\\ {\mathsf{\Phi }}_{\mathsf{\psi }}\end{array}\right]=\left[\begin{array}{c}{\mathrm{Q}}_{\mathsf{\varphi }1}+{\mathrm{Q}}_{\mathsf{\varphi }2}\left|{\mathrm{x}}_1\right|+{\mathrm{Q}}_{\mathsf{\varphi }3}\left|{\mathrm{x}}_2\right|\\ {\mathrm{Q}}_{\mathsf{\theta }1}+{\mathrm{Q}}_{\mathsf{\theta }2}\left|{\mathrm{x}}_3\right|+{\mathrm{Q}}_{\mathsf{\theta }3}\left|{\mathrm{x}}_4\right|\\ {\mathrm{Q}}_{\mathsf{\psi }1}+{\mathrm{Q}}_{\mathsf{\psi }2}\left|{\mathrm{x}}_5\right|+{\mathrm{Q}}_{\mathsf{\psi }3}\left|{\mathrm{x}}_6\right|\end{array}\right],$$

(60)

Based on the provided information and equations, the stability of the system has been proven.

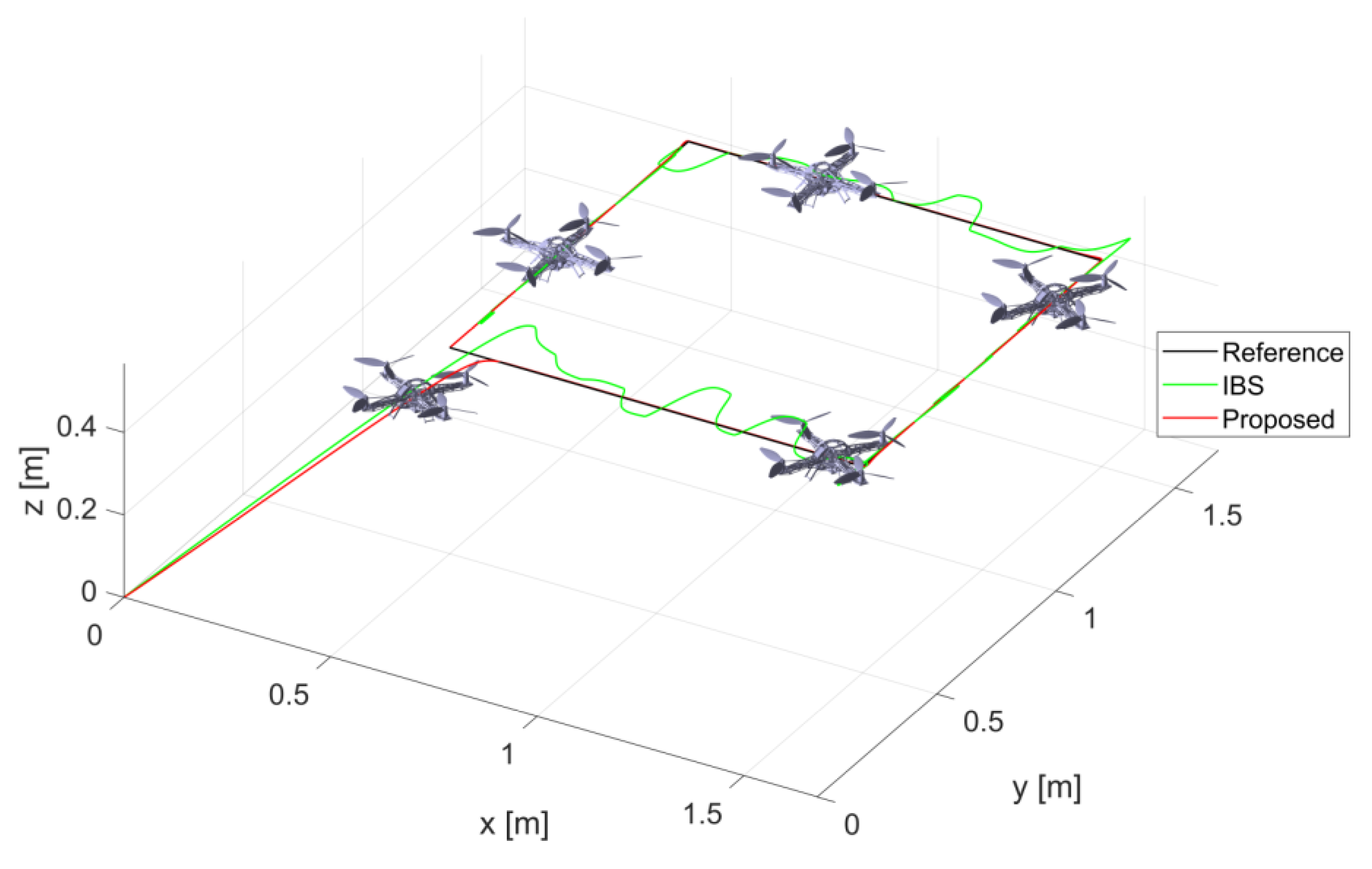
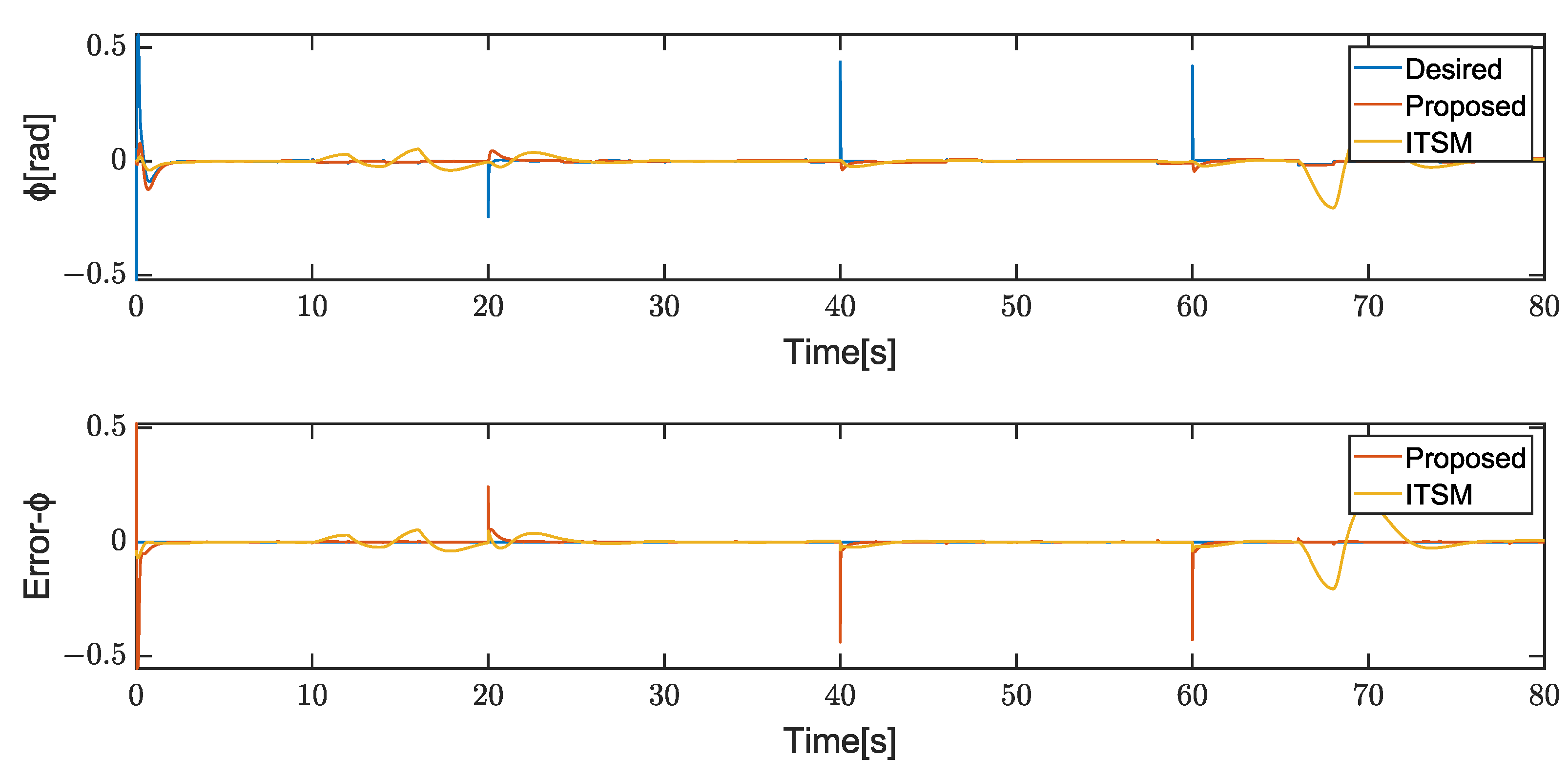
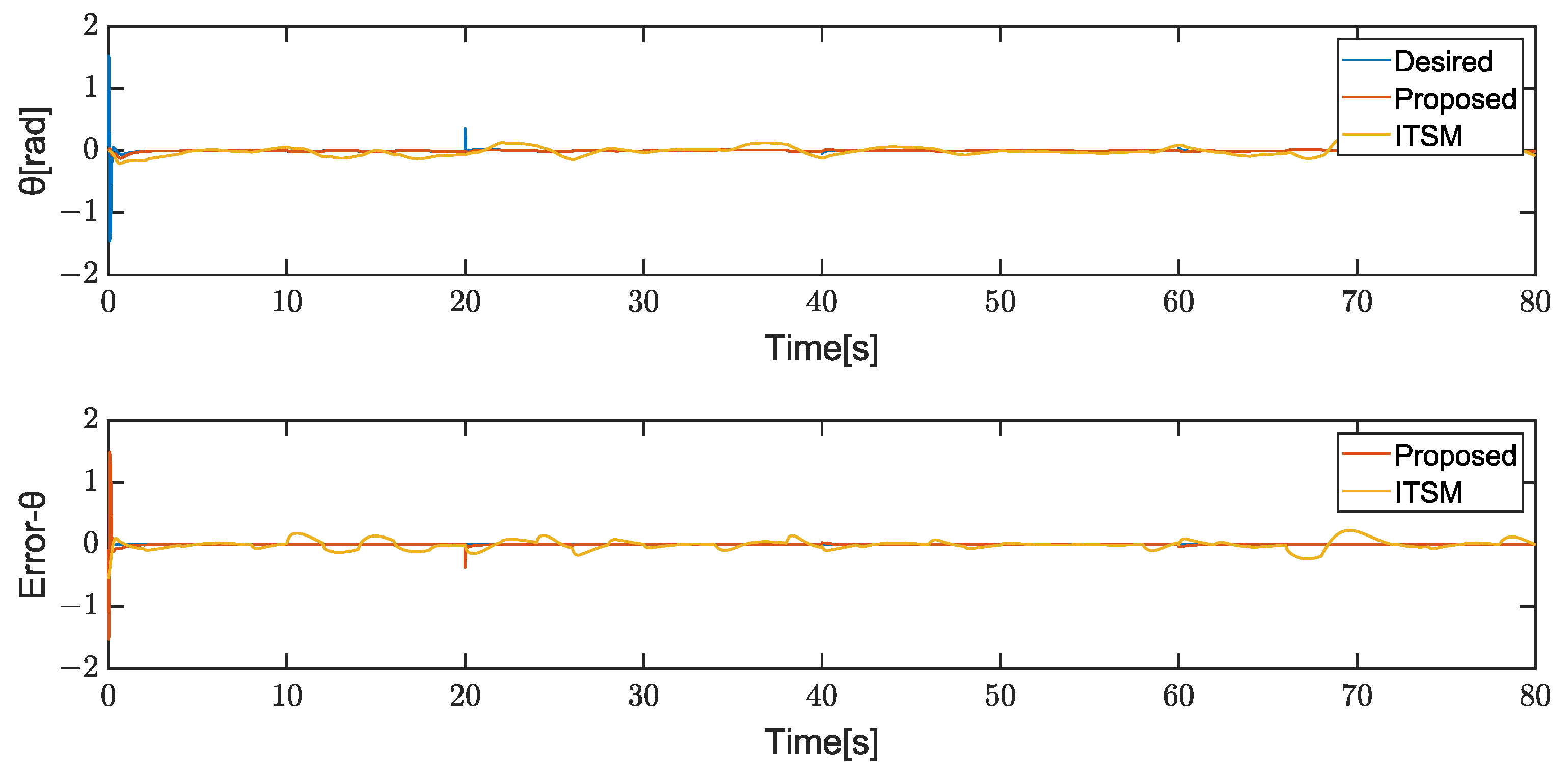
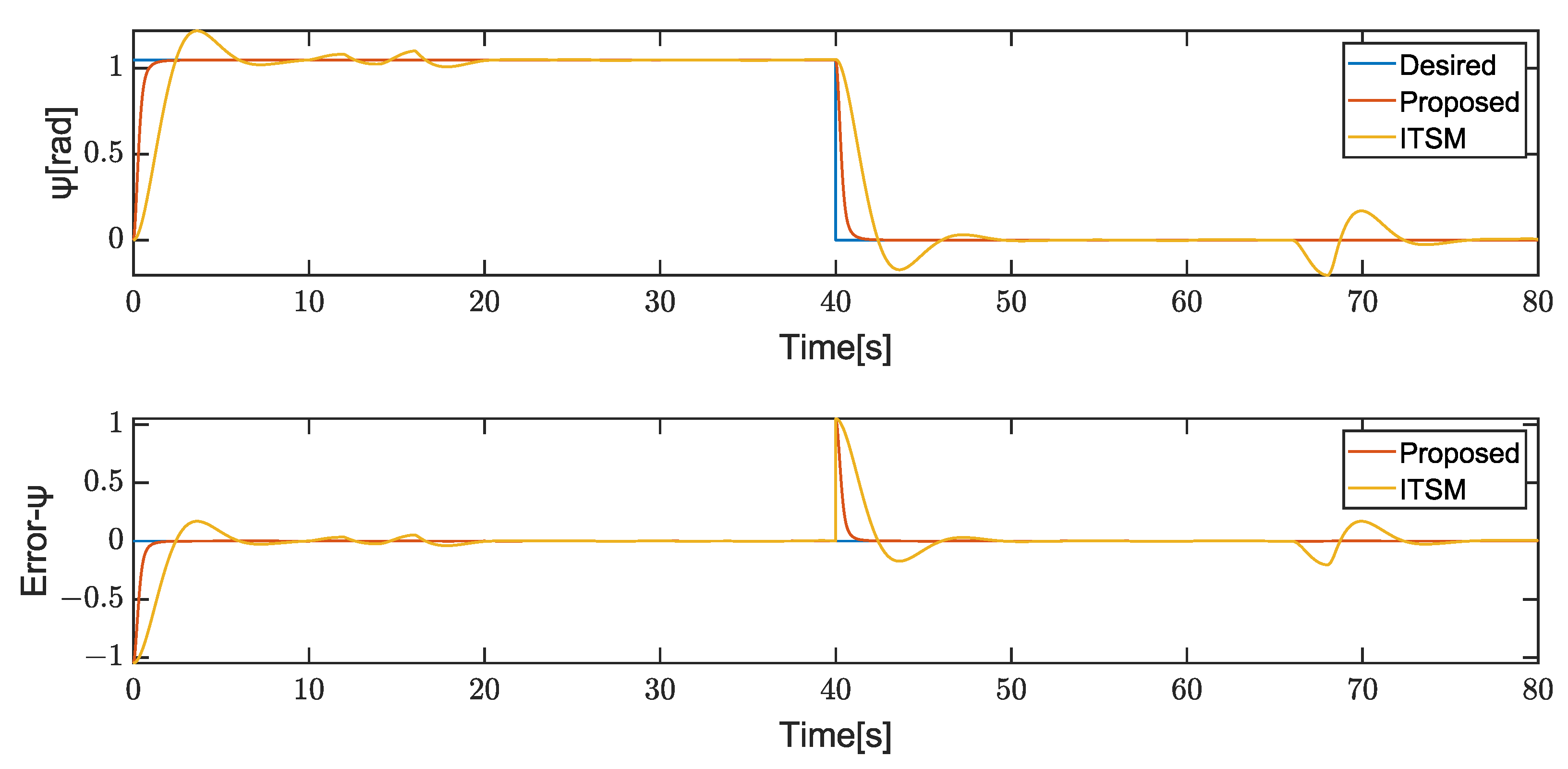
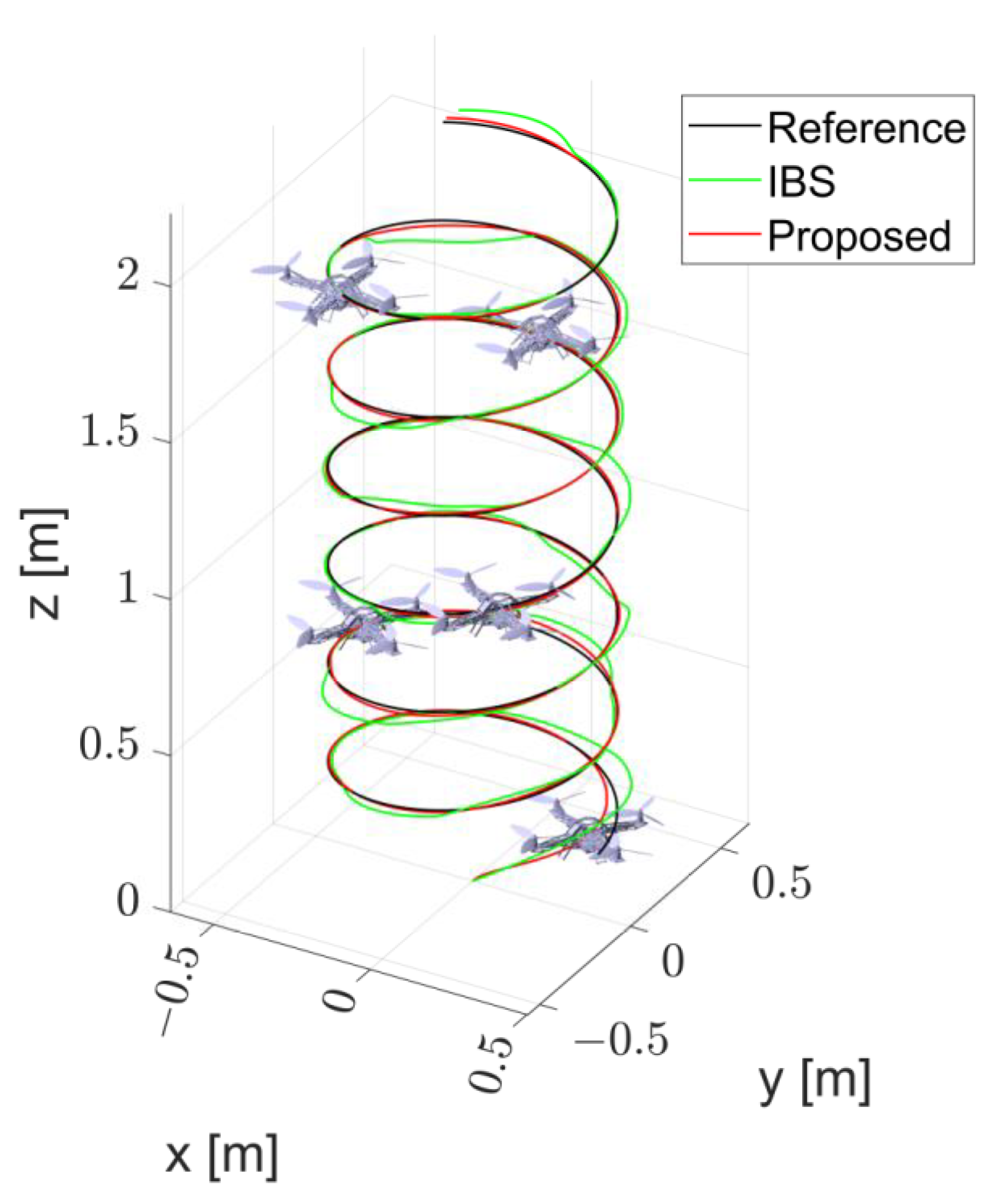
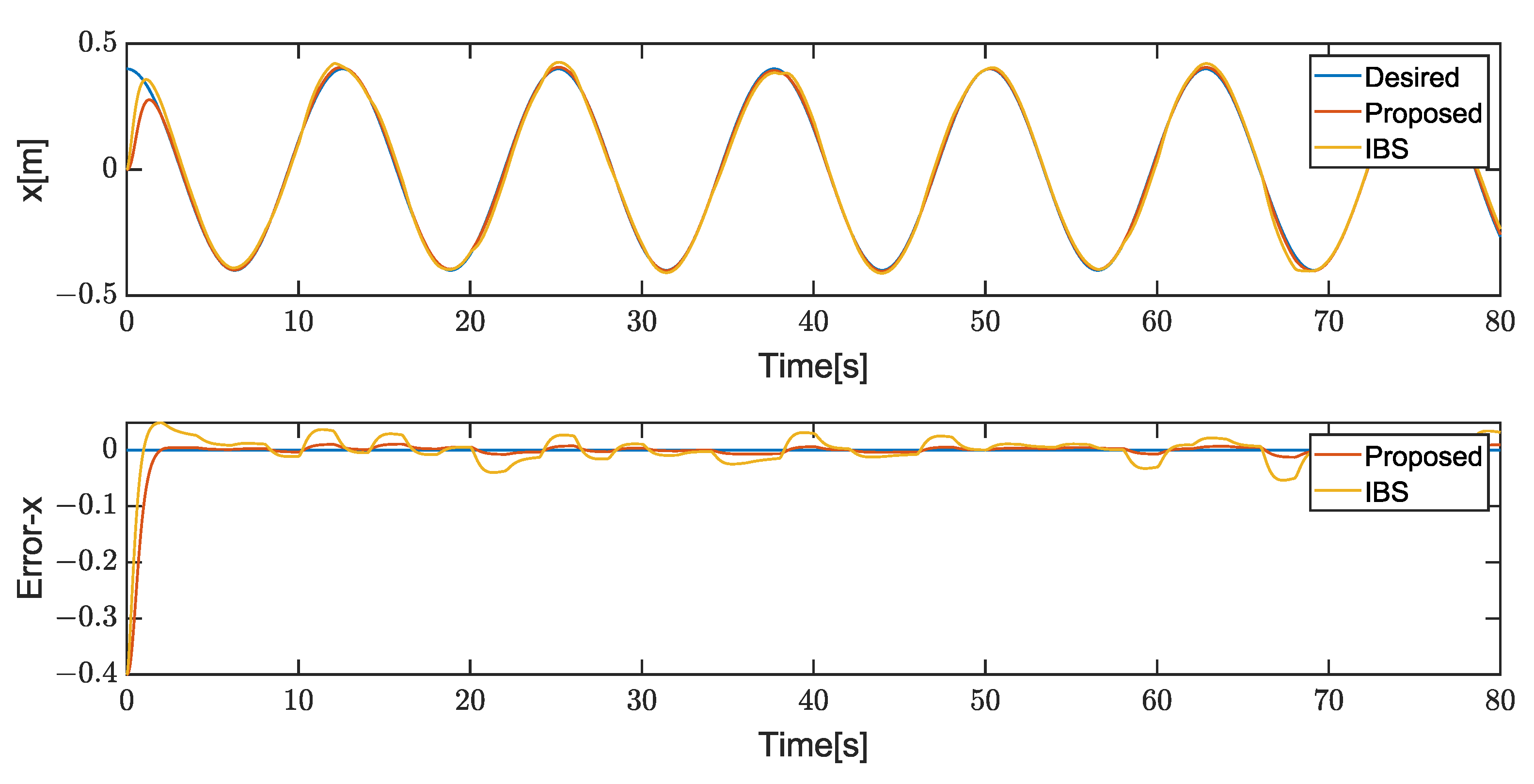
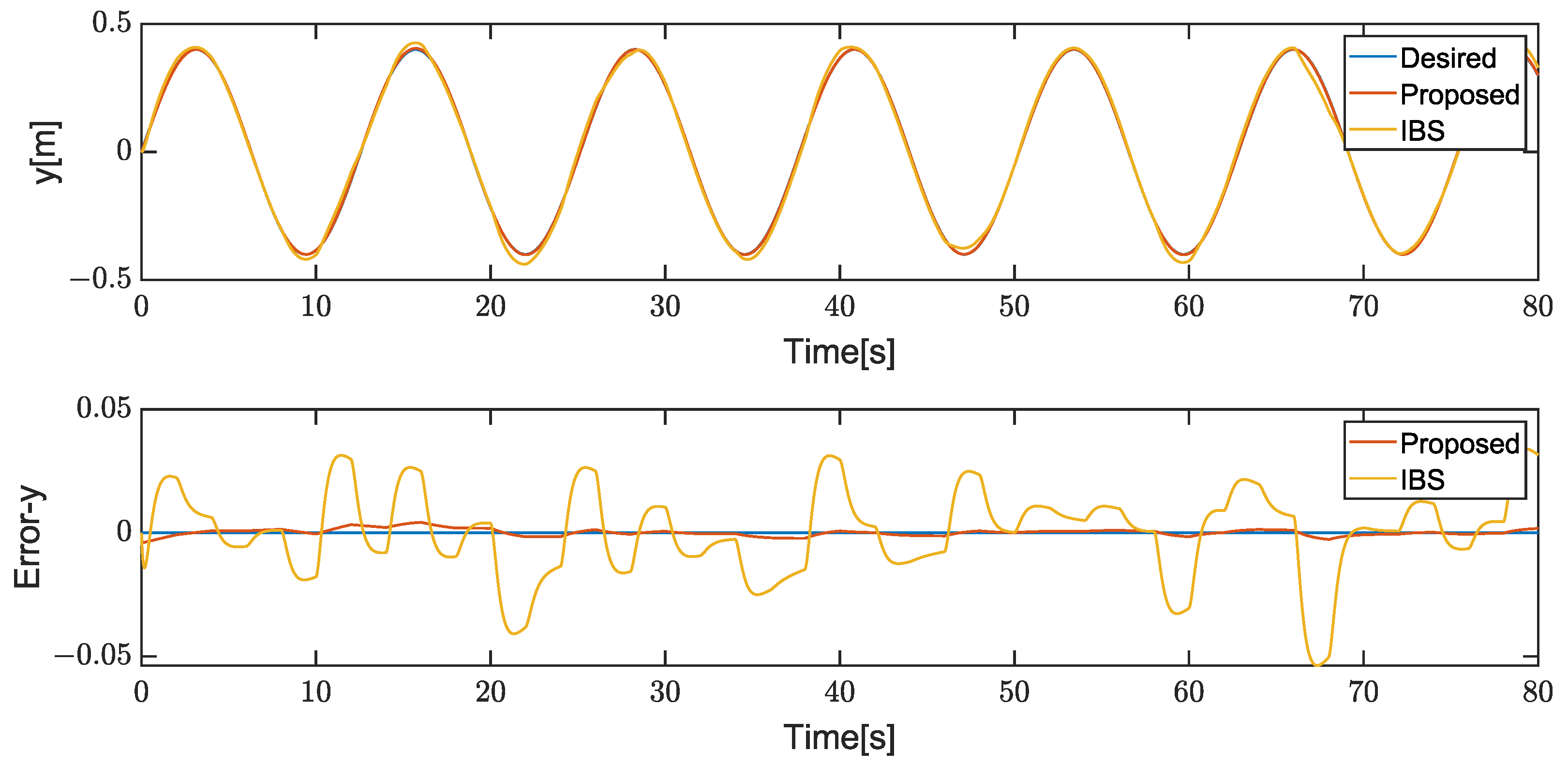
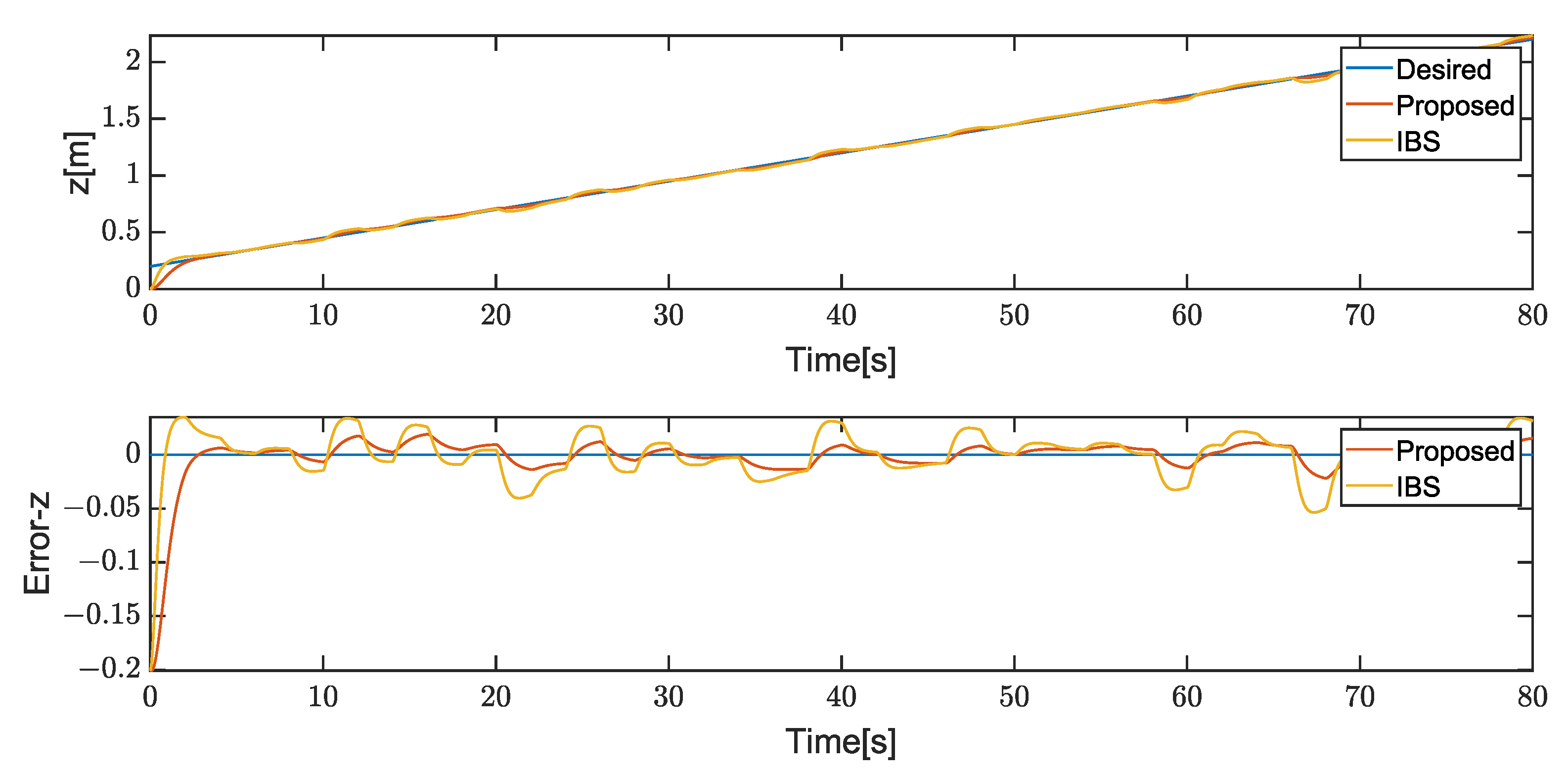
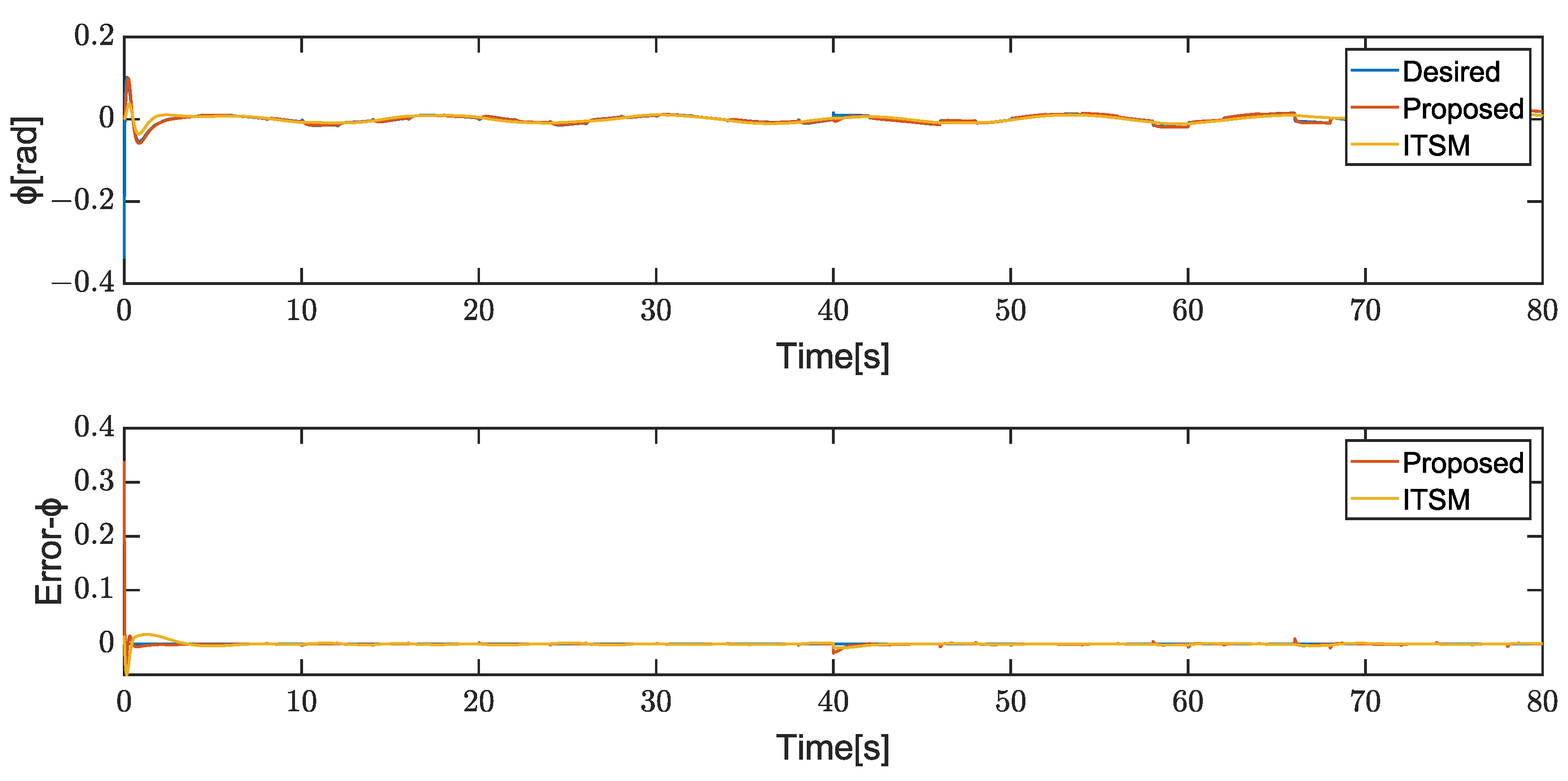
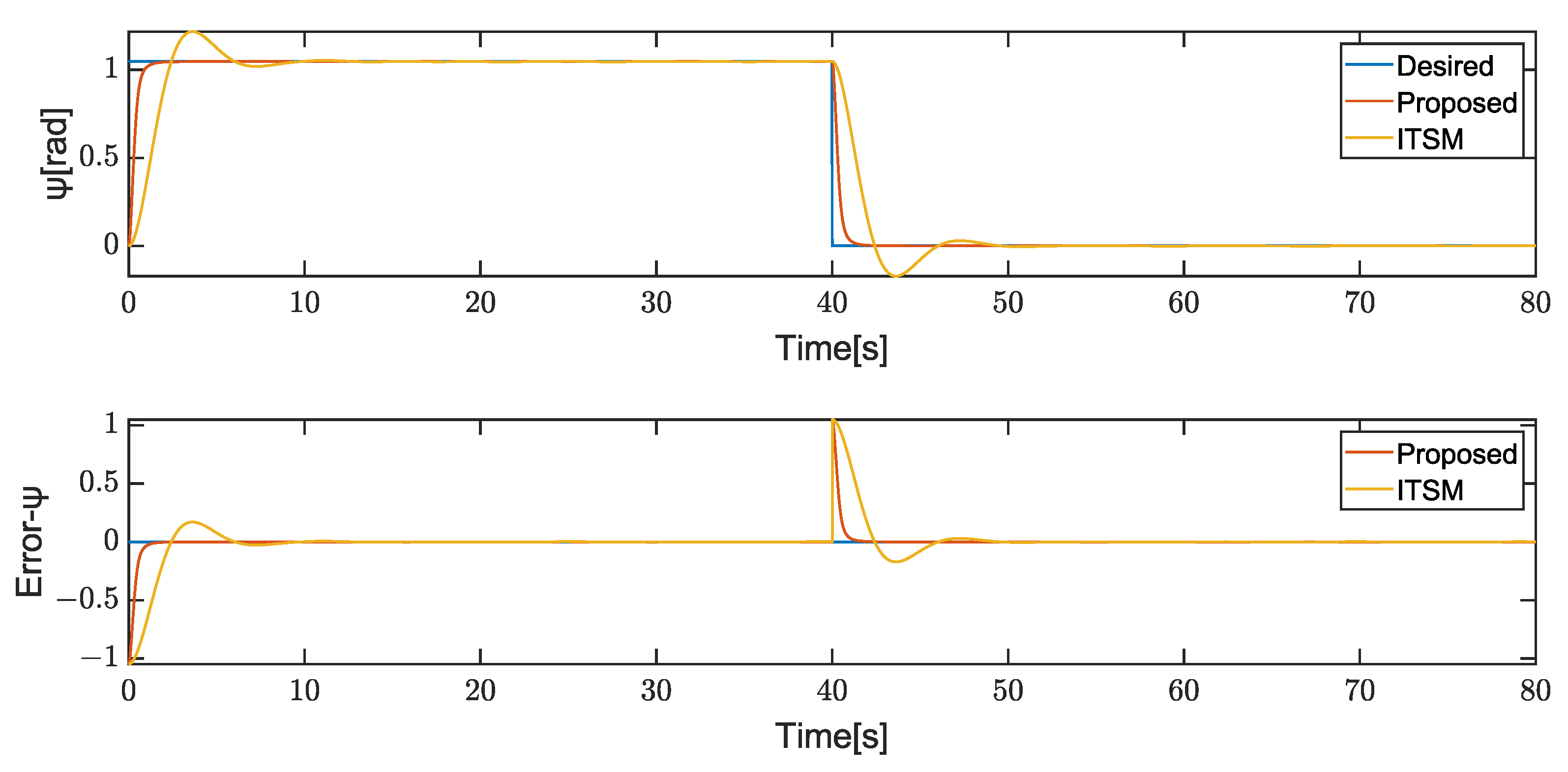
4. Results

This section presents the simulation results to validate the performance of the proposed control scheme. During the simulation tests, the initial position and attitude were set to ${\left[\mathrm{0,0},0\right]}^T$ m and ${\left[\mathrm{0,0},0\right]}^{\mathrm{T}}$ rad, respectively. The static parameters and control system parameters are listed in

Table 1. Static parameters of the quadrotor.

Parameter	Value	Meaning
m	0.56 kg	the mass of the quadrotor
g	9.8 $\mathrm{m}/{\mathrm{s}}^2$	gravitational acceleration
d	0.3 m	distance between the center of gravity and the rotation axis of one motor
${\mathrm{I}}_{\mathrm{x}\mathrm{x}}$	$3.5\times {10}^{-3}\mathrm{k}\mathrm{g}·{\mathrm{m}}^2$	moment of inertia about x-axis
${\mathrm{I}}_{\mathrm{y}\mathrm{y}}$	$3.5\times {10}^{-3}\mathrm{k}\mathrm{g}·{\mathrm{m}}^2$	moment of inertia about x-axis
${\mathrm{I}}_{\mathrm{z}\mathrm{z}}$	$7.0\times {10}^{-3}\mathrm{k}\mathrm{g}·{\mathrm{m}}^2$	moment of inertia about x-axis
${\mathrm{k}}_{\mathrm{L}}$	$4.2\times {10}^{-3}$	force coefficient during one motor rotation
${\mathrm{k}}_{\mathrm{M}}$	$3.8\times {10}^{-2}$	torque coefficient during one motor rotation
${\mathrm{k}}_{\mathrm{F}}$	$5.6\times {10}^{-4}$	drag coefficient due to air resistance
${\mathrm{k}}_{\mathrm{T}}$	$5.6\times {10}^{-4}$	drag torque coefficient due to air resistance

and

Table 2. Control system parameters.

Parameter	Value
${\mathrm{k}}_7,{\mathrm{k}}_9,{\mathrm{k}}_{11}$	0.01
${\mathsf{\xi }}_7,{\mathsf{\xi }}_9,{\mathsf{\xi }}_{11}$	4.25
${\mathsf{\alpha }}_8,{\mathsf{\alpha }}_{10},{\mathsf{\alpha }}_{12}$	2.5
${\mathsf{\delta }}_{\mathsf{\varphi }1},{\mathsf{\delta }}_{\mathsf{\theta }1},{\mathsf{\delta }}_{\mathsf{\psi }1}$	28.5, 50, 28.5
${\mathsf{\delta }}_{\mathsf{\varphi }2},{\mathsf{\delta }}_{\mathsf{\theta }2},{\mathsf{\delta }}_{\mathsf{\psi }2}$	6, 6, 12
${\mathsf{\rho }}_{\mathsf{\varphi }1},{\mathsf{\rho }}_{\mathsf{\theta }1},{\mathsf{\rho }}_{\mathsf{\psi }1}$	3
${\mathsf{\rho }}_{\mathsf{\varphi }2},{\mathsf{\rho }}_{\mathsf{\theta }2},{\mathsf{\rho }}_{\mathsf{\psi }2}$	2.5
${\mathsf{\sigma }}_{\mathsf{\varphi }},{\mathsf{\sigma }}_{\mathsf{\theta }},{\mathsf{\sigma }}_{\mathsf{\psi }}$	1.7

respectively.

The proposed control scheme is compared with the integral backstepping control and the integral terminal sliding mode. The simulations are performed with external disturbances caused by wind gusts or other factors.

The external disturbances are assumed to follow a Gaussian distribution. The “Random Number” block in Simulink was utilized to generate random numbers with a mean of 0 and a standard deviation of 10 as disturbances. The sampling time was set to 2 s. To ensure that the disturbances in the position loop stay within the range of −1.5 to 1.5 $\mathrm{m}/{\mathrm{s}}^2$ and that the disturbances in the attitude loop stay within the range of −2 to 2 $\mathrm{r}\mathrm{a}\mathrm{d}/{\mathrm{s}}^2$, the generated random numbers should be multiplied by appropriate scaling factors.

4.1. Case1

In this case, the quadrotor was required to track a simple rectangle trajectory. External disturbances are taken into account. A 3D trajectory plot provides a visual representation of the tracking performance of a control scheme (Figure 5). It allows for a comprehensive view of how well a control scheme is able to follow the desired trajectory in 3D space. The simulation results are presented in Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11. To provide a more intuitive representation of the control performance, error curves for the $\mathrm{x}$, $\mathrm{y}$, and $\mathrm{z}$ directions and Euler angles were plotted.

The desired trajectories are defined as follows:

$${\mathrm{x}}_{5\mathrm{d}}=\left\{\begin{array}{c}\frac{\mathsf{\pi }}{3},\hspace{1em}0\le \mathrm{x}<40\\ 0,\hspace{1em}40\le \mathrm{x}<80\end{array}\right.,$$

(61)

$${\mathrm{x}}_{7\mathrm{d}}=\left\{\begin{array}{c}\begin{array}{cc}0.5+0.05\mathrm{t}& 0\le \mathrm{t}<20\end{array}\\ \begin{array}{cc}1.5& 20\le \mathrm{t}<40\end{array}\\ \begin{array}{c}\begin{array}{cc}1.5-0.05\left(\mathrm{t}-40\right)& 40\le \mathrm{t}<60\end{array}\\ \begin{array}{cc}0.5& 60\le \mathrm{t}<80\end{array}\end{array}\end{array}\right.,$$

(62)

$${\mathrm{x}}_{9\mathrm{d}}=\left\{\begin{array}{c}\begin{array}{cc}0.5& 0\le \mathrm{t}<20\end{array}\\ \begin{array}{cc}0.5+0.05\left(\mathrm{t}-20\right)& 20\le \mathrm{t}<40\end{array}\\ \begin{array}{c}\begin{array}{cc}1.5& 40\le \mathrm{t}<60\end{array}\\ \begin{array}{cc}1.5-0.05\left(\mathrm{t}-60\right)& 60\le \mathrm{t}<80\end{array}\end{array}\end{array}\right.,$$

(63)

$${\mathrm{x}}_{11\mathrm{d}}=0.5,$$

(64)

As the initial position and attitude are set to 0, the quadrotor attempts to approach the desired trajectory quickly, which results in excessively large desired roll and pitch angles during the initial stages of the simulation, leading to significant tracking errors.

The results demonstrate that both controllers track the desired position and attitude in the presence of disturbances in Figure 5, Figure 9, Figure 10 and Figure 11, while the proposed controller behaves excellently. Even when there is a sudden change in the yaw angle, the proposed controller still rapidly reacts and tracks the new trajectory, as shown in Figure 11. Through comparison, it is evident that the proposed controller exhibits better performance than its counterparts.

Finally, in comparison with IBS-ITSM, the proposed controller possesses better performance. The square trajectory used in this case is relatively simple. In the next case, a more complex trajectory will be employed to further demonstrate the supremacy of the proposed controller.

4.2. Case2

In this scenario, the quadrotor is required to track a sophisticated trajectory under the influence of external disturbances. The simulation results are presented in Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18.

The desired trajectories are defined as follows:

$${\mathrm{x}}_{5\mathrm{d}}=\left\{\begin{array}{c}\frac{\mathsf{\pi }}{3},\hspace{1em}0\le \mathrm{t}<40\\ 0,\hspace{1em}40\le \mathrm{t}<80\end{array}\right.,$$

(65)

$${\mathrm{x}}_{7\mathrm{d}}=0.4\cos \left(0.5\mathrm{t}\right),$$

(66)

$${\mathrm{x}}_{9\mathrm{d}}=0.4\sin \left(0.5\mathrm{t}\right),$$

(67)

$${\mathrm{x}}_{11\mathrm{d}}=0.2+0.025\mathrm{t},$$

(68)

From Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18, it can be observed that the tracking performance of the IBS-ITSM control scheme is not ideal, exhibiting relatively large fluctuations in the presence of disturbances. In contrast, the proposed controller successfully tracked the desired trajectory and attitude faster and more accurately, demonstrating the robustness and superiority of the proposed controller.

5. Conclusions

In this article, the quadrotor dynamic model that factors in parameter uncertainty and external disturbances was derived by utilizing the Newton–Euler equation. An AIBS control was proposed in a position loop, with the desired attitude deduced from decoupling equations stemming from the desired position. Furthermore, a novel ABFNITSM control was proposed for attitude tracking, incorporating the use of integral elements, backstepping, adaptive estimation techniques, and dead-zone techniques, built upon terminal sliding mode control. To mitigate chattering, the introduction of a saturation function was employed. The stability of the control system was confirmed through the employment of Lyapunov theory. Finally, through contrastive analysis with IBS-ITSM, better performance and robust resistance against external random disturbances were exhibited by the proposed AIBS-ABFNITSM control scheme.

6. Future Work

Future research will encompass the validation of the AIBS-ABFNITSM control scheme’s performance in trajectory-tracking tasks utilizing an actual quadrotor. Given Euler angles’ inherent limitations, the exploration of the application of quaternions in the trajectory-tracking control of a quadrotor’s attitude warrants further investigation.