Design of Pseudo-Command Restricted Controller for Tailless Unmanned Aerial Vehicles Based on Attainable Moment Set
Abstract
:1. Introduction
- First, the innovative AMB algorithm is proposed, which not only reduces the complexity of calculation to ensure online computation, but also eliminates dependence on control allocation algorithms and the convex hull property of the reachable set.
- Second, based on AMB, we propose a flight performance assurance (FPA) system, which can not only adaptively compensate for deviations outside the AMB, but also alter the aggressiveness of FPA online and predictively modify the command.
- Third, to effectively avoid the loss of control caused by insufficient capability to perform the snake-shaped maneuver, an FPA-NDI controller is designed and its effectiveness and advantages are validated by comparative simulations.
2. TUAVs Model
2.1. Control Effectors
2.2. High-Fidelity Simulation Model
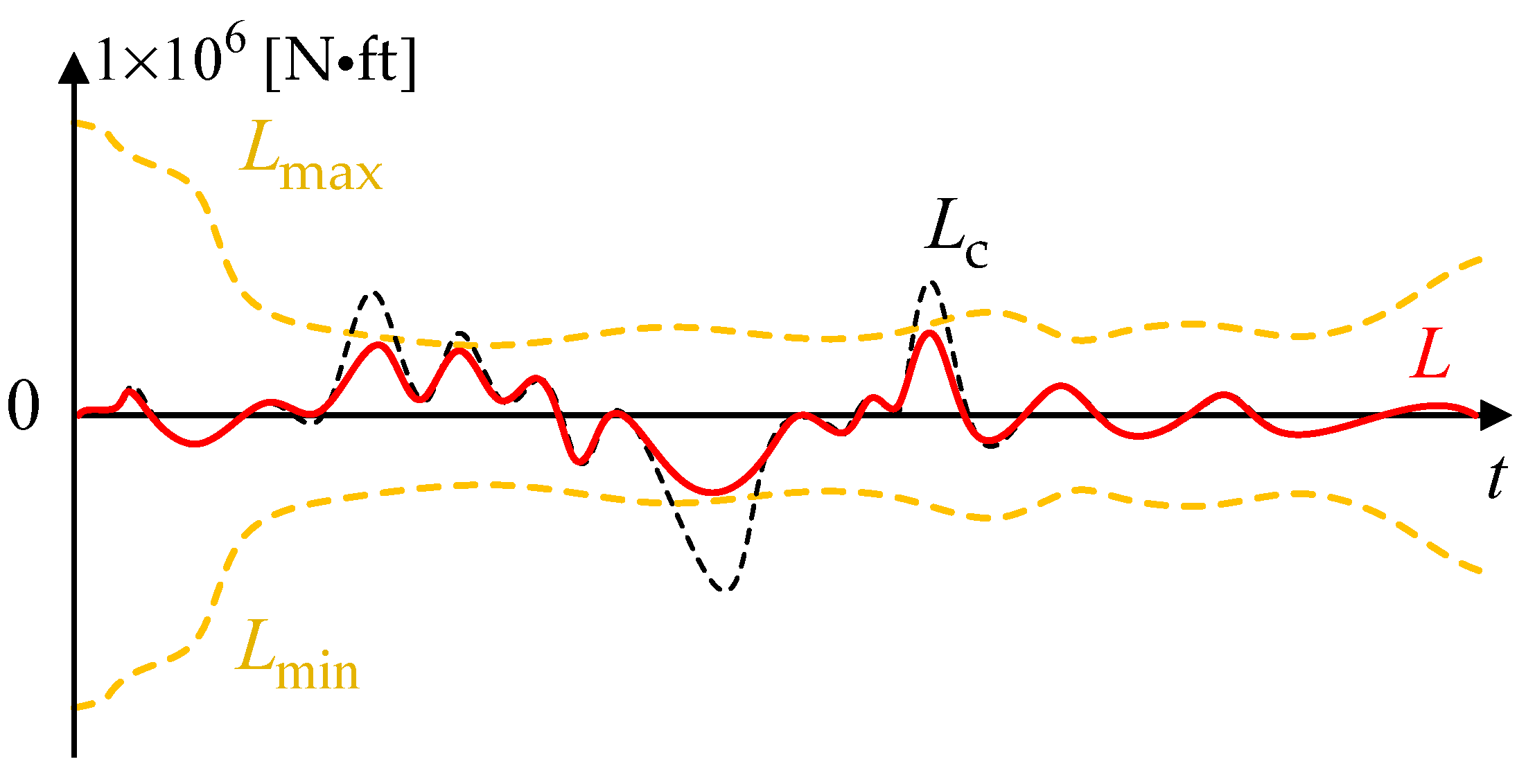
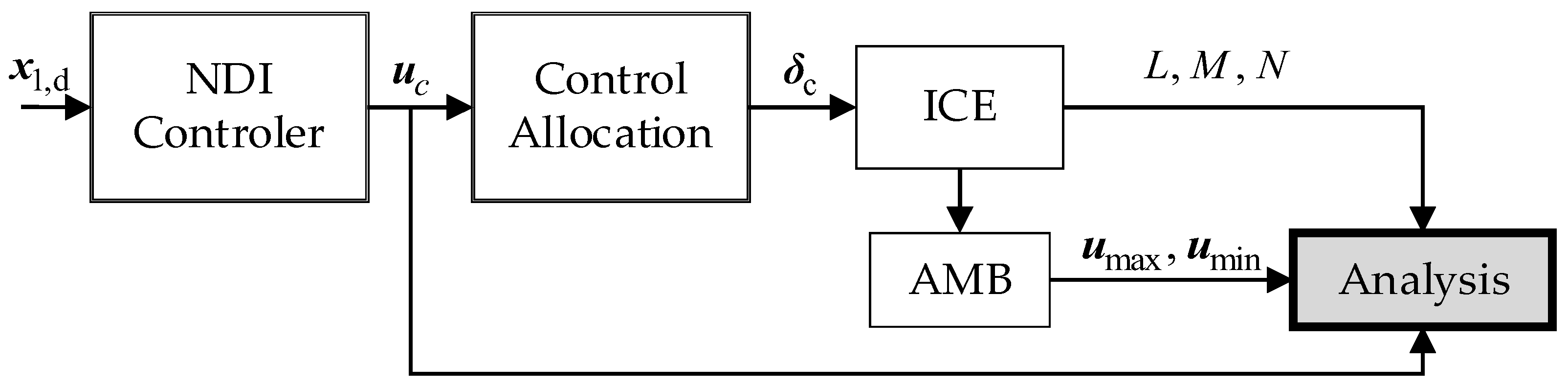
3. AMB Algorithm and FPA System
3.1. Constrained Moments Based on AMB
| Algorithm 1. AMB algorithm |
| function |
3.2. Flight Performance Assurance System Design with AMB
4. FPA-NDI Controller Design
4.1. Attitude Control
4.2. Stability Analysis
- (1)
- The state tracking error will gradually converge, which satisfies ;
- (2)
- The state variable in the compensation system (23) is bounded and the aerodynamic torque command constraint is not violated.
- (1)
- Firstly, the stability of the fast-period and slow-period models of the system under is proved, and the radially unbounded positive definite Lyapunov function is designed as follows:where is positive definite. The first order derivative of time along Equation (27) for is obtained:where and are the filtering errors generated by the command filter, and is the control allocation error. Substituting Equations (24) and (30) into the above equation yields:where and are the minimum eigenvalues of matrices and , respectively. Therefore, it is possible to use a reasonable design of control parameters to achieve global asymptotic boundedness for Equation (9) when the filtering errors at each level and the control allocation error are bounded. The state tracking error of the slow-period model and the tracking command converge when is proved. Therefore, the first part of Theorem 1 is proved.
- (2)
- Assuming that there is a constant vector , which satisfies , , the compensation system parameter is set. For the compensation system (22), the Lyapunov function is designed as follows:
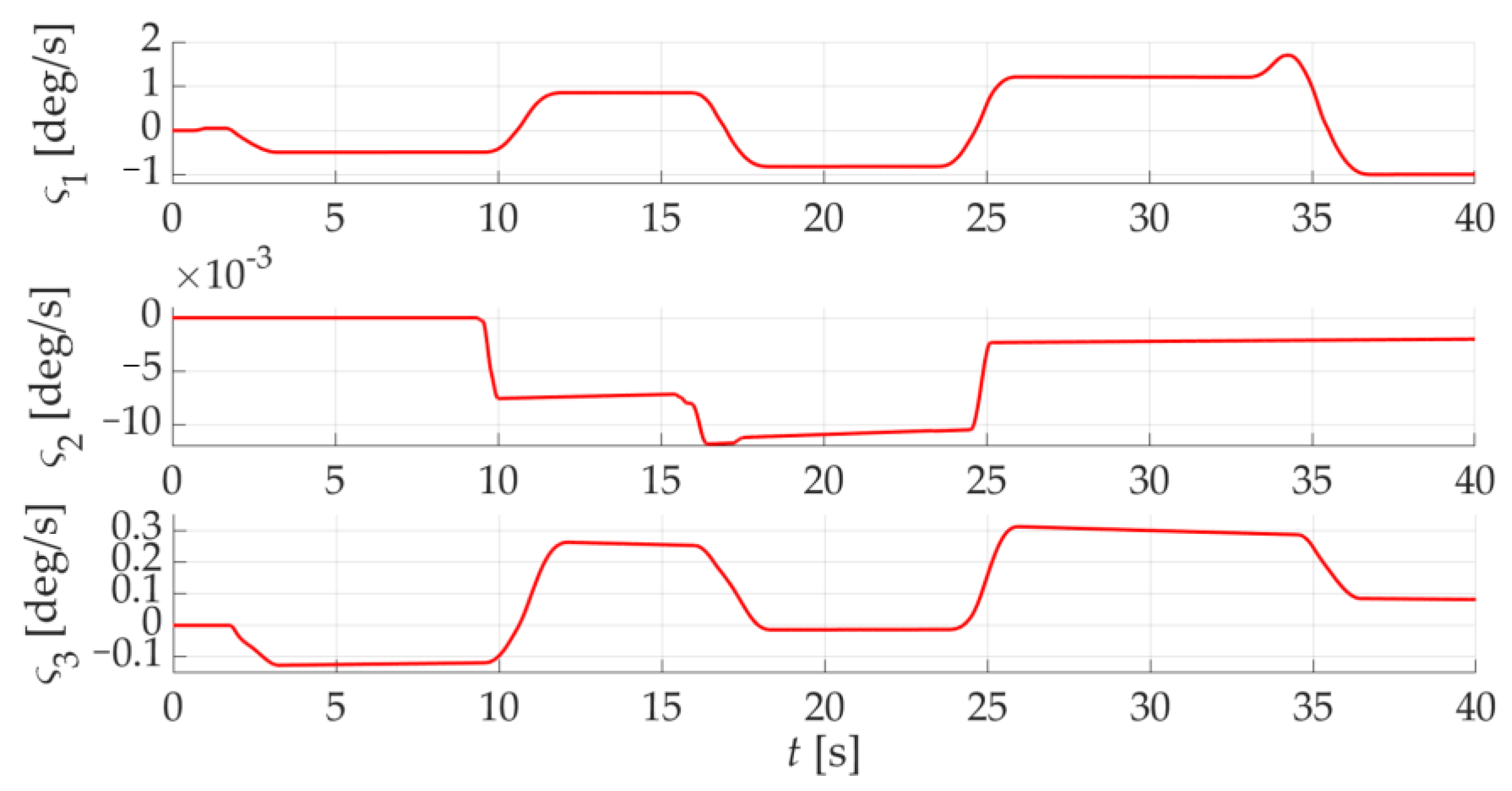
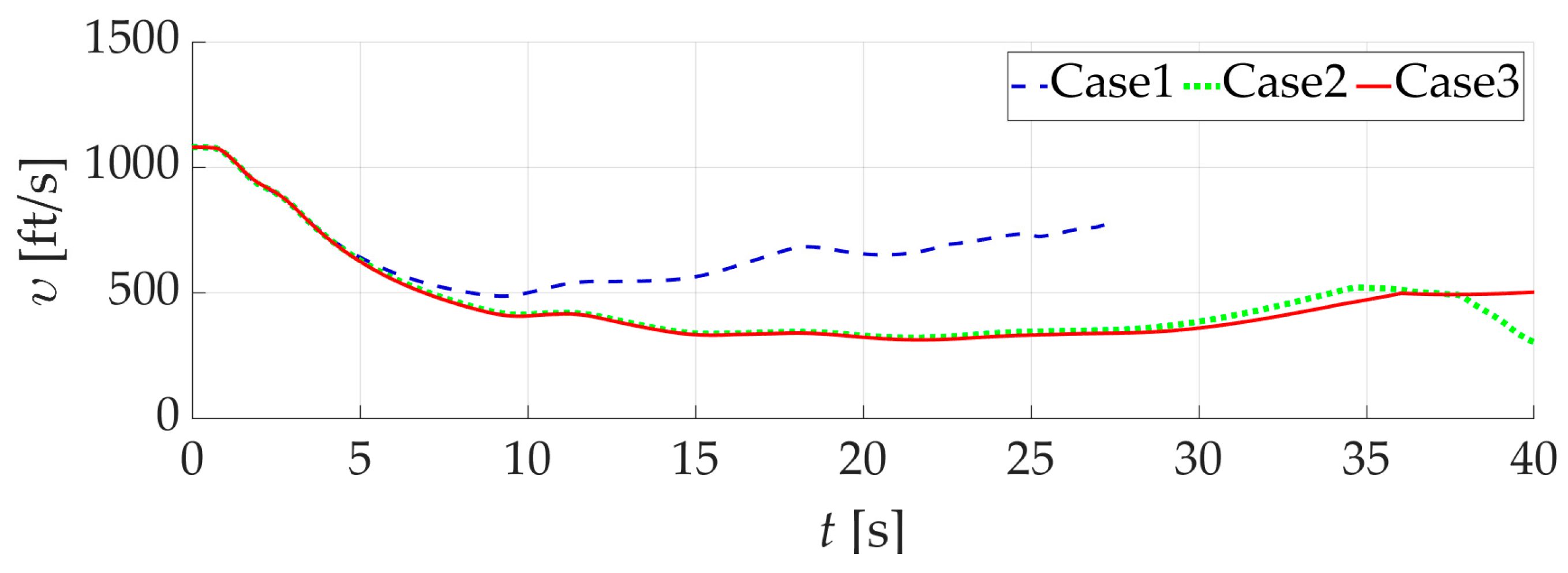
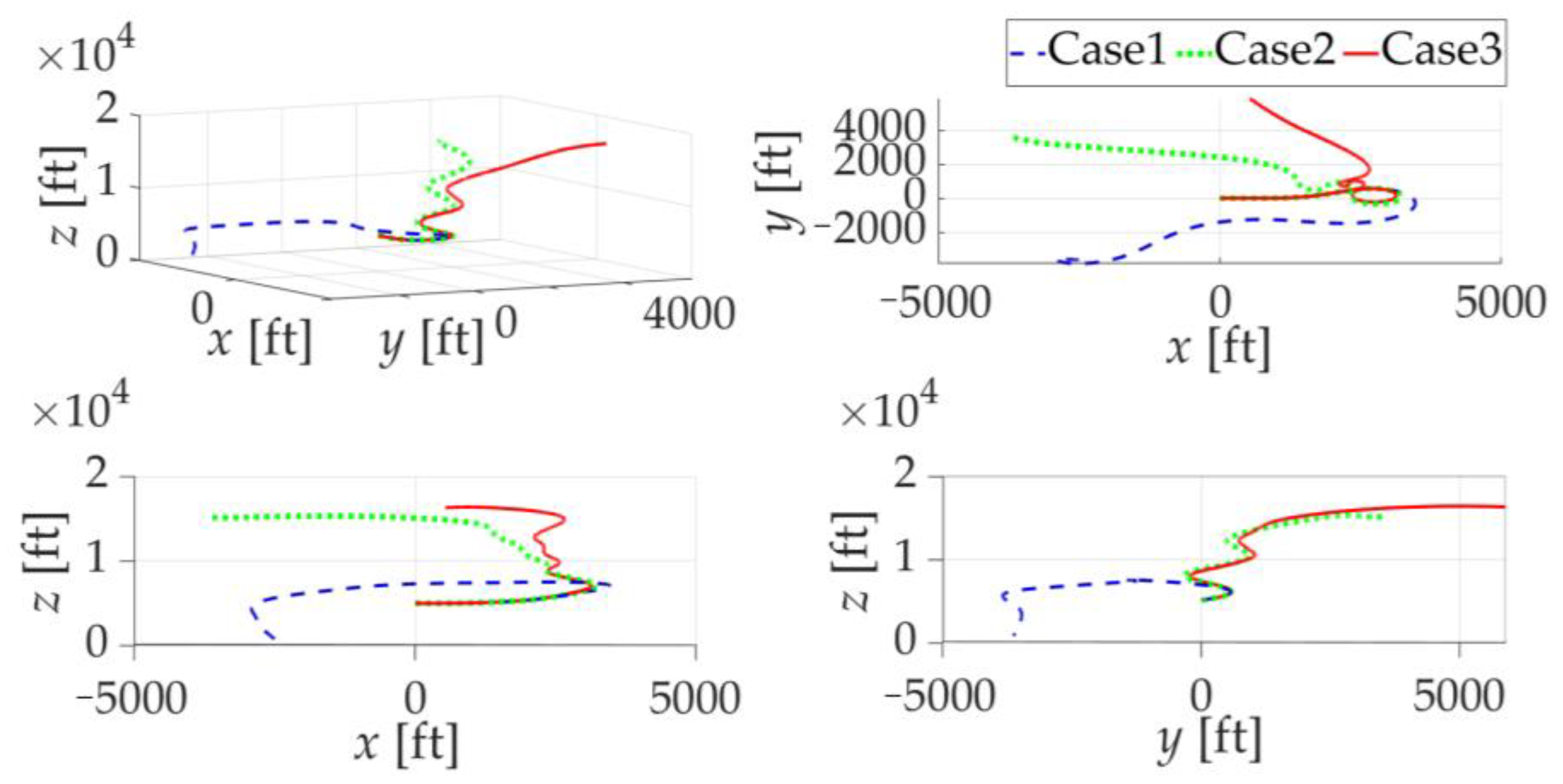
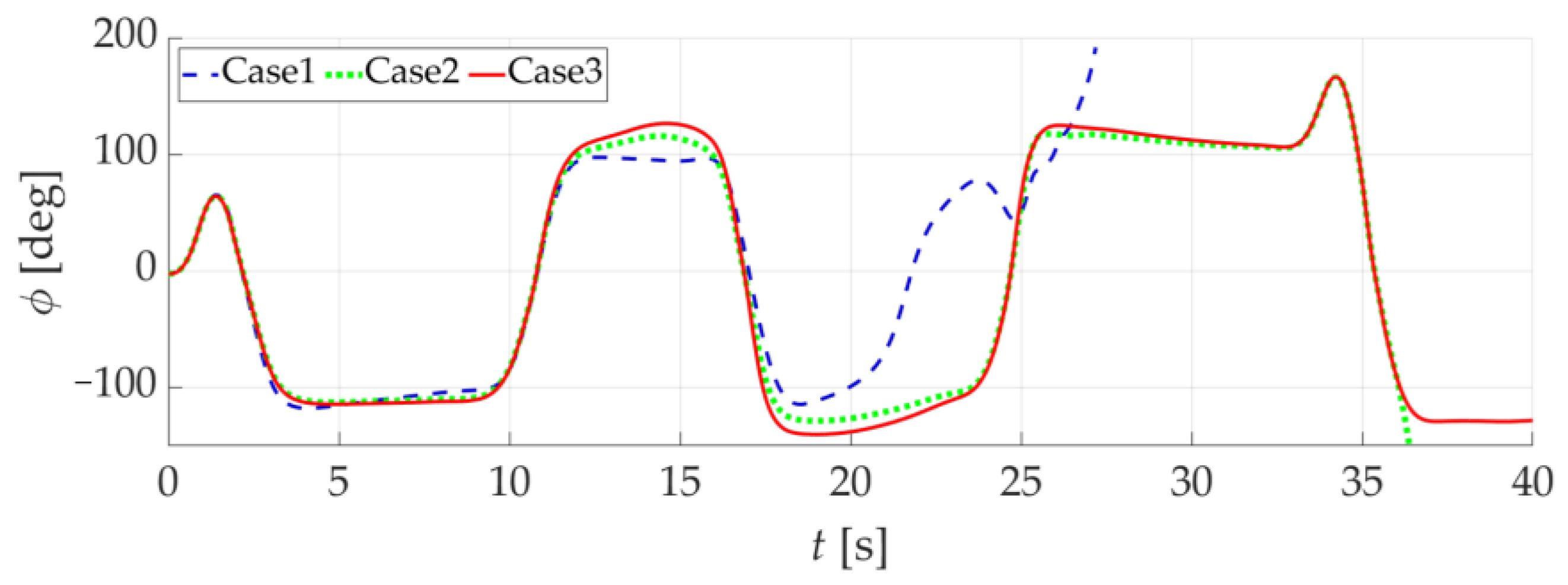
5. Experiment Evaluation and Comparison
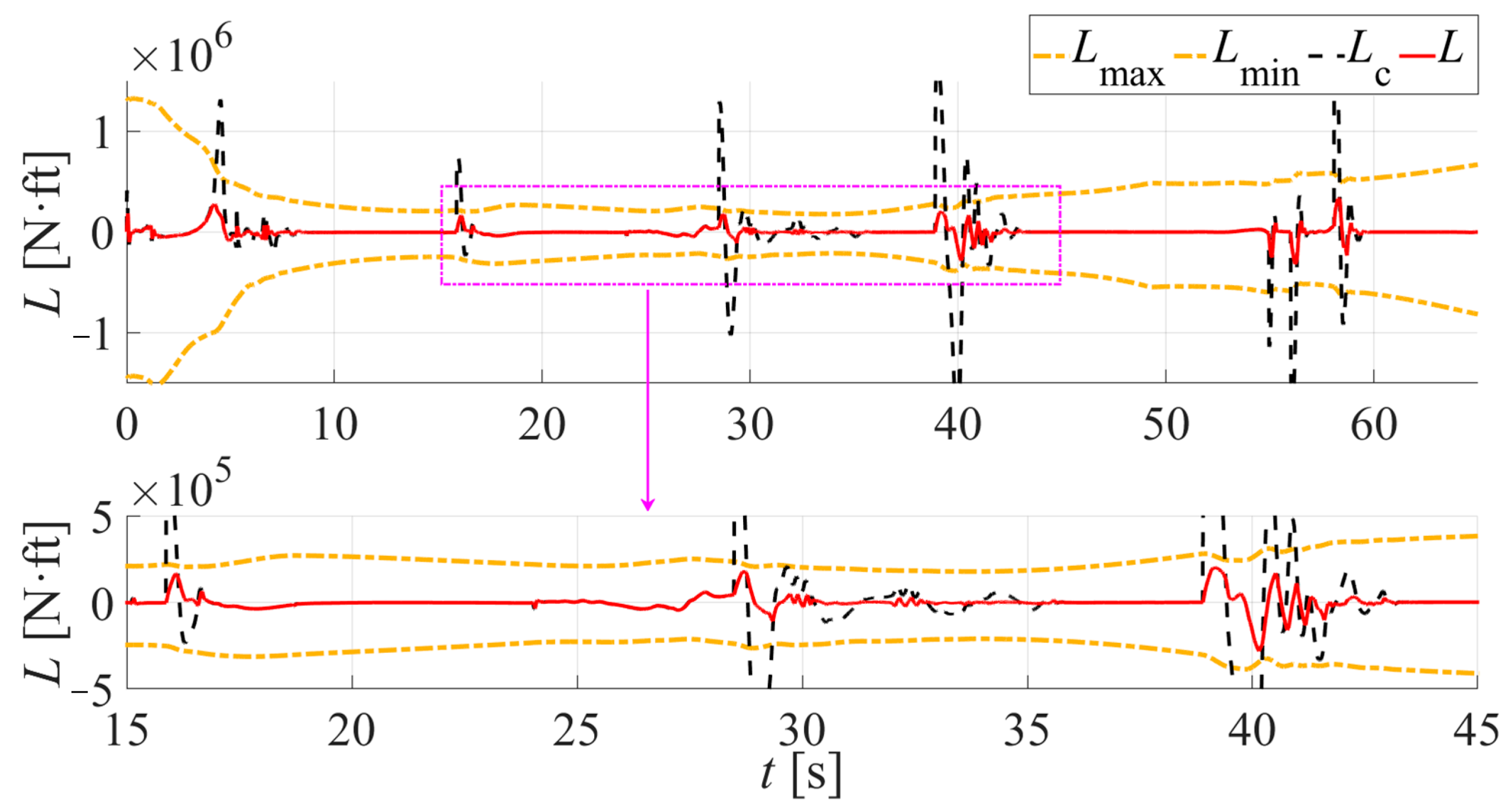
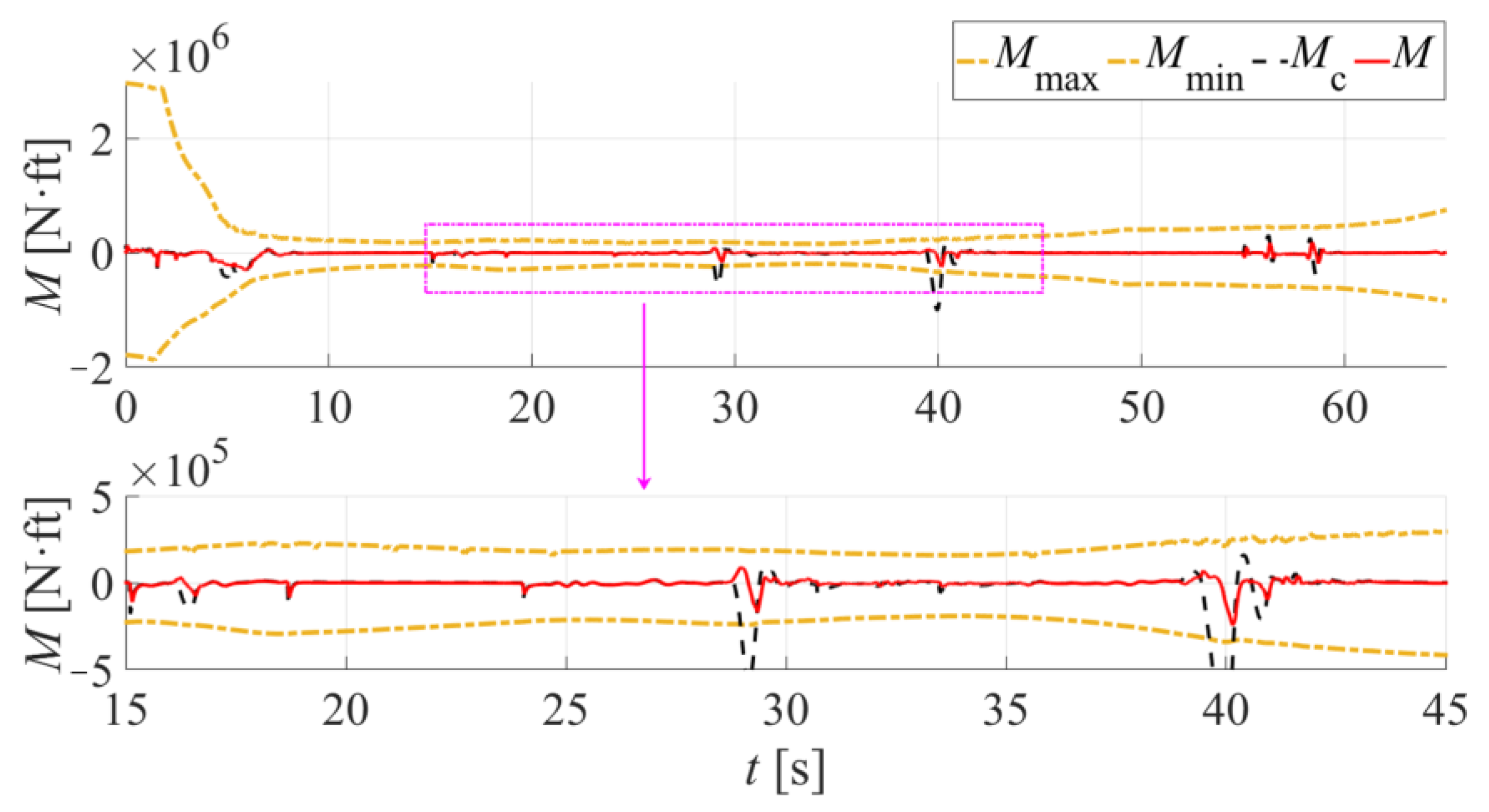
5.1. Scenario 1: Simulation Verification for Algorithm AMB
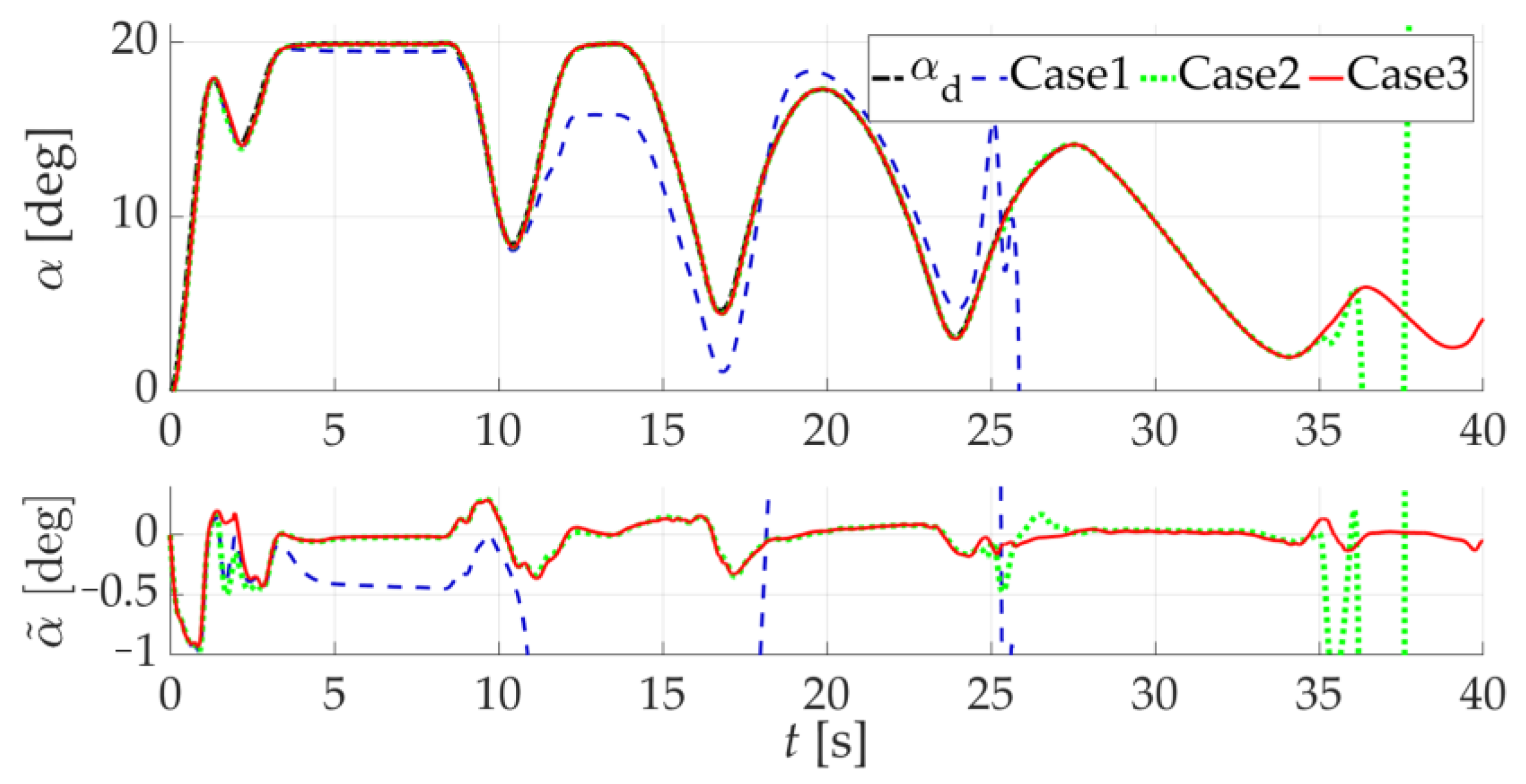
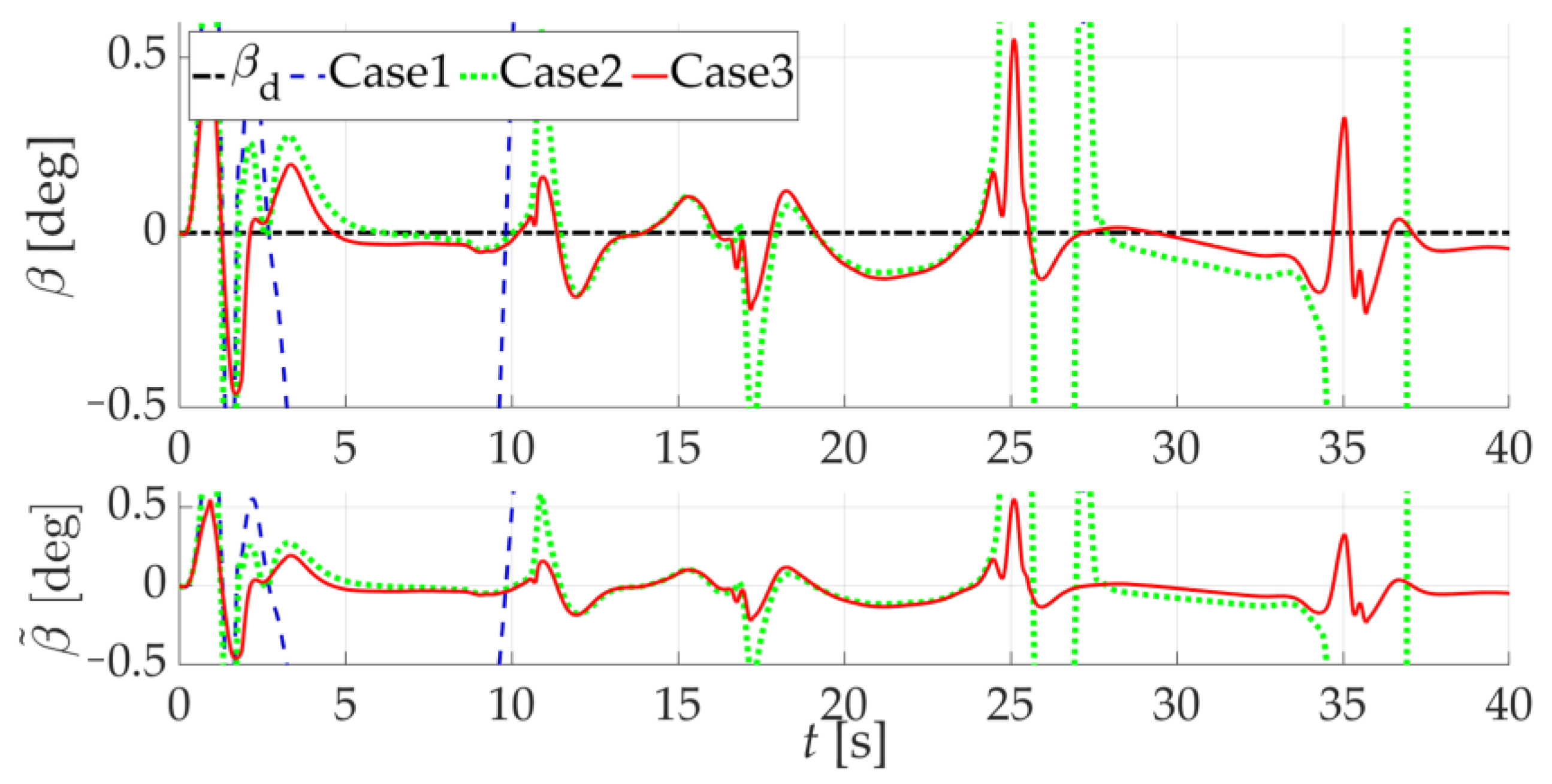
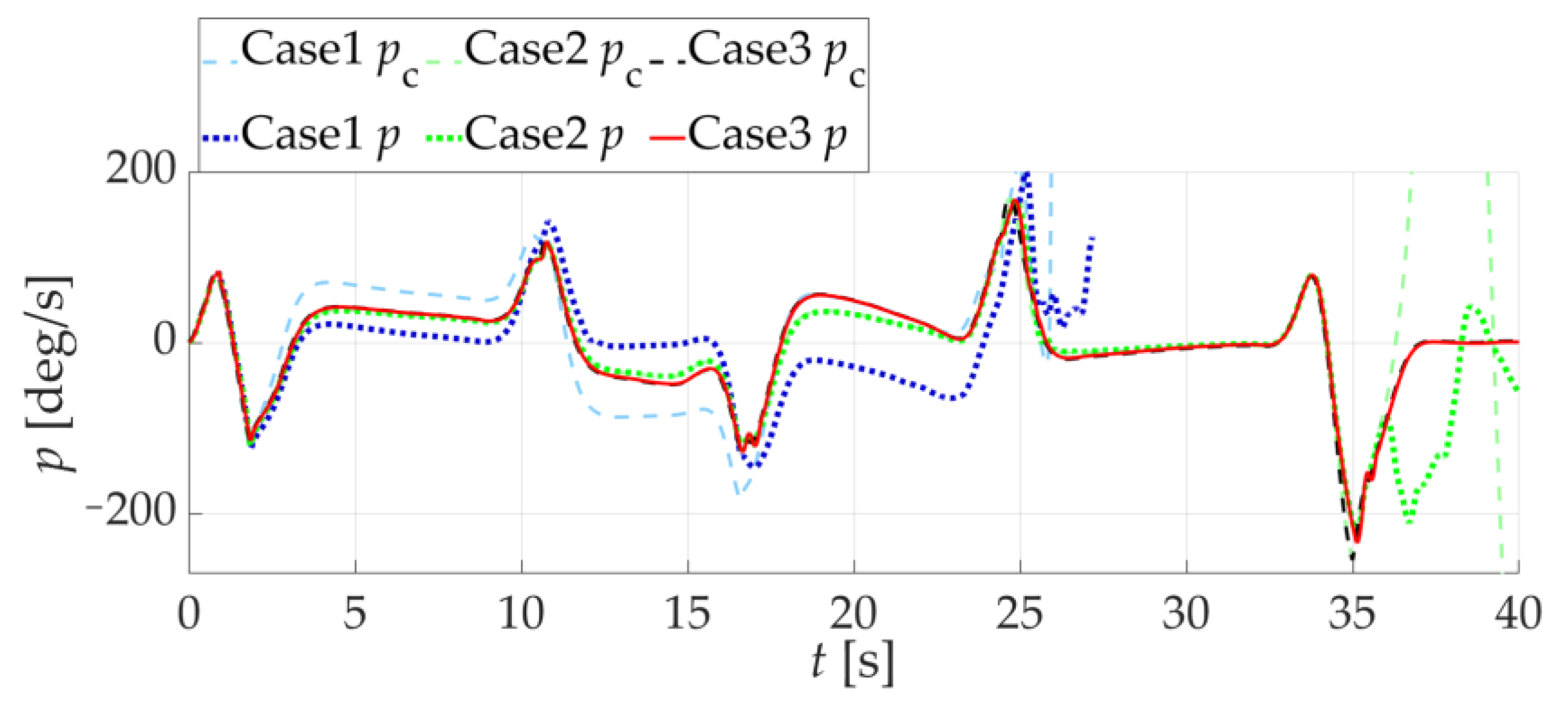
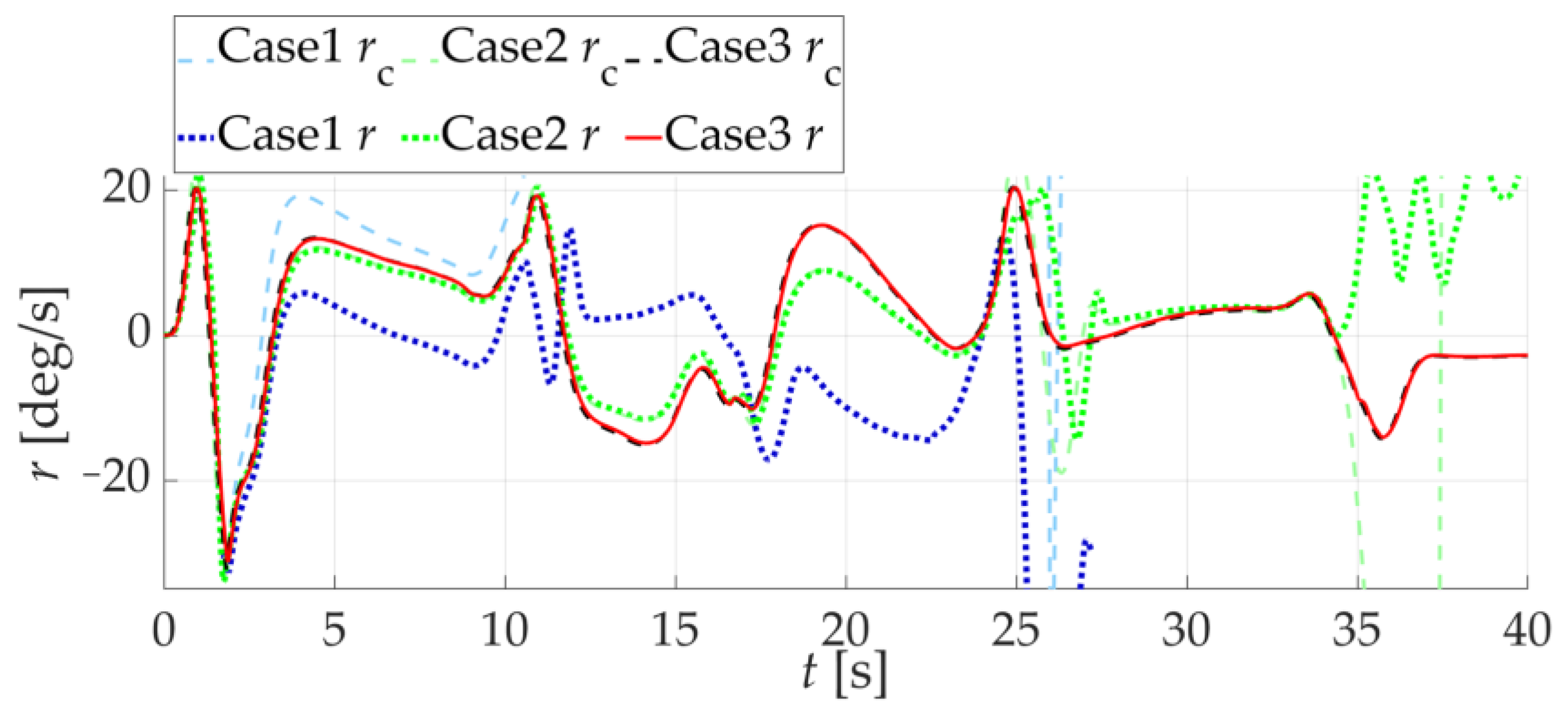
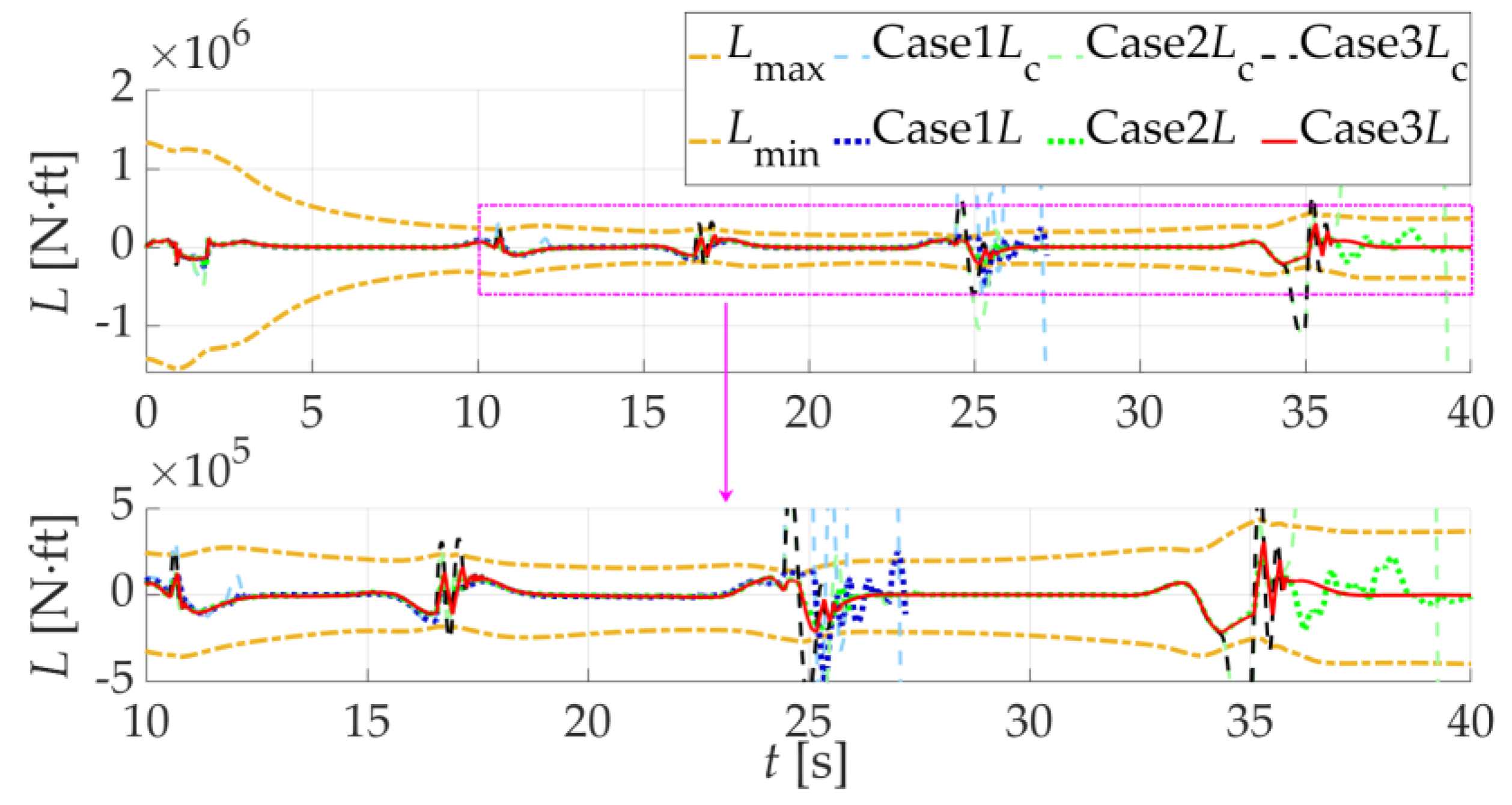
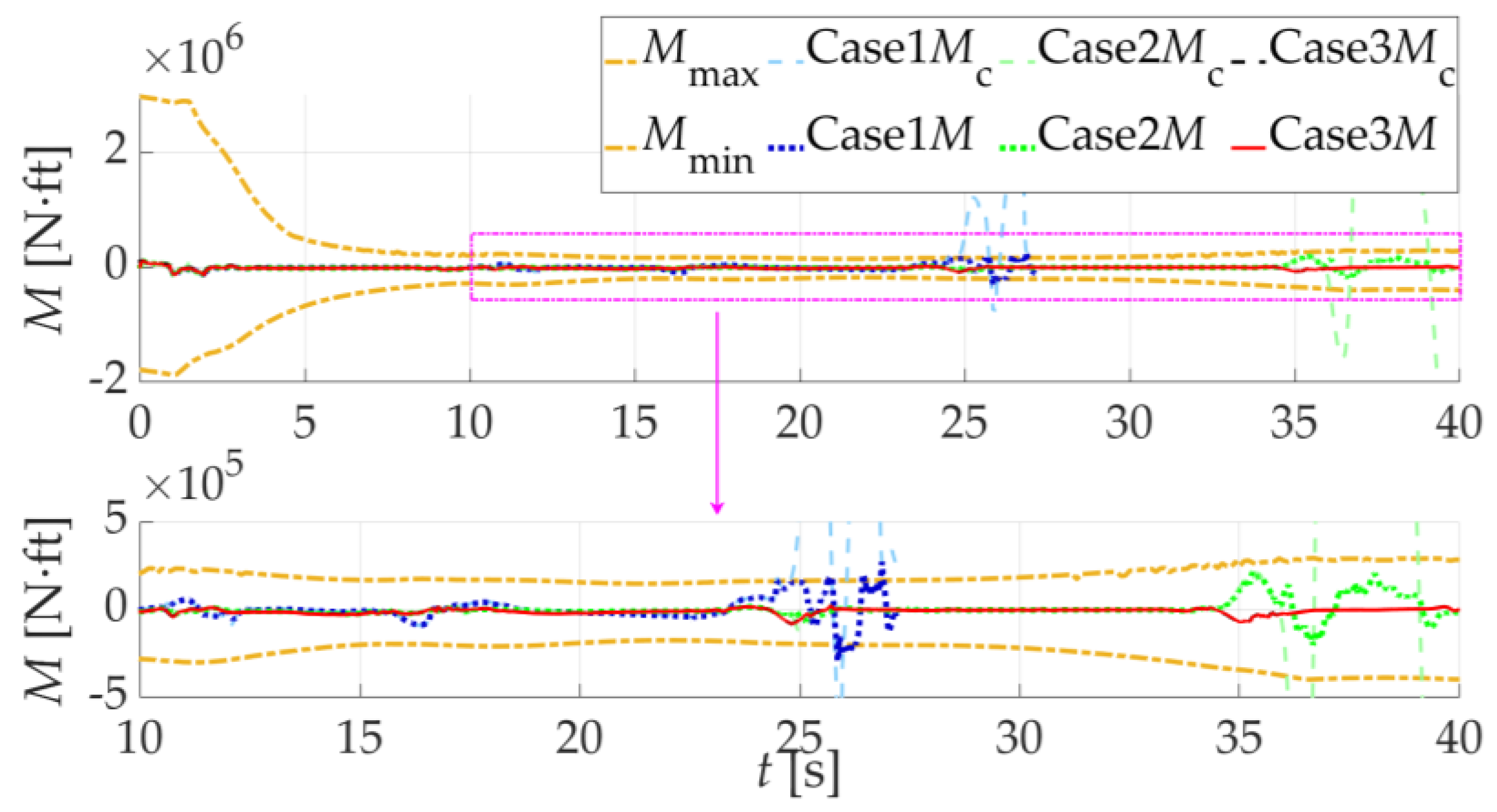
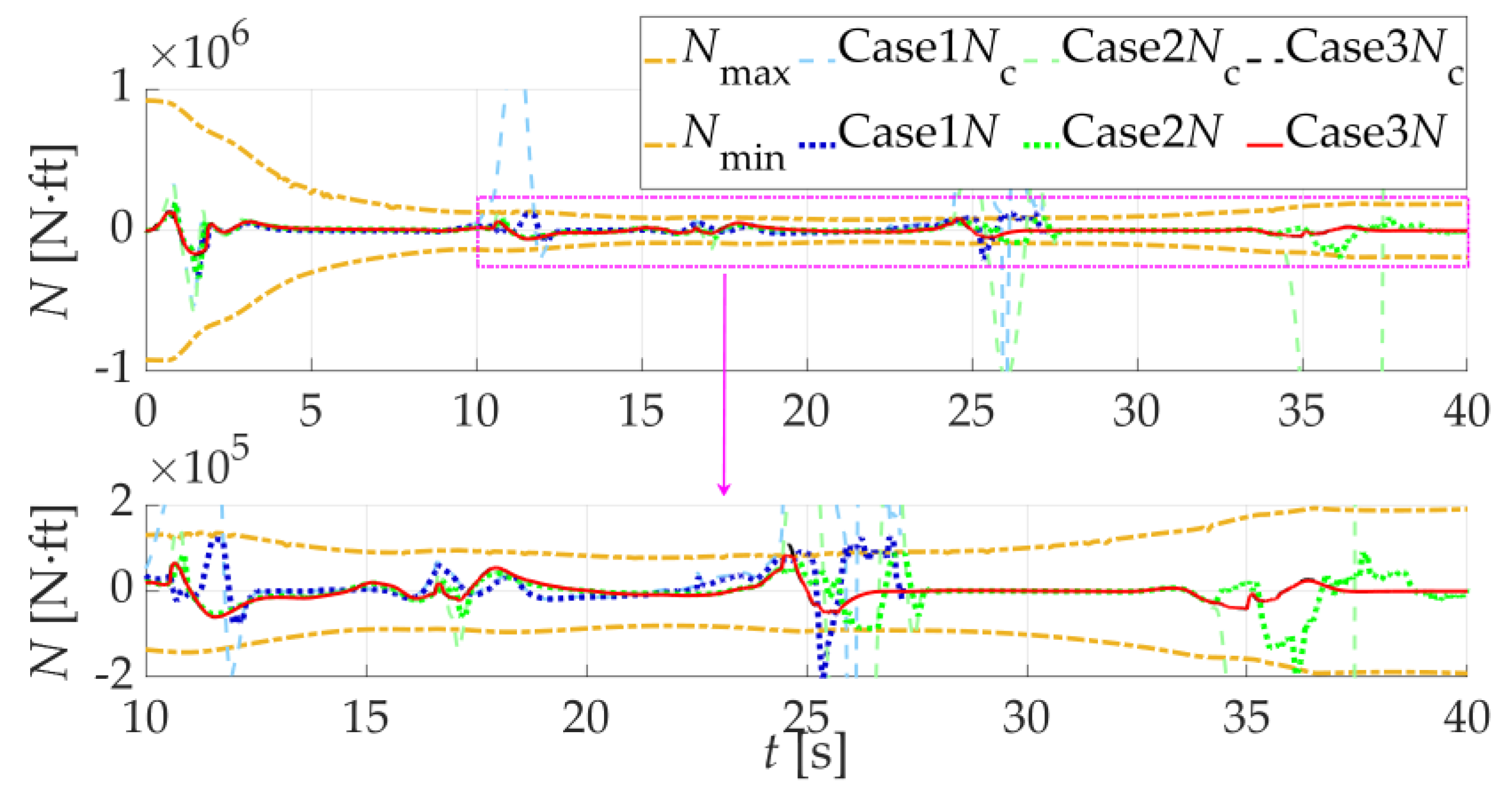
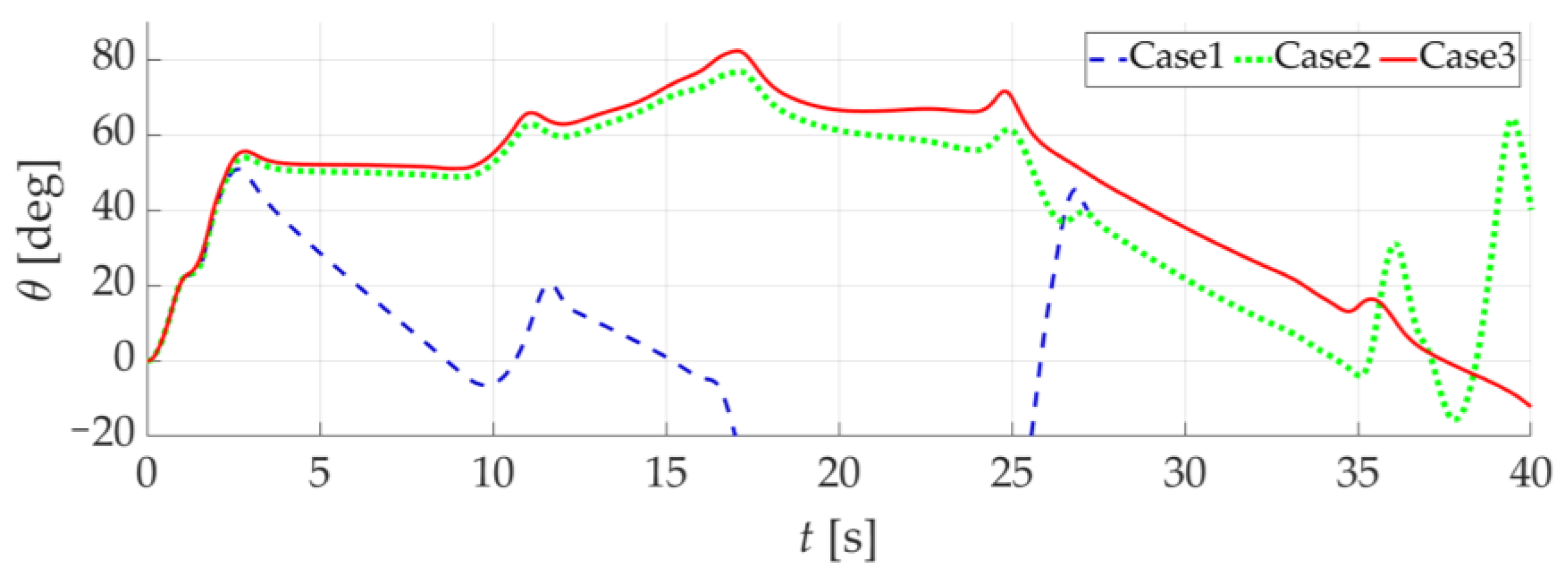
5.2. Scenario 2: Comparison of NDI Controller Simulation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shayan, K. Online Actor-Critic-Based Adaptive Control for a Tailless Aircraft with Innovative Control Effectors. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–21 January 2021. [Google Scholar]
- Harris, J.; Elliott, C.M.; Tallant, G. L1 Adaptive Nonlinear Dynamic Inversion Control for the Innovative Control Effectors Aircraft. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Cong, J.; Hu, J.; Wang, Y.; He, Z.; Han, L.; Su, M. Fault-Tolerant Attitude Control Incorporating Reconfiguration Control Allocation for Supersonic Tailless Aircraft. Aerospace 2023, 10, 241. [Google Scholar] [CrossRef]
- Zhu, J.; He, R.; Tang, G.; Bao, W. Pendulum Maneuvering Strategy for Hypersonic Glide Vehicles. Aerosp. Sci. Technol. 2018, 78, 62–70. [Google Scholar] [CrossRef]
- Guo, Q.; Teng, L. Maneuvering Target Tracking with Multi-Model Based on the Adaptive Structure. IEEJ Trans. Electr. Electron. Eng. 2022, 17, 865–871. [Google Scholar] [CrossRef]
- Wan, J.; Ren, P.; Guo, Q. Application of Interactive Multiple Model Adaptive Five-Degree Cubature Kalman Algorithm Based on Fuzzy Logic in Target Tracking. Symmetry 2019, 11, 767. [Google Scholar] [CrossRef]
- Yu, X.; Luo, S.; Liu, H. Integrated Design of Multi-Constrained Snake Maneuver Surge Guidance Control for Hypersonic Vehicles in the Dive Segment. Aerospace 2023, 10, 765. [Google Scholar] [CrossRef]
- Maolin, W.; Shenghao, F.; Fei, L.; Renli, L.; Nan, Y. Research on Control Law Design of Fixed Wing Unmanned Aerial Vehicle in Aerobatic Maneuvers. In Proceedings of the 2022 34th Chinese Control and Decision Conference (CCDC), Hefei, China, 15–17 August 2022; pp. 4665–4670. [Google Scholar] [CrossRef]
- Lungu, M.; Flores, G.; Dinu, D.-A.; Ciuca, G.M. Autonomous Landing of Tailless, Blended Wing, and Variable Centre of Mass UAV Using Adaptive Control. In Proceedings of the 2022 8th International Conference on Control, Decision and Information Technologies (CoDIT), Istanbul, Turkey, 17–20 May 2022; pp. 112–117. [Google Scholar] [CrossRef]
- Yu, Z.; Li, Y.; Lv, M.; Pei, B.; Fu, A. Event-Triggered Adaptive Fuzzy Fault-Tolerant Attitude Control for Tailless Flying-Wing UAV with Fixed-Time Convergence. IEEE Trans. Veh. Technol. 2023, 1–12. [Google Scholar] [CrossRef]
- Nie, B.; Liu, Z.; Guo, T.; Fan, L.; Ma, H.; Sename, O. Design and Validation of Disturbance Rejection Dynamic Inverse Control for a Tailless Aircraft in Wind Tunnel. Appl. Sci. 2021, 11, 1407. [Google Scholar] [CrossRef]
- Stolk, A.R.J. Minimum Drag Control Allocation for the Innovative Control Effector Aircraft. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2017. [Google Scholar]
- Su, M.; Hu, J.; Wang, Y.; He, Z.; Cong, J.; Han, L. A Multiobjective Incremental Control Allocation Strategy for Tailless Aircraft. Int. J. Aerosp. Eng. 2022, 2022, 6515234. [Google Scholar] [CrossRef]
- Yin, M.; Chu, Q.P.; Zhang, Y.; Niestroy, M.A.; De Visser, C.C. Probabilistic Flight Envelope Estimation with Application to Unstable Overactuated Aircraft. J. Guid. Control. Dyn. 2019, 42, 2650–2663. [Google Scholar] [CrossRef]
- He, Z.; Hu, J.; Wang, Y.; Cong, J.; Bian, Y.; Han, L. Attitude-Tracking Control for Over-Actuated Tailless UAVs at Cruise Using Adaptive Dynamic Programming. Drones 2023, 7, 294. [Google Scholar] [CrossRef]
- Durham, W.C. Attainable Moments for the Constrained Control Allocation Problem. J. Guid. Control. Dyn. 1994, 17, 1371–1373. [Google Scholar] [CrossRef]
- Kou, L.; He, S.; Li, Y.; Xiang, J. Constrained Control Allocation of a Quadrotor-Like Autonomous Underwater Vehicle. J. Guid. Control. Dyn. 2021, 44, 659–666. [Google Scholar] [CrossRef]
- Yu, Y.; Li, R.; Ji, W.; Lu, Z.; Tian, G. Refinements of the Dynamic Inversion Part of Hierarchical 4WIS/4WID Trajectory Tracking Controllers; SAE International: Detroit, MI, USA, 2023. [Google Scholar] [CrossRef]
- Ghobadi, M.; Shafaee, M.; Nadoushan, M.J. Reliability Approach to Optimal Thruster Configuration Design for Spacecraft Attitude Control Subsystem. J. Aerosp. Technol. Manag. 2020, 12, e2320. [Google Scholar] [CrossRef]
- Pfeifle, O.; Fichter, W. Incremental Control Allocation with Axis Prioritization on the Boundary of the Attainable Control Set. In Proceedings of the AIAA SciTech 2023 Forum, National Harbor, MD, USA, 23–27 January 2023; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2023. [Google Scholar] [CrossRef]
- Lu, Z.; Hong, H.; Diepolder, J.; Holzapfel, F. Maneuverability Set Estimation and Trajectory Feasibility Evaluation for eVTOL Aircraft. J. Guid. Control. Dyn. 2023, 46, 1184–1196. [Google Scholar] [CrossRef]
- Bolander, C.R.; Hunsaker, D.F.; Myszka, D.; Joo, J.J. Attainable Moment Set and Actuation Time of a Bio-Inspired Rotating Empennage. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Zheng, F.; Liu, L.; Chen, Z.; Chen, Y.; Cheng, F. Hybrid Multi-Objective Control Allocation Strategy for Compound High-Speed Rotorcraft. ISA Trans. 2020, 98, 207–226. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Guo, H.; Ma, J. Aerodynamic Layout Optimization Design of a Barrel-Launched UAV Wing Considering Control Capability of Multiple Control Surfaces. Aerosp. Sci. Technol. 2019, 93, 105297. [Google Scholar] [CrossRef]
- Lei, H.; Chen, B.; Liu, Y.; Lv, Y. Modified Kalman Particle Swarm Optimization: Application for Trim Problem of Very Flexible Aircraft. Eng. Appl. Artif. Intell. 2021, 100, 104176. [Google Scholar] [CrossRef]
- Zhang, N. Research on Command Allocation Method for Flying Wing Aircraft. IOP Conf. Ser. Mater. Sci. Eng. 2020, 887, 012020. [Google Scholar] [CrossRef]
- Qu, X.; Shi, J.; Zhou, H.; Zuo, L.; Lyu, Y. Reconfigurable Flight Control System Design for Blended Wing Body UAV Based on Control Allocation. In Proceedings of the 2018 18th International Conference on Control, Automation and Systems (ICCAS), PyeongChang, Republic of Korea, 17–20 October 2018. [Google Scholar]
- Matamoros, I.; De Visser, C.C. Incremental Nonlinear Control Allocation for a Tailless Aircraft with Innovative Control Effectors. In Proceedings of the 2018 AIAA Guidance, Navigation, and Control Conference, Kissimmee, FL, USA, 8–12 January 2018; American Institute of Aeronautics and Astronautics: Kissimmee, FL, USA, 2018. [Google Scholar] [CrossRef]
- Niestroy, M.A.; Dorsett, K.M.; Markstein, K. A Tailless Fighter Aircraft Model for Control-Related Research and Development. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Grapevine, TX, USA, 9–13 January 2017; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2017. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, J.; Yang, L.; Guo, X. Weighted Pseudo-Inverse Based Control Allocation of Heterogeneous Redundant Operating Mechanisms for DPC Aircraft. In Proceedings of the 2018 15th International Conference on Control, Automation, Robotics and Vision (ICARCV), Singapore, 18–21 November 2018; pp. 367–370. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, D.; Liu, L.; Zhao, Y.; Sun, L.; Yao, Z. Path Prediction Method for Automotive Applications Based on Cubic Spline Interpolation. In Proceedings of the 2022 International Conference on Advanced Robotics and Mechatronics (ICARM), Guilin, China, 9–11 July 2022; pp. 1086–1091. [Google Scholar]
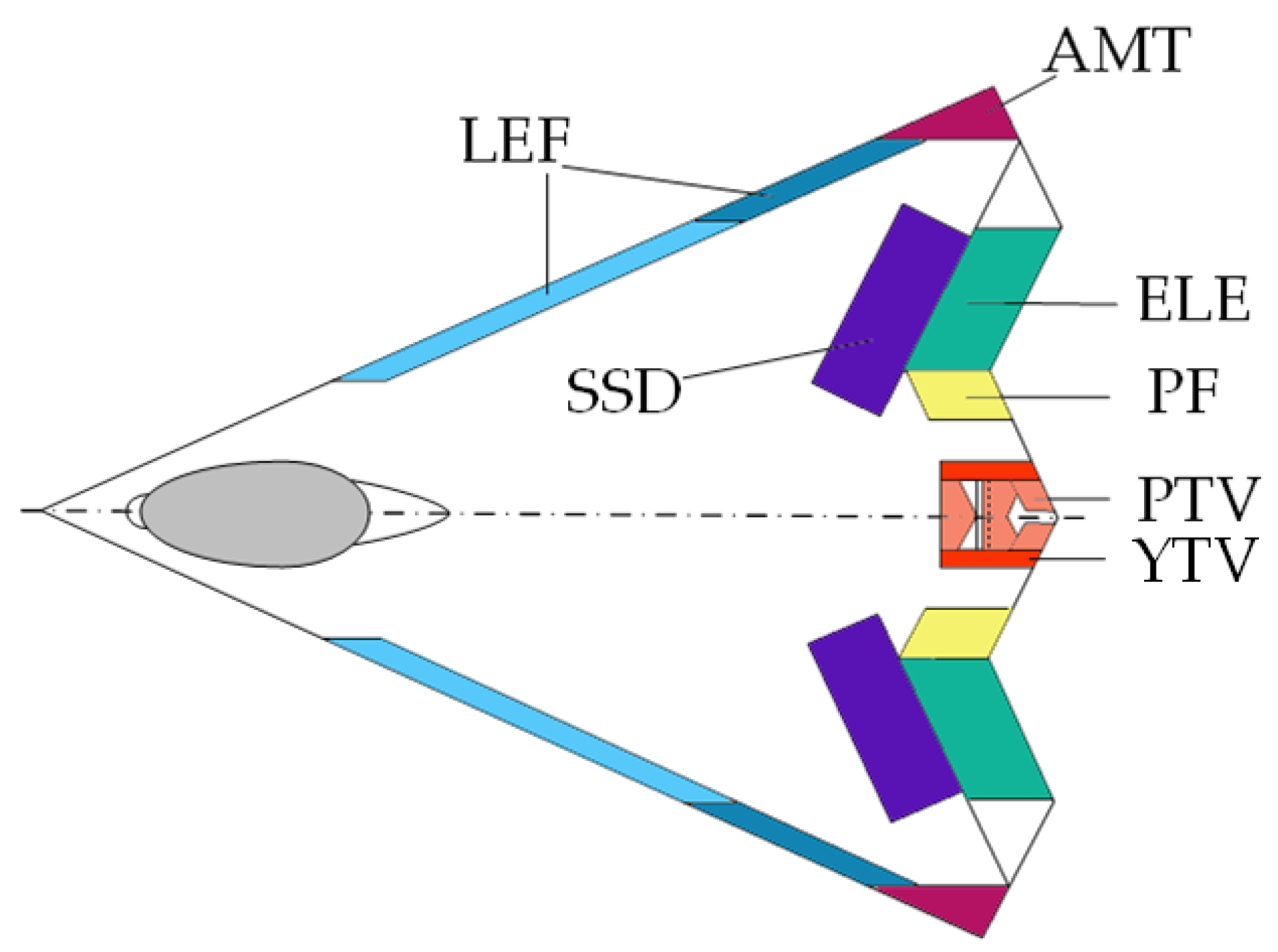











| Variable | Nomenclature | Unit |
|---|---|---|
| = geodetic coordinates | ft | |
| = airspeed | ft/s | |
| = flight path angle and sideslip angle | deg | |
| = attack angle, sideslip angle, bank angle of V | deg | |
| = roll angle, pitch angle, yaw angle | deg | |
| = body-axis roll, pitch, and yaw rate | deg/s |
| ICE Parameters | Value | Unit | Effectors | Action Range (deg) |
|---|---|---|---|---|
| lilef | [0, 40] | |||
| rilef | [0, 40] | |||
| lolef | [−40, 40] | |||
| rolef | [−40, 40] | |||
| lamt | [0, 60] | |||
| ramt | [0, 60] | |||
| lele | [−30, 30] | |||
| rele | [−30, 30] | |||
| lssd | [0, 60] | |||
| rssd | [0, 60] | |||
| pf | [−30, 30] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, L.; Hu, J.; Wang, Y.; Cong, J.; Zhang, P. Design of Pseudo-Command Restricted Controller for Tailless Unmanned Aerial Vehicles Based on Attainable Moment Set. Drones 2024, 8, 101. https://doi.org/10.3390/drones8030101
Han L, Hu J, Wang Y, Cong J, Zhang P. Design of Pseudo-Command Restricted Controller for Tailless Unmanned Aerial Vehicles Based on Attainable Moment Set. Drones. 2024; 8(3):101. https://doi.org/10.3390/drones8030101
Chicago/Turabian StyleHan, Linxiao, Jianbo Hu, Yingyang Wang, Jiping Cong, and Peng Zhang. 2024. "Design of Pseudo-Command Restricted Controller for Tailless Unmanned Aerial Vehicles Based on Attainable Moment Set" Drones 8, no. 3: 101. https://doi.org/10.3390/drones8030101
APA StyleHan, L., Hu, J., Wang, Y., Cong, J., & Zhang, P. (2024). Design of Pseudo-Command Restricted Controller for Tailless Unmanned Aerial Vehicles Based on Attainable Moment Set. Drones, 8(3), 101. https://doi.org/10.3390/drones8030101






