Ground Effect on the Thrust Performance of Staggered Rotor System
Abstract
:1. Introduction
2. Methods
2.1. Experimental Setup and Instrumentation
2.2. Operating Conditions
2.3. Performance Metrics
- -
- T represents the thrust,
- -
- ρ represents the density of the air,
- -
- A represents the rotor disk area,
- -
- Ω represents the rotation speed,
- -
- R represents the rotor radius.
- -
- CT can be derived from Equation (1) and expressed as:
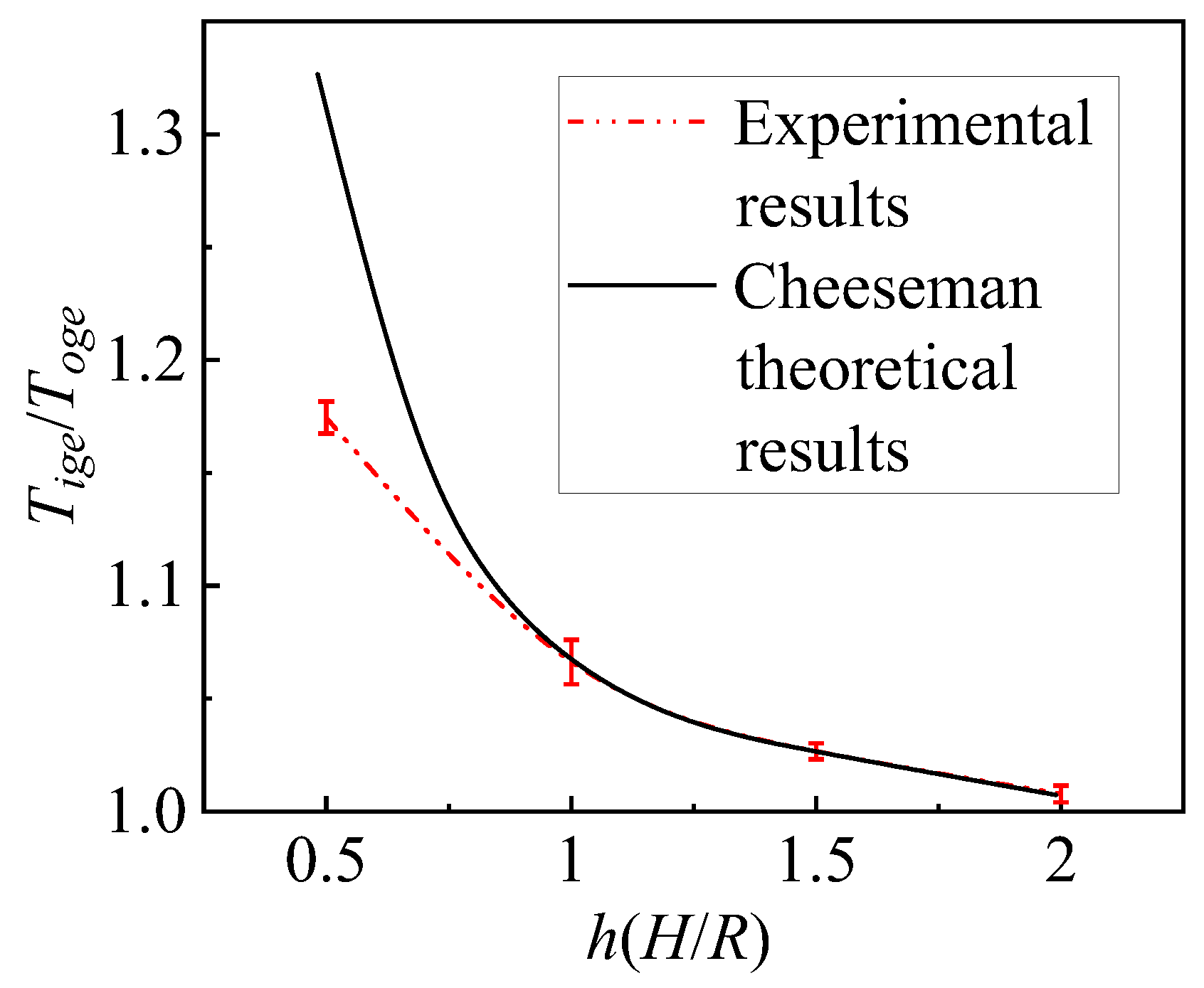
3. Error Analysis and Validation
4. Results and Analysis
4.1. Isolated Rotor Performance
4.2. Staggered Rotor System Performance
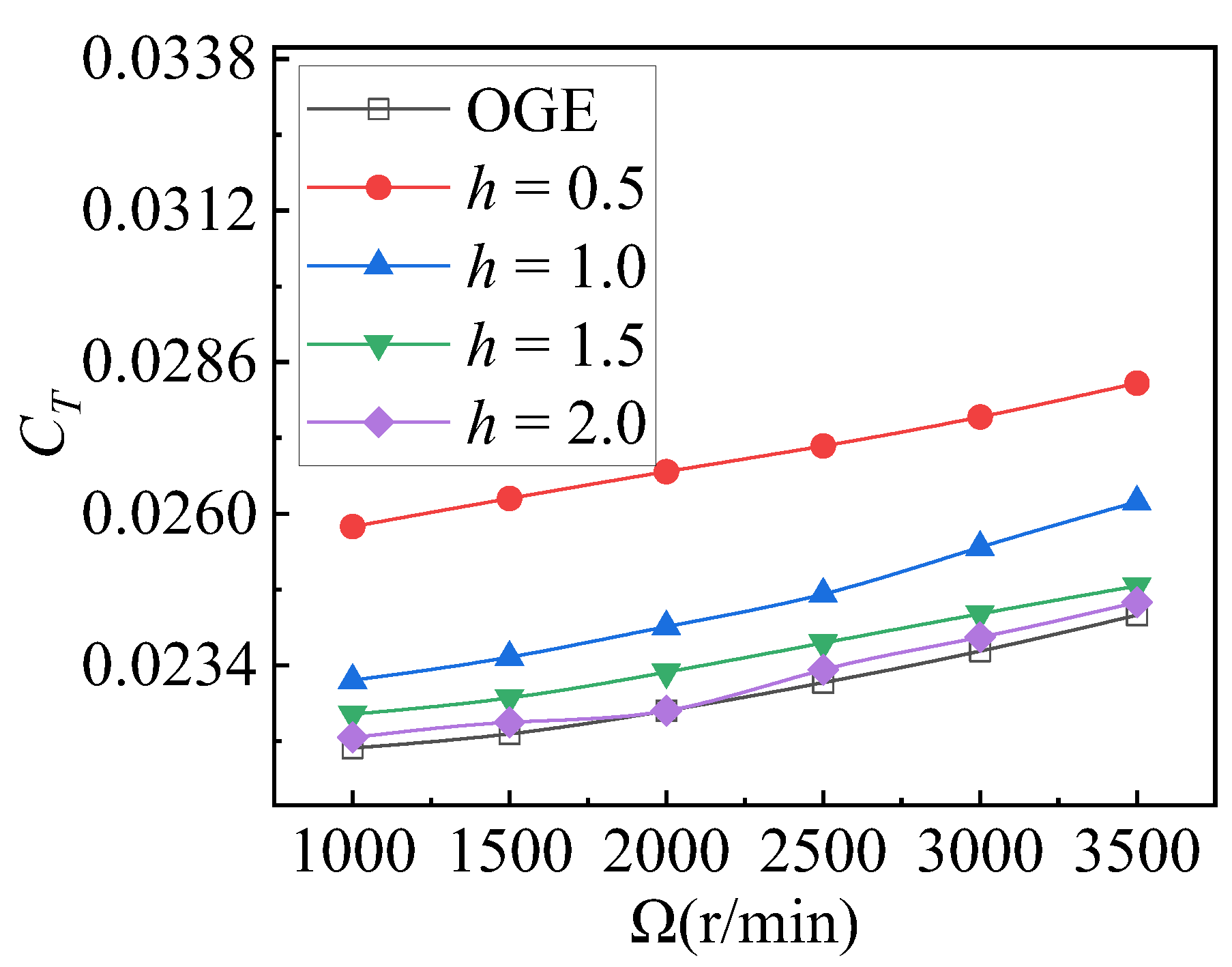
4.2.1. Effects of Rotor Speed
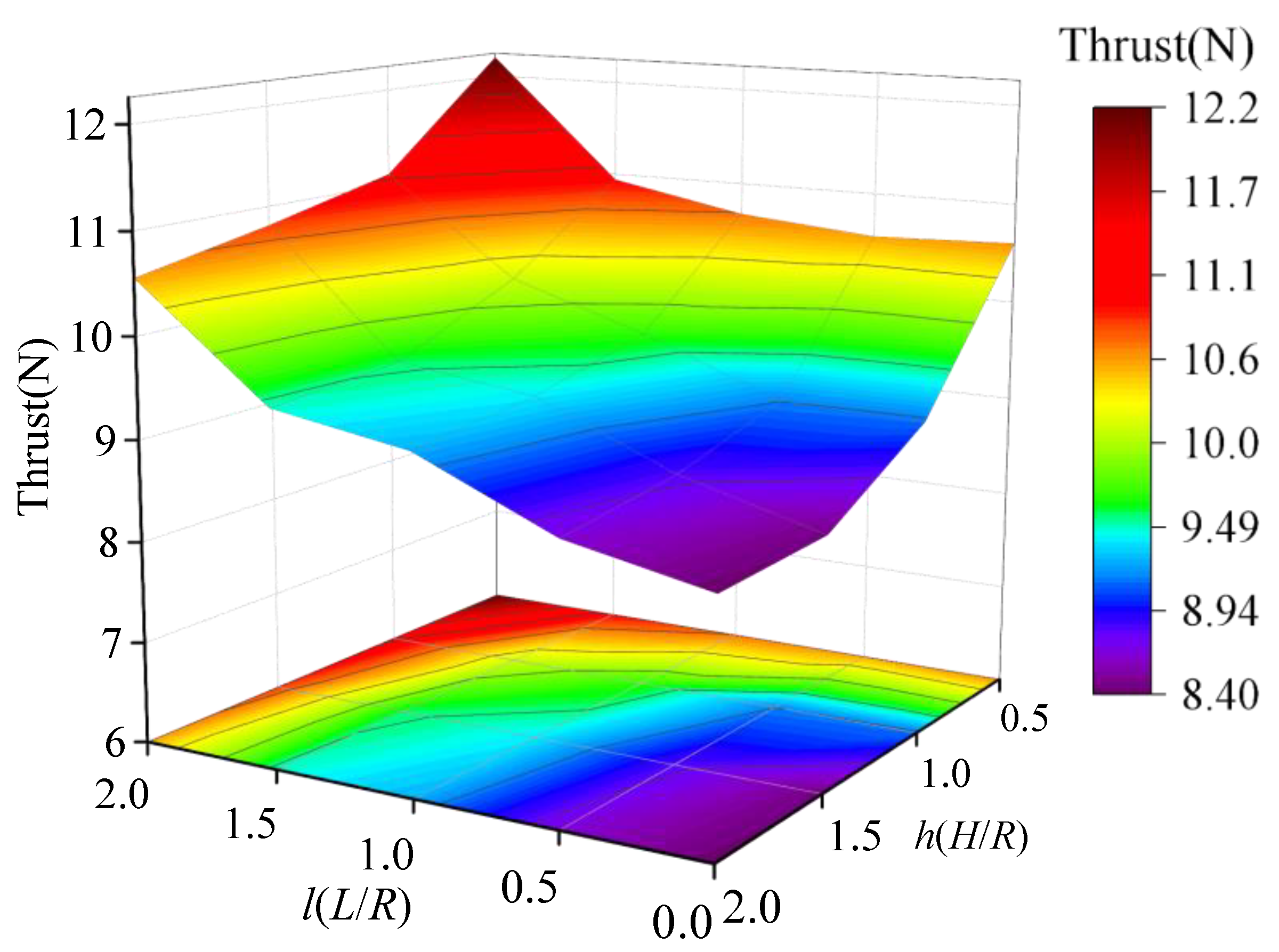
4.2.2. Effects of Ground Distance
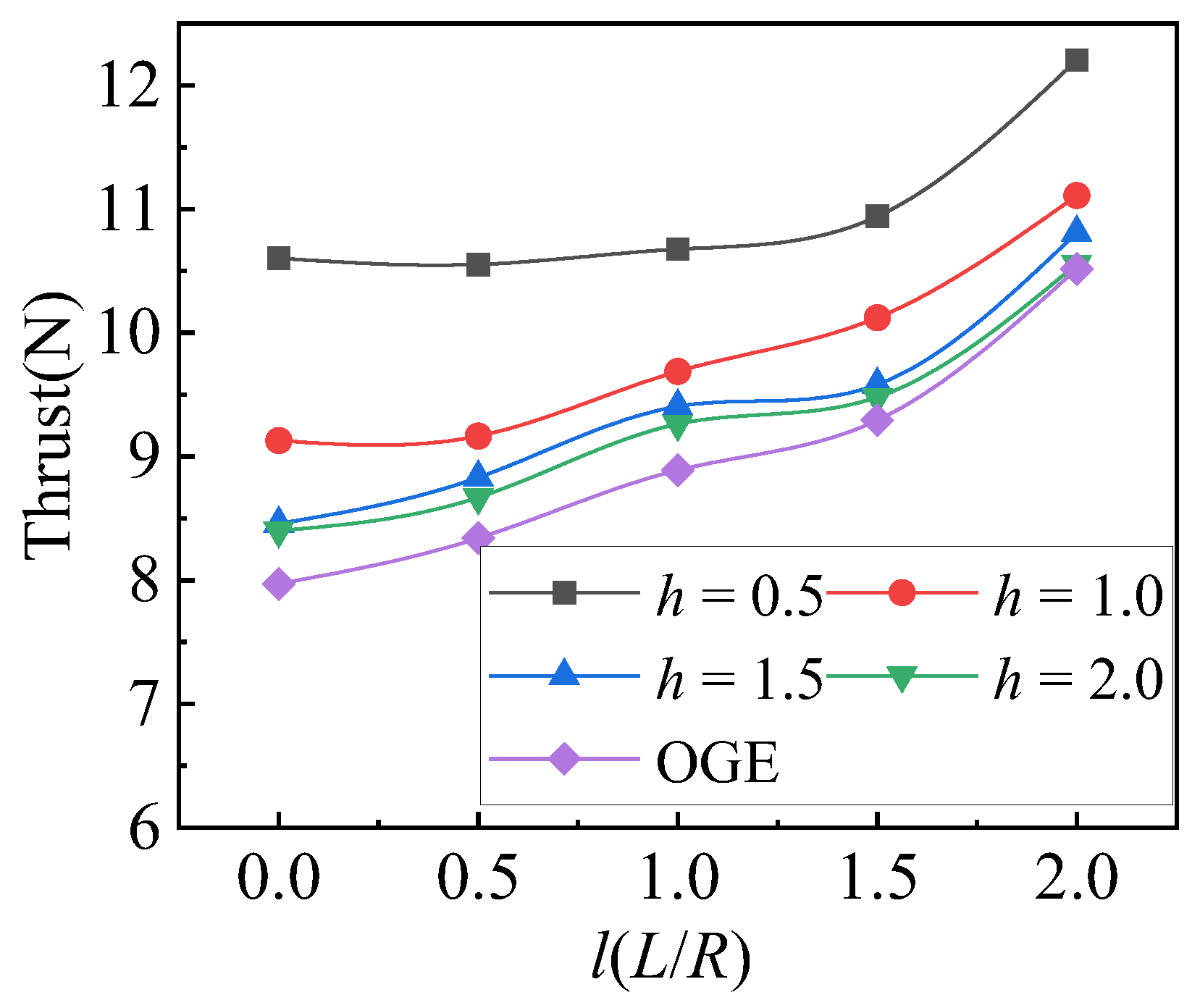
4.2.3. Effects of Lateral Distance
5. Discussion
5.1. Combination of Rotor to Rotor Interactions and Ground Effect
5.1.1. Impact on Thrust IGE
5.1.2. Impact on Thrust Ratio IGE
5.2. Effect on the Top and Bottom Rotors at h = 2.0
6. Conclusions and Future Work
- (1)
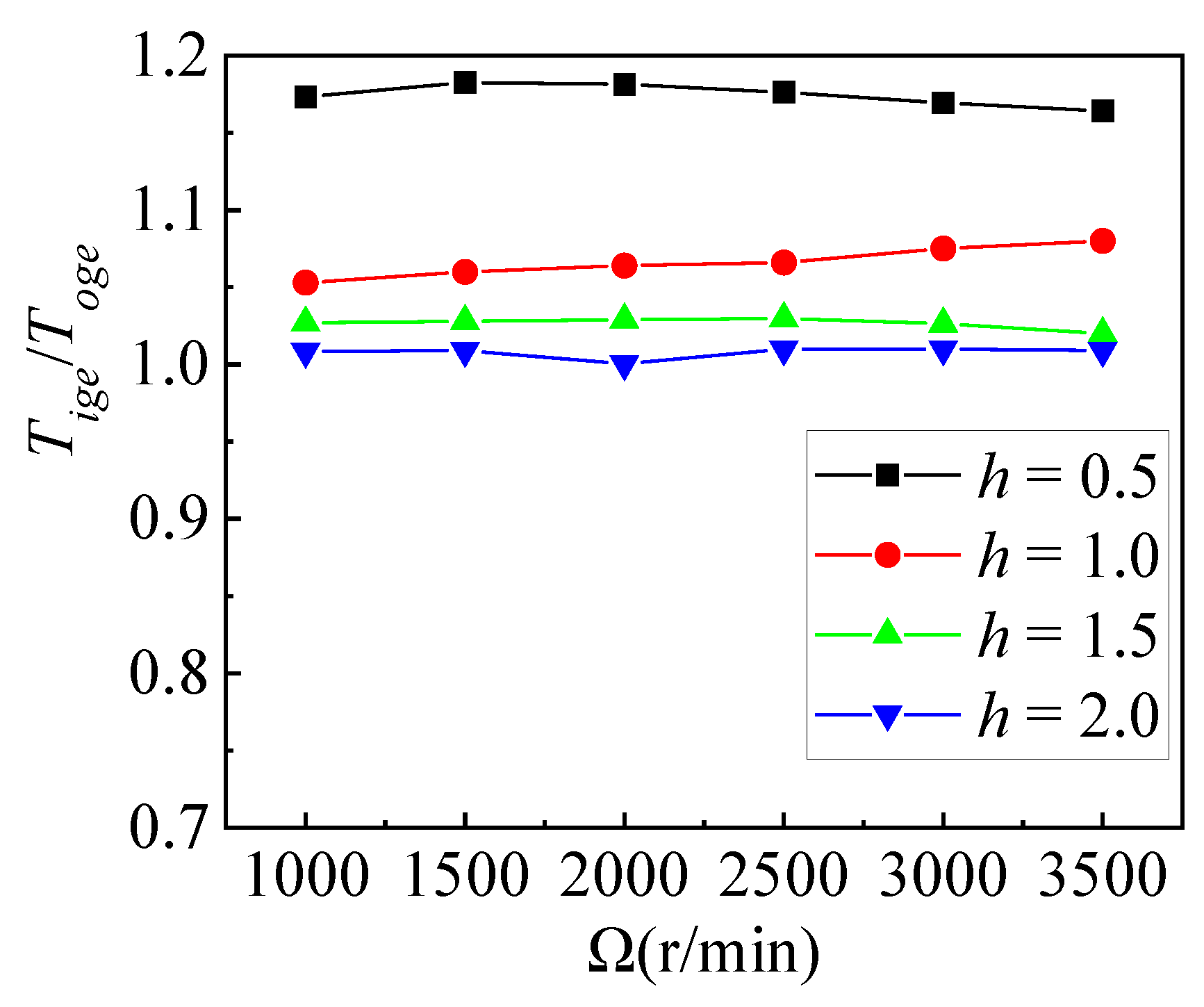
- In the ground effect, increasing rotor speed improves the thrust performance of both isolated rotor and staggered rotors, but the rotor speed barely affects the ratio of thrust IGE or OGE.
- (2)
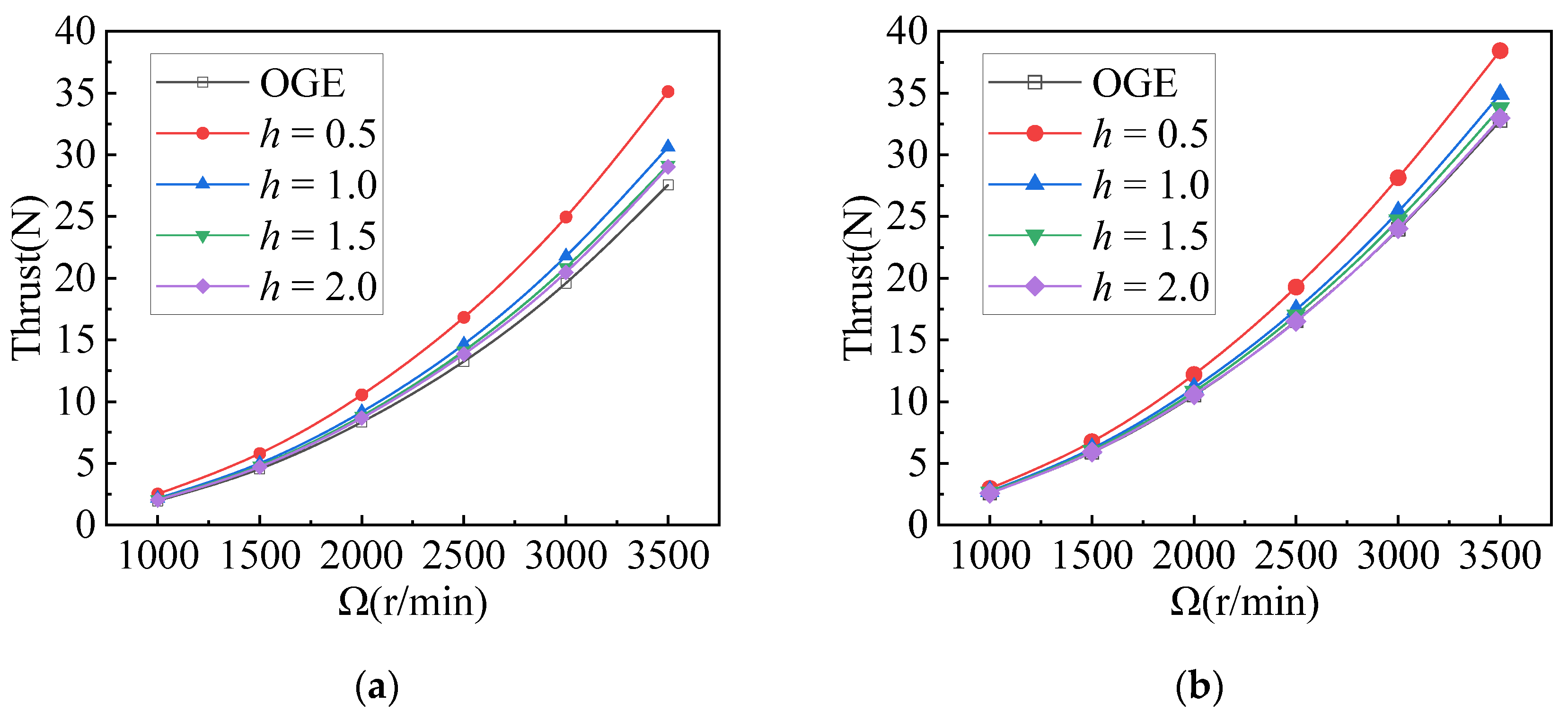
- As the distance above the ground increases, both isolated rotors and staggered rotors experience a decrease in thrust performance and thrust ratio. The position where the ground effect disappears for staggered rotor systems is farther away (hoge > 2.0) compared to the position where the ground effect disappears for isolated rotor systems.
- (3)
- As the lateral distance expands, the staggered rotor thrust improves, but the ratio of thrust decreases.
- (4)
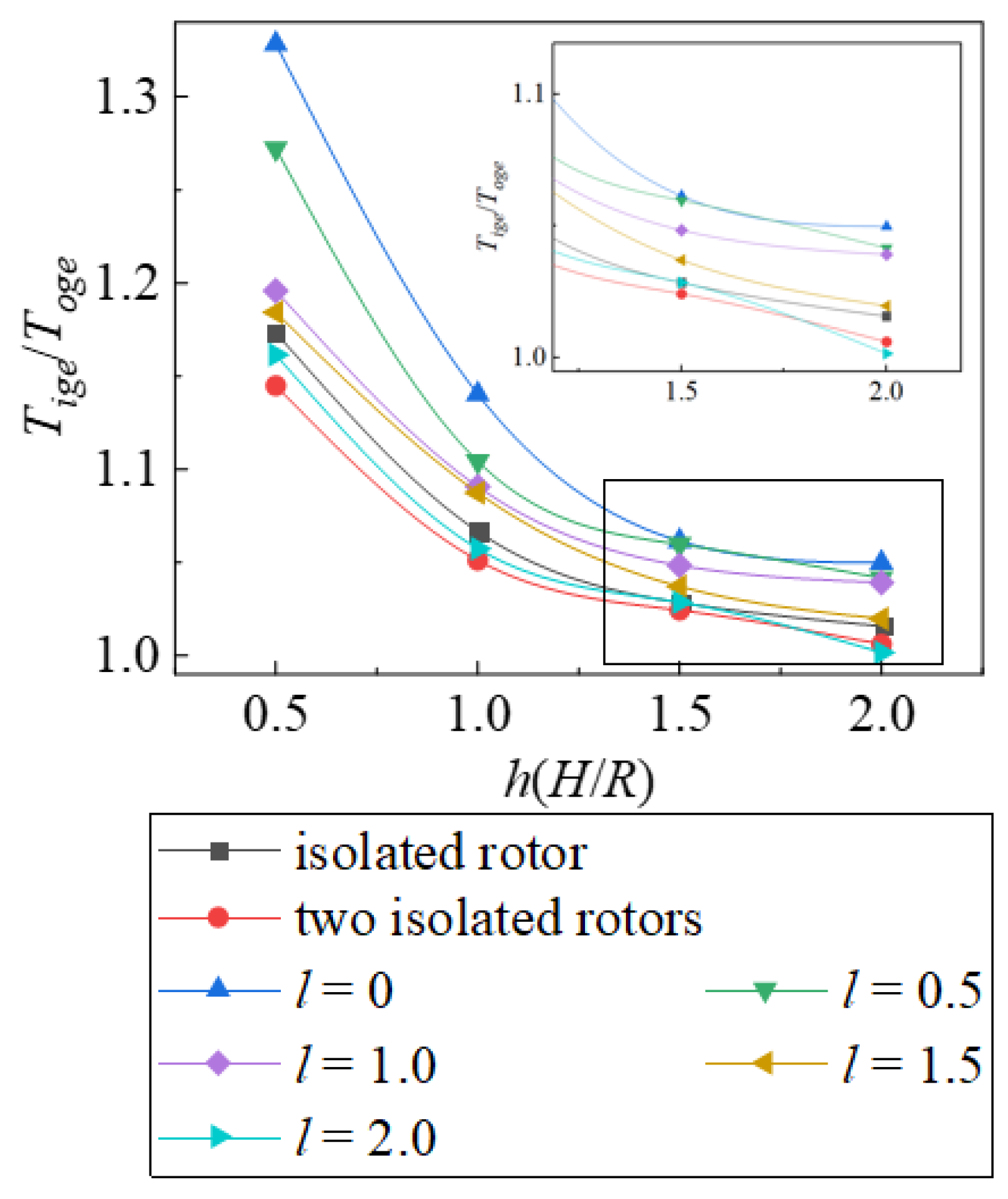
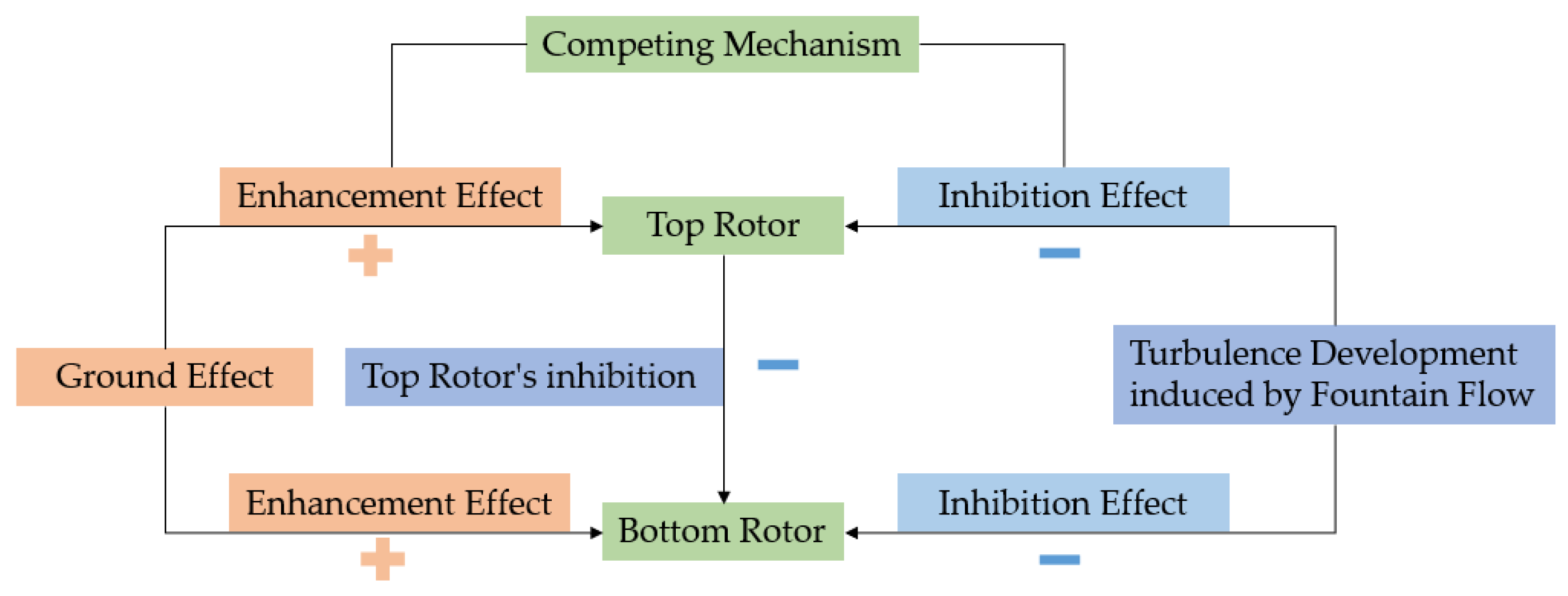
- The weakening effect of mutual interaction between staggered rotors and the strengthening effect of ground effect both coexist. The impacts of these two effects distribute differently: while the increase in lateral spacing leads to a uniform reduction in the interaction between rotors, affecting both thrust performance and thrust ratio almost evenly, the enhancement of ground effect due to decreasing distance from the ground experiences a sharp increase within the 0.5 ≤ h(H/R) ≤ 1.0 interval.
- (5)
- At h(H/R) = 2.0, certain configurations of staggered rotor systems are still influenced by ground effect. In this scenario, the thrust variation of bottom rotor behaves similarly with OGE state while the top rotor thrust experience an increase.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Doo, J.; Pavel, M.; Didey, A.; Hange, C.; Diller, N.; Tsairides, M.; Smith, M.; Bennet, E.; Bromfield, M.; Mooberry, J. NASA Electric Vertical Takeoff and Landing (eVTOL) Aircraft Technology for Public Services—A White Paper; NASA: Washington, DC, USA, 2021.
- Thipphavong, D.P.; Apaza, R.; Barmore, B.; Battiste, V.; Burian, B.; Dao, Q.; Verma, S.A. Urban Air Mobility Airspace Integration Concepts and Considerations. In Proceedings of the 2018 Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Ugwueze, O.; Statheros, T.; Bromfield, M.A.; Horri, N. Trends in eVTOL Aircraft Development: The Concepts, Enablers and Challenges. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023. [Google Scholar]
- Ugwueze, O.; Statheros, T.; Horri, N.; Bromfield, M.A.; Simo, J. An Efficient and Robust Sizing Method for eVTOL Aircraft Configurations in Conceptual Design. Aerospace 2023, 10, 311. [Google Scholar] [CrossRef]
- Zhang, H.; Zou, Y.; Zhang, Q.; Liu, H. Future urban air mobility management: Review. Acta Aeronaut. Et Astronaut. Sin. 2021, 42, 24638. [Google Scholar] [CrossRef]
- Li, Y.; Liu, M. Path Planning of Electric VTOL UAV Considering Minimum Energy Consumption in Urban Areas. Sustainability 2022, 14, 13421. [Google Scholar] [CrossRef]
- Qu, W.; Xu, C.; Tan, X.; Tang, A.; He, H.; Liao, X. Preliminary Concept of Urban Air Mobility Traffic Rules. Drones 2023, 7, 54. [Google Scholar] [CrossRef]
- Matus-Vargas, A.; Rodriguez-Gomez, G.; Martinez-Carranza, J. Ground effect on rotorcraft unmanned aerial vehicles: A review. Intell. Serv. Robot. 2021, 14, 99–118. [Google Scholar] [CrossRef]
- Darvishpoor, S.; Roshanian, J.; Raissi, A.; Hassanalian, M. Configurations, flight mechanisms, and applications of unmanned aerial systems: A review. Prog. Aerosp. Sci. 2020, 121, 100694. [Google Scholar] [CrossRef]
- Cheeseman, I.; Bennett, W. The Effect of the Ground on a Helicopter Rotor in Forward Flight; Her Majesty’s Stationery Office: London, UK, 1955. [Google Scholar]
- Hayden, J.S. The Effect of the Ground on Helicopter Hovering Power Required. In Proceedings of the AHS Forum 32, Washington, DC, USA, 10–12 May 1976. [Google Scholar]
- Hwang, J.Y.; Kwon, O.J. Assessment of S-76 rotor hover performance in ground effect using an unstructured mixed mesh method. Aerosp. Sci. Technol. 2019, 84, 223–236. [Google Scholar] [CrossRef]
- Kalra, T.S.; Lakshminarayan, V.K.; Baeder, J.D. CFD validation of micro hovering rotor in ground effect. In Proceedings of the AHS International Specialists Conference Proceedings on Aeromechanics, San Francisco, CA, USA, 20–22 January 2010. [Google Scholar]
- Sugiura, M.; Tanabe, Y.; Sugawara, H.; Matayoshi, N.; Ishii, H. Numerical Simulations and Measurements of the Helicopter Wake in Ground Effect. J. Aircr. 2017, 54, 209–219. [Google Scholar] [CrossRef]
- Milluzzo, J.I.; Leishman, J.G. Vortical Sheet Behavior in the Wake of a Rotor in Ground Effect. AIAA J. 2017, 55, 24. [Google Scholar] [CrossRef]
- Conyers, S.A.; Rutherford, M.J.; Valavanis, K.P. An empirical evaluation of ground effect for small-scale rotorcraft. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 1244–1250. [Google Scholar]
- Lee, T.E.; Leishman, J.G.; Ramasamy, M. Fluid Dynamics of Interacting Blade Tip Vortices with a Ground Plane. J. Am. Helicopter Soc. 2010, 55, 022005. [Google Scholar] [CrossRef]
- Danjun, L.; Yan, Z.; Zongying, S.; Geng, L. Autonomous landing of quadrotor based on ground effect modelling. In Proceedings of the 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 5647–5652. [Google Scholar]
- Sanchez-Cuevas, P.; Heredia, G.; Ollero, A. Characterization of the aerodynamic ground effect and its influence in multirotor control. Int. J. Aerosp. Eng. 2017, 2017, 1823056. [Google Scholar] [CrossRef]
- He, X.; Leang, K.K. Quasi-steady in-ground-effect model for single and multirotor aerial vehicles. AIAA J. 2020, 58, 5318–5331. [Google Scholar] [CrossRef]
- Yonezawa, K.; Akiba, K.; Liu, H.; Sugawara, H.; Tanabe, Y.; Tokutake, H.; Sunada, S. Numerical Investigations of Ground Effect of a Quadcopter. In Proceedings of the 2021 Asia-Pacific International Symposium on Aerospace Technology (APISAT 2021), Volume 1, Jeju, Republic of Korea, 15–17 November 2021; Lecture Notes in Electrical Engineering. Springer Nature: Berlin/Heidelberg, Germany, 2023; pp. 733–744. [Google Scholar]
- Dekker, H.N.; Ragni, D.; Baars, W.J.; Scarano, F.; Tuinstra, M. Aerodynamic Interactions of Side-by-Side Rotors in Ground Proximity. AIAA J. 2022, 60, 4267–4277. [Google Scholar] [CrossRef]
- Healy, R.; McCauley, J.; Gandhi, F.; Sahni, O. A Computational Examination of Side-by-Side Rotors in Ground Effect. J. Am. Helicopter Soc. 2023, 68, 32007–32024. [Google Scholar] [CrossRef]
- Tanabe, Y.; Sugawara, H.; Sunada, S.; Yonezawa, K.; Tokutake, H. Quadrotor Drone Hovering in Ground Effect. J. Robot. Mechatron. 2021, 33, 339–347. [Google Scholar] [CrossRef]
- Otsuka, H.; Kohno, M.; Nagatani, K. Fountain Flow Visualization in Quadrotor Wake Decreasing Rotor Thrust In-Ground Effect. J. Aircr. 2023. [Google Scholar] [CrossRef]
- Cameron, C.G.; Karpatne, A.; Sirohi, J. Performance of a Mach-Scale Coaxial Counter-Rotating Rotor in Hover. J. Aircr. 2016, 53, 746–755. [Google Scholar] [CrossRef]
- Lim, J.W.; Mcalister, K.W.; Johnson, W. Hover Performance Correlation for Full-Scale and Model-Scale Coaxial Rotors. J. Am. Helicopter Soc. 2009, 54, 32005–3200514. [Google Scholar] [CrossRef]
- Lei, Y.; Wang, J.; Li, Y. The Aerodynamic Performance of a Novel Overlapping Octocopter Considering Horizontal Wind. Aerospace 2023, 10, 902. [Google Scholar] [CrossRef]
- Zhu, H.; Nie, H.; Zhang, L.; Wei, X.; Zhang, M. Design and assessment of octocopter drones with improved aerodynamic efficiency and performance. Aerosp. Sci. Technol. 2020, 106, 106206. [Google Scholar] [CrossRef]
- Silwal, L.; Bhagwat, M.; Raghav, V. Aerodynamic Interactions of Counter-Rotating Coaxial Rotors Hovering in Ground Effect. J. Aircr. 2022, 59, 1416–1425. [Google Scholar] [CrossRef]
- Ghosh, S.; Lohry, M.; Rajagopalan, R. Rotor configurational effect on rotorcraft brownout. In Proceedings of the 28th AIAA Applied Aerodynamics Conference, Chicago, IL, USA, 28 June–1 July 2010; p. 4238. [Google Scholar]
- Ramasamy, M.; Yamauchi, G.K. Using Model-Scale Tandem-Rotor Measurements in Ground Effect to Understand Full-Scale CH-47D Outwash. J. Am. Helicopter Soc. 2017, 62, 012004. [Google Scholar] [CrossRef]
- Tan, J.F.; Sun, Y.M.; Barakos, G.N. Vortex approach for downwash and outwash of tandem rotors in ground effect. J. Aircr. 2018, 55, 2491–2509. [Google Scholar] [CrossRef]
- Mehrabi, A.; Davari, A.R. Outwash flow measurement around the subscale tandem rotor in ground effect. Eng. Sci. Technol. Int. J. 2020, 23, 1374–1384. [Google Scholar] [CrossRef]
- Zhu, H.; Nie, H.; Wei, X.; Zhang, M. Design and experimental testing of safe flight control system for novel vertical take-off and landing aircraft. J. Vibroengineering 2022, 24, 481–500. [Google Scholar] [CrossRef]
- Zhu, H.; Nie, H.; Zhang, L.; Deng, S.; Wei, X. Aerodynamic Design Optimization of a Staggered Rotors Octocopter Based on Surrogate Model. J. Aerosp. Eng. 2021, 34, 04021036. [Google Scholar] [CrossRef]
- Leishman, J.G. Principles of Helicopter Aerodynamics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Kline, S.J.; Mcclintock, F.A. Describing Uncertainties in Single-Sample Experiments. Mech. Eng. 1953, 75, 3–8. [Google Scholar]
- Lakshminarayan, V.K.; Baeder, J.D. Computational Investigation of Microscale Coaxial-Rotor Aerodynamics in Hover. J. Aircr. 2010, 47, 940–955. [Google Scholar] [CrossRef]
- Lu, C.; Qi, H.; Xu, G. Unsteady flow field interaction of coaxial rotor. J. Aerosp. Power 2019, 34, 1459–1470. [Google Scholar] [CrossRef]

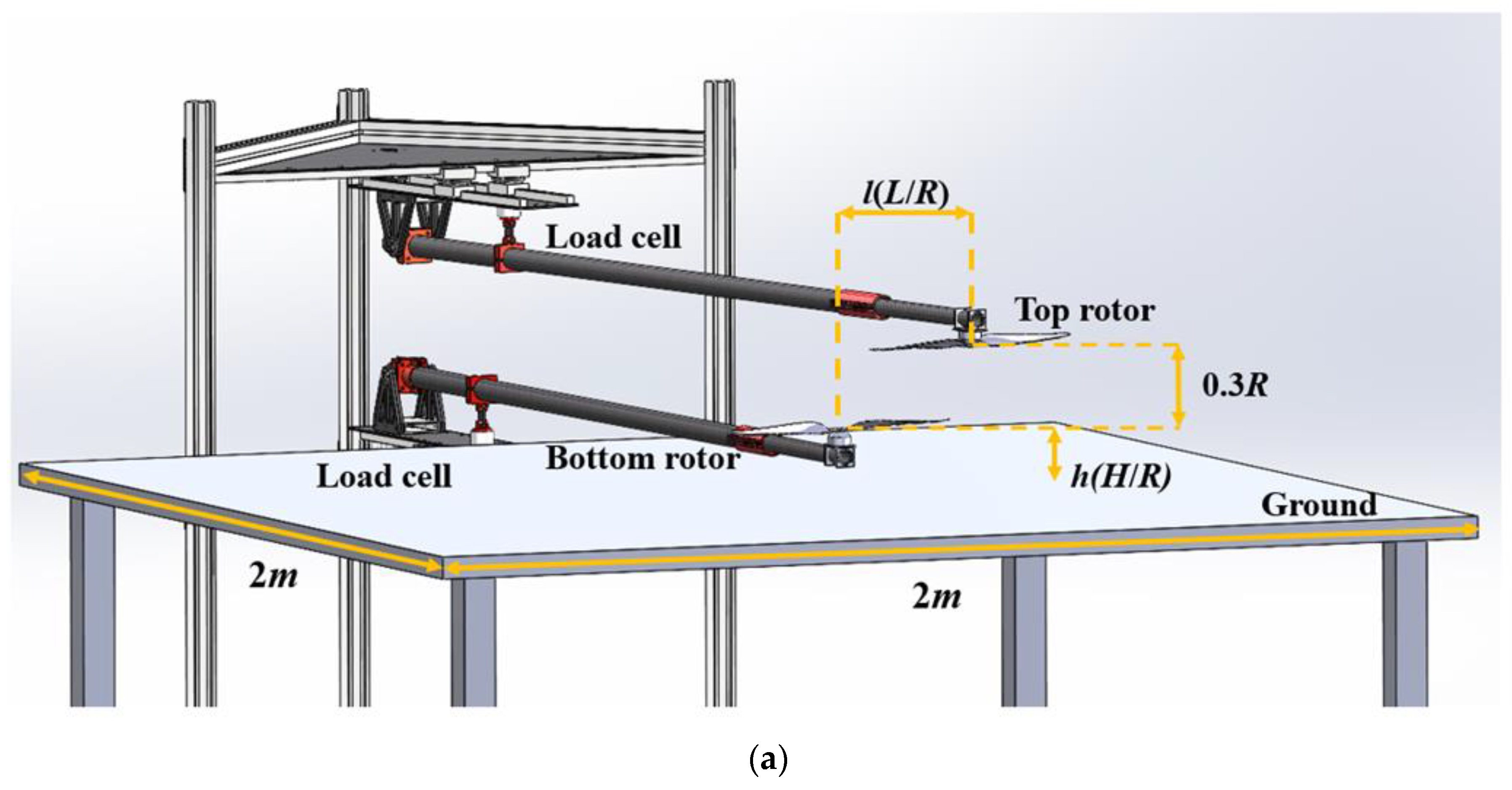
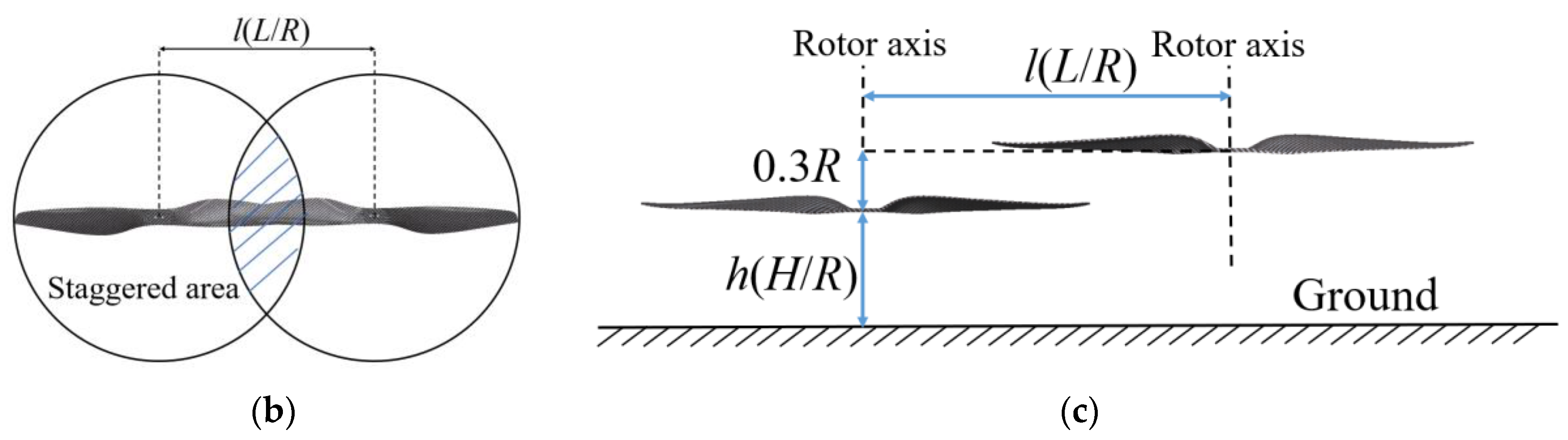
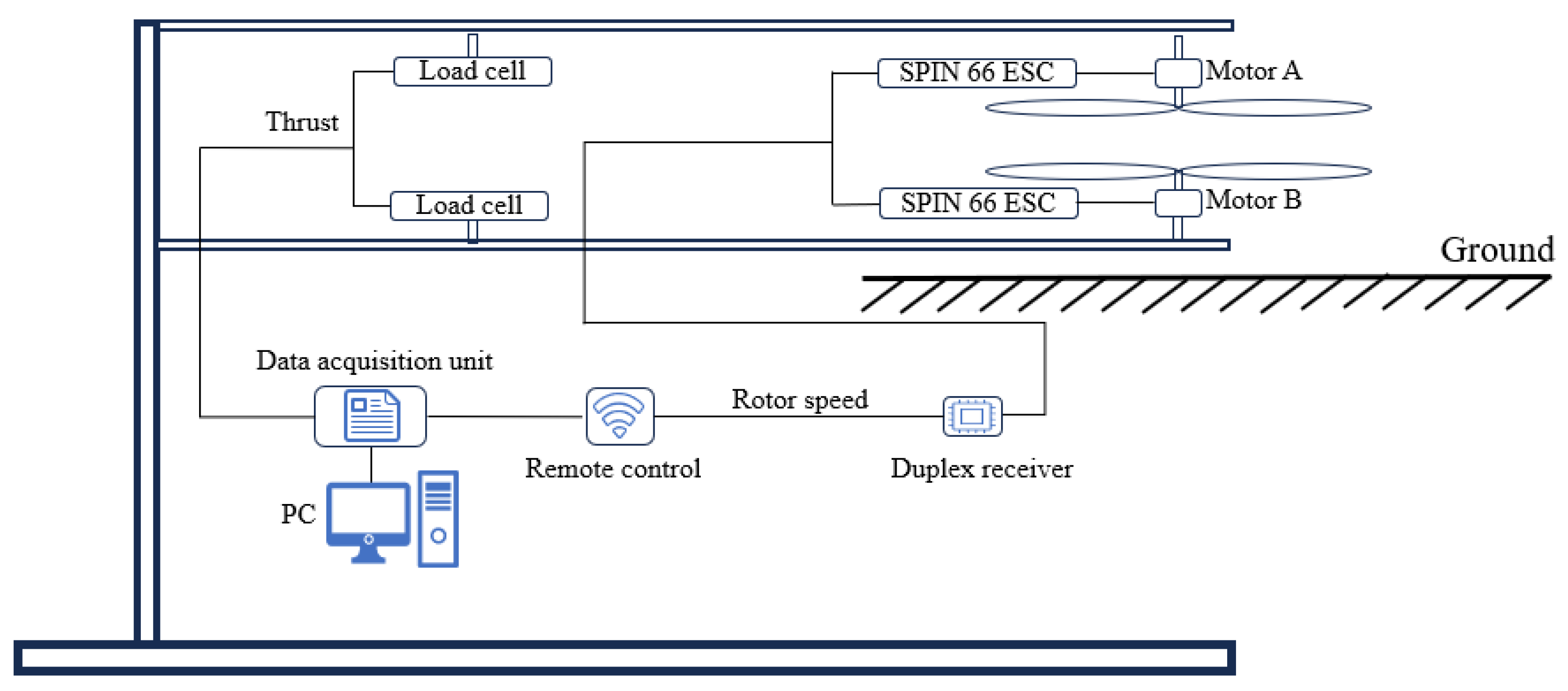






| Equipment | Details |
|---|---|
| Propeller | T-MOTOR 1855 (T-motor, Nanchang, China) |
| Motor | JFRC U4114 Brushless DC motor (KV: 320 RPM/V) (RCmodel, Yongzhou, Chnia) |
| Load cell | ZNLBM-IIX (Sensitivity: 1.5 mV/V) (Shenghongchuang, Xi’an, China) |
| Electronic governor | Master SPIN 66 Pro ESC (Provide angular velocity feedback) (JETI model, Hong Kong, China) |
| Receiver | JETI DUPLEX channel receiver (Signal reception) (JETI model, Hong Kong, China) |
| Variables | Values |
|---|---|
| RPM | 1000, 1500, 2000, 2500, 3000, 3500 |
| l | 0, 0.5, 1, 1.5, 2.0, 2.0 |
| h | 0.5, 1.0, 1.5, 2.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; Wei, S.; Nie, H.; Du, Y.; Wei, X. Ground Effect on the Thrust Performance of Staggered Rotor System. Drones 2024, 8, 118. https://doi.org/10.3390/drones8040118
Zhu H, Wei S, Nie H, Du Y, Wei X. Ground Effect on the Thrust Performance of Staggered Rotor System. Drones. 2024; 8(4):118. https://doi.org/10.3390/drones8040118
Chicago/Turabian StyleZhu, He, Shaoxiong Wei, Hong Nie, Yuhao Du, and Xiaohui Wei. 2024. "Ground Effect on the Thrust Performance of Staggered Rotor System" Drones 8, no. 4: 118. https://doi.org/10.3390/drones8040118
APA StyleZhu, H., Wei, S., Nie, H., Du, Y., & Wei, X. (2024). Ground Effect on the Thrust Performance of Staggered Rotor System. Drones, 8(4), 118. https://doi.org/10.3390/drones8040118







