Collaborative Task Allocation and Optimization Solution for Unmanned Aerial Vehicles in Search and Rescue
Abstract
:1. Introduction
2. Literature Review and Related Work
2.1. Models of Multi-UAV Collaborative Task Allocation for Search and Rescue
2.2. Algorithms of UAV Cooperative Task Allocation in Disaster Relief Operations
3. Description of the Problem and Multi-UAV Cooperative Task Allocation Method
3.1. Problem Description
3.2. Symbols and Decision-Making Variables
3.3. Effect of Loaded Materials on UAV Flight Time
3.4. Effect of Service Time on UAV Behaviour
3.5. Establishment of RMURPTW Model
4. Description of the Innovative Hybrid Algorithm
4.1. Particle Swarm Optimization
4.2. Grey Wolf Optimizer
- Encircling. Wolves surrounding their prey can be represented as:where is the distance between the prey and the wolves; and are the grey wolves position vector and the prey position vector, respectively; and are the coefficient vectors of the grey wolves; is the number of current iterations.where the convergence factor decreases linearly from 2 to 0 during the iteration; and are random variables on [0, 1]; has a range of [−2, 2], and is in [0, 2].
- Pursuing. Wolves , , and in the pack are closest to the prey, so the distance between the other grey wolves and these three wolves can be determined first, which in turn determines the best direction to attack the prey.where , , , , denotes the position vector of the grey wolf when it evolves to generation .
- Attacking. The last step of the prey behavior is attacking, which is the stage where the wolves need to hunt their prey; i.e., the GWO algorithm obtains the optimal solution. The attacking is mainly realized by a linear decrease of , making the positional adjustment coefficient vary in the interval . When , the wolves have an increased global search capability that contributes to the global search; when , the wolves are pushed to attack the prey.
4.3. Description of the PSOGWO Algorithm
4.3.1. Encoding and Decoding
- Update the position to according to the position update formula and find the minimum value and maximum value in .
- Apply an interval transformation to the components in , transforming to . The interval transformation formula is shown below:
- Rounding the components in makes become , i.e., changing continuous data to discrete data.
- At this point the components in are all positive integers between , but it may still not be possible to construct a full permutation of n. Keep only the first of the duplicate numbers in and fill in the rest by the numbers that do not appear to ensure the construction of a complete full permutation.
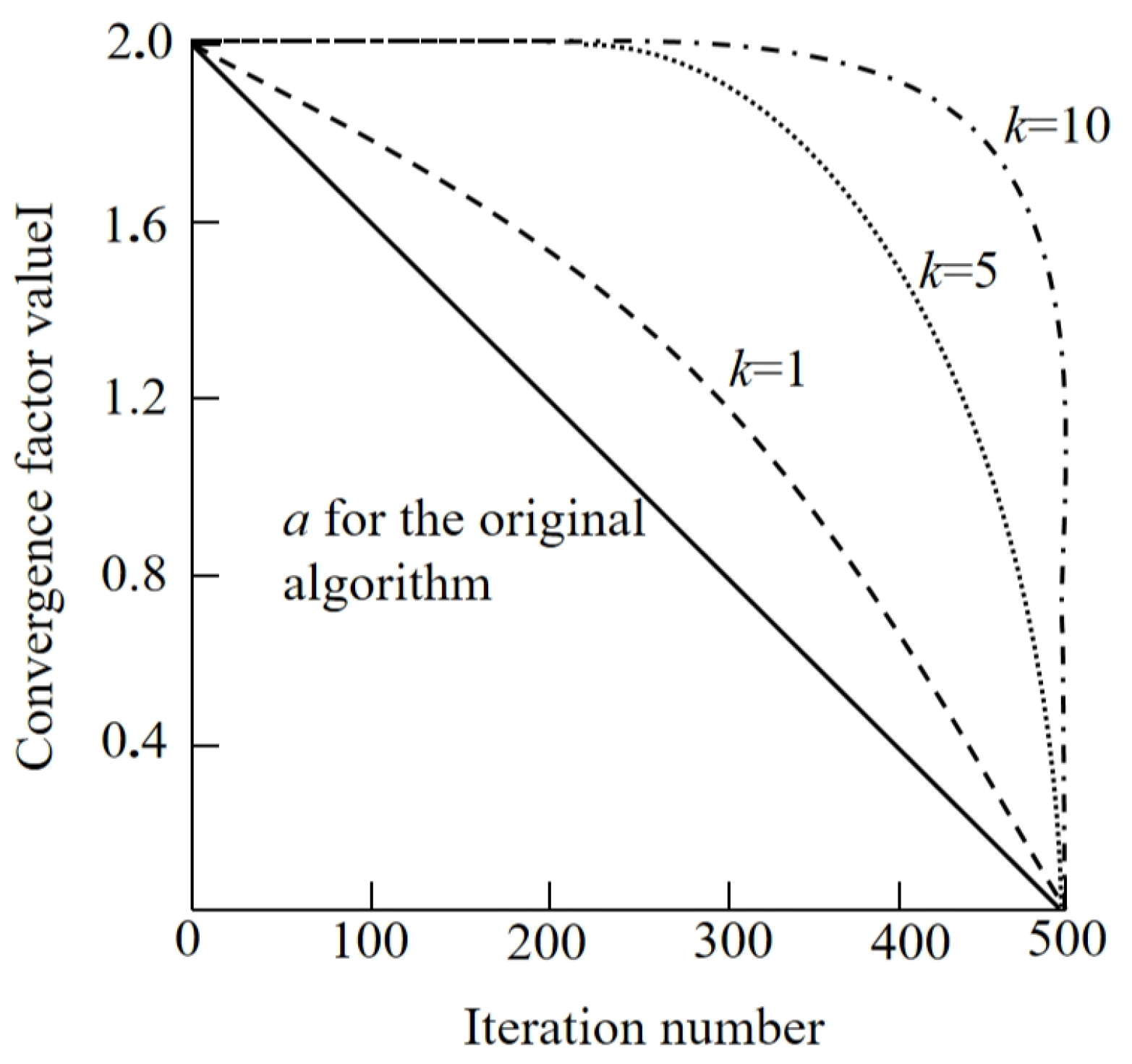
4.3.2. Nonlinear Convergence Factor
4.3.3. Individual Update Strategy
4.3.4. Dynamic Weighting Rules
4.3.5. The PSOGWO Algorithm Flow
- Step 1:
- Determine of initial population size, the maximum number of iterations and the current number of iterations .
- Step 2:
- Initialize individuals and groups of particles, initialize wolves, wolves, wolves.
- Step 3:
- Update the convergence factor according to Equation (25) and initialize and according to Equations (19) and (20), respectively.
- Step 4:
- Calculate the particle position using Equations (26)~(32).
- Step 5:
- Calculating the fitness of all particles, i.e., the rescue cost.
- Step 6:
- Updating individual best, and global best.
- Step 7:
- Update the velocity and position of the ith particle, and then add 1 to the current iteration number.
- Step 8:
- If the current iteration number is lower than , the particles update their positions according to Equations (26)~(32); if the maximum iteration number is attained, the loop is stopped and the optimal position is output.
5. Results
5.1. Experiments Setup
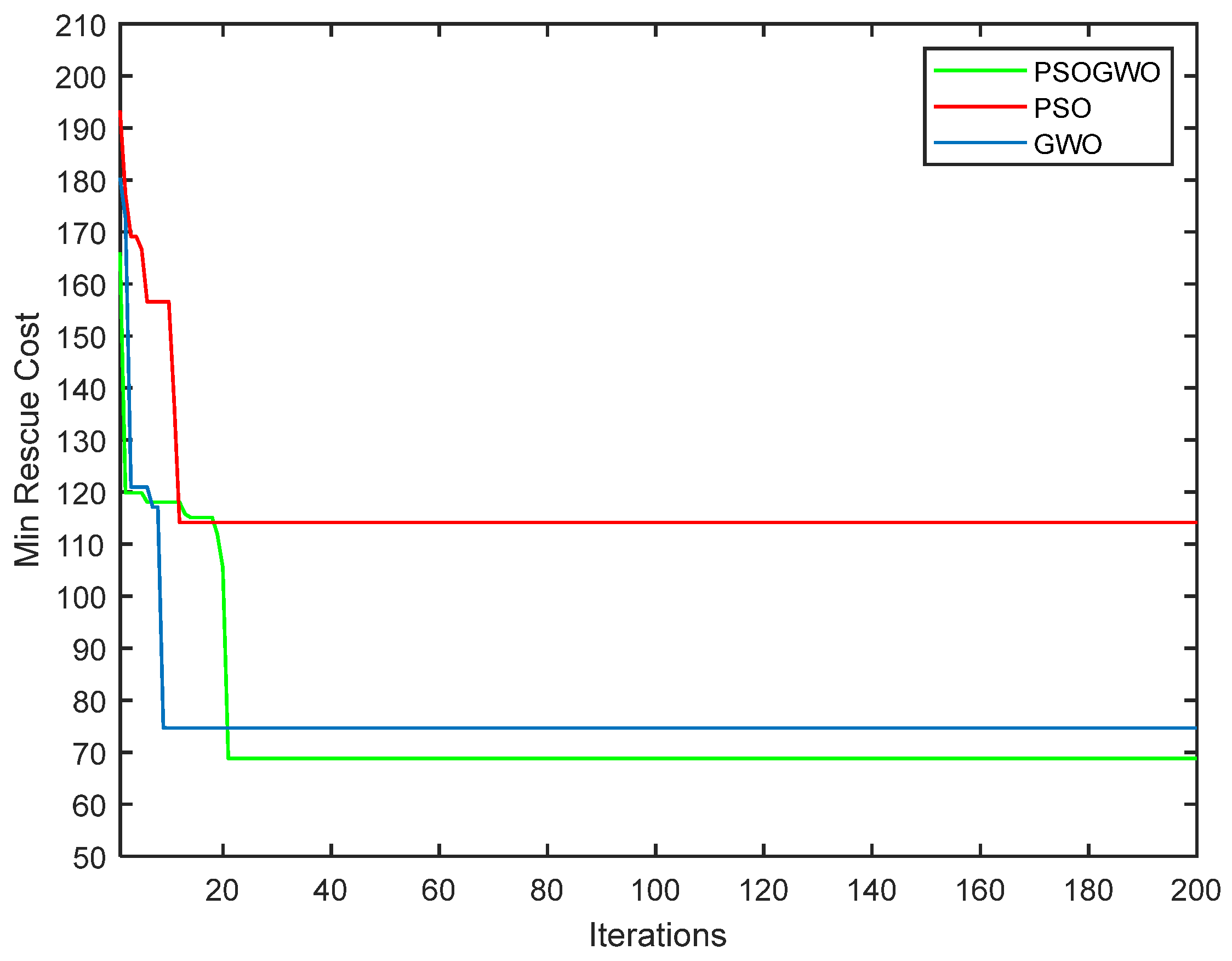
5.2. Comparison among Different Algorithm
5.3. The Optimal Allocation Results
5.4. Comparison among Multiple UAV
6. Discussion
6.1. The Use of Improved VRP Models in SAR
6.2. The PSOGWO Algorithm for Solving the Improved VRP in SAR
6.3. Comparison among Multiple UAV
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qi, J.; Song, D.; Shang, H.; Wang, N.; Hua, C.; Wu, C.; Qi, X.; Han, J. Search and rescue rotary-wing uav and its application to the lushan ms 7.0 earthquake. J. Field Robot. 2016, 33, 290–321. [Google Scholar] [CrossRef]
- Erdelj, M.; Król, M.; Natalizio, E. Wireless sensor networks and multi-UAV systems for natural disaster management. Comput. Netw. 2017, 124, 72–86. [Google Scholar] [CrossRef]
- Zhu, M.; Du, X.; Zhang, X.; Luo, H.; Wang, G. Multi-UAV rapid-assessment task-allocation problem in a postearthquake scenario. IEEE Access 2019, 7, 74542–74557. [Google Scholar] [CrossRef]
- Harikumar, K.; Senthilnath, J.; Sundaram, S. Multi-UAV oxyrrhis marina-inspired search and dynamic formation control for forest fire fighting. IEEE Trans. Autom. Sci. Eng. 2018, 16, 863–873. [Google Scholar] [CrossRef]
- Pham, H.; La, H.; Feil-Seifer, D.; Deans, M. A distributed control framework of multiple unmanned aerial vehicles for dynamic wildfifire tracking. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 1537–1548. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, R. Wireless communications with unmanned aerial vehicles: Opportunities and challenges. IEEE Commun. 2016, 54, 36–42. [Google Scholar] [CrossRef]
- Sharma, A.; Vanjani, P.; Paliwal, N.; Basnayaka, C.; Jayakody, D.; Wang, H.; Muthuchidambaranathan, P. Communication and networking technologies for UAVs: A survey. J. Netw. Comput. Appl. 2020, 168, 102739. [Google Scholar] [CrossRef]
- Alzahrani, B.; Oubbati, O.S.; Barnawi, A.; Atiquzzaman, M.; Alghazzawi, D. UAV assistance paradigm: State-of-the-art in applications and challenges. J. Netw. Comput. Appl. 2020, 166, 102706. [Google Scholar] [CrossRef]
- Jevtiü, A.; Andina, D.; Jaimes, A.; Gomez, J.; Jamshidi, M. Unmanned Aerial Vehicle route optimization using ant system algorithm. In Proceedings of the 2010 5th International Conference on System of Systems Engineering, Loughborough, UK, 22–24 June 2010; pp. 1–6. [Google Scholar]
- Zillies, J.; Westphal, S.; Scheidt, D.; Thakur, D.; Kumar, V.; Pappas, G.; Scheidt, D. A Column Generation Approach for Optimized Routing and Coordination of a UAV Fleet. In Proceedings of the 2016 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Lausanne, Switzerland, 23–27 October 2016; pp. 350–357. [Google Scholar]
- Bakhshipour, M.; Jabbari Ghadi, M.; Namdari, F. Swarm robotics search and rescue: A novel artificial intelligence-inspired optimization approach. Appl. Soft Comput. 2017, 57, 708–726. [Google Scholar] [CrossRef]
- Senthilkumar, K.; Bharadwaj, K. Multi-robot exploration and terrain coverage in an unknown environment. Robot. Auton. Syst. 2012, 60, 123–132. [Google Scholar] [CrossRef]
- Kim, Y.-D.; Son, G.-J.; Kim, H.; Song, C.; Lee, J.-H. Smart disaster response in vehicular tunnels: Technologies for search and rescue applications. Sustainability 2018, 10, 2509. [Google Scholar] [CrossRef]
- Lodeiro-Santiago, M.; Santos-González, I.; Caballero-Gil, P.; Caballero-Gil, C. Secure system based on UAV and BLE for improving SAR missions. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 3109–3120. [Google Scholar] [CrossRef]
- Beck, Z.; Teacy, L.; Rogers, A. Online Planning for Collaborative Search and Rescue by Heterogeneous Robot Teams; In Proceedings ofthe 15th International Conference on Autonomous Agents and Multiagent Systems, Singapore, 9–13 May 2016.
- Choi, S.; Zhu, W. Performance Optimisation of Mobile Robots for Searchand-Rescue. Appl. Mech. Mater. 2012, 232, 403–407. [Google Scholar] [CrossRef]
- Chatziparaschis, D.; Lagoudakis, M.G.; Partsinevelos, P. Aerial and ground robot collaboration for autonomous mapping in search and rescue missions. Drones 2020, 4, 79. [Google Scholar] [CrossRef]
- Straub, J.; Marsh, R.; Mohammad, A. Robotic disaster recovery efforts with adhoc deployable cloud computing. In Sensors, and Command, Control, Communications, and Intelligence (C3I) Technologies for Homeland Security and Homeland Defense XII; SPIE: Bellingham, WA, USA, 2013; Volume 8711, pp. 163–166. [Google Scholar]
- Kurdi, H.; Al-Megren, S.; Aloboud, E.; Alnuaim, A.A.; Alomair, H.; Alothman, R.; Muhayya, A.B.; Alharbi, N.; Alenzi, M.; Youcef-Toumi, K. Bee-inspired task allocation algorithm for multi-UAV search and rescue missions. Int. J. Bio-Inspired Comput. 2020, 16, 252–263. [Google Scholar] [CrossRef]
- Ding, Y.; Pan, Q. Path Planning for Mobile Robot Search and Rescue based on Improved Ant Colony Optimization Algorithm. Appl. Mech. Mater. 2011, 66, 1039–1044. [Google Scholar] [CrossRef]
- Abdulsaheb, J.A.; Kadhim, D.J. Classical and heuristic approaches for mobile robot path planning: A survey. Robotics 2023, 12, 93. [Google Scholar] [CrossRef]
- Majeed, A.; Hwang, S.O. A multi-objective coverage path planning algorithm for UAVs to cover spatially distributed regions in urban environments. Aerospace 2021, 8, 343. [Google Scholar] [CrossRef]
- Shima, T.; Rasmussen, S.; Sparks, A.; Passino, K. Multiple task allocations for cooperating uninhabited aerial vehicles using genetic algorithms. Comput. Oper. Res. 2006, 33, 3252–3269. [Google Scholar] [CrossRef]
- Ye, F.; Chen, J.; Tian, Y.; Jiang, T. Cooperative task allocation of a heterogeneous multi-UAV system using an adaptive genetic algorithm. Electronics 2020, 9, 687. [Google Scholar] [CrossRef]
- Hayat, S.; Yanmaz, E.; Brown, T.; Bettstetter, C. Multi-objective UAV path planning for search and rescue. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May 2017–3 June 2017; pp. 5569–5574. [Google Scholar]
- Pishkenari, H.; Mahboobi, S.; Alasty, A. Optimum synthesis of fuzzy logic controller for trajectory tracking by differential evolution. Sci. Iran. 2011, 18, 261–267. [Google Scholar] [CrossRef]
- Couceiro, M.; Rocha, R.; Ferreira, N. Ensuring ad hoc connectivity in distributed search with Robotic Darwinian Particle Swarms. In Proceedings of the 2011 IEEE International Symposium on Safety, Security, and Rescue Robotics, , Kyoto, Japan, 1–5 November 2011; pp. 284–289. [Google Scholar]
- Abdelkader, M.; Koubaa, A. Unmanned Aerial Vehicles Applications: Challenges and Trends; Springer: Cham, Switzerland, 2023; p. 127. [Google Scholar]
- Madridano, Á.; Al-Kaff, A.; Martín, D.; de la Escalera, A. Trajectory planning for multi-robot systems: Methods and applications. Expert Syst. Appl. 2021, 173, 114660. [Google Scholar] [CrossRef]
- Kurdi, H.A.; Aloboud, E.; Alalwan, M.; Alhassan, S.; Alotaibi, E.; Bautista, G.; How, J.P. Autonomous task allocation for multi-UAV systems based on the locust elastic behavior. Appl. Soft Comput. 2018, 71, 110–126. [Google Scholar] [CrossRef]
- Oh, G.; Kim, Y.; Ahn, J. Market-based task assignment for cooperative timing missions in dynamic environments. J. Intell. Robot. Syst. 2017, 87, 97–123. [Google Scholar] [CrossRef]
- Hassanalian, M.; Abdelkefi, A. Classifications, applications, and design challenges of drones: A review. Prog. Aerosp. Sci. 2017, 91, 99–131. [Google Scholar] [CrossRef]
- Technical Specifications of MK8-3500 Standard. Available online: https://files.mikrokopter.de/EN_mk8_flyer.pdf (accessed on 25 January 2017).
- Shankar, K.; Eswaran, P. Secure Visual Secret Share (VSS) Creation Scheme in Visual Cryptography using Elliptic Curve Cryptography with Optimization Technique. Aust. J. Basic Appl. Sci. 2015, 9, 150–163. [Google Scholar]
- Kumar, R.; Singh, L.; Tiwari, R. Path Planning for the Autonomous Robots Using Modified Grey Wolf Optimization Approach. J. Intell. Fuzzy Syst. 2021, 40, 9453–9470. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Almomani, O. A Features Selection Model for Net-work Instrusion Dection System Based on PSO, GWO, FFA and GA algorithms. Symmetry 2020, 12, 1046. [Google Scholar] [CrossRef]
- Salmen, A.; Ahmad, I.; Al Madani, S. Particle swarm optimization for task allocation problem. Microprocess. Microsyst. 2002, 26, 363–371. [Google Scholar] [CrossRef]
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle swarm optimization: A comprehensive survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]

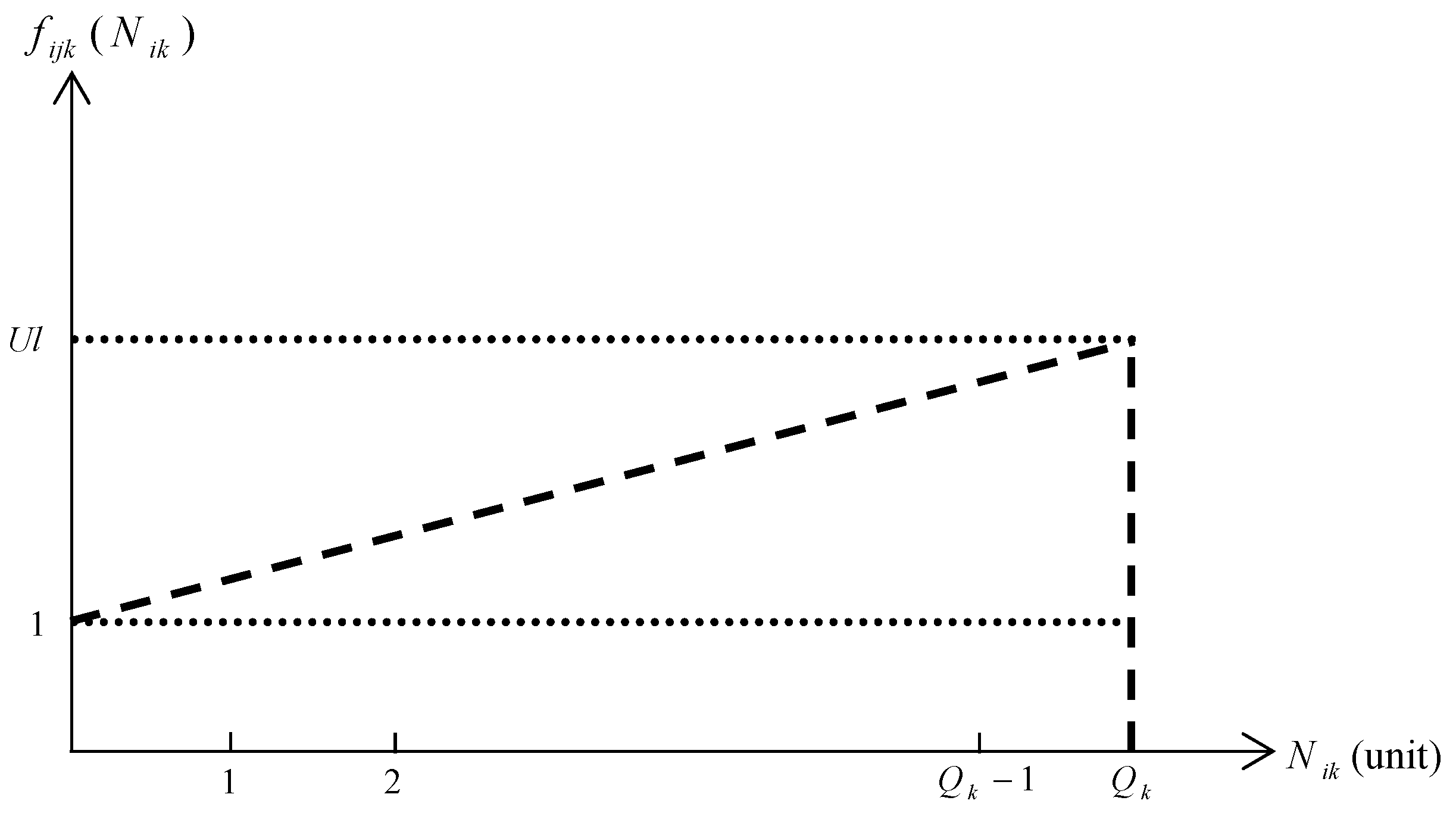

| Notation | Explanation |
|---|---|
| , directed graphdata | |
| set of rescue target points, | |
| set of all vertices, , represent a base | |
| index of rescue target points, | |
| set of arcs, where denote the arcs between nodes | |
| distance between the rescue target points and | |
| group of homogeneous UAVs, | |
| earliest time window of the rescue target point | |
| optimal early time window for the rescue target point | |
| optimal last time window for the rescue target point | |
| latest time window of the rescue target point | |
| service time of the UAV at the rescue target point to complete the mission | |
| demands of the rescue target point | |
| load capacity of UAV | |
| the maximum flight distance traveled by UAV | |
| starting service time of UAV on point | |
| decision-making variable. If UAV travels in link , , else, | |
| decision-making variable. 1, if UAV is being used, 0, otherwise | |
| the service start time for UAV at point | |
| time for UAV to arrive at point | |
| traveled distance for UAV after visiting point i | |
| cost per unit distance traveled for UAV | |
| fixed sortie costs for UAV | |
| UAV waiting cost per unit of time | |
| UAV penalty cost per unit of time |
| Rescue Mission No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 2 | 2 | 2 | 3 | 3 | |
| 1 | 4 | 3 | 1 | 2 | 2 | 1 |
| UAV No. | Decoding Scheme |
|---|---|
| 1 | 0 → 1 → 0 |
| 2 | 0 → 4 → 5 → 3 → 2 → 0 |
| 3 | 0 → 7 → 6 → 0 |
| Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Need/kg | 8 | 6 | 4.5 | 2.2 | 7.5 | 11 | 2 | 1.5 | 5 | 7.5 |
| Number | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| X Coordinate | 1.9 | 0 | 0.2 | 1.1 | 1.6 | 1.4 | 1.8 | 3.5 | 4.3 | 2 | 3.2 |
| Y Coordinate | 0.9 | 0.9 | 1.4 | 1.7 | 0 | 2.1 | 1.9 | 1.6 | 0.2 | 2.4 | 2.9 |
| Number | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Start Window | 14:00 | 14:21 | 14:02 | 14:04 | 14:05 | 14:15 | 14:11 | 14:05 | 14:02 | 14:05 | 14:09 |
| End Window | 14:30 | 14:27 | 14:03 | 14:05 | 14:06 | 14:21 | 14:14 | 14:10 | 14:04 | 14:07 | 14:15 |
| UAV | Route | Flight Range/km |
|---|---|---|
| UAV1 | 0 → 2 → 1 → 0 | 2.31 |
| UAV2 | 0 → 3 → 0 | 2.26 |
| UAV3 | 0 → 4 → 6 → 0 | 3.86 |
| UAV4 | 0 → 8 → 7 → 10 → 0 | 7.54 |
| UAV5 | 0 → 9 → 5 → 0 | 3.47 |
| Capacity | N-UAV | Routes | Rescue Time/s | Rescue Cost/$ |
|---|---|---|---|---|
| 20 | 9 | 0 → 3 → 11 → 17 → 0; 0 → 7 → 12 → 0; 0 → 18 → 14 → 10 → 0; 0 → 13 → 2 → 0; 0 → 4 → 1 → 6 → 0; 0 → 12 → 5 → 0; 0 → 15 → 20 → 0; 0 → 16 → 5 → 8 → 0; 0 → 9 → 19 → 0; | 10,500 | 152 |
| 30 | 7 | 0 → 10 → 17 → 5 → 14 → 0; 0 → 13 → 2 → 6 → 0; 0 → 10 → 9 → 3 → 0; 0 → 12 → 11 → 20 → 0; 0 → 15 → 8 → 0; 0 → 16 → 19 → 7 → 1 → 0; 0 → 18 → 4 → 0; | 9826 | 246 |
| 40 | 5 | 0 → 14 → 16 → 9 → 0; 0 → 20 → 15 → 8 → 7 → 4 → 0; 0 → 19 → 11 → 6 → 0; 0 → 18 → 12 → 1 → 2 → 0; 0 → 13 → 17 →10 → 5 → 3 → 0; | 8905 | 380 |
| 50 | 5 | 0 → 8 → 14 → 15 → 20 → 9 → 1 → 0; 0 → 18 → 16 → 3 → 0; 0 → 15 → 6 → 7 → 4 → 0; 0 → 19 → 12 → 5 → 0; 0 →17 → 10 → 13 → 11 → 2 → 0; | 8689 | 530 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, D.; Jiang, H.; Wang, L.; Zhu, X.; Chen, Y.; Yu, Q. Collaborative Task Allocation and Optimization Solution for Unmanned Aerial Vehicles in Search and Rescue. Drones 2024, 8, 138. https://doi.org/10.3390/drones8040138
Han D, Jiang H, Wang L, Zhu X, Chen Y, Yu Q. Collaborative Task Allocation and Optimization Solution for Unmanned Aerial Vehicles in Search and Rescue. Drones. 2024; 8(4):138. https://doi.org/10.3390/drones8040138
Chicago/Turabian StyleHan, Dan, Hao Jiang, Lifang Wang, Xinyu Zhu, Yaqing Chen, and Qizhou Yu. 2024. "Collaborative Task Allocation and Optimization Solution for Unmanned Aerial Vehicles in Search and Rescue" Drones 8, no. 4: 138. https://doi.org/10.3390/drones8040138
APA StyleHan, D., Jiang, H., Wang, L., Zhu, X., Chen, Y., & Yu, Q. (2024). Collaborative Task Allocation and Optimization Solution for Unmanned Aerial Vehicles in Search and Rescue. Drones, 8(4), 138. https://doi.org/10.3390/drones8040138






