Computer Vision-Based Path Planning with Indoor Low-Cost Autonomous Drones: An Educational Surrogate Project for Autonomous Wind Farm Navigation
Abstract
:1. Introduction
- Maximizing inspection coverage: Path planning algorithms help determine the most efficient routes for drones to follow while ensuring complete coverage of the wind turbine farms [8]. A well-developed path planning algorithm can ensure thorough inspection and reduce the risk of undetected turbines by minimizing the overlaps and avoiding missed areas.
- Time and cost efficiency: Proper path planning enables drones to navigate optimal routes based on relative distances and weather, minimizing unnecessary flight time and energy consumption [9]. By reducing the inspection time, path planning contributes to cost savings and increases the overall efficiency of wind turbine inspection.
- Collision avoidance and safety: Path planning algorithms incorporate collision avoidance mechanisms to prevent accidents and ensure the safety of the drone, wind turbine, and surrounding structures [10]. By considering the physical constraints and obstacles in the environment, path planning algorithms guide drones in a safe and controlled manner.
- Data accuracy and consistency: Well-planned inspection paths facilitate consistent data collection, ensuring uniform image and sensor data quality around the points of interest [11]. This improves data collection for machine learning (ML) model training and enables accurate results when the trained ML models are tested for crack and anomaly detection.
- Indoor navigation: GPS signals are often unreliable indoors due to signal blockage or multipath effects. Computer vision allows drones to navigate indoor environments where GPS signals are weak or nonexistent [19].
- Precision and accuracy: Computer vision enables drones to perceive their surroundings with high precision, allowing for obstacle avoidance and enhanced path planning when combined with GPS data. This is crucial for tasks that require precise movements, such as inspection of infrastructure or delivery in dense urban areas [4,15].
- Real-time adaptability: Computer vision systems can process real-time data from cameras, enabling drones to adapt their paths on the fly, based on changing environmental conditions or unexpected obstacles. This adaptability is essential for safe and efficient drone operations [20].
- Security: GPS signals can be susceptible to jamming or spoofing attacks, compromising the security of drone navigation [21]. Computer vision-based systems are less vulnerable to such attacks, enhancing the security of drone operations. Thus, taking advantage of the combination of GPS data and computer vision through the live camera feed of the drone is beneficial.
- Collaborative swarm robotics: Drones often work in swarms for environmental monitoring or search and rescue missions. Computer vision enables drones to communicate and coordinate with each other, leading to more efficient swarm behavior without relying solely on GPS signals [22].
- Research and development: Advancements in computer vision algorithms and hardware technology have opened up new avenues for research and development. Researchers are exploring innovative techniques such as simultaneous localization and mapping (SLAM) [23] and deep learning-based object recognition to enhance drone navigation capabilities.
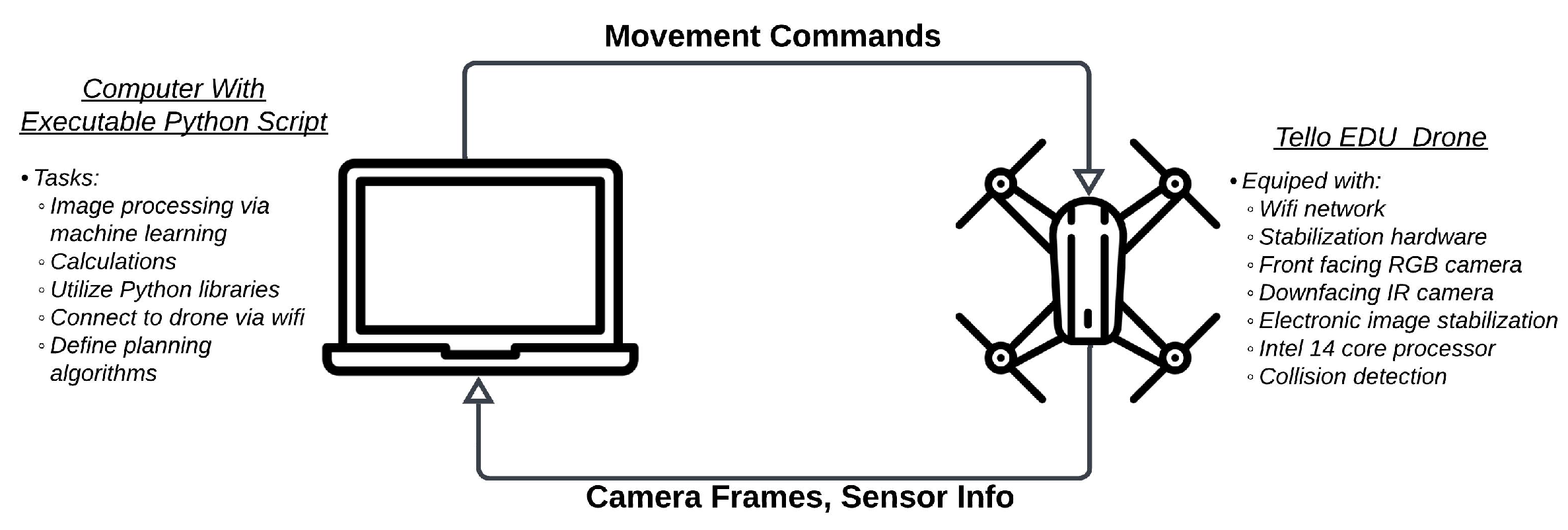
- Computer vision-based path planning: A path planning approach for autonomous drones that relies on computer vision techniques is proposed. This approach enables drones to navigate based on front and bottom-facing visuals to aid in GPS-based inspections or where GPS signals are weak or unavailable.
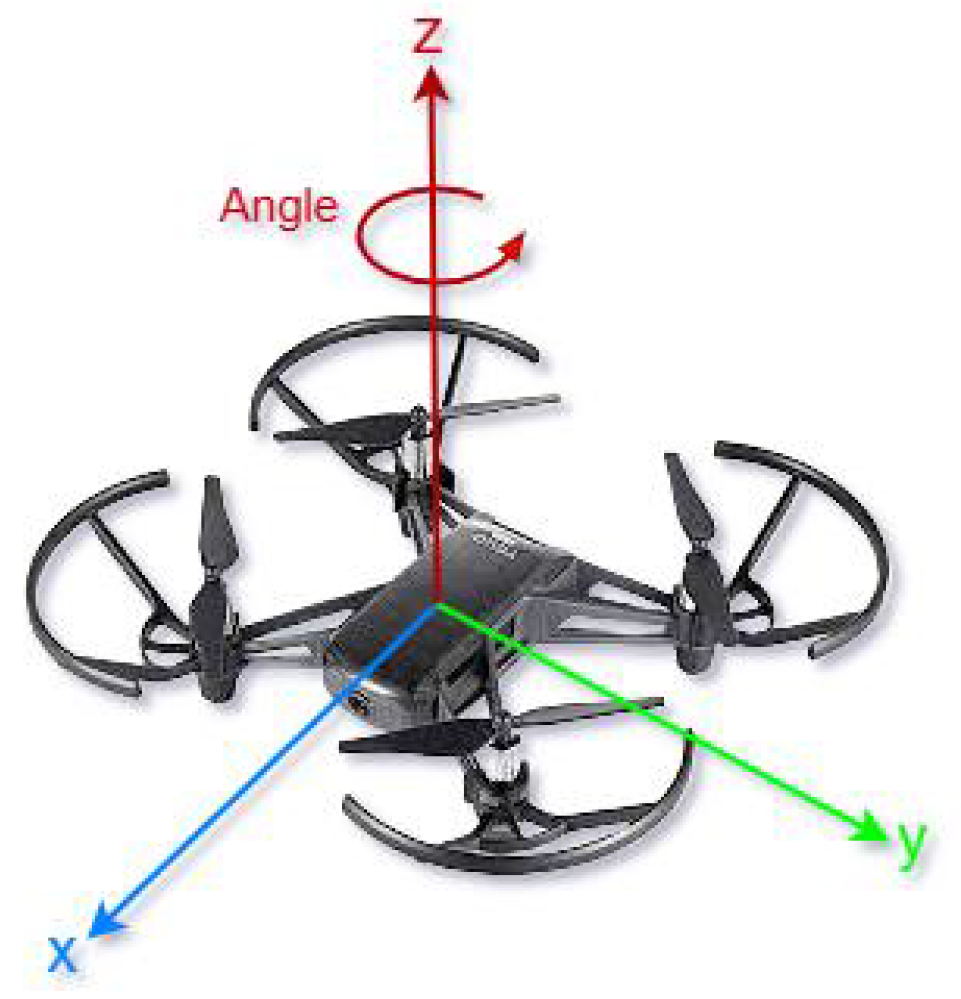
- Indoor navigation of low-cost autonomous drones: The research demonstrates that it is possible to develop low-cost autonomous drone systems that can perform complex tasks in indoor environments such as real-time decision-making, adaptability, determining real positions on the defined Cartesian coordinate system (CCS), and self-correction of its position as necessary without the use of GPS.
- Small-scale proof of concept: The research provides a small-scale proof of concept for indoor navigation that surrogates wind farm navigation and computer vision-based adaptability.
- Educational aspects and applications: This paper also resembles a project that can be used in machine learning and drone-related introductory courses. The GitHub repository with a README.md file showing how to use the developed autonomous drone system with functions, drone commands, images, and videos, is included. Such tools to accelerate on-boarding can be reused for various applications and lectures. In addition, the pseudo-code has been provided for implementation in Algorithms 1–4. The effectiveness of the developed computer vision-based navigation system for low-cost drones is attractive for educational purposes.
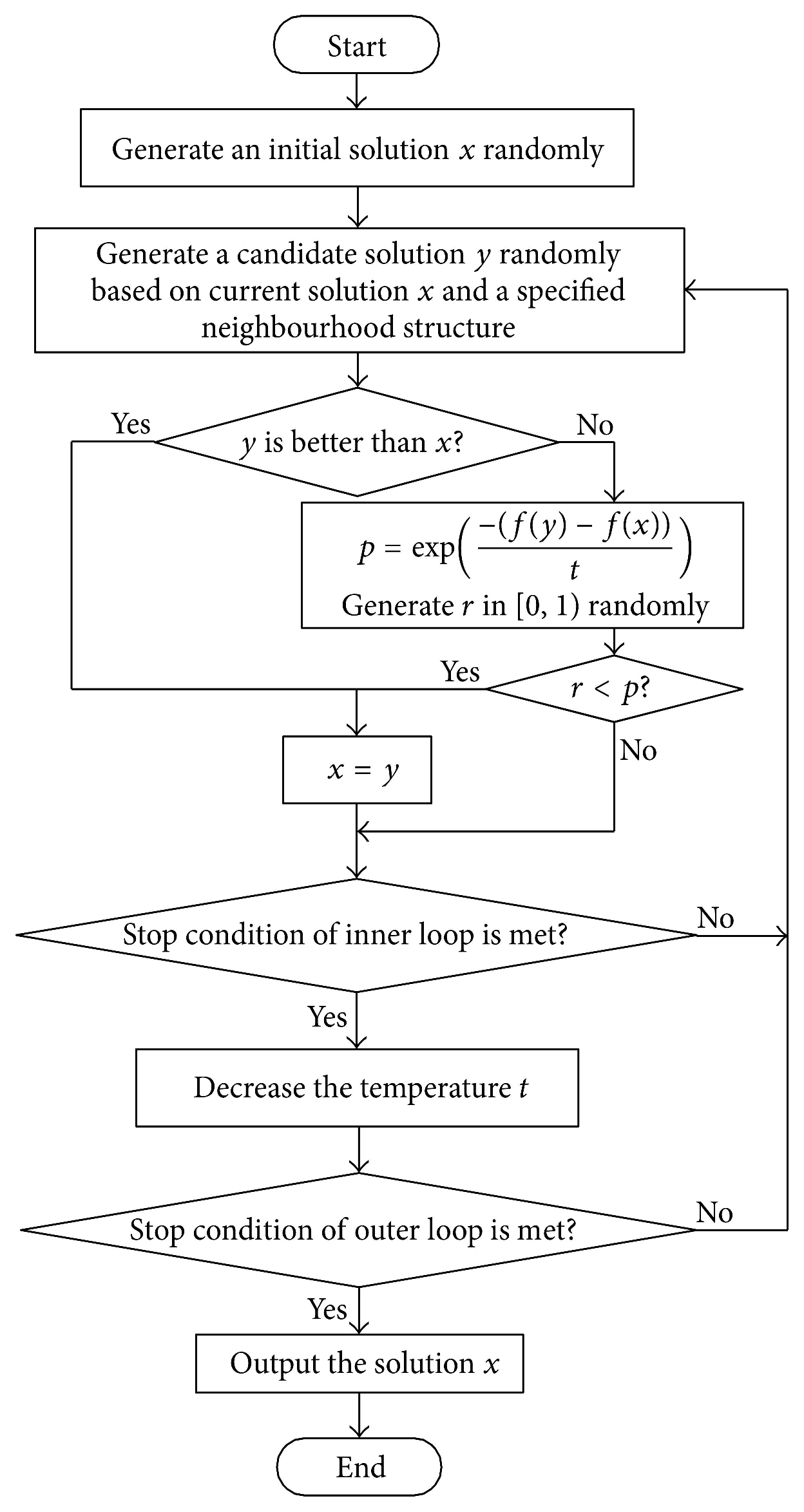
| Algorithm 1 Simulated annealing traveling salesman (SATS). |
|
| Algorithm 2 Coordinate calibration algorithm (CCA). |
| Inputs: fan identification per QR code identification of expected fan to be found Outputs: newly updated x coordinate of drone newly updated y coordinate of drone
|
| Algorithm 3 Robust coordinate calibration algorithm (RCCA). |
| Inputs: fan identification of the QR code scanned identification of expected fan to be found Outputs: newly updated x coordinate of drone newly updated y coordinate of drone
|
| Algorithm 4 Snake path flight algorithm (SPFA). |
| Inputs: Step length the drone moves forward and backward Step length the drone moves left -axis boundary of experiment -axis boundary of experiment Functions: if there are no fans detected in the frame then return else Move the drone laterally to center the fan in the frame Move the drone forward toward the fan, stopping in close proximity Lower the drone and move closer to the fan to be in range to read the QR code Once the QR code is in a readable range and scanned, raise the drone back to the original height end if
|
2. Previous Related Works
3. Proposed Autonomous Path Planning for Indoor Cartesian Coordinate System
- Link: GitHub repository: Surrogate wind farm navigation with the Tello EDU drone: https://github.com/MoShekaramiz/Tello_Edu_Surrogated_Wind_Fram.
3.1. Simulated Annealing
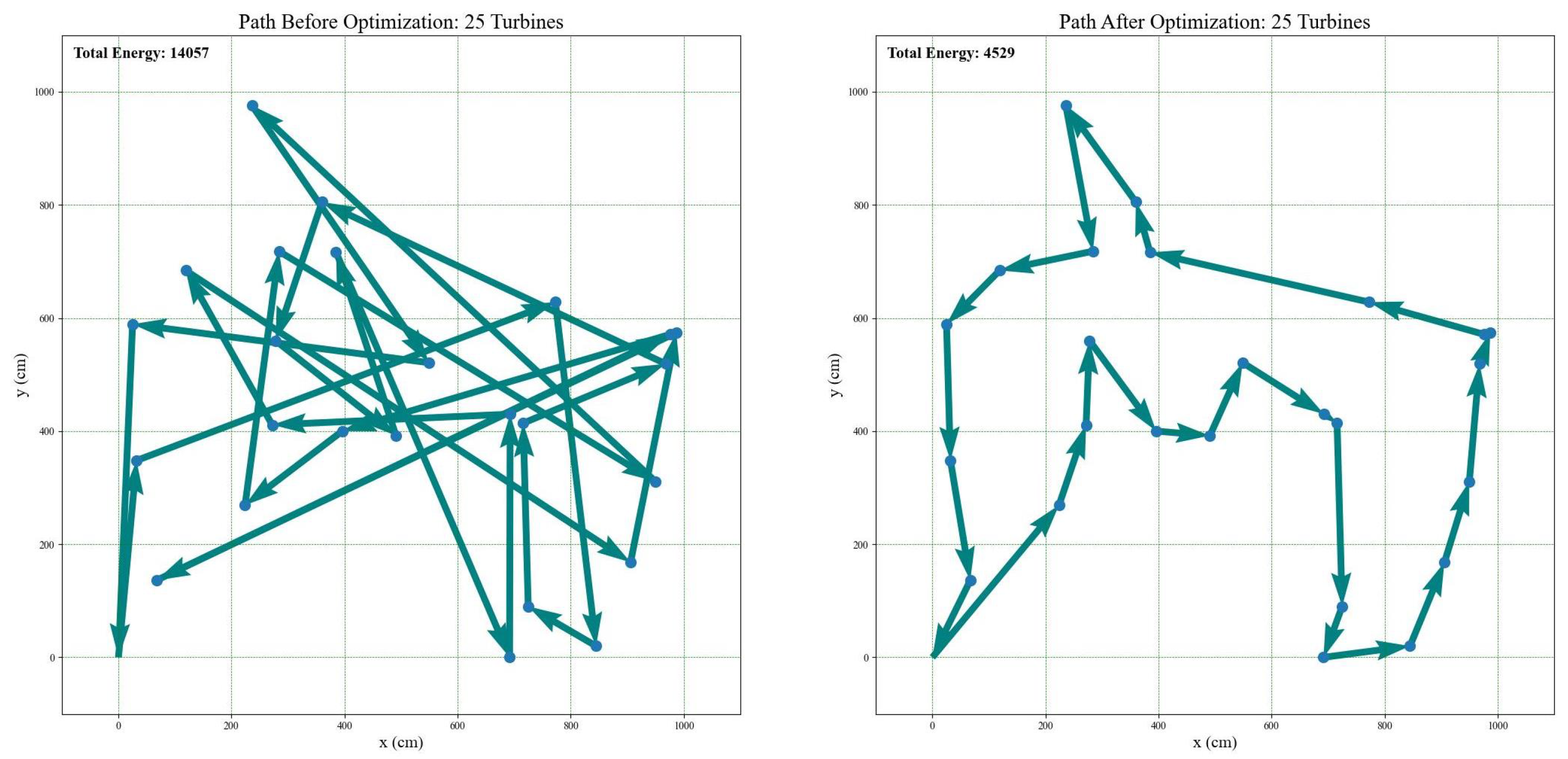
3.2. Generating Optimized Traveling Salesman Path in Python
- Link: GitHub repository: Surrogate wind farm navigation with the Tello EDU drone: https://github.com/MoShekaramiz/Tello_Edu_Surrogated_Wind_Fram.
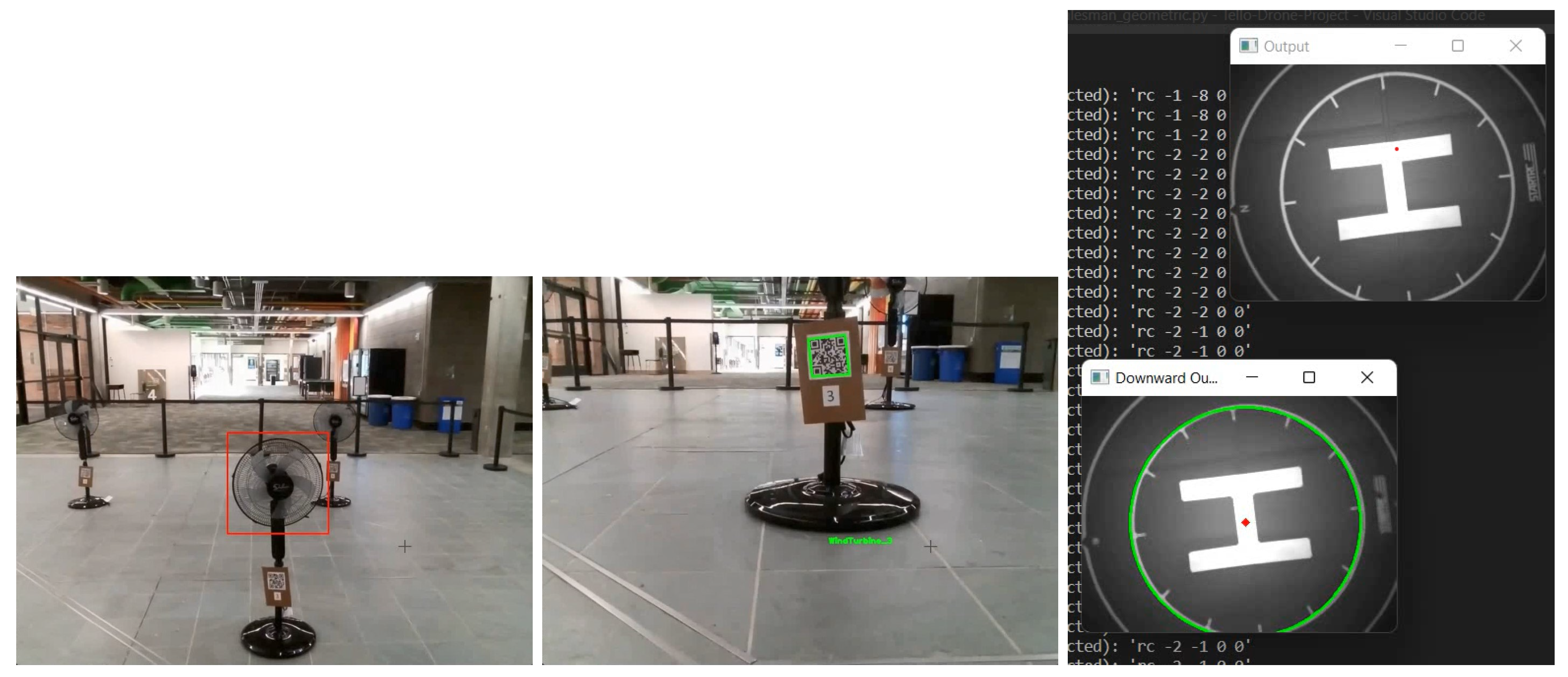
4. Proposed Computer Vision-Based Navigation
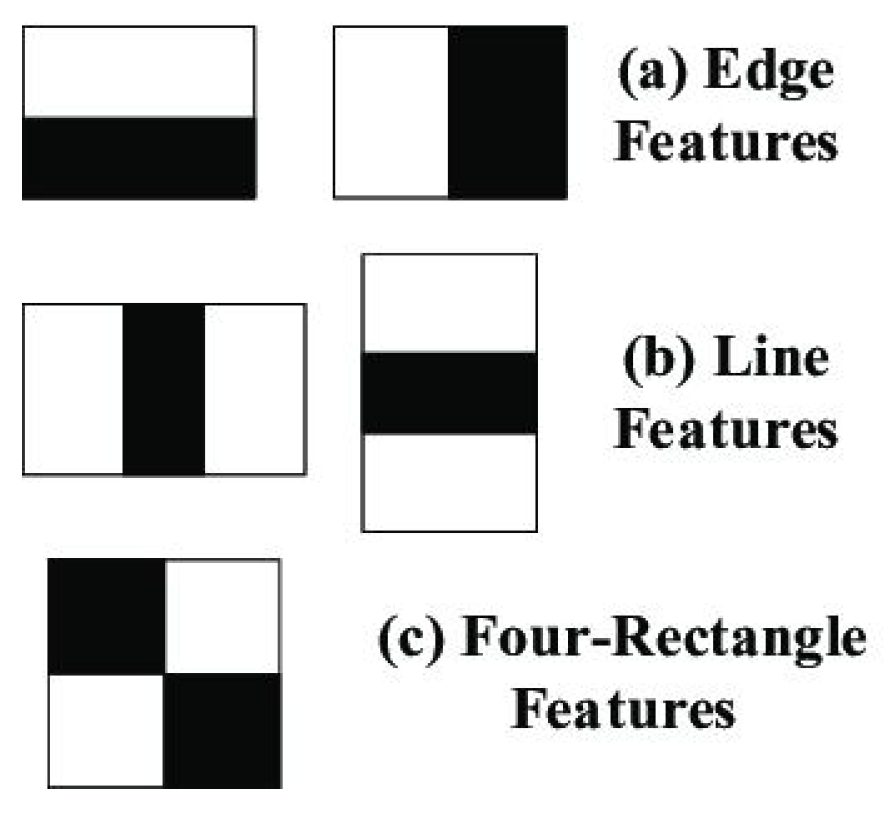
4.1. Object Detection via Cascade Classifier
- Link: GitHub repository: Surrogate wind farm navigation with the Tello EDU drone: https://github.com/MoShekaramiz/Tello_Edu_Surrogated_Wind_Fram.
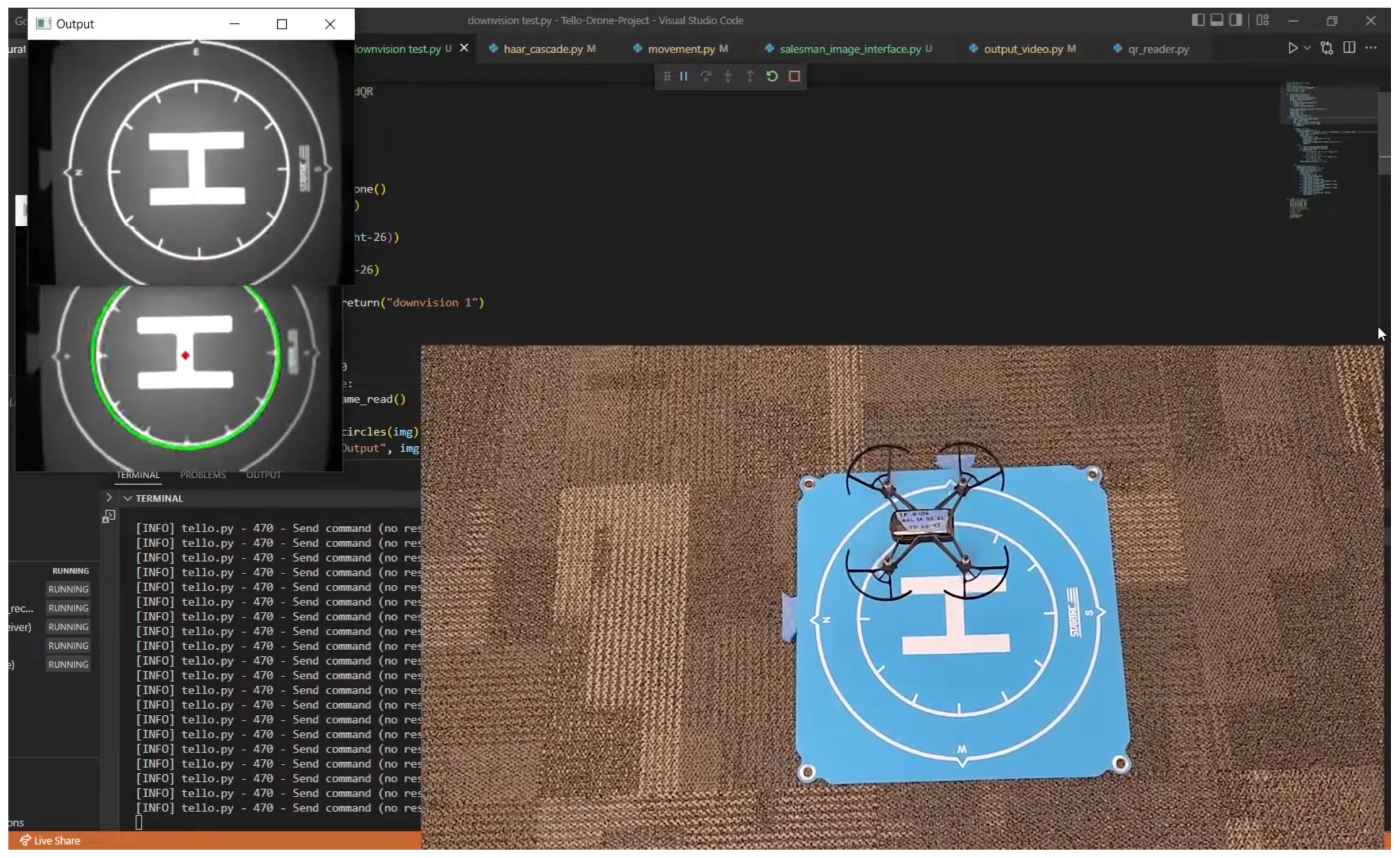
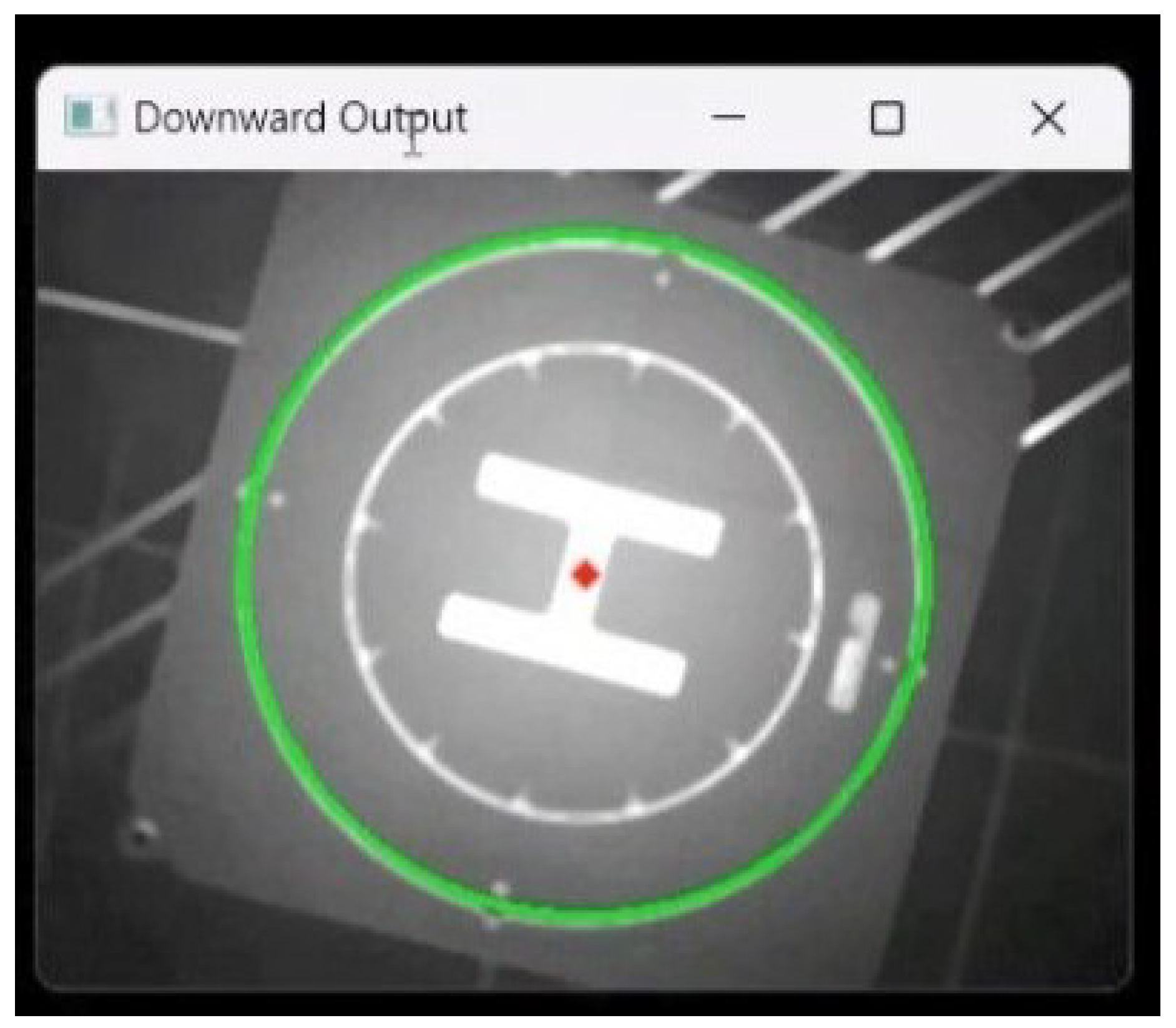
4.2. Vision Positioning System for Calibration and Precise Landing
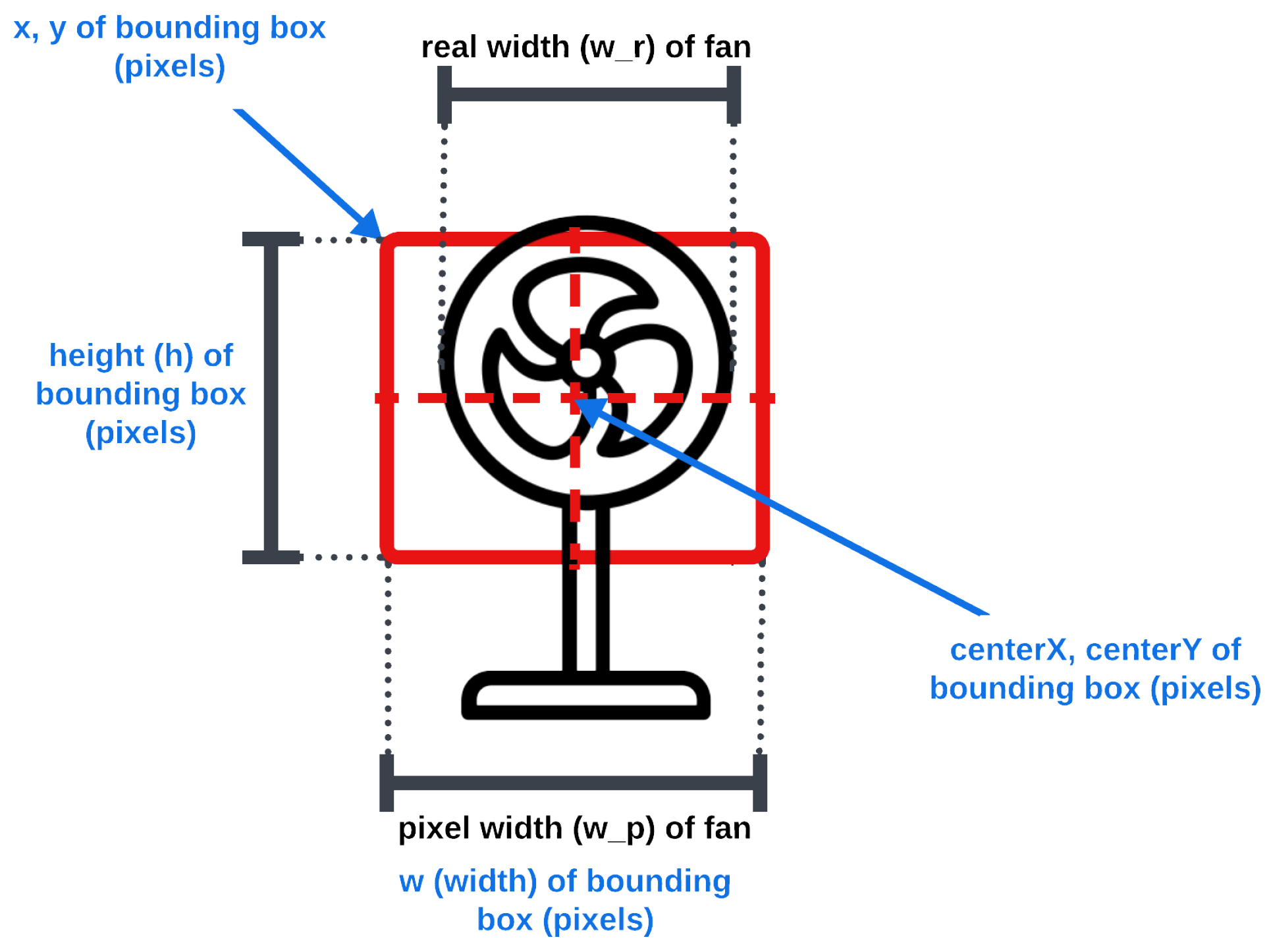
4.3. Trigonometric Calculations for the Path Using a Bounding Box
- d is the approximate distance of the detected object to the drone’s camera (cm),
- is the calculated focal length of the camera for a resolution image,
- is the real-world width of the object (cm), and
- is the width of the object in the frame (pixels).
- is the angle to turn the drone to center the detected object in the frame (degrees),
- x is the location of the center of the bounding box in the frame (from pixels 0–720),
- is the field of view of the drone in degrees (82.6° for Tello drones), and 360 is half the image width in pixels.
- For cases where x is less than half the image width, is counterclockwise; otherwise, it is clockwise.
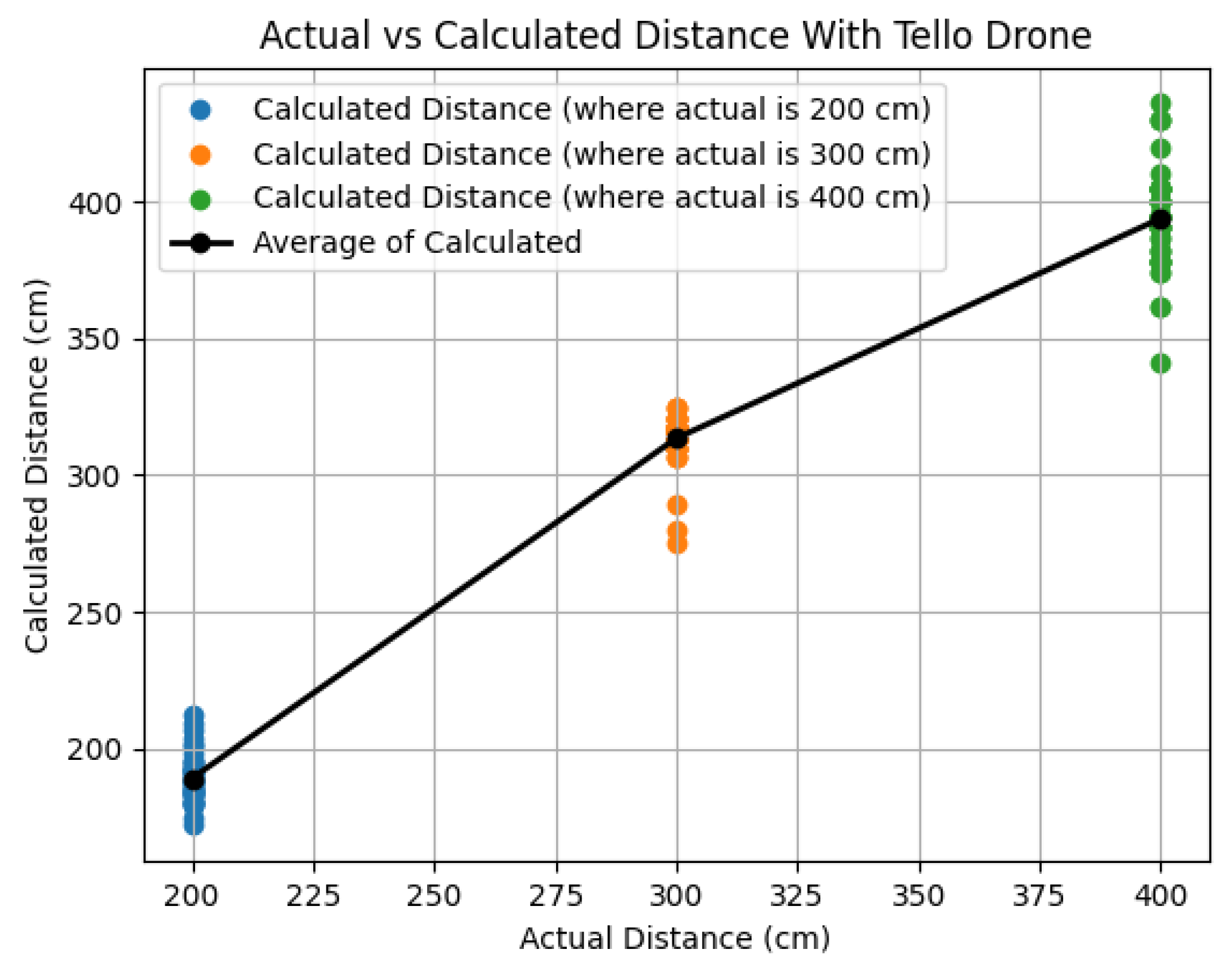
| Actual Distance (cm) | Average Calculated Distance (cm) | Average Error (%) |
|---|---|---|
| 200 | 189.1458 | 5.4271 |
| 300 | 313.5417 | 4.5139 |
| 400 | 393.9167 | 1.520825 |
5. Integration of Path Planning with Computer Vision
- Link: GitHub repository: Surrogate wind farm navigation with the Tello EDU drone: https://github.com/MoShekaramiz/Tello_Edu_Surrogated_Wind_Fram.
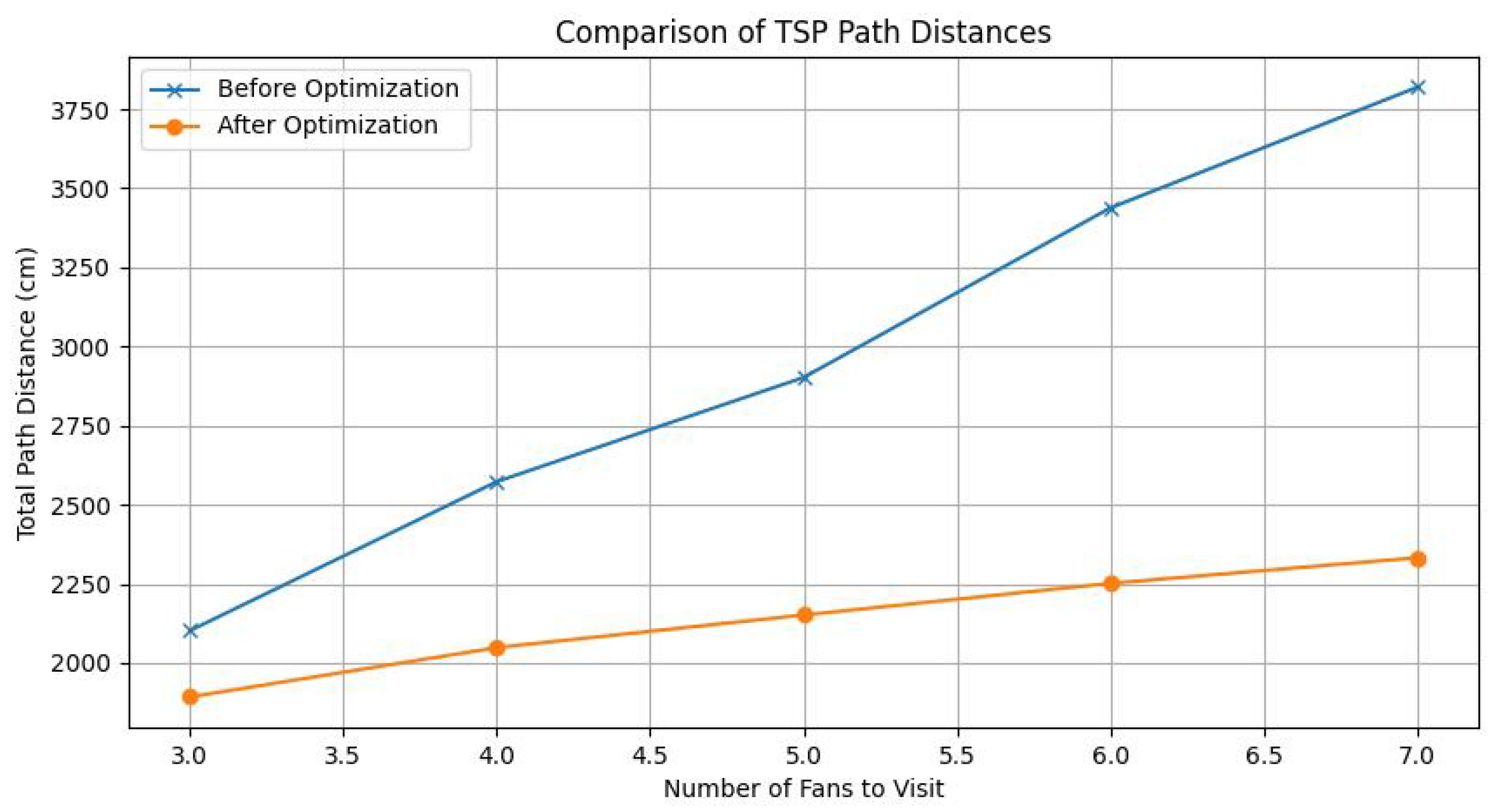
6. Traveling Salesman-Based Analyses and Exploration
6.1. Traveling Salesman-Based Experiments with Correct Takeoff Locations
6.2. Traveling Salesman-Based Experiments with Incorrect Takeoff Locations
7. Snake Path Area Search Analysis and Exploration
7.1. Snake Path Area Search Experiments with a Given Number of Fans
7.2. Snake Path Area Search Experiments Repeated with Unknown Number of Fans
8. Educational Contributions
- Link: GitHub repository: Surrogate wind farm navigation with the Tello EDU drone: https://github.com/MoShekaramiz/Tello_Edu_Surrogated_Wind_Fram.
- Link: Drone tutorial code explanations and demonstrations: Quick-Drone-Tutorial.
- The presented research and proof of concept for the use of computer vision in the path planning of drones can be used to improve existing educational programs, as well as develop new educational practices, materials, theories, and educational programs that focus on the use of computer vision in drone path planning.
- The effectiveness of the developed non-GPS computer vision-based navigation system for low-cost drones makes it an attractive candidate for large-scale educational purposes.
- The project can be used in machine learning and drone-related courses to teach students how to implement course concepts in real-world applications and overcome challenges. Projects of this caliber, involving autonomous drones and computer vision, enhance students’ understanding and ability to apply course concepts to real-world applications while persevering through the associated challenges.
- The educational aspect of the project reveals how to implement the experiments, simulated annealing, and image processing in detail using Python, ML libraries, path planning with Tello drones, computer vision tools and techniques using OpenCV, and patience in running a lot of experiments to confirm the results.
- The research can also be used to inspire students to pursue careers in the fields of computer vision, autonomous drones, and robotics, and to help students think critically about the role of technology in society.
9. Conclusions
- (a)
- The ability to achieve precise drone navigation within an indoor environment using computer vision methods.
- (b)
- The successful completion of traversal, detection, and landing tasks for most flights, as demonstrated by tests conducted on a surrogate small-scale wind farm model.
- (c)
- It offers a cost-effective alternative to GPS-based systems, making it appealing for educational applications and scenarios for GPS-denied environments.
- (d)
- It has the potential to enhance the autonomy and accuracy of wind farm navigation significantly by integrating visual-based adjustments alongside GPS technology.
10. Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CCA | coordinate calibration algorithm |
| CCS | Cartesian coordinate system |
| CNN | convolutional neural network |
| FOV | field of view |
| GPS | global positioning system |
| GPU | graphics processing unit |
| IR | Infrared |
| LSBA | list-based simulated annealing |
| ML | machine learning |
| POV | point of view |
| QR | quick response |
| RC | remote control |
| RCCA | robust coordinate calibration algorithm (with incorrect takeoff location) |
| RGB | red–green–blue (used to describe the digital color camera type) |
| SA | simulated annealing |
| SATS | simulated annealing traveling salesman |
| SLAM | simultaneous localization and mapping |
| SPFA | snake path flight algorithm |
| TSP | traveling salesman problem |
| UAV | unmanned aerial vehicle |
| VPS | vision positioning system |
Appendix A
| Randomly Selected Fans for Path (Order-Dependent) | Pass (P) or Fail (F) | Total Flight Time (s) |
|---|---|---|
| 7, 3, 1 | P | 287 |
| 5, 7, 6 | F1, P, P, P, P | NA, 159, 133, 187, 200 |
| 3, 7, 5 | P | 183 |
| 7, 2, 1 | P | 213 |
| 6, 2, 7 | P | 205 |
| 6, 4, 7 | P | 214 |
| 5, 6, 1 | P | 217 |
| 7, 3, 6 | P | 210 |
| 5, 7, 4 | P | 238 |
| 6, 4, 7 | P | 283 |
| 6, 2, 4 | P | 139 |
| 6, 3, 7, 5 | P | 285 |
| 1, 6, 7, 5 | P | 304 |
| 1, 3, 4, 7 | P | 362 |
| 1, 6, 2, 5 | P | 346 |
| 6, 4, 7, 5 | F2, P, P, P, P | NA, 245, 241, 309, 268 |
| 4, 2, 6, 3 | P | 268 |
| 3, 2, 6, 1 | F3, P, P, P, P | NA, 269, 239, 227, 290 |
| 4, 2, 6, 1 | P | 265 |
| 5, 4, 6, 3, 1 | P | 201 |
| 3, 6, 2, 4, 7 | P | 213 |
| 7, 4, 2, 3, 1 | P | 238 |
| 1, 3, 6, 2, 4 | F4, P, P, P, P | NA, 268, 253, 204, 233 |
| 4, 2, 6, 3, 1 | P | 234 |
| 5, 4, 2, 6, 1 | P | 283 |
| 1, 3, 6, 4, 5 | P | 174 |
| 1, 6, 2, 4, 5 | P | 216 |
| 1, 3, 4, 7, 5 | P | 204 |
| 3, 6, 2, 4, 5 | P | 278 |
| 5, 4, 2, 6, 3, 1 | P | 261 |
| 1, 3, 6, 4, 7, 5 | P | 278 |
| 1, 3, 2, 4, 7, 5 | P | 290 |
| 1, 3, 2, 4, 7, 5 | P | 276 |
| 5, 4, 2, 6, 3, 1 | P | 406 |
| 1, 6, 2, 4, 7, 5 | P | 237 |
| 1, 3, 6, 2, 4, 5 | P | 294 |
| 1, 3, 2, 4, 7, 5 | P | 260 |
| 7, 4, 2, 6, 3, 1 | F5, F6, F5, P, P | NA, NA, NA, 295, 359 |
| 3, 6, 2, 4, 7, 5 | P | 311 |
| 1, 3, 6, 2, 4, 7, 5 | P | 334 |
| 1, 3, 6, 2, 4, 7, 5 | P | 353 |
| 1, 3, 6, 2, 4, 7, 5 | P | 361 |
| 1, 3, 6, 2, 4, 7, 5 | P | 303 |
| 1, 3, 6, 2, 4, 7, 5 | P | 374 |
| 1, 3, 6, 2, 4, 7, 5 | P | 319 |
| 1, 3, 6, 2, 4, 7, 5 | P | 288 |
| 1, 3, 6, 2, 4, 7, 5 | P | 347 |
| 1, 3, 6, 2, 4, 7, 5 | P | 312 |
| 1, 3, 6, 2, 4, 7, 5 | P | 286 |
| Randomly Selected Fans for Path (Order-Dependent) | Pass (P) or Fail (F) | Total Flight Time (s) | Incorrect Takeoff Location (cm) |
|---|---|---|---|
| 1, 4, 7 | P1 | 275 | (−254, 254) |
| 1, 3, 4 | P | 177 | (−152, −152) |
| 5, 4, 3 | P | 180 | (152, −152) |
| 3, 2, 4 | P2 | 203 | (−254, −254) |
| 1, 3, 2 | P3 | 284 | (254, 254) |
| 3, 4, 7 | P4 | 247 | (297, 211) |
| 6, 2, 7 | P5 | 266 | (−147, 241) |
| 5, 7, 1 | P6 | 250 | (330, 119) |
| 7, 6, 1 | P7 | 233 | (610, 61) |
| 4, 2, 6 | P8 | 220 | (−89, 152) |
| 5, 4, 2, 6, 1 | P9 | 275 | (−254, 254) |
| 3, 6, 2, 4, 7 | P10 | 177 | (−152, −152) |
| 5, 7, 4, 2, 3 | P11 | 180 | (152, −152) |
| 5, 4, 2, 6, 3 | P12 | 203 | (−254, −254) |
| 3, 6, 2, 4, 5 | P13 | 284 | (254, 254) |
| 1, 6, 4, 7, 5 | P14 | 247 | (297, 211) |
| 5, 7, 2, 6, 1 | P15 | 266 | (0, 279) |
| 5, 4, 6, 3, 1 | P16 | 250 | (450, 307), |
| 5, 4, 2, 6, 1 | P17 | 233 | (589, 272), |
| 1, 6, 2, 4, 5 | P18 | 220 | (376, 369), |
| Randomly Selected Fan Location(s) | Pass (P) or Fail (F) | Total Flight Time (s) | ||
|---|---|---|---|---|
| 2 | P | 91 | ||
| 7 | P | 151 | ||
| One Fan | 10 | P | 249 | average: 155 |
| 1 | P | 123 | ||
| 0 | 5 | P | 161 | |
| 1, 9 | P | 231 | ||
| 11, 6 | P | 209 | ||
| Two Fans | 5, 7 | P | 266 | average: 229.6 |
| 8, 10 | P | 303 | ||
| 6, 7 | P | 139 | ||
| 2, 9, 11 | P | 317 | ||
| 2, 7, 11 | P | 367 | ||
| Three Fans | 1, 3, 5 | P | 285 | average: 318.6 |
| 4, 6, 8 | P | 305 | ||
| 1, 3, 10 | P | 319 | ||
| 1, 2, 3, 11 | P | 343 | ||
| 1, 2, 4, 7 | P | 264 | ||
| Four Fans | 1, 2, 7, 11 | P | 287 | average: 335.4 |
| 4, 6, 9, 11 | P | 383 | ||
| 3, 8, 11, 12 | P | 400 | ||
| 1, 3, 5, 9, 11 | P | 391 | ||
| 7, 8, 9, 11, 12 | P | 350 | ||
| Five Fans | 1, 3, 6, 2, 7 | P | 312 | average: 389.8 |
| 3, 8, 7, 9, 5 | P | 485 | ||
| 1, 2, 7, 10, 12 | P | 411 | ||
| Randomly Selected Fan Location(s) | Pass (P) or Fail (F) | Total Flight Time (s) | ||
|---|---|---|---|---|
| 8 | P | 298 | ||
| 7 | P | 313 | ||
| One Fan | 5 | P | 369 | average: 327.6 |
| 4 | P | 324 | ||
| 10 | P | 334 | ||
| 4, 8 | P | 363 | ||
| 3, 12 | P | 321 | ||
| Two Fans | 1, 9 | P | 337 | average: 337.4 |
| 6, 10 | P | 325 | ||
| 6, 11 | P | 341 | ||
| 8, 10, 11 | P | 325 | ||
| 1, 5, 6 | P | 319 | ||
| Three Fans | 7, 10, 11 | P | 337 | average: 315 |
| 2, 5, 6 | P | 274 | ||
| 7, 9, 11 | P | 320 | ||
| 3, 4, 8, 10 | P | 383 | ||
| 1, 2, 4, 12 | P | 330 | ||
| Four Fans | 1, 4, 5, 8 | P | 324 | average: 362.6 |
| 3, 6, 8, 10 | P | 451 | ||
| 1, 2, 8, 9 | P | 325 | ||
| 1, 4, 8, 10, 11 | P | 400 | ||
| 1, 3, 5, 8, 11 | P | 393 | ||
| Five Fans | 1, 4, 5, 11, 12 | P | 358 | average: 373 |
| 1, 4, 8, 9, 11 | P | 441 | ||
| 1, 2, 9, 10, 11 | P | 273 | ||
References
- Walford, C. Wind Turbine Reliability: Understanding and Minimizing Wind Turbine Operation and Maintenance Costs; SANDIA Report; SAND2006-1100; Sandia National Laboratories: Albuquerque, NM, USA, 2006; pp. 1–26.
- Besnard, F.; Bertling, L. An approach for condition-based maintenance optimization applied to wind turbine blades. IEEE Trans. Sustain. Energy 2010, 1, 77–83. [Google Scholar] [CrossRef]
- Nordin, M.H.; Sharma, S.; Khan, A.; Gianni, M.; Rajendran, S.; Sutton, R. Collaborative unmanned vehicles for inspection, maintenance, and repairs of offshore wind turbines. Drones 2022, 6, 137. [Google Scholar] [CrossRef]
- Guo, H.; Cui, Q.; Wang, J.; Fang, X.; Yang, W.; Li, Z. Detecting and positioning of wind turbine blade tips for UAV-based automatic inspection. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Yokohama, Japan, 28 July–2 August 2019; pp. 1374–1377. [Google Scholar]
- Yang, C.; Xun, L.; Hua, Z.; Yan, K.; John, S. Towards accurate image stitching for drone-based wind turbine blade inspection. Renew. Energy 2023, 203, 267–279. [Google Scholar] [CrossRef]
- Causa, F.; Franzone, A.; Fasano, G. Strategic and tactical path planning for urban air mobility: Overview and application to real-world use cases. Drones 2020, 7, 11. [Google Scholar] [CrossRef]
- Chung, H.M.; Maharjan, S.; Zhang, Y.; Eliassen, F.; Strunz, K. Placement and routing optimization for automated inspection with unmanned aerial vehicles: A study in offshore wind farm. IEEE Trans. Ind. Inform. 2020, 17, 3032–3043. [Google Scholar] [CrossRef]
- Chung, H.M.; Maharjan, S.; Zhang, Y.; Eliassen, F.; Yuan, T. Edge intelligence empowered UAVs for automated wind farm monitoring in smart grids. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Taipei, Taiwan, 7–11 December 2020; pp. 1–6. [Google Scholar]
- Cao, P.; Liu, Y.; Qiu, M.; Yang, C.; Xie, S. MEC-driven UAV routine inspection system in wind farm under wind influence. In Proceedings of the 12th International Conference on Intelligent Computation Technology and Automation (ICICTA), Xiangtan, China, 26–27 October 2019; pp. 672–677. [Google Scholar]
- Zhang, S.; Li, Y.; Ye, F.; Geng, X.; Zhou, Z.; Shi, T. A Hybrid Human-in-the-Loop Deep Reinforcement Learning Method for UAV Motion Planning for Long Trajectories with Unpredictable Obstacles. Drones 2023, 7, 311. [Google Scholar] [CrossRef]
- Apostolidis, S.D.; Vougiatzis, G.; Kapoutsis, A.C.; Chatzichristofis, S.A.; Kosmatopoulos, E.B. Systematically Improving the Efficiency of Grid-Based Coverage Path Planning Methodologies in Real-World UAVs’ Operations. Drones 2023, 7, 399. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Z. Automatic detection of wind turbine blade surface cracks based on UAV-taken images. IEEE Trans. Ind. Electron. 2017, 64, 7293–7303. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Z.; Luo, X. A two-stage data-driven approach for image-based wind turbine blade crack inspections. IEEE/ASME Trans. Mechatronics 2019, 24, 1271–1281. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, J.; Xu, R.; Cao, Z.; Jin, Z.; Guo, Z.; Wang, W.; Li, K. Three dimensional fully autonomous inspection method for wind power employing unmanned aerial vehicle based on 5G wireless communication and artificial intelligence. In Proceedings of the IEEE 5th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 16–18 December 2022; Volume 5, pp. 800–805. [Google Scholar]
- Stokkeland, M.; Klausen, K.; Johansen, T.A. Autonomous visual navigation of unmanned aerial vehicle for wind turbine inspection. In Proceedings of the IEEE International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 998–1007. [Google Scholar]
- Moreno, S.; Peña, M.; Toledo, A.; Treviño, R.; Ponce, H. A new vision-based method using deep learning for damage inspection in wind turbine blades. In Proceedings of the IEEE 15th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE), Mexico City, Mexico, 5–7 September 2018; pp. 1–5. [Google Scholar]
- Car, M.; Markovic, L.; Ivanovic, A.; Orsag, M.; Bogdan, S. Autonomous wind-turbine blade inspection using LiDAR-equipped unmanned aerial vehicle. IEEE Access 2020, 8, 131380–131387. [Google Scholar] [CrossRef]
- Xu, Y.; Gu, H.; Dai, Q.; Lu, G.; Gu, J.; Hua, L. Motion tracking detection and tracking technology based on aerial video. In Proceedings of the IEEE 11th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC), Hangzhou, China, 24–25 August 2019; Volume 2, pp. 122–125. [Google Scholar]
- Valenti, F.; Giaquinto, D.; Musto, L.; Zinelli, A.; Bertozzi, M.; Broggi, A. Enabling computer vision-based autonomous navigation for unmanned aerial vehicles in cluttered GPS-denied environments. In Proceedings of the 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 3886–3891. [Google Scholar]
- Jung, S.; Hwang, S.; Shin, H.; Shim, D.H. Perception, guidance, and navigation for indoor autonomous drone racing using deep learning. Robot. Autom. Lett. 2018, 3, 2539–2544. [Google Scholar] [CrossRef]
- Khan, S.Z.; Mohsin, M.; Iqbal, W. On GPS spoofing of aerial platforms: A review of threats, challenges, methodologies, and future research directions. PeerJ Comput. Sci. 2021, 7, e507. [Google Scholar] [CrossRef] [PubMed]
- Schilling, F.; Lecoeur, J.; Schiano, F.; Floreano, D. Learning vision-based flight in drone swarms by imitation. IEEE Robot. Autom. Lett. 2019, 4, 4523–4530. [Google Scholar] [CrossRef]
- Krul, S.; Pantos, C.; Frangulea, M.; Valente, J. Visual SLAM for indoor livestock and farming using a small drone with a monocular camera: A feasibility study. Drones 2021, 5, 41. [Google Scholar] [CrossRef]
- Ghazi, G.; Voyer, J. Use of a DJI Tello Drone as an Educational Platform in the Field of Control Engineering. In Proceedings of the Canadian Engineering Education Association (CEEA), Kelowna, BC, Canada, 17–21 June 2023. [Google Scholar]
- Verner, I.M.; Cuperman, D.; Reitman, M. Exploring robot connectivity and collaborative sensing in a high-school enrichment program. Robotics 2021, 10, 13. [Google Scholar] [CrossRef]
- Dorling, K.; Heinrichs, J.; Messier, G.G.; Magierowski, S. Vehicle routing problems for drone delivery. IEEE Trans. Syst. Man, Cybern. Syst. 2016, 47, 70–85. [Google Scholar] [CrossRef]
- Sundar, K.; Rathinam, S. Algorithms for routing an unmanned aerial vehicle in the presence of refueling depots. IEEE Trans. Autom. Sci. Eng. 2013, 11, 287–294. [Google Scholar] [CrossRef]
- Crevier, B.; Cordeau, J.F.; Laporte, G. The multi-depot vehicle routing problem with inter-depot routes. Eur. J. Oper. Res. 2007, 176, 756–773. [Google Scholar] [CrossRef]
- da Silva, Y.M.; Andrade, F.A.; Sousa, L.; de Castro, G.G.; Dias, J.T.; Berger, G.; Lima, J.; Pinto, M.F. Computer Vision Based Path Following for Autonomous Unmanned Aerial Systems in Unburied Pipeline Onshore Inspection. Drones 2022, 6, 410. [Google Scholar] [CrossRef]
- Caballero, F.; Merino, L. DLL: Direct LIDAR Localization. A map-based localization approach for aerial robots. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 5491–5498. [Google Scholar]
- Mur-Artal, R.; Tardós, J.D. Visual-inertial monocular SLAM with map reuse. IEEE Robot. Autom. Lett. 2017, 2, 796–803. [Google Scholar] [CrossRef]
- Pinney, B.; Duncan, S.; Shekaramiz, M.; Masoum, M.A. Drone path planning and object detection via QR codes; a surrogate case study for wind turbine inspection. In Proceedings of the IEEE Intermountain Engineering, Technology and Computing (IETC), Orem, UT, USA, 13–14 May 2022; pp. 1–6. [Google Scholar]
- Pinney, B.; Stockett, B.; Shekaramiz, M.; Masoum, M.A.; Seibi, A.; Rodriguez, A. Exploration and Object Detection via Low-Cost Autonomous Drone. In Proceedings of the IEEE Intermountain Engineering, Technology and Computing (IETC), Provo, UT, USA, 12–13 May 2023; pp. 49–54. [Google Scholar]
- Giernacki, W.; Rao, J.; Sladic, S.; Bondyra, A.; Retinger, M.; Espinoza-Fraire, T. DJI Tello quadrotor as a platform for research and education in mobile robotics and control engineering. In Proceedings of the IEEE International Conference on Unmanned Aircraft Systems (ICUAS), Dubrovnik, Croatia, 21–24 June 2022; pp. 735–744. [Google Scholar]
- Bai, O.; Chu, H. Drones in education: A critical review. Turk. J. Comput. Math. Educ. (TURCOMAT) 2021, 12, 1722–1727. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Cook, W.J. In Pursuit of the Traveling Salesman: Mathematics at the Limits of Computation; Princeton University Press: Princeton, NJ, USA, 2015; ISBN 9780691163529. [Google Scholar]
- Zhan, S.h.; Lin, J.; Zhang, Z.j.; Zhong, Y.W. List-based simulated annealing algorithm for traveling salesman problem. Comput. Intell. Neurosci. 2016, 2016, 1712630. [Google Scholar] [CrossRef] [PubMed]
- Nourani, Y.; Andresen, B. A comparison of simulated annealing cooling strategies. J. Phys. Math. Gen. 1998, 31, 8373. [Google Scholar] [CrossRef]
- Rego, C.; Gamboa, D.; Glover, F.; Osterman, C. Traveling salesman problem heuristics: Leading methods, implementations and latest advances. Eur. J. Oper. Res. 2011, 211, 427–441. [Google Scholar] [CrossRef]
- Priambodo, A.; Arifin, F.; Nasuha, A.; Winursito, A. Face Tracking for Flying Robot Quadcopter based on Haar Cascade Classifier and PID Controller. In Proceedings of the Journal of Physics: Conference Series, Yogyakarta, Indonesia, 5 October 2021; Volume 2111, p. 012046. [Google Scholar]
- Lane, C.; Jones, O.; Miloro, C.; Frye, M. Development of Semi-Autonomous Flight & Detection Systems Using Small Drones. In Proceedings of the IEEE/AIAA 41st Digital Avionics Systems Conference (DASC), Portsmouth, VA, USA, 18–22 September 2022; pp. 1–9. [Google Scholar]
- Viola, P.; Jones, M. Rapid object detection using a boosted cascade of simple features. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition. (CVPR), Kauai, HI, USA, 8–14 December 2001; Volume 1, p. I. [Google Scholar]
- Miller, J.; Seegmiller, C.; Masoum, M.A.; Shekaramiz, M.; Seibi, A.C. Hyperparameter Tuning of Support Vector Machines for Wind Turbine Detection Using Drones. In Proceedings of the IEEE Intermountain Engineering, Technology and Computing (IETC), Provo, UT, USA, 12–13 May 2023; pp. 55–60. [Google Scholar]
- N’diaye, L.M.; Phillips, A.; Masoum, M.A.; Shekaramiz, M. Residual and wavelet based neural network for the fault detection of wind turbine blades. In Proceedings of the IEEE Intermountain Engineering, Technology and Computing (IETC), Orem, UT, USA, 13–14 May 2022; pp. 1–5. [Google Scholar]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodriguez, A.A.; Shekaramiz, M.; Masoum, M.A.S. Computer Vision-Based Path Planning with Indoor Low-Cost Autonomous Drones: An Educational Surrogate Project for Autonomous Wind Farm Navigation. Drones 2024, 8, 154. https://doi.org/10.3390/drones8040154
Rodriguez AA, Shekaramiz M, Masoum MAS. Computer Vision-Based Path Planning with Indoor Low-Cost Autonomous Drones: An Educational Surrogate Project for Autonomous Wind Farm Navigation. Drones. 2024; 8(4):154. https://doi.org/10.3390/drones8040154
Chicago/Turabian StyleRodriguez, Angel A., Mohammad Shekaramiz, and Mohammad A. S. Masoum. 2024. "Computer Vision-Based Path Planning with Indoor Low-Cost Autonomous Drones: An Educational Surrogate Project for Autonomous Wind Farm Navigation" Drones 8, no. 4: 154. https://doi.org/10.3390/drones8040154
APA StyleRodriguez, A. A., Shekaramiz, M., & Masoum, M. A. S. (2024). Computer Vision-Based Path Planning with Indoor Low-Cost Autonomous Drones: An Educational Surrogate Project for Autonomous Wind Farm Navigation. Drones, 8(4), 154. https://doi.org/10.3390/drones8040154









