Control and Application of Tree Obstacle-Clearing Coaxial Octocopter with Flexible Suspension Saw
Abstract
:1. Introduction
- The drone’s rotors may collide with tree obstacles during operation, potentially causing crashes.
- When the drone makes contact with tree obstacles, it may experience impact forces. Excessive impact forces could damage the drone.
- The operational tools of the drone represent a significant dynamic load for traditional drones. Maintaining stable position and attitude control under significant dynamic loads is a critical challenge.
- During operation, the drone is in a hovering state, and tree obstacles inevitably exert reaction forces and moments on the drone. These forces and moments pose significant disturbances, and overcoming these disturbances is a key research problem.
2. Overall Scheme
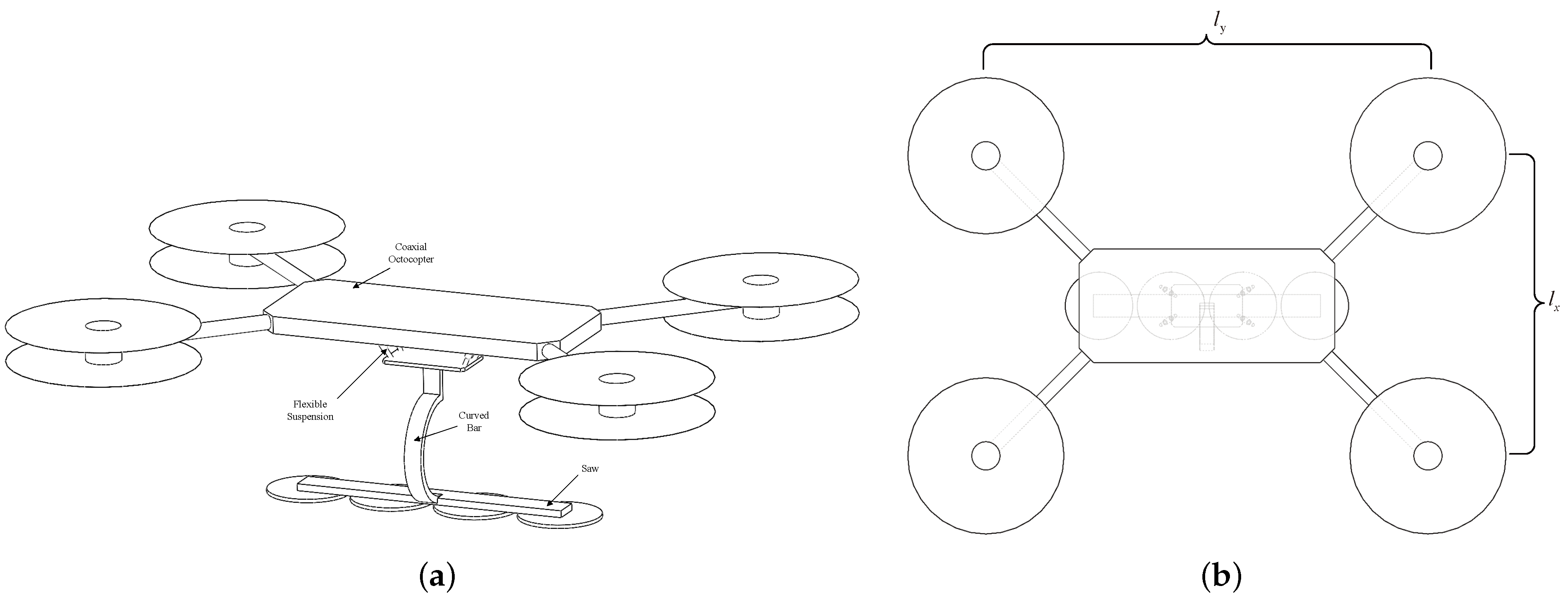
2.1. Structural Scheme
- A coaxial octocopter platform;
- A saw system composed of four pairs of saws;
- A flexible suspension system for buffering damping.
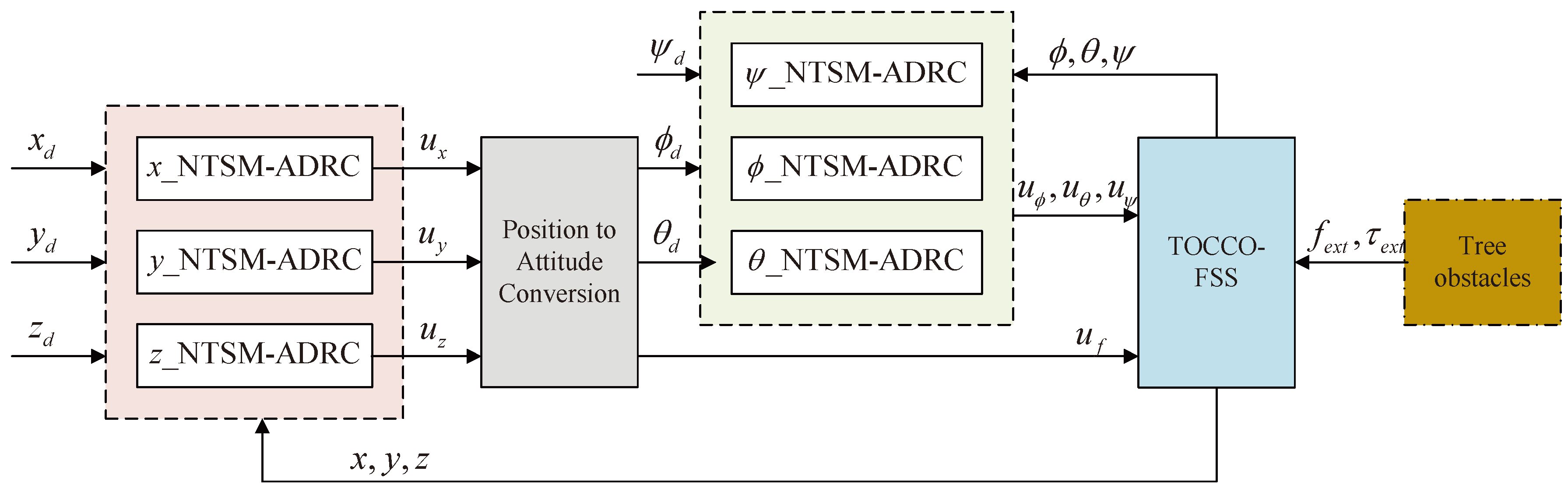
2.2. Control Methods Scheme
- Propose and model the novel TOCCO-FSS. Moreover, perform overall dynamic modeling using the Lagrange dynamic equation;
- Analyze the effects of contact operations on drones and model contact reaction forces and moments;
- In response to the perturbations of reaction forces and moments and the TOCCO-FSS internal parameter variations that exist in the contact operation, design the position and attitude control with the Non-Singular Terminal Sliding-Mode Active Disturbance Rejection Control (NTSM-ADRC) and analyze its stability;
- By conducting simulations and physical experiments, the effectiveness of the TOCCO-FSS design, modeling, and control was validated, demonstrating its practical application value.
3. Modeling
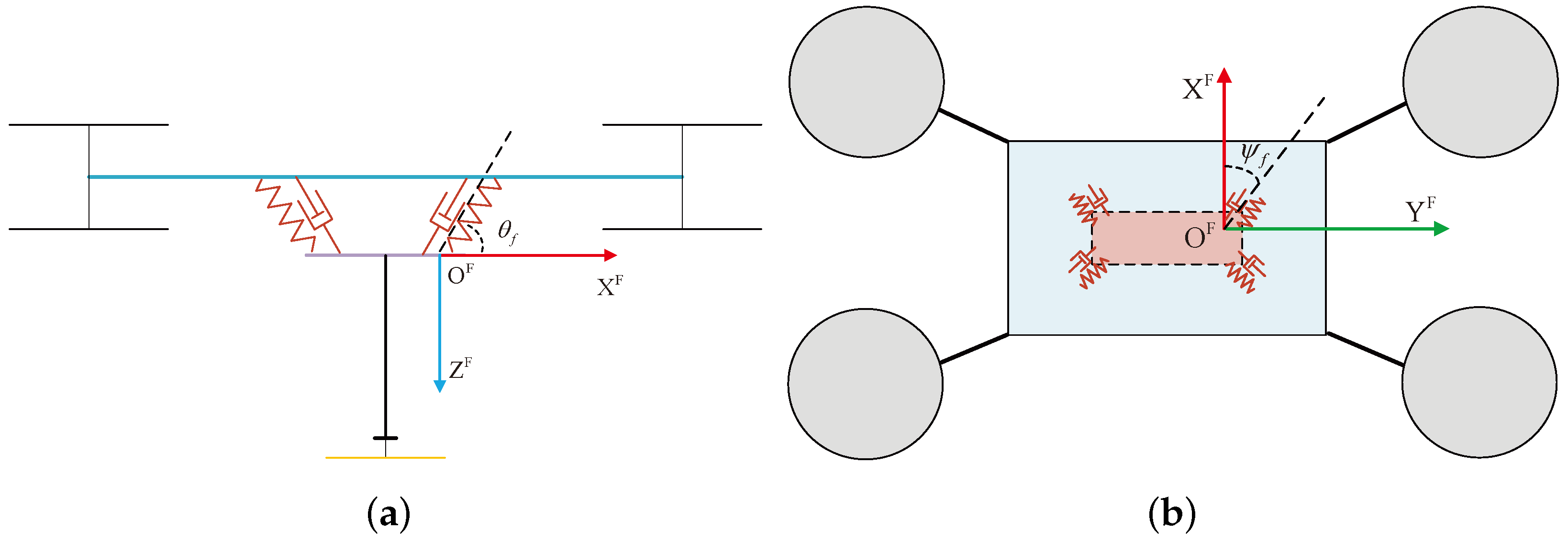
3.1. Flexible Suspension Modeling
- The TOCCO-FSS saw and the airframe are considered to be rigid bodies, and the two parts are connected by a flexible suspension system;
- Due to the relatively light structural weight of the flexible suspension system compared to the body and the saws, its mass can be neglected;
- The flexible suspension system can be equivalently modeled as a three-dimensional spring-damper system in space, and it is connected at the center of mass of the drone. Its front view and top view are shown in Figure 6. It consists of four identical diagonally arranged spring-damper units, which are symmetrically inclined with respect to the XY axes in the body coordinate system;
- Since the saws achieve maximum cutting efficiency when cutting tree obstacles horizontally, the structural design constrains the rotational motion of the flexible suspension system. It provides buffering and vibration damping for translational movements along the XYZ axes in space but does not allow for rotational movement;
3.2. Kinematic Modeling
3.3. Dynamic Modeling
3.4. Contact Operation Modeling
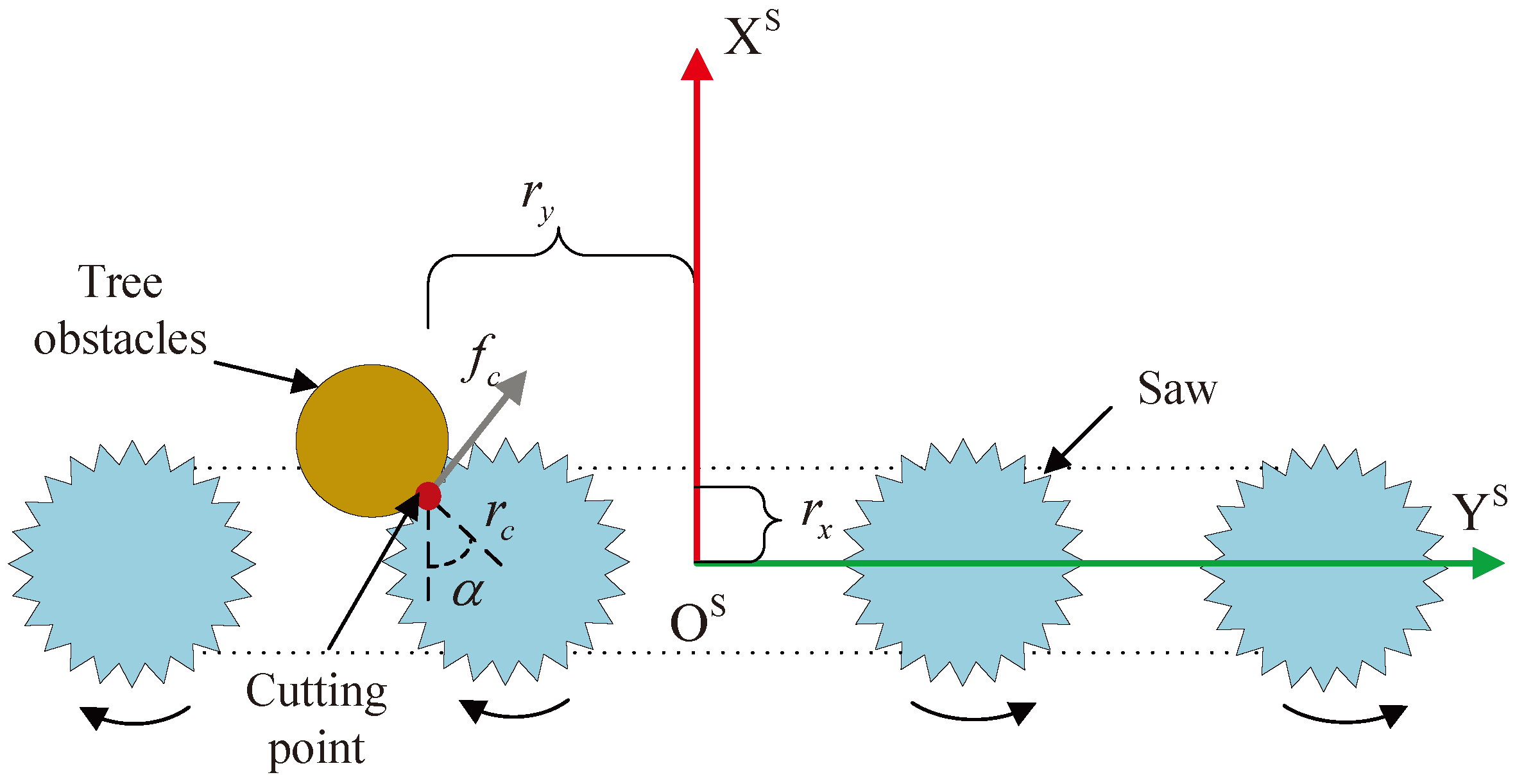
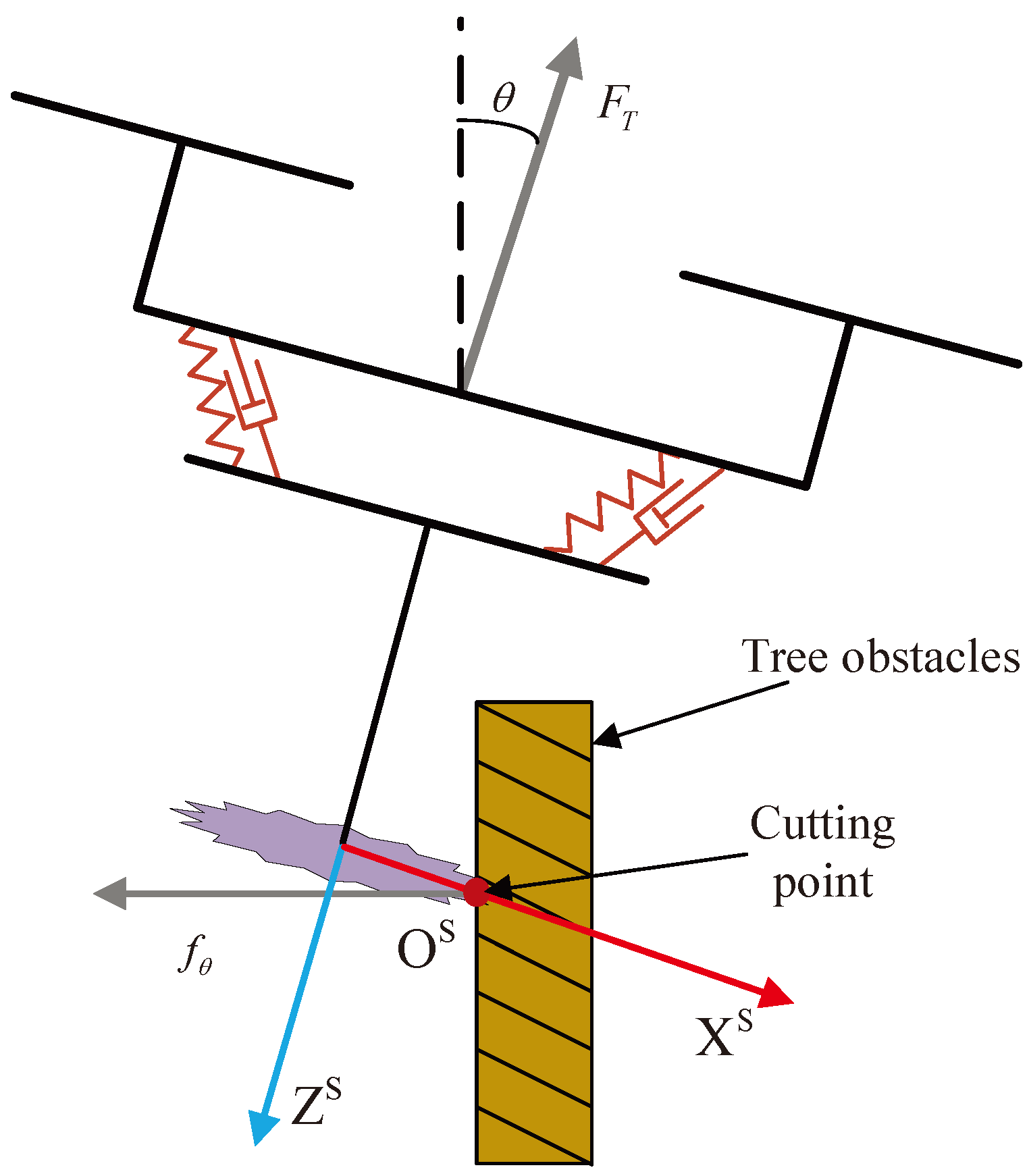
3.4.1. Cutting Disturbance Analysis
3.4.2. Contact Disturbance Analysis
4. Control
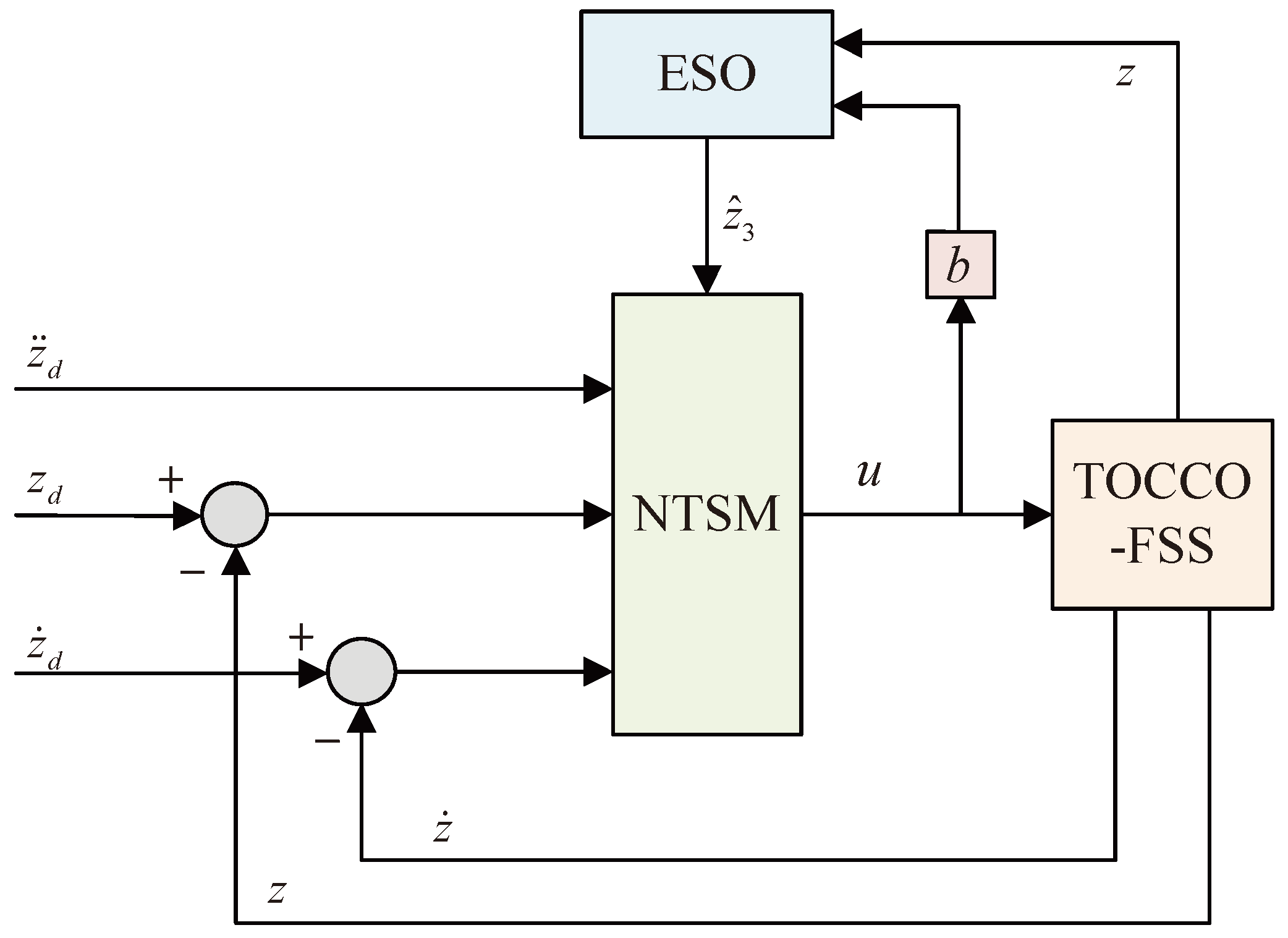
4.1. Control Output
4.2. Extended State Observer
4.3. Non-Singular Terminal Sliding-Mode Control
4.4. Stability Analysis
4.4.1. Analysis of Non-Singular Terminal Sliding-Mode Controller
4.4.2. Analysis of Extended State Observer
5. Experiment
5.1. Simulation
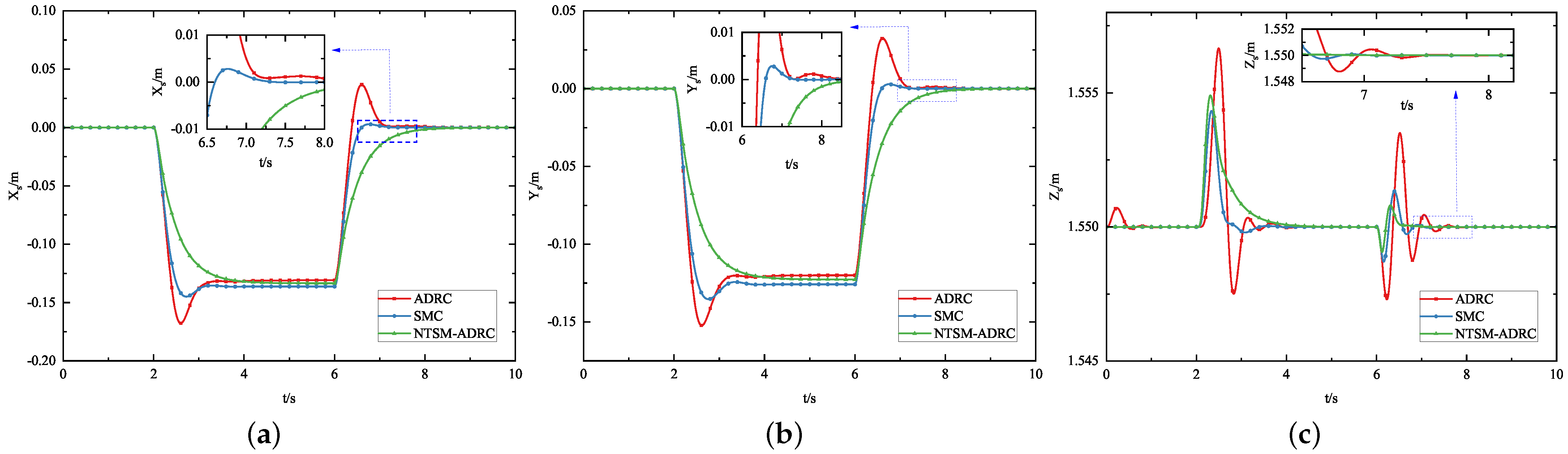
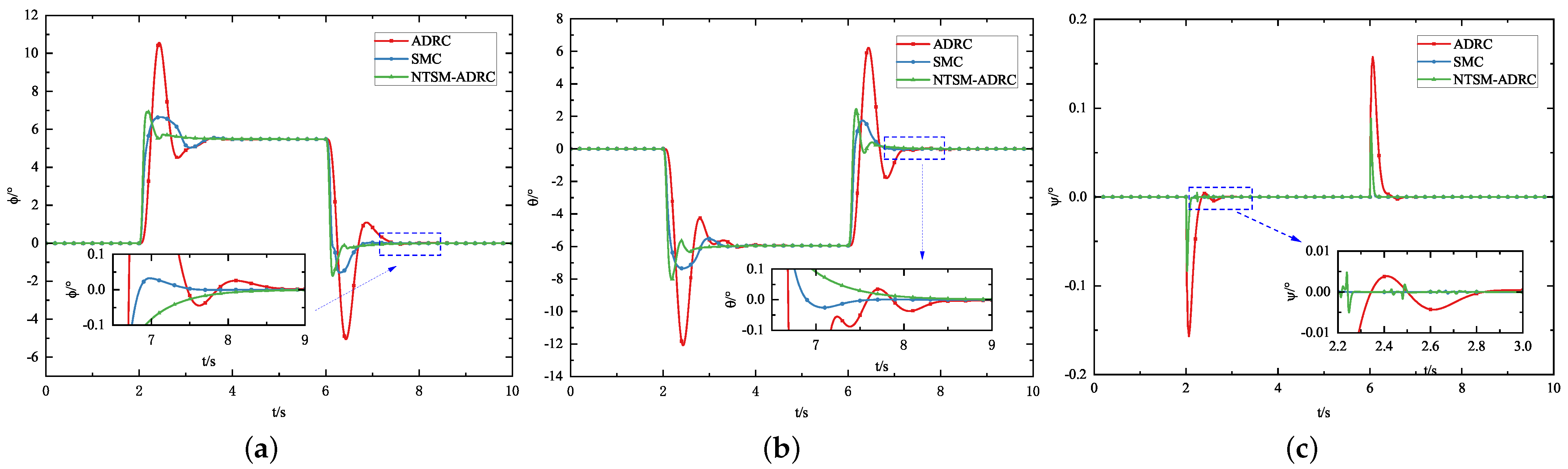
5.1.1. Attitude Control Experiment
5.1.2. Position Control Experiment
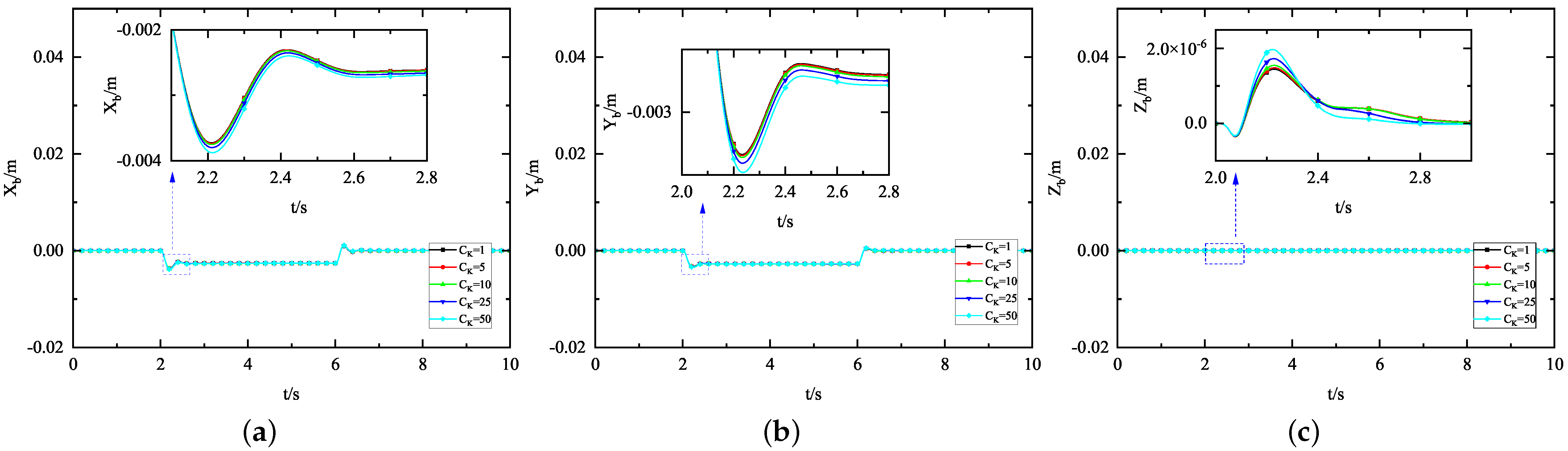
5.1.3. Flexible Coefficient Experiment
5.1.4. Contact Operation Experiment
5.1.5. Contact Operation Experiment with Different Flexible Coefficients
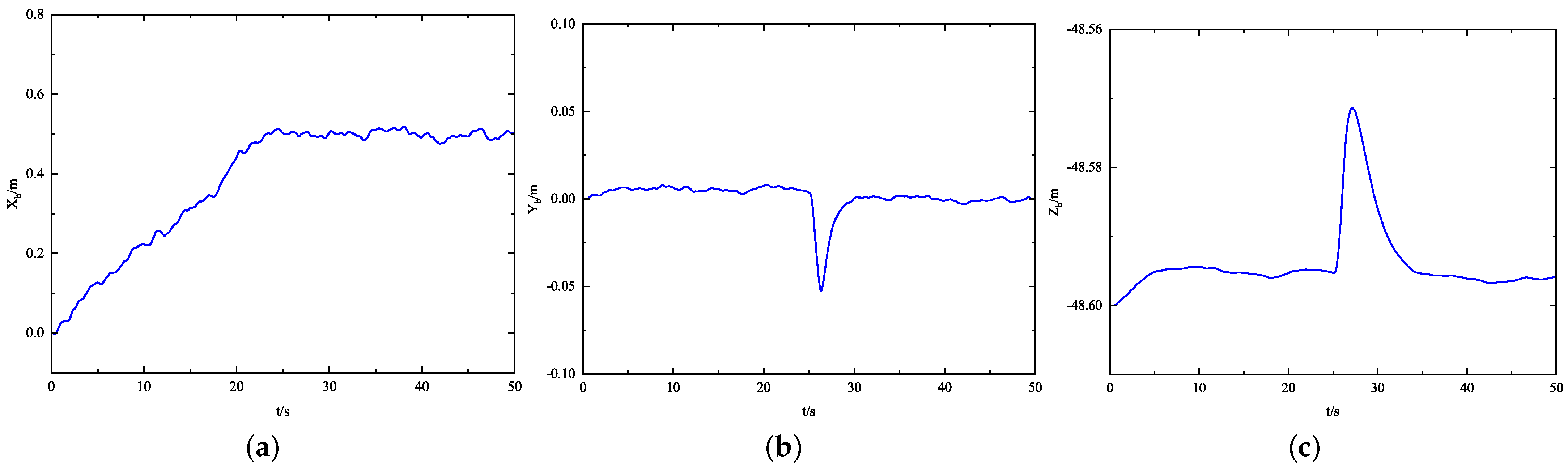
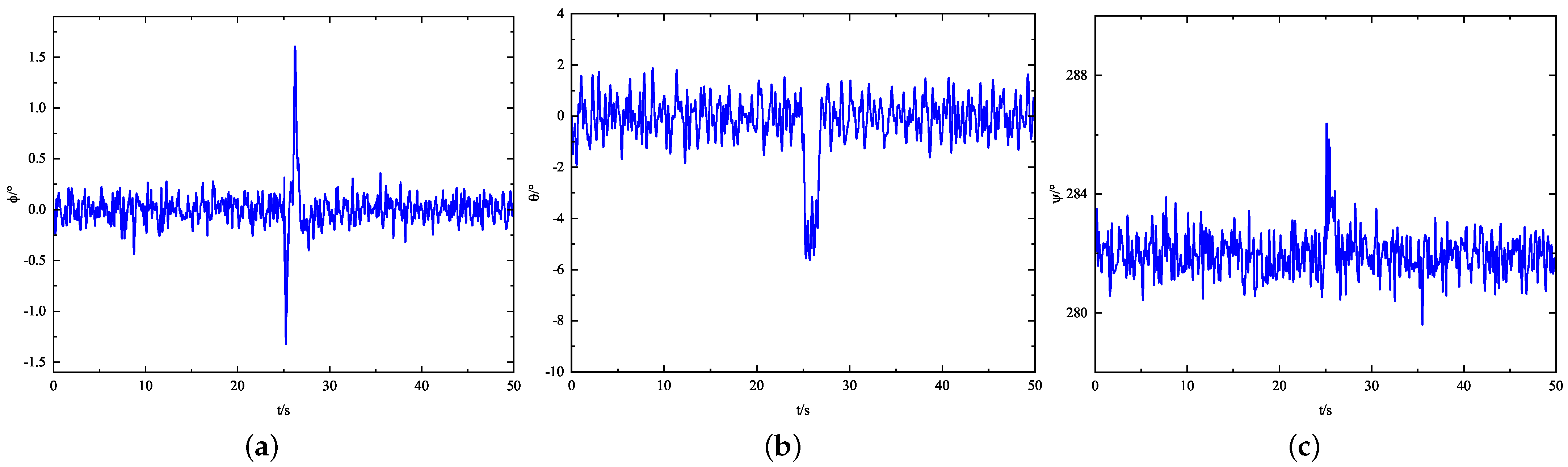
5.2. Physical Experiment
6. Conclusions
- A novel TOCCO-FSS scheme is proposed and modeled by the Lagrange dynamics equations, and then the contact operation disturbances are analyzed and modeled;
- The position and attitude control of Non-Singular Terminal Sliding-Mode Active Disturbance Rejection Control (NTSM-ADRC) has been designed and its stability has been analyzed with respect to the reaction force and moment disturbances that exist in contact operations;
- The effectiveness of the TOCCO-FSS design, modeling, and control has been verified through simulation and physical experiments, proving its relevance for practical applications.
- The flexible suspension can cause oscillations of the saw, which may reduce the efficiency of tree-obstacle clearing.
- The drone currently carries a flexible suspension saw and takes off and lands using a landing platform. Reliable takeoff and landing methods need further investigation.
- When clearing tree obstacles, the flexible suspension saw still forms an angle with the obstacles. Achieving vertical cutting of tree obstacles is another research direction.
- More physical flight experiments are needed to verify the adaptability of the TOCCO-FSS under different tree conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Luque-Vega, L.F.; Castillo-Toledo, B.; Loukianov, A.; Gonzalez-Jimenez, L.E. Power Line Inspection via an Unmanned Aerial System based on the Quadrotor Helicopter. In Proceedings of the MELECON 2014—2014 17th IEEE Mediterranean Electrotechnical Conference, Beirut, Lebanon, 13–16 April 2014; IEEE: Piscatway, NJ, USA, 2014; pp. 393–397. [Google Scholar]
- Wu, M.; Chen, W.; Tian, X. Optimal energy consumption path planning for quadrotor UAV transmission tower inspection based on simulated annealing algorithm. Energies 2022, 15, 8036. [Google Scholar] [CrossRef]
- Peng, X.; Qian, J.; Mai, X. Automatic power line inspection technology of large unmanned helicopter and its application. South. Power Syst. Technol. 2016, 10, 24–31. [Google Scholar]
- Liu, Z.; Du, Y.; Chen, Y.; Ma, J.G.; Wu, X.; Yao, J. Simulation and experiment on the safety distance of typical ±500 kV DC transmission lines and towers for UAV inspection. High Volt. Eng. 2020, 13, 3223. [Google Scholar]
- Roncolatto, R.A.; Romanelli, N.W.; Hirakawa, A.; Horikawa, O.; Vieira, D.M.; Yamamoto, R.; Finotto, V.C.; Sverzuti, V.; Lopes, I.P. Robotics Applied to Work Conditions Improvement in Power Distribution Lines Maintenance. In Proceedings of the 2010 1st International Conference on Applied Robotics for the Power Industry, Montreal, QC, Canada, 5–7 October 2010; IEEE: Piscatway, NJ, USA, 2010; pp. 1–6. [Google Scholar]
- Foudeh, H.A.; Luk, P.; Whidborne, J. Application of norm optimal iterative learning control to quadrotor unmanned aerial vehicle for monitoring overhead power system. Energies 2019, 45, 3223. [Google Scholar] [CrossRef]
- Menéndez, O.; Pérez, M.; Auat Cheein, F. Visual-based positioning of aerial maintenance platforms on overhead transmission lines. Appl. Sci. 2019, 9, 165. [Google Scholar] [CrossRef]
- Suarez, A.; Salmoral, R.; Zarco-Periñan, P.J.; Ollero, A. Experimental evaluation of aerial manipulation robot in contact with 15 kV power line: Shielded and long reach configurations. IEEE Access 2021, 9, 94573–94585. [Google Scholar] [CrossRef]
- Alhassan, A.B.; Zhang, X.; Shen, H.; Xu, H. Power transmission line inspection robots: A review, trends and challenges for future research. Int. J. Electr. Power Energy Syst. 2020, 118, 105862. [Google Scholar] [CrossRef]
- Hamaza, S.; Georgilas, I.; Richardson, T. An Adaptive-Compliance Manipulator for Contact-Based Aerial Applications. In Proceedings of the 2018 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Auckland, New Zealand, 9–12 July 2018; IEEE: Piscatway, NJ, USA, 2018; pp. 730–735. [Google Scholar]
- Hartung, J.; Cox, W.C., III. Airborne Tree Trimming Apparatus. U.S. Patent No. 4984757, 15 January 1991. [Google Scholar]
- Molina, J.; Hirai, S.T. Aerial pruning mechanism, initial real environment test. Robot. Biomimetics 2017, 4, 1–11. [Google Scholar]
- Molina, J.; Hirai, S. Pruning Tree-Branches Close to Electrical Power Lines Using a Skew-Gripper and a Multirotor Helicopter. In Proceedings of the 2017 IEEE International Conference on Advanced Intelligent Mechatronics, Munich, Germany, 3–7 July 2017; IEEE: Piscatway, NJ, USA, 2017; pp. 1123–1128. [Google Scholar]
- Azami, N.; Zarafshan, P.; Kermani, A.M.; Khashehchi, M.; Kouravand, S. Design and Analysis of an Armed-Octorotor to Prune Trees near the Power Lines. In Proceedings of the International Conference of Iranian Aerospace Society, Tehran, Iran, 7–8 December 2016; pp. 1–6. [Google Scholar]
- Xu, C.; Yang, Z.; Jiang, Y.; Zhang, Q.; Xu, H.; Xu, X. The Design and Control of a Double- Saw Cutter on the Aerial Trees-Pruning Robot. In Proceedings of the IEEE Internation- al Conference on Robotics and Biomimetics, Kuala Lumpur, Malaysia, 12–15 December 2018; pp. 2095–2100. [Google Scholar]
- Xu, H.; Yang, Z.; Zhou, G.; Liao, L.; Xu, C.; Wu, J.; Zhang, Q.; Zhang, C. A Novel Aerial Manipulator with Front Cutting Effector: Modeling, Control, and Evaluation. Complexity 2021, 2021, 1–17. [Google Scholar] [CrossRef]
- Liao, L.W.; Yang, Z.; Wang, C.; Xu, C.; Xu, H.; Wang, Z.; Zhang, Q. Flight control method of aerial robot for tree obstacle clearing with hanging telescopic cutter. Control Theory Appl. 2023, 40, 343–352. [Google Scholar]
- Chamseddine, A.; Theilliol, D.; Sadeghzadeh, I.; Zhang, Y.; Weber, P. Optimal reliability design for over-actuated systems based on the MIT rule: Application to an octocopter helicopter testbed. Reliab. Eng. Syst. Saf. 2014, 132, 196–206. [Google Scholar] [CrossRef]
- Caccavale, F.; Giglio, G.; Muscio, G.; Pierri, F. Cooperative Impedance Control for Multiple UAVs with a Robotic Arm. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 September–2 October 2015; IEEE: Piscatway, NJ, USA, 2015; pp. 2366–2371. [Google Scholar]
- Sugar, T.G. A novel selective compliant actuator. Mechatronics 2002, 12, 1157–1171. [Google Scholar] [CrossRef]
- Tao, Y.; Wang, T.; Wang, Y.; Guo, L.; Xiong, H.; Xu, D. A new variable stiffness robot joint. Ind. Robot. Int. J. 2015, 42, 371–378. [Google Scholar] [CrossRef]
- Katav, A.; Shapiro, A. Accurate Transportation Nonlinear Control for Flexible Cable-Suspended Load Carried by a Multi-Copter. In Proceedings of the 62nd Israel Annual Conference on Aerospace Sciences, IACAS, Tel-Aviv, Israel, 15 March 2023. Haifa, Israel, 16 March 2023. [Google Scholar]
- Geronel, R.S.; Botez, R.M.; Bueno, D.D. On the Effect of Flexibility on the Dynamics of a Suspended Payload Carried by a Quadrotor. Designs 2022, 6, 31. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and Bandwidth-Parameterization based Controller Tuning. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; IEEE: Piscatway, NJ, USA, 2003; pp. 4989–4996. [Google Scholar]
- Wang, H.; Ye, X.; Tian, Y.; Zheng, G.; Christov, N. Model-free–based terminal SMC of quadrotor attitude and position. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2519–2528. [Google Scholar] [CrossRef]
- Nasmyth, K.; Haering, C.H. The structure and function of SMC and kleisin complexes. Annu. Rev. Biochem. 2005, 74, 595–648. [Google Scholar] [CrossRef] [PubMed]
- Hassani, H.; Mansouri, A.; Ahaitouf, A. Performance evaluation of an improved non-singular sliding mode attitude control of a perturbed quadrotor: Experimental validation. J. Vib. Control 2024, 30, 1297–1312. [Google Scholar] [CrossRef]
- Silva, A.L.; Santos, D.A. Fast nonsingular terminal sliding mode flight control for multirotor aerial vehicles. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4288–4299. [Google Scholar] [CrossRef]
- Riache, S.; Kidouche, M.; Rezoug, A. Adaptive robust nonsingular terminal sliding mode design controller for quadrotor aerial manipulator. Telecommun. Comput. Electron. Control 2019, 17, 1501–1512. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, H.; Liu, D. Investigation of the hydraulic servo system of the rolling mill using nonsingular terminal sliding mode-active disturbance rejection control. Math. Probl. Eng. 2020, 17, 1–12. [Google Scholar] [CrossRef]




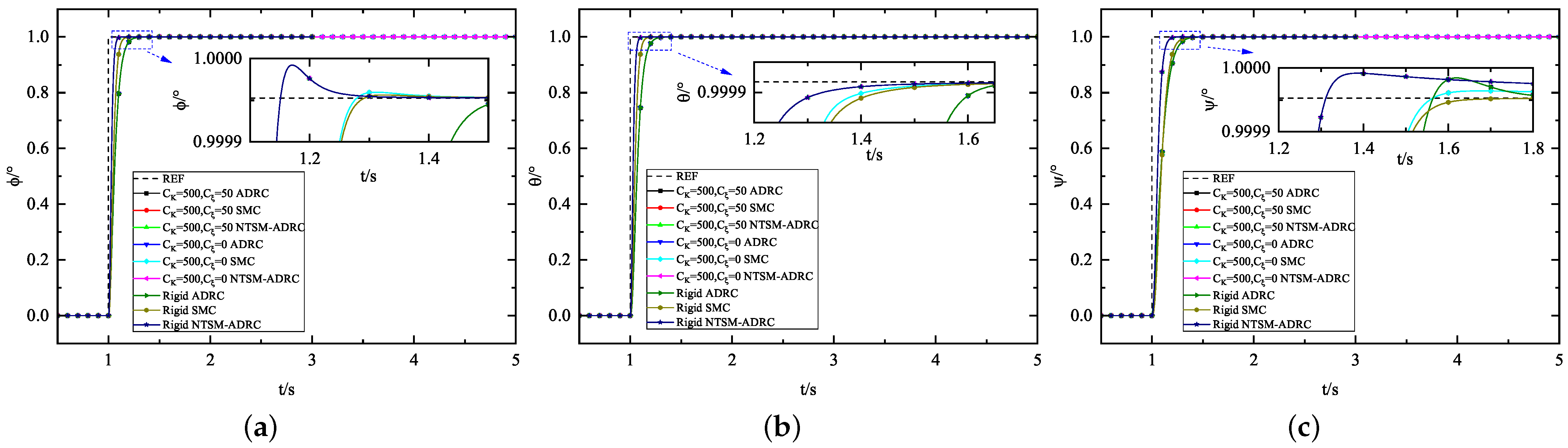
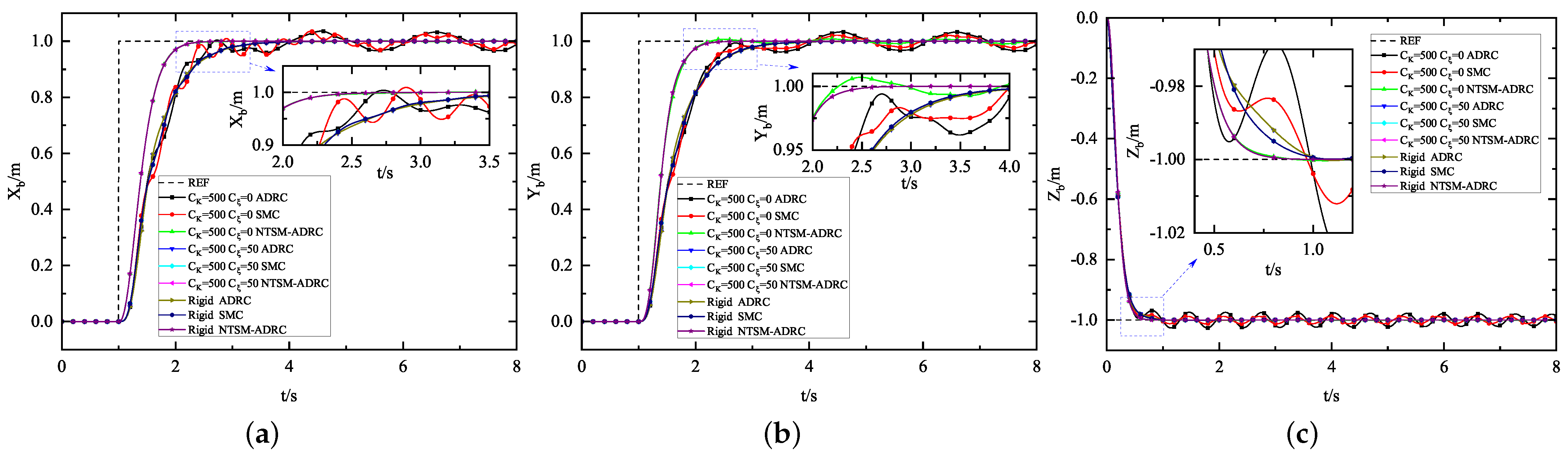
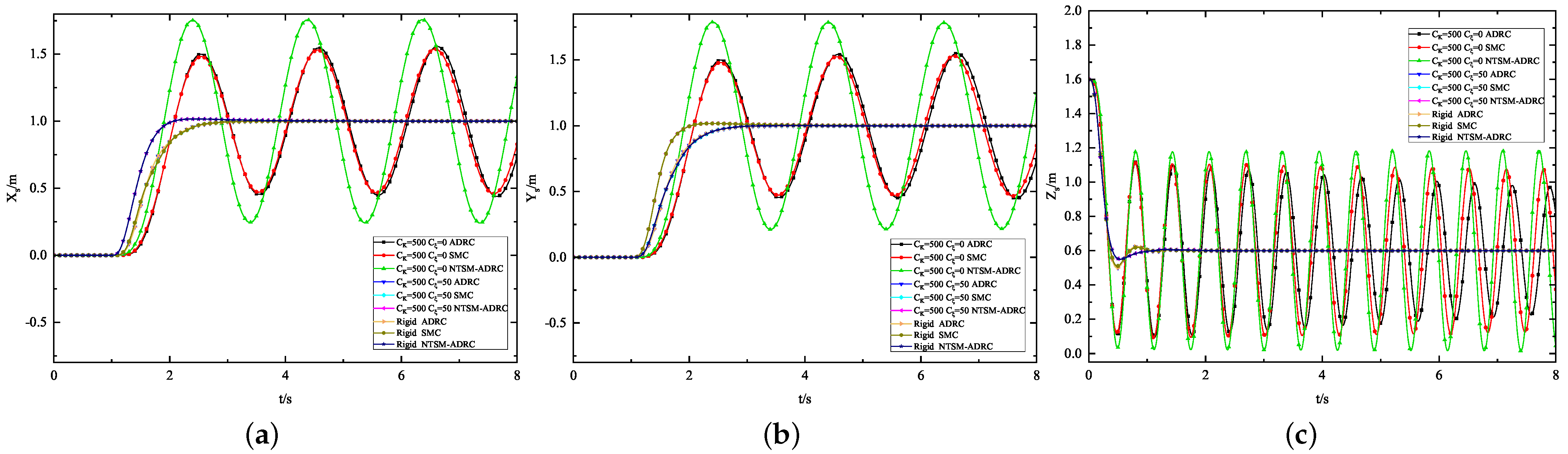
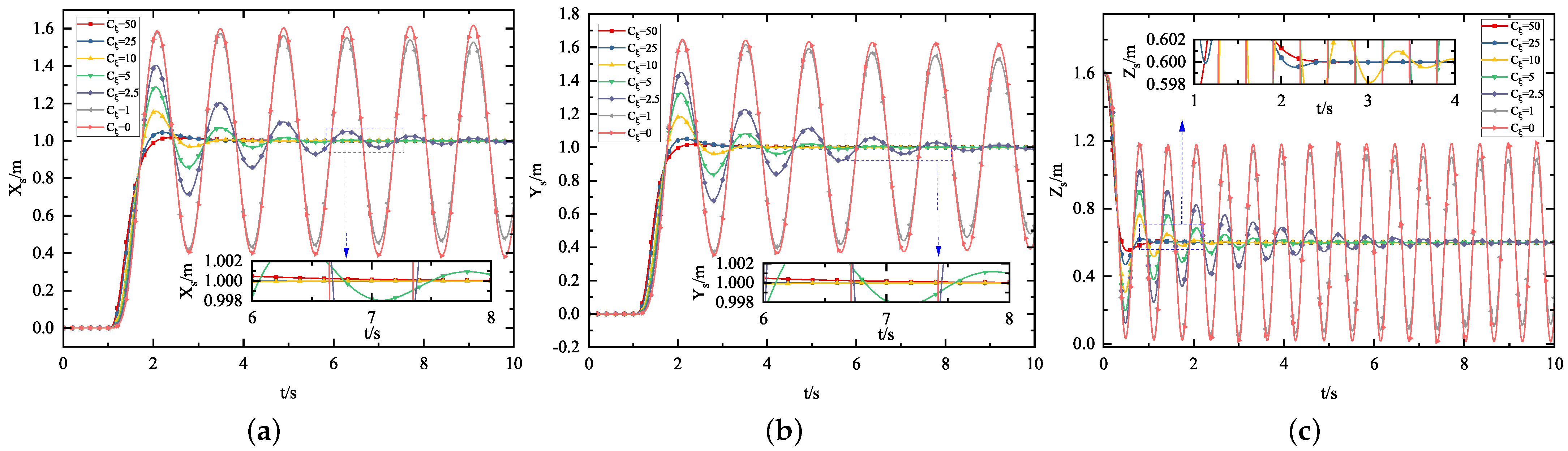
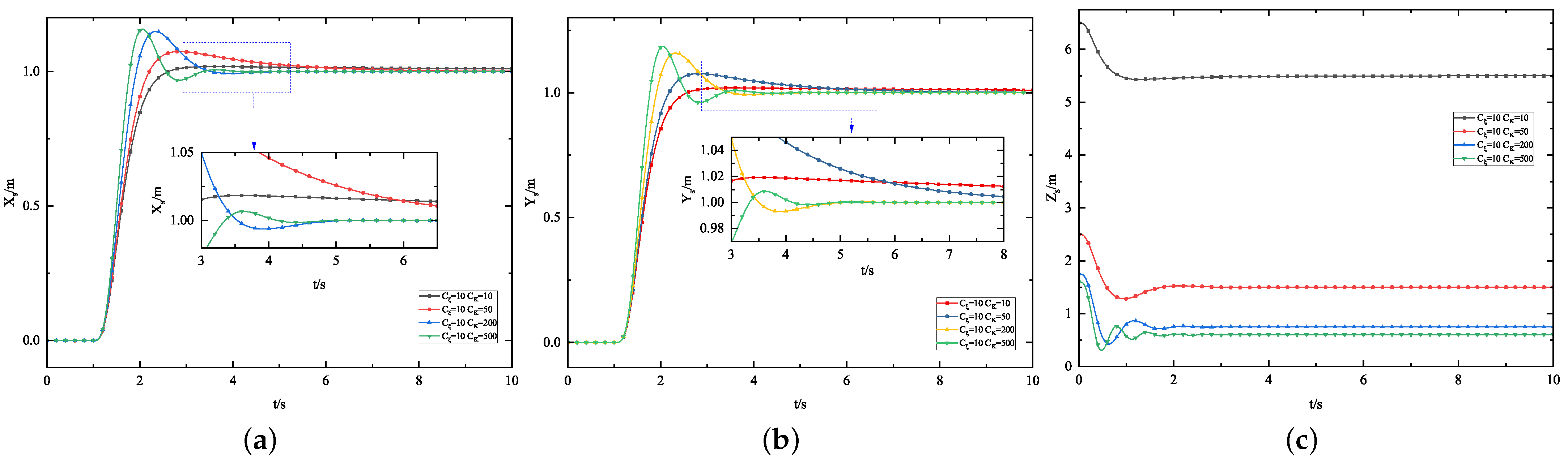
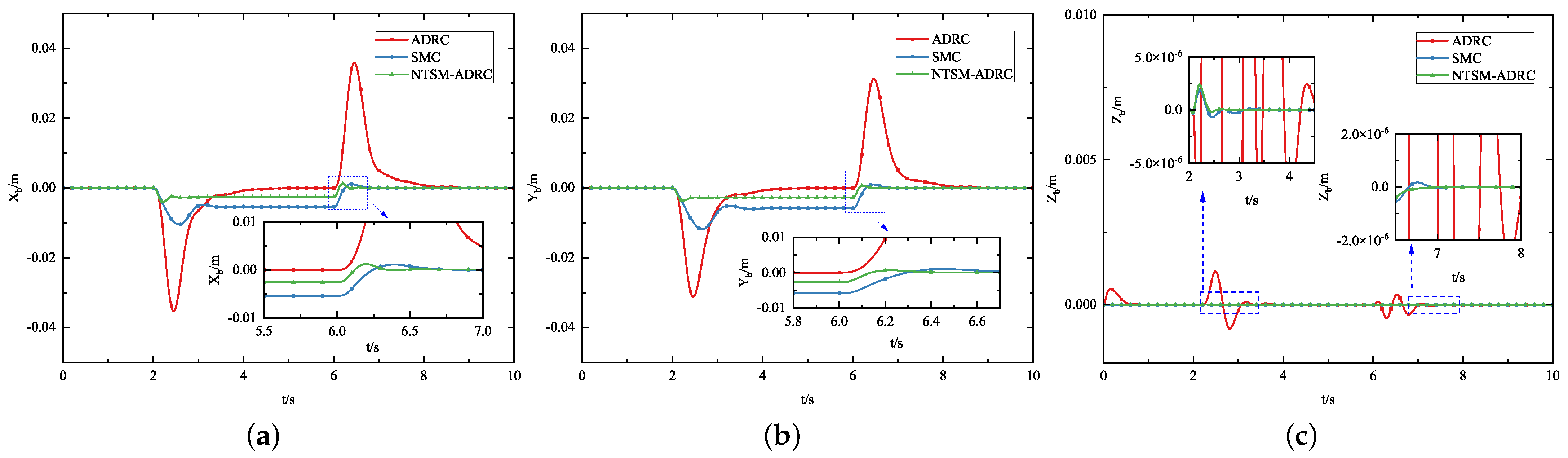







| Experimental Content | Purpose |
|---|---|
| Attitude Control Experiment | Verification of the effect of using different control methods on attitude control under elasticity, rigidity and spring-damping |
| Position Control Experiment | Verification of the effect of using different control methods on position control under elasticity, rigidity and spring-damping |
| Flexible Coefficient Experiment | Verification of the effect of different elastic-damping coefficients on position |
| Contact Operation Experiment | Verification of the effect of using different control methods on contact operation |
| Pyhsical Experiment | Validation of the effectiveness of TOCCO-FSS in practical applications |
| Parameters | Value | Unit |
|---|---|---|
| Airframe quality, | 20.2 | kg |
| Airframe width, | 2.5 | m |
| Airframe length, | 1.5 | m |
| Inertia tensor of airframe in x-axis, | 4.2 | |
| Inertia tensor of airframe in y-axis, | 2.5 | |
| Inertia tensor of airframe in z-axis, | 3.2 | |
| Lift coefficient, | ||
| Antitorque coefficient, | ||
| Saw hanging lengths, | 1.5 | m |
| Saw quality, | 5.15 | kg |
| Inertia tensor of saw in x-axis, | 2.2 | |
| Inertia tensor of saw in y-axis, | 1.1 | |
| Inertia tensor of saw in z-axis, | 1.6 | |
| Roll angle of flexible suspension, | 60 | deg |
| Yaw angle of flexible suspension, | 45 | deg |
| Steel modulus of the spring, | 8000 | MPa |
| Number of coils of the spring, | 20 | − |
| Outer diameter of the spring, | 35 | mm |
| Wire diameter of the spring, | 2.5 | mm |
| Maximum impact force of the damper, | 500 | N |
| Maximum velocity of the damper, | 10 |
| Parameters | x | y | z | ||||
|---|---|---|---|---|---|---|---|
| ESO | 0.01 | 0.01 | 0.01 | 0.05 | 0.05 | 0.02 | |
| 6 | 6 | 6 | 3 | 3 | 6 | ||
| 11 | 11 | 11 | 5 | 5 | 10 | ||
| 6 | 6 | 6 | 3 | 3 | 6 | ||
| tanh | 0.01 | 0.01 | 0.01 | 0.1 | 0.1 | 0.1 | |
| NTSM | 3 | 3 | 3 | 1.5 | 1.5 | 4 | |
| p | 5 | 5 | 5 | 5 | 5 | 5 | |
| q | 3 | 3 | 3 | 3 | 3 | 3 | |
| 5 | 5 | 5 | 3 | 3 | 6 | ||
| k | 8 | 8 | 8 | 5 | 5 | 10 |
| Parameters | Value | Unit |
|---|---|---|
| Airframe quality, | 25 | kg |
| Saw quality, | 6.2 | kg |
| Suspension saw lengths, | 1.5 | m |
| Airframe width, | 2.5 | m |
| Airframe length, | 1.5 | m |
| Steel modulus of the spring, | 8000 | MPa |
| Number of coils of the spring, | 20 | − |
| Outer diameter of the spring, | 35 | mm |
| Wire diameter of the spring, | 2.5 | mm |
| Maximum impact force of the damper, | 500 | N |
| Maximum velocity of the damper, | 10 | |
| Roll angle of flexible suspension, | 60 | deg |
| Yaw angle of flexible suspension, | 45 | deg |
| Rotor size | 32 | inch |
| Battery voltage | 54 | V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, L.; Yang, Z.; Zhuo, H.; Xu, N.; Wang, W.; Tao, K.; Liang, J.; Zhang, Q. Control and Application of Tree Obstacle-Clearing Coaxial Octocopter with Flexible Suspension Saw. Drones 2024, 8, 328. https://doi.org/10.3390/drones8070328
Liao L, Yang Z, Zhuo H, Xu N, Wang W, Tao K, Liang J, Zhang Q. Control and Application of Tree Obstacle-Clearing Coaxial Octocopter with Flexible Suspension Saw. Drones. 2024; 8(7):328. https://doi.org/10.3390/drones8070328
Chicago/Turabian StyleLiao, Luwei, Zhong Yang, Haoze Zhuo, Nuo Xu, Wei Wang, Kun Tao, Jiabing Liang, and Qiuyan Zhang. 2024. "Control and Application of Tree Obstacle-Clearing Coaxial Octocopter with Flexible Suspension Saw" Drones 8, no. 7: 328. https://doi.org/10.3390/drones8070328
APA StyleLiao, L., Yang, Z., Zhuo, H., Xu, N., Wang, W., Tao, K., Liang, J., & Zhang, Q. (2024). Control and Application of Tree Obstacle-Clearing Coaxial Octocopter with Flexible Suspension Saw. Drones, 8(7), 328. https://doi.org/10.3390/drones8070328







