ERRT-GA: Expert Genetic Algorithm with Rapidly Exploring Random Tree Initialization for Multi-UAV Path Planning
Abstract
1. Introduction
2. Related Work
3. Preparatory Knowledge
3.1. Optimal Boundary Value Problem
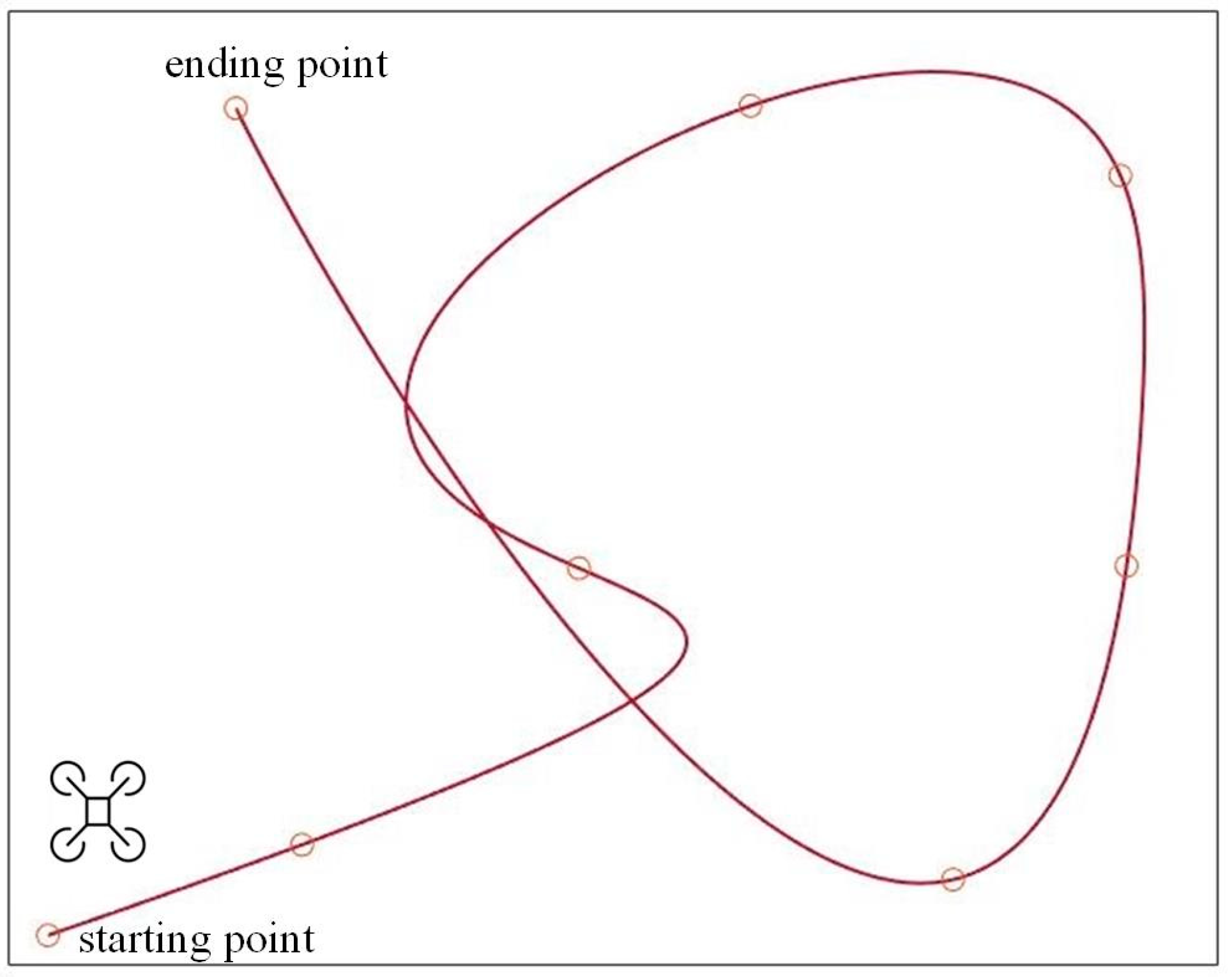
3.2. Multi-Segment Trajectory Generation
4. Algorithm Model
4.1. Problem Model Paradigm
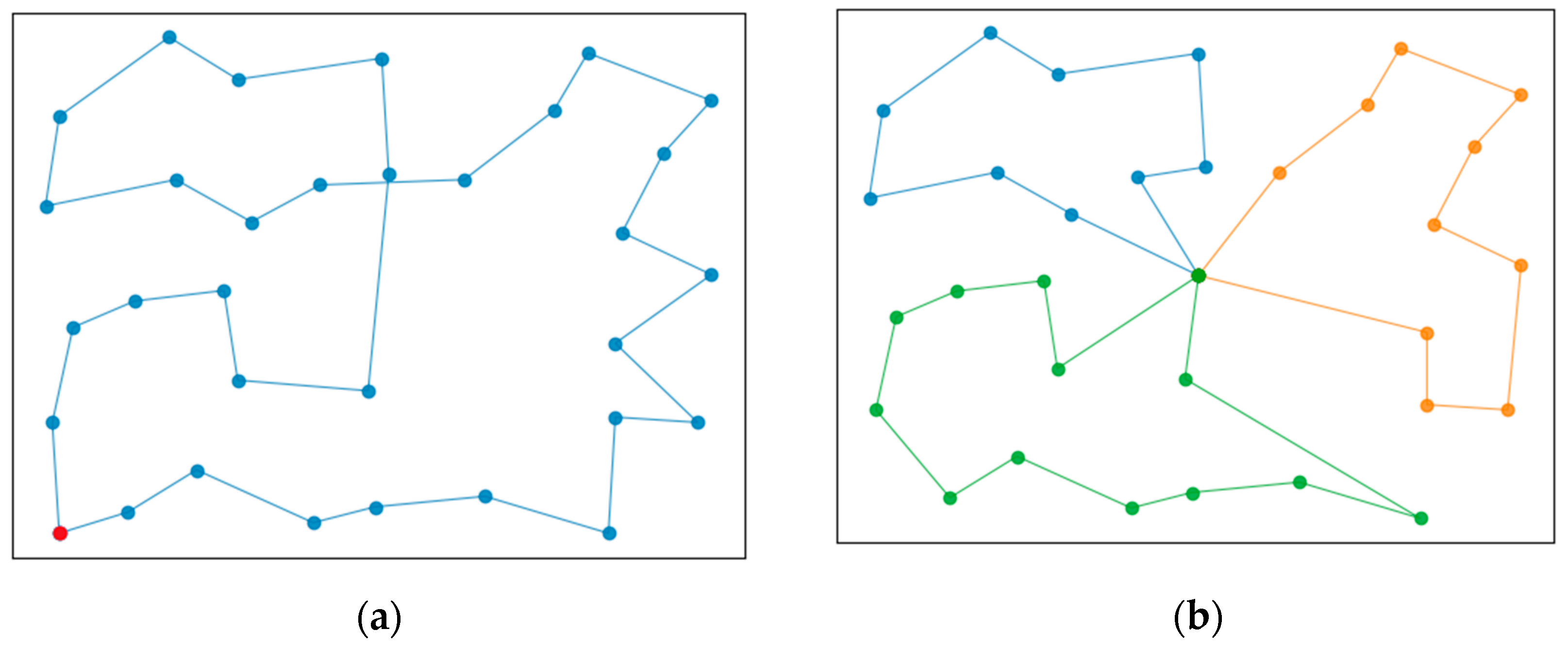
4.2. Task Assignment Based on Improved PSO-GA
| Algorithm 1: PSO-genetic algorithm |
| Input: iteration time , population number Output: List of all waypoints for each drone |
|
4.3. ERRT-GA for Path Planning
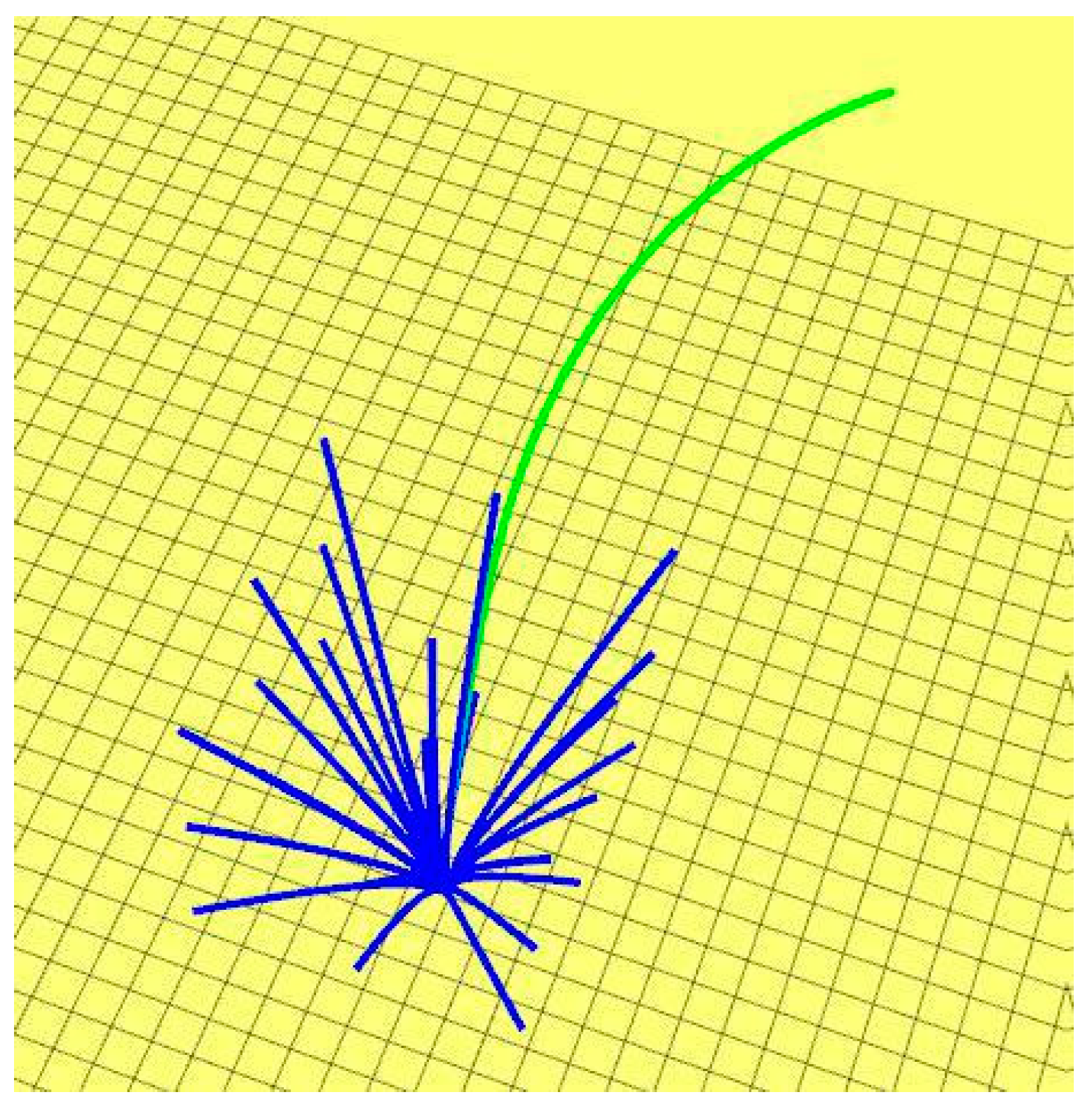
4.3.1. Population Initialization
| Algorithm 2: RRT-initial Algorithm |
| Input: population number NP Output: path of population |
|
4.3.2. Expert Genetic Iteration
| Algorithm 3: Expert Genetic Algorithm |
| Input: population number NP, path of population , iteration time Output: best path of the population |
|
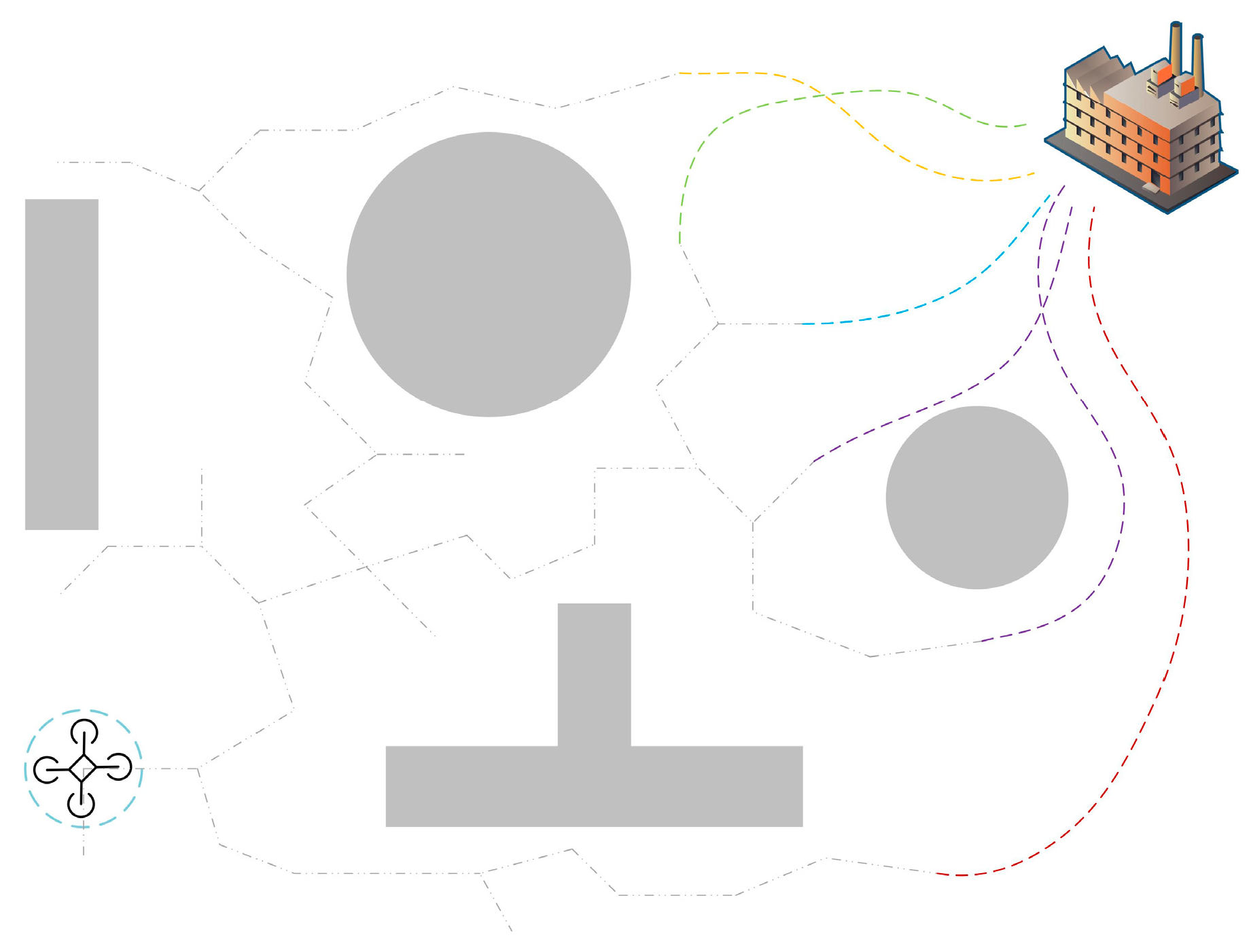
4.3.3. Multi-UAV Path Conflict Detection
| Algorithm 4: Multi-UAV evolutionary path planning Algorithm |
| Input: iteration time , population number NP Output: Smooth trajectory for all drone Trajectory |
|
5. Experiment and Result Analysis
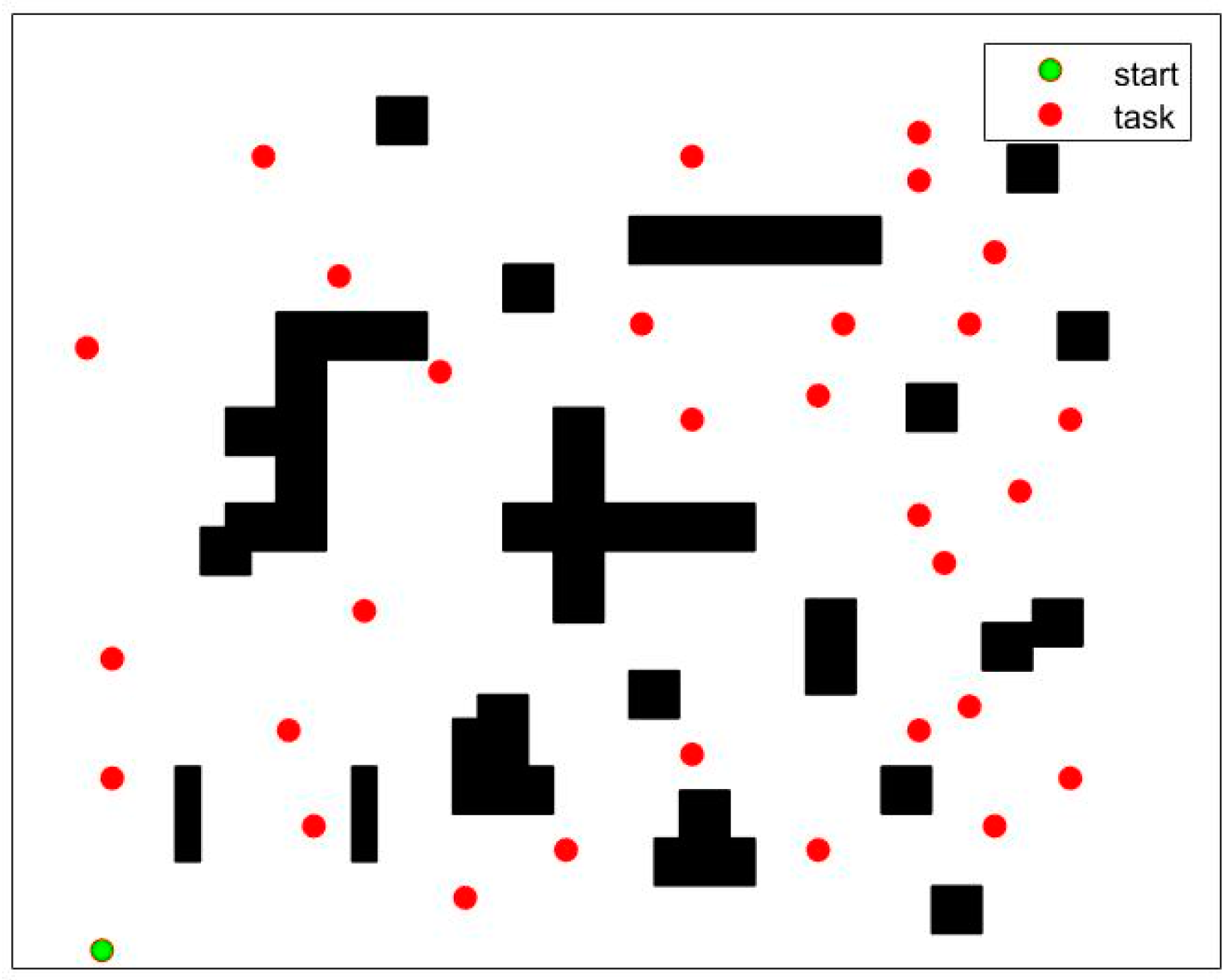
5.1. Experiment Settings
5.2. Experiment and Analysis
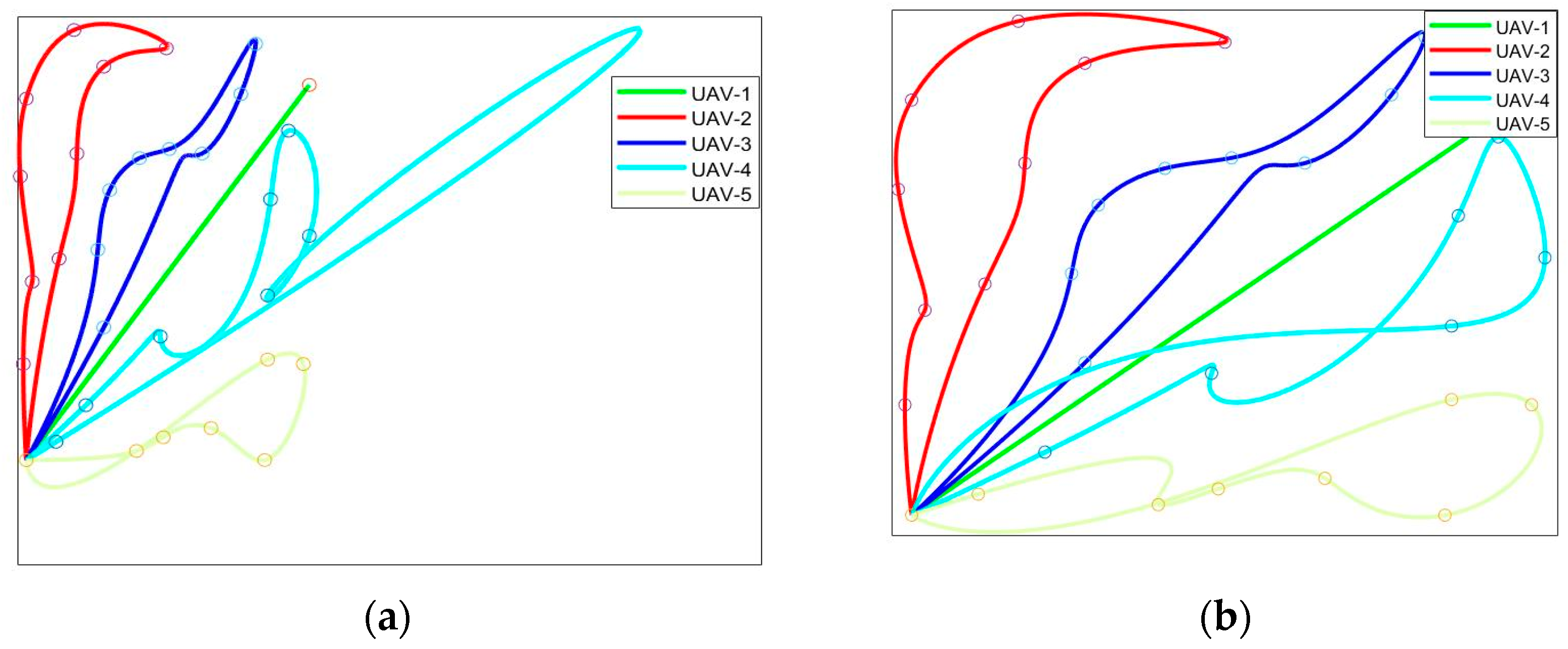
5.2.1. Task Assignment
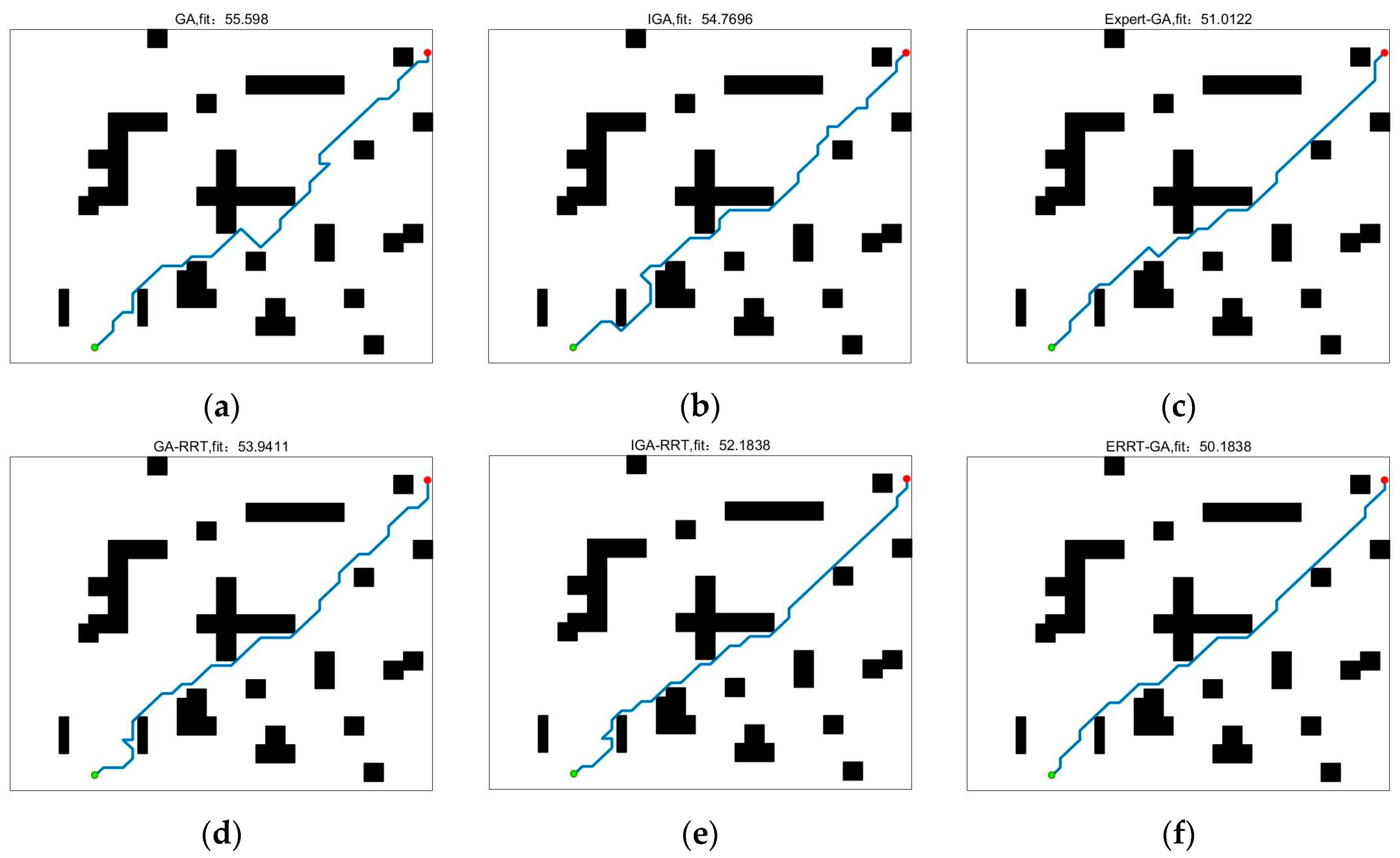
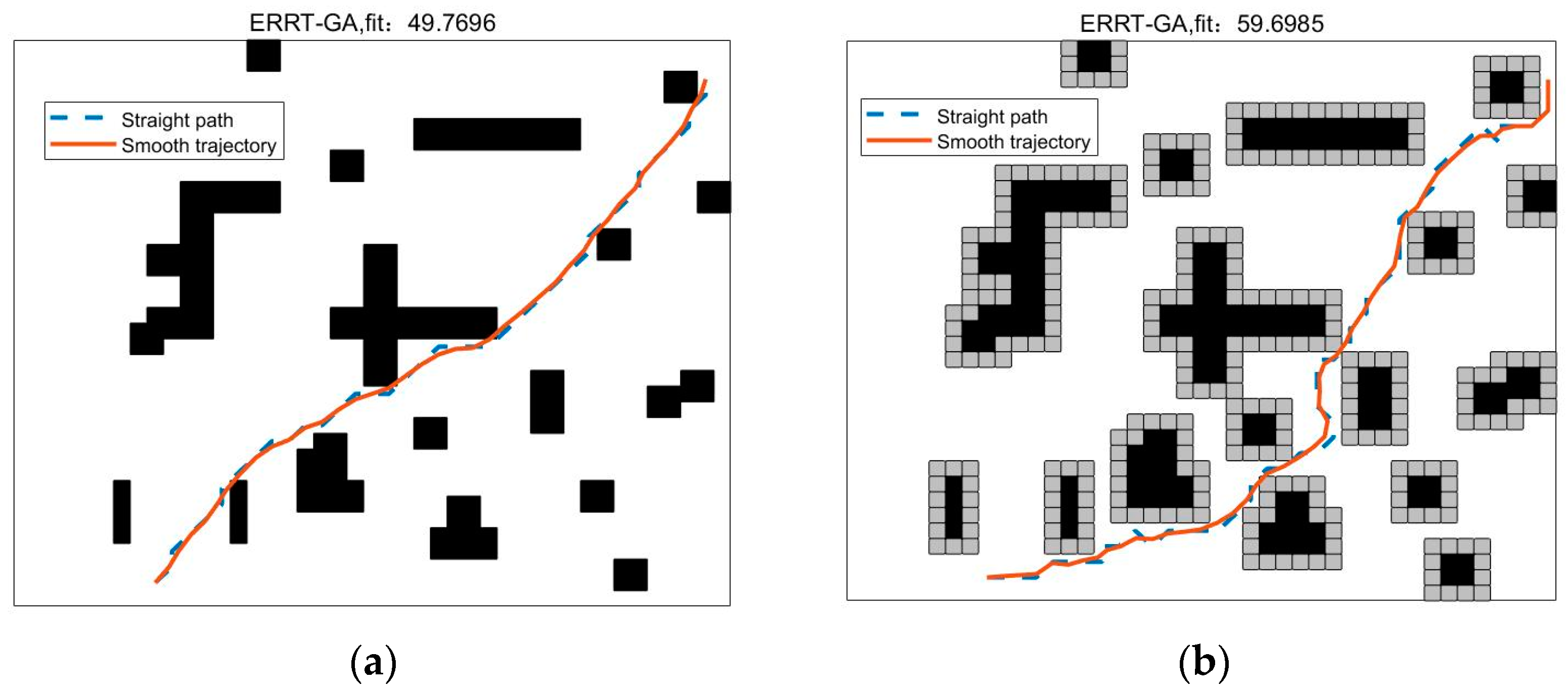
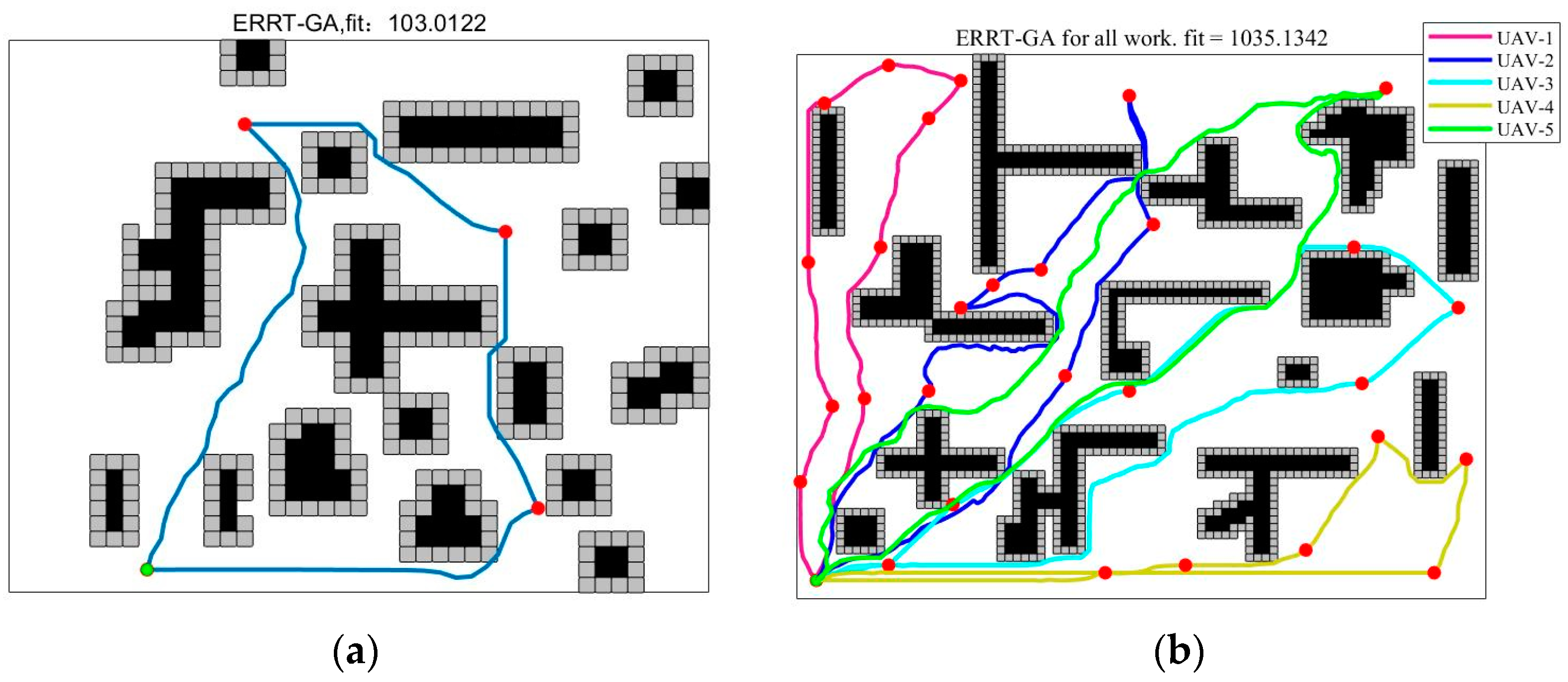
5.2.2. Path Planning
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tanaka, T.S.T.; Wang, S.; Jørgensen, J.R.; Gentili, M.; Vidal, A.Z.; Mortensen, A.K.; Acharya, B.S.; Beck, B.D.; Gislum, R. Review of Crop Phenotyping in Field Plot Experiments Using UAV-Mounted Sensors and Algorithms. Drones 2024, 8, 212. [Google Scholar] [CrossRef]
- Asadzadeh, S.; de Oliveira, W.J.; de Souza Filho, C.R. UAV-based remote sensing for the petroleum industry and environmental monitoring: State-of-the-art and perspectives. J. Pet. Sci. Eng. 2022, 208, 109633. [Google Scholar] [CrossRef]
- Mohd Noor, N.; Abdullah, A.; Hashim, M. Remote sensing UAV/drones and its applications for urban areas: A review. IOP Conf. Ser. Earth Environ. Sci. 2018, 169, 012003. [Google Scholar]
- Erdelj, M.; Natalizio, E. UAV-assisted disaster management: Applications and open issues. In Proceedings of the 2016 International Conference on Computing, Networking and Communications (ICNC), Kauai, HI, USA, 15–18 February 2016; pp. 1–5. [Google Scholar]
- Kakiuchi, R.; Tran, D.T.; Lee, J.H. Evaluation of human behaviour detection and interaction with information projection for drone-based night-time security. Drones 2023, 7, 307. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, S.; Hu, X. Multi-constrained cooperative path planning of multiple drones for persistent surveillance in urban environments. Complex Intell. Syst. 2021, 7, 1633–1647. [Google Scholar] [CrossRef]
- Saeed, R.A.; Omri, M.; Abdel-Khalek, S.; Ali, E.S.; Alotaibi, M.F. Optimal path planning for drones based on swarm intelligence algorithm. Neural Comput. Appl. 2022, 34, 10133–10155. [Google Scholar] [CrossRef]
- Yosuf, R.H.; Mokhtar, R.A.; Saeed, R.A.; Alhumyani, H.; Abdel-Khalek, S. Scheduling Algorithm for Grid Computing Using Shortest Job First with Time Quantum. Intell. Autom. Soft Comput. 2022, 31, 581–590. [Google Scholar] [CrossRef]
- Aggarwal, S.; Kumar, N. Path planning techniques for unmanned aerial vehicles: A review, solutions, and challenges. Comput. Commun. 2020, 149, 270–299. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Stentz, A. Optimal and efficient path planning for partially-known environments. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; pp. 3310–3317. [Google Scholar]
- Koenig, S.; Likhachev, M. D*lite. In Proceedings of the Eighteenth National Conference on Artificial Intelligence and Fourteenth Conference on Innovative Applications of Artificial Intelligence, Edmonton, AB, Canada, 28 July–1 August 2002; pp. 476–483. [Google Scholar]
- Fransen, K.; van Eekelen, J. Efficient path planning for automated guided vehicles using A*(Astar) algorithm incorporating turning costs in search heuristic. Int. J. Prod. Res. 2023, 61, 707–725. [Google Scholar] [CrossRef]
- Fan, G.; Xing, X.; Han, Y.; Chen, M.; Gui, H. Path planning for ground target reconnaissance based on improved Astar algorithm. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021; pp. 2092–2097. [Google Scholar]
- LaValle, S. Rapidly-Exploring Random Trees: A New Tool for Path Planning; Research Report 9811; Department of Computer Science, Iowa State University: Ames, IA, USA, 1998. [Google Scholar]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Gammell, J.D.; Srinivasa, S.S.; Barfoot, T.D. Informed RRT*: Optimal sampling-based path planning focused via direct sampling of an admissible ellipsoidal heuristic. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2997–3004. [Google Scholar]
- Lindqvist, B.; Agha-Mohammadi, A.A.; Nikolakopoulos, G. Exploration-RRT: A multi-objective path planning and exploration framework for unknown and unstructured environments. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 3429–3435. [Google Scholar]
- Ge, J.; Liu, L.; Dong, X.; Tian, W. Trajectory planning of fixed-wing UAV using kinodynamic RRT algorithm. In Proceedings of the 2020 10th International Conference on Information Science and Technology (ICIST), Bath, London, Plymouth, UK, 9–15 September 2020; pp. 44–49. [Google Scholar]
- Meng, Q.; Chen, K.; Qu, Q. PPSwarm: Multi-UAV Path Planning Based on Hybrid PSO in Complex Scenarios. Drones 2024, 8, 192. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, X.; Deng, P.; Kang, J.; Gao, Z.; Liu, L. An Energy-Balanced Path Planning Algorithm for Multiple Ferrying UAVs Based on GA. Int. J. Aerosp. Eng. 2020, 2020, 3516149. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Liu, S.; Zhou, J.; Papavassiliou, C. Three-dimensional underwater path planning based on modified wolf pack algorithm. IEEE Access 2017, 5, 22783–22795. [Google Scholar] [CrossRef]
- Wang, Y.; Li, W.; Jiang, R. A novel hybrid algorithm based on improved particle swarm optimization algorithm and genetic algorithm for multi-UAV path planning with time windows. In Proceedings of the 2022 IEEE 5th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 16–18 December 2022; Volume 5, pp. 1005–1009. [Google Scholar]
- Wang, X.; Meng, X. UAV online path planning based on improved genetic algorithm. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 4101–4106. [Google Scholar]
- Yang, T.; Yang, F.; Li, D. A New Autonomous Method of Drone Path Planning Based on Multiple Strategies for Avoiding Obstacles with High Speed and High Density. Drones 2024, 8, 205. [Google Scholar] [CrossRef]
- Rahim, S.; Razaq, M.M.; Chang, S.Y.; Peng, L. A reinforcement learning-based path planning for collaborative UAVs. In Proceedings of the 37th ACM/SIGAPP Symposium on Applied Computing, New York, NY, USA, 25–29 April 2022; pp. 1938–1943. [Google Scholar]
- Huang, X.; Wang, W.; Ji, Z.; Cheng, B. Representation Enhancement-Based Proximal Policy Optimization for UAV Path Planning and Obstacle Avoidance. Int. J. Aerosp. Eng. 2023, 2023, 6654130. [Google Scholar] [CrossRef]
- Sharon, G.; Stern, R.; Felner, A.; Sturtevant, N.R. Conflict-based search for optimal multi-agent pathfinding. Artif. Intell. 2015, 219, 40–66. [Google Scholar] [CrossRef]
- Li, J.; Ruml, W.; Koenig, S. Eecbs: A bounded-suboptimal search for multi-agent path finding. Proc. AAAI Conf. Artif. Intell. 2021, 35, 12353–12362. [Google Scholar] [CrossRef]
- Li, J.; Harabor, D.; Stuckey, P.J.; Ma, H.; Gange, G.; Koenig, S. Pairwise symmetry reasoning for multi-agent path finding search. Artif. Intell. 2021, 301, 103574. [Google Scholar] [CrossRef]
- Li, J.; Tinka, A.; Kiesel, S.; Durham, J.W.; Kumar, T.S.; Koenig, S. Lifelong multi-agent path finding in large-scale warehouses. Proc. AAAI Conf. Artif. Intell. 2021, 35, 11272–11281. [Google Scholar] [CrossRef]
- Chen, J.; Li, J.; Fan, C.; Williams, B.C. Scalable and safe multi-agent motion planning with nonlinear dynamics and bounded disturbances. Proc. AAAI Conf. Artif. Intell. 2021, 35, 11237–11245. [Google Scholar] [CrossRef]
- Mueller, M.W.; Hehn, M.; D’Andrea, R. A computationally efficient motion primitive for quadrocopter trajectory generation. IEEE Trans. Robot. 2015, 31, 1294–1310. [Google Scholar] [CrossRef]
- Lian, L.; Zong, X.; He, K.; Yang, Z. Trajectory optimization of unmanned surface vehicle based on improved minimum snap. Ocean. Eng. 2024, 302, 117719. [Google Scholar] [CrossRef]
- Mellinger, D.; Kumar, V. Minimum snap trajectory generation and control for quadrotors. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2520–2525. [Google Scholar]
- Stellato, B.; Banjac, G.; Goulart, P.; Bemporad, A.; Boyd, S. OSQP: An operator splitting solver for quadratic programs. Math. Program. Comput. 2020, 12, 637–672. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical report-tr06; Erciyes University, Engineering Faculty, Computer Engineering Department: Kayseri, Türkiye, 2005. [Google Scholar]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B 1996, 26, 29–41. [Google Scholar] [CrossRef]
- Loscos, D.; Martí-Oliet, N.; Rodríguez, I. Generalization and completeness of stochastic local search algorithms. Swarm Evol. Comput. 2022, 68, 100982. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Muñoz, A.; Rubio, F. Evaluating genetic algorithms through the approximability hierarchy. J. Comput. Sci. 2021, 53, 101388. [Google Scholar] [CrossRef]
- Cheng, Z.; Sun, Y.; Liu, Y. Path planning based on immune genetic algorithm for UAV. In Proceedings of the 2011 International Conference on Electric Information and Control Engineering, Wuhan, China, 15–17 April 2011; pp. 590–593. [Google Scholar]
- Tu, G.T.; Juang, J.G. Path planning and obstacle avoidance based on reinforcement learning for UAV application. In Proceedings of the 2021 International Conference on System Science and Engineering (ICSSE), Ho Chi Minh City, Vietnam, 26–28 August 2021; pp. 352–355. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Li, Y.; Dong, D.; Guo, X. Mobile robot path planning based on improved genetic algorithm with A-star heuristic method. In Proceedings of the 2020 IEEE 9th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 11–13 December 2020; Volume 9, pp. 1306–1311. [Google Scholar]







| Time | Position | Velocity | Acceleration |
|---|---|---|---|
| 0 | 0 | ||
| 0 | 0 |
| Map Size | Task Number | UAV Number | ITERMAX (Task) | ITERMAX (Path) |
|---|---|---|---|---|
| [43, 36] and [86, 72] | 31 | 10 | 3000 | 200 |
| Algorithm | NP = 10 | NP = 50 | NP = 100 |
|---|---|---|---|
| GA | 0.3132 s | ∞ | ∞ |
| Expert-GA | 0.2955 s | 1.4241 s | 2.8302 s |
| Ours (ERRT-GA) | 0.3365 s | 1.4803 s | 2.8922 s |
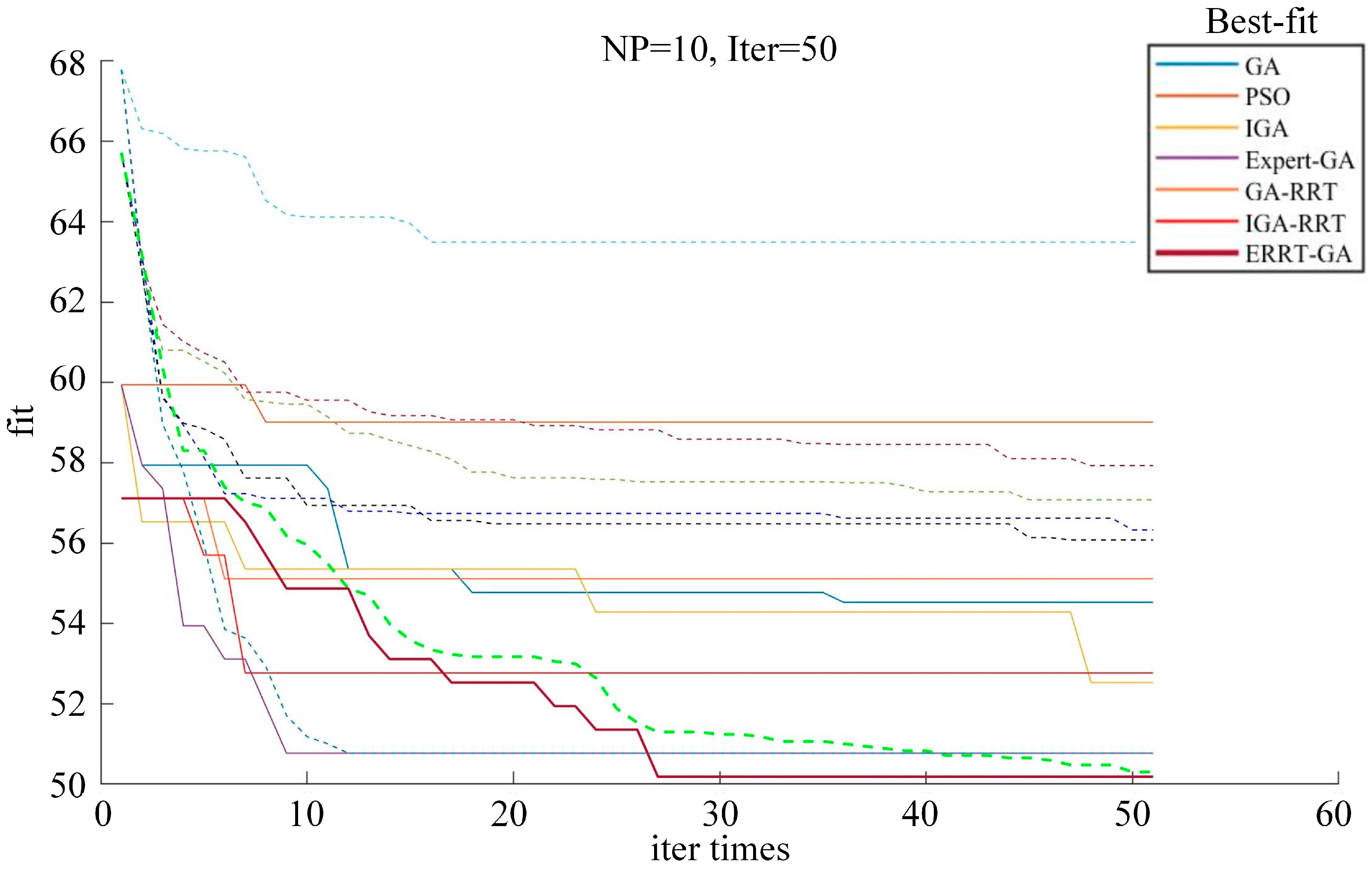
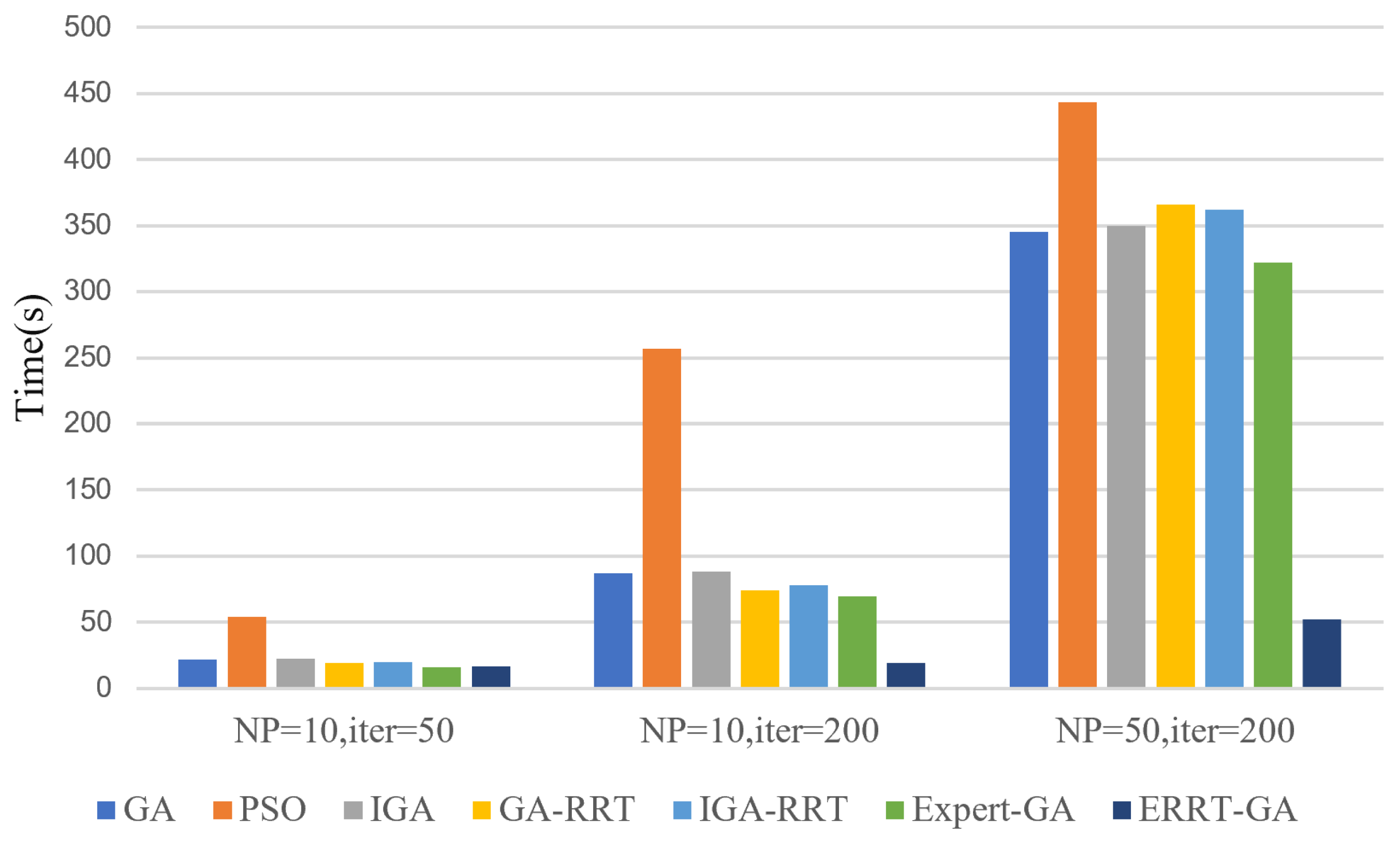
| Algorithm | Mean Fit | Best Fit | Convergence Times | Time |
|---|---|---|---|---|
| GA | 57.07 | 54.52 | 36 | 21.88 s |
| PSO | 63.49 | 59.01 | 8 | 54.11 s |
| IGA | 58.01 | 52.52 | 48 | 22.11 s |
| GA-RRT | 56.32 | 55.11 | 6 | 19.08 s |
| IGA-RRT | 56.23 | 52.76 | 7 | 19.95 s |
| Expert-GA | 50.76 | 50.76 | 9 | 15.86 s |
| ERRT-GA | 50.18 | 50.18 | 27 | 16.74 s |
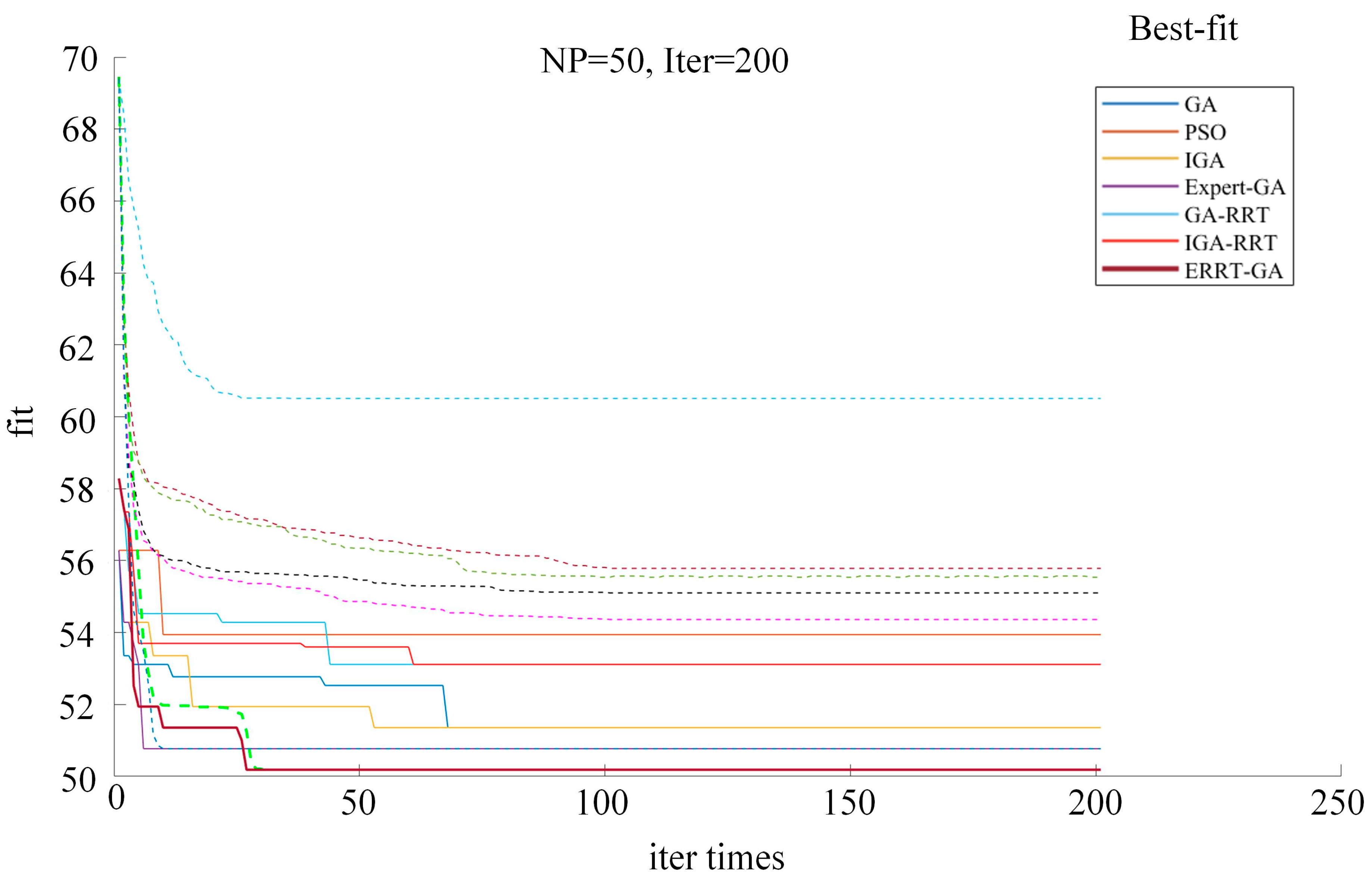
| Algorithm | Mean Fit | Best Fit | Convergence Times | Time |
|---|---|---|---|---|
| GA | 55.43 | 53.94 | 174 | 87.11 s |
| PSO | 63.49 | 59.01 | 8 | 256.58 s |
| IGA | 56.11 | 52.52 | 48 | 88.11 s |
| GA-RRT | 55.78 | 53.11 | 114 | 74.02 s |
| IGA-RRT | 55.42 | 52.70 | 7 | 79.74 s |
| Expert-GA | 50.18 | 50.18 | 62 | 61.61 s |
| ERRT-GA | 50.18 | 50.18 | 27 | 63.80 s |
| Algorithm | Mean Fit | Best Fit | Convergence Times | Time |
|---|---|---|---|---|
| GA | 54.38 | 51.35 | 68 | 345.82 s |
| PSO | 60.51 | 53.94 | 10 | 446.22 s |
| IGA | 55.11 | 51.35 | 53 | 348.96 s |
| GA-RRT | 55.93 | 53.11 | 44 | 359.15 s |
| IGA-RRT | 55.81 | 53.11 | 61 | 362.69 s |
| Expert-GA | 50.76 | 50.76 | 6 | 324.81 s |
| ERRT-GA | 50.18 | 50.18 | 27 | 296.85 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Niu, Z.; Jiang, B.; Zhang, Y.; Chen, S.; Li, Z.; Gao, M.; Zhu, M. ERRT-GA: Expert Genetic Algorithm with Rapidly Exploring Random Tree Initialization for Multi-UAV Path Planning. Drones 2024, 8, 367. https://doi.org/10.3390/drones8080367
Xu H, Niu Z, Jiang B, Zhang Y, Chen S, Li Z, Gao M, Zhu M. ERRT-GA: Expert Genetic Algorithm with Rapidly Exploring Random Tree Initialization for Multi-UAV Path Planning. Drones. 2024; 8(8):367. https://doi.org/10.3390/drones8080367
Chicago/Turabian StyleXu, Hong, Zijing Niu, Bo Jiang, Yuhang Zhang, Siji Chen, Zhiqiang Li, Mingke Gao, and Miankuan Zhu. 2024. "ERRT-GA: Expert Genetic Algorithm with Rapidly Exploring Random Tree Initialization for Multi-UAV Path Planning" Drones 8, no. 8: 367. https://doi.org/10.3390/drones8080367
APA StyleXu, H., Niu, Z., Jiang, B., Zhang, Y., Chen, S., Li, Z., Gao, M., & Zhu, M. (2024). ERRT-GA: Expert Genetic Algorithm with Rapidly Exploring Random Tree Initialization for Multi-UAV Path Planning. Drones, 8(8), 367. https://doi.org/10.3390/drones8080367






