Towards Safer UAV Operations in Urban Air Mobility: 3D Automated Modelling for CFD-Based Microweather Systems
Highlights
- An automated workflow was developed to generate geometrically consistent urban CFD meshes from open-source data.
- CFD simulations of Ourense reveal complex wind patterns and regions of high turbulence, validated through experimental measurements using anemometers.
- The methodology enables reliable prediction of urban wind fields without requiring proprietary or high-cost 3D city models.
- The generated CFD outputs can be integrated into UAV trajectory optimisation frameworks to enhance flight safety and efficiency in urban areas.
Abstract
1. Introduction
- Enhanced terrain model integration: The proposed approach is specifically designed for areas with significant elevation changes and steep slopes. In addition to producing error-free geometries, a new geometry-smoothing method is introduced to prevent wakes near the computational domain boundaries, ensuring numerical stability.
- Development of adaptive geometry modelling tools: The proposed framework includes tools to adjust the geometric level of detail according to available computational resources. It introduces a novel method for implicit building modelling based on porosity models. This low-detail approach considers the effects of these elements on wind flow without increasing mesh complexity, making it particularly useful for large-scale simulations.
- Suitability analysis of a preliminary microweather system for vertiport operations: The developed CFD model was coupled with a mesoscale weather forecast to obtain high-resolution wind predictions. Using this approach, a probabilistic evaluation was conducted to quantify the prediction uncertainties.
2. Methodology
2.1. The 3D Geometric Model Generation
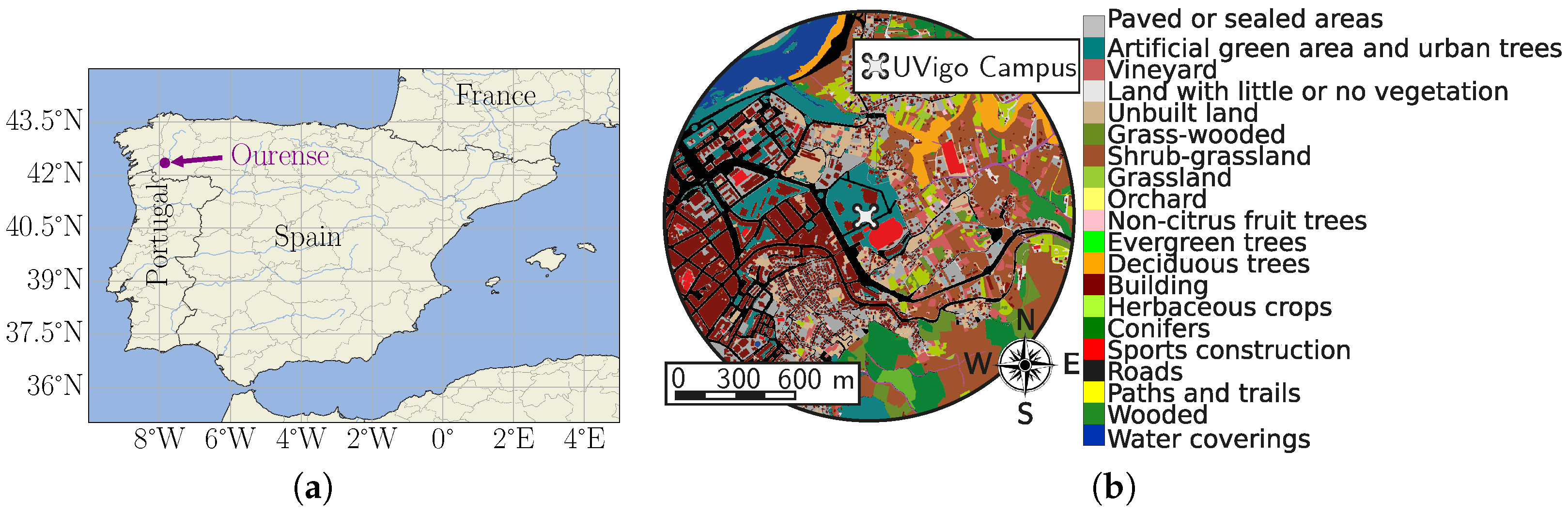
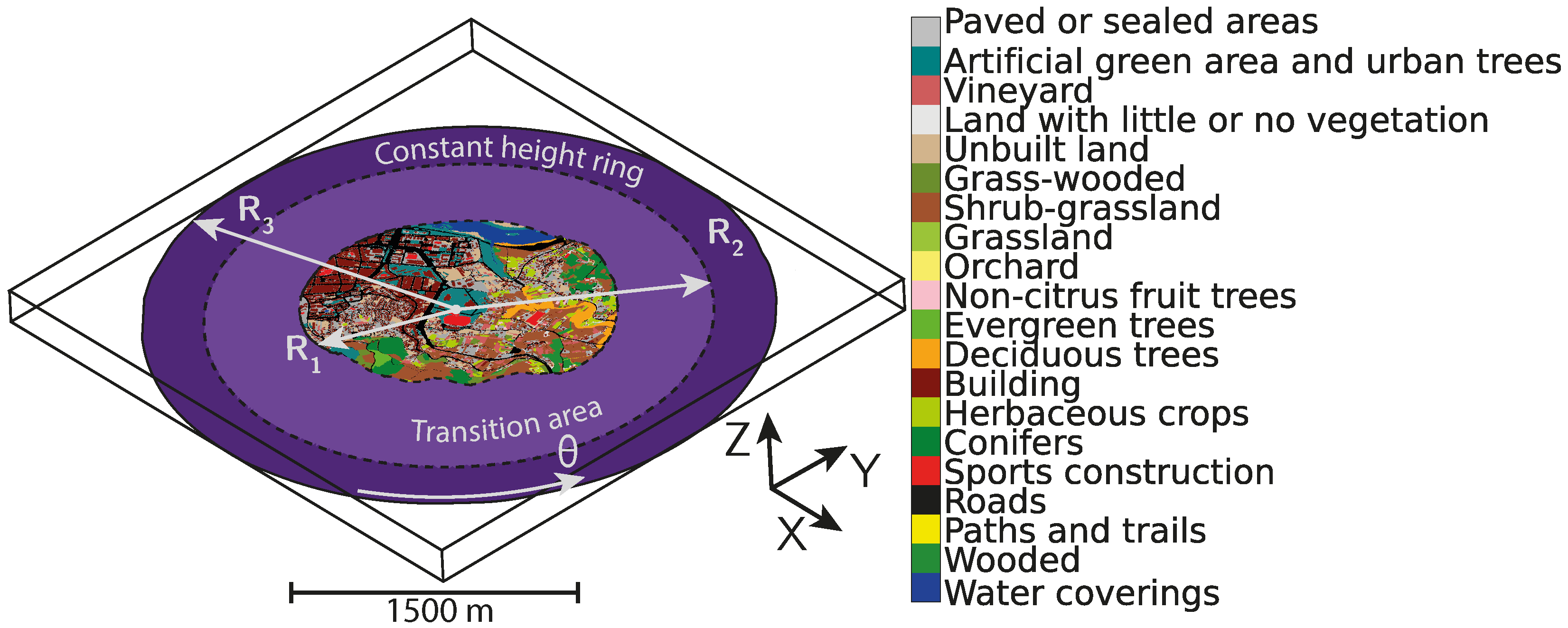
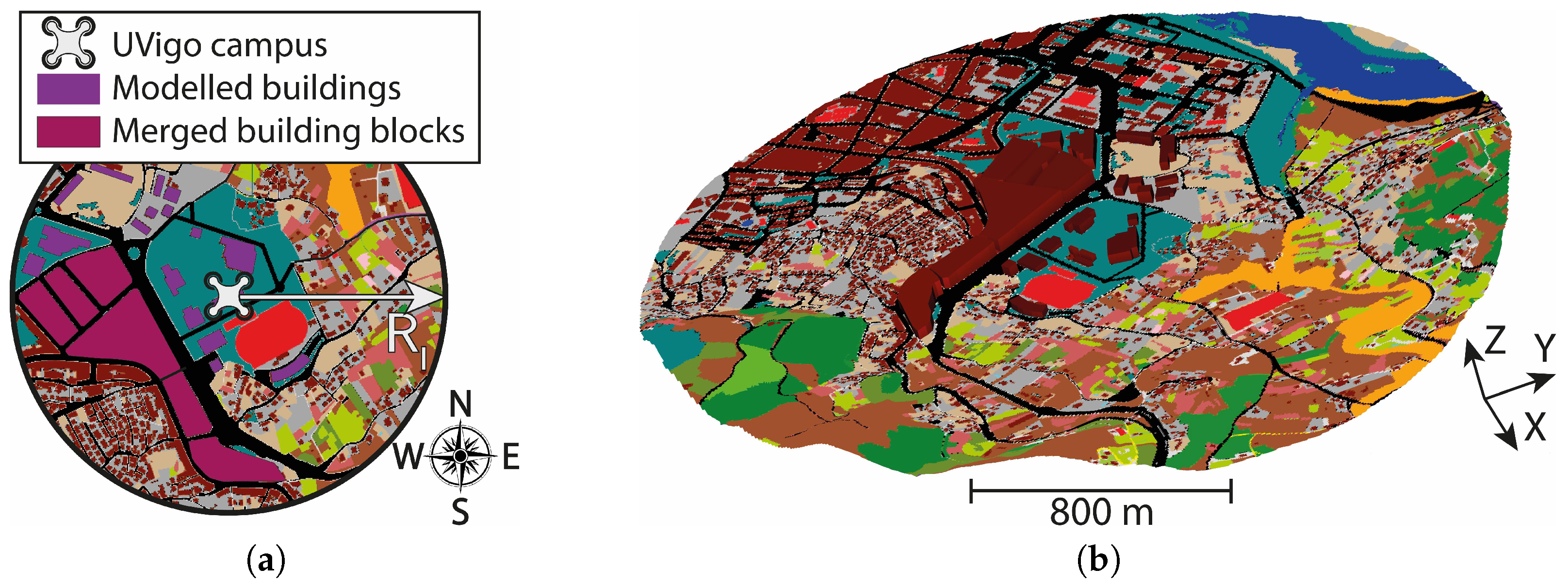
2.1.1. Area of Study Definition
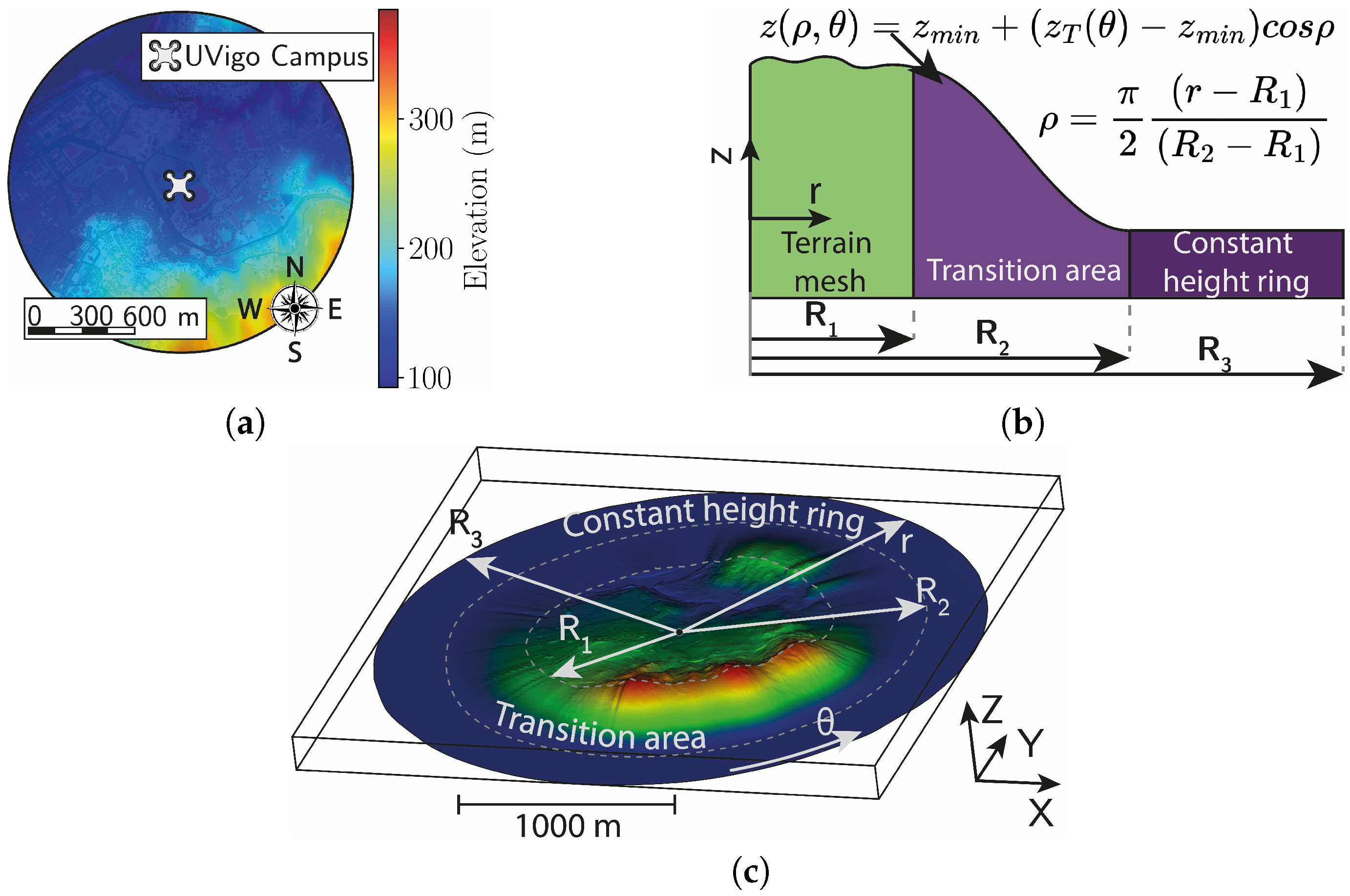
2.1.2. Terrain Geometry
- Transition area (): This provides a smooth elevation transition between the terrain mesh and the constant height ring, using a cosine elevation profile (Figure 2b). It spans from the limits of the terrain mesh ( = 1 km) to the constant height ring ( = 1.6 km). This last value was chosen based on the recommendations from An et al. [42], which suggest avoiding slopes steeper than 30° near the domain boundaries. With this configuration, the maximum slope is 22°, considering for steepest case of the variable.
- Constant height ring (): A flat surface with a constant elevation equal to the minimum terrain height (). Its purpose is to ensure organised inflow and outflow. It extends up to a radius of 2 km.
2.1.3. Land Semantic Classification
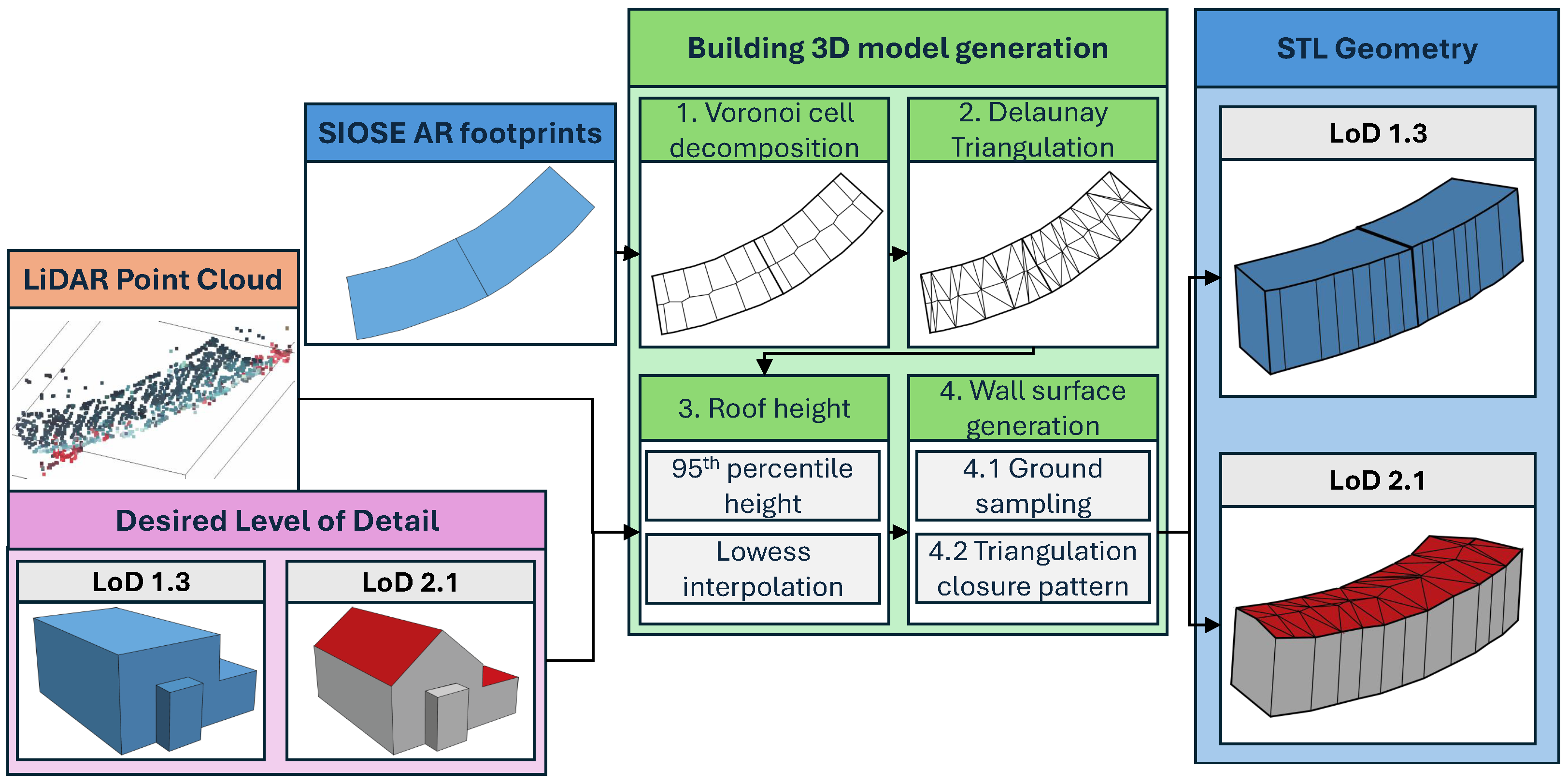
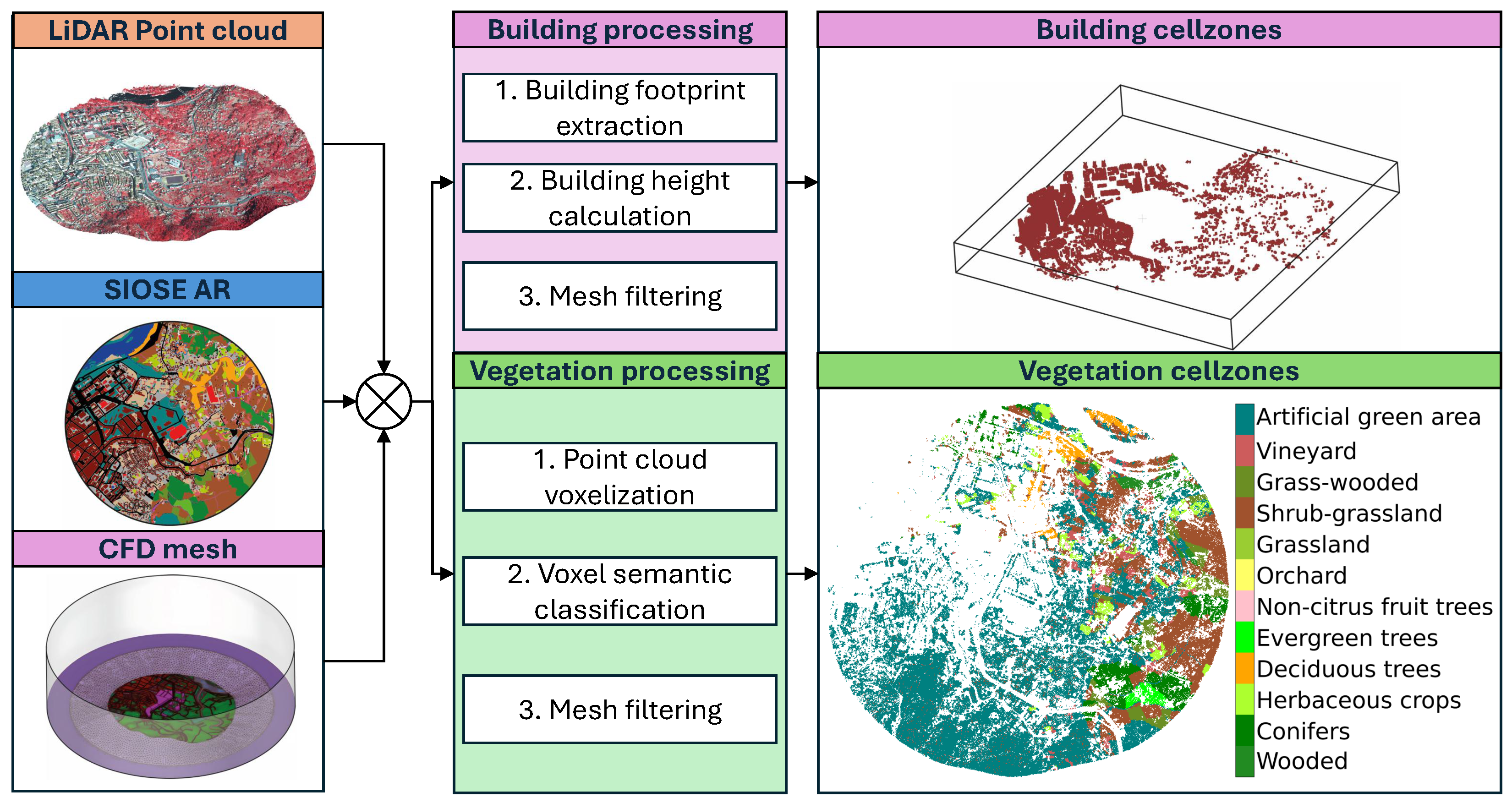
2.1.4. Buildings’ Geometry
- LoD 1.3: Buildings are represented as simple blocks with flat roofs.
- LoD 2.1: Simplified roof elevation variations are included, excluding fine details.
- Voronoi cell decomposition: Building footprints are decomposed into convex polygons using Voronoi cells from boundary points, fully covering the domain.
- Delaunay triangulation: Applied to each Voronoi cell to create a 2D surface without gaps or overlaps.
- Roof height calculation: Roof heights are derived from IGN LiDAR point clouds. Points within the ground floor polygon are extracted, and heights are assigned to Delaunay points according to LoD:
- LoD 1.3: Roofs are modelled as flat surfaces at the 95th percentile height of the point cloud.
- LoD 2.1: Roofs are modelled through a Lowess interpolation, adjusted with point cloud heights.
- Wall surface generation: Building side walls are created from the roof’s outer points. Terrain height is sampled, and an extrusion is performed, closing the building volume with a triangulation pattern.
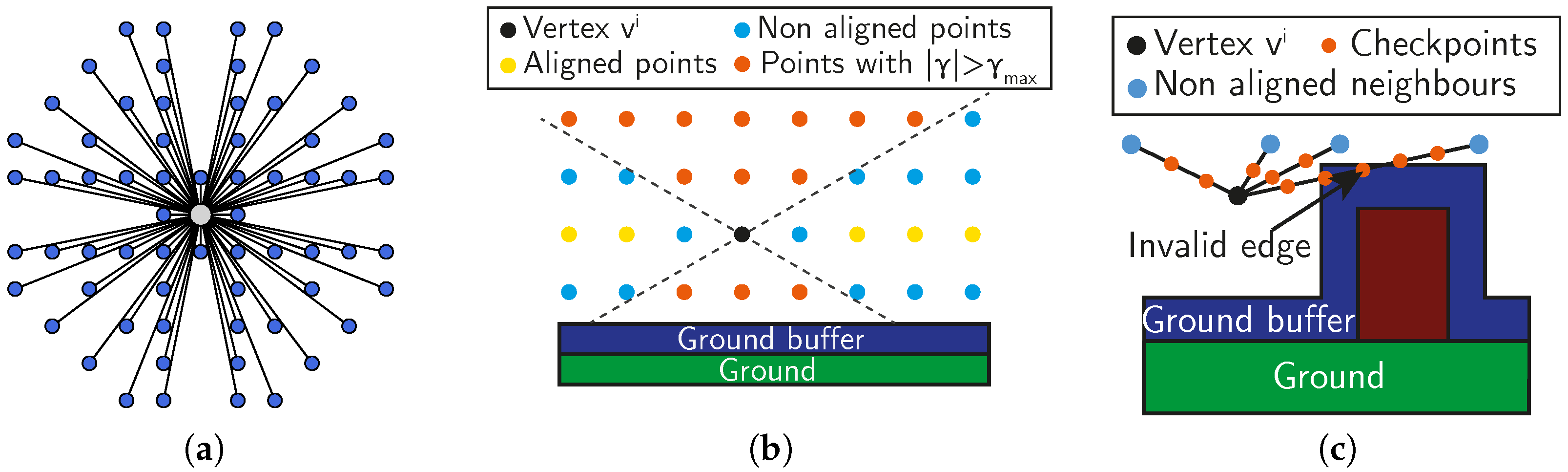
2.1.5. Geometry Simplification
2.2. CFD Wind Simulation
2.2.1. CFD Mesh Generation
2.2.2. Vegetation and Urban Structures Modelling
2.2.3. Boundary Conditions
2.2.4. Simulation Setup
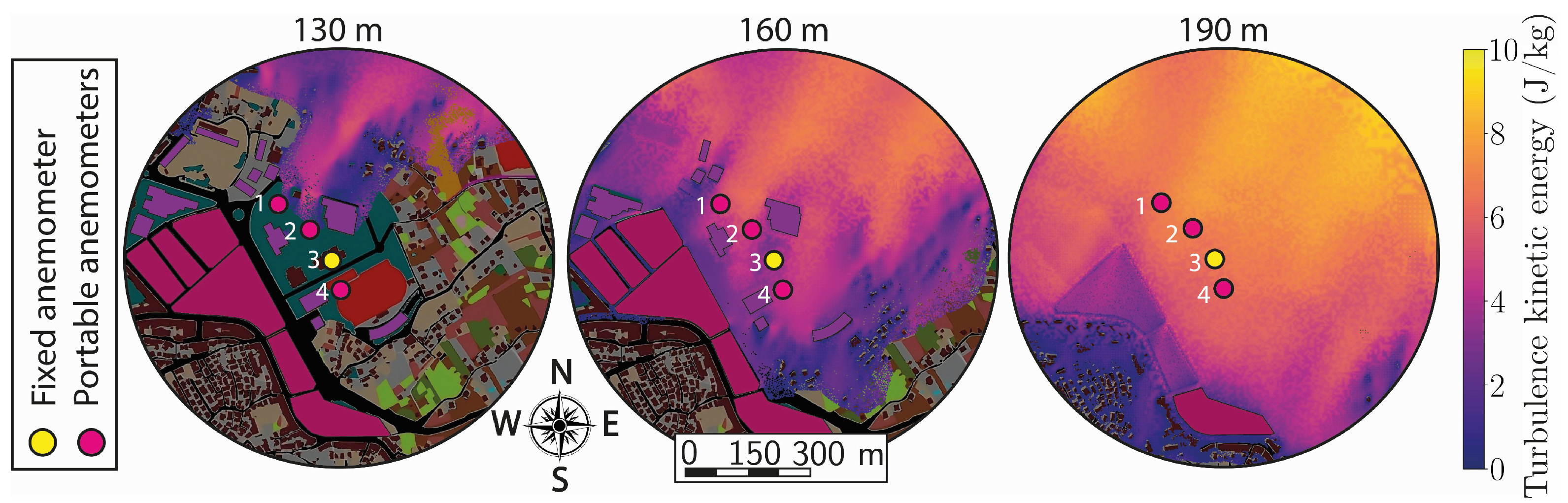
2.3. CFD Validation
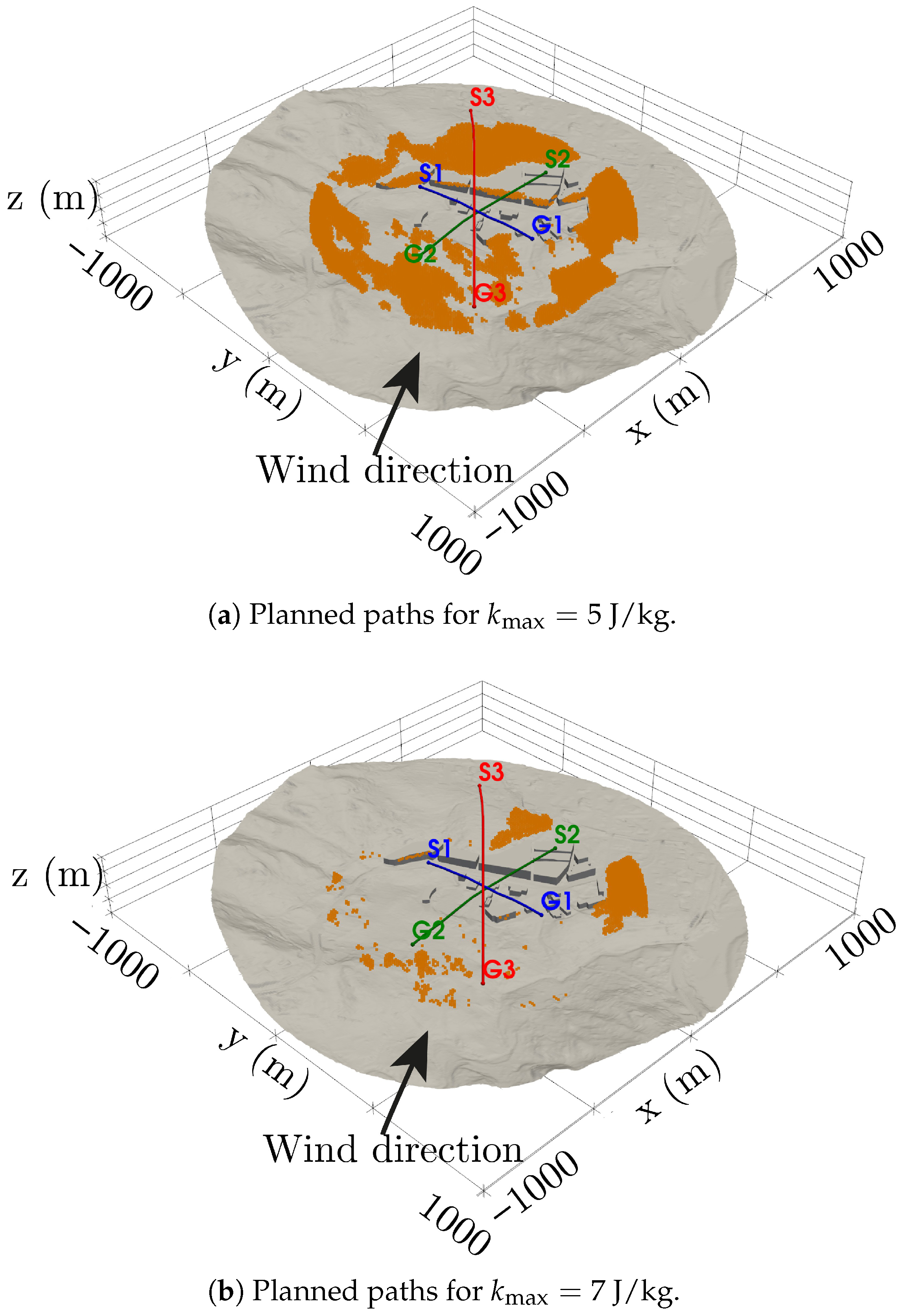
2.4. UAV Path Planning Application
2.4.1. Airspace Mesh Generation
2.4.2. Path Planner
- Heading angle constraint: To avoid abrupt changes in direction, a maximum allowable variation in heading angle of is established. For each edge connecting node to its neighbour , the heading angle difference is computed, where corresponds to the heading angle of edge , and corresponds to that of the preceding edge arriving at node .
| Algorithm 1 Trajectory optimiser algorithm. |
|
3. Results
3.1. CFD Simulation Results
3.2. CFD Validation
3.3. Path Planner Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- González-Jorge, H.; Martínez-Sánchez, J.; Bueno, M.; Arias, P. Unmanned Aerial Systems for Civil Applications: A Review. Drones 2017, 1, 2. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Khan, M.A.; Noor, F.; Ullah, I.; Alsharif, M.H. Towards the Unmanned Aerial Vehicles (UAVs): A Comprehensive Review. Drones 2022, 6, 147. [Google Scholar] [CrossRef]
- Cheng, N.; Wu, S.; Wang, X.; Yin, Z.; Li, C.; Chen, W.; Chen, F. AI for UAV-Assisted IoT Applications: A Comprehensive Review. IEEE Internet Things J. 2023, 10, 14438–14461. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, F.; Feng, D.; Du, S.; Zhong, G.; Deng, C.; Zhou, J. A Logistics UAV Parcel-Receiving Station and Public Air-Route Planning Method Based on Bi-Layer Optimization. Appl. Sci. 2023, 13, 1842. [Google Scholar] [CrossRef]
- Aurambout, J.P.; Gkoumas, K.; Ciuffo, B. Last mile delivery by drones: An estimation of viable market potential and access to citizens across European cities. Eur. Transp. Res. Rev. 2019, 11, 30. [Google Scholar] [CrossRef]
- She, R.; Ouyang, Y. Efficiency of UAV-based last-mile delivery under congestion in low-altitude air. Transp. Res. Part C Emerg. Technol. 2021, 122, 102878. [Google Scholar] [CrossRef]
- Barrado, C.; Boyero, M.; Brucculeri, L.; Ferrara, G.; Hately, A.; Hullah, P.; Martin-Marrero, D.; Pastor, E.; Rushton, A.P.; Volkert, A. U-Space Concept of Operations: A Key Enabler for Opening Airspace to Emerging Low-Altitude Operations. Aerospace 2020, 7, 24. [Google Scholar] [CrossRef]
- Tepylo, N.; Straubinger, A.; Laliberte, J. Public perception of advanced aviation technologies: A review and roadmap to acceptance. Prog. Aerosp. Sci. 2023, 138, 100899. [Google Scholar] [CrossRef]
- Reiche, C.; Cohen, A.P.; Fernando, C. An Initial Assessment of the Potential Weather Barriers of Urban Air Mobility. IEEE Trans. Intell. Transp. Syst. 2021, 22, 6018–6027. [Google Scholar] [CrossRef]
- Mohamed, A.; Marino, M.; Watkins, S.; Jaworski, J.; Jones, A. Gusts Encountered by Flying Vehicles in Proximity to Buildings. Drones 2023, 7, 22. [Google Scholar] [CrossRef]
- Gendron, É.; Leclerc, M.A.; Hovington, S.; Perron, É.; Rancourt, D.; Lussier-Desbiens, A.; Hamelin, P.; Girard, A. Assessing wind impact on semi-autonomous drone landings for in-contact power-line inspection. Drone Syst. Appl. 2024, 12, 1–16. [Google Scholar] [CrossRef]
- Geronel, R.S.; Botez, R.M.; Bueno, D.D. Dynamic responses due to the Dryden gust of an autonomous quadrotor UAV carrying a payload. Aeronaut. J. 2023, 127, 116–138. [Google Scholar] [CrossRef]
- Mendez, A.P.; Whidborne, J.F.; Chen, L. Wind Preview-Based Model Predictive Control of Multi-Rotor UAVs Using LiDAR. Sensors 2023, 23, 3711. [Google Scholar] [CrossRef]
- Simon, N.; Ren, A.Z.; Piqué, A.; Snyder, D.; Barretto, D.; Hultmark, M.; Majumdar, A. FlowDrone: Wind Estimation and Gust Rejection on UAVs Using Fast-Response Hot-Wire Flow Sensors. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 5393–5399. [Google Scholar] [CrossRef]
- Semenov, S.; Jian, Y.; Jiang, H.; Chernykh, O.; Binkovska, A. Mathematical model of intelligent UAV flight path planning. Adv. Inf. Syst. 2025, 9, 49–61. [Google Scholar] [CrossRef]
- Steiner, M. Urban Air Mobility: Opportunities for the Weather Community. Bull. Am. Meteorol. Soc. 2019, 100, 2131–2133. [Google Scholar] [CrossRef]
- Adkins, K.A.; Becker, W.; Ayyalasomayajula, S.; Lavenstein, S.; Vlachou, K.; Miller, D.; Compere, M.; Muthu Krishnan, A.; Macchiarella, N. Hyper-Local Weather Predictions with the Enhanced General Urban Area Microclimate Predictions Tool. Drones 2023, 7, 428. [Google Scholar] [CrossRef]
- Zhang, S.; Kwok, K.C.; Liu, H.; Jiang, Y.; Dong, K.; Wang, B. A CFD study of wind assessment in urban topology with complex wind flow. Sustain. Cities Soc. 2021, 71, 103006. [Google Scholar] [CrossRef]
- Qi, Y.; Ishihara, T. Numerical study of turbulent flow fields around of a row of trees and an isolated building by using modified k-ε model and LES model. J. Wind Eng. Ind. Aerodyn. 2018, 177, 293–305. [Google Scholar] [CrossRef]
- Ampatzidis, P.; Cintolesi, C.; Petronio, A.; Di Sabatino, S.; Kershaw, T. Evaporating waterbody effects in a simplified urban neighbourhood: A RANS analysis. J. Wind Eng. Ind. Aerodyn. 2022, 227, 105078. [Google Scholar] [CrossRef]
- Nithya, D.S.; Quaranta, G.; Muscarello, V.; Liang, M. Review of Wind Flow Modelling in Urban Environments to Support the Development of Urban Air Mobility. Drones 2024, 8, 147. [Google Scholar] [CrossRef]
- Blocken, B. LES over RANS in building simulation for outdoor and indoor applications: A foregone conclusion? Build. Simul. 2018, 11, 821–870. [Google Scholar] [CrossRef]
- Paden, I.; García-Sánchez, C.; Ledoux, H. Towards automatic reconstruction of 3D city models tailored for urban flow simulations. Front. Built Environ. 2022, 8, 899332. [Google Scholar] [CrossRef]
- Deininger, M.E.; von der Grün, M.; Piepereit, R.; Schneider, S.; Santhanavanich, T.; Coors, V.; Voß, U. A Continuous, Semi-Automated Workflow: From 3D City Models with Geometric Optimization and CFD Simulations to Visualization of Wind in an Urban Environment. ISPRS Int. J. Geo-Inf. 2020, 9, 657. [Google Scholar] [CrossRef]
- Slotnick, J.P.; Khodadoust, A.; Alonso, J.J.; Darmofal, D.L.; Gropp, W.; Lurie, E.A.; Mavriplis, D.J. CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences; NASA Center for AeroSpace Information: Hanover, MD, USA, 2014. [Google Scholar]
- Biljecki, F.; Ledoux, H.; Du, X.; Stoter, J.; Soon, K.H.; Khoo, V.H.S. The most common geometric and semantic errors in CityGML datasets. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, IV-2/W1, 13–22. [Google Scholar] [CrossRef]
- Lin, L.; Liu, Y.; Hu, Y.; Yan, X.; Xie, K.; Huang, H. Capturing, Reconstructing, and Simulating: The UrbanScene3D Dataset. arXiv 2022, arXiv:2107.04286. [Google Scholar] [CrossRef]
- Zhao, J.; Stoter, J.; Ledoux, H. A Framework for the Automatic Geometric Repair of CityGML Models. In Cartography from Pole to Pole: Selected Contributions to the XXVIth International Conference of the ICA, Dresden 2013; Springer: Berlin/Heidelberg, Germany, 2014; Chapter 14; pp. 187–202. [Google Scholar] [CrossRef]
- Mirzaei, P.A. CFD modeling of micro and urban climates: Problems to be solved in the new decade. Sustain. Cities Soc. 2021, 69, 102839. [Google Scholar] [CrossRef]
- Blocken, B. Computational Fluid Dynamics for urban physics: Importance, scales, possibilities, limitations and ten tips and tricks towards accurate and reliable simulations. Build. Environ. 2015, 91, 219–245. [Google Scholar] [CrossRef]
- Boikos, C.; Siamidis, P.; Oppo, S.; Armengaud, A.; Tsegas, G.; Mellqvist, J.; Conde, V.; Ntziachristos, L. Validating CFD modelling of ship plume dispersion in an urban environment with pollutant concentration measurements. Atmos. Environ. 2024, 319, 120261. [Google Scholar] [CrossRef]
- Badach, J.; Wojnowski, W.; Gebicki, J. Spatial aspects of urban air quality management: Estimating the impact of micro-scale urban form on pollution dispersion. Comput. Environ. Urban Syst. 2023, 99, 101890. [Google Scholar] [CrossRef]
- Brozovsky, J.; Simonsen, A.; Gaitani, N. Validation of a CFD model for the evaluation of urban microclimate at high latitudes: A case study in Trondheim, Norway. Build. Environ. 2021, 205, 108175. [Google Scholar] [CrossRef]
- Blocken, B.; van der Hout, A.; Dekker, J.; Weiler, O. CFD simulation of wind flow over natural complex terrain: Case study with validation by field measurements for Ria de Ferrol, Galicia, Spain. J. Wind Eng. Ind. Aerodyn. 2015, 147, 43–57. [Google Scholar] [CrossRef]
- Ledoux, H.; Biljecki, F.; Dukai, B.; Kumar, K.; Peters, R.; Stoter, J.; Commandeur, T. 3dfier: Automatic reconstruction of 3D city models. J. Open Source Softw. 2021, 6, 2866. [Google Scholar] [CrossRef]
- Mahgoub, A.O.; Ghani, S. Numerical and experimental investigation of utilizing the porous media model for windbreaks CFD simulation. Sustain. Cities Soc. 2021, 65, 102648. [Google Scholar] [CrossRef]
- Li, R.; Niu, J.; Zhao, Y.; Wang, L.L.; Shi, X.; Gao, N. Wind tunnel experiments on the aerodynamic effects of a single potted tree: Hot-wire anemometry and PIV measurements. Urban Clim. 2025, 62, 102520. [Google Scholar] [CrossRef]
- Pardo-del Viejo, L.; Fernández-Rodríguez, S. CFD with LIDAR applied to buildings and vegetation for environmental construction. Autom. Constr. 2024, 167, 105710. [Google Scholar] [CrossRef]
- Huo, H.; Chen, F. Study of effects of different vegetation model parameter settings on quantitative CFD simulation of urban spatial air temperature and wind-field. Int. J. Remote Sens. 2023, 45, 7234–7247. [Google Scholar] [CrossRef]
- Aldao, E.; Fontenla-Carrera, G.; Veiga-López, F.; González-Jorge, H.; Morais, M.J.; Matos, J.C. Evaluating the Influence of Wind on UAV Path Planning for Bridge Inspections. In Proceedings of the 2025 International Conference on Unmanned Aircraft Systems (ICUAS), Charlotte, NC, USA, 14–17 May 2025; pp. 236–242. [Google Scholar] [CrossRef]
- Instituto Geográfico Nacional. Centro de Descargas, 2024. Available online: https://centrodedescargas.cnig.es/CentroDescargas/home (accessed on 4 October 2024).
- An, K.; Wong, S.M.; Fung, J.C.H.; Ng, E. Revisit of prevailing practice guidelines and investigation of topographical treatment techniques in CFD-Based air ventilation assessments. Build. Environ. 2020, 169, 106580. [Google Scholar] [CrossRef]
- Biljecki, F.; Ledoux, H.; Stoter, J. An improved LOD specification for 3D building models. Comput. Environ. Urban Syst. 2016, 59, 25–37. [Google Scholar] [CrossRef]
- Silva, J.; Ribeiro, C.; Guedes, R.; Rua, M.C.; Ulrich, F. Roughness length classification of Corine Land Cover classes. In Proceedings of the EWEC 2007, Milan, Italy, 7–10 May 2007. [Google Scholar]
- MeteoGalicia. Modelos Meteorológicos Deterministas, 2024. Available online: https://www.meteogalicia.gal/web/observacion/meteovisor (accessed on 4 October 2024).
- SIMSCALE. Advanced Modelling PWC, 2024. Available online: https://www.simscale.com/docs/analysis-types/pedestrian-wind-comfort-analysis/advanced-modelling/ (accessed on 4 October 2024).
- Iio, A.; Ito, A. A Global Database of Field-Observed Leaf Area Index in Woody Plant Species, 1932–2011; ORNL Distributed Active Archive Center: Oak Ridge, TN, USA, 2014. [Google Scholar] [CrossRef]
- Bekkers, C.C.; Angelou, N.; Dellwik, E. Drag coefficient and frontal area of a solitary mature tree. J. Wind Eng. Ind. Aerodyn. 2022, 220, 104854. [Google Scholar] [CrossRef]
- Aldao, E.; Veiga-López, F.; Chanel, C.P.; Watanabe, Y.; González-Jorge, H. Dynamic UAV trajectory optimisation for parcel delivery with integrated third-party risk mitigation. Reliab. Eng. Syst. Saf. 2025, 262, 111178. [Google Scholar] [CrossRef]
- GU, R.; ZHAO, Y.; REN, X. Integrating wind field analysis in UAV path planning: Enhancing safety and energy efficiency for urban logistics. Chin. J. Aeronaut. 2025, 103605. [Google Scholar] [CrossRef]
- Gao, M.; Hugenholtz, C.H.; Fox, T.A.; Kucharczyk, M.; Barchyn, T.E.; Nesbit, P.R. Weather constraints on global drone flyability. Sci. Rep. 2021, 11, 12092. [Google Scholar] [CrossRef] [PubMed]





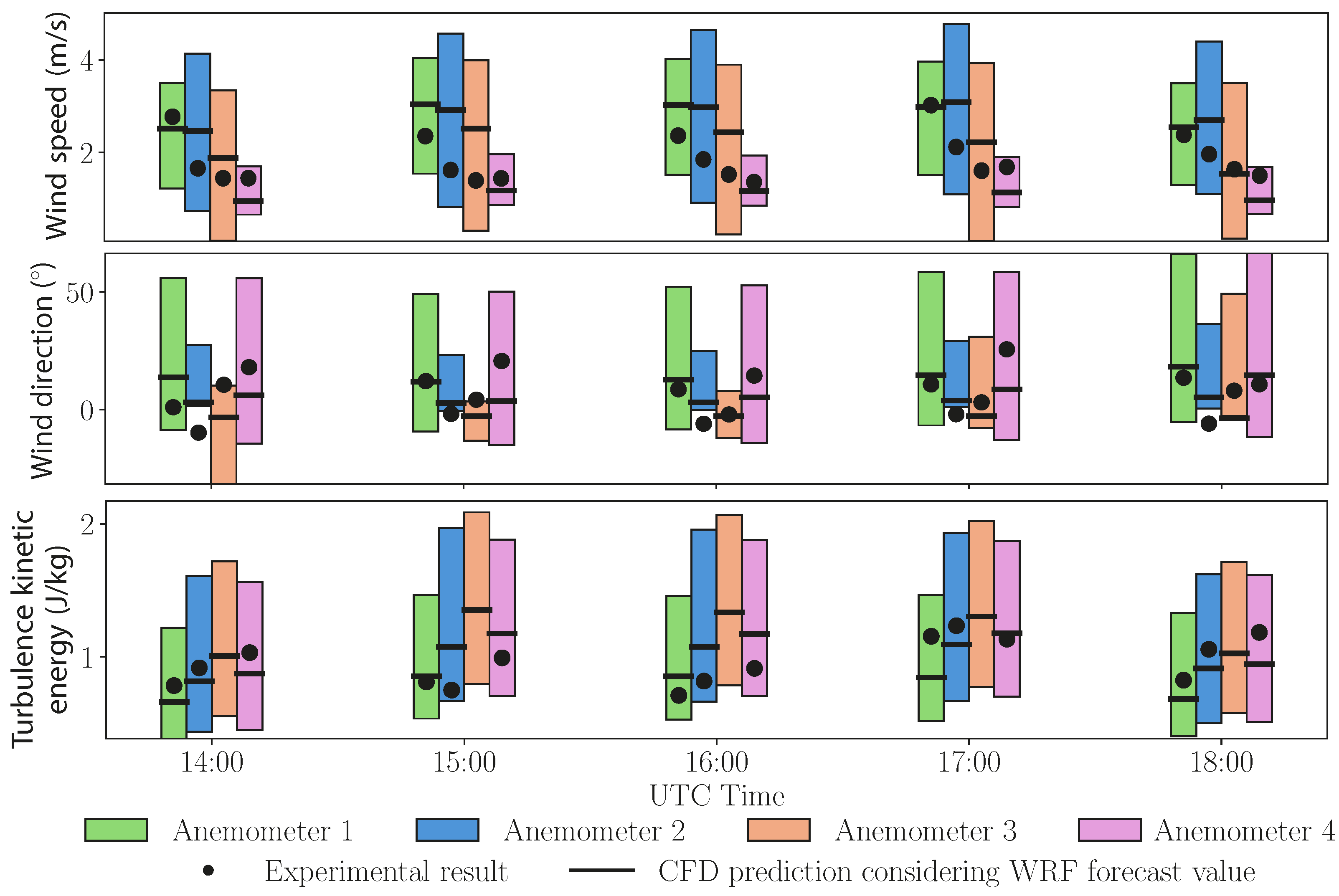
| Mesh | Cells (Million) | Simulation Time (h) | Deviation vs. Mesh 3 (%) |
|---|---|---|---|
| Mesh 1 | 20 | 1.3 | 6.1 |
| Mesh 2 | 34 | 2.0 | 1.3 |
| Mesh 3 | 41 | 7.5 | 0.0 |
| UTC Time | Local Time (CEST) | Wind Speed (m/s) | Wind Direction (°) |
|---|---|---|---|
| 14:00 | 16:00 | 4.74 | 25.21 |
| 15:00 | 17:00 | 5.79 | 22.04 |
| 16:00 | 18:00 | 5.76 | 23.68 |
| 17:00 | 19:00 | 5.71 | 27.00 |
| 18:00 | 20:00 | 4.89 | 31.63 |
| Wind Speed | Wind Direction | Turbulence Kinetic Energy (k) | ||||
|---|---|---|---|---|---|---|
| UTC Time | Mean Error (m/s) | Bias (m/s) | Mean Error (°) | Bias (°) | Mean Error (J/kg) | Bias (J/kg) |
| 14:00 | 0.58 | 0.25 | 12.9 | 4.2 | 0.13 | 0.13 |
| 15:00 | 0.89 | 0.72 | 9.5 | 6.5 | 0.18 | 0.18 |
| 16:00 | 0.76 | 0.61 | 6.4 | 0.3 | 0.22 | 0.22 |
| 17:00 | 0.71 | 0.36 | 9.6 | 5.7 | 0.17 | 0.14 |
| 18:00 | 0.45 | 0.04 | 8.9 | 1.1 | 0.18 | 0.18 |
| Overall | 0.68 | 0.39 | 9.5 | 3.6 | 0.17 | 0.17 |
| Trajectory | Origin (m) | Destination (m) | Path Length (m) | Straight-Line Distance (m) |
|---|---|---|---|---|
| Trajectory 1 | 604.07 | 604.07 | ||
| Trajectory 2 | 784.53 | 800.54 | ||
| Trajectory 3 | 1029.09 | 1071.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aldao, E.; Veiga-Piñeiro, G.; Domínguez-Estévez, P.; Martín, E.; Veiga-López, F.; Fontenla-Carrera, G.; González-Jorge, H. Towards Safer UAV Operations in Urban Air Mobility: 3D Automated Modelling for CFD-Based Microweather Systems. Drones 2025, 9, 730. https://doi.org/10.3390/drones9110730
Aldao E, Veiga-Piñeiro G, Domínguez-Estévez P, Martín E, Veiga-López F, Fontenla-Carrera G, González-Jorge H. Towards Safer UAV Operations in Urban Air Mobility: 3D Automated Modelling for CFD-Based Microweather Systems. Drones. 2025; 9(11):730. https://doi.org/10.3390/drones9110730
Chicago/Turabian StyleAldao, Enrique, Gonzalo Veiga-Piñeiro, Pablo Domínguez-Estévez, Elena Martín, Fernando Veiga-López, Gabriel Fontenla-Carrera, and Higinio González-Jorge. 2025. "Towards Safer UAV Operations in Urban Air Mobility: 3D Automated Modelling for CFD-Based Microweather Systems" Drones 9, no. 11: 730. https://doi.org/10.3390/drones9110730
APA StyleAldao, E., Veiga-Piñeiro, G., Domínguez-Estévez, P., Martín, E., Veiga-López, F., Fontenla-Carrera, G., & González-Jorge, H. (2025). Towards Safer UAV Operations in Urban Air Mobility: 3D Automated Modelling for CFD-Based Microweather Systems. Drones, 9(11), 730. https://doi.org/10.3390/drones9110730










