One- and Two-Equation Models to Simulate Ion Transport in Charged Porous Electrodes
Abstract
:1. Introduction
2. Theoretical Development
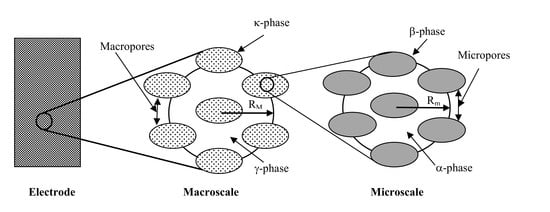
2.1. Model Description
2.2. Microscale Equations (α–β System)
2.2.1. Electrostatic Potential
2.2.2. Ionic Concentrations Equation
2.3. Macroscale Equations (γ-κ System)
2.3.1. Electrostatic Potential
The κ-Region
The γ-Region
2.3.2. One-Equation Model for Electrostatic Potential
2.3.3. Closure for the Potential One-Equation Model
2.3.4. Ionic Concentration Equations
The κ-Region
The γ-Region
2.3.5. One-Equation Model for Ionic Concentrations
2.3.6. Closure for Ionic Concentrations One-Equation Model
2.3.7. Two-Equation Model for the Electrostatic Potential
2.3.8. Two-Equation Model for the Ionic Concentrations
2.3.9. Closure for the Ionic Concentrations Two-Equation Model
3. Closure Problem Solution
3.1. Introduction
3.2. Calculation of One-Equation Model Transport Parameters
3.3. Calculation of Two-Equation Model Transport Parameters
3.4. Comparison of One- and Two-Equation Model Transport Parameters
4. Results and Discussion
4.1. Transport Parameters
4.2. Comparison of One-Equation and Two-Equation Models
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix A.1. Closure Problems
Appendix A.1.1. Problem 1
Appendix A.1.2. Problem 2
Appendix A.1.3. Problem 3
Appendix A.1.4. Problem 4
Appendix A.1.5. Problem 5
Appendix A.1.6. Problem 6
Appendix B
Appendix B.1. Analytical Solution of Closure Problem 3
References
- Whitaker, S. Theory and Application of Transport in Porous Media: The Method of Volume Averaging; Kluwer Academic: London, UK, 1999; p. 219. [Google Scholar]
- Whitaker, S. Local Thermal Equilibrium: An Application to Packed Bed Catalytic Reactor Design. Chem. Eng. Sci. 1986, 41, 2029–2039. [Google Scholar] [CrossRef]
- Whitaker, S. Improved Constraints for the Principle of Local Thermal Equilibrium. Ind. Eng. Chem. Res. 1991, 30, 983–997. [Google Scholar] [CrossRef]
- Kaviany, M. Principles of Heat Transfer in Porous Media; Springer-Verlag: New York, NY, USA, 1991. [Google Scholar]
- Quintard, M.; Whitaker, S. One and two-equation Models for Transient Diffusion Processes in Two-phase Systems. In Advances in Heat Transfer; Academic Press: New York, NY, USA, 1993; Volume 23, pp. 369–465. [Google Scholar]
- Quintard, M.; Whitaker, S. Local thermal equilibrium for transient heat conduction: Theory and comparison with numerical experiments. Int. J. Heat Mass Trans. 1995, 38, 2779–2796. [Google Scholar] [CrossRef]
- Del Rìo, J.A.; Whitaker, S. Maxwell’s Equations in Two-Phase Systems I: Local Electrodynamic Equilibrium. Transp. Porous Media 2000, 39, 159–186. [Google Scholar] [CrossRef]
- Del Rìo, J.A.; Whitaker, S. Maxwell’s Equations in Two-Phase Systems II: Two-Equation Model. Transp. Porous Media 2000, 39, 259–287. [Google Scholar]
- Tsouris, C.; Mayes, R.; Kiggans, J.; Sharma, K.; Yiacoumi, S.; DePaoli, D.; Dai, S. Mesoporous Carbon for Capacitive Deionization of Saline Water. Environ. Sci. Technol. 2011, 45, 10243–10249. [Google Scholar] [CrossRef] [PubMed]
- Johnson, A.M.; Newman, J. Desalting by Means of Carbon Electrodes. J. Electrochem. Soc. 1971, 118, 510–517. [Google Scholar] [CrossRef]
- Biesheuvel, P.M.; Bazant, M.Z. Nonlinear Dynamics of Capacitive Charging and Desalination by Porous Electrodes. Phys. Rev. E 2010, 81, 031502. [Google Scholar] [CrossRef] [PubMed]
- Gabitto, J.F.; Tsouris, C. Volume Averaging Study of the Capacity Deionization Process in Homogeneous Porous Media. Transp. Porous Media 2015, 109, 61–80. [Google Scholar] [CrossRef]
- Biesheuvel, P.M.; Yu, F.; Bazant, M.Z. Diffuse charge and Faradaic reactions in porous electrodes. Phys. Rev. E 2011, 83, 061507. [Google Scholar] [CrossRef] [PubMed]
- Biesheuvel, P.M.; Fu, Y.; Bazant, M.Z. Electrochemistry and Capacitive Charging of Porous Electrodes in Asymmetric Multicomponent Electrolytes. Russ. J. Electrochem. 2012, 48, 580–592. [Google Scholar] [CrossRef]
- Biesheuvel, P.M.S.; Porada, S.; Levi, M.; Bazant, M.Z. Attractive Forces in Microporous Carbon Electrodes for Capacitive Deionization. J. Solid State Electrochem. 2014, 18, 1365. [Google Scholar] [CrossRef]
- Gabitto, J.F.; Tsouris, C. Volume Averaging Study of the Capacity Deionization Process in Dual-Porosity Electrodes. Transp. Porous Media 2016, 113, 173–205. [Google Scholar] [CrossRef]
- Gabitto, J.F.; Tsouris, C. One and Two-Equation Models in the Capacity Deionization Process. In Proceedings of the AIChE Annual Meeting, Minneapolis, MN, USA, 29 October–3 November 2017. [Google Scholar]
- Gabitto, J.F.; Tsouris, C. Ion Transport Processes in Charged Porous Media. In Proceedings of the AIChE Annual Meeting, Minneapolis, MN, USA, 29 October–3 November 2017. [Google Scholar]
- Quintard, M.; Whitaker, S. Transport in Chemical and Mechanical Heterogeneous Porous Media IV: large-scale Mass Equilibrium for Solute Transport with Adsorption. Adv. Water Resour. 1998, 22, 33–57. [Google Scholar] [CrossRef]
- Ulson de Souza, U.A.A.; Whitaker, S. The Modeling of a Textile Dyeing Process Utilizing the Method of Volume Averaging. Braz. J. Chem. Eng. 2003, 20, 445–453. [Google Scholar] [CrossRef]
- Valdès-Parada, F.J.; Goyeau, B.; Ochoa-Tapia, J.A.; Whitaker, S. Diffusive Mass transfer between a Microporous Medium and a Homogeneous Fluid: Jump Boundary Conditions. Chem. Eng. Sci. 2006, 61, 1692–1704. [Google Scholar]
- Gray, W.G.; Lee, P.C.Y. On the Theorems for Local Volume Averaging of Multiphase Systems. Int. J. Multiph. Flow 1977, 3, 333–340. [Google Scholar] [CrossRef]
- Nozad, I.; Carbonell, R.G.; Whitaker, S. Heat Conduction in Multiphase Systems I: Theory and Experiment for Two-Phase Systems. Chem. Eng. Sci. 1985, 40, 843–855. [Google Scholar] [CrossRef]
- Carbonell, R.G.; Whitaker, S. Dispersion in Pulsed Systems-II Theoretical Developments for Passive Dispersion in Porous Media. Chem. Eng. Sci. 1983, 38, 1795–1802. [Google Scholar] [CrossRef]
- Chang, H.-C. Multiscale Analysis of Effective Transport in Periodic Heterogeneous Media. Chem. Eng. Commun. 1982, 15, 83–91. [Google Scholar] [CrossRef]
- Chang, H.-C. Effective Diffusion and Conduction in Two-Phase Media: A Unified Approach. AIChE J. 1983, 29, 846–853. [Google Scholar] [CrossRef]
- Ochoa, J.A. Diffusion and Reaction in Heterogeneous Porous Media. Ph.D. Thesis, Department of Chemical Engineering, University of California, Davis, CA, USA, 1988. [Google Scholar]
- Ochoa-Tapia, J.A.; Del Rio, J.A.; Whitaker, S. Bulk and Surface Diffusion in Porous Media: An Application of the Surface-Averaging Theorem. Chem. Eng. Sci. 1993, 48, 2061–2082. [Google Scholar] [CrossRef]
- Maxwell, J.C. Treatise on Electricity and Magnetism; Clarendon Press: Oxford, UK, 1881; Volume I. [Google Scholar]






© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gabitto, J.; Tsouris, C. One- and Two-Equation Models to Simulate Ion Transport in Charged Porous Electrodes. Colloids Interfaces 2018, 2, 4. https://doi.org/10.3390/colloids2010004
Gabitto J, Tsouris C. One- and Two-Equation Models to Simulate Ion Transport in Charged Porous Electrodes. Colloids and Interfaces. 2018; 2(1):4. https://doi.org/10.3390/colloids2010004
Chicago/Turabian StyleGabitto, Jorge, and Costas Tsouris. 2018. "One- and Two-Equation Models to Simulate Ion Transport in Charged Porous Electrodes" Colloids and Interfaces 2, no. 1: 4. https://doi.org/10.3390/colloids2010004
APA StyleGabitto, J., & Tsouris, C. (2018). One- and Two-Equation Models to Simulate Ion Transport in Charged Porous Electrodes. Colloids and Interfaces, 2(1), 4. https://doi.org/10.3390/colloids2010004