Anomalous Interfacial Structuring of a Non-Halogenated Ionic Liquid: Effect of Substrate and Temperature

Abstract

We investigate the interfacial properties of the non-halogenated ionic liquid (IL), trihexyl(tetradecyl)phosphonium bis(mandelato)borate, [P_6,6,6,14][BMB], in proximity to solid surfaces, by means of surface force measurement. The system consists of sharp atomic force microscopy (AFM) tips interacting with solid surfaces of mica, silica, and gold. We find that the force response has a monotonic form, from which a characteristic steric decay length can be extracted. The decay length is comparable with the size of the ions, suggesting that a layer is formed on the surface, but that it is diffuse. The long alkyl chains of the cation, the large size of the anion, as well as crowding of the cations at the surface of negatively charged mica, are all factors which are likely to oppose the interfacial stratification which has, hitherto, been considered a characteristic of ionic liquids. The variation in the decay length also reveals differences in the layer composition at different surfaces, which can be related to their surface charge. This, in turn, allows the conclusion that silica has a low surface charge in this aprotic ionic liquid. Furthermore, the effect of temperature has been investigated. Elevating the temperature to 40 °C causes negligible changes in the interaction. At 80 °C and 120 °C, we observe a layering artefact which precludes further analysis, and we present the underlying instrumental origin of this rather universal artefact.

1. Introduction

Ionic liquids (ILs) consist of cations and anions, and are, thus, salts. Unlike their crystalline counterparts, e.g., table salt, they are liquid below 100 °C [1]. Room temperature ionic liquids, or RTILs, display liquid-like behavior at room temperature and, increasingly, the term ionic liquid is used to refer to RTILs; though, as pointed out by Macfarlane et al., there is little to be gained by overly strict definitions [2,3]. In ILs, at least one of the ionic species is organic, bulky, and asymmetric. The balance of enthalpic and entropic interactions in ILs favors the liquid state, and it also gives ILs specific properties, such as being a good solvent for a range of organic and inorganic materials, low vapor pressure, high viscosity, low conductivity, and a high electrochemical window [4,5]. Once used primarily as “green” solvents, e.g., for cellulose [6], ILs are now finding applications in tribology and super capacitors [7,8,9,10,11,12].

An important property of ILs is that they form interfacial layers in proximity to solid surfaces, with characteristics similar to the behavior of both molecular solvents and surfactants. That is to say, their ordering can be thought of both as solvation structures and as analogous to adsorption, particularly for charged surfaces. Close to a negatively charged surface, such as mica, a cationic rich layer is usually found to compensate for the charge of the surface. This behavior is analogous to surfactant adsorption and the formation of monolayers although, in this case, there is no solvent. Generally, it is thought that adsorbed cations overscreen the surface charge, or crowd at the surface, resulting in an inner layer that is thicker than a monolayer in the case of crowding, and a second outer layer that is rich in anions [13]. Overscreening in ILs is similar to the adsorption of polyelectrolytes and counter ions. The scenario reverses for positively charged surfaces, such as BaF₂, onto which the anions are primarily adsorbed [14]. The bulk structure of ILs is also important in their near-surface structure [5]. In proximity to uncharged surfaces or surfaces with low potential, the 3D structure of the bulk IL is assumed to continue up to the surface, with structural constraints imposed by the geometry of the surface, analogous to solvation forces [15].

Formation of stable IL interfacial layers depends on the chemical structure of the ions, the presence or otherwise of contaminants, such as water, and the surface properties, such as surface charge and roughness. Investigation of the layers with atomic force microscopy (AFM) and surface force apparatus (SFA) have generally shown layering, or “push-through” transitions [16,17,18,19,20,21,22]. A transition corresponds to the removal of a coherent interfacial layer by the force probe. In this case, the layers act as barriers between the two approaching surfaces. It also shows that the layers are strongly bound to the surface or to a near-surface layer. The distances associated with the “push-through” transitions correspond to ion pairs or individual ion layers. The interfacial layers of ILs have also been shown to be electroresponsive with AFM [12,22], SFA [16], and neutron reflectivity (NR) measurements [23], due to the ability to tune the surface charge and, thus, the relative numbers of the different ionic species in the interfacial layer.

The near-surface structure of ILs is of increasing interest in tribology, e.g., in controlling friction. It has been shown that an interfacial layer rich in cations has a lower friction coefficient than one rich in anions [12], and even a small concentration of IL in oil has profound effect on lowering friction [7,9]. Through careful selection of the ions and substrate, however, such frictional properties can be reversed, so that anion-rich surfaces can also facilitate low friction and, in some cases, superlubricity can be achieved [24]. Some ionic species may even be surface-active; these species bind strongly to the surface via self-assembly, electrostatic or tribochemical reactions, reduce solid–solid contact, and prevent wear [7,10,25].

The interfacial layering of ILs, as well as multilayers formed further away from the solid surface, can also control interparticle interactions in a colloidal context. In the outer Helmholtz layer, the potential depends on the ionic composition and interfacial ordering of ionic species adsorbed onto the solid [16]. The long-ranged electrostatic interactions observed in ILs appear to depend crucially on the charge at this plane, and Perkins and coworkers have exhaustively addressed this subject recently [16,26,27].

The effect of temperature on the interfacial layering is also important for tribology—interfacial layers provide lubrication, but often need to function at elevated temperature. Further interest arises from other observations in the chemical physics literature. It has been found, for example, that the interfacial layers are relatively insensitive to temperature but, on the other hand, dramatic transitions in long-range forces have been observed [20,28]. In one case, the decay length of electrostatic interactions was even observed to decrease with temperature, contrary to predictions of Debye–Hückel theory [29], which was rationalized in terms of an increase in dissociated ionic concentration with temperature. There are, thus, compelling reasons to investigate the temperature dependence of ILs, in an attempt to understand, from a molecular perspective, how the ionic composition and interfacial ordering are affected by the temperature.

In this manuscript, we investigate the interfacial ordering of the non-halogenated IL, trihexyl(tetradecyl)phosphonium bis(mandelato)borate, [P_6,6,6,14][BMB] at various temperatures and on various substrates, using AFM force measurement. The choice of this IL is motivated by its high thermal and hydrolytic stability, and its friction- and wear-reducing properties, as neat lubricant and as additive to biodegradable oils. Further, its lack of halogenation means that it is a greener and non-toxic candidate for lubrication applications [30]. Its structure is shown in Figure 1. This IL has also been shown to be electroresponsive [23], therefore, it is of interest for tribotronic applications, where its interfacial ordering will be decisive for its performance.

2. Materials and Methods

The IL [P_6,6,6,14][BMB] was kindly provided by Luleå University of Technology (Luleå, Sweden) and its synthesis is reported elsewhere [30]. Prior to the measurements, the IL was dried inside a vacuum oven for 72 h at 60 °C. The procedure reduces the residual water content and removes dissolved gases that were produced during synthesis. The density of the IL at 25 °C was measured using vibrating tube densitometer (Anton Paar, DMA 4100M, Graz, Austria) to be 1007 kg/m³. One thus estimates an upper limit for the ion pair dimension of about 1.1 nm for cubic packing at room temperature. The density was also measured at 40 °C and 80 °C to be 997 kg/m³ and 972 kg/m³, respectively. The viscosity of the IL was measured using parallel plate rheometer (TA Instruments, HR3, New Castle, DE, USA) to be 4.12, 1.198, and 0.139 Pa.s, respectively, at 25, 40, and 80 °C. The refractive index was measured with Abbe refractometer (ORT-1, Kern, Balingen, Germany) to be 1.504 at room temperature. All AFM measurements, including calibrations, imaging, and force measurements, were carried out on a Nanoscope IIIa Multimode AFM from Bruker (Santa Barbara, CA, USA).

Sharp diamond-like carbon-coated AFM tips (Multi75DLC, NanoAndMore) were used in the force measurements. The cantilevers were cleaned by dipping in Milli-Q water and absolute ethanol, followed by drying in a stream of nitrogen. The spring constant of the cantilevers was calibrated using the Sader method [31]. The constants varied slightly between the cantilevers, but were of the order of 2 N/m; in each case, the spring constant was obtained with a precision of about 5%. The tip radius was measured using AFM imaging of conical calibration gratings (TGTZ-400, Ted Pella Inc., Redding, CA, USA) and found to be 40 ± 8 nm.

Mica, gold, and silica were used as surfaces. Mica substrates (ruby muscovite mica, optical grade, S&J trading Inc., New York, NY, USA) were cut to size 1 cm², and freshly cleaved prior to each measurement. A silicon wafer (p-type, Boron, <100>, 500 μm, University Wafer Inc., Boston, MA, USA) was cut into 1 cm² pieces. The pieces were cleaned for 20 min in a 3:1 H₂SO₄/H₂O piranha solution, rinsed with Milli-Q water, and then dried in a stream of filtered nitrogen prior to use. An oxide layer naturally grows on top of silicon upon exposure to oxygen, therefore, these substrates are referred to as silica hereafter. The same clean silica pieces were used to evaporate a thin film of gold atop. The films were prepared by electron beam evaporation (Auto 306, Edwards High Vacuum International, Wilmington, MA, USA). The gold film thickness was about 170 Å. To ensure good adhesion between silica and gold, a thin layer of titanium, about 30 Å, was evaporated as an adhesive layer. Before AFM measurements, the gold-coated silica pieces were rinsed with filtered ethanol, and dried in a stream of nitrogen, then exposed to UV/ozone (Procleaner™, BioForce Nanosciences, Salt Lake City, UT, USA) for 10 min.

The scheme of the AFM experiments is depicted in Figure 1. Generally, 6 points were selected on the surface for the force measurements while, at each point, 20 force profiles were collected. The approach velocity was 20 nm/s. The average of the measured force versus apparent separation curves are shown in Figure 2, Figure 3, Figure 4 and Figure 5, where each condition was repeated on at least two occasions. The measurements were performed from room temperature up to 120 °C in a closed fluid cell. To control the temperature, a Peltier heating element is connected to the sample stage underneath the solid substrate. The heating element turns on and off in response to proportional–integral–derivative (PID) feedback loop of a controller unit. The PID values are set to maximize the stability of the element in maintaining a set temperature. The AFM cantilever was used as an internal sensor of temperature to ensure that the bulk of IL has reached the set temperature. The AFM cantilever is coated with a thin reflective gold layer on its upper surface. Due to the difference in the thermal expansion of gold and silicon, the cantilever bends dynamically under temperature gradients, which can be detected with AFM. When the temperature stabilizes, this bending phenomenon ceases, and the cantilever deflection remains stable. All measurements were performed after this equilibrium was achieved, which typically takes about 20 min.

In the force measurements, one obtains deflection versus z-piezo displacement. These quantities are converted to force versus tip–solid separation, using the spring constant of the cantilever and the optical lever sensitivity (OLS). The latter parameter is obtained using a hard-contact method, whereby the deflection of the cantilever upon contact with a hard surface is assumed to be equivalent to the displacement of the z-piezo—the so-called constant compliance [32].

Measurements at high temperature were performed in a similar fashion, however, due to thermal instability discussed in an ensuing section, it was not possible to calculate the OLS using the hard-contact method. For this reason, the force profiles were analyzed using the OLS obtained at room temperature, i.e., 37.0 ± 0.5 nm/V.

Further evaluation of thermal instability was performed in an experiment where the cantilever was placed in contact with the solid substrate in the absence of liquid, with setpoint adjusted to 1.0 V, while the integral gain was set to zero. Zero integral gain results in no correction to the deflection of the cantilever (via a movement of the piezo) as its value deviates from the setpoint value during contact [32].

The force profiles were interpreted in terms of an expression of the sum of van der Waals and steric repulsion forces [16]:

$$\frac{F}{R}=-\frac{A}{6D^2}+2\pi W_0\exp \left(-\frac{D}{{\lambda }_0}\right)$$

(1)

where R is the radius of tip, A the Hamaker constant, W₀ the steric prefactor, and λ₀ the steric decay length, which is characteristic of the length of the adsorbed ions. Since the measured forces have a range about 2 nm, no electrostatic double layer forces were included in the model. Due to the low approach velocity and the small radius of the tip, hydrodynamic forces are negligible.

AFM images were obtained in air with a sharp tip (HQ:CSC38, MikroMasch) at a low contact force of 5–8 nN, and over an area of 1 µm². The spring constant of the cantilever used for imaging was calibrated to be 0.060 ± 0.003 N/m using the Sader method [31]. The images were flattened by subtracting a quadratic fit from each line. The roughness was then calculated to be 0.10 ± 0.01 nm RMS on mica, 0.60 ± 0.10 nm RMS on gold, and 0.60 ± 0.04 nm RMS on silica. The AFM images are shown in Figure 1.

3. Results and Discussion

A force versus apparent separation profile, for an AFM tip approaching a mica surface in [P_6,6,6,14][BMB] at room temperature, is shown in Figure 2. One observes a monotonic repulsion which decays to zero at about 2 nm from the (apparent) surface. Note that an absolute zero of separation cannot be obtained in AFM force measurements, and zero separation is thus conventionally defined in terms of constant compliance of the cantilever deflection with actuator movement [32,33]. A best fit to Equation (1) of the individual force profiles, measured on approach, yields a Hamaker constant 1.5 ± 0.2 (×10⁻²⁰) J, a steric prefactor of 0.11 ± 0.01 J/m², and a steric decay length of 0.52 ± 0.02 nm. An adhesion, defined as the depth of the minimum, is observed on the retraction curves with a value of 3.1 ± 0.4 nN.

The fitted Hamaker constant may be compared with the calculated value in air. The dielectric constant, refractive index, and absorption frequency of diamond and mica are, respectively, ${\epsilon }_{\mathrm{diamond}}=5.66$, $n_{\mathrm{diamond}}=2.375$, $v_{\mathrm{e},\mathrm{diamond}}=2.6\times {10}^{15}$ s⁻¹, ${\epsilon }_{\mathrm{mica}}=6.2$, $n_{\mathrm{mica}}=1.6$, and $v_{\mathrm{e},\mathrm{mica}}=3.0\times {10}^{15}$ s⁻¹ [15]. Using these values, one obtains a Hamaker constant in air equal to 16.6 × 10⁻²⁰ J (calculated using Equation 13,15 in [15]). From mixing rules, one would expect that the Hamaker constant reduces in [P_6,6,6,14][BMB]. As expected, the fitted Hamaker constant is about an order of magnitude smaller than the value for in air. Similar reductions in the Hamaker constants were reported for interactions between mica and gold in 1-butyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide [BMIM][TFSI], and between silicon oxide and graphene in 1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide [EMIM][TFSI] [16,22], but this is not a characteristic of ILs, rather, the fact that the surfaces are immersed in a medium of dielectric constant larger than 1 [15]. In general, however, aprotic ILs have surprisingly low dielectric constants [16]. Apparent screening of the van der Waals interaction in protic ILs has also been observed [34], and was interpreted in terms of the liquid salt behavior leading to the extinguishing of electrostatic interactions.

The steric decay length is found to be comparable with an estimation of the ion size from the density data, 0.55 nm. This agreement suggests that the force is due to an interfacial layer at the surface of mica. A priori, it cannot be determined whether this corresponds to a highly confined film of liquid, or an adsorbed film. Indeed, the two descriptions are not necessarily different. Due to the high negative surface charge density of mica, however, with a maximum 30 µC/cm² [35], it is likely that the interfacial layer is cation-rich [36]. Note that the value of the steric decay length does not agree with any of the dimensions of the cation calculated using molecular modeling (Figure 1). These dimensions do not take into account the packing constraints and free volume effects, which are implicit in the density approximation. The steric decay length is slightly larger than the value of 0.5 nm obtained by Gebbie et al. for the system gold–[BMIM][TFSI]–mica obtained at an applied potential of 0 V [16]. Since this parameter must be related to the composition of the ionic liquid, and characteristic dimensions thereof, it is not surprising that the value is larger for [P_6,6,6,14] than [BMIM], due to its bulkier structure. There is, as yet, no other direct experimental evidence for the orientation of this cation at the mica interface, however, modeling studies suggest that the longest alkyl chains of the phosphonium cation lie preferentially flat on the surface of gold, reducing the effective layer thickness even at high negative surface charge density [37]. These predictions are broadly in agreement with neutron reflectance measurements, though the layer thicknesses obtained in solvent studies are somewhat larger [23]. The steric prefactor in these studies relates to the difficulty of dislodging the layer and is presumably, thus, related to the ordering of the layer, the viscosity of the liquid, and the strength of the interaction with the substrate. The prefactor found here (0.11 J/m²) is rather larger than that for [BMIM][TFSI] (1.6 mJ/m²). This correlates well with the significantly larger viscosity of [P_6,6,6,14][BMB].

Various studies have shown multiple transitions, or steps, in force curves measured in ILs as the force probe encounters structured interfacial multilayers [17,18,19,20,21,22]. We are not aware of similar observations having been reported for [P_6,6,6,14]-based ILs although, thus far, measurements have been limited to [P_6,6,6,14][TFSI] and trihexyl(tetradecyl)phosphonium bis(2,4,4-trimethylpentyl)phosphinate [P_6,6,6,14][(ⁱC₈)₂PO₂] on a stainless steel surface [21]. While it could be argued that the lack of steps for these ILs may be due to the roughness of the steel, measurements on the same type of surface using ILs based on other cations, such as imidazolium and a shorter-chained phosphonium, [P_4,4,4,1], did indeed show such force barriers [21]. On the surface of mica, which is molecularly smooth, we find a similar monotonic repulsion which indicates that the layers formed by this IL are diffuse, an effect that may be attributed to (i) the length and flexibility of the alkyl chains in the [P_6,6,6,14] cation, (ii) the bulkiness and the delocalization of charges in [BMB] anion, (iii) the anions’ racemic mixture of chiral species, as well as (iv) crowding of the cation at the surface of mica [37].

The force versus apparent separation profile at 40 °C, on mica, is shown in Figure 3. A monotonic repulsion similar to the response at room temperature is observed. Fitting to the individual force profiles was performed by fixing the value of the Hamaker constant to that at room temperature, 1.5 × 10⁻²⁰ J. Best fits to Equation (1) give a steric prefactor of 0.16 ± 0.02 J/m², and a steric decay length of 0.59 ± 0.03 nm. We, thus, observe no significant difference between the force responses at 40 °C and at room temperature. The retraction curves at 40 °C, however, give an adhesion force of 1.8 ± 0.6 nN, which is comparable to, though smaller than, the adhesion force at room temperature. This is likely due to a reduction in viscosity with increasing temperature, and suggests that the attraction (note that the minimum is not at “zero” separation) may have a fluid dynamic component [38]. Such a force is dependent on the viscosity and the rate of separation, as well as the surface separation, and typically gives rise to this sort of soft minimum at a finite value of separation.

To investigate the possible role of the surface, we performed similar experiments with [P_6,6,6,14][BMB] using gold and silica substrates. Force versus apparent separation profiles, at room temperature and at 40 °C on gold, are shown in Figure 4. Once again, a monotonic repulsion is observed, similar to the response on mica, however, the force decays more rapidly from the surface. Best fits to Equation (1), for the individual force profiles at room temperature, give a Hamaker constant of 1.4 ± 0.7(×10⁻²⁰) J, a steric prefactor of 0.12 ± 0.01 J/m², and a steric decay length of 0.33 ± 0.01 nm. The smaller decay length on gold, as compared with mica, indicates that the interfacial layer formed on gold has a smaller thickness. Molecular dynamics (MD) simulations were previously used to study the structuring of this IL on gold electrodes [37]. It was found that, on neutral gold, the innermost layer consists of both cations and anions, and PC₆ and PC₁₄ alkyl chains are predominantly parallel to the surface. It was shown that the density fluctuations have a first peak located 0.4 nm away from the surface [37]. Our experimental value is comparable with MD calculations, and suggests that, indeed, the cation adopts a conformation more parallel to the surface.

Unlike the surface of mica which, due to its (ion exchanged) negative surface charge, has the possibility to adsorb cations preferentially, the gold surface has a lower intrinsic charge and, thus, the interfacial layer is likely to be approximately equally rich in cations and anions [37]. The anion is smaller than the cation (see dimensions in Figure 1). The thicker interfacial layer on mica is, thus, consistent with the idea of a larger cation fraction, and/or a different conformation. In fact, at a surface charge density lower than −20 µC/cm², MD simulations suggest that anions are completely expelled from the first layer [37]. Even at the highest surface charge density in the MD simulations (100 µC/cm²), however, no alternating cation–anion layers were formed. Once again, lack of interfacial layering by this particular IL is probably due to the length and flexibility of the alkyl chains, as well as charge neutralization by the first layer. It is unwise to consider the behavior in terms of the cation alone, however, and the bulkiness and delocalized charge of the anions may also contribute to the lack of layering.

The individual force profiles on gold at 40 °C were also fitted with Equation (1), while keeping the Hamaker constant equal to that obtained at room temperature. Best fits give a steric prefactor of 0.10 ± 0.01 J/m², and steric decay length of 0.36 ± 0.02 nm. As for mica, there is thus no significant difference observed between the force responses at 40 °C and those at room temperature. The retraction curves at 40 °C give an adhesion minimum of 1.6 ± 0.1 nN which is, once again, smaller than the adhesion force at room temperature, 4.3 ± 0.2 nN.

The data for [P_6,6,6,14][BMB] on silica at room temperature and at 40 °C are shown in Figure 5. Once again, a monotonic repulsion is observed, which is highly reminiscent of the response on mica and gold. The best fit to Equation (1) for the individual force profiles at room temperature gave a Hamaker constant of 1.5 ± 0.2 (×10⁻²⁰) J, a steric prefactor of 0.11 ± 0.03 J/m², and a steric decay length of 0.35 ± 0.03 nm. The steric decay length is comparable to the value on gold rather than that of mica, which is somewhat surprising, since the surface of silica is usually considered negatively charged. This charging behavior is in aqueous systems, however, where dissociation of silanol groups is favorable via the formation of hydrogen bonded hydronium complexes [39,40]. Such a charging mechanism is forbidden, without a suitable hydrogen-bonding moiety in aprotic ion liquids, though it should be recognized that, for protic ionic liquids, such a charging mechanism should be possible [28,34]. Indeed, it has been shown that undissociated silanol groups are likely to be responsible for the decomposition of orthoborate anions [41]. Mica, on the other hand, has an intrinsic aluminosilicate lattice charge, due to the isomorphic substitution of aluminum for silicon atoms in the lattice. This negative charge is neutralized by adsorbed metal counterions which can, thus, be expected to ion exchange with, or “dissolve in”, the IL.

While the reduced steric behavior is well described in terms of a different orientation of the cation in the near-surface layer, the issue of roughness should also be addressed. It is generally accepted [15], and shown with simulations [42], that oscillatory solvation forces are smeared out on rough surfaces, if the roughness is larger than the molecular dimension of the fluid. For ILs, however, there is evidence that the roughness plays a less important role in the observation of stratified layers. For example, stratified layers were observed on stainless steel surfaces with roughness larger than the size of the ionic species (RMS = 0.89 nm), in 1-ethyl-3-methylimidazolium tris(pentafluoroethyl)trifluorophosphate [EMIM][FAP], 1-hexyl-3-methylimidazolium tris(pentafluoroethyl)trifluorophosphate [HMIM][FAP], and 1-hexyl-3-methylimidazolium iodide [HMIM][I] ILs [21]. Sheehan et al. also performed a systematic study of the effect of roughness on stratified layers formed by 1-hexyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide [HMIM][TFSI] on silica, where it was found that that roughness somewhat promoted difficulty to squeeze out the innermost layer, while it smeared out the outermost layer [43]. Here, we see an almost constant prefactor, with a sharper decay on gold and silica (i.e., the opposite of a smearing effect). It is thus concluded, that the similarity of the steric decay lengths on the surfaces of silica and gold is not associated with their (rather different) topography but, rather, is due to an approximately equal population of cations and anions in the near-surface layer, with cations aligned parallel to the surface.

Individual force profiles on silica at 40 °C were also fitted using Equation (1), while keeping the Hamaker constant equal to the value at room temperature. Best fits give a steric prefactor of 0.10 ± 0.02 J/m², and steric decay length of 0.34 ± 0.03 nm. The retraction curves at 40 °C give an adhesion force of 0.9 ± 0.2 nN which, in line with the previous observations, is smaller than the adhesion force at room temperature, 2.5 ± 0.3 nN. The temperature trend from room temperature to 40 °C is thus the same on all surfaces, and is characterized only by a reduction in adhesion.

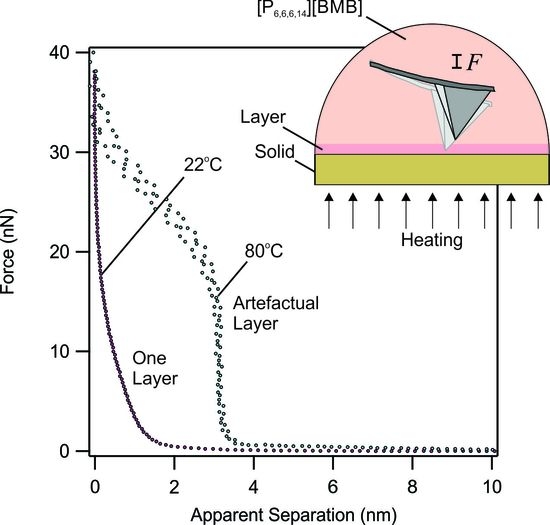
The question can then be posed as to whether a different response is observed at more elevated temperatures, analogously to the dramatic changes observed by Hjalmarsson et al. [28]. Figure 6 shows representative force profiles obtained at 80 °C and 120 °C on a mica surface. The force behavior has the “push-through” appearance expected for interfacial solvation-like layers, as commonly observed in ILs [16,17,18,19,20,21,22]. The apparent layers observed here have sizes in the range of about 4 nm at 80 °C, and 2 nm at 120 °C. These sizes are molecularly relevant, e.g., an ion pair of [P_6,6,6,14][BMB] IL is expected to have dimensions of about 1.1 nm, as calculated from the IL density and assuming cubic packing. Using molecular modeling calculations (Ref. [44]) shown in Figure 1, an ion pair may have a dimension between 1.2 and 2.5 nm which is, nevertheless, larger than the calculations based on the density value. Considering the former value, the step sizes would thus correspond to four layers and two layers of ion pairs, respectively, apparently being expelled from the small gap between the AFM tip and the solid substrate. The observation of an increased number of apparent layers with increasing temperature, and/or decreasing approach velocity, is highly reproducible. It is thus tempting to ascribe these observations to thermal transitions in the interfacial layers.

These observations were investigated more closely with a view to understanding this phenomenon. Figure 7 shows the AFM cantilever deflection as a function of time and temperature where it was placed in contact with a temperature-controlled solid substrate surface in the absence of ionic liquid. The deflection setpoint was adjusted to 1.0 V, while the integral gain was set to zero and, thereby, no correction to the deflection was applied. One observes that while the deflection remains almost constant at room temperature and at 40 °C, it fluctuates at 80 °C. These fluctuations further display a sinusoidal behavior at 120 °C. Such features were observed regardless of the type of the AFM cantilever used or the liquid medium; for example, they were also present in hexadecane or if an uncoated cantilever was used and cannot, thus, be due to ionic liquid ordering. Instead, the origin of these fluctuations has been traced to the thermal instability of the Peltier heating element. To maintain a constant set temperature, the Peltier element turns on and off, repeatedly, in response to a PID feedback loop connected to the temperature controller unit. While heating, the element expands in the z-direction, which results in extension of the solid substrate towards the tip, causing an increase in the deflection. Similarly, during cooling, contraction of the Peltier element moves the solid substrate away from the tip, leading to a reduction in the deflection. During these events, the measured contact force (which is obtained directly from the cantilever deflection) changes its gradient, giving an appearance of a layer-like transition (Figure 6). Comparison between the intervals of artefactual relaxation responses in Figure 6, with the time intervals of thermal instabilities in Figure 7, corroborates this conclusion: at 80 °C, the former process has a frequency of about 0.4 Hz (in terms of the number of artefactual relaxation events per second) while the latter has an oscillation frequency of about 0.4 Hz. The agreement persists at 120 °C, where the frequency of both is around 0.8 Hz. This phenomenon is thus entirely artefactual, and we caution against misinterpretation of such observations.

4. Conclusions

Force measurements in [P_6,6,6,14][BMB] on a range of substrates reveal differences in the ordering of the interfacial layers but, also, a systematic absence of multilayer behavior. Indeed, no well-defined barrier is formed at all. It would thus appear that the multilayer phenomenon is not a universal feature of ionic liquids at interfaces. Instead, a monotonic squeeze-out phenomenon is observed in all cases, suggesting that the large size and flexibility of the cation, which is the counterion to the surface charge, combined with its highly delocalized charge, leads to a lack of stratification in the interfacial region which precludes step-like behavior. This behavior is likely to be reinforced by the bulky and inflexible anion, though further studies using systematically varied ion structures would be necessary to pin down the relative importance of the two species. It is interesting to contrast this behavior with the adsorption of such ions (surfactants) from aqueous solutions, where the added self-assembly interactions lead to more ordered layers, rather than less. It would also be interesting to see whether a larger radius of curvature for the confining interaction (for example, more akin to the surface force apparatus geometry) would lead to a difference in the observed layering tendency, though we note that for layered systems, no such geometry dependence has hitherto been observed.

Nonetheless, the details of this monotonically repulsive interaction allow conclusions to be drawn about the composition of the interfacial film. The highly reproducible nature of the interaction allows a decay length to be assigned, with high precision. For negatively charged mica, the decay length is longer, indicating a preponderance of the larger cations in the interfacial film. On both gold and silica, the decay length (or layer thickness) is considerably smaller, reflecting the fact that the surfaces have a lower charge density, and that the interfacial film contains a more even balance between cations and anions. We note that the experimental dimensions inferred from the decay are in excellent agreement with earlier simulations of this IL on gold [37].

The fact that the force profile on silica is more reminiscent of that of gold than mica, provides a vital piece of evidence as to the charging behavior of silica in aprotic ionic liquids, since it implies a considerably lower charge density than mica. This contrasts with their aqueous behavior, where a silica surface can reach silanol site densities almost double that of the charge density of mica. It would thus appear that silanol dissociation is not favored in these aprotic liquids.

Finally, there was very little change in the interaction over the range between room temperature and 40 °C, which is consistent with studies in other IL systems [20], albeit ones showing more distinct layering. While multilayer phenomena were, indeed, apparently observed at elevated temperatures, we have, here, demonstrated that they arise from an artefact of the temperature control system shared by the majority of instruments. We warn against possible misinterpretation of such data, particularly where the time scale of the feedback is comparable to that of the force measurements.