Electrohydrodynamic Instabilities in Free Emulsion Films

Abstract

Electrohydrodynamic instabilities were induced in thin water-in-oil emulsion films by application of external DC electric field. The dominant wavelengths of instabilities were measured for constant electric fields of various strengths. The dominant wavelengths agreed reasonably well with theoretical predictions based on a linear stability model. The linear stability model used in this study took into account experimentally measured repulsive disjoining pressure and calculated Maxwell stress. The observation of such instabilities can help to understand the rupture mechanism of emulsion films under the influence of electric field.

1. Introduction

Electric-field-induced breakdown of emulsion films has broad applications in industrial and biological systems. In the petroleum industry, for instance, electrocoalescence is widely used to demulsify water-in-oil emulsions [1,2,3,4]. Formation of pores in bilayer lipid membranes (BLM) using electric fields (electroporation) has also been used to transfer molecules into the cell body [5,6]. While the electric-field-induced breakdown of bilayer lipid membranes is well studied, the breakdown mechanism for common emulsion films encountered in industry is still not well understood. Electroporation in emulsion films is unlikely because they are rather thick. Emulsion films consist of two adsorbed layers with a considerable solvent core. The thickness of these films is on the order of tens of nanometers [7,8,9]. Bilayers, on the other hand, are much thinner, typically a few nanometers, and virtually without a solvent core [10]. Furthermore, pore nucleation in bilayers is experimentally detectable by a sudden increase in conductance of the film at the onset of pore formation but has not been reported for typical emulsion films [11,12]. Dielectric breakdown, which manifests as the growth of conduction paths through a nonconductive medium beyond a critical electric field strength, is another possible mechanism. However, the dielectric strengths of typical organic solvents are an order of magnitude greater than those required for the breakdown of thin films [13].

Electric-field-induced instabilities have been observed in wetting films, where a thin liquid film is squeezed between a solid substrate and air. Electric fields have been used as a means to transfer patterns onto polymer films [14,15,16]. However, experimental evidence for the existence of such instabilities in free emulsion films is scarce [17]. Herein, we report evidence of electric-field-induced instabilities in free water-in-oil emulsion films. The dominant wavelengths of these instabilities were measured as a function of applied DC (direct current) electric fields strengths. Experimentally measured disjoining pressure and calculated Maxwell stress are used in a linear stability model to interpret the experimental results for dominant wavelengths.

2. Materials and Methods

2.1. Materials

The oil phase was a solution of Tegopren 7008 (Degussa, Essen, Germany) in n-decane (Fisher Scientific, Pittsburgh, PA, USA). Tegopren 7008 is a high-molecular-weight (>10,000 Da) block copolymer with strong emulsifying properties for water-in-oil type emulsions [18]. The oil phase was prepared at two different Tegopren 7008 concentrations: 0.058 wt.% (“film A”) and 0.52 wt.% (“film B”). The aqueous phase was 1 wt.% solution of sodium chloride in Milli-Q water, 18.2 MΩ·cm.

The porous glass plate was treated hydrophobic by soaking it for 24 h in a solution of 20 wt.% dichlorodimethylsilane (purity >99.5%, Fluka) in cyclohexene (reagent grade, Fisher Scientific, Pittsburgh, PA, USA).

2.2. Experimental Setup

A schematic diagram of the experimental setup is shown in Figure 1. A single thin emulsion film is formed in the modified Scheludko–Exerowa cell that allows for application of DC or AC (alternating current) polarizations to single water-in-oil emulsion films [19]. The cell consisted of a hydrophobic porous glass plate, in which a small hole has been drilled to hold the film. The porous plate, soaked with oil, separated two aqueous phases (electrically insulated). Both aqueous phases were de-ionized water with addition of sodium chloride (1 wt.%) to increase the conductivity of the solutions. Platinum wire electrodes were placed in the aqueous phases. The electrodes were connected to a Solartron 1287 potentiostat (Solartron, Farnborough, UK) and used to apply DC electric field. The films were observed and recorded in reflected light with Zeiss Axio Observer microscope and Leica DFC500 digital camera. The disjoining pressure isotherms were measured by applying external pressure on the film and measuring the film thickness. The external pressure was controlled via Hamilton Syringe Drive PSD/2 and pressure transducer from Omega. The film thickness was measured following conventional interferometry techniques used in thin-film applications [20,21]. Hg-arc lamp, a green interference filter 546 nm, and a low-noise Hamamatsu Si photodiode S8745-01 were used for registration of photo signal.

3. Results and Discussion

Both Tegopren 7008 concentrations, “film A” (0.058 wt.%) and “film B” (0.52 wt.%) formed stable films with long lifetimes and good stability against applied electric fields. The thin films were obtained by slowly withdrawing oil from the porous plate through a capillary until a plane parallel film was formed. The films were allowed to drain for at least 30 min to achieve the final equilibrium thicknesses before any electric field was applied. The equilibrium thicknesses of films A and B were 57 and 72 nm, respectively.

Figure 2a is a micrograph of a film at rest. Relatively uniform light distribution across the plane of the film indicates uniform film thickness. Once the films reached their equilibrium thicknesses, a step potential was applied across the film through platinum electrodes using the Solartron 1287 potentiostat. Upon applying the electric field, instabilities appeared in a form of small white dots or ripples as shown in Figure 2b,c. In these pictures, the white dots represent thicker film areas. To study the behavior of the films, step electric potentials varying from 0 to 900 mV with 100 mV increments were applied. Each measurement started with a uniform and well-equilibrated film, as shown in Figure 2a. No instabilities were observed below 200 mV, while the films ruptured at potentials above 900 mV. Once the electric field was removed, the instabilities disappeared, and the films reestablished their uniform thickness at equilibrium state. When a constant electric field was maintained, however, the white spots slowly merged, mostly through a mode similar to the coarsening process observed in wetting films [22]. A few coalescence events were also observed. The images shown in Figure 2b,c correspond to the first frames captured right after applying the potential.

The comparison of images obtained at different conditions showed a clear correlation between the applied potential and the distribution of the spots: the stronger the electric field, the greater the number density of the spots. To characterize the instabilities, we measured the nearest neighbor-to-neighbor distance distribution of the spots. The inset in Figure 2c shows the distribution of the measured distances. The maximum of the normal distribution of the distances was considered to be the dominant or the fastest-growing wavelength for the instabilities.

The dominant wavelength, λ_max, corresponding to the applied potentials is plotted in Figure 3. It is assumed that the applied potential across the electrodes translates into equivalent electric potential across the film. This assumption is justified given the amount of electrolyte in the aqueous phase, thus its high electric conductivity, compared to very low conductivity of the oily film liquid. Electrode polarization is neglected due to the low current (current density) flowing through the system. The figure shows a reduction in the wavelength of the fastest-growing instabilities when the potential is increased. Furthermore, the dominant wavelengths for both systems (i.e., for film A and film B) are similar; in particular, they are indistinguishable at potentials greater than 400 mV.

We explain this observation by using linear stability theory [23,24,25,26], taking into account the surface forces acting in the film. Before using the linear stability theory, one needs to emphasize its underlying assumption. In this theory, the Navier–Stokes equations are linearized assuming the amplitude of the instabilities is much smaller than the thickness of the film. Despite this approximation, the linear model provides a simple and straightforward solution that explains the underlying mechanism of electric-field-induced rupture [23,24,25].

Now, let us analyze the pressure difference, Δp, between the perturbed state and the initial state before the application of electric field. If we follow Mileva and Radoev [26], Δp can be presented as:

$$-\Delta p=p_{\gamma }\left(\delta \right)+P_{ST}\left(h+2\delta \right)-P_{ST}\left(h\right)$$

(1)

where p_γ, δ, h are the local capillary pressure, the displacement of film surface from initial position due to instability, and the initial film thickness, respectively. P_ST(h + 2δ) and P_ST(h) are stabilizing pressures acting on the film. In our case, we have two major pressure contributions: disjoining pressure Π(h) which includes all surface forces acting in the film (e.g., Van der Waals, electrostatic, and steric forces) and Maxwell stress due to the applied electric field.

$$P_{st}\left(h\right)=\Pi \left(h\right)-\frac{1}{2}{\epsilon \left(\frac{U}{h}\right)}^2$$

(2)

In Equation (2), ε and U are the permittivity of oil phase and applied potential, respectively. Π(h) by definition is positive when stabilizing the film and the Maxwell stress is acting in the opposite direction. By assuming an immobile film interfaces due to the adsorption of the surfactant molecules and performing perturbation analysis followed by Fourier transformation [25,26], one can obtain the following expression for the wavenumber of the fastest-growth instability mode, q_max:

$$q_{max}^2=\frac{{\left(\frac{d{P}_{st}}{dh}\right)}_{h_0}}{\gamma }=\frac{1}{\gamma }\left\{{\left(\frac{d\Pi }{dh}\right)}_{h_0}+\frac{\epsilon U^2}{h_0^3}\right\}$$

(3)

where γ, h₀ are the interfacial tension and equilibrium film thickness. As shown by Herminghaus [23], for wetting films with no surfactant, the contribution of Van der Waals force to the dominant wavelength is negligible compared to that of an electric field. In an emulsion film with adsorbed surfactant layer, however, the contribution of repulsive interactions should be taken into account. To quantify the contribution of stabilizing surface forces, disjoining pressures of the films were measured, and the results are shown in Figure 4. In the measurement of the disjoining pressures, no electric force was applied. Therefore, the disjoining pressure consists of all interactions including Van der Waals, electrostatic (due to surface charges), and steric forces. We used the slope of the linear fit of the experimental data points in proximity of h₀ as an estimate of the derivative of the disjoining pressure at the equilibrium film thickness, as shown in the Figure 4.

Now, one may calculate the fastest-growing wavelengths of the instabilities (λ_max = 2π/q_max) using Equation (3). These are shown by the solid and dashed lines in Figure 3 for films A and B, respectively. Considering limitations of linear stability theory, a reasonable agreement between theory and the experimental data is achieved. The model follows the trend of the experimental data. Furthermore, the model shows that almost identical dominant wavelengths are expected for potentials greater than 400 mV. The relatively high interfacial tension in film A is counterbalanced by the greater slope of disjoining pressure vs. film thickness and lower film thickness, yielding a dominant wavelength similar to that for film B.

Table 1. Experimental data for film thickness, interfacial tension, and the derivative of disjoining pressure that were used in the model.

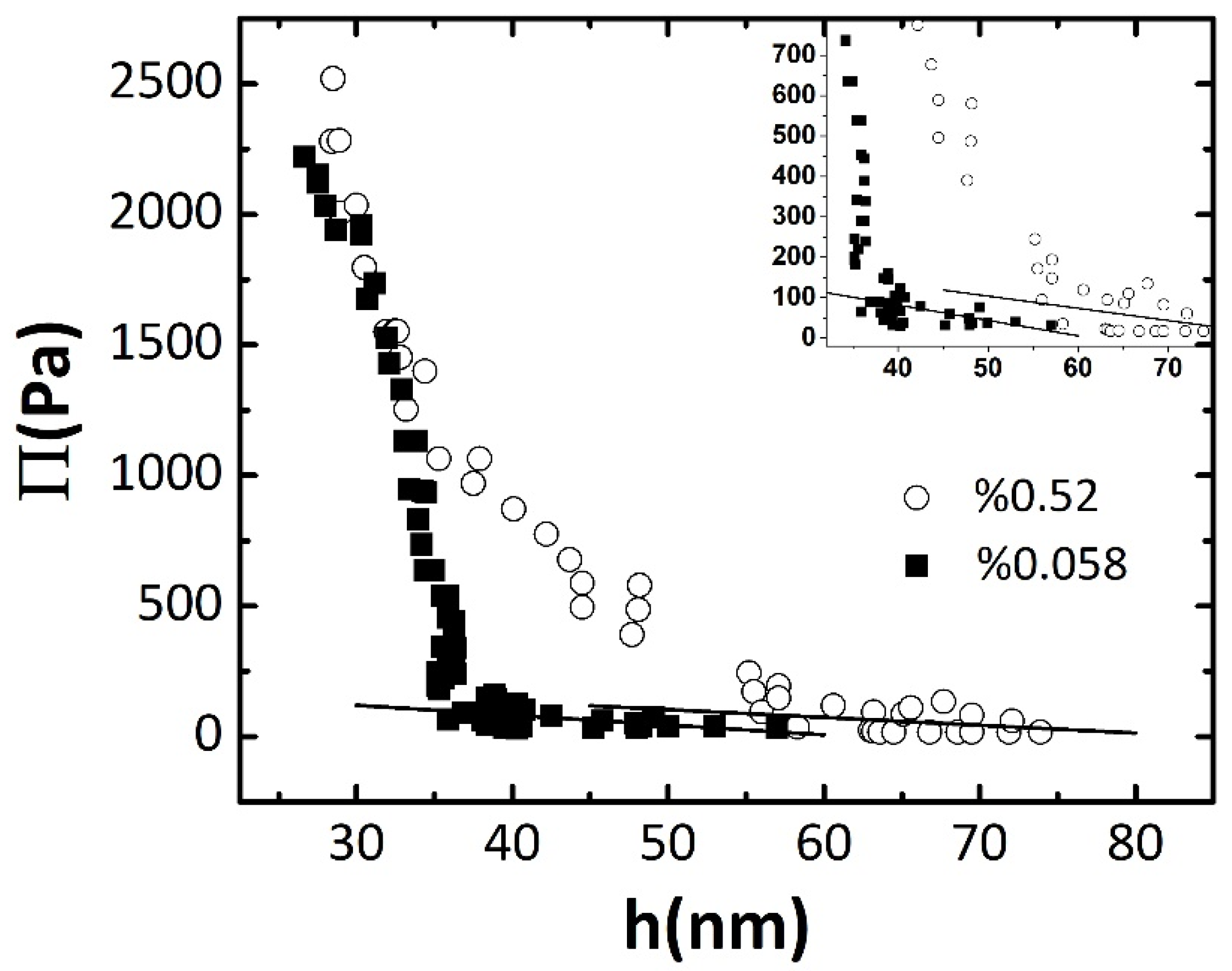
Conc. (wt.%)	Equilibrium Thickness (nm)	Equilibrium Interfacial Tension (mJ/m2)	$\raisebox{1ex}{$\mathit{\partial }\mathit{\Pi }$}\!\left/ \!\raisebox{-1ex}{$\mathit{\partial }\mathit{h}$}\right.$(Pa/nm)
0.058	57 ± 1	5.8 ± 0.5	−3.8
0.52	72 ± 1	3.2 ± 0.5	−3.0

shows the experimental data for film thickness, interfacial tension, and derivative of the disjoining pressure used in the model.

The linear stability model allows to calculate the critical wavenumber and wavelength of the instability:

$$q_{cr}=\frac{2\pi }{{\lambda }_{cr}}={\left[\frac{2}{\gamma }\left\{{\left(\frac{d\Pi }{dh}\right)}_{h_0}+\frac{\epsilon U^2}{h_0^3}\right\}\right]}^{\frac{1}{2}}$$

(4)

Since (dΠ/dh)_h0 < 0, the value of q_cr has a real value if $\epsilon U^2/h_0^3>\left|{(d\Pi /dh)}_{h_0}\right|$. When q_cr is real, for a given electric field, there exist wavelengths that destabilize the film (those with λ > λ_cr). However, for electric potentials that make $\epsilon U^2/h_0^3<\left|{(d\Pi /dh)}_{h_0}\right|$, q_cr has no real roots. This condition is satisfied for electric potentials below 0.19 and 0.25 V for films A and B, respectively. In other words, the film is stable for all wavelengths at potentials below these values due to the stabilizing repulsive disjoining pressure. This corroborates our observations—no instabilities were detected below 0.2 V.

4. Conclusions

Upon application of an electric field across water-oil-water emulsion films, instability patterns were observed as small white dots in the film’s microscopic images. The characteristic lengths of these instabilities were measured for constant electric fields of various strengths. The experimentally observed dominant and critical wavelengths agreed reasonably well with theoretical predictions based on the linear stability model. The linear stability model used in this study took into account experimentally measured disjoining pressure and calculated Maxwell stress. The reported results demonstrated that the formation of electrohydrodynamic instabilities is a possible mechanism for breakup of thick emulsion films. DC polarization studies of single thin emulsion films are a promising approach for understanding of electro-induced coalescence of W/O emulsions.