Electrophoretic Mobility and Electric Conductivity of Salt-Free Suspensions of Charged Soft Particles
Abstract
:1. Introduction
2. Analysis
2.1. Electrostatic Potential Profile
2.2. Ionic Electrochemical Potential Energy Profile
2.3. Fluid Flow Field
2.4. Electrophoretic Velocity
2.5. Electric Conductivity
3. Results and Discussion
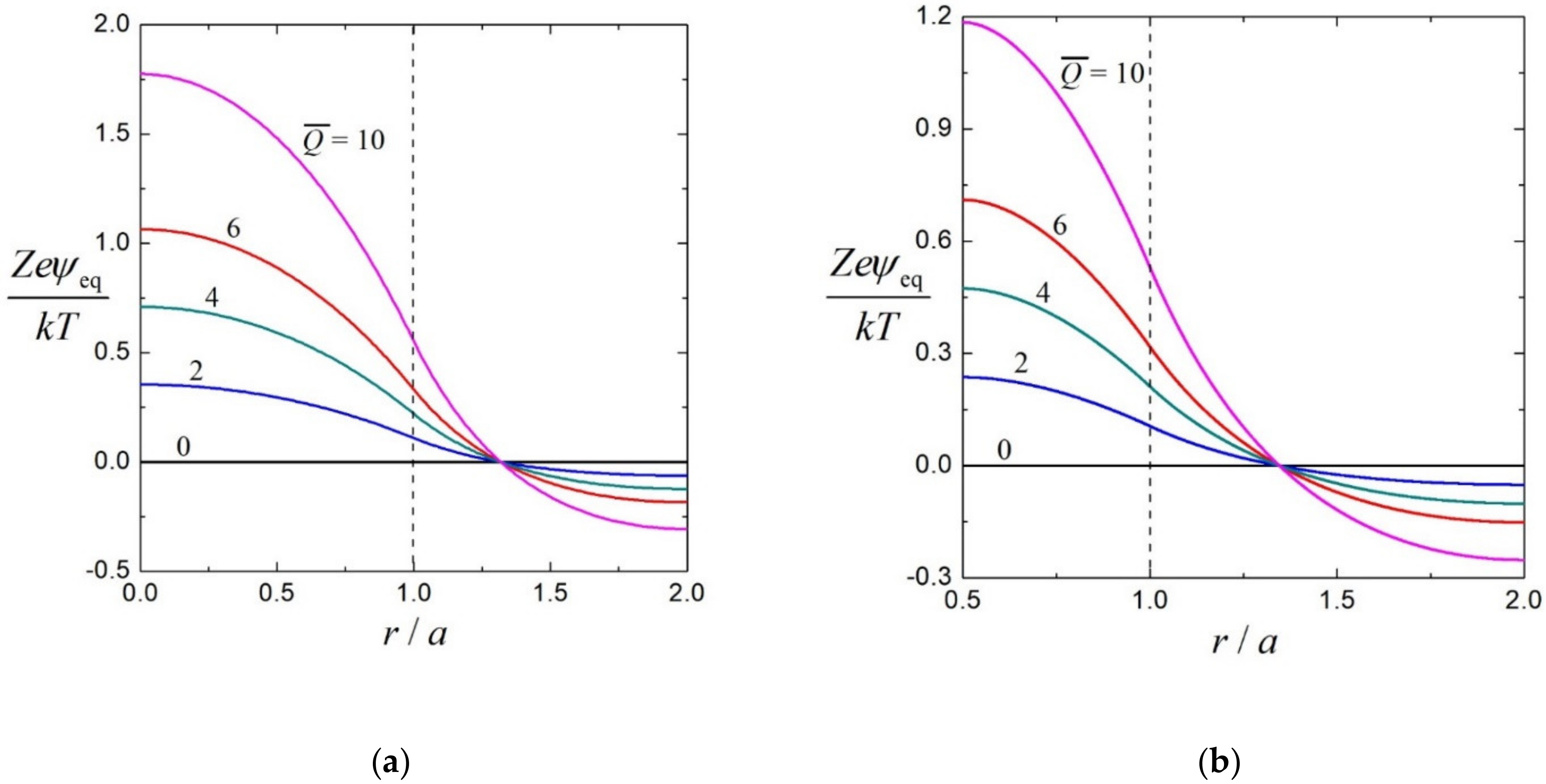
3.1. Equilibrium Electrostatic Potential
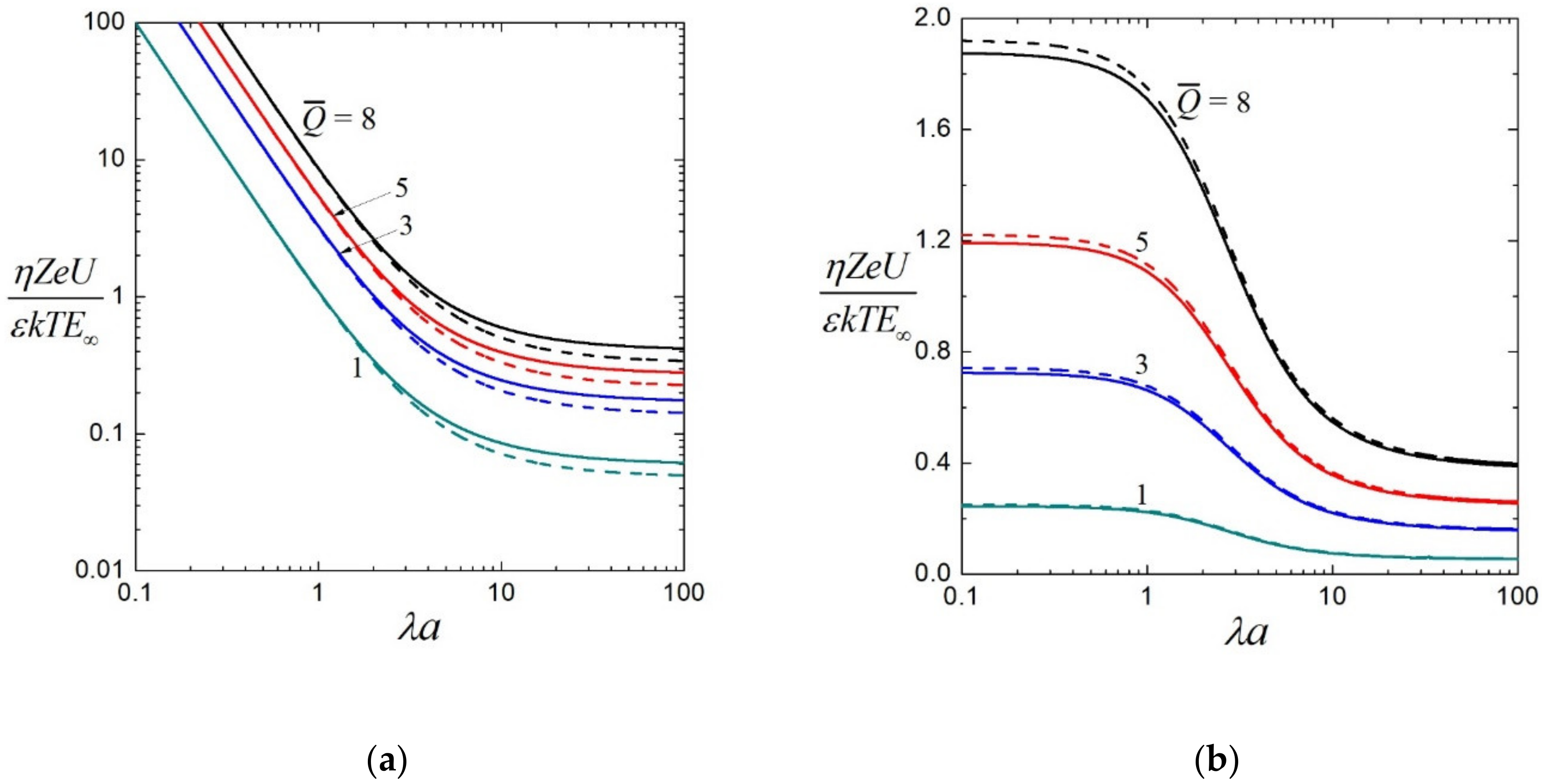
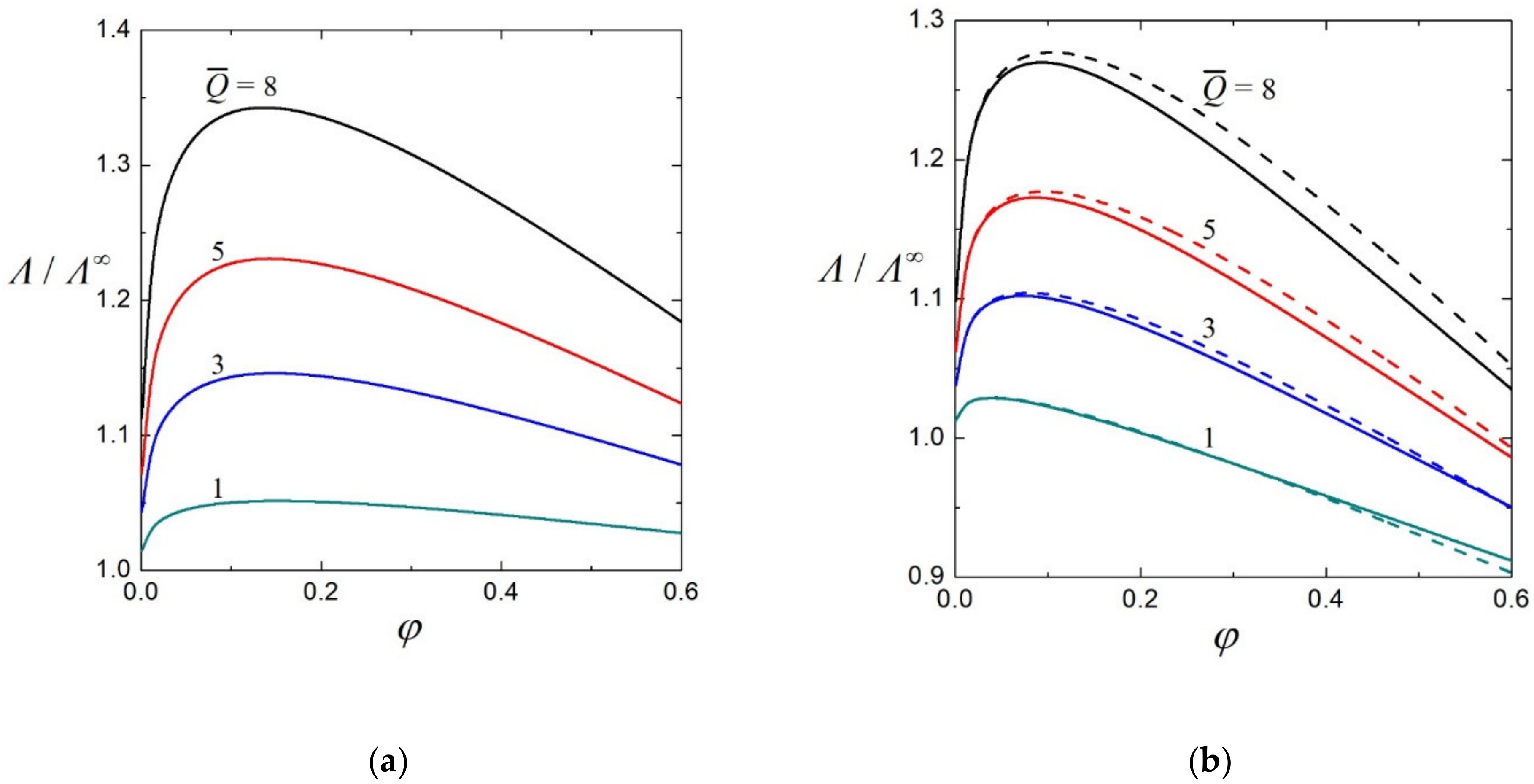
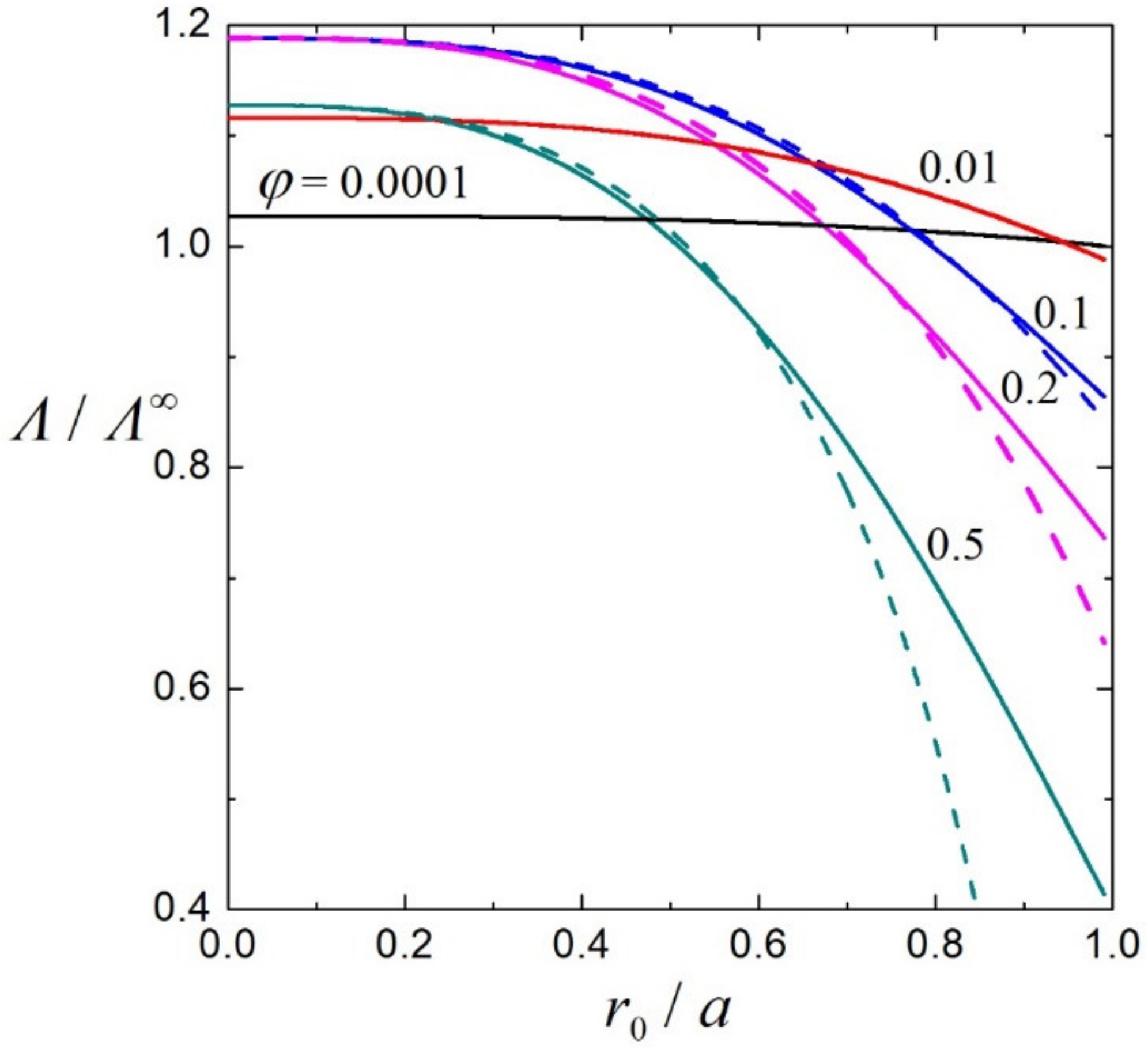
3.2. Electrophoretic Mobility
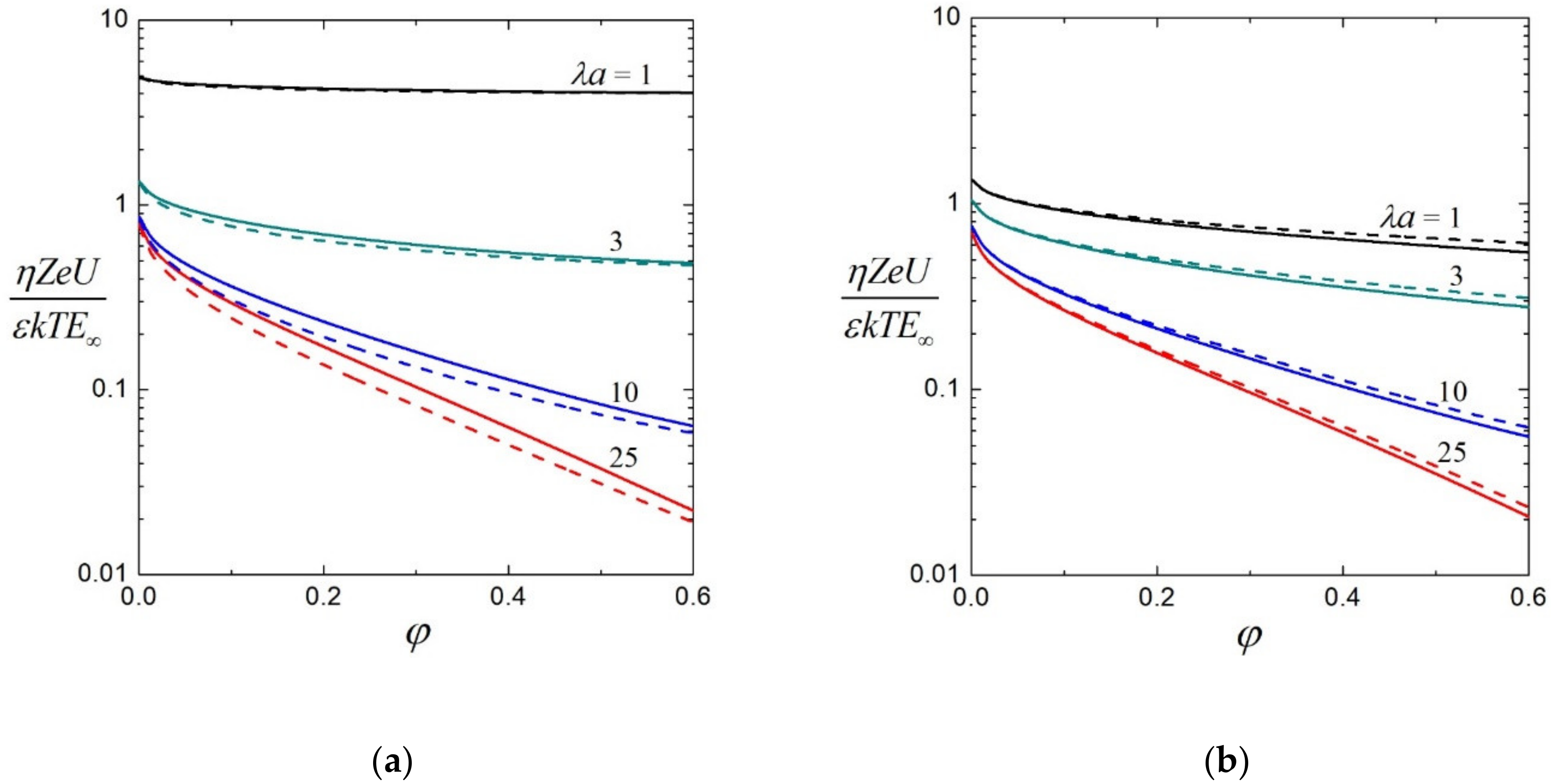
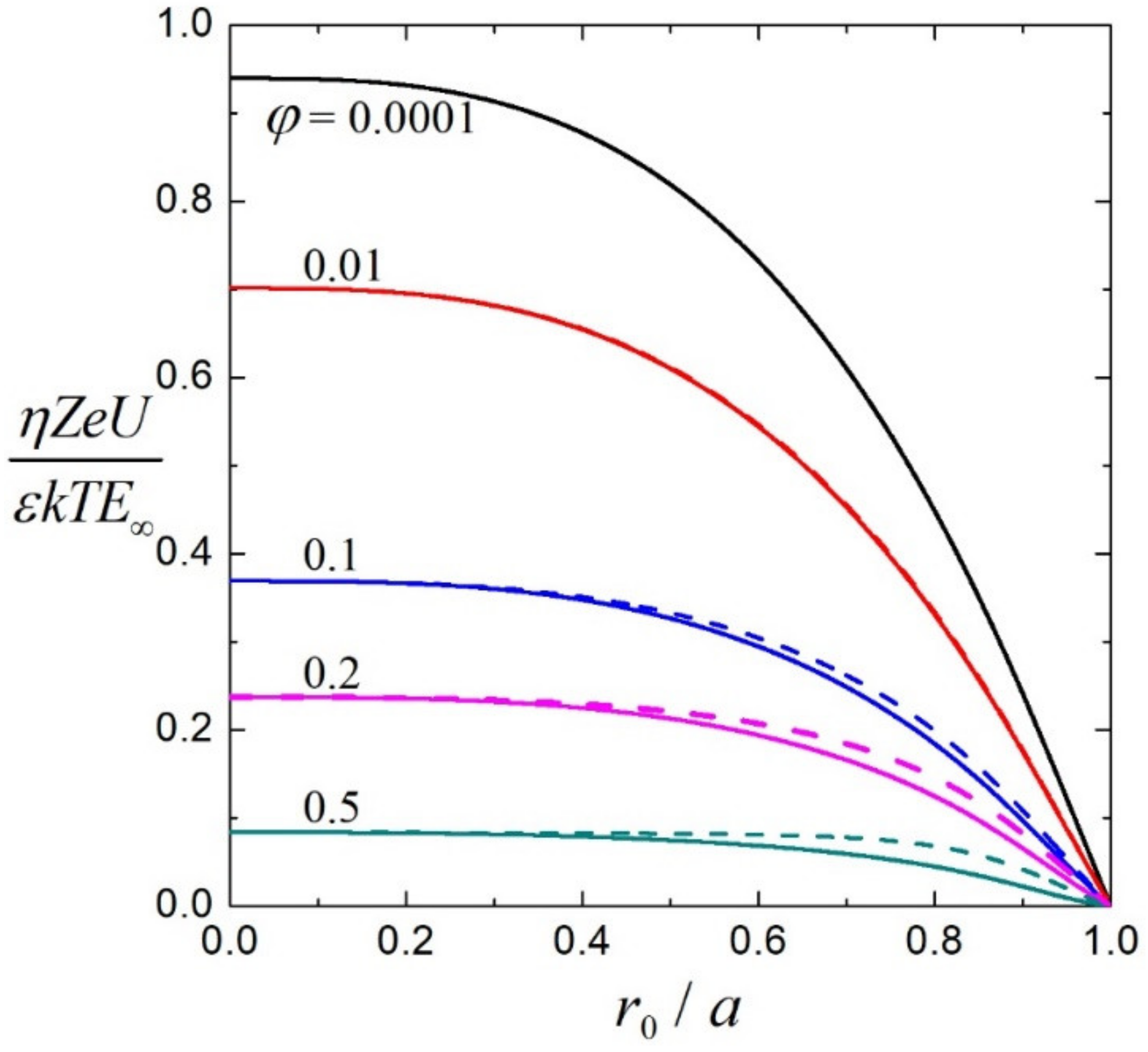
3.3. Effective Electric Conductivity
4. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Levine, S.; Neale, G.H. The Prediction of Electrokinetic Phenomena within Multiparticle Systems I. Electrophoresis and Electroosmosis. J. Colloid Interface Sci. 1974, 47, 520–529. [Google Scholar] [CrossRef]
- O’Brien, R.W. The Electric Conductivity of a Dilute Suspension of Charged Particles. J. Colloid Interface Sci. 1981, 81, 234–248. [Google Scholar] [CrossRef]
- Zharkikh, N.I.; Shilov, V.N. Theory of Collective Electrophoresis of Spherical Particles in the Henry Approximation. Colloid J. USSR (Eng. Transl.) 1982, 43, 865–870. [Google Scholar]
- Ohshima, H.; Healy, T.W.; White, L.R. Approximate Analytic Expressions for the Electrophoretic Mobility of Spherical Colloidal Particles and the Conductivity of Their Dilute Suspensions. J. Chem. Soc. Faraday Trans. 2 1983, 79, 1613–1628. [Google Scholar] [CrossRef]
- Chen, S.B.; Keh, H.J. Axisymmetric Electrophoresis of Multiple Colloidal Spheres. J. Fluid Mech. 1992, 238, 251–276. [Google Scholar] [CrossRef]
- Liu, Y.C.; Keh, H.J. Electric Conductivity of a Dilute Suspension of Charged Composite Spheres. Langmuir 1998, 14, 1560–1574. [Google Scholar] [CrossRef]
- Ohshima, H. Electrical Conductivity of a Concentrated Suspension of Spherical Colloidal Particles. J. Colloid Interface Sci. 1999, 212, 443–448. [Google Scholar] [CrossRef]
- Borkovec, M.; Behrens, S.H.; Semmler, M. Observation of the Mobility Maximum Predicted by the Standard Electrokinetic Model for Highly Charged Amidine Latex Particles. Langmuir 2000, 16, 5209–5212. [Google Scholar] [CrossRef]
- Ding, J.M.; Keh, H.J. The Electrophoretic Mobility and Electric Conductivity of a Concentrated Suspension of Colloidal Spheres with Arbitrary Double-Layer Thickness. J. Colloid Interface Sci. 2001, 236, 180–193. [Google Scholar] [CrossRef] [Green Version]
- Carrique, F.; Cuquejo, J.; Arroyo, F.J.; Jimenez, M.L.; Delgado, Á.V. Influence of Cell-Model Boundary Conditions on the Conductivity and Electrophoretic Mobility of Concentrated Suspensions. Adv. Colloid Interface Sci. 2005, 118, 43–50. [Google Scholar] [CrossRef]
- Zholkovskij, E.K.; Masliyah, J.H.; Shilov, V.N.; Bhattacharjee, S. Electrokinetic Phenomena in Concentrated Disperse Systems: General Problem Formulation and Spherical Cell Approach. Adv. Colloid Interface Sci. 2007, 134–135, 279–321. [Google Scholar] [CrossRef] [PubMed]
- Keh, H.J.; Liu, C.P. Electric Conductivity and Electrophoretic Mobility in Suspensions of Charged Porous Spheres. J. Phys. Chem. C 2010, 114, 22044–22054. [Google Scholar] [CrossRef]
- Liu, H.C.; Keh, H.J. Electrophoresis and Electric Conduction in a Suspension of Charged Soft Spheres. Colloid Polym. Sci. 2016, 294, 1129–1141. [Google Scholar] [CrossRef]
- Galli, M.; Sáringer, S.; Szilágyi, I.; Trefalt, G. A Simple Method to Determine Critical Coagulation Concentration from Electrophoretic Mobility. Colloids Interfaces 2020, 4, 20. [Google Scholar] [CrossRef]
- Lin, W.C.; Keh, H.J. Diffusiophoresis in Suspensions of Charged Soft Particles. Colloids Interfaces 2020, 4, 30. [Google Scholar] [CrossRef]
- Lai, Y.C.; Keh, H.J. Transient Electrophoresis of a Charged Porous Particle. Electrophoresis 2020, 41, 259–265. [Google Scholar] [CrossRef]
- Delgado, Á.V.; Carrique, F.; Roa, R.; Ruiz-Reina, E. Recent Developments in Electrokinetics of Salt-Free Concentrated Suspensions. Curr. Opin. Colloid Interface Sci. 2016, 24, 32–43. [Google Scholar] [CrossRef]
- Ohshima, H. Ion Size Effect on Counterion Condensation around a Spherical Colloidal Particle in a Salt-Free Medium Containing Only Counterions. Colloid Polym. Sci. 2018, 296, 1293–1300. [Google Scholar] [CrossRef]
- Su, Y.W.; Keh, H.J. Electrokinetic Flow of Salt-Free Solutions in a Fibrous Porous Medium. J. Phys. Chem. B 2019, 123, 9724–9730. [Google Scholar] [CrossRef]
- Ohshima, H. Electrophoretic Mobility of a Spherical Colloidal Particle in a Salt-Free Medium. J. Colloid Interface Sci. 2002, 248, 499–503. [Google Scholar] [CrossRef]
- Ohshima, H. Electrokinetic Phenomena in a Dilute Suspension of Spherical Colloidal Particles in a Salt-Free Medium. Colloids Interfaces A 2003, 222, 207–211. [Google Scholar] [CrossRef]
- Ohshima, H. Electrophoretic Mobility of a Soft Particle in a Salt-Free Medium. J. Colloid Interface Sci. 2004, 269, 255–258. [Google Scholar] [CrossRef]
- Carrique, F.; Ruiz-Reina, E.; Arroyo, F.J.; Delgado, Á.V. Cell Model of the Direct Current Electrokinetics in Salt-Free Concentrated Suspensions: The Role of Boundary Conditions. J. Phys. Chem. B 2006, 110, 18313–18323. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chiang, C.-P.; Lee, E.; He, Y.-Y.; Hsu, J.-P. Electrophoresis of a Spherical Dispersion of Polyelectrolytes in a Salt-Free Solution. J. Phys. Chem. B 2006, 110, 1490–1498. [Google Scholar] [CrossRef] [PubMed]
- He, Y.-Y.; Wu, E.; Lee, E. Electrophoresis in Suspensions of Charged Porous Spheres in Salt-Free Media. Chem. Eng. Sci. 2010, 65, 5507–5516. [Google Scholar] [CrossRef]
- Luo, R.H.; Keh, H.J. Electrophoresis and electric conduction in a salt-free suspension of charged particles. Electrophoresis 2021, 42. [Google Scholar] [CrossRef]
- Kong, C.Y.; Muthukumar, M. Monte Carlo study of adsorption of a polyelectrolyte onto charged surfaces. J. Chem. Phys. 1998, 109, 1522. [Google Scholar] [CrossRef]
- Hierrezuelo, J.; Szilagyi, I.; Vaccaro, A.; Borkovec, M. Probing Nanometer-Thick Polyelectrolyte Layers Adsorbed on Oppositely Charged Particles by Dynamic Light Scattering. Macromolecules 2010, 43, 9108–9116. [Google Scholar] [CrossRef]
- Lin, W.-C. Electrophoresis and Electric Conduction in Salt-Free Suspensions of Charged Soft Particles. Master’s Thesis, National Taiwan University, Taipei, Taiwan, 2021. [Google Scholar]
- Keh, H.J.; Chen, W.C. Sedimentation Velocity and Potential in Concentrated Suspensions of Charged Porous Spheres. J. Colloid Interface Sci. 2006, 296, 710–720. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, W.C.; Keh, H.J. Electrophoretic Mobility and Electric Conductivity of Salt-Free Suspensions of Charged Soft Particles. Colloids Interfaces 2021, 5, 45. https://doi.org/10.3390/colloids5040045
Lin WC, Keh HJ. Electrophoretic Mobility and Electric Conductivity of Salt-Free Suspensions of Charged Soft Particles. Colloids and Interfaces. 2021; 5(4):45. https://doi.org/10.3390/colloids5040045
Chicago/Turabian StyleLin, Wei C., and Huan J. Keh. 2021. "Electrophoretic Mobility and Electric Conductivity of Salt-Free Suspensions of Charged Soft Particles" Colloids and Interfaces 5, no. 4: 45. https://doi.org/10.3390/colloids5040045






