Charged Colloids at the Metal–Electrolyte Interface

Abstract

We discuss the peculiarities of the structure of the interface between a metal and a stable colloidal dispersion of charged nanoparticles in an electrolyte. It is demonstrated that a quasi-2D ionic structure of elevated density arises in its vicinity due to the effect of electrostatic image forces. The stabilized colloidal particles, being electroneutral and spatially distributed objects in the bulk of the electrolyte and approaching the interface, are attracted to it. In their turn, the counterions forming their coat partially retract into the 2D-layer, which results in an acquisition by the colloidal particle of the effective charge $e{Z}^{*}\gg e$ and which, together with its mirror image, creates the electric dipole. The formed dipoles, possessing the moments directed perpendicularly to the interface, form the gas with repulsion between particles. The intensity of this repulsion, evidently, depends on the value of the effective charge $e{Z}^{*}$ acquired by the nanoparticle having lost a number of counterions. It can be related to the value of the excess osmotic pressure $P_{osm}$ measured in the experiment. On the other hand, this effective charge can be connected by means of the simple geometric consideration with the structural charge $eZ$ of the nanoparticle core being in the bulk of the electrolyte.

1. Introduction

In recent years, liquid thermoelectric materials are emerging as a cheaper alternative to the semiconductor-based solid counterpart for low-grade waste heat recovery technologies [1,2,3]. Incorporation of nanometer-sized colloidal particles can considerably change the transport properties of the host electrolyte. For example, a breakthrough in the enhancement of the Seebeck signal has been achieved by means of dispersion of charged colloidal particles in such systems [4,5].

In view of thermocell applications, a special attention requires the study of the behavior of colloidal particles being in the vicinity of the electrodes. Various experiments [6,7,8,9] indicate that colloidal particles are attracted by the metal–electrolyte interface. Herewith, its origin by definition is supposed to be of the Van der Waals type, which, indeed, always results in attraction of the neutral particles to the interface. Yet, this kind of attraction should be preserved between colloids also along the metal–electrolyte interface. The latter statement contradicts the experiment: the interaction between colloidal particles localized in the vicinity of the interface has the character of repulsion [6,7,8,9].

The alternative to the Van der Waals mechanism of such an interaction of the colloidal particle with the metal–electrolyte interface could be the attraction to its electrostatic mirror image. The method of mirror charges is widely used in electrostatics to simplify calculations of the electric field distribution of a charge placed in the vicinity of an interface between two dielectric media. It allows one to automatically satisfy the boundary conditions imposed by Maxwell equations on electric field intensity and the electrical induction vectors at the interface. It is notorious that this elegant method was proposed by W. Thomson (later Lord Kelvin) [10] for more than a decade before Maxwell formulated his electrodynamics. In the case under consideration of the metal–electrolyte interface, the method of mirror charges requires modification, since the potential of the electric field in the bulk of the electrolyte ceases to be a harmonic function: its properties here are defined by the Poisson equation. A corresponding extension of the theory was proposed at the beginning of XX-th century in the seminal papers of Wagner [11] and Onsager-Samaras [12], where it was found that the image force today bearing their name, is noticeably transformed with respect to dielectric media. Recently, the ideas of Wagner and Onsager-Samaras were developed by the authors on purpose to explain the details of the Seebeck effect in colloidal electrolytic solutions [13]. The Wagner–Onsager–Samaras mechanism, developed for the point-like charges and for the colloidal particles, is valid at the relatively large distances from the metal–electrolyte interface. Yet, its dominance ceases in the boundary domain where the direct colloid’s contact with the metal surface occurs. The origin and details of namely these contact interactions are discussed in this paper.

Point in fact, when the colloidal particles are neutral, they cannot exist independent in a dilute solution. Rather, they coagulate due to the Van der Waals forces acting between them. In order to prevent such coagulation processes, one can immerse individual colloidal particles of bare radius $R_0$ in the electrolyte (specific for each kind of particle), such that their surface species dissociate in the electrolyte, the counterions being freely dissolved while the NPs keep surface ions (e.g., hydroxyl groups, citrate, etc. [14,15,16]), resulting in a very large structural charge $eZ$ ($\left|Z\right|\gg 10$). Its sign can be either positive or negative, depending on the surface group type. If the concentration of free ions in the electrolyte (ionic strength) is small enough [16], the obtained dispersion is considered as colloidally stabilized.

The large structural core charge attracts counterions from the surrounding solvent, creating an electrostatic screening coat of the order of Debye length ${\lambda }_0$ containing an opposite charge $-eZ$ (see Figure 1a). Consequently, such complexes become neutral and their size can be estimated as the sum of the bare radius of charged core and the effective thickness of the screening coat: $2(R_0+{\lambda }_0)$. In these conditions, nanoparticles approaching within the distances $\delta r=r-(R_0+{\lambda }_0)\le {\lambda }_0$ between them begin to repel each other, preventing coagulation. The corresponding theory of stabilized electrolyte was developed in Refs. [17,18,19] and is called the DLVO theory. A typical manifestation of the stabilization phenomenon occurs in very dilute dispersions, where the system can be considered as a perfect gas of NPs, especially in the region of concentrations where

$$n_{\odot }{\left({\lambda }_0+R_0\right)}^3\ll 1,$$

(1)

where $n_{\odot }$ is the density of the colloidal particles. It is important to note that the stabilized solution is homogeneous under the condition described in Equation (1).

Here, the structure of the colloidal particle, immersed in the bulk of an electrolyte, is spherically symmetric and is determined by means of the solution of the Poisson equation with the zero boundary conditions at infinity [20]. Close to the interface, a non-homogeneous electric field in the electrolyte is formed due to the redistribution of ions. As a consequence, the colloidal complexes are pulled into the region of stronger electric field; the boundary conditions change and the electrostatic problem has to be revisited. Here, the difference between the electrostatic forces of attraction to the metallic electrode acting on the charged counterions of the screening coat and on the colloidal particle core enters in play. Indeed, such attraction forces are very different for the weakly charged counterions in the coating layer and the strongly charged ($eZ$) particle core of the colloid. Correspondingly, the counterions partially leave the coat (see Figure 1b), which results in the acquisition by the colloidal particle of the effective charge $e{Z}^{*}\gg e$ and which, together with its mirror image, creates the electric dipole [21]. These dipoles, possessing the moments directed perpendicularly to the interface, form a $2D$ gas with repulsion between particles. The intensity of this repulsion, evidently, depends on the value of the effective charge $e{Z}^{*}$ acquired by the nanoparticle that lost some number of counterions. Namely, such a repulsion is demonstrated by the abovementioned experiments [6,7,8,9] performed with colloidal solutions on a metal substrate. On the other hand, this charge can be related by means of a simple geometric consideration to the structural charge $eZ$ of the nanoparticle core being in the bulk of the electrolyte.

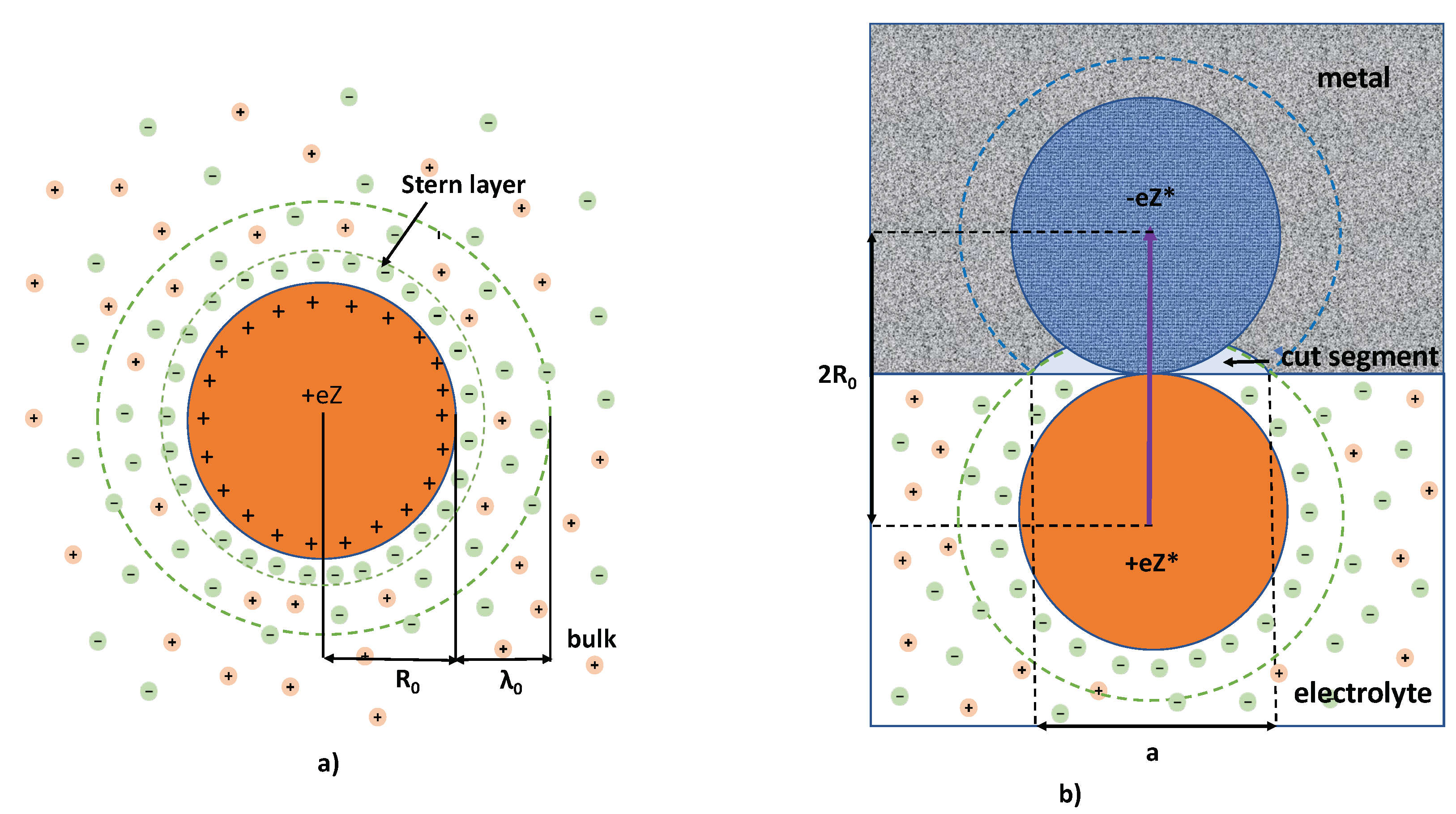
Figure 1. The schematic presentation of the multiply-charged colloidal particle surrounded by the cloud of counterions: (a) in the bulk of electrolyte; (b) in the vicinity of electrolyte–metal interface. In (a) is presented the standard scheme of the colloid structure assumed in the DLVO theory. Its core of the radius $R_0$ carries the charge $eZ$, while ${\lambda }_0$ appears in the DLVO theory as the characteristic screening length. The “Stern layer” is the auxilary characteristics of the screening coat, which is determined in the early theories [22,23], as the size of the region of elevate electrostatic energy $e\phi \gg k_{B}T$. The screening coat of the volume $\frac{4\pi }{3}[{(R_0+{\lambda }_0)}^3-R_0^3]$ possesses the opposite charge $-eZ$. Hence, the entire colloidal particle in the DLVO model is neutral. In (b), the colloidal particle is schematically shown in contact with the electrode (metallic plane). Here, the counterions previously contained in the spherical segment partially leave the coat (see b). This process results in acquisition by the colloidal particle of the effective charge $e{Z}^{*}$ (see Equation (8)), which, together with its mirror image, creates the electric dipole. Note that the effective charge considered here is that of static colloidal particles, to be distinguished from the dynamic effective charge of moving particles [4].

Figure 1. The schematic presentation of the multiply-charged colloidal particle surrounded by the cloud of counterions: (a) in the bulk of electrolyte; (b) in the vicinity of electrolyte–metal interface. In (a) is presented the standard scheme of the colloid structure assumed in the DLVO theory. Its core of the radius $R_0$ carries the charge $eZ$, while ${\lambda }_0$ appears in the DLVO theory as the characteristic screening length. The “Stern layer” is the auxilary characteristics of the screening coat, which is determined in the early theories [22,23], as the size of the region of elevate electrostatic energy $e\phi \gg k_{B}T$. The screening coat of the volume $\frac{4\pi }{3}[{(R_0+{\lambda }_0)}^3-R_0^3]$ possesses the opposite charge $-eZ$. Hence, the entire colloidal particle in the DLVO model is neutral. In (b), the colloidal particle is schematically shown in contact with the electrode (metallic plane). Here, the counterions previously contained in the spherical segment partially leave the coat (see b). This process results in acquisition by the colloidal particle of the effective charge $e{Z}^{*}$ (see Equation (8)), which, together with its mirror image, creates the electric dipole. Note that the effective charge considered here is that of static colloidal particles, to be distinguished from the dynamic effective charge of moving particles [4].

The structural nanoparticle core charge $eZ\gg e$ is the important characteristic of the solution containing the stabilized nanoparticles. Yet, in the frameworks of the existing theories based on the bulk properties of the solution, it does not appear explicitly either in the expression for conductivity [20], nor for the Seebeck coefficient [13]. Below, we propose the mechanism that explains the observed attraction of colloidal nano-particles to the metal surface and the nature of their repulsion along the latter. Finally, we discuss the possibility of determination of the value of core charge $eZ\gg e$ exploiting the properties of the two-dimensional system of colloids, which occurs at the metal–colloidal solution interface.

2. The Structure of Interface between a Metal and Stabilized Electrolyte

Let us start from the standard electrostatic problem of the interaction between the point charge Q, placed in the insulator semi-space (with dielectric constant $ϵ$), with the metallic semi-space. It can be replaced by the attraction of the charge to its mirror image [10,24]:

$$F_{ϵ}\left(z\right)=-\frac{Q^2}{4ϵz^2},$$

(2)

where z is the distance from the point charge Q to the plane.

When the first semi-space is filled with an electrolyte, the electrostatic image force $F_{ϵ}$ (Equation (2)) is screened at the distances of the order of the Debye length as one moves away from the plane. As it was demonstrated by Wagner, Onsager, and Samaras [11,12]:

$$F_{\mathrm{WOS}}\left(z\right)=F_{ϵ}\left(z\right)exp\left(-\frac{2z}{{\lambda }_0}\right).$$

(3)

The corresponding electrostatic energy of the charge Q in this configuration acquires the form

$$U_{\mathrm{WOS}}\left(z\right)=-{\int }_z^{\infty }{F}_{\mathrm{WOS}}\left(x\right)dx=-\frac{Q^2}{2{\lambda }_0ϵ}\Gamma \left(-1,\frac{2z}{{\lambda }_0}\right),$$

(4)

where $\Gamma \left(s,x\right)$ is the upper incomplete gamma function. In other words, a charged point-like particle located in the electrolyte at distances exceeding the Debye length ${\lambda }_0$ from the electrode interacts exponentially weaker with it.

Let us face the behavior of a colloidal particle in the vicinity of the interface between a metal and electrolyte. Until the distance from the center of colloidal particle to the interface z noticeably exceeds the Debye length ($z\gg {\lambda }_0$), the latter keeps its integrity and electroneutrality. Approaching the interface ($z<{\lambda }_0$) this complex object loses part of its screening counterions and acquires a finite number of charges. The framework of the Poisson equation with infinite boundary conditions [20] is no longer applicable here. The finite colloidal particle core size $R_0$ serves as the natural cut off of the image force potential singularity at small distances ( $z<R_0$) [25].

In the previous work of the authors [13], the value of the colloidal particles’ surface concentration $N_{\odot }$ was found. This was performed by means of the integration of the difference between the Poisson-Boltzmann distribution of the colloids in the modified (by Oshima, see [25])) $U_{\mathrm{WOS}}\left(z\right)$ potential and their homogeneous density $n_{\odot }$:

$$\begin{array}{cc}{N}_{\odot }=\hfill & n_{\odot }\left\{{\int }_{R_0}^{R_0+{\lambda }_0}\left(exp\left[\frac{Z^2{e}^2\Gamma \left(-1,2+\frac{2R_0}{{\lambda }_0}\right)}{{\lambda }_0{k}_{B}Tϵ}exp\left(-\frac{z-R_0}{{\lambda }_0}\right)\right]-1\right)dz\right.\hfill \\ \hfill & +\left.{\int }_{R_0+{\lambda }_0}^{\infty }\left(exp\left[\frac{Z^2{e}^2}{2{\lambda }_0{k}_{B}Tϵ}\Gamma \left(-1,\frac{2z}{{\lambda }_0}\right)\right]-1\right)dz\right\}.\hfill \end{array}$$

(5)

The conservation of the number of colloidal particles in dispersion implies the condition

$$N=2N_{\odot }·S+n_{\odot }·S·L=const,$$

(6)

where S is the surface of the interface, L is the linear size of the sample, and N is the total number of colloids introduced in the solution. The latter retains its value in the process of mutual adjustment between two colloidal fractions approaching equilibrium.

Definition (5), together with the requirement (6), contains all the necessary information concerning the properties of the $2D$ colloidal fraction in terms of the $3D$ homogeneous density $n_{\odot }$ of colloids with an arbitrary ratio ${\lambda }_0/R_0$. Yet, the value of the charge $0\le e{Z}^{*}\left(z\right)\le eZ$ acquired by a colloidal particle, as a result of the partial lost of counterions from the coat, remains indefinite.

Far from the interface, the colloidal gas is rarefied (the condition (1) is satisfied); the bulk physical characteristics of the colloidal solutions (osmotic pressure [26,27], conductivity [20], and the Seebeck coefficient [13]) were found to be independent of the value of the core structural charge $eZ$. As the density of colloidal particles increases and the criterion (1) approaches its upper limit, the effective charge of the colloidal core enters in the gamble [28].

In turn, in the vicinity of the interface, the colloidal particles are localized at the distances of the order of $R_0$ from it, and in view of their partial loss of the counterions, the role of the effective charge $e{Z}^{*}\left(z\right)$ cannot be ignored at any colloidal concentration $n_{\odot }$.

For further discussion, it is crucial to find the binding energy of the colloidal particle $E_{\odot }$ in the vicinity of the metallic plane. In Ref. [25], Ohshima performed the study of its dependence on the distance to the interface (z) for an arbitrary relation between $R_0$ and ${\lambda }_0$. One can observe from Figure 4 of Ref. [25] that $E_{\odot }\left(z\right)$ remains negative for all z and reaches its minimum when the core of the colloidal particle touches the plane: i.e., $z=R_0$ (see Figure 1b).

The analysis of the binding energy $E_{\odot }$’s dependence on the colloid’s core size, as it can be observed from the Ohshima’s numerical results, demonstrates that this energy depends on $R_0$ much more strongly than it could be expected for the Coulomb interaction of the point charge Q with its electrostatic image ($E_Q=Q^2/2R_0$). This fact can be explained taking into consideration that the acquired by the colloid effective charge $e{Z}^{*}$ itself depends on the value of $R_0$.

Operating in geometrical terms, one can identify $e{Z}^{*}$ with the charge of the spherical segment cut by the plane $z=R_0$ from the screening coat (see Figure 1b). The values of the segment chord a and the corresponding volume $V^{*}$ are determined by (see Figure 1b):

$$a=\sqrt{2{\lambda }_0{R}_0+{\lambda }_0^2},V^{*}=\pi {\lambda }_0^2(R_0+\frac{2{\lambda }_0}{3}).$$

(7)

The corresponding value of the acquiring effective charge is determined by the ratio of $V^{*}$ and the full volume of the counterions coat $\frac{4}{3}[{(R_0+{\lambda }_0)}^3-R_0^3]$ (see Figure 1a). Therefore, indeed, in our simple geometric model, the acquired effective charge $e{Z}^{*}$ depends on the colloid core radius:

$$e{Z}^{*}=eZ\frac{(3R_0+2{\lambda }_0){\lambda }_0}{4[3R_0^2+3R_0{\lambda }_0+{\lambda }_0^2]},$$

(8)

and the binding energy takes form:

$$E_{\odot }=-\frac{e^2{Z}^{*2}}{2ϵR_0}=-\frac{e^2{Z}^2}{32ϵR_0}\frac{{(3R_0+2{\lambda }_0)}^2{\lambda }_0^2}{{[3R_0^2+3R_0{\lambda }_0+{\lambda }_0^2]}^2}.$$

(9)

This expression demonstrates that the binding energy of the large colloid ($R_0\gg {\lambda }_0$) in the vicinity of the metallic plane decreases with the increase of its size much more rapidly than for the point charge (compare $E_{\odot }\sim R_0^{-3}$ and $E_Q\sim R_0^{-1}$).

One can observe that the Debye length enters in the binding energy (Equation (9)) in the form of the dimensionless parameter ${\lambda }_0/R_0$, exactly like it appears in the Ohshima’s theory [25]. It is important to stress the independence of ${\lambda }_0$ on the value of the structural charge over a wide range of $eZ$.

To confirm the correctness of our model, we calculated $E_{\odot }\left(R_0\right)$ according to Equation (9) in the region $R_0\le {\lambda }_0$ and found good agreement with the results of Oshima’s numerical analysis for three values: $R_0=0.1{\lambda }_0;0.5{\lambda }_0;1.0{\lambda }_0$ (see Figure 2). Extrapolating this equivalence, we also apply below our model for the range of colloid core sizes exceeding the Debye length: $R_0\ge {\lambda }_0$.

The surface concentration $N_{\odot }$ of colloidal particles in this interface layer can be evaluated by equating the corresponding chemical potential with that of one of the colloids in bulk

$${\mu }_s={\mu }_b.$$

(10)

Let us imagine the box with the face surface S and the height $R_0+{\lambda }_0$, built at the interface. First, let us fill it with the colloidal particles’ gas without electrostatic interaction with the metallic semi-space (its density will be $n_{\odot }$). The corresponding chemical potential ${\mu }_b$ of the colloidal particle in the approximation of a weak electrolyte is determined by the total number of particles in the box [19]:

$${\mu }_b=k_{B}Tln\left[2n_{\odot }·S·(R_0+{\lambda }_0)\right]+{\psi }_b(P,T),$$

(11)

where ${\psi }_b(P,T)$ is some function of pressure and temperature (by means of the factor 2 under the logarithm, we took into account the availability of the two electrodes). Now, let us switch on the electrostatic interactions. The surface concentration of the colloidal particles will become $N_{\odot }$, and consequently the chemical potential ${\mu }_s$ of the particle localized in the interface layer can be written as

$${\mu }_s=k_{B}Tln\left(2N_{\odot }·S\right)+{\psi }_s(P,T),$$

(12)

with ${\psi }_s(P,T)$ as another function of pressure and temperature. Comparing Equations (11) and (12) and recognizing that the difference of the additive functions is determined by the colloidal particle binding energy in the interface layer (${\psi }_s(P,T)-{\psi }_b(P,T)=E_{\odot }$), one finds:

$$N_{\odot }=n_{\odot }(R_0+{\lambda }_0)exp\left(\frac{|E_{\odot }|}{k_{B}T}\right).$$

(13)

By the sign $|...|$ we stressed that the binding energy $E_{\odot }$ is negative (see Equation (9)), i.e., the argument in the activation exponent is positive. One can see that the Equation (13) qualitatively resembles the cited above relation (5), yet in the former we have succeeded in avoiding cumbersome integration. Let us recall that all these considerations were performed with the assumption $R_0\ge {\lambda }_0$.

The normalization relation (6) between $N_{\odot }$ and $n_{\odot }$ allows one to track down the process of filling the interface layer by partially undressing colloidal particles as their number in the cuvette increases (for instance, such a process occurs at the beginning of the steady stage of the Seebeck effect in [4,13]). One can see that Equations (10)–(13) confirm the observed saturation effect ($N_{\odot }\left(N\right)\to const$).

3. Determination of the Effective Colloidal Charge

As it was already mentioned in the Introduction, the structural charge $eZ$ is the important characteristic of the solution containing the stabilized nanoparticles. Yet, the study of its bulk properties hardly allows one to determine this physical value. Indeed, the equation of the state of the $3D$ colloidal gas relates the corresponding osmotic pressure $P_b$ to the dimensionless concentration $\varphi =n_{\odot }{V}_{\odot }$ [26,27]:

$$\frac{P_b\left(\varphi \right)V_{\odot }}{k_{B}T\varphi }=\frac{1+{\varphi }^{*}+{\varphi }^{*2}-{\varphi }^{*3}}{{\left(1-{\varphi }^{*}\right)}^3}.$$

(14)

Here, $V_{\odot }=\frac{4}{3}\pi R_0^3$ is the volume of the colloidal particle and ${\varphi }^{*}=\varphi {\left(1+{\lambda }_0/R_0\right)}^3$ is the effective concentration accounting for the screening coat. One can observe that the structural charge $eZ$ does not enter in Equation (14), as in its derivation the interaction between the colloidal particles was considered in the solid spheres’ approximation.

The situation turns out to be quite different for the equation of state of the $2D$ colloidal gas localized in the interface layer. The acquired effective charge $e{Z}^{*}$ can be determined relating the concentrations $N_{\odot }$ to the observable on the experiment osmotic pressure $P_s$ by means of the virial expansion. As it was discussed above, here, the colloids form the dipoles with their electrostatic images. These dipoles are oriented perpendicularly to the interface plane and hence, repel each other. It is essential that the potential energy of this interaction is positive and can be presented as a function of the distance between their centers [24]:

$$U\left(r\right)=\frac{8R_0^2{Z}^{*2}{e}^2}{ϵr^3}.$$

(15)

In this case, in full agreement to the virial expansion theory [19], the corresponding osmotic pressure $P_s$ is determined by the formula explicitly accounting for the interaction effects:

$$\begin{array}{c}\hfill P_s=N_{\odot }T\left\{1+\frac{N_{\odot }}{2}\int \left[1-exp\left(-\frac{8e^2{R}_0^2{Z}^{*2}}{ϵr^3{k}_{B}T}\right)\right]dS\right\},\end{array}$$

(16)

where $dS=2\pi rdr$. The last integral can be easily calculated:

$$\begin{array}{ccc}{P}_s\hfill & =\hfill & N_{\odot }{k}_{B}T\left\{1+\frac{4\pi N_{\odot }}{3}{\left[\frac{e^2{R}_0^2{Z}^{*2}}{ϵk_{B}T}\right]}^{2/3}{\int }_0^{\infty }\left[1-e^{-y}\right]\frac{dy}{y^{5/3}}\right\}\hfill \\ \hfill & \approx \hfill & N_{\odot }{k}_{B}T\left[1+\frac{16\pi N_{\odot }}{3}{\left(\frac{e^2{R}_0^2{Z}^{*2}}{ϵk_{B}T}\right)}^{2/3}\right],\hfill \end{array}$$

(17)

where the value of the integral is $4.01$. Hence, the measurable deviation of the $2D$ osmotic pressure $\Delta P_s$ from its ideal value $P_{s0}=N_{\odot }{k}_{B}T$ allows one to determine the value of the acquired effective charge of the colloidal particle ($e{Z}^{*}$) and consequently to restore the value of the structural charge of its core in the bulk:

$$eZ=\frac{2(3R_0^2+3R_0{\lambda }_0+{\lambda }_0^2)}{R_0{\lambda }_0(3R_0+2{\lambda }_0)}{\left(\frac{\Delta P_s}{P_s}\right)}^{3/4}\frac{{\left(ϵk_{B}T\right)}^{1/2}}{{\left(\pi N_{\odot }\right)}^{3/4}}.$$

(18)

According to the Ref. [8], an alternating external electric field $E_{\perp }\left(\omega \right)$, applied perpendicularly to the metal–electrolyte interface, modulates the interaction between the forming $2D$ gas colloids. Looking at Equation (17) one recognizes that the compressibility of the $2D$ colloidal gas should also oscillate with the same frequency $\omega$, following the perturbing electric field $E_{\perp }\left(\omega \right)$. As a consequence, one should expect the existence of the parametric resonance for acoustic waves propagating along the metal–electrolyte interface in the interacting $2D$ gas of the colloidal particles.

Indeed, the density perturbation $\delta N_{\odot }\left(T\right)$ obeys the wave equation

$$\frac{{\partial }^2\delta N_{\odot }}{{\partial }^{2}t}-S^2\Delta \delta N_{\odot }=0,$$

(19)

with $S^2=\partial P_s\left(\omega \right)/\partial {\rho }_{\odot }$, where ${\rho }_{\odot }=M_{\odot }{N}_{\odot }\left(T\right)$, and $P_s$ is determined by Equation (17). The parametric resonance in the two-dimensional oscillations of the colloids’ density (an analogue of sound waves in air) arises when the doubled frequency of the electric field $2\omega$ coincides with one of the eigen-frequencies of Equation (19).

4. Discussion

We demonstrated that the colloidal particles, being globally neutral in the electrolyte bulk thanks to their layer of counterions, acquire the finite charge approaching the metal–electrolyte interface. This circumstance noticeably effects the major part of the colloidal system properties.

A. Localization of the colloidal particles at the electrolyte–metal interface is easily observable visually [6,7,8,9]. The analysis of the activation temperature dependence of their surface concentration $N_{\odot }\left(T\right)$ at a fixed value of the colloidal particles number N in solution (see Equations (6) and (13) allows one to extract the value of the localization energy $E_{\odot }$ and, consequently, the value of the colloidal particle effective charge $e{Z}^{*}$.

B. The virial equation of the state of a dilute colloidal solution (14) lies in the basis of the DLVO theory. It is also used for the analysis of the hydrodynamic fluctuations of various origins [29]. The consequences of its non-linearity in the $3D$ case find their experimental confirmation in the measurements of the form-factor and its relationship to the compressibility of the gas [27]. Considerable progress is achieved in the studies of the wave scattering at a rough surface of two dielectrics, which present a special request for radio physics (this is also wave scattering at the surface of seas and oceans; see, for example [30]). Knowledge of the $2D$ equation of state (17) will allow one to relate the intensity of light scattered by the interface to the properties of the rough metal–electrolyte boundary (roughness is associated with the presence of charged colloidal particles on a flat metal boundary). Such kinds of experiments studying the light scattering on surfaces with $2D$ colloids are still lacking.

C. The internal electric field in the bulk of a large enough ($2d\gg {\lambda }_0$) flat electrolyte capacitor is screened by the ions. The non-zero field occurs only within the Debye layers (of the thickness ${\lambda }_0$) along the capacitor plates (see Ref. [21]); namely, the latter determines the capacitance of the device. According to Figure 3, the colloidal particles of the dimensions ${\lambda }_0\le R_0\ll d$, localized at the metallic boundary, pierce the holes of the radius $a/2$ (see Equation (7)) in a flat Debye layer providing an anomalous value of the capacitance $C_0$. As a consequence, the capacitance of a capacitor with a $2D$ system of colloids of a density $N_{\odot }$ at the metal–electrolyte boundaries decreases, as

$$\frac{\delta C}{C_0}\approx -\pi a^2{N}_{\odot }/4$$

(20)

which allows one to directly measure the density $N_{\odot }$ and parameter a.

In summary, the discussed phenomenon of the colloidal particle accumulation at the metal–electrolyte interface interestingly diversifies the physics of dilute colloidal solutions. The image forces at the boundaries of an electrolyte noticeably affect the entire range of contact phenomena. For example, their bright manifestation is the electrostatic renormalization of the surface tension in dilute electrolytes, which was studied in detail by the authors of Refs. [11,12]. Other series of phenomena related to the electrostatic image forces are the little explored adsorption of a charged fraction of the electrolyte at a solid boundary with the formation of the double Debye layers [31]. The role of electrostatic forces acting on colloidal particles in thin capillaries with dielectric walls also presents a challenging problem to be investigated.