Climate on the Blanca Massif, Sangre de Cristo Mountains, Colorado, USA, during the Last Glacial Maximum
Abstract
:1. Introduction
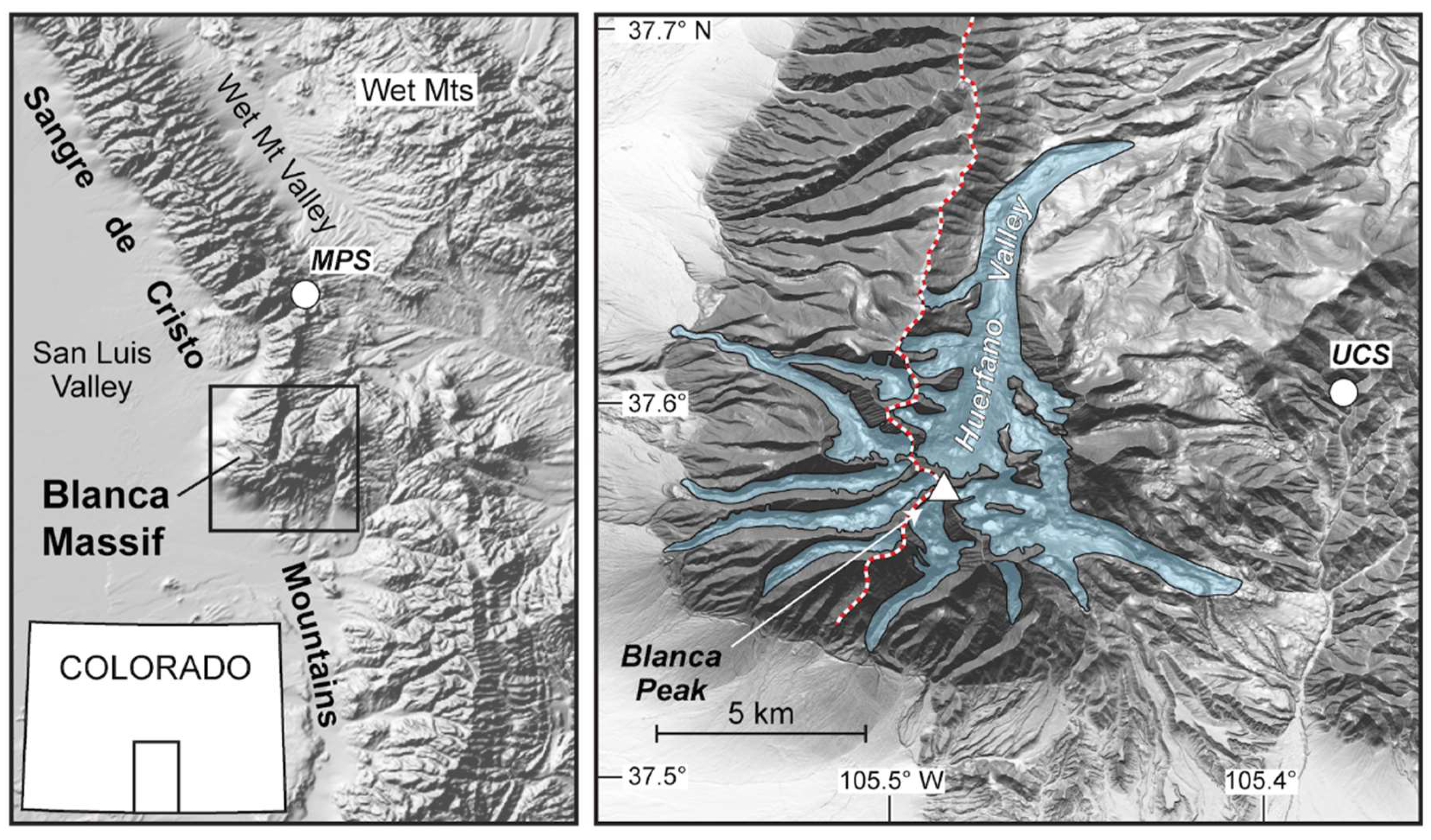
2. Regional Setting
2.1. Geologic and Geomorphic Setting
2.2. Modern Climatology
2.3. Timing of the Local LGM
3. Materials and Methods
3.1. Glacier Reconstruction
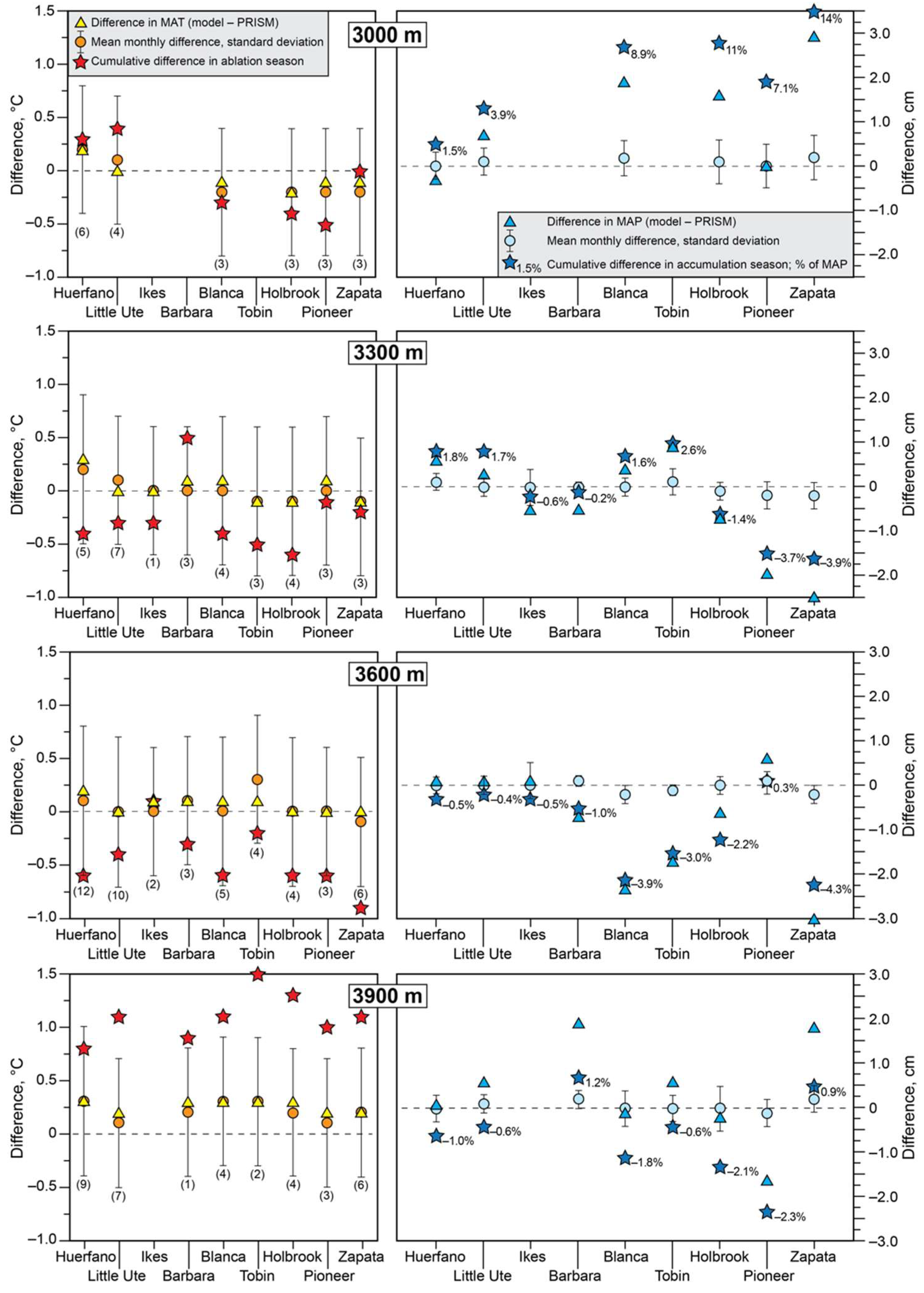
3.2. Temperature-Index Modeling
4. Results
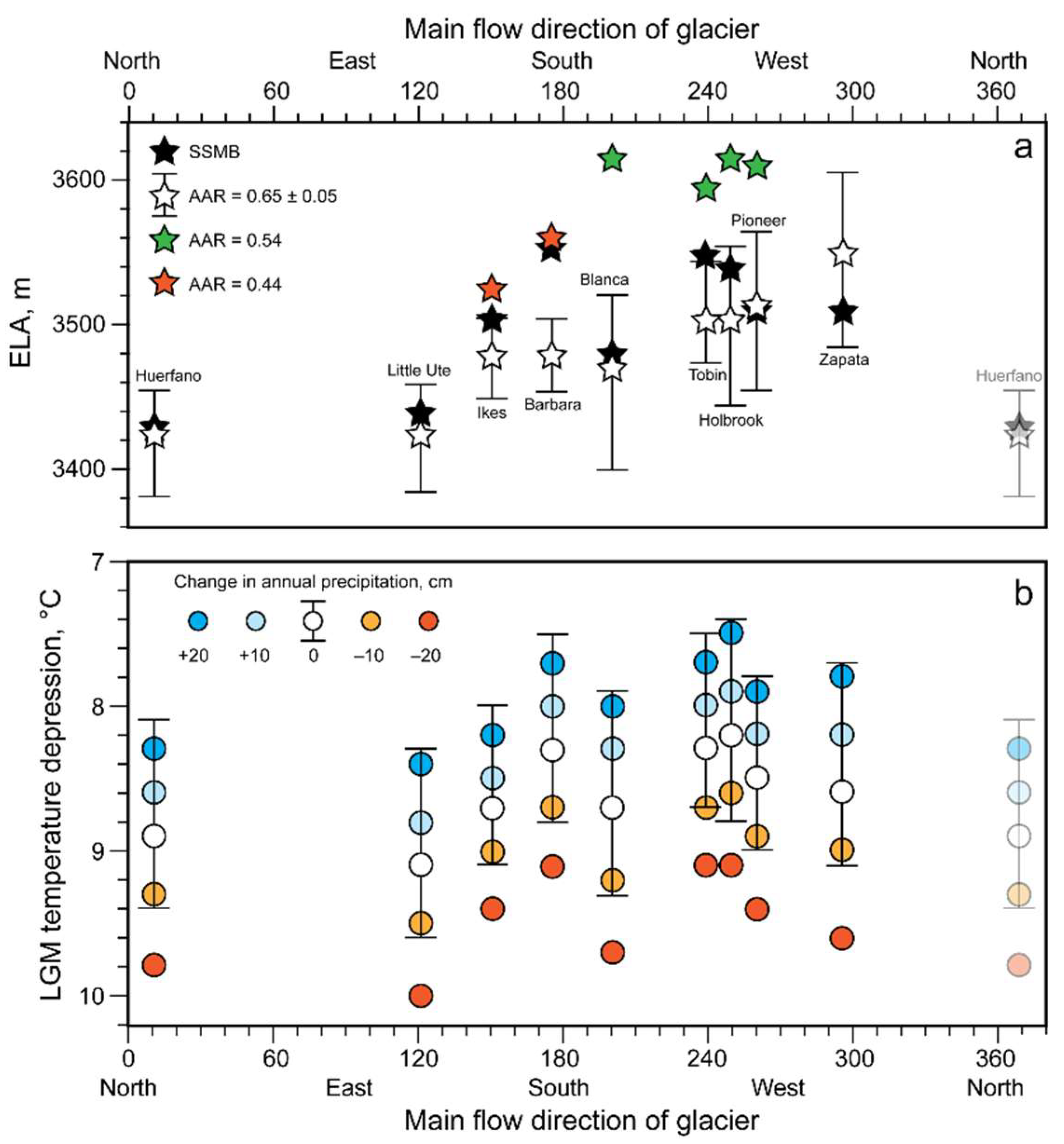
4.1. Glacier Reconstruction and ELA Determination
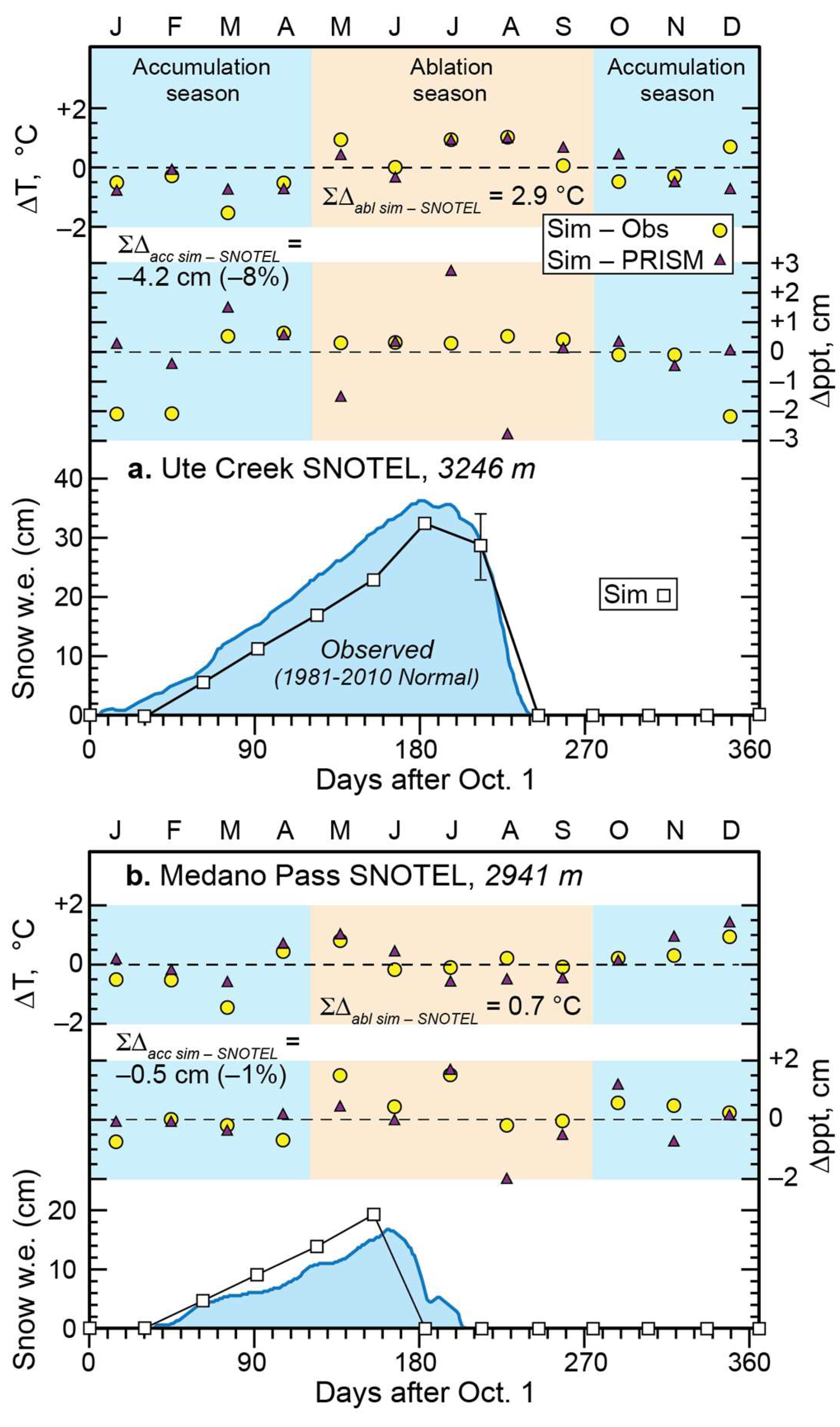
4.2. Temperature-Index Modeling: Model Skill
4.3. Steady-State Mass Balances of Paleoglaciers and Implications for LGM Climate
5. Discussion
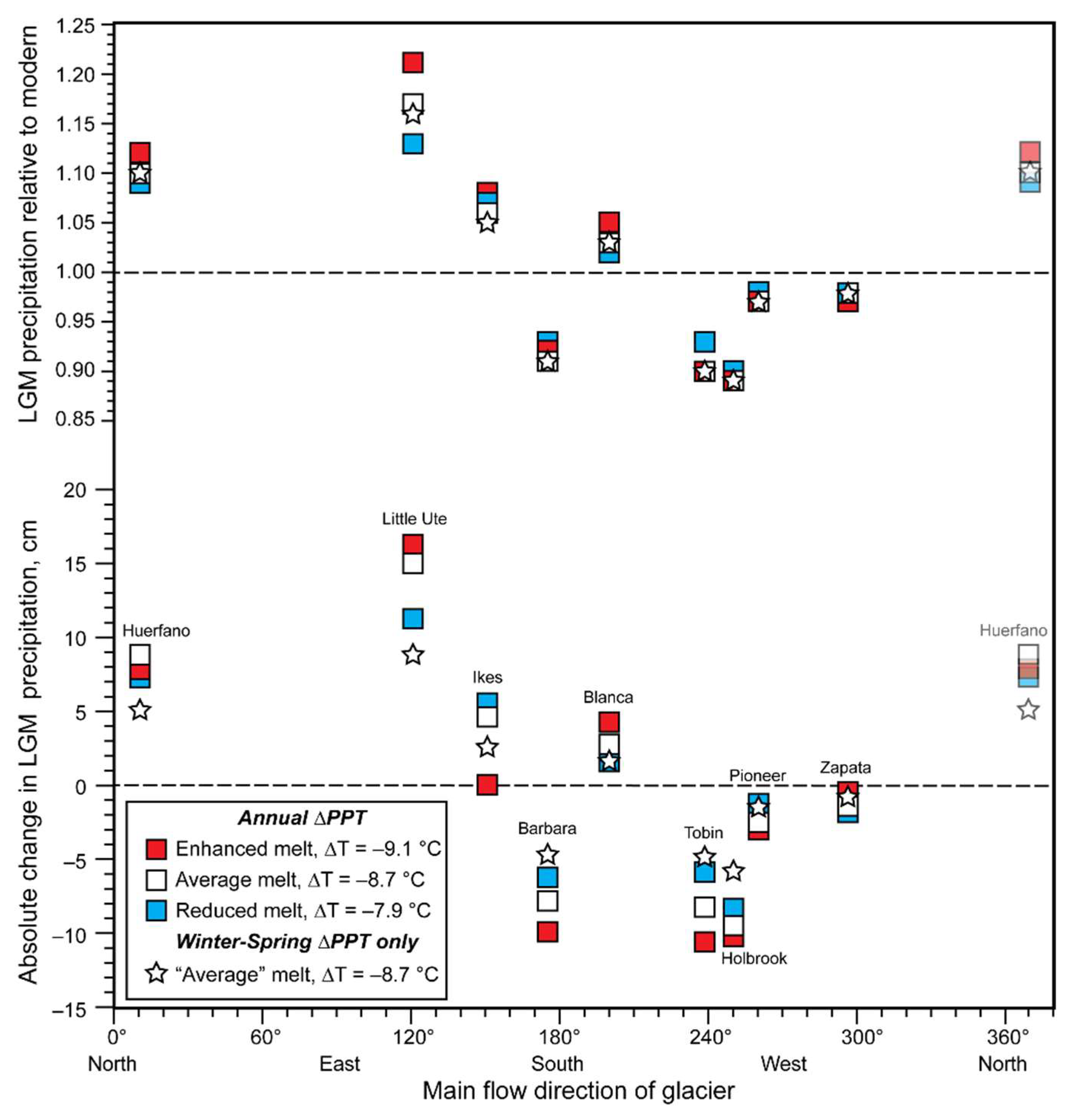
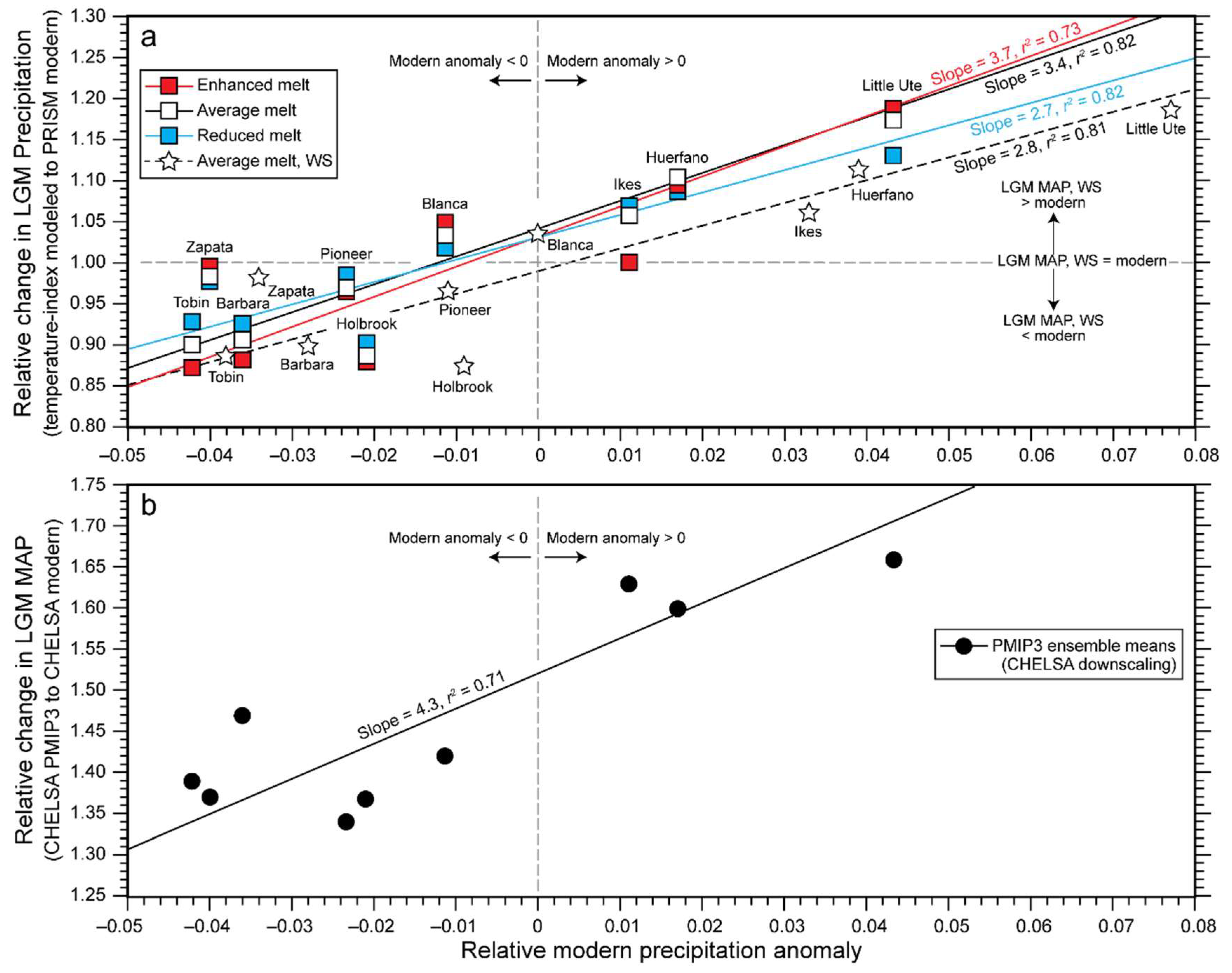
5.1. Directional Dependence of ELAs and Inferred Change of Precipitation during the LGM
5.2. LGM Climate on the Blanca Massif
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Leonard, E.M. Climatic change in the Colorado Rocky Mountains: Estimates based on modern climate at late Pleistocene equilibrium lines. Arct. Alp. Res. 1989, 21, 245–255. [Google Scholar] [CrossRef]
- Leonard, E.M. Modeled patterns of Late Pleistocene glacier inception and growth in the Southern and Central Rocky Mountains, USA: Sensitivity to climate change and paleoclimatic implications. Quat. Sci. Rev. 2007, 26, 2152–2166. [Google Scholar] [CrossRef]
- Refsnider, K.A.; Brugger, K.A.; Leonard, E.M.; McCalpin, J.P.; Armstrong, P.P. Last glacial maximum equilibrium-line altitude trends and precipitation patterns in the Sangre de Cristo Mountains, southern Colorado, USA. Boreas 2009, 38, 663–678. [Google Scholar] [CrossRef]
- Brugger, K.A. Climate in the southern Sawatch Range and Elk Mountains, Colorado, USA, during the Last Glacial Maximum: Inferences using a simple degree-day model. Arct. Antarct. Alp. Res. 2010, 42, 164–178. [Google Scholar] [CrossRef] [Green Version]
- Dühnforth, M.; Anderson, R.S. Reconstructing the glacial history of green lakes valley, North Boulder Creek, Colorado Front Range. Arct. Antarct. Alp. Res. 2011, 43, 527–542. [Google Scholar] [CrossRef]
- Leonard, E.M.; Laabs, B.J.C.; Plummer, M.A.; Kroner, R.K.; Brugger, K.A.; Spiess, V.M.; Refsnider, K.A.; Xia, Y.; Caffee, M.W. Late Pleistocene glaciation and deglaciation in the Crestone Peaks area, Sangre de Cristo Mountains, USA-chronology and paleoclimate. Quat. Sci. Rev. 2017, 158, 127–144. [Google Scholar] [CrossRef] [Green Version]
- Brugger, K.A.; Laabs, B.; Reimers, A.; Bensen, N. Late Pleistocene glaciation in the Mosquito Range, Colorado, USA: Chronology and climate. J. Quat. Sci. 2019, 34, 187–202. [Google Scholar] [CrossRef]
- Brugger, K.A.; Ruleman, C.A.; Caffee, M.W.; Mason, C.C. Climate during the Last Glacial Maximum in the Northern Sawatch Range, Colorado, USA. Quaternary 2019, 2, 36. [Google Scholar] [CrossRef] [Green Version]
- Oster, J.L.; Ibarra, D.E.; Winnick, M.J.; Maher, K. Steering of westerly storms over western North America at the Last Glacial Maximum. Nat. Geosci. 2015, 8, 201–205. [Google Scholar] [CrossRef]
- Lyle, M.; Heusser, L.; Ravelo, C.; Yamamoto, M.; Barron, J.; Diffenbaugh, N.S.; Herbert, T.; Andreasen, D. Out of the Tropics: The Pacific, Great Basin Lakes, and the late Pleistocene water cycle in the western United States. Science 2012, 337, 1629–1633. [Google Scholar] [CrossRef] [Green Version]
- Lora, J.M.; Mitchell, J.L.; Tripati, A.E. Abrupt reorganization of North Pacific and western North American climate during the last glaciation. Geophys. Res. Lett. 2016, 43, 11796–11804. [Google Scholar] [CrossRef]
- Lora, J.M.; Mitchell, J.L.; Risi, C.; Tripati, A.E. North Pacific atmospheric rivers and their influence on western North America at the Last Glacial Maximum. Geophys. Res. Lett. 2017, 44, 1051–1059. [Google Scholar] [CrossRef]
- Ibarra, D.E.; Oster, J.L.; Winnick, M.J.; Caves Rugenstein, J.K.; Byrne, M.; Chamberlain, C.P. Warm and cold wet states in the western United States during the Pliocene-Pleistocene. Geology 2018, 46, 355–358. [Google Scholar] [CrossRef]
- Morrill, C.; Lowry, D.P.; Hoell, A. Thermodynamic and dynamic causes of pluvial conditions during the last glacial maximum. Geophys. Res. Lett. 2018, 45, 335–345. [Google Scholar] [CrossRef]
- Hudson, A.M.; Hatchett, B.J.; Quade, J.; Boyle, D.P.; Bassett, S.D.; Ali, G.; De los Santos, M.G. North-south dipole in winter hydroclimate in the western United States during the last glaciation. Sci. Rep. 2019, 9, 4826. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lora, J.M.; Ibarra, D.E. The North American hydrologic cycle through the last deglaciation. Quat. Sci. Rev. 2019, 226, 105991. [Google Scholar] [CrossRef]
- Tulenko, J.P.; Caffee, W.; Schweinsberg, A.D.; Briner, J.P.; Leonard, E.M. Delayed and rapid deglaciation of alpine valleys in the Sawatch Range, southern Rocky Mountains, USA. Geochronology 2020, 2, 245–255. [Google Scholar] [CrossRef]
- Braconnot, P.; Harrison, S.P.; Kageyama, M.; Bartlein, P.J.; Masson-Delmotte, V.; Abe-Oche, A.; Otto-Bleisner, B.; Zhao, Y. Evaluation of climate models using paleoclimatic data. Nat. Clim. Chang. 2012, 2, 417–424. [Google Scholar] [CrossRef]
- Kageyama, M.; Albani, S.; Braconnot, P.; Harrison, S.P.; Hopcroft, P.O.; Ivanovic, R.F.; Lambert, F.; Marti, O.; Peltier, W.R.; Peterschmitt, J.-Y.; et al. The PMIP4 contribution to CMIP6-Part 4: Scientific objectives and experimental design of the PMIP4-CMIP6 last glacial maximum experiments and PMIP4 sensitivity experiments. Geosci. Model Dev. 2017, 10, 4035–4055. [Google Scholar] [CrossRef] [Green Version]
- Ricketts, J.W.; Kelley, S.A.; Karlstrom, K.E.; Schmandt, B.; Donahue, M.S.; van Wijk, J. Synchronous opening of the Rio Grande rift along its entire length at 25–10 Ma supported by apatite (U-Th)/He and fission-track thermochronology, and evaluation of possible driving mechanisms. GSA Bull. 2016, 128, 397–424. [Google Scholar] [CrossRef]
- Drenth, B.J.; Grauch, V.J.S.; Turner, K.T.; Rodriguez, B.D.; Thompson, R.A.; Bauer, P.W. A shallow rift basin segmented in space and time: The southern San Luis Basin, Rio Grande rift, northern New Mexico, U.S.A. Rocky Mount. Geol. 2019, 54, 97–131. [Google Scholar] [CrossRef] [Green Version]
- Chapin, C.E.; Kelley, S.A.; Cather, S.M. The Rocky Mountain Front, southwestern USA. Geosphere 2014, 10, 1043–1060. [Google Scholar] [CrossRef] [Green Version]
- Lindsey, D.A.; Johnson, B.J.; Andriessen, P.A.M. Laramide and Neogene structure of the Sangre de Cristo Range, south-central Colorado. In Rocky Mountain Foreland Basins and Uplifts; Lowell, J.D., Ed.; Rocky Mountain Association of Geologists: Denver, CO, USA, 1983; pp. 219–228. ISBN 978-0-9339-7905-5. [Google Scholar]
- Lindsey, D.A. The Geologic Story of Colorado’s Sangre de Cristo Range; U.S. Geological Survey: Reston, VA, USA, 2010; 14p.
- Johnstone, S.A.; Hudson, A.M.; Nicovitch, S.; Ruleman, C.A.; Sare, R.M.; Thompson, R.A. Establishing chronologies for alluvial-fan sequences with analysis of high resolution topographic data: San Luis Valley, Colorado, USA. Geosphere 2018, 14, 2487–2504. [Google Scholar] [CrossRef]
- Nicovitch, S. Construction and Modification of Debris-Flow Alluvial Fans as Captured in Geomorphic and Sedimentary Record. Ph.D. Thesis, Montana State University, Bozeman, MT, USA, 2020; p. 283. [Google Scholar]
- Siebenthal, C.E. Notes on glaciation in the Sangre de Cristo Range, Colorado. J. Geol. 1907, 15, 15–22. [Google Scholar] [CrossRef]
- Glaciers of the American West. Available online: https://glaciers.us/glaciers.research.pdx.edu/glaciers-colorado-2.html (accessed on 24 July 2021).
- Daly, C.; Halbleib, M.; Smith, J.I.; Gibson, W.P.; Doggett, M.K.; Taylor, G.H.; Curtis, J.; Pasteris, P.P. Physiographically sensitive mapping of climatological temperature and precipitation across the coterminous United States. Int. J. Climatol. 2008, 28, 2031–2064. [Google Scholar] [CrossRef]
- Higgins, R.W.; Yao, Y.; Wang, X.L. Influence of the North American Monsoon System on the U.S. summer precipitation regime. J. Clim. 1997, 10, 2600–2622. [Google Scholar] [CrossRef]
- Collins, D.L.; Doesken, N.J.; Stanton, W.P. Colorado floods and droughts. National Water Summary 1988–89: Hydrologic events and floods and droughts. Water Sup. Pap. 1991, 2375, 207–214. [Google Scholar] [CrossRef]
- Gutmann, E.D.; Rasmussen, R.M.; Lui, C.; Ikeda, K.; Gochis, D.J.; Clark, M.P.; Dudhia, J.; Thompson, G. A comparison of statistical and dynamical downscaling of winter precipitation over complex terrain. J. Clim. 2012, 25, 262–281. [Google Scholar] [CrossRef] [Green Version]
- Boatman, J.F.; Reinking, R.F. Synoptic and mesoscale circulation and precipitation mechanisms in shallow upslope storms over the western high plains. Mon. Weather Rev. 1984, 112, 1725–1744. [Google Scholar] [CrossRef] [Green Version]
- Mock, C.J. Climatic controls and spatial variation of precipitation in the western United States. J. Clim. 1996, 9, 1111–1125. [Google Scholar] [CrossRef] [Green Version]
- Brugger, K.A. Cosmogenic 10Be and 36Cl ages from late Pleistocene terminal moraine complexes in the Taylor River drainage basin, central Colorado, U.S.A. Quat. Sci. Rev. 2007, 26, 494–499. [Google Scholar] [CrossRef]
- Young, N.E.; Briner, J.P.; Leonard, E.M.; Licciardi, J.M.; Lee, K. Assessing climatic and non-climatic forcing of Pinedale glaciation and deglaciation in the western United States. Geology 2011, 39, 171–174. [Google Scholar] [CrossRef] [Green Version]
- Schweinsberg, A.D.; Briner, J.P.; Licciardi, J.M.; Schroba, R.R.; Leonard, E.M. Cosmogenic 10Be exposure dating of Bull Lake and Pinedale moraine sequences in the upper Arkansas River valley Colorado Rocky Mountains, USA. Quat. Res. 2020, 97, 125–139. [Google Scholar] [CrossRef]
- McCalpin, J. Quaternary geology and neotectonics of the west flank of the Sangre de Cristo Mountains, south-central Colorado. Colo. Sch. Mines Q. 1982, 77, 1–97. [Google Scholar]
- Johnson, B.R.; Bruce, R.M. Reconnaissance Geologic Map of Parts of the Twin Peaks and Blanca Peak Quadrangles, Alamosa, Costilla, and Huerfano Counties, Colorado; Miscellaneous Field Studies Map 2169; USGS: Reston, VA, USA, 1991. [CrossRef]
- Cuffey, K.M.; Paterson, W.S.B. The Physics of Glaciers, 4th ed.; Elsevier: Boston, MA, USA, 2010. [Google Scholar]
- Nye, J.F. The flow of a glacier in a channel of rectangular, elliptic or parabolic cross-section. J. Glaciol. 1965, 5, 661–690. [Google Scholar] [CrossRef] [Green Version]
- Bindschadler, R.; Harrison, W.D.; Raymond, C.F.; Crossen, R. Geometry and dynamics of a surge-type glacier. J. Glaciol. 1977, 18, 181–194. [Google Scholar] [CrossRef] [Green Version]
- Hock, R. Glacier melt: A review of processes and their modelling. Prog. Phys. Geogr. 2005, 29, 362–391. [Google Scholar] [CrossRef]
- Yang, W.; Guo, X.; Yao, T.; Yang, K.; Zhoa, L.; Li, S.; Zhu, M. Summertime surface energy budget and ablation modeling in the ablation zone of a maritime Tibetan glacier. J. Geophys. Res. 2011, 116, D14116. [Google Scholar] [CrossRef]
- Vincent, C.; Six, D. Relative contribution of solar radiation and temperature in enhanced temperature-index melt models from a case study at Glacier de Saint-Sorlin, France. Ann. Glaciol. 2013, 54, 11–17. [Google Scholar] [CrossRef] [Green Version]
- Réveillet, M.; Vincent, C.; Six, D.; Rabatel, A. Which empirical model is best suited to simulate glacier mass balances? J. Glaciol. 2017, 63, 39–54. [Google Scholar] [CrossRef] [Green Version]
- Gabbi, J.; Carenzo, M.; Pellicciotto, F.; Bauder, A.; Funk, M. A comparison of empirical and physically based glacier surface melt models for long-term simulation of glacier response. J. Glaciol. 2014, 60, 1140–1154. [Google Scholar] [CrossRef] [Green Version]
- Pellicciotti, F.; Brock, B.; Strasser, U.; Burlando, P.; Funk, M.; Corripio, J. An enhanced temperature-index glacier melt model including a shortwave radiation balance: Development and testing for Haut Glacier d’Arolla, Switzerland. J. Glaciol. 2005, 175, 573–587. [Google Scholar] [CrossRef]
- Matthews, T.; Hodgkins, R.; Wilby, R.L.; Gudmundsson, S.; Pálsson, F.; Björnsson, H.; Carr, S. Conditioning temperature-index model parameters on synoptic weather types for glacier melt simulations. Hydrol. Process. 2015, 29, 1027–1045. [Google Scholar] [CrossRef] [Green Version]
- Porter, S.C. Equilibrium-line altitudes of late Quaternary glaciers in the Southern Alps, New Zealand. Quat. Res. 1975, 5, 27–47. [Google Scholar] [CrossRef]
- Meierding, T.C. Late Pleistocene glacial equilibrium-line altitudes in the Colorado Front Range: A comparison of methods. Quat. Res. 1982, 18, 289–310. [Google Scholar] [CrossRef]
- Kern, Z.; László, P. Size specific steady-state accumulation-area ratio: An improvement for equilibrium-line estimation of small paleoglaciers. Quat. Sci. Rev. 2010, 29, 2781–2787. [Google Scholar] [CrossRef]
- Molotch, N.P.; Bales, R.C. Scaling snow observations from the point to the grid element: Implications for observational netwtwork design. Water Resour. Res. 2005, 41, W11421. [Google Scholar] [CrossRef] [Green Version]
- Rasmussen, R.; Baker, B.; Kochendorfer, J.; Myers, T.; Landolt, S.; Fisher, A.; Black, J.; Theriault, J.; Kucera, P.; Gochis, D.; et al. The NOAA/FAA/NCAR winter precipitation test bed: How well are we measuring snow. Bull. Am. Meteor. Soc. 2012, 93, 811–829. [Google Scholar] [CrossRef] [Green Version]
- Meyer, J.D.D.; Jin, J.; Wang, S.-Y. Systematic patterns of the inconsistency between snow water equivalent and accumulated precipitation as reported by the snowpack telemetry network. J. Hydromet. 2012, 13, 1970–1976. [Google Scholar] [CrossRef]
- Oyler, J.W.; Dobrowski, S.Z.; Ballantyne, A.P.; Klene, A.E.; Running, S.W. Artificial amplification of warming trends across the mountains of the western United States. Geophys. Res. Lett. 2014, 42, 153–161. [Google Scholar] [CrossRef] [Green Version]
- Strachan, S.; Daly, C. Testing the daily PRISM air temperature model on semiarid mountain slopes. J. Geophys. Res. Atmos. 2017, 122, 5697–5715. [Google Scholar] [CrossRef]
- Ma, C.; Fassnacht, S.R.; Kampf, S.K. How temperature sensor change affects warming trends and modeling: An evaluation across the state of Colorado. Water Resour. Res. 2019, 55, 9748–9764. [Google Scholar] [CrossRef]
- Johnson, J.B.; Marks, D. The detection and correction of snow water equivalent pressure sensor errors. Hydrol. Process. 2004, 18, 3513–3525. [Google Scholar] [CrossRef]
- Kirkham, J.D.; Koch, I.; Saloranta, T.M.; Litt, M.; Stigter, E.E.; Møen, K.; Thapa, A.; Melvold, K.; Immerzeel, W.W. Near real-time measurement of snow water equivalent in the Nepal Himalayas. Front. Earth Sci. 2019, 7, 177. [Google Scholar] [CrossRef] [Green Version]
- Brugger, K.A. Late Pleistocene climate inferred from the Taylor River glacier complex, southern Sawatch Range, Colorado. Geomorphology 2006, 75, 318–329. [Google Scholar] [CrossRef] [Green Version]
- Lowry, D.P.; Morrill, C. Is the Last Glacial Maximum a reverse analog for future hydroclimate changes in the America? Clim. Dyn. 2019, 52, 4407–4427. [Google Scholar] [CrossRef]
- Tsagris, M.; Athineou, G.; Sajib, A.; Amson, E.; Waldstein, M.J. Directional: A Collection of R Functions for Directional Data Analysis; R Package Version 4.9. Available online: https://CRAN.R-project.org/package=Directional (accessed on 2 May 2020).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013; Available online: http://www.R-project.org/ (accessed on 7 December 2014).
- Cornelissen, G. Cosinor-based rhythmometry. Theor. Biol. Med. Model. 2014, 11, 16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karger, D.N.; Conrad, O.; Böhner, J.; Kawohl, T.; Kreft, H.; Soria-Auza, R.W.; Zimmermann, N.E.; Linder, H.P.; Kessler, M. Climatologies at high resolution for the earth’s land surface areas. Sci. Data 2017, 4, 170122. [Google Scholar] [CrossRef] [Green Version]
- Karger, D.N.; Conrad, O.; Böhner, J.; Kawohl, T.; Kreft, H.; Soria-Auza, R.W.; Zimmermann, N.E.; Linder, H.P.; Kessler, M. Data from: Climatologies at high resolution for the earth’s land surface areas. Datadryad 2018. [Google Scholar] [CrossRef]
- Beck, H.E.; Wood, E.F.; McVicar, T.R.; Zambrano-Bigiarini, M.; Alvarez-Garreton, C.; Baez-Villanueva, O.M.; Sheffield, J.; Karger, D.N. Bias Correction of Global High-Resolution Precipitation Climatologies Using Streamflow Observations from 9372 Catchments. J. Clim. 2020, 33, 1299–1315. [Google Scholar] [CrossRef] [Green Version]
- Oster, J.L.; Weisman, I.E.; Sharp, W.D. Multi-proxy stalagmite records from northern California reveal dynamic patterns of regional hydroclimate over the last glacial cycle. Quat. Sci. Rev. 2020, 241, 106411. [Google Scholar] [CrossRef]
- Bhattacharya, T.; Tierney, J.E.; DiNezio, P. Glacial reduction of the North American monsoon via surface cooling and atmospheric ventilation. Geophys. Res. Lett. 2017, 44, 5113–5122. [Google Scholar] [CrossRef] [Green Version]
- Lachniet, M.S.; Asmerom, Y.; Bernal, J.P.; Polyak, V.J.; Vazquez-Selem, L. Orbital pacing and ocean circulation-induced collapses of the Mesoamerican monsoon over the past 22,000 y. Proc. Natl. Acad. Sci. USA 2013, 110, 9255–9260. [Google Scholar] [CrossRef] [Green Version]
- Lora, J.M. Components and mechanisms of hydrologic cycle changes over North America at the Last Glacial Maximum. J. Clim. 2018, 31, 7035–7051. [Google Scholar] [CrossRef]
- Varuolo-Clarke, A.M.; Reed, K.A.; Medeiros, B. Characterizing the North American monsoon in the Community Atmospheric Model: Sensitivity to resolution and topography. J. Clim. 2019, 32, 8355–8372. [Google Scholar] [CrossRef]
- COHMAP Members. Climatic changes of the last 18,000 years: Observations and model simulations. Science 1988, 241, 1043–1052. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.-J.; Crowley, T.J.; Erickson, D.J.; Govindasamy, B.; Duffy, P.B.; Lee, B.Y. High-resolution climate simulation of the last glacial maximum. Clim. Dyn. 2008, 31, 1–16. [Google Scholar] [CrossRef]
- Wang, N.; Jiang, D.; Lang, X. Northern westerlies during the Last Glacial Maximum: Results from CMIP5 simulations. J. Clim. 2018, 31, 1135–1153. [Google Scholar] [CrossRef]
- Hu, Y.; Xia, Y.; Liu, Z.; Wang, Y.; Lu, Z.; Wang, T. Distorted Pacific-North American teleconnections at the Last Glacial Maximum. Clim. Past. 2020, 16, 199–209. [Google Scholar] [CrossRef] [Green Version]
- Brocklehurst, S.H.; MacGregor, K.R. The role of wind in the evolution of glaciated mountain ranges: Field observations and insights from numerical modelling. AGU Fall Meet. Abstr. 2005, 2005, H51C-0390. [Google Scholar]
- Outcalt, S.I.; McPhail, D.S. A Survey of Neoglaciation in the Front Range of Colorado; University of Colorado Studies Series in Earth Science: Boulder, CO, USA, 1965; Volume 4, p. 124. [Google Scholar]
- Hoffman, M.J.; Fountain, A.G.; Achuff, J.M. 20th-century variations in area of cirque glaciers and glacierets, Rocky Mountain National Park, Rocky Mountains, Colorado, USA. Ann. Glaciol. 2007, 46, 349–354. [Google Scholar] [CrossRef] [Green Version]





| Glacier | Area km2 | Length, km * | Average Ice Thickness, m *,† | Maximum Ice Thickness m *,† | Driving Stresses, kPa ** | AAR-Derived ELA, m † | ||
|---|---|---|---|---|---|---|---|---|
| AAR = 0.65 | AAR = 0.54 | AAR = 0.44 | ||||||
| Huerfano | 17.84 | 11.9 | 150 | 250 | 89–121 | 3425 | na | na |
| Little Ute | 9.32 | 8.1 | 70 | 130 | 72–138 | 3425 | na | na |
| Ikes | 0.84 | 2.7 | 25 | 55 | 52–88 | 3480 | na | 3525 |
| Barbara | 0.65 | 2.3 | 20 | 55 | 76–150 | 3480 | na | 3560 |
| Blanca | 3.06 | 6.2 | 60 | 130 | 99–148 | 3470 | 3615 | na |
| Tobin | 1.53 | 4.2 | 35 | 80 | 46–142 | 3505 | 3590 | na |
| Holbrook | 3.63 | 7.4 | 60 | 125 | 56–116 | 3505 | 3615 | na |
| Pioneer | 2.45 | 5.9 | 55 | 100 | 64–109 | 3515 | 3610 | na |
| Zapata | 5.46 | 7.4 | 55 | 100 | 51–101 | 3550 | na | na |
| Model Parameter | Temperature Depression, °C | Steady-State ELA, m * | ||||||
|---|---|---|---|---|---|---|---|---|
| Precipitation Change (F), cm | 0 | 10 | 20 | −10 | −20 | |||
| Melt Factors (mƒ) Snow/Ice | 0.0045/0.008 | 0.0065/0.010 | 0.0025/0.006 | 0.0045/0.008 | ||||
| m w.e. °C−1 d−1 | (Average Melt) | (Enhanced Melt) | (Reduced melt) | |||||
| Glacier | ||||||||
| Huerfano | 8.9 | 9.4 | 8.1 | 8.6 | 8.3 | 9.3 | 9.8 | 3430 |
| Little Ute | 9.1 | 9.6 | 8.3 | 8.8 | 8.4 | 9.5 | 10 | 3440 |
| Ikes | 8.7 | 9.1 | 8 | 8.5 | 8.2 | 9 | 9.4 | 3505 |
| Barbara | 8.3 | 8.8 | 7.5 | 8 | 7.7 | 8.7 | 9.1 | 3555 |
| Blanca | 8.7 | 9.3 | 7.9 | 8.3 | 8 | 9.2 | 9.7 | 3480 |
| Tobin | 8.3 | 8.7 | 7.5 | 8 | 7.7 | 8.7 | 9.1 | 3555 |
| Holbrook | 8.2 | 8.8 | 7.4 | 7.9 | 7.5 | 8.6 | 9.1 | 3540 |
| Pioneer | 8.5 | 9 | 7.8 | 8.2 | 7.9 | 8.9 | 9.4 | 3510 |
| Zapata | 8.6 | 9.1 | 7.7 | 8.2 | 7.8 | 9 | 9.6 | 3510 |
| Means | 8.6 ± 0.3 | 9.1 ± 0.3 | 7.8 ± 0.3 | 8.3 ± 0.3 | 7.9 ± 0.3 | 9.0 ± 0.3 | 9.5 ± 0.3 | |
| Glacier | Average Melt | Enhanced Melt | Reduced Melt | Average Melt | |
|---|---|---|---|---|---|
| ∆T, °C | 8.6 | 9.1 | 7.8 | 8.6 | |
| mf | 0.0045/0.008 | 0.0065/0.010 | 0.0025/0.006 | 0.0045/0.008 | |
| ∆MAP, cm (%) | ∆MAP, cm (%) | ∆MAP, cm (%) | ∆WS, cm (%) | ||
| Huerfano | 8.7 (10) | 7.9 (9) | 7.2 (9) | 5.1 (10) | |
| Little Ute | 15.0 (17) | 16.2 (19) | 11.3 (13) | 8.8 (16) | |
| Ikes | 4.6 (6) | 0.0 (0) | 5.6 (7) | 2.7 (5) | |
| Barbara | −7.8 (−9) | −9.9 (−12) | −6.2 (−7) | −4.6 (−9) | |
| Blanca | 2.9 (3) | 4.2 (5) | 1.6 (2) | 1.7 (3) | |
| Tobin | −8.2 (−10) | −10.5 (−13) | −5.9 (−7) | −4.8 (−10) | |
| Holbrook | −9.5 (−11) | −10.1 (−12) | −8.3 (−10) | −5.7 (−11) | |
| Pioneer | −2.5 (−3) | −3.0 (−4) | −1.3 (−2) | −1.5 (−3) | |
| Zapata | −1.4 (−2) | −0.4 (0) | −1.9 (−2) | −0.8 (−2) |
| Data Set | Shapiro–Wilk | Circular Correlation | Confidence Interval about Maximum | |||
|---|---|---|---|---|---|---|
| W | p | r2 | p | Lower Bound | Upper Bound | |
| (Compass Directions, °) | ||||||
| AAR-derived ELAs | 0.94 | 0.56 | 0.70 | <0.006 | 227 | 287 |
| SSMB-ELAs | 0.91 | 0.31 | 0.66 | <0.009 | 200 | 255 |
| ∆MAP, average melt | 0.94 | 0.58 | 0.71 | <0.005 | 37 | 90 |
| ∆MAP, enhanced melt | 0.92 | 0.41 | 0.59 | <0.017 | 26 | 93 |
| ∆MAP, reduced melt | 0.94 | 0.68 | 0.73 | <0.004 | 40 | 91 |
| ∆WS, average melt | 0.94 | 0.62 | 0.71 | <0.005 | 37 | 90 |
| Modern anomalies | 0.91 | 0.31 | 0.73 | <0.004 | 46 | 100 |
| ∆MAP, PMIP3 | 0.91 | 0.30 | 0.98 | <0.001 | 82 | 96 |
| Model | TemperatureDepression, °C | ∆MAP, cm | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Huerfano | Little Ute | Ikes | Barbara | Blanca | Tobin | Holbrook | Pioneer | Zapata | ||
| NCAR-CCSM4 | 8.6 ± 0.2 | 23.8 ± 2.0 | 26.9 ± 1.2 | 26.9 ± 0.7 | 24.6 ± 1.3 | 21.8 ± 3.2 | 19.4 ± 3.4 | 18.6 ± 4.5 | 17.1 ± 3.9 | 18.3 ± 5.4 |
| MRI-CGCM3 | 6.7 ± 0.4 | 37.1 ± 2.6 | 38.2 ± 3.3 | 37.7 ± 1.2 | 38.7 ± 1.5 | 37.3 ± 3.8 | 36.2 ± 3.4 | 35.5 ± 4.3 | 34.1 ± 3.7 | 35.1 ± 5.4 |
| CNRM-CM5 | 5.8 ± 0.4 | 26.5 ± 2.1 | 28.2 ± 1.6 | 27.7 ± 0.9 | 26.0 ± 1.3 | 23.7 ± 3.4 | 21.8 ± 3.3 | 21.2 ± 4.3 | 20.0 ± 3.8 | 21.6 ± 5.2 |
| FGOALS-g2 | 15.2 ± 0.4 | 17.1 ± 2.0 | 18.7 ± 1.4 | 17.9 ± 0.9 | 15.5 ± 1.2 | 13.9 ± 2.7 | 12.6 ± 2.4 | 11.8 ± 3.6 | 10.7 ± 3.1 | 11.9 ± 4.4 |
| IPSL-CM5A-LR | 13.6 ± 0.6 | 1.8 ± 2.0 | 3.6 ± 1.5 | 3.2 ± 0.8 | −1.2 ± 1.0 | −2.4 ± 1.4 | −3.3 ± 1.4 | −3.9 ± 2.0 | −4.7 ± 1.7 | −4.1 ± 2.8 |
| MIROC-ESM | 13.6 ± 0.3 | 13.9 ± 2.1 | 17.6 ± 2.4 | 17.5 ± 0.8 | 12.4 ± 2.1 | 9.6 ± 1.8 | 8.3 ± 1.8 | 7.5 ± 2.3 | 6.9 ± 2.2 | 7.8 ± 3.2 |
| MPI-ESM-P | 8.9 ± 0.3 | 16.9 ± 2.0 | 17.9 ± 1.3 | 17.3 ± 0.8 | 14.9 ± 1.3 | 13.0 ± 2.9 | 11.6 ± 2.7 | 11.2 ± 3.5 | 10.2 ± 3.0 | 11.6 ± 4.2 |
| Ensemble mean | 10.4 ± 3.7 | 19.5 ± 11.1 | 21.6 ± 10.9 | 21.2 ± 10.9 | 18.7 ± 12.6 | 16.7 ± 12.5 | 15.2 ± 12.3 | 14.6 ± 12.3 | 13.5 ± 12.1 | 14.6 ± 12.2 |
| MAP, cm | ||||||||||
| CHELSA Modern | 32.6 ± 4.0 | 32.6 ± 3.4 | 33.8 ± 1.0 | 40.0 ± 0.4 | 40.1 ± 1.5 | 39.4 ± 1.2 | 39.5 ± 1.9 | 39.3 ± 1.7 | 39.9 ± 1.7 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brugger, K.A.; Leonard, E.M.; Refsnider, K.A.; Dolan, P. Climate on the Blanca Massif, Sangre de Cristo Mountains, Colorado, USA, during the Last Glacial Maximum. Quaternary 2021, 4, 27. https://doi.org/10.3390/quat4030027
Brugger KA, Leonard EM, Refsnider KA, Dolan P. Climate on the Blanca Massif, Sangre de Cristo Mountains, Colorado, USA, during the Last Glacial Maximum. Quaternary. 2021; 4(3):27. https://doi.org/10.3390/quat4030027
Chicago/Turabian StyleBrugger, Keith A., Eric M. Leonard, Kurt A. Refsnider, and Peter Dolan. 2021. "Climate on the Blanca Massif, Sangre de Cristo Mountains, Colorado, USA, during the Last Glacial Maximum" Quaternary 4, no. 3: 27. https://doi.org/10.3390/quat4030027
APA StyleBrugger, K. A., Leonard, E. M., Refsnider, K. A., & Dolan, P. (2021). Climate on the Blanca Massif, Sangre de Cristo Mountains, Colorado, USA, during the Last Glacial Maximum. Quaternary, 4(3), 27. https://doi.org/10.3390/quat4030027






