Chaos Synchronization in Visible Light Communications with Variable Delays Induced by Multipath Fading
Abstract
:1. Introduction
2. Working Models
2.1. Colpitts Chaotic Synchronization
2.2. VLC Multipath Channel Model
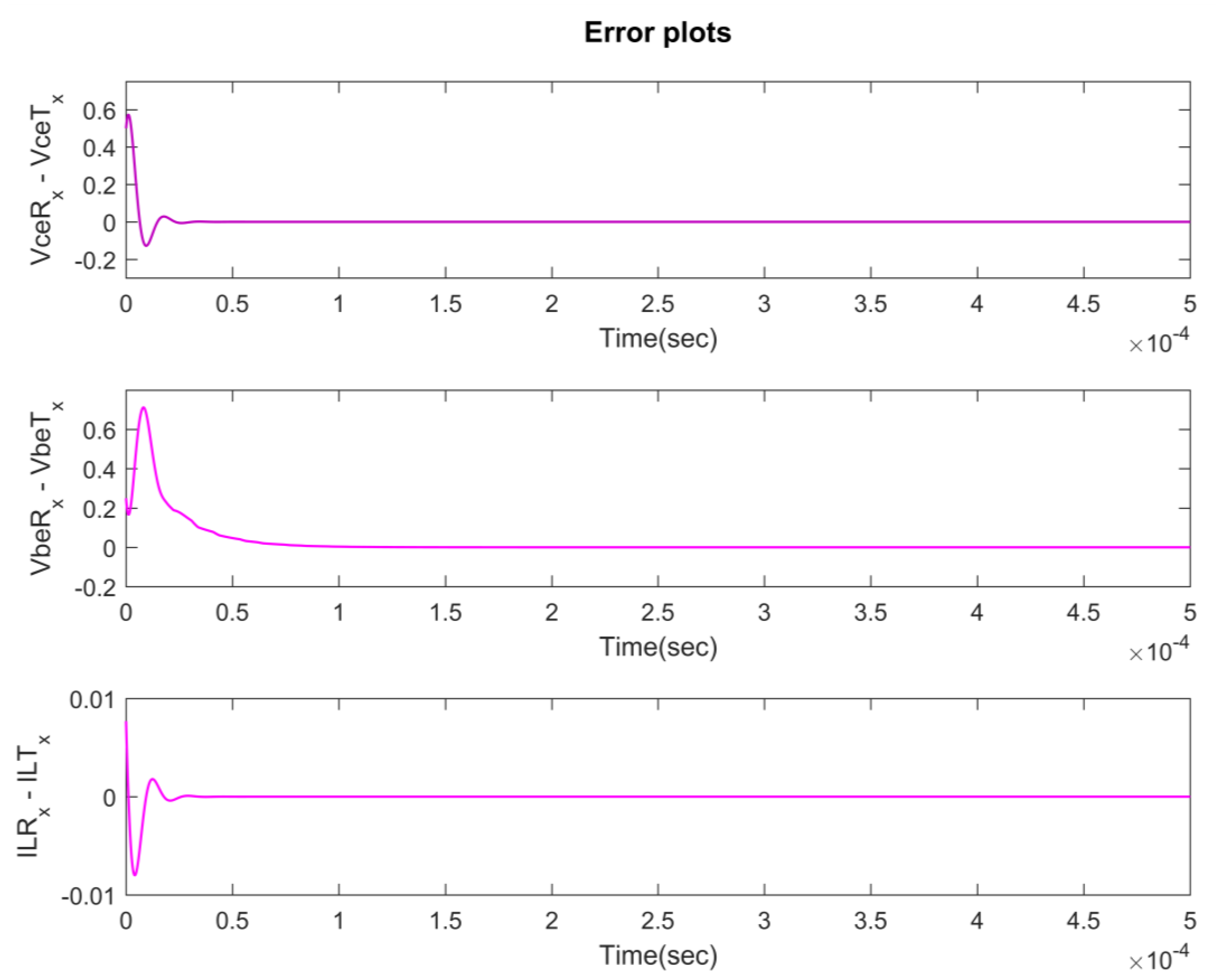
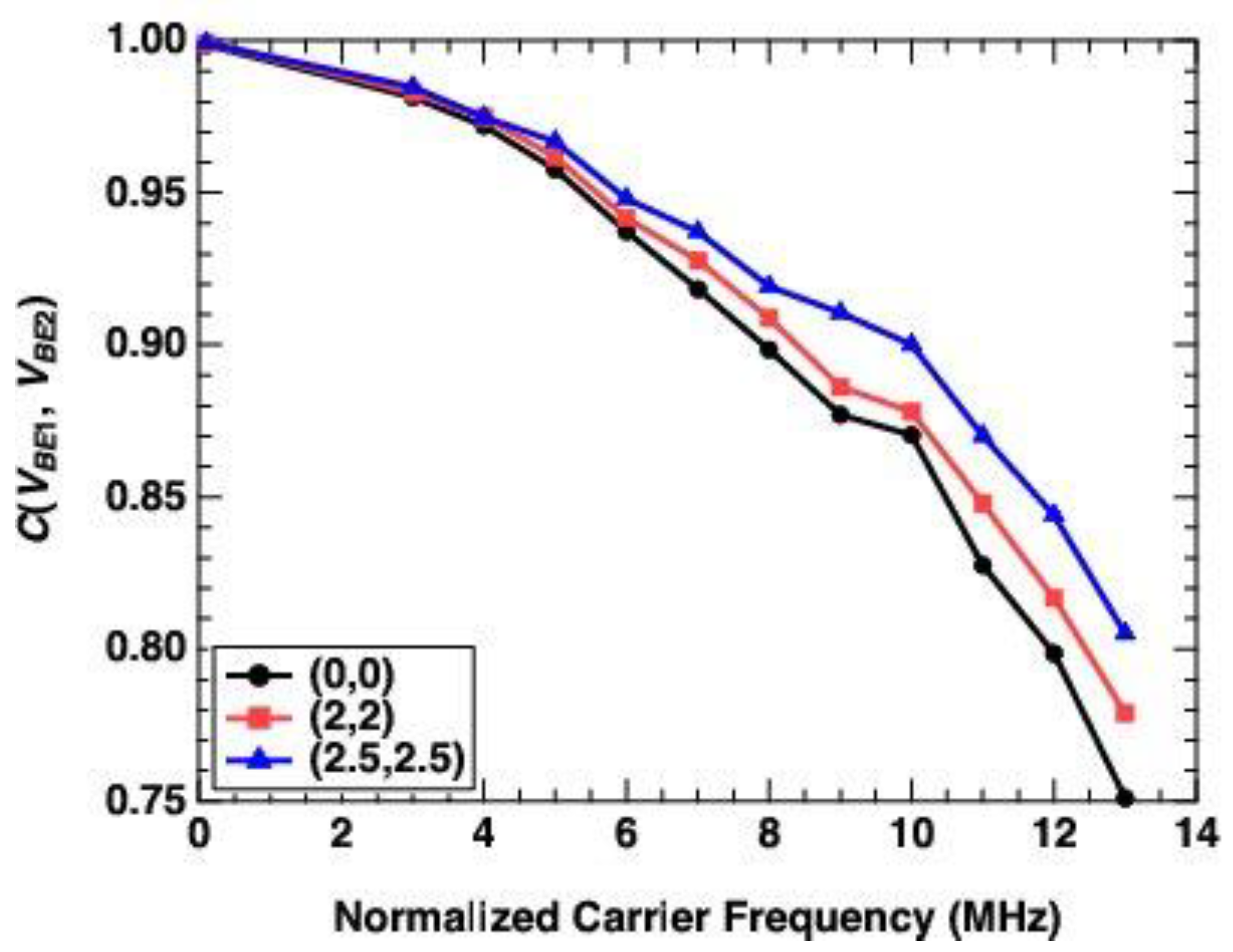
3. Results
4. Conclusions Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kocarev, L.; Lian, S. Chaos-Based Cryptography: Theory, Algorithms and Applications; Springer: Berlin, Germany, 2011; ISBN 9783662506530. [Google Scholar]
- Pecora, L.M.; Carroll, T.L. Synchronization of chaotic systems. Chaos 2015, 25, 097611. [Google Scholar] [CrossRef] [PubMed]
- Boccaletti, S.; Kurths, J.; Osipov, G.; Valladares, D.L.; Zhou, C.S. The synchronization of chaotic systems. Phys. Rep. 2002, 366, 1–101. [Google Scholar] [CrossRef]
- Alvarez, G.; Li, S. Some basic cryptographic requirements for chaos-based crypto systems. Int. J. Bifurc. Chaos 2006, 16, 2129–2151. [Google Scholar] [CrossRef]
- Le Minh, H.; O’Brien, D.; Faulkner, G.; Zeng, L.; Lee, K.; Jung, D.; Oh, Y.J. High-speed visible light communications using multiple-resonant equalization. IEEE Photonics Technol. Lett. 2008, 20, 1243–1245. [Google Scholar] [CrossRef]
- Grobe, L.; Paraskevopoulos, A.; Hilt, J.; Schulz, D.; Lassak, F.; Hartlieb, F.; Kotte, C.; Jungnickel, V.; Langer, K.D. High-speed Visible Light Communication Systems. IEEE Commun. Mag. 2013, 51, 60–66. [Google Scholar] [CrossRef]
- Jovicic, A.; Li, J.; Richardson, T. Visible light communication: Opportunities, challenges and the path to market. IEEE Commun. Mag. 2013, 51, 26–32. [Google Scholar] [CrossRef]
- Wu, S.; Wang, H.; Youn, C.H. Visible light communications for 5G wireless networking systems: From fixed to mobile communications. IEEE Netw. 2014, 28, 41–45. [Google Scholar] [CrossRef]
- Tsiropoulou, E.E.; Gialagkolidis, I.; Vamvakas, P.; Papavassiliou, S. Resource allocation in visible light communication networks: NOMA vs. OFDMA transmission techniques. In Proceedings of the International Conference on Ad-Hoc Networks and Wireless, Lille, France, 4–6 July 2016; Springer: Cham, Switzerland, 2016; pp. 32–46. [Google Scholar]
- Singhal, C.; De, S. (Eds.) Resource Allocation in Next-Generation Broadband Wireless Access Networks; IGI Global: Hershey, PA, USA, 2017. [Google Scholar]
- Bykhovsky, D.; Arnon, S. Multiple access resource allocation in visible light communication systems. J. Lightw. Technol. 2014, 32, 1594–1600. [Google Scholar] [CrossRef]
- Chen, Z.; Tsonev, D.; Haas, H. Improving SINR in indoor cellular visible light communication networks. In Proceedings of the IEEE International Conference on Communications (ICC), Sydney, Australia, 10–14 June 2014. [Google Scholar]
- IEEE Standard Association. IEEE Standard for Local and Metropolitan Area Networks—Part 15.7: Short-Rang Wireless Optical Communication Using Visible Light; IEEE Computer Society: Wahington, DC, USA, 2011. [Google Scholar]
- Chaleshtori, Z.N.; Chvojka, P.; Zvanovec, S.; Ghassemlooy, Z.; Haigh, P.A. A Survey on Recent Advances in Organic Visible Light Communications. In Proceedings of the IEEE 11th International Symposium on Communication Systems, Networks & Digital Signal Processing (CSNDSP), Budapest, Hungary, 18–20 July 2018. [Google Scholar]
- Bates, R.; Geldard, C.; Hassan, N.B.; Burton, A.; Luo, P. Comparison of LED illumination patterns for camera based car to car communications. In Proceedings of the 10th International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP), Prague, Czech Republic, 20–22 July 2016. [Google Scholar]
- Chen, C.W.; Wang, W.C.; Wu, J.T.; Chen, H.Y.; Liang, K.; Wei, L.Y.; Hsu, Y.H.; Chow, C.W.; Yeh, C.H.; Liu, Y.; et al. Visible light communications for the implementation of internet-of-things. Opt. Eng. 2016, 55, 060501. [Google Scholar] [CrossRef]
- Burton, A.; Le Minh, H.; Ghassemlooy, Z.; Rajbhandari, S.; Haigh, P.A. Smart receiver for visible light communications: Design and Analysis. In Proceedings of the 8th International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP), Poznan, Poland, 18–20 July 2012. [Google Scholar]
- Burton, A.; Ghassemlooy, Z.; Rajbhandari, S.; Liaw, S.K. Design and analysis of an angular-segmented full-mobility visible light communications receiver. Trans. Emerg. Telecommun. Technol. 2014, 25, 591–599. [Google Scholar] [CrossRef]
- Aguado, A.; Hugues-Salas, E.; Haigh, P.A.; Marhuenda, J.; Price, A.B.; Sibson, P.; Kennard, J.; Erven, C.; Rarity, J.G.; Thompson, M.G.; et al. First Experimental Demonstration of Secure NFV Orchestration over an SDN-Controlled Optical Network with Time-Shared Quantum Key Distribution Resources. In Proceedings of the 42nd European Conference on Optical Communication (ECOC), Düsseldorf, Germany, 18–22 September 2016. [Google Scholar]
- Jouguet, P.; Kunz-Jacques, S.; Leverrier, A.; Grangier, P.; Diamanti, E. Experimental demonstration of long-distance continuous-variable quantum key distribution. Nat. Photonics 2013, 5, 378–381. [Google Scholar] [CrossRef]
- Stinson, D.R. Cryptography: Theory and Practice; Chapman & Hall/CRC: Boca Raton, FL, USA, 2006; ISBN 9781584885085. [Google Scholar]
- Álvarez, G.; Li, S.; Montoya, F.; Pastor, G.; Romera, M. Breaking projective chaos synchronization secure communication using filtering and generalized synchronization. Chaos Solitons Fractals 2005, 24, 775–783. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Álvarez, G.; Chen, G. Breaking a chaos-based secure communication scheme designed by an improved modulation method. Chaos Solitons Fractals 2005, 25, 109–120. [Google Scholar] [CrossRef] [Green Version]
- Millerioux, G.; Amigó, J.M.; Daafouz, J. A Connection Between Chaotic and Conventional Cryptography. IEEE Trans. Circuits Syst. I Reg. Pap. 2008, 55, 1695–1703. [Google Scholar] [CrossRef]
- Ren, H.P.; Baptista, M.S.; Grebogi, C. Wireless communication with chaos. Phys. Rev. Lett. 2013, 110, 184101. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.P.; Bai, C.; Baptista, M.S.; Greborgi, C. Experimental validation of wireless communication with chaos. Chaos 2016, 26, 083117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kennedy, M.P. Chaos in the Colpitts oscillator. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1994, 41, 771–774. [Google Scholar] [CrossRef]
- Uchida, A.; Kawano, M.; Yoshimori, S. Dual synchronization of chaos in Colpitts electronic oscillators and its applications for communications. Phys. Rev. E 2003, 68, 056207. [Google Scholar] [CrossRef] [PubMed]
- Rubezic, V.; Ostojic, R. Synchronization of chaotic Colpitts oscillators with applications to binary communications. In Proceedings of the 6th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Pafos, Cyprus, 5–8 September 1999. [Google Scholar]
- Beal, A.; Blakely, J.N.; Corron, N.J.; Dean, R.N. High frequency oscillators for chaotic radar. In Proceedings of the SPIE Radar Sensor Technology, Baltimore, MD, USA, 18–21 April 2016. [Google Scholar]
- Ghassemlooy, Z.; Popoola, W.O.; Rajbhandari, S. Optical Wireless Communications: System and Channel Modelling with MATLAB; CRC Press, Taylor and Francis Group: Boca Raton, FL, USA, 8 August 2012; ISBN 9781138074804. [Google Scholar]
- Zeng, L.; O’Brien, D.; Le Minh, H.; Faulkner, G.E.; Lee, K.; Jung, D.; Oh, Y.J.; Won, E.T. High data rate multiple input multiple output (MIMO) optical wireless communications using white LED lighting. IEEE J. Sel. Areas Commun. 2009, 27, 1654–1662. [Google Scholar] [CrossRef]
- Haigh, P.A.; Ghassemlooy, Z.; Rajbhandari, S.; Papakonstantinou, I.; Popoola, W. Visible Light Communications: 170 Mb/s Using an Artificial Neural Network Equalizer in a Low Bandwidth White Light Configuration. J. Lightw. Technol. 2014, 32, 1807–1813. [Google Scholar] [CrossRef] [Green Version]
- Burton, A.; Le Minh, H.; Ghassemlooy, Z.; Rajbhandari, S. A study of LED lumination uniformity with mobility for visible light communications. In Proceedings of the International Workshop on Optical Wireless Communications (IWOW), Newcastle-upon-Tyne, UK, 22 October 2012. [Google Scholar]








| Parameters | Values |
|---|---|
| C1 (nF) | 58 |
| C2 (nF) | 58 |
| L (µH) | 100 |
| RL (Ω) | 36 |
| REE (Ω) | 430 |
| VCC (V) | 5 |
| VEE (V) | −5 |
| RON (Ω) | 375 |
| β | 230 |
| VTH | 0.7 |
| Carrier Frequency | Position 1 | Position 2 | Position 3 |
|---|---|---|---|
| (0, 0) | (2, 2) | (2.5, 2.5) | |
| T = 1, ω = 100 kHz | 0.9987 | 0.9992 | 0.9992 |
| T = 30, ωnorm = 3 MHz | 0.9814 | 0.9829 | 0.9848 |
| T = 40, ωnorm = 4 MHz | 0.9721 | 0.9749 | 0.9749 |
| T = 50, ωnorm = 5 MHz | 0.9577 | 0.9618 | 0.9669 |
| T = 60, ωnorm = 6 MHz | 0.9373 | 0.9417 | 0.9480 |
| T = 70, ωnorm = 7 MHz | 0.9183 | 0.9277 | 0.9371 |
| T = 80, ωnorm = 8 MHz | 0.8985 | 0.9088 | 0.9192 |
| T = 90, ωnorm = 9 MHz | 0.8770 | 0.8862 | 0.9106 |
| T = 100, ωnorm = 10 MHz | 0.8703 | 0.8780 | 0.9000 |
| T = 110, ωnorm = 11 MHz | 0.8275 | 0.8479 | 0.8701 |
| T = 120, ωnorm = 12 MHz | 0.7986 | 0.8168 | 0.8440 |
| T = 130, ωnorm = 13 MHz | 0.7510 | 0.7789 | 0.8050 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Canyelles-Pericas, P.; Haigh, P.A.; Ghassemlooy, Z.; Burton, A.; Dai, X.; The Son, T.; Le-Minh, H.; Binns, R.; Busawon, K. Chaos Synchronization in Visible Light Communications with Variable Delays Induced by Multipath Fading. Appl. Syst. Innov. 2018, 1, 45. https://doi.org/10.3390/asi1040045
Canyelles-Pericas P, Haigh PA, Ghassemlooy Z, Burton A, Dai X, The Son T, Le-Minh H, Binns R, Busawon K. Chaos Synchronization in Visible Light Communications with Variable Delays Induced by Multipath Fading. Applied System Innovation. 2018; 1(4):45. https://doi.org/10.3390/asi1040045
Chicago/Turabian StyleCanyelles-Pericas, Pep, Paul Anthony Haigh, Zabih Ghassemlooy, Andrew Burton, Xuewu Dai, Tran The Son, Hoa Le-Minh, Richard Binns, and Krishna Busawon. 2018. "Chaos Synchronization in Visible Light Communications with Variable Delays Induced by Multipath Fading" Applied System Innovation 1, no. 4: 45. https://doi.org/10.3390/asi1040045
APA StyleCanyelles-Pericas, P., Haigh, P. A., Ghassemlooy, Z., Burton, A., Dai, X., The Son, T., Le-Minh, H., Binns, R., & Busawon, K. (2018). Chaos Synchronization in Visible Light Communications with Variable Delays Induced by Multipath Fading. Applied System Innovation, 1(4), 45. https://doi.org/10.3390/asi1040045







