Mathematical Apparatus of Optimal Decision-Making Based on Vector Optimization
Abstract
:1. Introduction
2. Statement of a Problem: Creation of the Mathematical Model “Acceptance of an Optimal Solution”
- Creation of a mathematical model, which defines the inter-relation of each functional characteristic from parameters of the technical system, i.e., it is formed from the vector problem of mathematical programming;
- Choice of methods of the decision: we suggest using the methods based on normalization of criteria and the principle of the guaranteed result with equivalent criteria and with the set criterion priority;
- Development of the software which realizes these methods;
3. Theory. Axioms, the Principle of Optimality and Methods for Solving Vector Problems of Mathematical Programming
3.1. Vector Optimization with Equivalent Criteria
3.1.1. Axioms and the Principle of Optimality of Vector Optimization with Equivalent Criteria
3.1.2. Mathematical Algorithm of the Solution of a Vector Problem with Equivalent Criteria
- X0 = {λ0, X0}, an optimum point,
- fk(X0), k = , values of the criteria at this point,
- λk(X0) = , k = , sizes of the relative estimates,
3.1.3. Implementation of the Decision using the Example of a Vector Problem of Linear Programming with Equivalent Criteria
3.2. Vector Optimization with a Criterion Priority
3.2.1. Axioms and the Principle of Optimality of Vector Optimization with a Criterion Priority
- priority of one criterion of vector problems, with a criterion priority over other criteria,
- numerical expression of a priority,
- the set priority of a criterion,
- the lower (minimum) level from all criteria with a priority of one of them,
- a subset of points with priority by criterion (Axiom 2),
- a subset of points by priority criterion Sq, which is included in a set of points S, ∀q ∈ K X ∈ Sq ⊂ S, (such a subset of points can be used in problems of clustering, but is beyond this article);
- a subset of points by priority criterion S, which is included in a set of Pareto optimal points S°, ∀q∈K, X∈S ⊂ S0.
| Set of admissible points of X∈S → | Subset of points, optimum across Pareto, X∈S0 ⊂S → | Subset of points, optimum across Pareto X∈S ⊂ S0 ⊂ S → | Separate point of а ∀X∈S X∈S ⊂ S0 ⊂ S |
3.2.2. Mathematical Method of the Solution of a Vector Problem with Criterion Priority
- optimum points by each criterion separately X, k = and sizes of criterion functions in these points of f = fk(X), k = , which represent the boundary of a set of Pareto optimal points,
- anti-optimum points by each criterion of X = {xj, j = } and the worst unchangeable part of each criterion of f = fk(X), k = ,
- X0 = {λ0, X0}, an optimum point, as a result of the solution of VPMP at equivalent criteria, i.e., the result of the solution of a maximine problem and the λ-problem constructed on its basis,
- λ0, the maximum relative assessment which is the maximum lower level for all relative estimates of λk(X0), or the guaranteed result in relative units, λ0 guarantees that all relative estimates of λk(X0) are equal to or greater than λ0:
- in each point X, k = we determine sizes of all criteria of q = :{fq(X), q = }, k = , and relative estimatesλ(X) = {λq(X), q = , k = }, λk(X) = , ∀k ∈ K:
- at an optimum point at equivalent criteria X0 we calculate sizes of criteria and relative estimates:which satisfy the inequality of Equation (28). In other points X∈S0, in relative units the criteria of λ = λk(X) are always less than λ0, given the λ-problem of Equations (22) and (23).
- all criteria in physical units fk(xq) = {fk(xq), k = },
- all relative estimates of criteria λq = {λ, k = }, λk(xq) = , k = ,
- the vector of priorities Pq = {p = , k = },
- the maximum relative assessment λoq = min (pλk(xq), k = ).
4. Research, Analysis, and Formulation of the Problem of Decision-Making with Uncertain Data
4.1. Investigation of the Model of the “Object for Making an Optimal Decision” under Certainty and Uncertainty
4.1.1. Characteristics of Certainty and Uncertainty
4.1.2. Investigation of Condition of Uncertainty
- (a)
- random data,
- (b)
- fuzzy data, or
- (c)
- incomplete data, which are usually obtained from experimental data.
4.2. Conceptual Problem Definition of Decision Making under the Conditions of Uncertainty
4.3. The Analysis of Modern Methods of Decision Making to the Experimental Data
4.4. Transforming the Decision-Making Problem into Vector Problem
5. Statement and Optimal Decision Making with Experimental Data in Problems with One Parameter
5.1. Problem Definition of Decision Making of the First Type
5.2. The Solution of the Problem
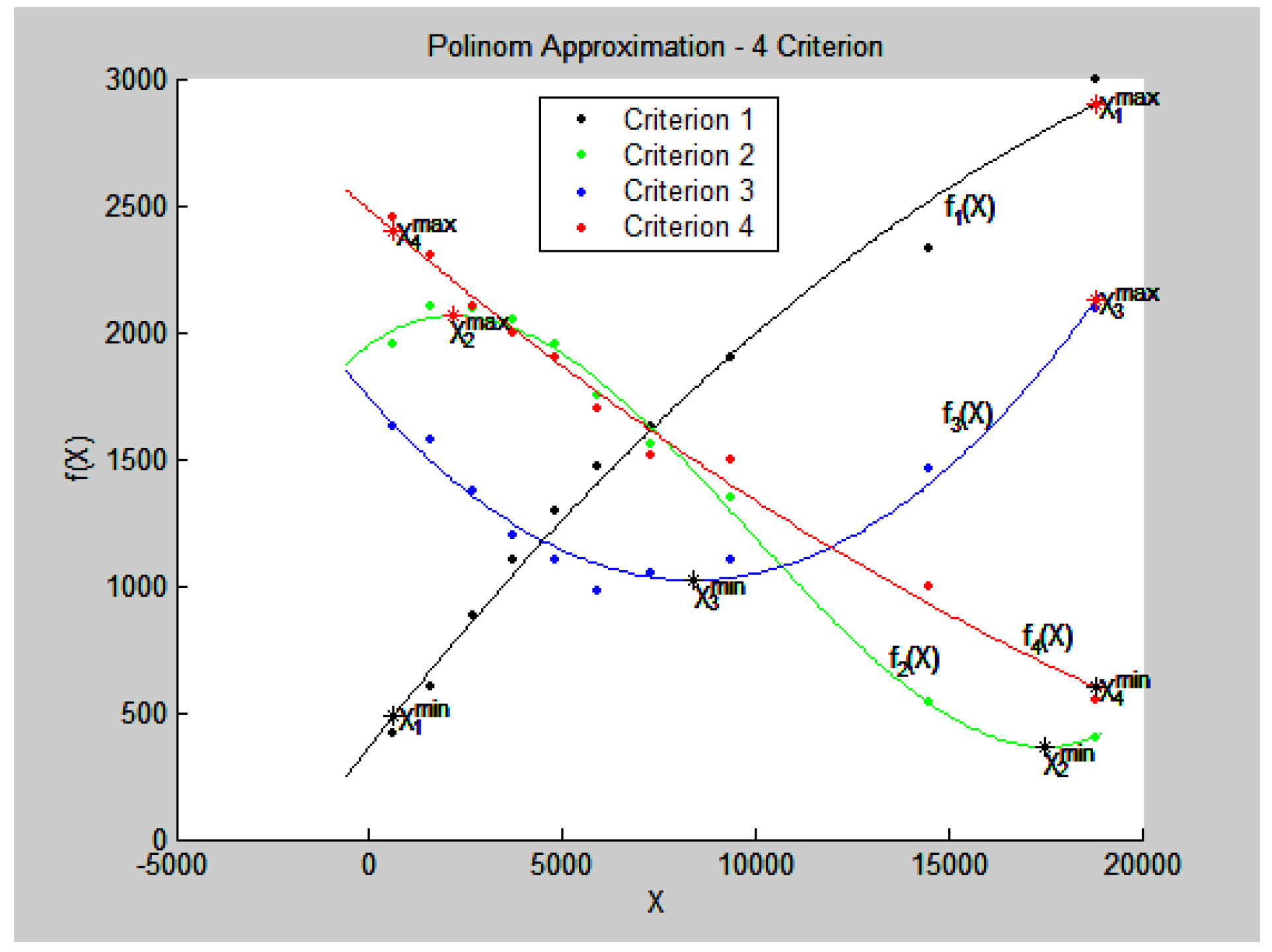
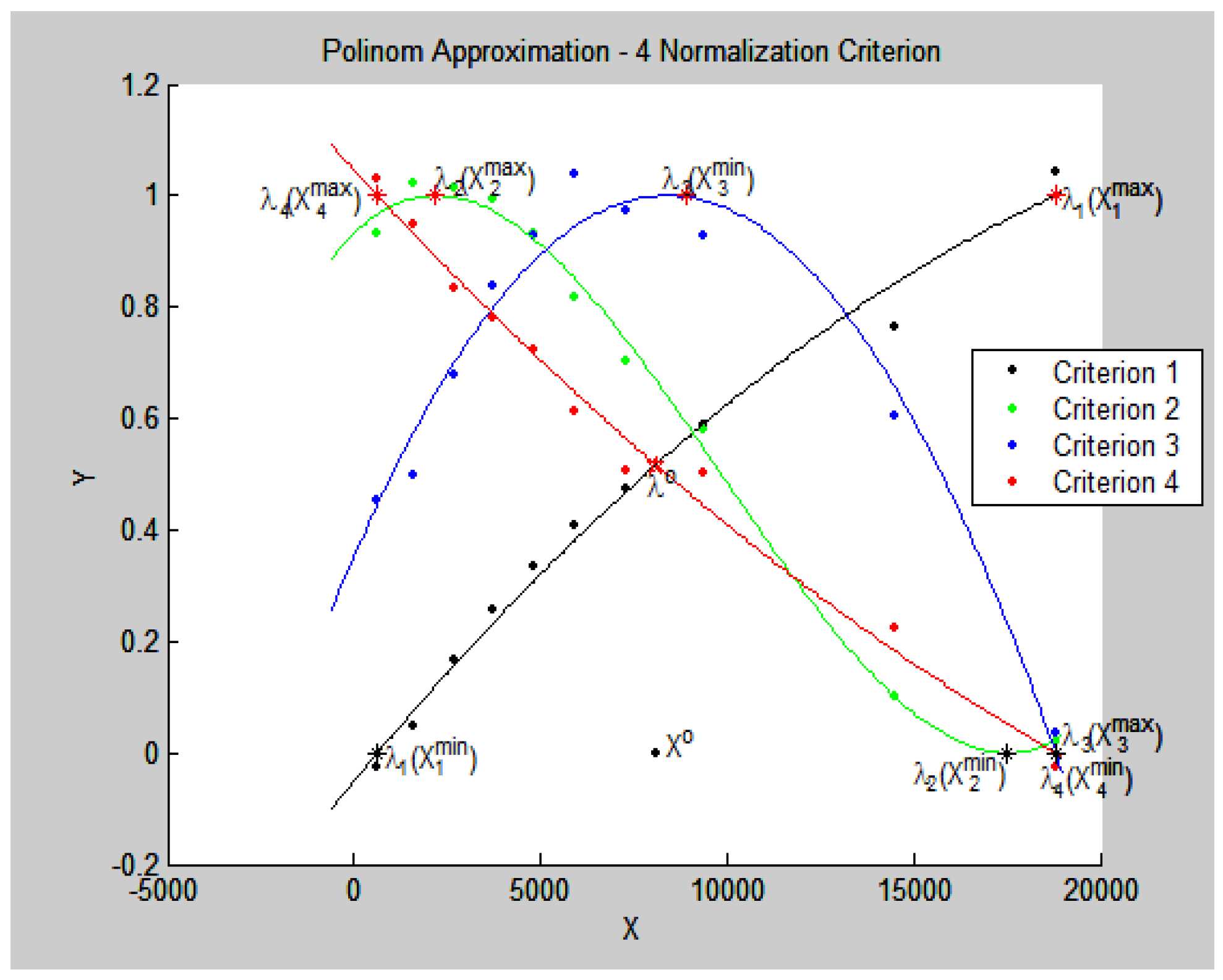
- λ1(x) = −1.325 × 10−9 x2 + 8.0762 × 10−5 x × 0.0504,
- λ2(x) = 5.5735 × 10−13 x3 − 1.6467 × 10−8 x2 + 6.4179 × 10−5 x + 0.9325,
- λ3(x) = −9.2080 × 10−9 x2 + 1.5451 × 10−4 x + 0.3519,
- λ4 (x) = 9.1530 × 10−10 x2 − 7.2811 × 10−5 x + 1.0455.
- the values of the criteria at this point of fk(X0), k = : f1(X0) = 17,310, f2(X0) = 1501.8, f3(X0) = 1022.3, f4(X0) = 152.7,
- the values of the relative estimates λk(X0), k = : λ1(X0) = 0.5163, λ2(X0) = 0.6692, λ3(X0) = 0.9992, λ4(X0) = 0.5165 (Figure 2).
6. Statement and Optimal Decision Making with Experimental Data in Problems with Two Parameters
6.1. Problem Definition of Decision Making of the Second Type with Two Parameters
6.2. Transformation of Experimental Data into a Vector Problem of Mathematical Programming
f2(x) = −0.3x12 − 6x1 − 0.3x22 + 12x2 − 150,
f3(x) = 0.5x12 − 20x1+0.5x22 − 8x2 + 232,
f4(x) = 0.6x12 − 9.6 x1 + 0.6x22 − 24x2 + 278.4,
f5(x) = x12 − 40x1 + x22 +20x2 + 500,
6.3. The Solution of a Vector Problem of Mathematical Programming–Decision-Making
- the optimum point X0 = {x1 = 5.0, x2 = 5.0, λ0 = 0.5833},
- the values of criteria: f1(X0) = −180, f2(X0) = −135, f3(X0) = 117, f4(X0) = 140.4, f4(X0) = 450,
- the values of the relative estimates λk(X0), k = : λ1(X0) = 0.5833, λ2(X0) = 0.5833, λ3(X0) = 0.6319, λ4(X0) = 0.6319, λ5(X0) = 0.5833),
- the maximal relative estimate λ0 = 0.5833 that is the maximal lower level for all relative estimates λ0 = min{λ1(X0), λ2(X0), λ3(X0), λ4(X0), λ5(X0)} = 0.5833.
7. Statement and Optimal Decision Making with Experimental Data in Problems with Three Parameters
7.1. Statement of the Problem of Decision Making in a System with Three Parameters
7.2. Construction of a Numerical Model of a System with Three Parameters in the Form of a Vector Problem
- Building a model under the conditions of certainty;
- Building a model under the conditions of uncertainty;
- Construction of a mathematical model of a technical system (i.e., the general part for the conditions of certainty and uncertainty).
7.2.1. Building a Model under the Conditions of Certainty
7.2.2. Building a Model under the Conditions of Uncertainty
7.2.3. Creation of a Mathematical Model of a Technical System under the Conditions of Definiteness and Uncertainty
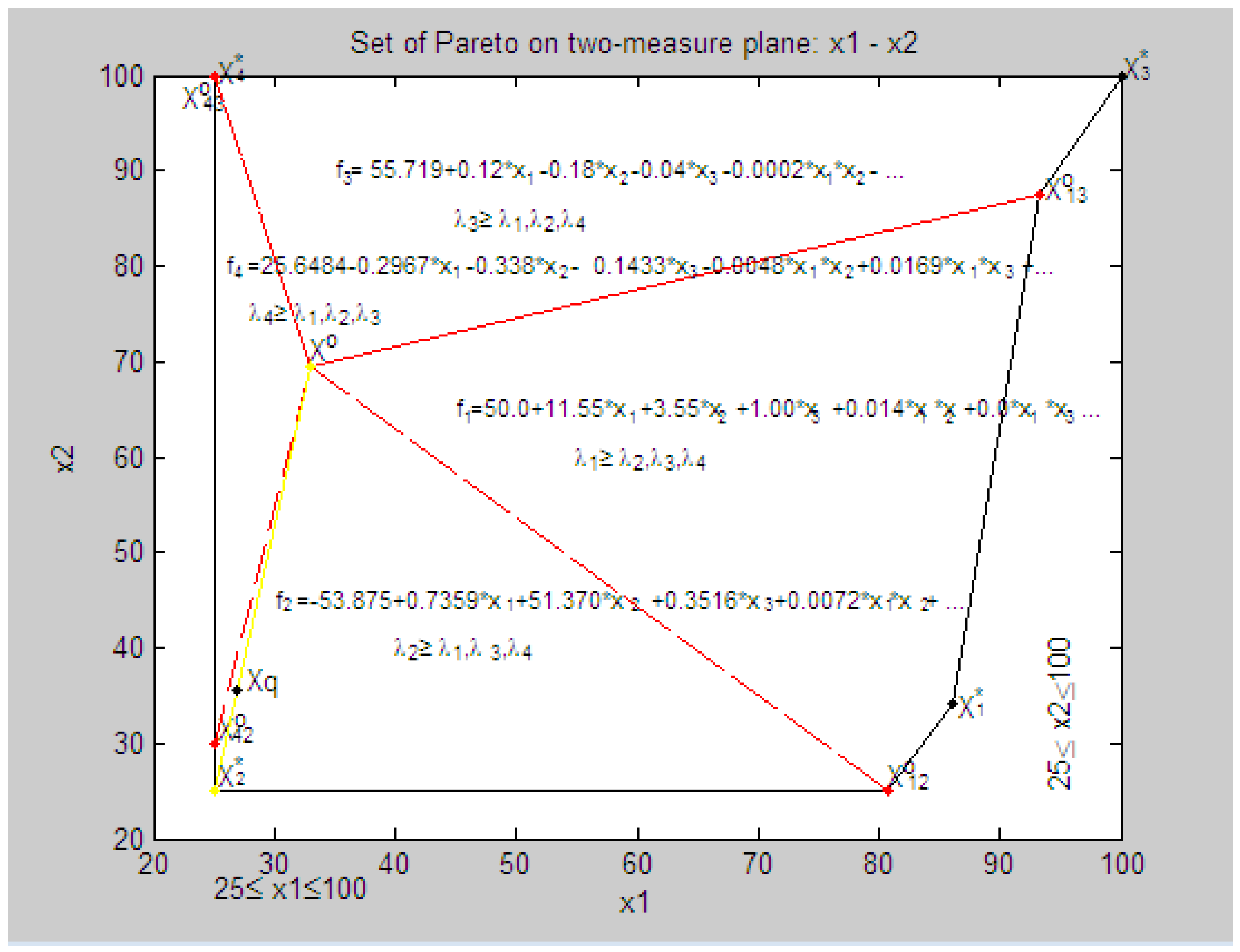
7.3. The Solution of the Vector Problem and Decision Making with Equivalent Criteria
7.4. Decision Making in a System with Three Parameters with a Criterion Priority
- all criteria in physical units fk(Xq) = {fk(Xq), k = }:f(Xq) = {f1(Xq) = 386.5, f2(Xq) = 1651.5, f3(Xq) = 137.9, f4(Xq) = 26.1},
- all relative estimates of criteria λq = {λ, k = }, λk(Xq) = , k = :λk(xq) = {λ1(xq) = 0.5392, λ2(xq) = 0.8530, λ3(xq) = 0.0827, λ4(xq) = 0.9334},
- vector of priorities Pq = {p = , k = }:Pq = [p = 1.5820, p = 1.0, p = 10.3123, p = 0.9139],
- the minimum relative assessment: min LXq = min (LXq): min LXq = min (λk(Xq)) = 0.0827,
- the relative assessment taking into account a criterion priority:λ00 = min (pλ1(Xq) = 0.7564, pλ2(Xq) = 0.7564, pλ3(Xq) = 0.7564, pλ4(Xq)) = 0.7564.
7.5. Analysis of the Results of the Final Decision
- parameters of the technical system X0 = {x1 = 33.03, x2 = 69.54, x3 = 25.0},
- the parameters of the technical system at a given priority criterion q = 2: Xq = {x1 = 26.88, x2 = 35.47, x3 = 25.0}.
8. The Methodology of Making Optimal Decisions with the Functional and Experimental Data (For Example, a Problem with Four Parameters)
- Formation of the requirement specification (source data) for numerical modeling and choice of optimum parameters of a system. The initial data is determined by the designer who operates the system.
- Creation of a mathematical and numerical model of the system under the conditions of definiteness and indeterminacy.
- The solution of the vector problem of mathematical programming (VPMP), i.e., a model of the system with equivalent criteria.
- Geometric interpretation of the results of the decision in a three-dimensional coordinate system in relative units.
- The solution of a vector problem of mathematical programming, i.e., a model of the system at the given priority of the criterion.
- Geometric interpretation of the results of the decision in a three-dimensional coordinate system in physical units.
8.1. Formation of Technical Specifications (Source Data) for the Numerical Simulation of the System
8.2. Creation of a Mathematical and Numerical Model of the System under the Conditions of Definiteness and Indeterminacy
- Choosing a mathematical model of the system,
- Building a model under certainty conditions,
- Construction under the conditions of uncertainty,
- Construction of a numerical model of the system under certainty and uncertainty.
8.2.1. Mathematical Model of the System
8.2.2. Building a Model under the Conditions of Certainty
8.2.3. Construction under the Conditions of Uncertainty
8.2.4. Construction of a Numerical Model of the System under Certainty and Uncertainty
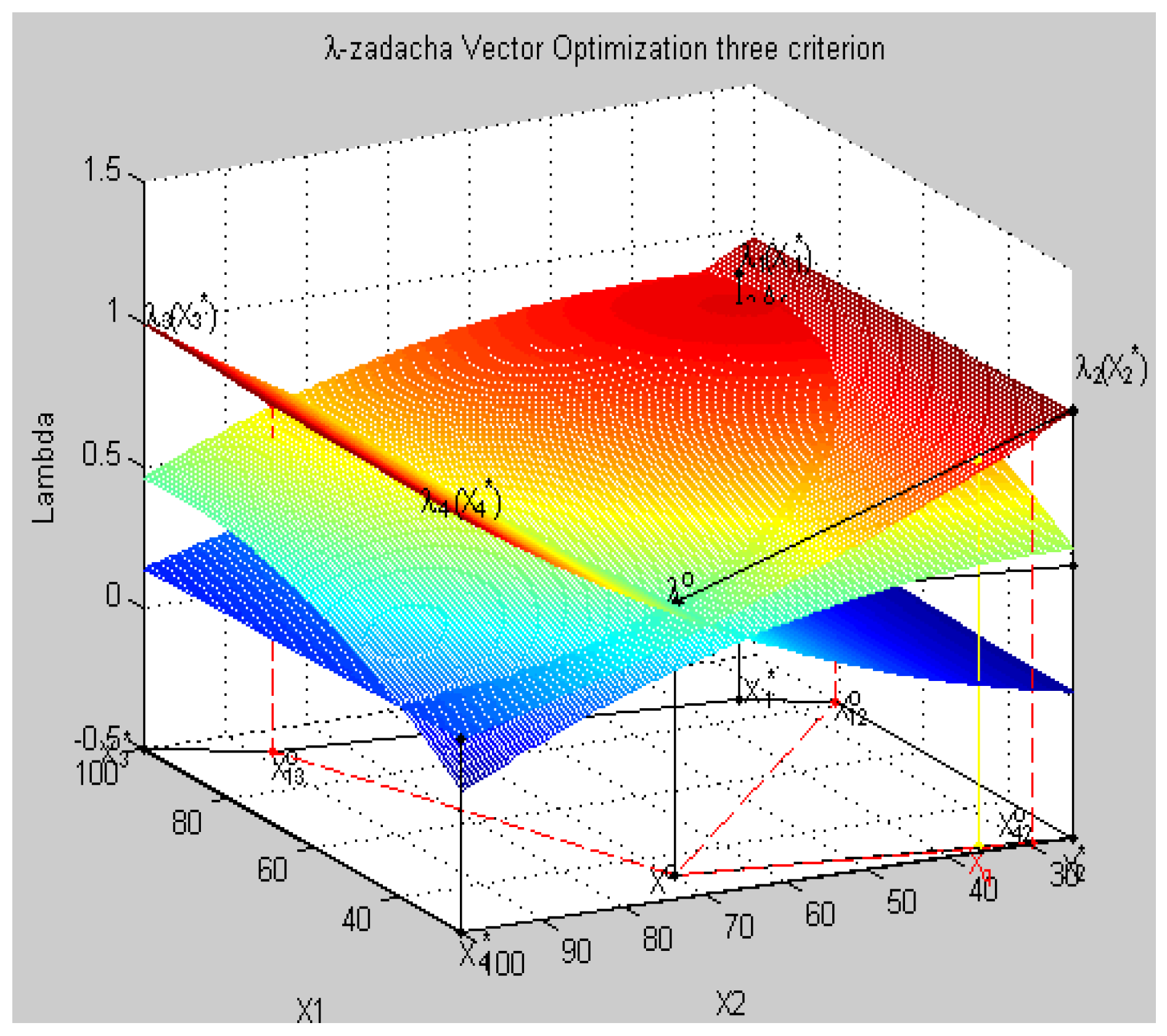
8.3. The Solution of the Vector Problem of Mathematical Programming (VPMP)—Model of the System with Equivalent Criteria
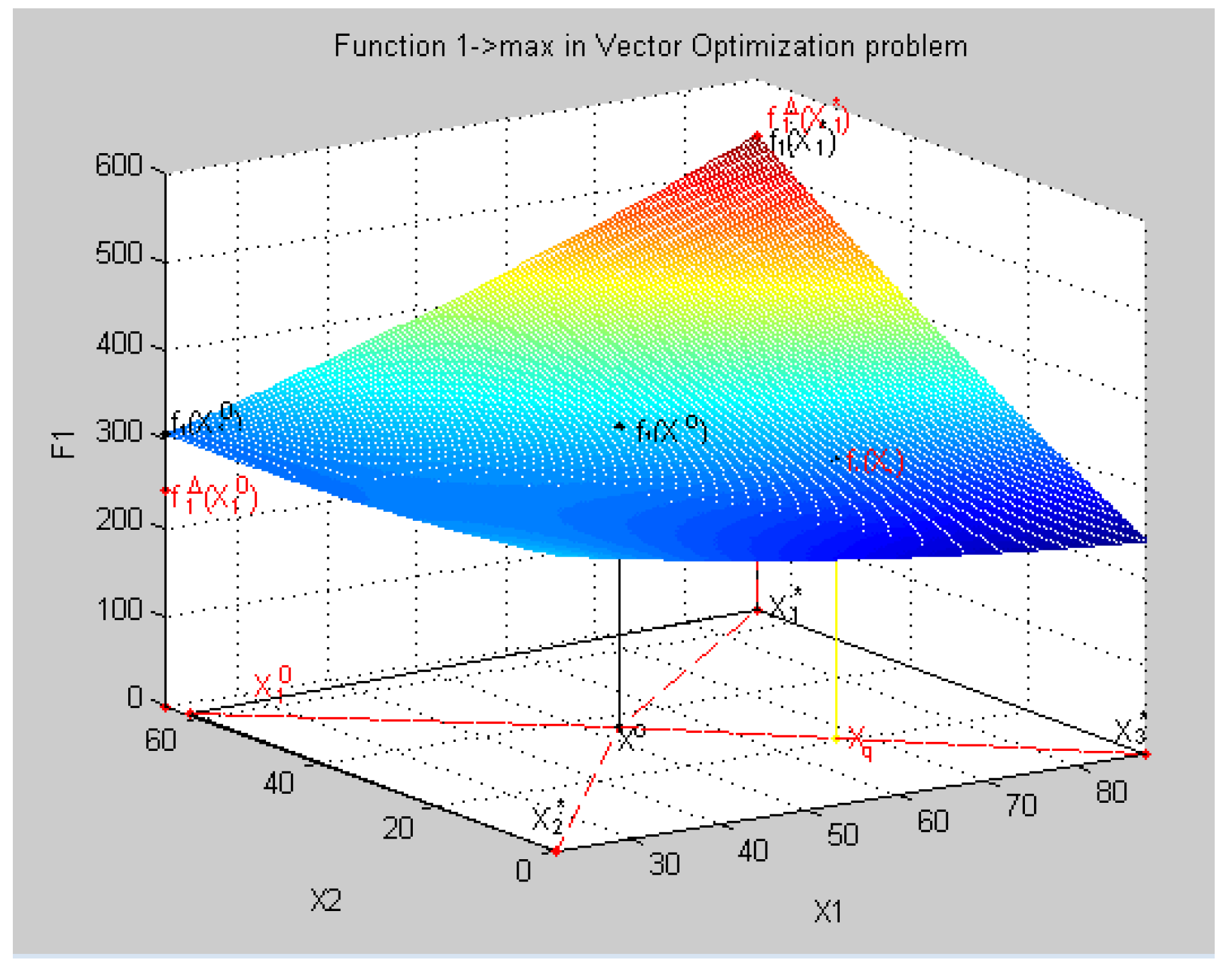
- X = {x1 = 88.0, x2 = 66.0, x3=8.8, x4 = 2.2}, f = f1(X) = −535.06,
- X = {x1 = 22.0, x2 = 0.0, x3=2.83, x4 = 6.25}, f = f2(X) = 1301.2,
- X = {x1 = 88.0, x2 = 0.0, x3=2.2, x4 = 8.8}, f = f3(X) = −100.15,
- X = {x1=22.0, x2 = 62.17, x3 = 2.2, x4 = 2.2}, f = f4(X) = 12.247.
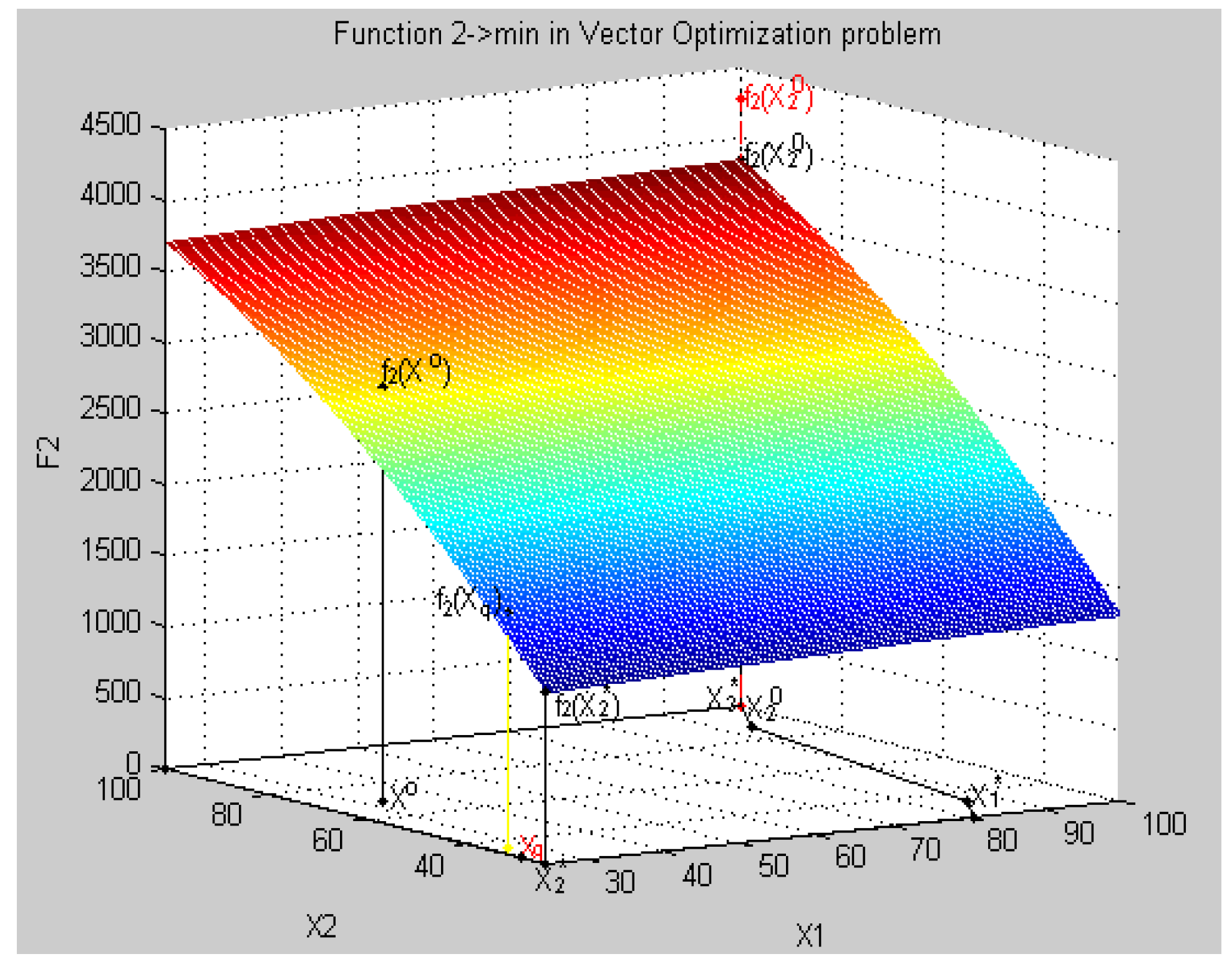
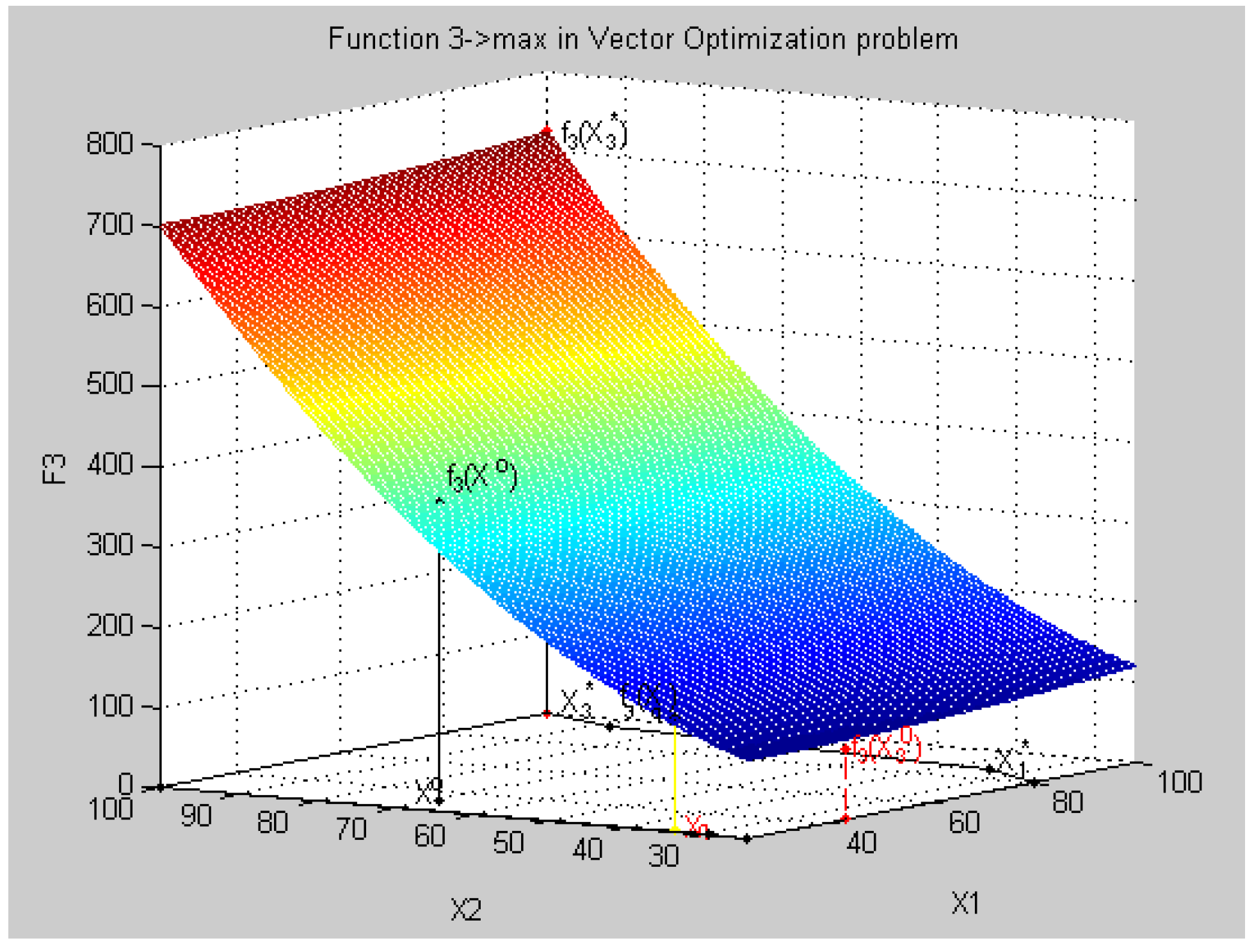
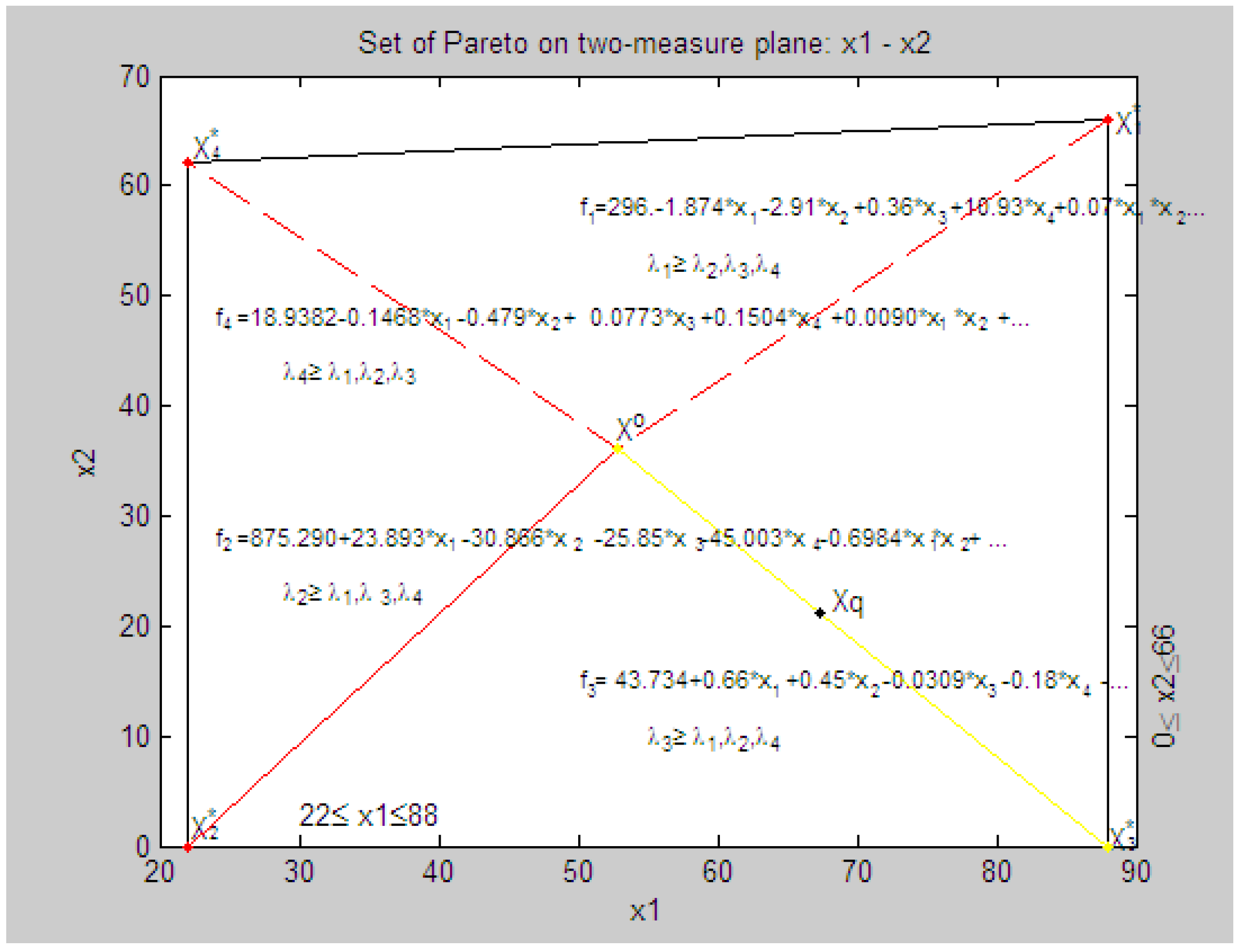
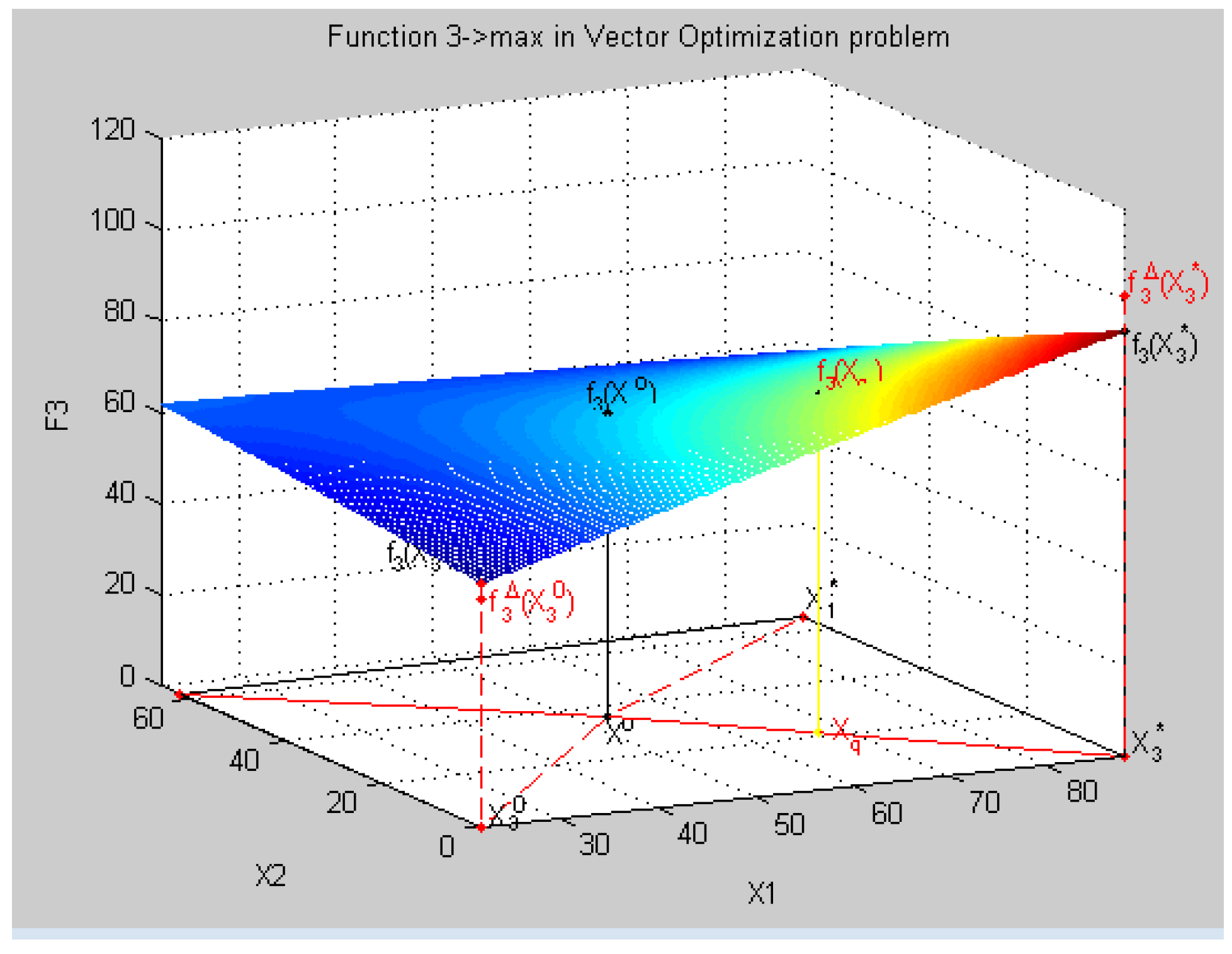
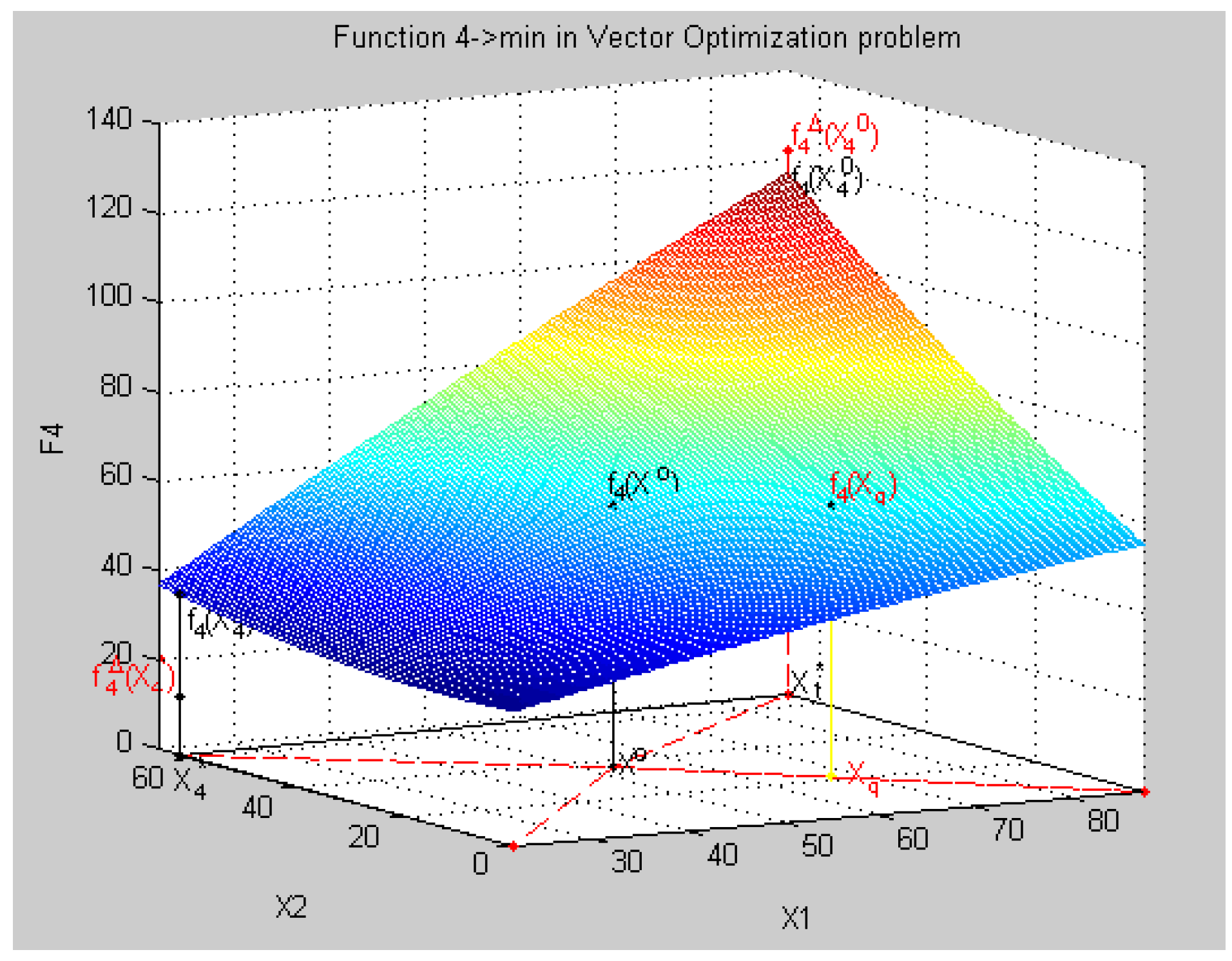
8.4. Geometric Interpretation of Results of the Decision in a Three-Dimensional Coordinate System in Relative Units
8.5. The Solution of a Vector Problem of Mathematical Programming—Model of the System at the Given Priority of the Criterion
- all criteria in physical units fk(Xq) = {fk(Xq), k = }:f(Xq) = {f1(Xq) = 313.45, f2(xq) = 2575.7, f3(xq) = 74.2, f4(xq) = 60.6},
- all relative estimates of criteria λq = {λ, k = }, λk(Xq) = , k = :λk(Xq) = {λ1(Xq) = 0.2405, λ2(xq) = 0.5102, λ3(xq) = 0.4825, λ4(xq) = 0.5586},
- the minimum relative assessment: minLXq = min(LXq): minLXq = min(λk(Xq)) = 0.2405,
- the vector of priorities Pq = {p = , k = }:Pq = (p = 2.0061, p = 0.9458, p = 1.0, p = 0.8637),
- the relative assessment taking into account a criterion priority:LXqPq = λk(Xq).*Pq = {pλ1(Xq), pλ2(Xq), pλ3(Xq), pλ4(Xq)}λk(Xq).*Pq = {0.7968 0. 7968 0. 7968 0. 7968},
- the the minimum relative assessment taking into account a criterion priority:λ00 = min (pλ1(Xq) = 0.4825, pλ2(Xq) = 0.4825, pλ3(Xq) = 0.4825, pλ4(Xq)) = 0.4825
8.6. Geometric Interpretation of Results of the Decision in a Three-Dimensional Coordinate System in Physical Units
- parameters of the system X0 = {x1 = 80.0, x2 = 69.11, x3 = 32.58, x4 = 20.0},
- the parameters of the system at a given priority criterion q = 3: Xq = {x1 = 67.313, x2 = 21.276}.
- point Xo, characteristics of f1(X0), f2(X0), f3(X0), f4(X0),
- relative estimates of λ1(X0), λ2(X0), λ3(X0), λ4(X0), and
- maximum relative level λ0 such that λ0 ≤ λk(X0) ∀k ∈ K
- point Xq, characteristics of f1(Xq), f2(Xq), f3(Xq), f4(Xq),
- relative estimates of λ1(Xq), λ2(Xq), λ3(Xq), λ4(Xq),
- maximum relative level λo such that λo ≤ pλk(Xq), k =
Funding
Conflicts of Interest
References
- Germeier, Y.B. Non_Antagonistic Games; Nauka: Moscow, Russia, 1976; Springer, 1986. [Google Scholar]
- Podinovskii, V.V. Analysis of Multicriteria Choice Problems by Methods of the Theory of Criteria Importance, Based on Computer Systems of Decision_Making Support. Comput. Syst. Sci. Int. 2008, 47, 221. [Google Scholar] [CrossRef]
- Malyshev, V.V.; Piyavskii, B.S.; Piyavskii, S.A. A decision making method under conditions of diversity of means of reducing uncertainty. Comput. Syst. Sci. Int. 2010, 49, 44–58. [Google Scholar] [CrossRef]
- Mashunin, Y.K. Solving composition and decomposition problems of synthesis of complex engineering systems by vector_optimization methods. Comput. Syst. Sci. Int. 1999, 38, 421. [Google Scholar]
- Mashunin, Y.K. Market Theory and Simulation Based on Vector Optimization; Universitetskaya kniga: Moscow, Russia, 2010. (In Russian) [Google Scholar]
- Mashunin, K.Y.; Mashunin, Y.K. Simulation Engineering Systems under Uncertainty and Optimal Descision Making. J. Comput. Syst. Sci. Int. 2013, 52, 519–534. [Google Scholar] [CrossRef]
- Mashunin, Y.K.; Mashunin, K.Y. Modeling of technical systems on the basis of vector optimization (2. with a Criterion Priority). Int. J. Eng. Sci. Res. Technol. 2014, 3, 224–240. [Google Scholar]
- Mashunin, Y.K.; Mashunin, K.Y. Simulation and Optimal Decision Making the Design of Technical Systems (2. The Decision with a Criterion Priority). Am. J. Model. Optim. 2016, 4, 51–66. [Google Scholar]
- Mashunin, Y.K. Vector optimization in the system optimal Decision Making the Design in economic and technical systems. Int. J. Emerg. Trends Technol. Comput. Sci. 2017, 7, 42–57. [Google Scholar]
- Mashunin, Y.K. Concept of Technical Systems Optimum Designing (Mathematical and Organizational Statement). In Proceedings of the International Conference on Industrial Engineering, Applications and Manufacturing, ICIEAM 2017, St. Petersburg, Russia, 16–19 May 2017; Proceedings 8076394; WOS: 000414282400287. ISBN 978-1-5090-5648-4. [Google Scholar]
- Keeney, R.L.; Raiffa, H. Decisions with Multiple Objectives–Preferences and Value Tradeoffs; Wiley: New York, NY, USA, 1976; Radio i svyaz’: Moscow, Russia, 1981. [Google Scholar]
- Mashunin, Y.K. Control Theory. The Mathematical Apparatus of Management of the Economy. Logos. Moscow. 2013. Available online: http://www.sciepub.com/reference/162155 (accessed on 11 October 2019). (In Russian).
- Mashunin, Y.K. Optimum Designing of the Technical Systems Concept (Numerical Realization). In Proceedings of the International Conference on Industrial Engineering, Applications and Manufacturing, ICIEAM 2017, St. Petersburg, Russia, 16–19 May 2017; ISBN 978-1-5090-5648-4. [Google Scholar]
- Cooke, T.; Lingard, H.; Blismas, N. The development and evaluation of a decision support tool for health and safety in construction design. Eng. Constr. Archit. Manag. 2008, 15, 336–351. [Google Scholar] [CrossRef]
- Mashunin, K.Y.; Mashunin, Y.K. Vector Optimization with Equivalent and Priority Criteria. J. Comput. Syst. Sci. Int. 2017, 56, 975–996. [Google Scholar] [CrossRef]
- Johannes, J. Vector Optimization: Theory, Applications, and Extensions; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2010; p. 510. [Google Scholar]
- Ansari, Q.; Jen Chih, Y. Recent Developments in Vector Optimization; Springer: Heidelberg, Germany; Dordrecht, The Netherlands; London, UK; New York, NY, USA, 2010. [Google Scholar]
- Hirotaka, N.; Yeboon, Y.; Min, Y. Sequential Approximate Multiobjective Optimization Using Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2009; p. 197. [Google Scholar]
- Shankar, R. Decision Making in the Manufacturing Environment: Using Graft Theory and Fuzzy Multiple Attribute Decision Making Methods; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Mashunin, Y.K.; Mashunin, K.Y. Modeling of technical systems on the basis of vector optimization (1. At equivalent criteria). Int. J. Eng. Sci. Res. Technol. 2014, 3, 84–96. [Google Scholar]
- Mashunin, Y.K. Methods and Models of Vector Optimization; Nauka: Moscow, Russia, 1986. [Google Scholar]
- Mashunin, Y.K.; Mashunin, K.Y. Simulation and Optimal Decision Making the Design of Technical Systems. Am. J. Model. Optim. 2015, 3, 56–67. [Google Scholar]
- Mashunin, Y.K.; Levitskii, V.L. Methods of Vector Optimization in Analysis and Synthesis of Engineering Systems. Monograph; DVGAEU: Vladivostok, Russia, 1996. (In Russian) [Google Scholar]
- Torgashov, A.Y.; Krivosheev, V.P.; Mashunin, Y.K.; Holland, C.D. Calculation and multiobjective optimization of static modes of mass_exchange processes by the example of absorption in gas separation. Izv. Vyssh. Uchebn. Zaved. Neft. Gaz. 2001, 3, 82–86. [Google Scholar]
- Mashunin, Y.K. Engineering system modeling on the base of vector problem of nonlinear optimization. In Control Applications of Optimization, Preprint of the Eleventh IFAC International Workshop; CAO: St._Petersburg, Russia, 2000. [Google Scholar]
- Ketkov, Y.L.; Ketkov, A.Y.; Shul’ts, M.M. MATLAB 6.x.: Numerical Programming; BKhV_Peterburg: St. Petersburg, Russia, 2004; p. 672. (In Russian) [Google Scholar]









| Type Resources | Costs of Resources of One Product | Possibilities of Firm on Resources | |||
|---|---|---|---|---|---|
| Type 1 | Type 2 | Type 3 | Type 4 | ||
| Labor (people/week) | 1 | 1 | 1 | 1 | 15 |
| Material (in kg) | 7 | 5 | 3 | 2 | 120 |
| Capacity (per hour) | 3 | 5 | 10 | 15 | 100 |
| Income from a unit of production | 4.0 | 5.0 | 9.0 | 11.0 | maximize |
| Profit , j = 1,...,4 | 2 | 10 | 6 | 20 | maximize |
| Output | x1 | x2 | x3 | x4 | To define |
| VPMP—Equations (1)–(4) | DMP_1—Equation (37) | DMP_2—Equation (38) |
|---|---|---|
| 2. Common Objective: Making the best decision | ||
| 3. Find the vector X from the admissible set, where the vector criterion F(X) is optimal | Objective: Find the alternative ai, i = , such that the set of criteria , k = is optimal | Objective: Find the vector alternative Xi, i = , such that the set of criteria F(X), is optimal |
| 4. The vector of parameters X and the dependence of criteria F(X) on it are given completely, the set of admissible points is finite: G(X)≤ 0, Xmin ≤ X ≤ Xmax. | Parameters are not given, the criteria are represented as the finite set of values, the set of admissible alternatives is finite | Parameters are given, the criteria are represented as separate values so that the functional dependence between them is not given, the set of admissible points is finite |
| Opt F(X) = {max F1(X) = {max fk(X), k = }, min F2(X) = {min fk(X), k = }}, G(X) ≤ 0, x≤ xj ≤ x, j = | 5. Transforming the Decision Making Problem into VMPP | |
| Using regression analysis, we transform each k-th k = set of values of criteria, , i = into the criterion function fk(x) | Using multiple regression, we transform each k-th k = set of values of criteria , i = into the criterion function | |
| 6. ↑ Problems are Equivalent→ | Opt F(x) = (f1(x))T. ≤ fk(x) ≤ , k = , xmin ≤ x ≤ xmax. | Opt F(X) = (f1(X(X))T. ≤ fk(X) ≤ , k = , Xmin ≤ X ≤ Xmax. |
| x | f1 | f2 | f3 | f4 |
|---|---|---|---|---|
| 630 | 4200 | 1950 | 1628 | 245 |
| 1580 | 6000 | 2100 | 1577 | 230 |
| 2662 | 8850 | 2090 | 1377 | 210 |
| 3704 | 11,000 | 2050 | 1200 | 200 |
| 4800 | 12,900 | 1950 | 1100 | 190 |
| 5929 | 14,730 | 1750 | 977 | 170 |
| 7284 | 16,310 | 1560 | 1050 | 151 |
| 9353 | 19,000 | 1350 | 1100 | 150 |
| 14,505 | 23,250 | 540 | 1457 | 100 |
| 18,810 | 29,970 | 400 | 2088 | 55 |
| x | λ1−max | λ2−max | λ3−min | λ4−max |
|---|---|---|---|---|
| 630 | -0.0276 | 0.933 | 0.451 | 1.0298 |
| 1580 | 0.0471 | 1.0214 | 0.4971 | 0.9463 |
| 2662 | 0.1653 | 1.0155 | 0.6781 | 0.8351 |
| 3704 | 0.2545 | 0.9919 | 0.8383 | 0.7795 |
| 4800 | 0.3334 | 0.933 | 0.9289 | 0.7239 |
| 5929 | 0.4093 | 0.8153 | 1.0402 | 0.6127 |
| 7284 | 0.4748 | 0.7034 | 0.9741 | 0.507 |
| 9353 | 0.5864 | 0.5798 | 0.9289 | 0.5014 |
| 14,505 | 0.7627 | 0.1029 | 0.6057 | 0.2234 |
| 18,810 | 1.0415 | 0.0205 | 0.0346 | −0.0269 |
| x1 | x2 | f1 | f2 | f3 | f4 | f5 |
|---|---|---|---|---|---|---|
| 0 | 0 | −80 | −150 | 232 | 278.4 | 500 |
| 0 | 2.5 | −102.5 | −121.875 | 215.125 | 222.15 | 556.25 |
| 0 | 5 | −130 | −97.5 | 204.5 | 173.4 | 625 |
| 0 | 7.5 | −162.5 | −76.875 | 200.125 | 132.15 | 706.25 |
| 0 | 10 | −200 | −60 | 202 | 98.4 | 800 |
| 2.5 | 0 | −102.5 | −166.875 | 185.125 | 258.15 | 406.25 |
| 2.5 | 2.5 | −125 | −138.75 | 168.25 | 201.9 | 462.5 |
| 2.5 | 5 | −152.5 | −114.375 | 157.625 | 153.15 | 531.25 |
| 2.5 | 7.5 | −185 | −93.75 | 153.25 | 111.9 | 612.5 |
| 2.5 | 10 | −222.5 | −76.875 | 155.125 | 78.15 | 706.25 |
| 5 | 0 | −130 | −187.5 | 144.5 | 245.4 | 325 |
| 5 | 2.5 | −152.5 | −159.375 | 127.625 | 189.15 | 381.25 |
| 5 | 5 | −180 | −135 | 117 | 140.4 | 450 |
| 5 | 7.5 | −212.5 | −114.375 | 112.625 | 99.15 | 531.25 |
| 5 | 10 | −250 | −97.5 | 114.5 | 65.4 | 625 |
| 7.5 | 0 | −162.5 | −211.875 | 110.125 | 240.15 | 256.25 |
| 7.5 | 2.5 | −185 | −183.75 | 93.25 | 183.9 | 312 |
| 7.5 | 5 | −212.5 | −159.375 | 82.625 | 135.15 | 381.25 |
| 7.5 | 7.5 | −245 | −138.75 | 78.25 | 93.9 | 462.5 |
| 7.5 | 10 | −282.5 | −121.875 | 80.125 | 60.15 | 556.25 |
| 10 | 0 | −200 | −240 | 82 | 242.4 | 200 |
| 10 | 2.5 | −222.5 | −211.875 | 65.125 | 186.15 | 256.25 |
| 10 | 5 | −250 | −187.5 | 54.5 | 137.4 | 325 |
| 10 | 7.5 | −282.5 | −166.875 | 50.125 | 96.15 | 406.25 |
| 10 | 10 | −320 | −150 | 52 | 62.4 | 500 |
| x1 | x2 | x3 | y1(X) → max | y2(X) → min |
|---|---|---|---|---|
| 25 | 25 | 25 | 412.5 | 1197.2 |
| 25 | 25 | 50 | 437.5 | 1232.8 |
| 25 | 25 | 75 | 462.5 | 1393.3 |
| 25 | 25 | 100 | 87.5 | 1303.8 |
| 25 | 50 | 25 | 312.5 | 2232.3 |
| 25 | 50 | 50 | 37.5 | 2267.7 |
| 25 | 50 | 75 | 62.5 | 2303.2 |
| 25 | 50 | 100 | 87.5 | 2338.8 |
| 25 | 75 | 25 | 212.5 | 3077.2 |
| 25 | 75 | 50 | 237.5 | 2862.8 |
| 25 | 75 | 75 | 262.5 | 3148.3 |
| 25 | 75 | 100 | 287.5 | 3183.7 |
| 25 | 100 | 25 | 12.5 | 3732.3 |
| 25 | 100 | 50 | 37.5 | 3767.7 |
| 25 | 100 | 75 | 62.5 | 3803.2 |
| 25 | 100 | 100 | 87.5 | 3838.8 |
| 50 | 25 | 25 | 512.5 | 1245.3 |
| 50 | 25 | 50 | 537.5 | 1303.8 |
| 50 | 25 | 75 | 562.5 | 1374.7 |
| 50 | 25 | 100 | 587.5 | 1445.8 |
| 50 | 50 | 25 | 512.5 | 2267.7 |
| 50 | 50 | 50 | 537.5 | 2338.8 |
| 50 | 50 | 75 | 562.5 | 2409.7 |
| 50 | 50 | 100 | 587.5 | 2480.8 |
| 50 | 75 | 25 | 412.5 | 3112.8 |
| 50 | 75 | 50 | 437.5 | 3183.7 |
| 50 | 75 | 75 | 462.5 | 3379.8 |
| 50 | 75 | 100 | 487.5 | 3325.8 |
| 50 | 100 | 25 | 212.5 | 3767.7 |
| 50 | 100 | 50 | 237.5 | 3838.8 |
| 50 | 100 | 75 | 262.5 | 3909.7 |
| 50 | 100 | 100 | 287.5 | 3980.8 |
| 75 | 25 | 25 | 612.5 | 1268.3 |
| 75 | 25 | 50 | 637.5 | 1374.7 |
| 75 | 25 | 75 | 662.5 | 1481.3 |
| 75 | 25 | 100 | 687.5 | 1587.8 |
| 75 | 50 | 25 | 612.5 | 2303.2 |
| 75 | 50 | 50 | 637.5 | 2409.7 |
| 75 | 50 | 75 | 662.5 | 2516.2 |
| 75 | 50 | 100 | 687.5 | 2622.7 |
| 75 | 75 | 25 | 512.5 | 3148.3 |
| 75 | 75 | 50 | 537.5 | 3254.8 |
| 75 | 75 | 75 | 562.5 | 3361.3 |
| 75 | 75 | 100 | 587.5 | 3467.8 |
| 75 | 100 | 25 | 312.5 | 3803.2 |
| 75 | 100 | 50 | 337.5 | 3909.7 |
| 75 | 100 | 75 | 362.5 | 4016.3 |
| 75 | 100 | 100 | 387.5 | 4122.7 |
| 100 | 25 | 25 | 612.5 | 1303.8 |
| 100 | 25 | 50 | 637.5 | 1445.8 |
| 100 | 25 | 75 | 662.5 | 1587.8 |
| 100 | 25 | 100 | 687.5 | 1729.7 |
| 100 | 50 | 25 | 612.5 | 2338.8 |
| 100 | 50 | 50 | 637.5 | 2480.8 |
| 100 | 50 | 75 | 662.5 | 2622.7 |
| 100 | 50 | 100 | 687.5 | 2764.7 |
| 100 | 75 | 25 | 512.5 | 3183.7 |
| 100 | 75 | 50 | 537.5 | 3325.8 |
| 100 | 75 | 75 | 562.5 | 3467.8 |
| 100 | 75 | 100 | 587.5 | 3609.8 |
| 100 | 100 | 25 | 312.5 | 3838.8 |
| 100 | 100 | 50 | 337.5 | 3980.8 |
| 100 | 100 | 75 | 362.5 | 4122.7 |
| 100 | 100 | 100 | 387.5 | 4264.8 |
| x1 | x2 | x3 | x4 | y2(X) →min | y3(X) →max |
|---|---|---|---|---|---|
| 22 | 0 | 2.2 | 2.2 | 1053.8 | 47.7 |
| 22 | 0 | 2.2 | 5.5 | 1067 | 47.3 |
| 22 | 0 | 2.2 | 8.8 | 1078 | 47.2 |
| 22 | 0 | 5.5 | 2.2 | 1111 | 50.7 |
| 22 | 0 | 5.5 | 5.5 | 1155 | 46.8 |
| 22 | 0 | 5.5 | 8.8 | 1152.8 | 46.3 |
| 22 | 0 | 8.8 | 2.2 | 1151.7 | 44.2 |
| 22 | 0 | 8.8 | 5.5 | 1148.4 | 43 |
| 22 | 0 | 8.8 | 8.8 | 1147.3 | 42.5 |
| 22 | 33 | 2.2 | 2.2 | 1964.6 | 58.3 |
| 22 | 33 | 2.2 | 5.5 | 1974.5 | 57.5 |
| 22 | 33 | 2.2 | 8.8 | 1983.3 | 57.1 |
| 22 | 33 | 5.5 | 2.2 | 1995.4 | 56.5 |
| 22 | 33 | 5.5 | 5.5 | 2003.1 | 55.1 |
| 22 | 33 | 5.5 | 8.8 | 2015.2 | 54.9 |
| 22 | 33 | 8.8 | 2.2 | 2027.3 | 54.8 |
| 22 | 33 | 8.8 | 5.5 | 2046 | 52.8 |
| 22 | 33 | 8.8 | 8.8 | 2058.1 | 53 |
| 22 | 66 | 2.2 | 2.2 | 2708.2 | 75.9 |
| 22 | 66 | 2.2 | 5.5 | 2585 | 71.5 |
| 22 | 66 | 2.2 | 8.8 | 2541 | 68.2 |
| 22 | 66 | 5.5 | 2.2 | 2519 | 66.4 |
| 22 | 66 | 5.5 | 5.5 | 2596 | 68.2 |
| 22 | 66 | 5.5 | 8.8 | 2662 | 70.4 |
| 22 | 66 | 8.8 | 2.2 | 2770.9 | 72.4 |
| 22 | 66 | 8.8 | 5.5 | 2783 | 71.5 |
| 22 | 66 | 8.8 | 8.8 | 2801.7 | 70.6 |
| 55 | 0 | 2.2 | 2.2 | 3284.6 | 100.5 |
| 55 | 0 | 2.2 | 5.5 | 3301.1 | 100.1 |
| 55 | 0 | 2.2 | 8.8 | 3307.7 | 99 |
| 55 | 0 | 5.5 | 2.2 | 3315.4 | 98.8 |
| 55 | 0 | 5.5 | 5.5 | 3320.9 | 97.9 |
| 55 | 0 | 5.5 | 8.8 | 3334.1 | 97.6 |
| 55 | 0 | 8.8 | 2.2 | 3347.3 | 97 |
| 55 | 0 | 8.8 | 5.5 | 3366 | 95.7 |
| 55 | 0 | 8.8 | 8.8 | 3378.1 | 95.3 |
| 55 | 33 | 2.2 | 2.2 | 1095.6 | 54.6 |
| 55 | 33 | 2.2 | 5.5 | 1111 | 50.6 |
| 55 | 33 | 2.2 | 8.8 | 1133 | 48.4 |
| 55 | 33 | 5.5 | 2.2 | 1147.3 | 47.7 |
| 55 | 33 | 5.5 | 5.5 | 1166 | 46.2 |
| 55 | 33 | 5.5 | 8.8 | 1188 | 45.1 |
| 55 | 33 | 8.8 | 2.2 | 1208.9 | 44.2 |
| 55 | 33 | 8.8 | 5.5 | 1232 | 42.2 |
| 55 | 33 | 8.8 | 8.8 | 1272.7 | 40.7 |
| 55 | 66 | 2.2 | 2.2 | 1995.4 | 61.8 |
| 55 | 66 | 2.2 | 5.5 | 2013 | 60.5 |
| 55 | 66 | 2.2 | 8.8 | 2035 | 59.4 |
| 55 | 66 | 5.5 | 2.2 | 2058.1 | 58.3 |
| 55 | 66 | 5.5 | 5.5 | 2095.5 | 57.2 |
| 55 | 66 | 5.5 | 8.8 | 2103.2 | 56.1 |
| 55 | 66 | 8.8 | 2.2 | 2120.8 | 54.8 |
| 55 | 66 | 8.8 | 5.5 | 2145 | 47.3 |
| 55 | 66 | 8.8 | 8.8 | 2183.5 | 51.3 |
| 88 | 0 | 2.2 | 2.2 | 2739 | 79.4 |
| 88 | 0 | 2.2 | 5.5 | 2761 | 78.1 |
| 88 | 0 | 2.2 | 8.8 | 2783 | 77 |
| 88 | 0 | 5.5 | 2.2 | 2801.7 | 75.9 |
| 88 | 0 | 5.5 | 5.5 | 2849 | 76.1 |
| 88 | 0 | 5.5 | 8.8 | 2893 | 76.6 |
| 88 | 0 | 8.8 | 2.2 | 2974.4 | 76.8 |
| 88 | 0 | 8.8 | 5.5 | 2959 | 715 |
| 88 | 0 | 8.8 | 8.8 | 2927.1 | 682 |
| 88 | 33 | 2.2 | 2.2 | 3315.4 | 1041 |
| 88 | 33 | 2.2 | 5.5 | 3336.3 | 1023 |
| 88 | 33 | 2.2 | 8.8 | 3355 | 1012 |
| 88 | 33 | 5.5 | 2.2 | 3378.1 | 1005 |
| 88 | 33 | 5.5 | 5.5 | 3399 | 990 |
| 88 | 33 | 5.5 | 8.8 | 3421 | 979 |
| 88 | 33 | 8.8 | 2.2 | 3440.8 | 970 |
| 88 | 33 | 8.8 | 5.5 | 3366 | 957 |
| 88 | 33 | 8.8 | 8.8 | 3503.5 | 935 |
| 88 | 66 | 2.2 | 2.2 | 1116.5 | 583 |
| 88 | 66 | 2.2 | 5.5 | 1144 | 561 |
| 88 | 66 | 2.2 | 8.8 | 1166 | 550 |
| 88 | 66 | 5.5 | 2.2 | 1208.9 | 530 |
| 88 | 66 | 5.5 | 5.5 | 1232 | 506 |
| 88 | 66 | 5.5 | 8.8 | 1276 | 484 |
| 88 | 66 | 8.8 | 2.2 | 1303.5 | 477 |
| 88 | 66 | 8.8 | 5.5 | 1342 | 440 |
| 88 | 66 | 8.8 | 8.8 | 1397 | 425 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mashunin, Y.K. Mathematical Apparatus of Optimal Decision-Making Based on Vector Optimization. Appl. Syst. Innov. 2019, 2, 32. https://doi.org/10.3390/asi2040032
Mashunin YK. Mathematical Apparatus of Optimal Decision-Making Based on Vector Optimization. Applied System Innovation. 2019; 2(4):32. https://doi.org/10.3390/asi2040032
Chicago/Turabian StyleMashunin, Yury K. 2019. "Mathematical Apparatus of Optimal Decision-Making Based on Vector Optimization" Applied System Innovation 2, no. 4: 32. https://doi.org/10.3390/asi2040032
APA StyleMashunin, Y. K. (2019). Mathematical Apparatus of Optimal Decision-Making Based on Vector Optimization. Applied System Innovation, 2(4), 32. https://doi.org/10.3390/asi2040032




