Performance of UAV-to-Ground FSO Communications with APD and Pointing Errors
Abstract
:1. Introduction
2. System and Channel Modeling
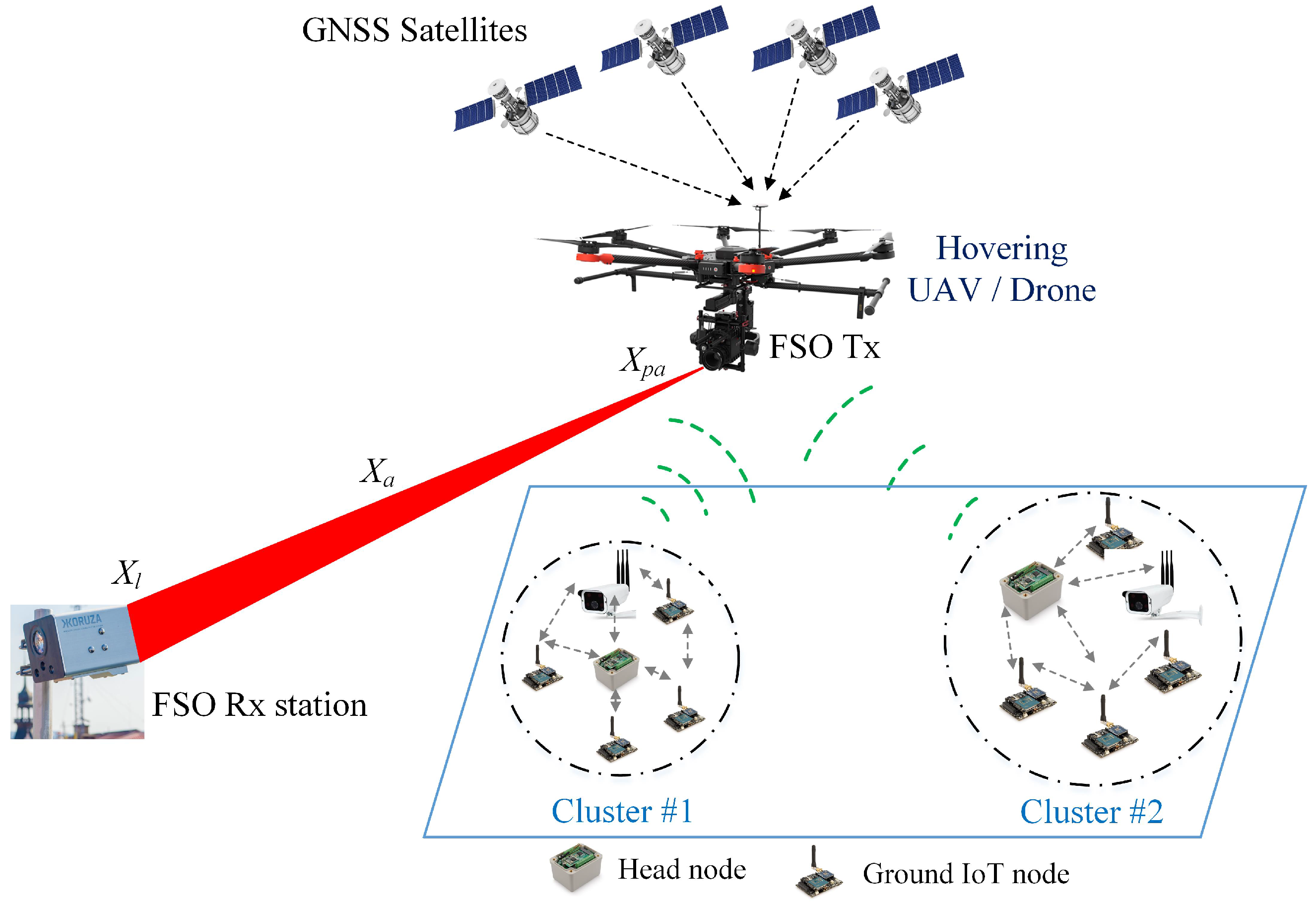
2.1. System Modeling
2.2. Channel Modeling
2.2.1. Atmospheric Attenuation and Turbulence
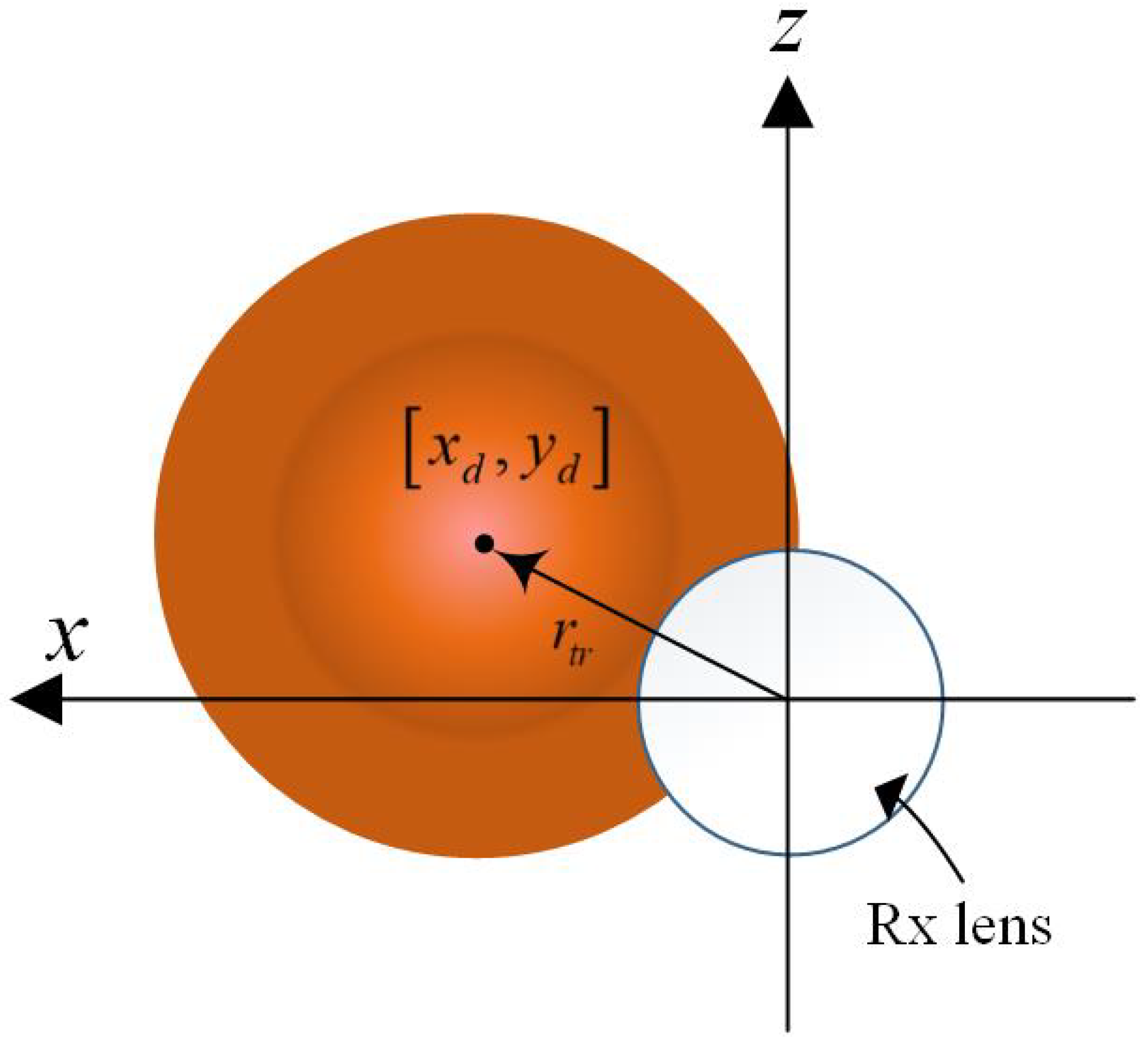
2.2.2. Pointing Error Loss
2.2.3. Combined Channel Models
3. Symbol Error Rate Calculation
3.1. SER Calculation of Weak to Moderate Links
3.2. SER Calculation of Moderate to Strong Links
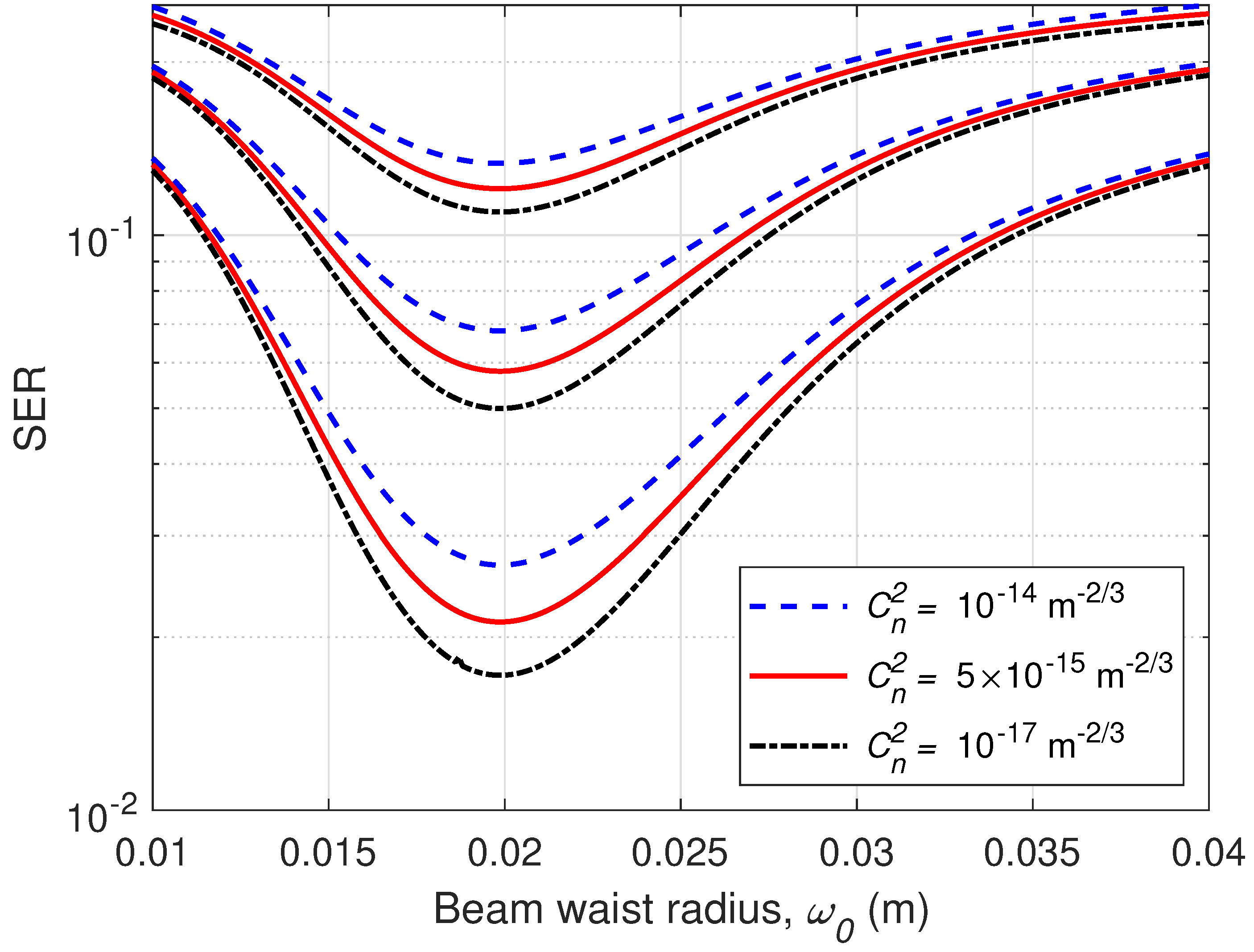
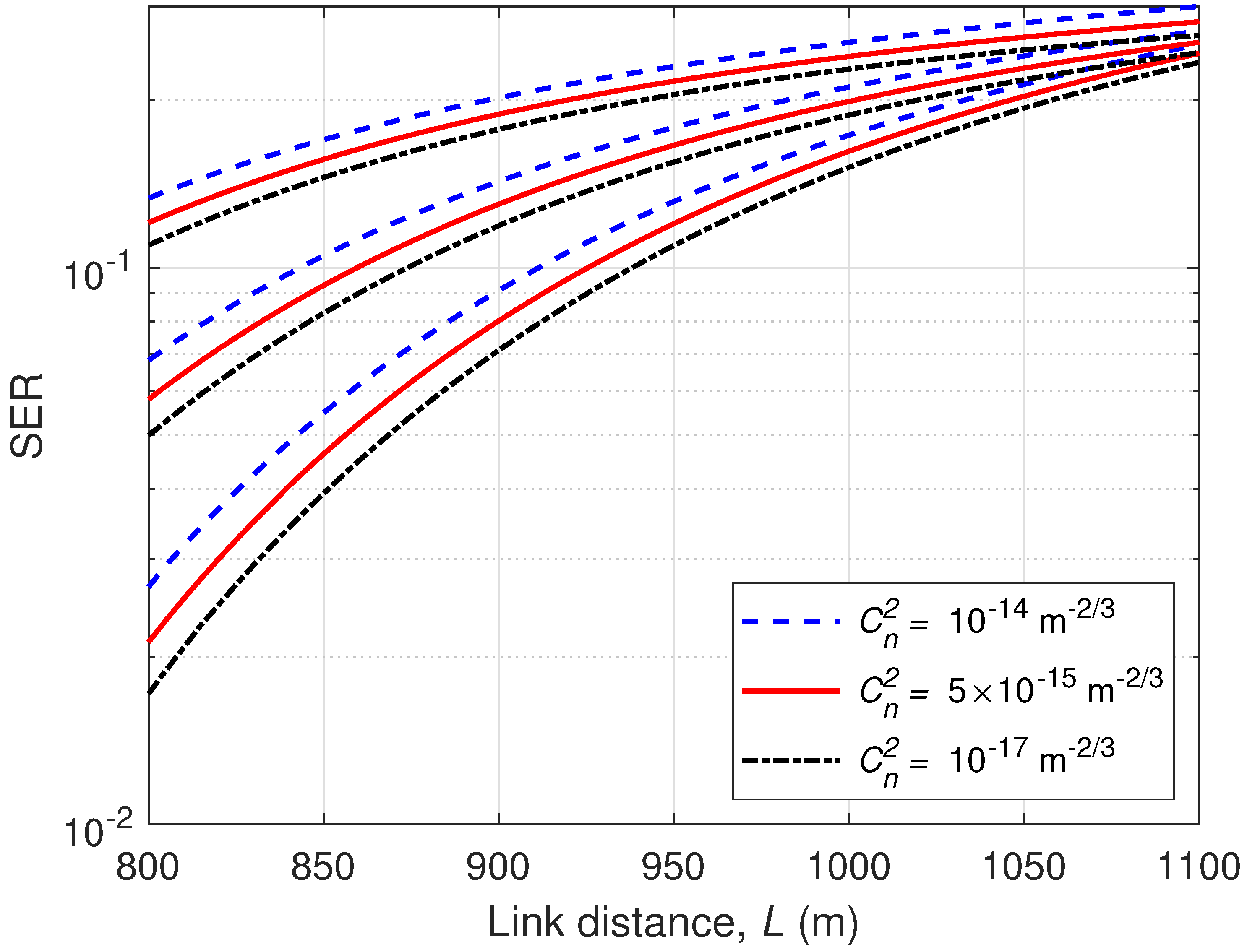
4. Performance Results
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chamola, V.; Kotesh, P.; Agarwal, A.; Naren; Gupta, N.; Guizani, M. A comprehensive review of unmanned aerial vehicle attacks and neutralization techniques. Ad. Hoc. Netw. 2021, 11, 102324. [Google Scholar] [CrossRef]
- Salhaoui, M.; Guerrero-González, A.; Arioua, M.; J Ortiz, F.; Oualkadi, A.E.; Torregrosa, C.L. Smart industrial IoT monitoring and control system based on UAV and cloud computing applied to a concrete plant. Sensors 2019, 19, 3316. [Google Scholar] [CrossRef] [Green Version]
- Hildmann, H.; Kovacs, E. Review: Using unmanned aerial vehicles (UAVs) as mobile sensing platforms (MSPs) for disaster response, civil security and public safety. Drones 2019, 3, 59. [Google Scholar] [CrossRef] [Green Version]
- Popescu, D.; Stoican, F.; Stamatescu, G.; Chenaru, O.; Ichim, L. A survey of collaborative UAV–WSN systems for efficient monitoring. Sensors 2019, 19, 4690. [Google Scholar] [CrossRef] [Green Version]
- Tien, P.V.; Nguyen, P.V.; Trung, H.D. Self-navigating UAVs for supervising moving objects over large-scale wireless sensor networks. Int. J. Aerosp. Eng. 2020, 2027340. [Google Scholar]
- Alzenad, M.; Shakir, M.Z.; Yanikomeroglu, H.; Alouini, M.-S. FSO-based vertical backhaul/fronthaul framework for 5G+ wireless networks. IEEE Commun. Mag. 2018, 56, 218–224. [Google Scholar] [CrossRef] [Green Version]
- Najafi, M.; Ajam, H.; Jamali, V.; Diamantoulakis, P.D.; Karagiannidis, G.K.; Schober, R. Statistical modeling of the FSO fronthaul channel for UAV-based communications. IEEE Trans. Commun. 2020, 68, 3720–3736. [Google Scholar] [CrossRef] [Green Version]
- Kurt, G.K.; Khoshkholgh, M.G.; Alfattani, S.; Ibrahim, A.; Darwish, T.S.J.; Alam, M.S.; Yanikomeroglu, H.; Yongacoglu, A. A vision and framework for the high altitude platform station (HAPS) networks of the future. IEEE Commun. Surv. Tutor. 2021, 23, 729–779. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Deng, Y.; Du, A.; Liu, J. Design of a free space optical communication system for an unmanned aerial vehicle command and control link. Photonics 2021, 8, 163. [Google Scholar] [CrossRef]
- Fotouhi, A.; Qiang, H.; Ding, M.; Hassan, M.; Giordano, L.G.; Garcia-Rodriguez, A.; Yuan, J. Survey on UAV cellular communications: Practical aspects, standardization advancements, regulation, and security challenges. IEEE Commun. Surv. Tutor. 2019, 21, 3417–3442. [Google Scholar] [CrossRef] [Green Version]
- Ding, J.; Mei, H.; I, C.-L.; Zhang, H.; Liu, W. Frontier progress of unmanned aerial vehicles optical wireless technologies. Sensors 2020, 20, 5476. [Google Scholar] [CrossRef]
- Dautov, K.; Kalikulov, N.; Kizilirmak, R.C. The Impact of Various Weather Conditions on Vertical FSO Links. In Proceedings of the 2017 IEEE 11th International Conference on Application of Information and Communication Technologies (AICT), Moscow, Russia, 20–22 September 2017. [Google Scholar]
- Trung, H.D.; Tuan, D.T. Performance of free-space optical communications using SC-QAM signals over strong atmospheric turbulence and pointing errors. In Proceedings of the 2014 IEEE Fifth International Conference on Communications and Electronics (ICCE), Danang, Vietnam, 30 July–1 August 2014; pp. 42–47. [Google Scholar]
- Khalighi, M.A.; Uysal, M. Survey on free space optical communication: A communication theory perspective. IEEE Commun. Surv. Tutor. 2014, 16, 2231–2258. [Google Scholar] [CrossRef]
- Dabiri, M.T.; Sadough, S.M.S.; Khalighi, M.A. Channel modeling and parameter optimization for hovering UAV-based free-space optical links. IEEE J. Sel. Areas Commun. 2018, 36, 2104–2113. [Google Scholar] [CrossRef] [Green Version]
- Heng, K.H.; Liu, N.; He, Y.; Zhong, W.D.; Cheng, T.H. Adaptive Beam Divergence for Inter-UAV Free Space Optical Communications. In Proceedings of the 2008 IEEE PhotonicsGlobal@Singapore, Singapore, 8–11 December 2008; pp. 1–4. [Google Scholar]
- Kaadan, A.; Refai, H.H.; LoPresti, P.G. Multielement FSO transceivers alignment for inter-UAV communications. J. Lightw. Technol. 2014, 32, 4785–4795. [Google Scholar] [CrossRef]
- Dabiri, M.T.; Sadough, S.M.S.; Ansari, I.S. Tractable optical channel modeling between UAVs. IEEE Trans. Veh. Technol. 2019, 68, 11543–11550. [Google Scholar] [CrossRef]
- Mai, V.V.; Kim, H. Beam size optimization and adaptation for high-altitude airborne free-space optical communication systems. IEEE Photonics J. 2019, 11, 1–13. [Google Scholar] [CrossRef]
- Wang, J.-Y.; Ma, Y.; Lu, R.-R.; Wang, J.-B.; Lin, M.; Cheng, J. Hovering UAV-based FSO communications: Channel modelling, performance analysis, and parameter optimization. arXiv 2021, arXiv:2104.05368. [Google Scholar]
- Khankalantary, S.; Dabiri, M.T.; Safic, H. BER performance analysis of drone-assisted optical wireless systems with APD receiver. Optics Commun. 2020, 463, 1–7. [Google Scholar] [CrossRef]
- Trung, H.D.; Hoa, N.T.; Trung, N.H.; Ohtsuki, T. A Closed-form expression for performance optimization of subcarrier intensity QAM signals-based relay-added FSO systems with APD. Phys. Commun. J. 2018, 31, 203–211. [Google Scholar] [CrossRef]
- Karp, S.; Gagliardi, R.M.; Moran, S.E.; Stotts, L.B. Optical Channel: Fibers, Clouds, Water, and the Atmosphere; Springer: New York, NY, USA, 1988. [Google Scholar]
- AlQuwaiee, H.; Yang, H.-C.; Alouini, M.-S. On the asymptotic capacity of dual-aperture FSO systems with generalized pointing error model. IEEE Trans. Wilress Commun. 2016, 15, 6502–6512. [Google Scholar] [CrossRef] [Green Version]
- Ai, D.H.; Trung, H.D.; Tuan, D.T. On the ASER performance of amplify-and-forward relaying MIMO/FSO systems using SC-QAM signals over log-normal and gamma-gamma atmospheric turbulence channels and pointing error impairments. J. Inf. Telecommun. 2020, 4, 267–281. [Google Scholar] [CrossRef] [Green Version]




| Description | Parameter | Value Setting |
|---|---|---|
| UAV and FSO Tx parameters | ||
| Operational wavelength | 1.55 | |
| Beam waist radius of Tx | 0.3–0.08 m | |
| The modulation index | m | 1 |
| In-phase, quadrature distances | 8, 4 | |
| Transmitted power per symbol | −15 ÷ 5 dBm | |
| Variance of position deviation | 30 cm | |
| Variance of orientation deviation | 6 cm | |
| FSO link parameters | ||
| Link length | L | 800 m ÷ 900 m |
| Attenuation coefficient | 3.436 | |
| Strength of weak turbulence | m | |
| Strength of moderate turbulence | m | |
| Strength of strong turbulence | m | |
| FSO Rx parameters | ||
| Lens radius | r | 0.04 m |
| Average APD gain | G | 18 ÷ 30 |
| Excess noise factor of APD | F | 2.75 |
| Electrical bandwidth of APD | Hz | |
| Optical filter bandwidth | m | |
| The Planck constant | m Kg/s | |
| APD’s load resistance | 1000 | |
| Receiver noise temperature | T | 3000 K |
| Ionization factor | 0.7 | |
| Boltzmann’s constant | J/K | |
| Amplifier noise figure | 2 | |
| Receiver aperture diameter | D | 0.08 m |
| Rx’s FOV angle | 20 mrad | |
| Variance of position deviation | 30 cm | |
| Variance of orientation deviation | 6 cm | |
| Spectral radiance of the background radiations | Watts/cm2-μm-srad |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trung, H.D. Performance of UAV-to-Ground FSO Communications with APD and Pointing Errors. Appl. Syst. Innov. 2021, 4, 65. https://doi.org/10.3390/asi4030065
Trung HD. Performance of UAV-to-Ground FSO Communications with APD and Pointing Errors. Applied System Innovation. 2021; 4(3):65. https://doi.org/10.3390/asi4030065
Chicago/Turabian StyleTrung, Ha Duyen. 2021. "Performance of UAV-to-Ground FSO Communications with APD and Pointing Errors" Applied System Innovation 4, no. 3: 65. https://doi.org/10.3390/asi4030065






