Design and Fabrication of Modified SMA-Connector Sensor for Detecting Water Adulteration in Honey and Natural Latex

Abstract

A detection system for water adulteration in honey is proposed. It consists of a modified SMA-connector sensor and a vector network analyzer. A modified SMA-connector sensor is applied to measure complex relative permittivity, electrical conductivity, and phase constant of honey samples with the open-ended method. The system is tested in the frequency range of 0.5–4.0 GHz at the sample temperature of 25 °C. The relationships between the complex relative permittivity, electrical conductivity, the phase constant, and the honey samples with different concentrations (0–30%w/w) are determined. The experimental results show that the real part of the complex relative permittivity is significantly proportional in honey samples with adulteration of water in the range of 0–30%w/w. The frequency of 0.6 GHz is a suitable frequency for detection with a real part of complex relative permittivity as an indicator. The frequency of 3.74 GHz is an appropriate frequency for detection with electrical conductivity as in indicator while the frequency of 4.0 GHz is suitable for detection with phase constant as an indicator. In addition, the data are analyzed with regression analysis. This technique is also performed on natural latex samples to determine the dry rubber content. The frequency of 0.5 GHz is a suitable frequency with a real part of complex relative permittivity as an indicator while the frequency of 4.0 GHz is a suitable frequency with an imaginary part of complex relative permittivity, electrical conductivity, and phase constant as the indicators. The results demonstrate that it is possible to apply this technique to determine the dry rubber content in the natural latex samples as well.

1. Introduction

Honey has been around since 7000 BC in the Stone Age [1]. It contains components such as organic acid, minerals and protein [2]. Honey products are usually directly consumed, and some of its products are used in the food industry for such things as infant food and ice cream. They also play a role in pharmaceuticals such as in the flavor of medicines [3]. The International Food Regulations have specified that pure honey must not contain any additives. However, additive sweeteners and water are widely used in honey. This adulteration is intended to increase volume and reduce cost, which is a major issue, since the contamination affects the nutritional value of honey. The color, concentration and viscosity of adulterated honey are quite similar to pure honey, making the adulterated honey even harder to detect by consumers. Consumers typically detect adulteration by sensory observations of the honey’s physical characteristics, which include color, viscosity and crystallization. The contamination can be detected by chemical analysis in the laboratory using methods such as chromatography, optical transmission analysis [3] and mass spectrometry [4]. These methods are complex processes. As such, the development of a fast, simple and low-cost method for honey adulteration detection is absolutely necessary.

Based on previous studies, many researchers have measured the complex relative permittivity and physical properties of materials associated with medical, constructional, industrial, or agricultural applications [5,6,7]. In [8], an open-ended coaxial probe is used to measure the complex relative permittivity of apples in a frequency range of 10–1800 MHz. The obtained relative permittivity can be used to determine properties such as moisture content and pH value of apples. A waveguide and coaxial transmission line technique are applied to measure the complex relative permittivity of eggs to predict the quality index of eggs [9]. In addition, the dielectric properties of honeydew melons are measured in order to compare it to the quality of honeydew melons [10]. There are also many other researchers interested in measuring the physical properties of food and agricultural materials [11,12,13,14,15].

Water, a main component in agricultural products i.e., honey, is sensitive to applied microwave frequencies and therefore the complex relative permittivity is dominantly influenced by the water content. The complex relative permittivity of a substance in an aqueous solution depends on water content. A water molecule is dipolar, which can be polarized in the range of microwave frequencies, and produce a tetrahedral molecular structure [4]. However, when other substances dissolve in water, the molecular structure of water changes, affecting polarization properties in the microwave frequency range, leading to a change in complex relative permittivity [4]. Measurement of the complex relative permittivity of honey sample can be applied to determine water content in honey sample, which is an indicator of honey quality in food industries. Understanding of the complex relative permittivity of honey is necessary to develop a model and thus assess the quality of honey. Although the dielectric properties of some agricultural materials have been studied, not many studies of the agricultural materials investigate the electrical conductivity and the phase constant with different microwave frequencies in the agricultural materials. There is little knowledge of how water content affects the complex relative permittivity, the electrical conductivity, and the phase constant of honey at microwave frequencies.

The complex relative permittivity (${\epsilon }_r$) of materials can be written as shown in Equation (1) [5]:

$${\epsilon }_r={\epsilon }_r^{\prime }-j{\epsilon }_r^{″},$$

(1)

where ${\epsilon }_r^{\prime }$ is the real part of complex relative permittivity, and ${\epsilon }_r^{″}$ is the imaginary part of complex relative permittivity. The δ is the loss angle of the material. It is also written in the form of loss tangent as in Equation (2) [5]:

$$tan\delta =\frac{{\epsilon }_r^{″}}{{\epsilon }_r^{\prime }},$$

(2)

which is the ratio of loss energy and stored energy in the material due to external electric fields [6]. In addition, the electrical conductivity $(\sigma )$ can be calculated as in Equation (3) [5]:

$$\sigma =2\pi f{\epsilon }_0{\epsilon }_r^{″},$$

(3)

where ${\epsilon }_0^{}$ is the permittivity of free space and $f$ is the electric frequency (Hz). The phase constant $(\beta )$ can be determined as in Equation (4) [5]:

$$\beta =\frac{2\pi f}{c_0}\sqrt{{\epsilon }_r^{\prime }}$$

(4)

where $c_0^{}$ is the speed of light.

In this paper, the complex relative permittivity, the electrical conductivity, and the phase constant of honey are characterized at the constant temperature (25 °C) over the frequency range of 0.5–4.0 GHz with different water contents using the open-ended transmission line technique. The proposed sensor is newly designed from the modification of a SMA-connector. The benefits of this technique are its compact design, ease of design, ability to be used in a wide range of frequencies, simple measuring process and non-destructive test, relatively high measurement accuracy and low-cost, all of which make this technique suitable for measuring the complex relative permittivity, electrical conductivity, and phase constant of honey. The obtained values are useful in the analysis of the relationship between water adulteration in honey, complex relative permittivity, electrical conductivity, and phase constant of honey. Knowledge of the properties of honey is an important step in the development of microwave sensors to determine the quality of honey for agricultural and food industries. Section 2 describes the materials and methods. In addition, it explains the experimental setup and the validation of the proposed sensor. Section 3 demonstrates the experimental results and discussions. Finally, the conclusions are presented in Section 4.

2. Materials and Methods

The honey sample preparation and the design of the proposed sensor are presented in this section. The details of the honey samples and the design are described as shown below.

2.1. Preparation of Honey Samples

All the characteristics of Thai honey according to the notification of the Ministry of Public Health of Thailand in 2000 defined the standards for Thai honey as shown in

Table 1. Honey standards of Thailand [16].

Composition	%w/w
Moisture	less than 21.0
Reducing sugar	at least 65.0
Sucrose	less than 5.0
Ash	less than 0.6
Insoluble substances	less than 0.1

[16].

The honey used in this study is 100% pure honey. Ten honey samples were analyzed for honey composition. The moisture and reducing sugar contents of samples have average values of 15.90 and 75.90%w/w, respectively. The sucrose and ash contents have average values of 1.30 and 0.4%w/w, respectively. The pure honey is mixed with distilled water at different water contents in the unit of %w/w. The honey samples mixed with water at different percentage are shown in Figure 1, which also shows the similar physical characteristics of color, flavor, taste and viscosity of honey adulterated with water.

2.2. Design of the Proposed Sensor

A SMA connector is one of connectors used in radio frequency and microwave devices [17,18,19]. The connector has the impedance of 50 $\mathrm{\Omega }$, and is typically designed for uses in the frequency range of 0–18 GHz. Figure 2 illustrates a photograph of the SMA connectors compared to a US quarter dollar.

The sensor used with the honey samples is a modified SMA connector. The low-cost modification involves trimming the pins to be an open-ended coaxial sensor, which can measure the complex relative permittivity of materials. Also, the results can be used to calculate the electrical conductivity, and the phase constant. The structure of the proposed sensor is shown in Figure 3.

In Figure 3a, A is the diameter of the inner coaxial core of 1.30 mm; B is the diameter of the outer coaxial core of 4.35 mm. The dielectric material in the connector is made of Teflon with ${\epsilon }_r$ of 2.08. The impedance of this connector is 50 $\mathrm{\Omega }$ that can be calculated by Equation (5) [20] as follows:

$$z=\frac{60}{\sqrt{{\epsilon }_r}}\ln \left(\frac{B}{A}\right)$$

(5)

The measurement of the complex relative permittivity (${\epsilon }_r$) of honey samples is based on the measurement of reflection coefficient $(S_{11}^{})$ when the connector is immersed in the honey samples. The change of the complex relative permittivity of the honey sample results in the change of the equivalent circuit of capacitor, reflection coefficient $(S_{11}^{})$ and admittance $(Y)$ as the model in Figure 4 [20].

From the equivalent circuit of the proposed sensor, $C_f$ is the capacitance independent of the material and $C_0$ is the capacitance of the capacitor filled with the air. The admittance ($Y$) of this sensor depends on the complex relative permittivity (${\epsilon }_r$) of material as in Equation (6) [20,21,22]:

$$\mathrm{Y}=\mathrm{j}\mathsf{\omega }{\mathsf{\epsilon }}_{\mathrm{r}}{\mathrm{C}}_0+\mathrm{j}\mathsf{\omega }{\mathrm{C}}_{\mathrm{f}},$$

(6)

when $Y$ is related to the reflection coefficient $(S_{11}^{})$ as in Equation (7) [20,21]:

$$Y=\frac{1}{Z_0}(\frac{1-S_{11}}{1+S_{11}}).$$

(7)

From Equations (6) and (7), the relationship of the complex relative permittivity and reflection coefficient can be derived by measuring the three reference materials with known complex relative permittivity and a material with unknown complex relative permittivity as in Equation (8) [5]:

$$\frac{\left({\epsilon }_{UN}-{\epsilon }_A\right)\left({\epsilon }_B-{\epsilon }_C\right)}{\left({\epsilon }_{UN}-{\epsilon }_B\right)\left({\epsilon }_C-{\epsilon }_A\right)}=\frac{\left(S_{11,UN}-S_{11,A}\right)\left(S_{11,B}-{\mathrm{S}}_{11,C}\right)}{\left(S_{11,UN}-S_{11,B}\right)\left({\mathrm{S}}_{11,C}-{\mathrm{S}}_{11,A}\right)}$$

(8)

Equation (8) is used to determine the complex relative permittivity (${\epsilon }_{UN}$) of the unknown material when the complex relative permittivity of the three materials (${\epsilon }_A,{\epsilon }_B,{\epsilon }_C$) and the reflection coefficient of all four materials (A, B, C, UN) are determined. $S_{11,A},S_{11,B},S_{11,C}$ and $S_{11,UN}$ values can be measured with a vector network analyzer and ${\epsilon }_A,{\epsilon }_B,{\epsilon }_C$ can be found in [5,6]. Therefore, the equation only needs to calculate ${\epsilon }_{UN}$. The sensor we designed and built must be tested for validation before using it with honey samples. The testing procedures are shown in Figure 5.

The validation of the sensor is a test to provide the reflection coefficient of four materials: air (A), distilled water (B), ethanol (C) and methanol (UN) which can be determined in the experiments as shown in Figure 5 by measuring it when the temperature of material is constant at the temperature of 25 °C. The complex relative permittivity of air (A), distilled water (B) and ethanol (C), which is used in Equation (8) can be found in [5,6].

After the reflection coefficient ($S_{11}$) is obtained from the vector network analyzer ($S_{11,A},S_{11,B},S_{11,C},S_{11,UN}$) and the complex relative permittivity (${\epsilon }_A,{\epsilon }_B,{\epsilon }_C$) is obtained from [5,6], all values are substituted to Equation (8) to solve for ${\epsilon }_{UN}$. The value of ${\epsilon }_{UN}$ in Equation (8) can be calculated and is shown in Figure 6, which is the complex relative permittivity of methanol. Also, the electrical conductivity, and phase constant are calculated and shown in Figure 6. For validation, the complex relative permittivity, the electrical conductivity, and the phase constant of methanol (${\epsilon }_{UN},\sigma ,\beta$) from [5,6] are used for comparison. The comparison demonstrates the accuracy of the complex relative permittivity both in real part and imaginary part (${\epsilon }_r={\epsilon }_r^{\prime }-j{\epsilon }_r^{″}$), electrical conductivity, and phase constant in the frequency range of 0.5–4.0 GHz. The proposed results accord well with the literature data as shown in Figure 6. The validation indicates that the proposed sensor can be properly used. From this validation, Equation (8) is modified as shown in Equation (9).

$${\epsilon }_{UN}=\frac{({\mathsf{\epsilon }}_{AIR}-{\epsilon }_{WATER}\mathrm{X})}{\left(1-\mathrm{X}\right)},$$

(9)

where X is $\left(\frac{S_{11,UN}-S_{11,AIR}}{S_{11,UN}-S_{11,WATER}}\right)\left(\frac{S_{11,WATER}-S_{11,ETHANOL}}{S_{11,ETHANOL}-S_{11,AIR}}\right)\left(\frac{{\epsilon }_{ETHANOL}-{\epsilon }_{AIR}}{{\epsilon }_{WATER}-{\epsilon }_{ETHANOL}}\right).$

3. Results and Discussions

The validation test of the sensor ensures that this sensor can be practically used in the frequency range of 0.5–4.0 GHz at 25 °C to measure the accurate complex relative permittivity, electrical conductivity, and phase constant of material. The measurement test of pure honey can be done by immersing the sensor in pure honey and connecting the other end of the cable to the vector network analyzer and recording the reflection coefficient of the pure honey. In this experiment, three samples with known complex relative permittivity are air (A), distilled water (B), and ethanol (C). Equation (9) is applied to determine the complex relative permittivity of the unknow material. The honey samples are considered the unknown material (UN). The experimental setup is shown in Figure 5.

The reflection coefficients are used to determine the complex relative permittivity according to Equation (9). Equations (3) and (4) are used to calculate the electrical conductivity and the phase constant. The results of complex relative permittivity both real part and imaginary part, electrical conductivity, and phase constant in the frequency range of 0.5–4.0 GHz are shown in Figure 7. Figure 7a demonstrates the complex relative permittivity in the microwave frequency range of 0.5–4.0 GHz. The complex relative permittivity of pure honey both real part and imaginary part monotonically decreased with increasing frequency. However, in Figure 7b,c, the electrical conductivity, and the phase constant of pure honey increased with increasing frequency. The real part values of complex relative permittivity range between 9.77 and 20.35 while the imaginary part values lie between 5.20 and 10.10. The electrical conductivity values range between 0.28 and 1.12 S/m while the phase constant values lie between 0.05 and 0.26 rad/mm. The real part of the honey sample decreases with increasing frequency (0.5–4.0 GHz), similar to water [23], since the honey sample contains up to 15.90%w/w moisture content.

The complex relative permittivity, the electrical conductivity, and the phase constant of honey samples in the frequency of 0.5–4.0 GHz are revealed in Figure 7. Further study is performed with water adulteration in honey samples. The sample preparation for the detection of water adulteration in honey can be done by preparing seven different adulterated honey samples as follows: pure honey, honey with water adulteration at 5–30%w/w. Each adulterated honey sample has five samples to measure for average values. The experiments are performed with the sample temperature of 25 °C.

After the measurement, the complex relative permittivity, the electrical conductivity, and the phase constant of the honey samples at different frequencies are calculated and shown in Figure 8, Figure 9 and Figure 10, respectively.

From Figure 8a, when the water content in the honey increases, the real part of the complex relative permittivity increases throughout the 0.5–4.0 GHz frequency range because the real part of the relative permittivity of water is as high as 78.3 [23], results in the real part of the complex relative permittivity of adulterated honey increases as well. Figure 8b shows the imaginary part of complex relative permittivity of the adulterated honey samples with water in the range of 0–30%w/w. The imaginary part of the complex relative permittivity increases when compared to the pure honey sample. However, each adulterated honey sample with different water content shows slight difference in the imaginary part of complex relative permittivity. The difference of the real part of complex relative permittivity of each honey sample is the highest at lower frequencies. A figure of merit (FOM1) for measuring the performance of this technique using the real part of complex relative permittivity is calculated in Equation (10).

$$FOM1=\frac{\mathsf{\Delta }{\epsilon }_r^{\prime }}{\mathsf{\Delta }\left(\%w/w\right)}$$

(10)

The FOM1 can help to judge how well the performance of this technique using the real part of permittivity is. From Figure 8a, the measured results show that the difference of the real part of complex relative permittivity ($∆{\epsilon }_r^{\prime }$) of pure honey and the honey sample (water adulteration for 30%w/w) is 33.24 at the frequency of 0.6 GHz and the temperature of 25 °C while the difference of water content of both samples is 30%w/w. Therefore, the FOM1 is equal to 1.108 (%w/w)⁻¹ at the frequency of 0.6 GHz. Figure 11 shows the FOM1. The FOM1 is performed at the frequency of 4.0 GHz as well. Its FOM1 is equal to 0.715 (%w/w)⁻¹. From the results, it shows that the real part of the complex relative permittivity is the most appropriate indicator in water adulteration detection in honey at 0.6 GHz, and the FOM1 is equal to 1.108 (%w/w)⁻¹.

Figure 9 shows the electrical conductivity of the adulterated honey samples with water in the range of 0–30%w/w. The electrical conductivity increases when compared to pure honey. The electrical conductivity is slightly changed in the frequency range of 0.5–1.5 GHz while the significant increase occurs in the higher frequency range of 1.5–4.0 GHz. A figure of merit (FOM2) for measuring the performance of this technique using the electrical conductivity is described in Equation (11).

$$FOM2=\frac{\mathsf{\Delta }\sigma }{\mathsf{\Delta }\left(\%w/w\right)}$$

(11)

Figure 12 demonstrates the FOM2 in the frequency range of 0.5–4.0 GHz. The maximum FOM2 is equal to 0.069 S/m * (%w/w)⁻¹ at the frequency of 3.74 GHz. Therefore, the frequency of 3.74 GHz is the most appropriate frequency when the electrical conductivity is considered the indicator.

Figure 10 shows the phase constant of the adulterated honey samples with water in the range of 0–30%w/w. The phase constant increases when compared to pure honey. The significant change occurs in the frequency range of 1.5–4.0 GHz. A figure of merit (FOM3) for measuring the performance of this technique using the phase constant is given by Equation (12).

$$FOM3=\frac{\mathsf{\Delta }\beta }{\mathsf{\Delta }\left(\%w/w\right)}$$

(12)

Figure 13 depicts the FOM3 in the frequency range of 0.5–4.0 GHz. The maximum FOM3 is equal to 0.007 rad/mm * (%w/w)⁻¹ at the frequency of 4.0 GHz. The frequency of 4.0 GHz is the most suitable frequency when the phase constant is considered the indicator.

From the FOMs, it can be concluded in

Table 2. Comparison of FOMs in experiments of honey samples.

FOM	Indicator	Suitable Frequency (GHz)
FOM1	Real part of complex relative permittivity $\left({\epsilon }_r^{\prime }\right)$	0.60
FOM2	Electrical conductivity $\left(\sigma \right)$	3.74
FOM3	Phase constant $\left(\beta \right)$	4.00

according to the indicators for measurements.

In regression analysis (R²) for the real part of complex relative permittivity, the electrical conductivity, and the phase constant, curve fitting is the process of determining which model best fits specific curves in the data set. It is found that the real part of complex relative permittivity at the frequency of 0.6 GHz has the polynomial relationship with the adulterations. The relationship is shown in Equation (13) and Figure 14 shows the curve fitting of real part of relative permittivity at 0.6 GHz on water adulteration in honey samples with R² of 0.9968.

$${\epsilon }_r^{\prime }=p1\ast x^2+p2\ast x+p3,$$

(13)

where p1 = −0.006279, p2 = 1.268, p3 = 20.05 and x = %w/w at 0.6 GHz.

It is found in the regression analysis for electrical conductivity that the electrical conductivity at the frequency of 3.74 GHz has the polynomial relationship with the adulterations. Equation (14) shows the relationship and Figure 15 shows the curve fitting of electrical conductivity at 3.74 GHz on water adulteration in honey samples with R² of 0.9833.

$$\sigma =p1\ast x^2+p2\ast x+p3,$$

(14)

where p1 = −0.0007925, p2 = 0.08857, p3 = 1.212 and x = %w/w at 3.74 GHz.

In the regression analysis for phase constant, it is found that the phase constant at the frequency of 4.0 GHz has the polynomial relationship with the adulterations. Equation (15) shows the equation and Figure 16 shows the regression of phase constant at 4.0 GHz on water adulteration in honey samples with R² of 0.9977.

$$\beta =p1\ast x^2+p2\ast x+p3,$$

(15)

where p1 = 6.634 × 10⁻⁶, p2 = 0.006855, p3 = 0.2673 and x = %w/w at 4.0 GHz.

From the curve fittings, it is shown that the real part of complex relative permittivity, the electrical conductivity, and the phase constant models given in Equations (13)–(15) could accurately describe the real part of permittivity (0.6 GHz), the electrical conductivity (3.74 GHz), and the phase constant (4.0 GHz) with the water adulteration in honey samples, respectively.

The proposed technique is successful in determination of the complex relative permittivity of the honey samples. Further study is performed on the natural latex samples to obtain the initial results. The experimental setup is shown in Figure 5. After the measurement is performed, the dry rubber content (DRC) of the natural latex is determined as shown in Figure 17. The obtained DRC is 35.27%w/w.

In Figure 18, the proposed technique can be used to determine the complex relative permittivity of the natural latex samples. The real part is in the range of 34–37 while the imaginary ranges from 7–14. From the results in Figure 18, it is possible to apply the proposed sensor to determine the DRC in different concentrations and choose the suitable frequency for the determination of the DRC.

Generally, DRC is inversely proportional to the water content of the natural latex sample. In the experiments for the natural latex samples with DRC in the range of 29.28–35.27%w/w, the complex relative permittivity, the electrical conductivity, and the phase constant of the natural latex samples at different frequencies are calculated and shown in Figure 19, Figure 20, Figure 21 and Figure 22, respectively. In Figure 19, when the DRC decreases due to the increasing water content in the natural latex samples, the real part of the complex relative permittivity increases over the frequency range of 0.5–4.0 GHz because of the high real part of the complex relative permittivity of water [23]. Therefore, the real part of the complex relative permittivity of natural latex samples increases as well. The maximum FOM1 is equal to 1.4462 (%w/w)⁻¹ at the frequency of 0.5 GHz. The frequency of 0.5 GHz is the most suitable frequency when the real part of the complex relative permittivity is considered the indicator. 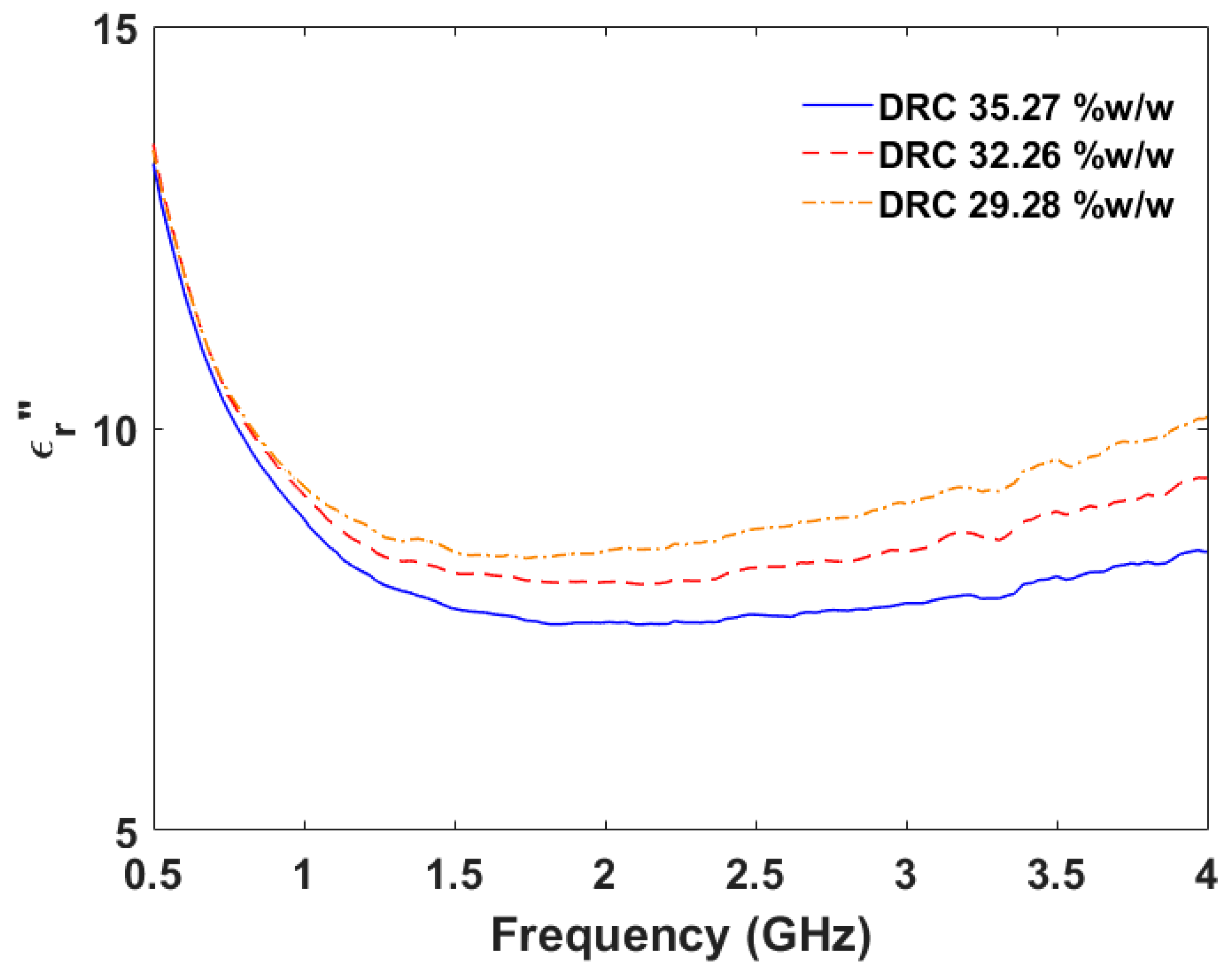Figure 20 shows the imaginary part of complex relative permittivity of the natural samples with different DRCs. The imaginary part of the complex relative permittivity increases when the DRC in the natural latex sample decreases. The maximum figure of merit is equal to 0.2759 (%w/w)⁻¹ at the frequency of 4.0 GHz. Therefore, the frequency of 4.0 GHz is the most appropriate frequency when the imaginary part of the complex relative permittivity is considered the indicator. Figure 21 demonstrates the electrical conductivity of the natural latex samples with different DRCs. When the DRC in the natural latex sample decreases, the electrical conductivity is slightly changed in the frequency range of 0.5–1.0 GHz while the significant increase occurs in the higher frequency range of 1.0–4.0 GHz. The maximum FOM2 is equal to 0.0612 S/m * (%w/w)⁻¹ at the frequency of 4.0 GHz. Therefore, when considering the electrical conductivity as an indicator, the frequency of 4.0 GHz is the optimum frequency. 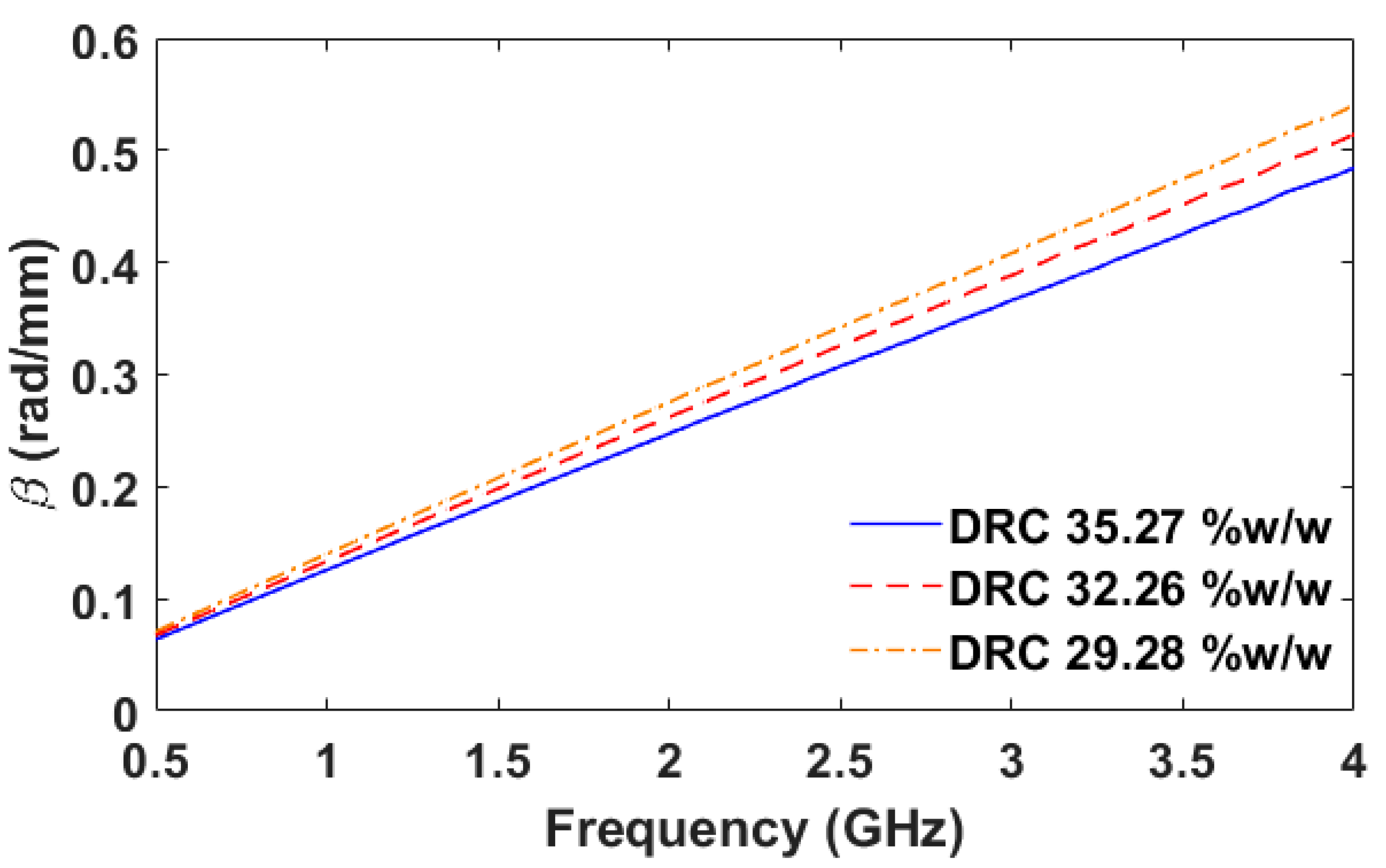Figure 22 depicts the phase constant of the natural latex samples with different DRCs. The phase constant is inversely proportional to the DRC over the frequency range of 0.5–4.0 GHz. The significant increase of the phase constant occurs over the frequency range of 0.7–4.0 GHz. The maximum FOM3 is equal to 0.0093 rad/mm * (%w/w)⁻¹ at the frequency of 4.0 GHz. When using the phase constant as an indicator, the frequency of 4.0 GHz is the most suitable frequency.

4. Conclusions

Water adulteration in honey is the simplest and most popular adulteration method because the physical properties of honey adulterated with water (color, smell, taste, viscosity and crystallization) are very similar to natural pure honey. A modified SMA-connector sensor is successfully fabricated and is accurately validated with the methanol for the frequency range of 0.5–4.0 GHz at the constant temperature of 25 °C. The modified SMA-connector sensor has been proposed to measure the complex relative permittivity, the electrical conductivity, and the phase constant of honey adulterated with water at 0–30%w/w in the frequency range of 0.5–4.0 GHz at the constant temperature of 25 °C. There is little difference in the imaginary part of the complex relative permittivity of honey samples adulterated with water at 5–30%w/w throughout the frequency range of 0.5–4.0 GHz at 25 °C. The real part of the complex relative permittivity of the honey sample adulterated with water is significantly different throughout the frequency range of 0.5–4.0 GHz at 25 °C. The frequency of 0.6 GHz is the most suitable to detect water adulteration in honey using the real part of complex relative permittivity since the FOM1 is the highest at 1.108 (%w/w)⁻¹. The electrical conductivity of the honey sample is directly proportional to the frequency. The electrical conductivity of the honey sample increases when the water adulteration increases. To use the electrical conductivity as an indicator to detect water adulteration in honey, the frequency of 3.74 GHz is the most appropriate frequency since the FOM2 is the highest at this frequency at 0.069 S/m * (%w/w)⁻¹. The phase constant of the honey sample is directly proportional to the frequency. For the phase constant as an indicator to detect water adulteration in honey, the frequency of 4.0 GHz is the most appropriate frequency because the maximum FOM3 is at this frequency at 0.007 rad/mm * (%w/w)⁻¹.

From this concept, the proposed sensor could have many other potential applications for determination of relative permittivity, such as alcohol content determination in some solutions, dry rubber content determination in fresh latex, and etc. Further study is performed in the natural latex. Normally, DRC is inversely proportional to the water content of the natural latex sample. The proposed method can be used to determine the complex relative permittivity of natural latex samples. The real part is in the range of 34–37 and the imaginary part is in the range of 7–14. In the experiments for the natural latex samples with DRC in the range of 29.28–35.27%w/w, the real part of the complex relative permittivity increases when the DRC decreases. The maximum FOM is equal to 1.4462 (%w/w)⁻¹ at the frequency of 0.5 GHz. The imaginary part of the complex relative permittivity increases when the DRC decreases. The maximum FOM is equal to 0.2759 (%w/w)⁻¹ at the frequency of 4.0 GHz. The electrical conductivity and the phase constant increase when the DRC decreases. The maximum FOMs for the electrical conductivity and the phase constant are 0.0612 S/m * (%w/w)⁻¹ and 0.0093 rad/mm * (%w/w)⁻¹ at the frequency of 4.0 GHz, respectively. The results demonstrate that it is possible to apply this technique to determine the DRC in the natural latex.