Enhancing Industrial Valve Diagnostics: Comparison of Two Preprocessing Methods on the Performance of a Stiction Detection Method Using an Artificial Neural Network
Abstract
1. Introduction
Stiction
2. Background Study
2.1. Multisensor Data Fusion
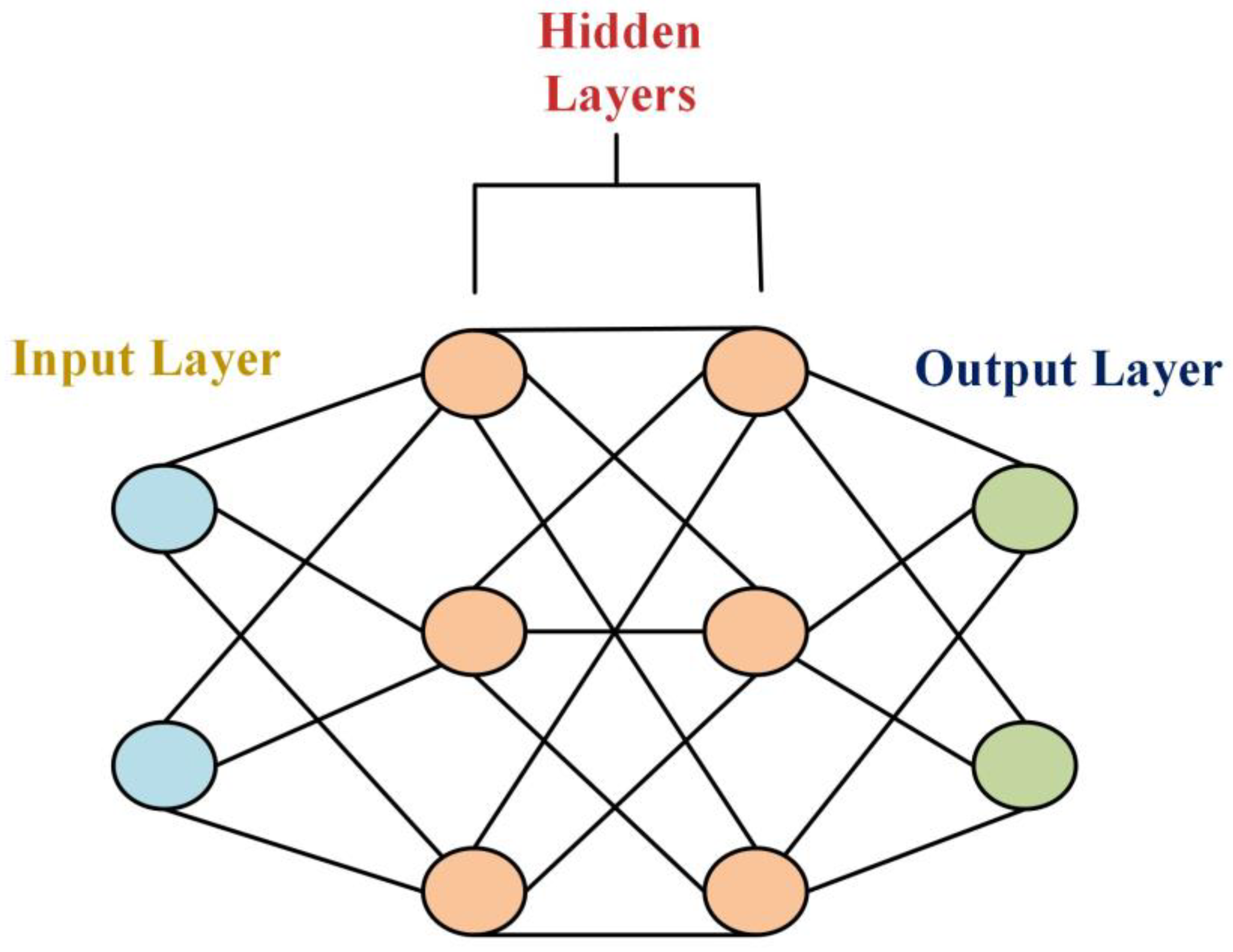
2.2. Neural Network
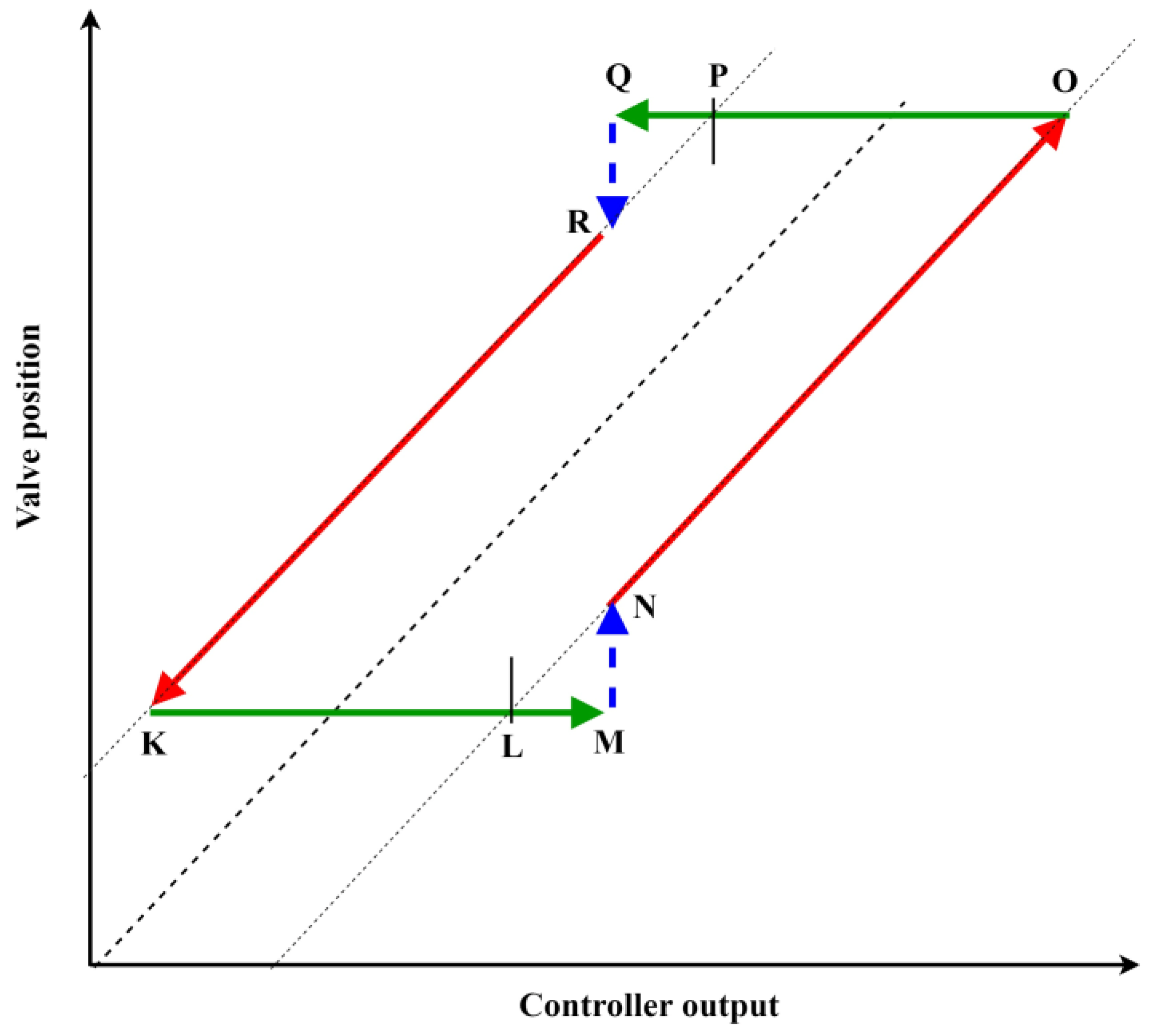
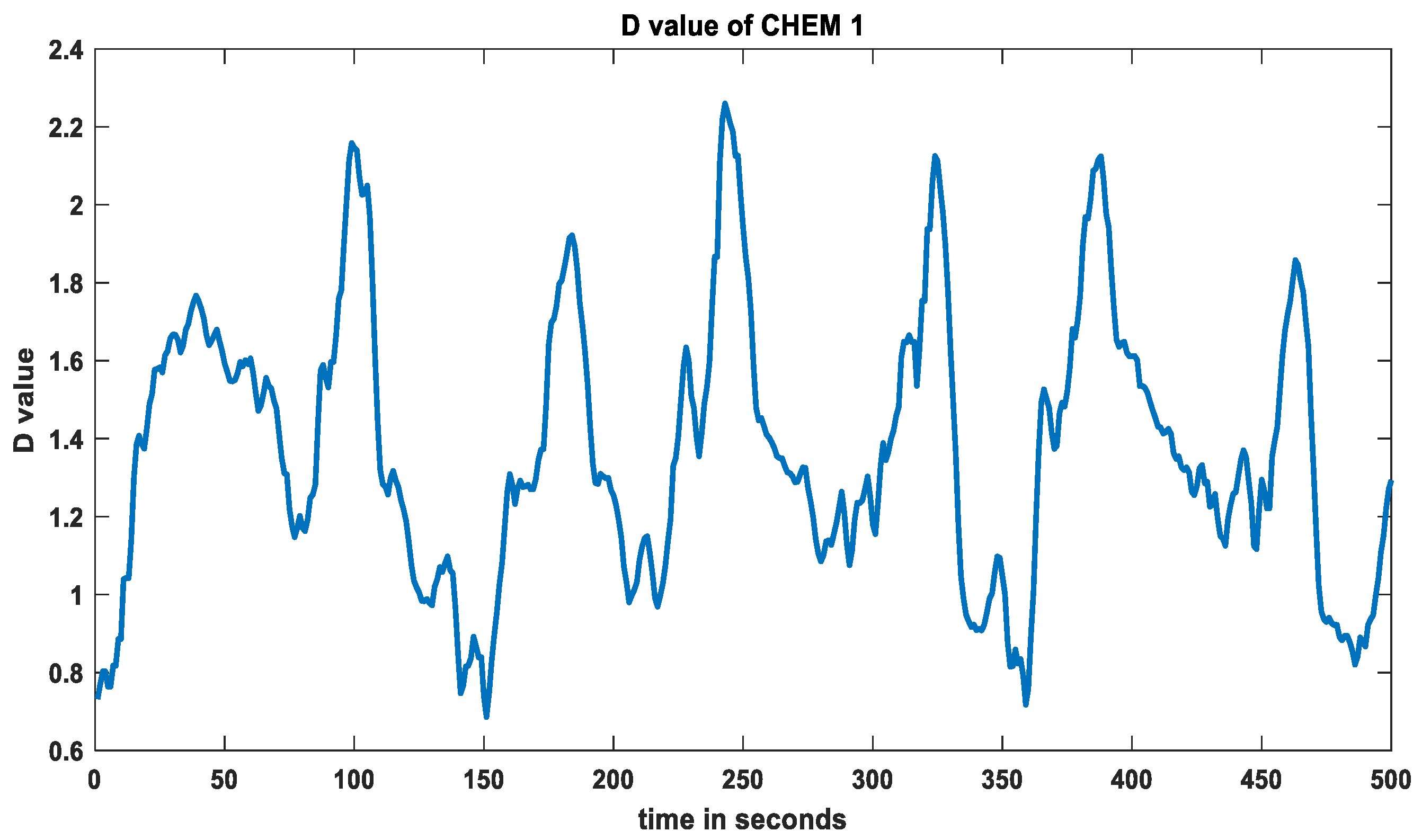
2.3. D-Value
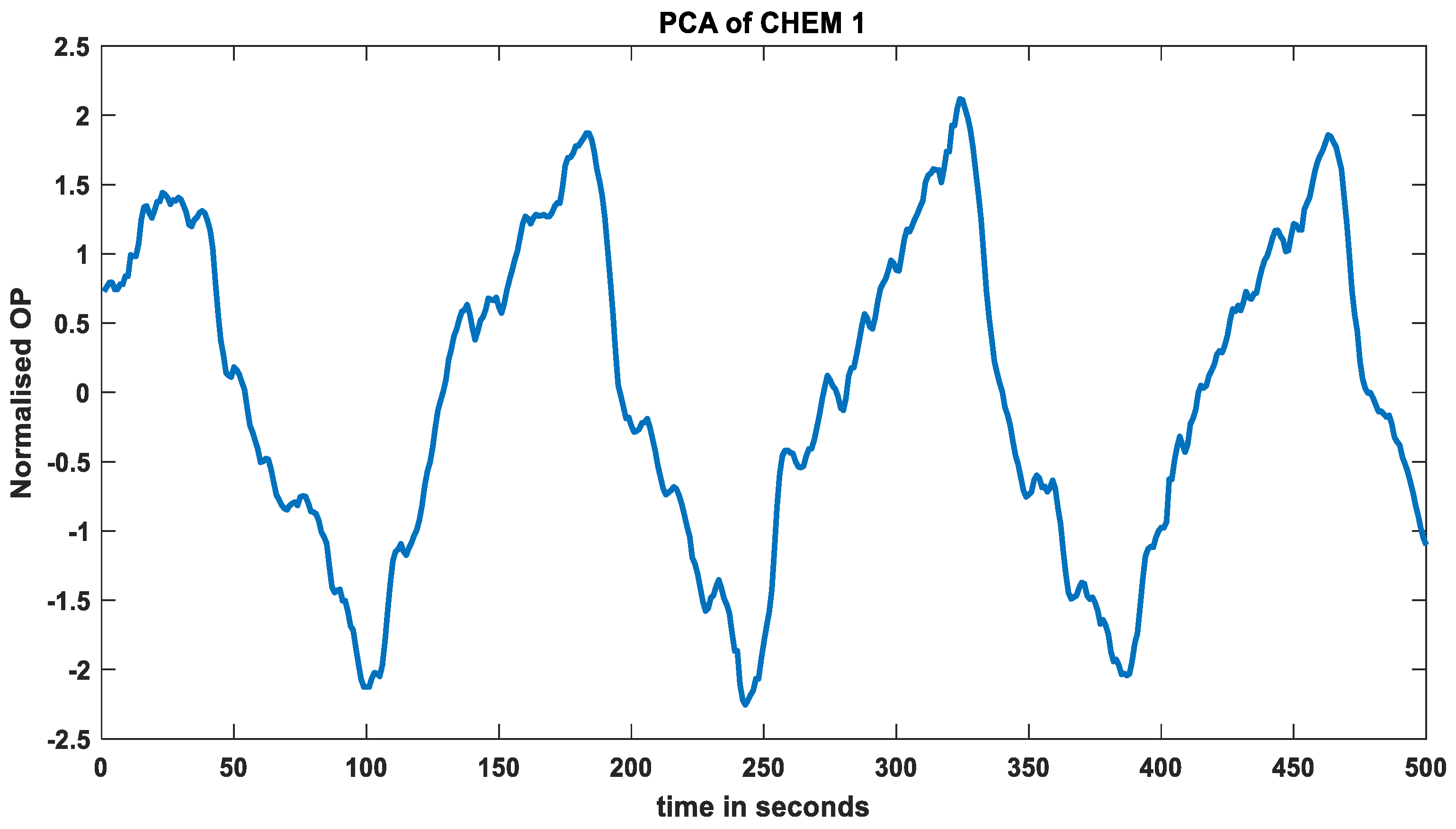
2.4. PCA
- Calculate the covariance matrix Σ of the data points.
- 2.
- Compute the eigenvectors of covariance matrix Σ.
- 3.
- Choose the first k eigenvectors, which are the new k-dimensions.
- 4.
- Transform the original n-dimensional data points into k-dimensions.
3. Methodology
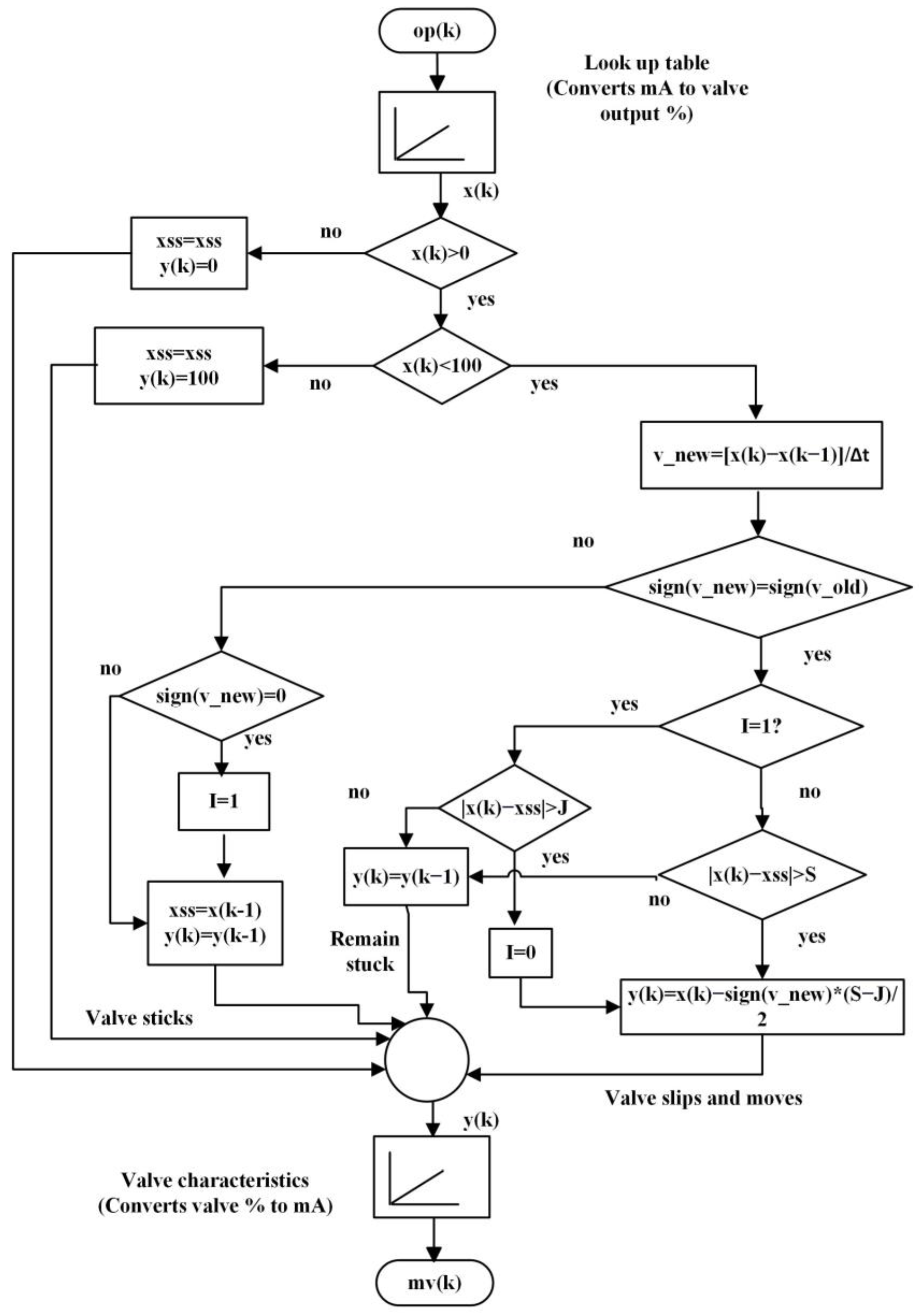
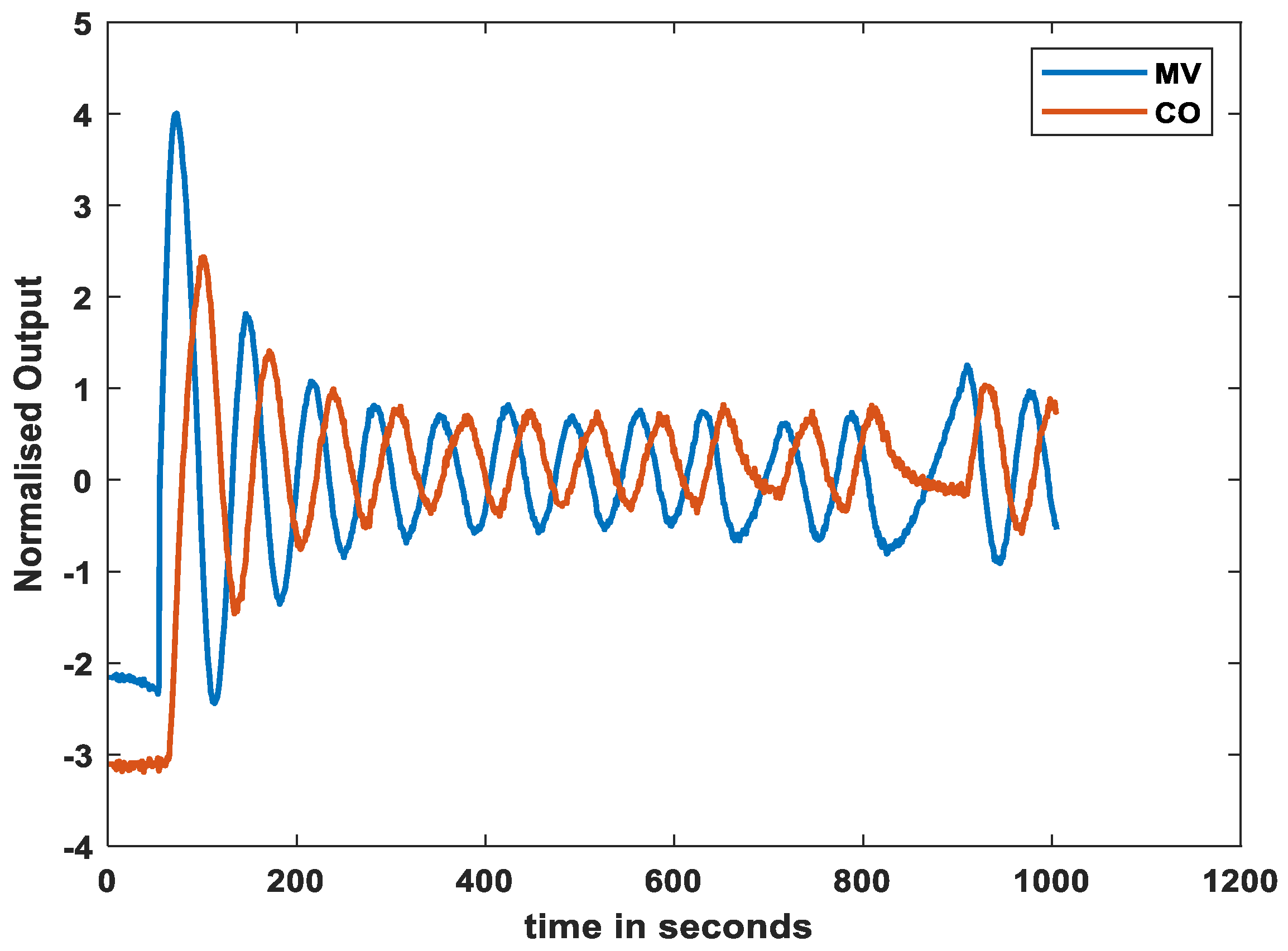
3.1. Artificial Data Generation
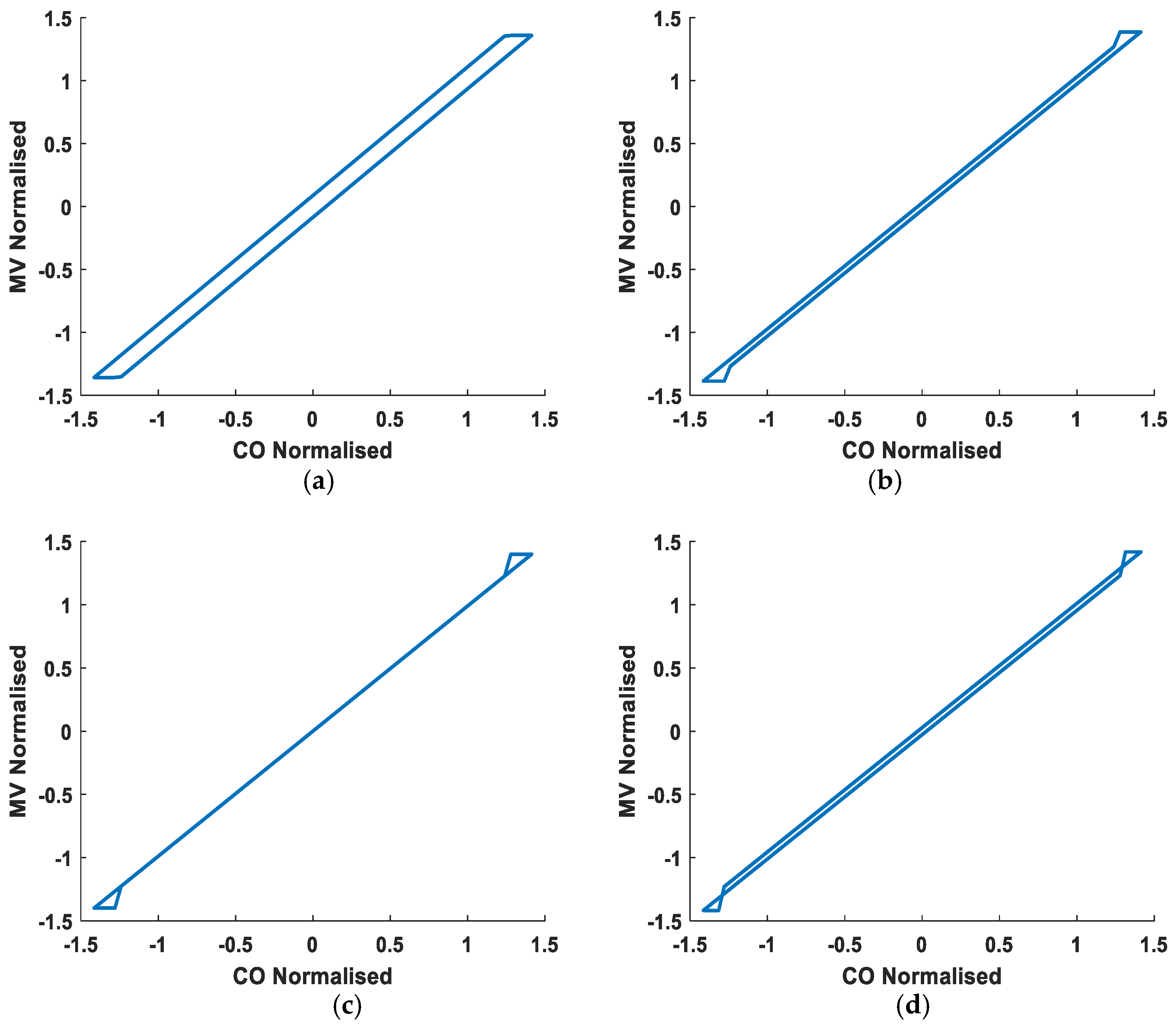
- Deadband: The response of the controller output to the valve position creates a deadband without any sudden jumps, as this case is simulated when J is a null value, J = 0, as presented in Figure 6a for S = 6.
- Undershoot: This region is created when the value of ‘J’ is less than the deadband, J < S, as represented in Figure 6b for S = 6 and J = 4.
- No offset: When the values of ‘S’ and ‘J’ are the same, J = S, this region is created, and it produces pure stick–slip behavior, as shown in Figure 6c for S = J = 6.
- Overshoot: If the ‘J’ value exceeds the ‘S’ value, J > S; this leads to an overshoot region of stiction as the jump amplitude is greater than the deadband, as depicted in Figure 6d for S = 4 and J = 6.
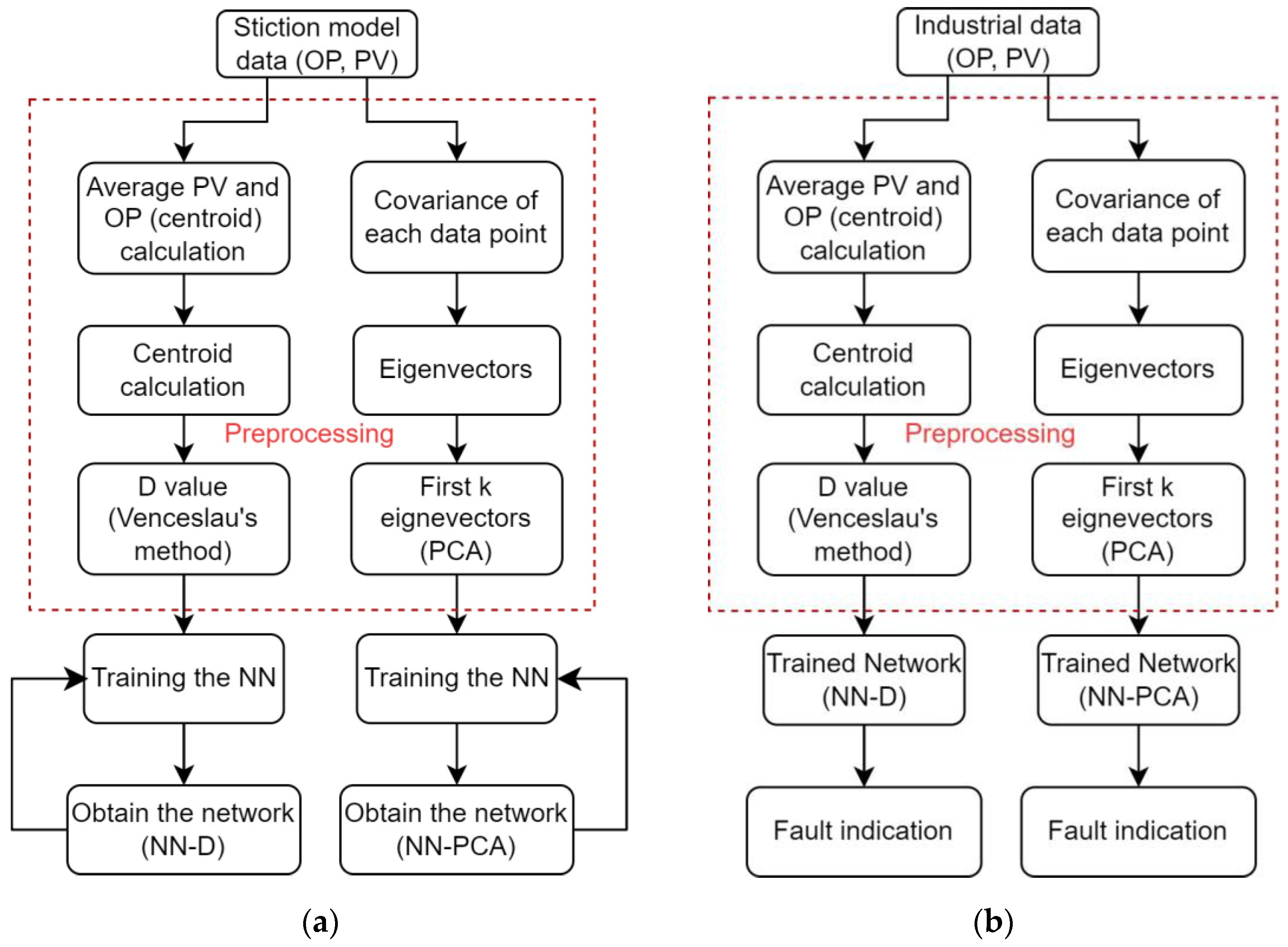
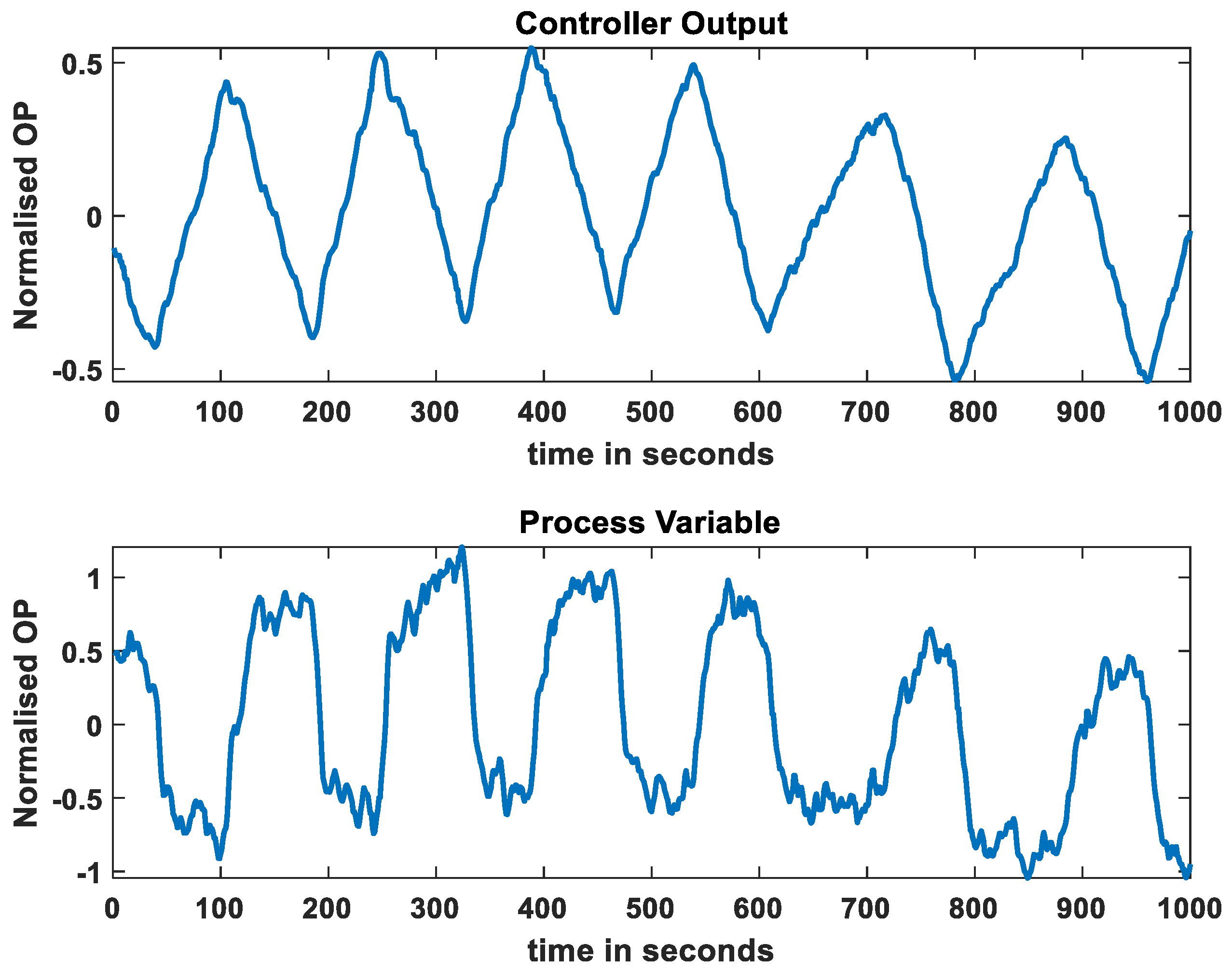
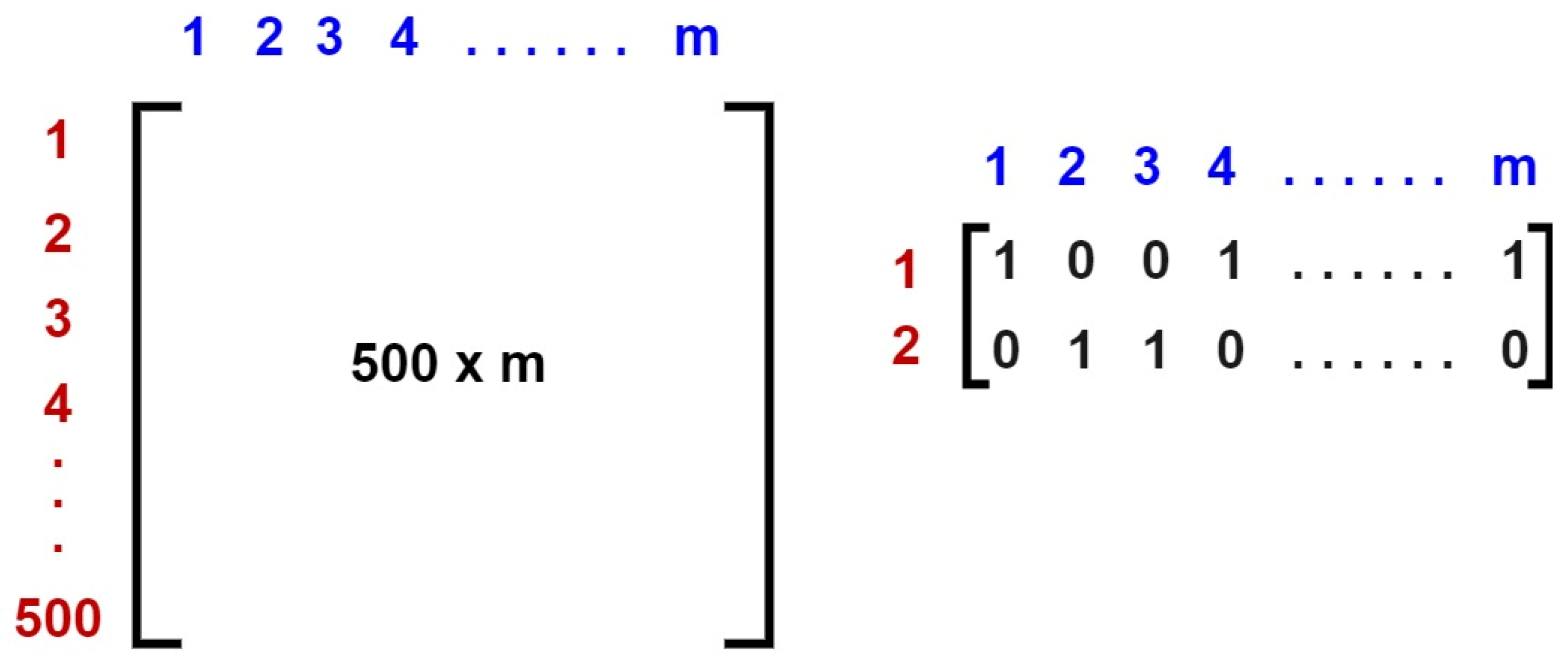
3.2. Data Preprocessing
3.3. NN Architecture
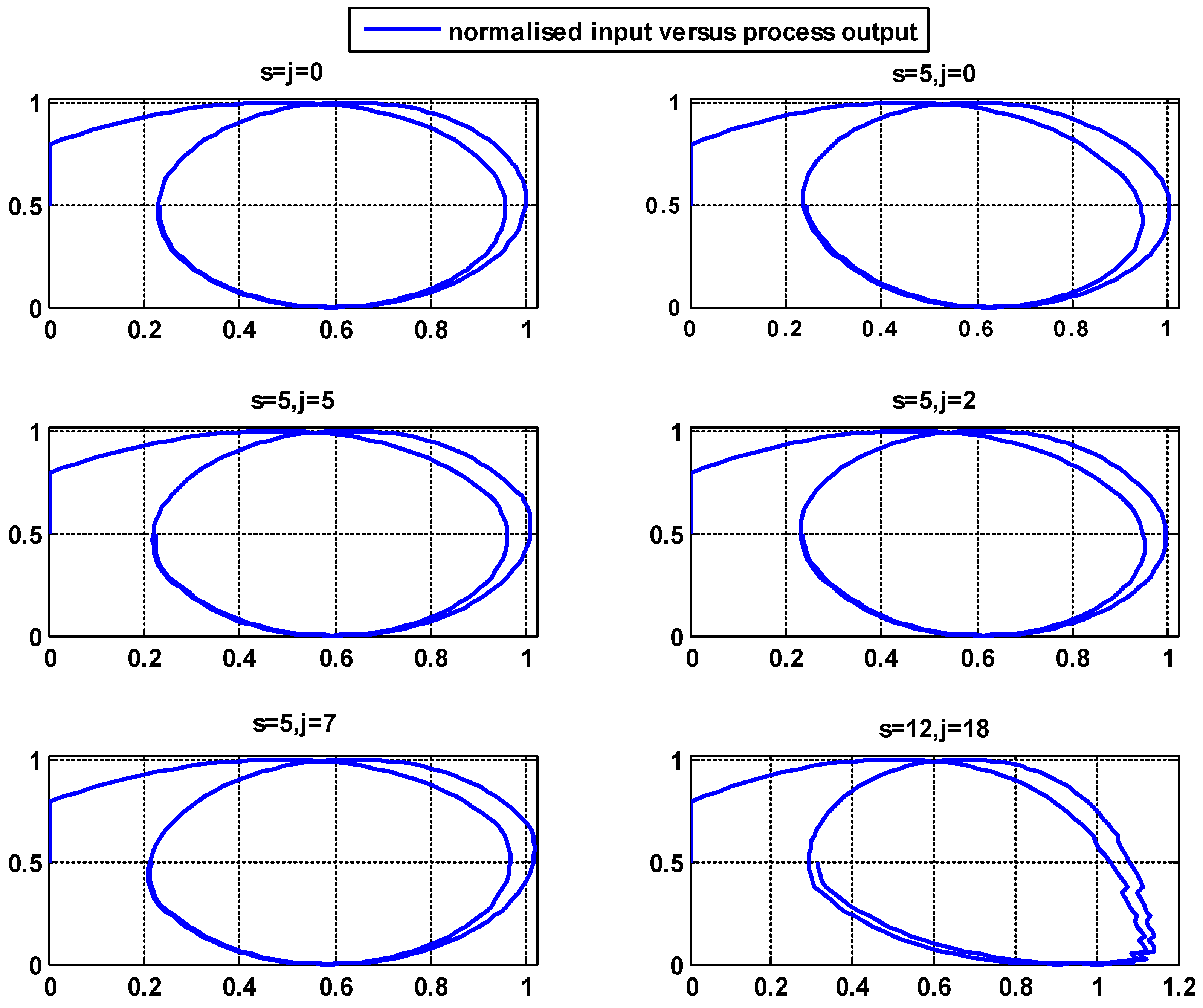
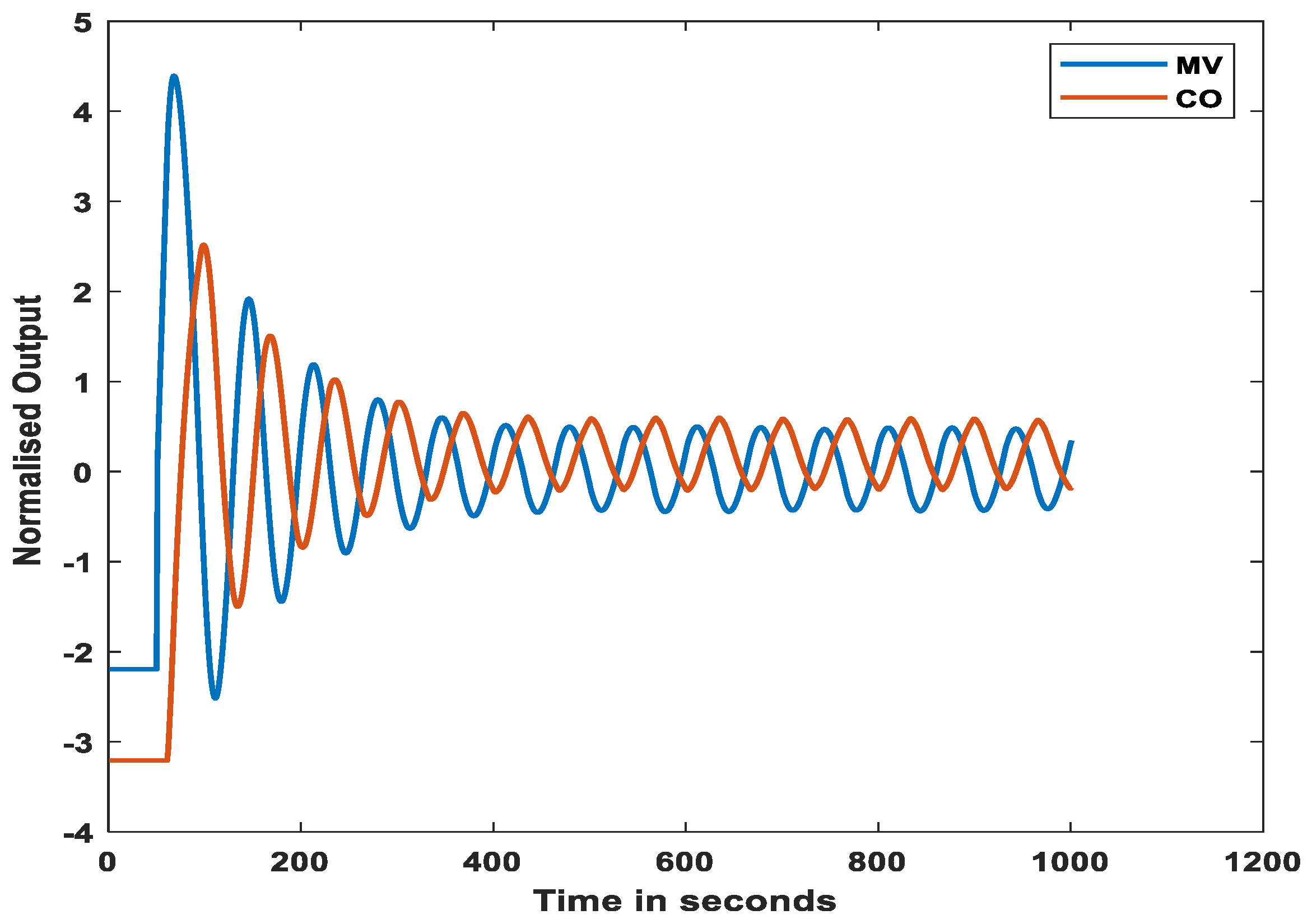
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Valette, E.; El-Haouzi, H.B.; Demesure, G. Industry 5.0 and its technologies: A systematic literature review upon the human place into IoT-and CPS-based industrial systems. Comput. Ind. Eng. 2023, 184, 109426. [Google Scholar] [CrossRef]
- Wolfe, M.T.; Patel, P.C. Same difference? The impact of low-, medium-, and high-tech industries on venture performance and survival. IEEE Trans. Eng. Manag. 2019, 68, 1907–1918. [Google Scholar] [CrossRef]
- Wang, Z.; Fan, Y. Monitoring-performance-indicator-related industrial process monitoring with a monitoring index identification model. Control Eng. Pract. 2023, 139, 105660. [Google Scholar] [CrossRef]
- Asrol, M.; Wahyudi, S.; Harito, C.; Utama, D.N.; Syafrudin, M. Improving Supplier Evaluation Model using Ensemble Method-Machine Learning for Food Industry. Procedia Comput. Sci. 2023, 227, 307–315. [Google Scholar] [CrossRef]
- LaNasa, P.J.; Upp, E.L. Fluid Flow Measurement: A Practical Guide to Accurate Flow Measurement; Butterworth-Heinemann: Oxford, UK, 2014; pp. 35–47. [Google Scholar]
- Elijah, O.; Ling, P.A.; Rahim, S.K.A.; Geok, T.K.; Arsad, A.; Kadir, E.A.; Abdurrahman, M.; Junin, R.; Agi, A.; Abdulfatah, M.Y. A survey on industry 4.0 for the oil and gas industry: Upstream sector. IEEE Access 2021, 9, 144438–144468. [Google Scholar] [CrossRef]
- Liu, J.; An, R.; Xiao, R.; Yang, Y.; Wang, G.; Wang, Q. Implications from substance flow analysis, supply chain and supplier’risk evaluation in iron and steel industry in Mainland China. Resour. Policy 2017, 51, 272–282. [Google Scholar] [CrossRef]
- Jia, Y.; Zhang, Z.G.; Xu, T. Improving the Performance of MMPP/M/C Queue by Convex Optimization–A Real-World Application in Iron and Steel Industry. IEEE Access 2020, 8, 185909–185918. [Google Scholar] [CrossRef]
- Xiao, H.; McDonald, D.; Fan, Y.; Umbanhowar, P.B.; Ottino, J.M.; Lueptow, R.M. Controlling granular segregation using modulated flow. Powder Technol. 2017, 312, 360–368. [Google Scholar] [CrossRef]
- Nawaz, M.; Maulud, A.S.; Zabiri, H.; Suleman, H. Review of multiscale methods for process monitoring, with an emphasis on applications in chemical process systems. IEEE Access 2022, 10, 49708–49724. [Google Scholar] [CrossRef]
- Shah, R.B.; Tawakkul, M.A.; Khan, M.A. Comparative evaluation of flow for pharmaceutical powders and granules. Aaps Pharmscitech 2008, 9, 250–258. [Google Scholar] [CrossRef]
- Wang, Z.; Tang, S.; Guo, G.; Yang, Y.; He, D.; Yang, L.; Han, M.; Hou, Y. Adaptive Quality Control with Uncertainty for a Pharmaceutical Cyber-Physical System Based on Data and Knowledge Integration. IEEE Trans. Ind. Inform. 2024, 20, 3339–3350. [Google Scholar] [CrossRef]
- Bugallo, P.M.B.; Stupak, A.; Andrade, L.C.; López, R.T. Material Flow Analysis in a cooked mussel processing industry. J. Food Eng. 2012, 113, 100–117. [Google Scholar] [CrossRef]
- Alves, N.N.; Messaoud, G.B.; Desobry, S.; Costa, J.M.C.; Rodrigues, S. Effect of drying technique and feed flow rate on bacterial survival and physicochemical properties of a nondairy fermented probiotic juice powder. J. Food Eng. 2016, 189, 45–54. [Google Scholar] [CrossRef]
- Hawashin, D.; Salah, K.; Jayaraman, R.; Musamih, A. Using Composable NFTs for Trading and Managing Expensive Packaged Products in the Food Industry. IEEE Access 2023, 11, 10587–10603. [Google Scholar] [CrossRef]
- Odunlami, O.A.; Amoo, T.E.; Adisa, H.A.; Elehinafe, F.B.; Oladimeji, T.E. Application of mass transfer in the pulp and paper Industry− overview, processing, challenges, and prospects. Results Eng. 2023, 20, 101498. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, L.; Lu, S.; Hou, X.; Hou, D.; Ma, J. Porous ceramsite catalytic ozonation for the treatment of pulp and paper mill wastewater in a continuous-flow reactor. Chem. Eng. Sci. 2024, 288, 119855. [Google Scholar] [CrossRef]
- Liu, W.; Hu, J.; Zhao, X.; Pan, H.; Lakhiar, I.A.; Wang, W. Development and experimental analysis of an intelligent sensor for monitoring seed flow rate based on a seed flow reconstruction technique. Comput. Electron. Agric. 2019, 164, 104899. [Google Scholar] [CrossRef]
- He, F.; Ma, X.; Shen, K.; Wang, C. Study on material and energy flow in steel forging production process. IEEE Access 2019, 8, 12921–12932. [Google Scholar] [CrossRef]
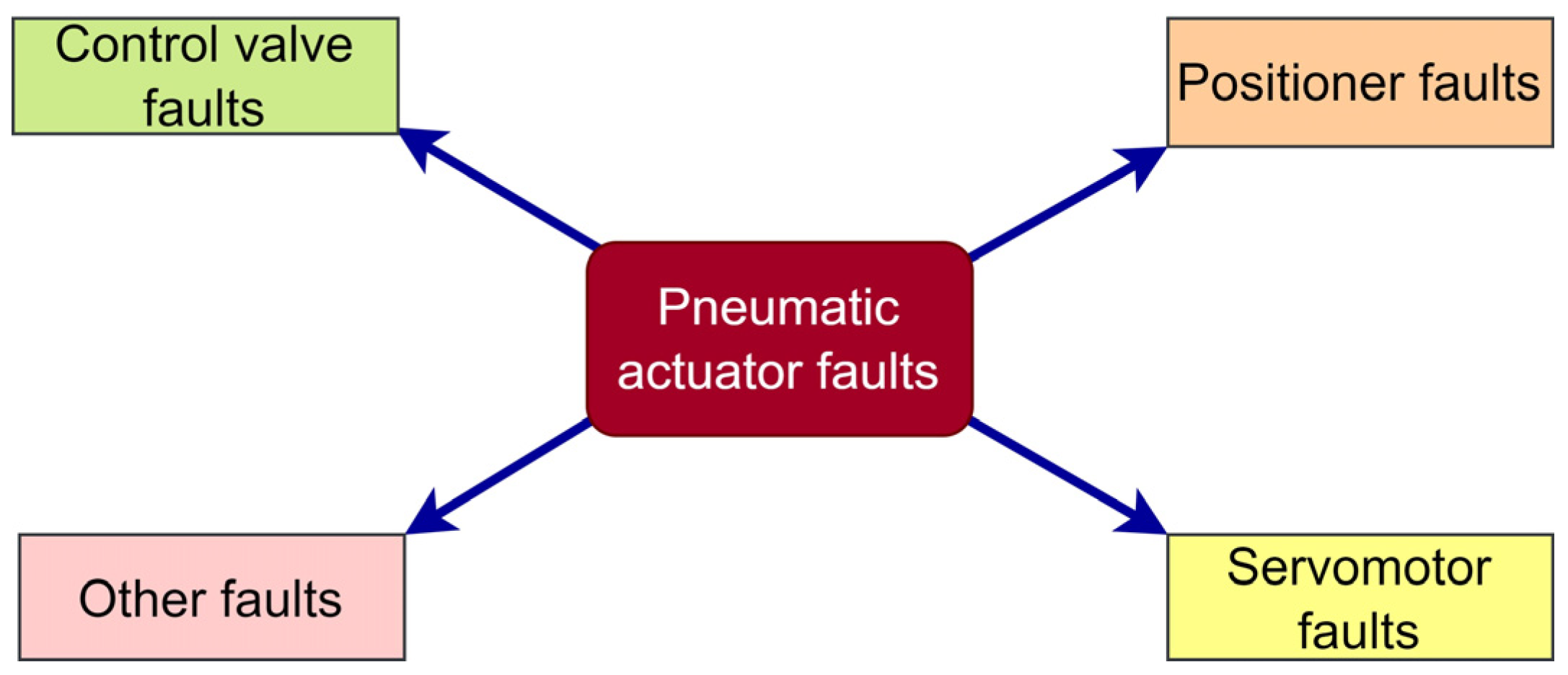
- Navada, B.R.; Santhosh, K.V. Is fault detection and diagnosis in pneumatic actuator a topic of concern? J. Adv. Res. Fluid Mech. Therm. Sci. 2021, 77, 102–129. [Google Scholar] [CrossRef]
- Ji, H.; He, X.; Shang, J.; Zhou, D. Incipient fault detection with smoothing techniques in statistical process monitoring. Control Eng. Pract. 2017, 62, 11–21. [Google Scholar] [CrossRef]
- Zhang, S.; Luo, M.; Qian, H.; Liu, L.; Yang, H.; Zhang, Y.; Liu, X.; Xie, Z.; Yang, L.; Zhang, W. A review of valve health diagnosis and assessment: Insights for intelligence maintenance of natural gas pipeline valves in China. Eng. Fail. Anal. 2023, 153, 107581. [Google Scholar] [CrossRef]
- Shi, J.; Yi, J.; Ren, Y.; Li, Y.; Zhong, Q.; Tang, H.; Chen, L. Fault diagnosis in a hydraulic directional valve using a two-stage multi-sensor information fusion. Measurement 2021, 179, 109460. [Google Scholar] [CrossRef]
- Ji, X.; Ren, Y.; Tang, H.; Shi, C.; Xiang, J. An intelligent fault diagnosis approach based on Dempster-Shafer theory for hydraulic valves. Measurement 2020, 165, 108129. [Google Scholar] [CrossRef]
- Ma, D.; Liu, Z.; Gao, Q.; Huang, T. Fault diagnosis of a solenoid valve based on multi-feature fusion. Appl. Sci. 2022, 12, 5904. [Google Scholar] [CrossRef]
- Ttito Ugarte, L.; Bernardini, F. An Overview on the Use of Machine Learning Algorithms for Identifying Anomalies in Industrial Valves. In World Conference on Information Systems and Technologies; Springer Nature: Cham, Switzerland, 2024; pp. 3–12. [Google Scholar]
- Andrade, A.; Lopes, K.; Lima, B.; Maitelli, A. Development of a methodology using artificial neural network in the detection and diagnosis of faults for pneumatic control valves. Sensors 2021, 21, 853. [Google Scholar] [CrossRef]
- Sun, F.; Xu, H.; Zhao, Y.H.; Zhang, Y.D. Data-driven fault diagnosis of control valve with missing data based on modeling and deep residual shrinkage network. J. Zhejiang Univ. Sci. A 2022, 23, 303–313. [Google Scholar] [CrossRef]
- Jo, S.H.; Seo, B.; Oh, H.; Youn, B.D.; Lee, D. Model-based fault detection method for coil burnout in solenoid valves subjected to dynamic thermal loading. IEEE Access 2020, 8, 70387–70400. [Google Scholar] [CrossRef]
- Han, X.; Jiang, J.; Xu, A.; Huang, X.; Pei, C.; Sun, Y. Fault detection of pneumatic control valves based on canonical variate analysis. IEEE Sens. J. 2021, 21, 13603–13615. [Google Scholar] [CrossRef]
- An, Z.; Cheng, L.; Guo, Y.; Ren, M.; Feng, W.; Sun, B.; Ling, J.; Chen, H.; Chen, W.; Luo, Y.; et al. A novel principal component analysis-informer model for fault prediction of nuclear valves. Machines 2022, 10, 240. [Google Scholar] [CrossRef]
- Durand, H.; Parker, R.; Alanqar, A.; Christofides, P.D. Elucidating and handling effects of valve-induced nonlinearities in industrial feedback control loops. Comput. Chem. Eng. 2018, 116, 156–175. [Google Scholar] [CrossRef]
- Brasio, A.S.; Romanenko, A.; Fernandes, N.C. Modeling, detection and quantification, and compensation of stiction in control loops: The state of the art. Ind. Eng. Chem. Res. 2014, 53, 15020–15040. [Google Scholar] [CrossRef]
- Daneshwar, M.A.; Noh, N.M. Detection of stiction in flow control loops based on fuzzy clustering. Control Eng. Pract. 2015, 39, 23–34. [Google Scholar] [CrossRef]
- Choudhury, M.S.; Thornhill, N.F.; Shah, S.L. Modeling valve stiction. Control Eng. Pract. 2005, 13, 641–658. [Google Scholar] [CrossRef]
- Xie, L.; Cong, Y.; Horch, A. An improved valve stiction simulation model based on ISA standard tests. Control Eng. Pract. 2013, 21, 1359–1368. [Google Scholar] [CrossRef]
- di Capaci, R.B.; Scali, C.; Pannocchia, G. System identification applied to stiction quantification in industrial control loops: A comparative study. J. Process Control 2016, 46, 11–23. [Google Scholar] [CrossRef]
- di Capaci, R.B.; Vaccari, M.; Pannocchia, G.; Scali, C. Identification and estimation of valve stiction by the use of a smoothed model. IFAC-PapersOnLine 2018, 51, 684–689. [Google Scholar] [CrossRef]
- Daneshwar, M.A.; Noh, N.M. Identification of a process with control valve stiction using a fuzzy system: A data-driven approach. J. Process Control 2014, 24, 249–260. [Google Scholar] [CrossRef]
- Horch, A. A simple method for detection of stiction in control valves. Control Eng. Pract. 1999, 7, 1221–1231. [Google Scholar] [CrossRef]
- Rossi, M.; Scali, C. A comparison of techniques for automatic detection of stiction: Simulation and application to industrial data. J. Process Control 2005, 15, 505–514. [Google Scholar] [CrossRef]
- Yamashita, Y. An automatic method for detection of valve stiction in process control loops. Control Eng. Pract. 2006, 14, 503–510. [Google Scholar] [CrossRef]
- Zakharov, A.; Zattoni, E.; Xie, L.; Garcia, O.P.; Jämsä-Jounela, S.L. An autonomous valve stiction detection system based on data characterization. Control Eng. Pract. 2013, 21, 1507–1518. [Google Scholar] [CrossRef]
- Maruta, H.; Kano, M.; Kugemoto, H.; Shimizu, K. Modeling and detection of stiction in pneumatic control valve. Trans. Soc. Instrum. Control Eng. 2004, 40, 825–833. [Google Scholar] [CrossRef][Green Version]
- Kok, T.L.; Aldrich, C.; Zabiri, H.; Taqvi, S.A.A.; Olivier, J. Application of unthresholded recurrence plots and texture analysis for industrial loops with faulty valves. Soft Comput. 2022, 26, 10477–10492. [Google Scholar] [CrossRef]
- Shang, L.; Zhang, Y.; Zhang, H. Valve Stiction Detection Method Based on Dynamic Slow Feature Analysis and Hurst Exponent. Processes 2023, 11, 1913. [Google Scholar] [CrossRef]
- Zheng, D.; Sun, X.; Damarla, S.K.; Shah, A.; Amalraj, J.; Huang, B. Valve stiction detection and quantification using a k-means clustering based moving window approach. Ind. Eng. Chem. Res. 2021, 60, 2563–2577. [Google Scholar] [CrossRef]
- Dambros, J.W.; Farenzena, M.; Trierweiler, J.O. Stiction detection in low sampling rate signals. Can. J. Chem. Eng. 2018, 96, 1735–1745. [Google Scholar] [CrossRef]
- Bounoua, W.; Aftab, M.F.; Omlin, C.W.P. Stiction detection in industrial control valves using Poincaré plot-based convolutional neural networks. IFAC-PapersOnLine 2023, 56, 11687–11692. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, Y.; Gu, Y.; Ruan, X.; Wang, J. Multiple-timescale feature learning strategy for valve stiction detection based on convolutional neural network. IEEE/ASME Trans. Mechatron. 2021, 27, 1478–1488. [Google Scholar] [CrossRef]
- Henry, Y.Y.S.; Aldrich, C.; Zabiri, H. Detection and severity identification of control valve stiction in industrial loops using integrated partially retrained CNN-PCA frameworks. Chemom. Intell. Lab. Syst. 2020, 206, 104143. [Google Scholar] [CrossRef]
- Amiruddin, A.A.A.M.; Zabiri, H.; Jeremiah, S.S.; Teh, W.K.; Kamaruddin, B. Valve stiction detection through improved pattern recognition using neural networks. Control Eng. Pract. 2019, 90, 63–84. [Google Scholar] [CrossRef]
- Venceslau, A.R.; Guedes, L.A.; Silva, D.R. Artificial neural network approach for detection and diagnosis of valve stiction. In Proceedings of the 2012 IEEE 17th International Conference on Emerging Technologies & Factory Automation (ETFA 2012), Kraków, Poland, 17–21 September 2012; IEEE: New York, NY, USA, 2012; pp. 1–4. [Google Scholar]
- Navada, B.R.; Venkata, S. Fusion-based online identification technique for pneumatic actuator faults. Eng. Sci. 2021, 17, 56–69. [Google Scholar] [CrossRef]
- Navada, B.R.; Santhosh, K.V. Analysis of Stiction Fault in Pneumatic Control Valves. In Advances in Control Instrumentation Systems: Select Proceedings of CISCON; Springer: Singapore, 2019; pp. 215–226. [Google Scholar]
| Parameter | Description | Parameter Range |
|---|---|---|
| S | Stick–slip parameters | 0.1: 0.25: 10 |
| J | Stick–jump parameters | 0.1: 0.25: 10 |
| V | White noise variance | 0, 0.010.5, 0.020.5, 0.030.5, 0.040.5, 0.050.5 |
| Parameter | Description | Parameter Range |
|---|---|---|
| Kp | Controller gain | 1: 0.05: 2 |
| KI | Integral gain | 0.05: 0.01: 0.3 |
| V | White noise variance | 0, 0.010.5, 0.020.5, 0.030.5, 0.040.5, 0.050.5 |
| Parameter | Description | Parameter Range |
|---|---|---|
| A | Amplitude | 1: 0.5: 2. |
| Frequency | 0.01: 0.01: 0.11 | |
| Phase | 0: 0.25π: 1.75π | |
| V | White noise variance | 0, 0.010.5, 0.020.5, 0.030.5, 0.040.5, 0.050.5 |
| Variance | Performance % |
|---|---|
| 0.050.5 | 69.24 |
| 0.040.5 | 73.4 |
| 0.030.5 | 65.9 |
| 0.020.5 | 65.8 |
| 0.010.5 | 62.3 |
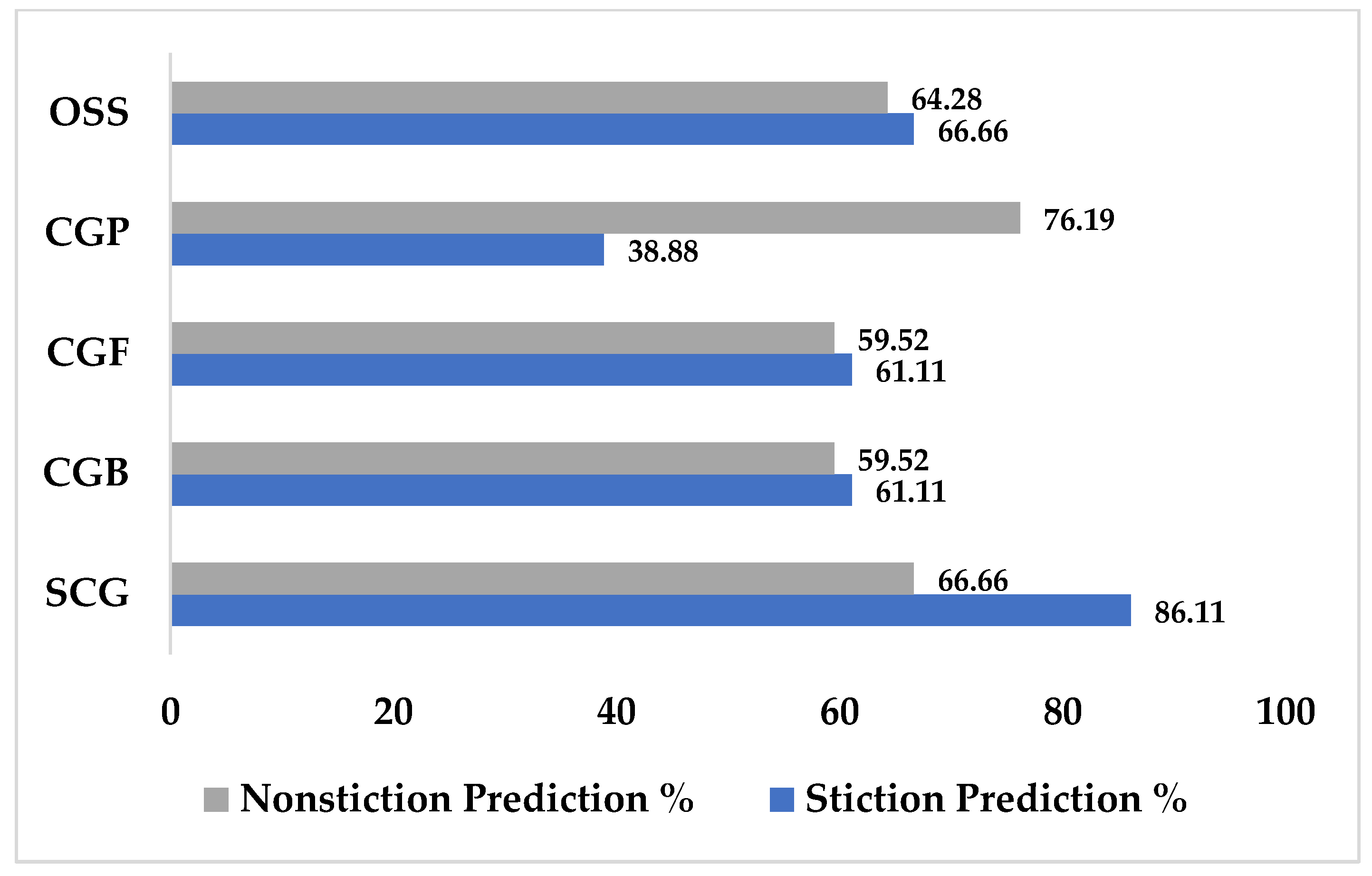
| Learning Algorithm | Performance % |
|---|---|
| Conjugate Gradient with Powell/Beale Restart (CGB) | 60.317 |
| Fletcher–Powell Conjugate Gradient (CGF) | 60.31 |
| Polak–Ribere Conjugate Gradient (CGP) | 57.53 |
| Scaled Conjugate Gradient (SCG) | 76.38 |
| One Step Secant (OSS) | 65.47 |
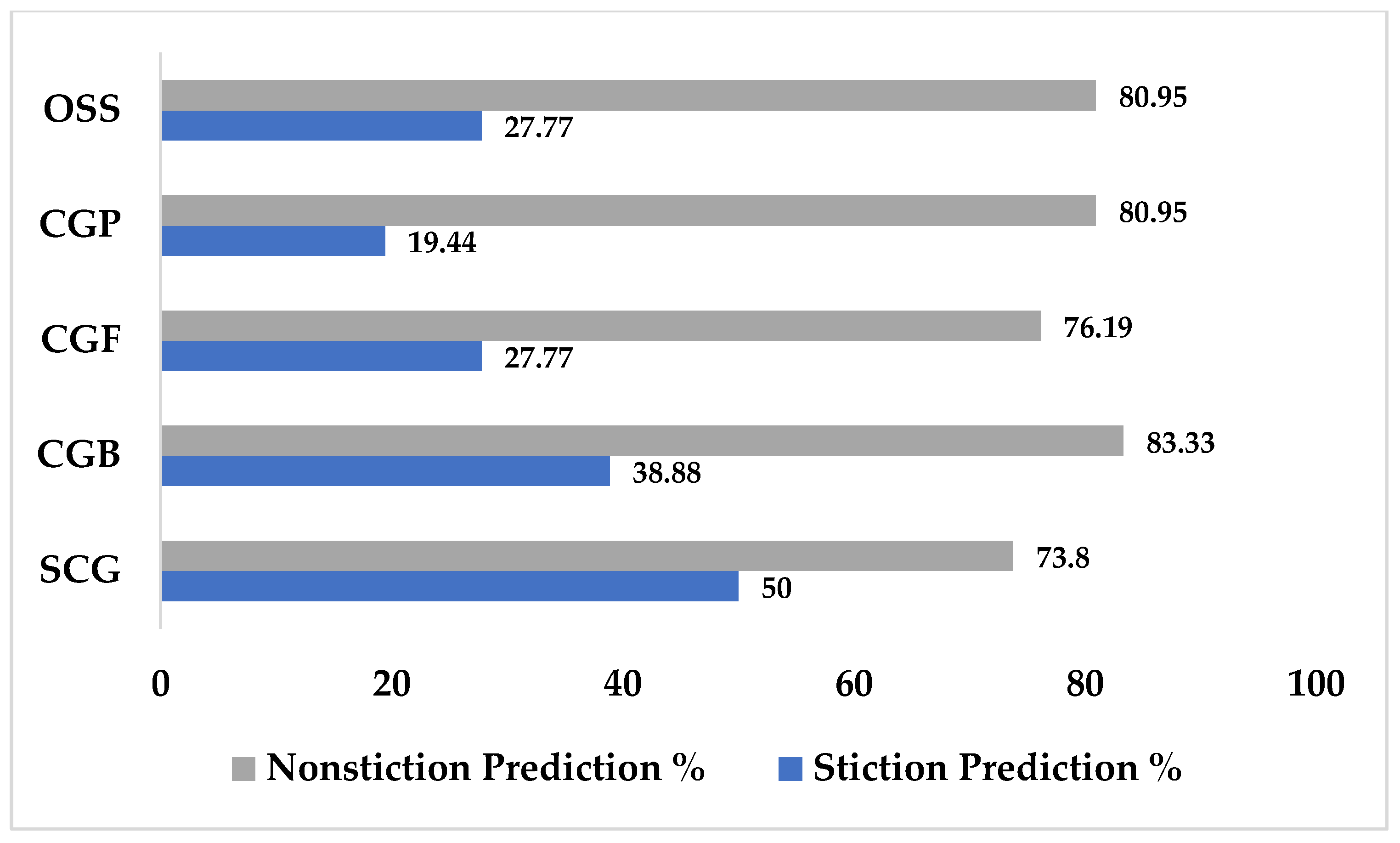
| Learning Algorithm | Performance % |
|---|---|
| Conjugate Gradient with Powell/Beale Restart (CGB) | 61.11 |
| Fletcher–Powell Conjugate Gradient (CGF) | 51.98 |
| Polak–Ribere Conjugate Gradient (CGP) | 50.19 |
| Scaled Conjugate Gradient (SCG) | 61.90 |
| One Step Secant (OSS) | 54.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Published by MDPI on behalf of the International Institute of Knowledge Innovation and Invention. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Navada, B.R.; Sravani, V.; Venkata, S.K. Enhancing Industrial Valve Diagnostics: Comparison of Two Preprocessing Methods on the Performance of a Stiction Detection Method Using an Artificial Neural Network. Appl. Syst. Innov. 2024, 7, 104. https://doi.org/10.3390/asi7060104
Navada BR, Sravani V, Venkata SK. Enhancing Industrial Valve Diagnostics: Comparison of Two Preprocessing Methods on the Performance of a Stiction Detection Method Using an Artificial Neural Network. Applied System Innovation. 2024; 7(6):104. https://doi.org/10.3390/asi7060104
Chicago/Turabian StyleNavada, Bhagya Rajesh, Vemulapalli Sravani, and Santhosh Krishnan Venkata. 2024. "Enhancing Industrial Valve Diagnostics: Comparison of Two Preprocessing Methods on the Performance of a Stiction Detection Method Using an Artificial Neural Network" Applied System Innovation 7, no. 6: 104. https://doi.org/10.3390/asi7060104
APA StyleNavada, B. R., Sravani, V., & Venkata, S. K. (2024). Enhancing Industrial Valve Diagnostics: Comparison of Two Preprocessing Methods on the Performance of a Stiction Detection Method Using an Artificial Neural Network. Applied System Innovation, 7(6), 104. https://doi.org/10.3390/asi7060104






