The Nanosecond Impulsive Breakdown Characteristics of Air, N2 and CO2 in a Sub-mm Gap
Abstract
:1. Introduction
2. Materials and Methods
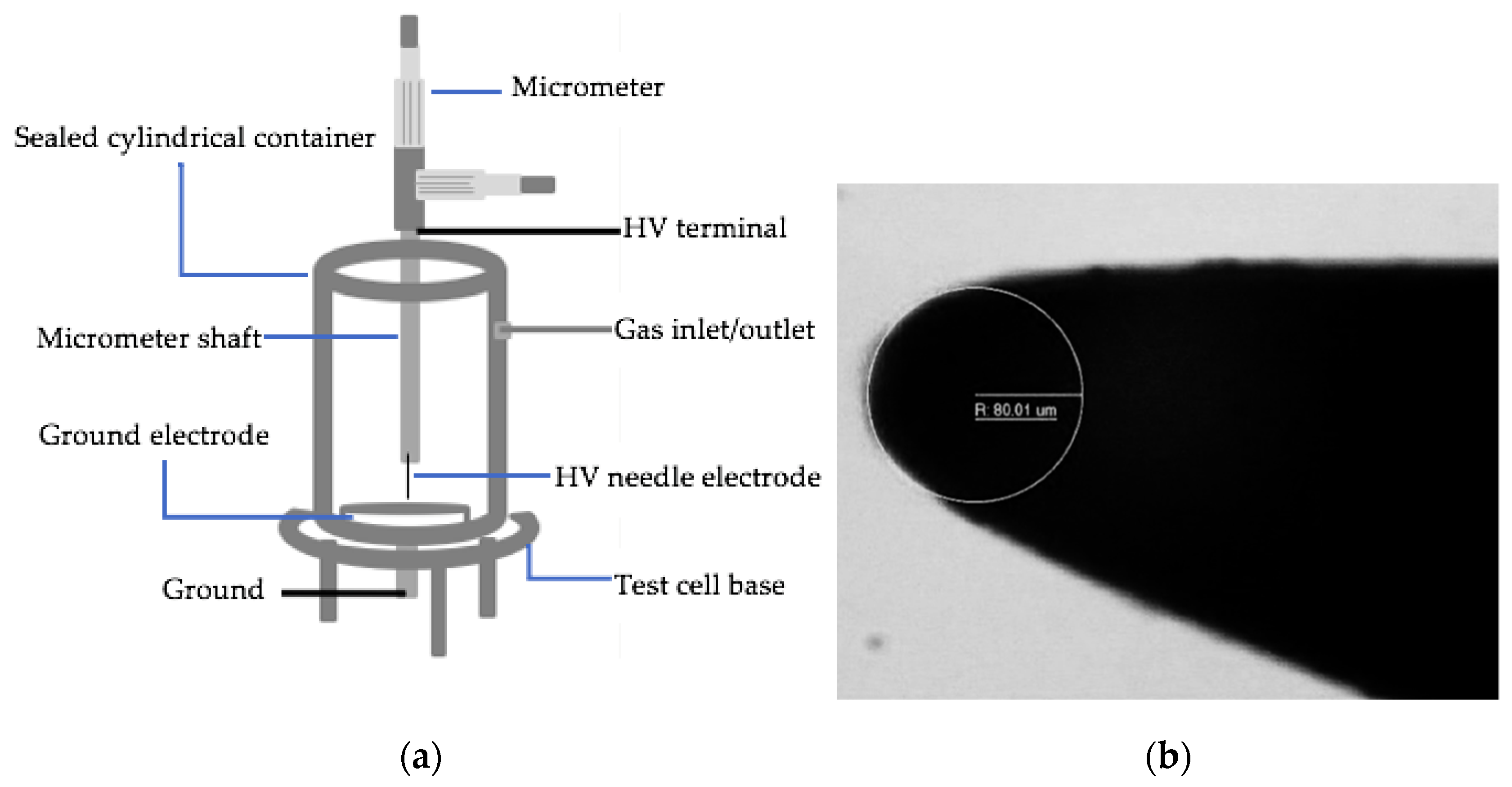
2.1. Electrode Topology and Test Cell
2.2. Gases and Gas-Handling System
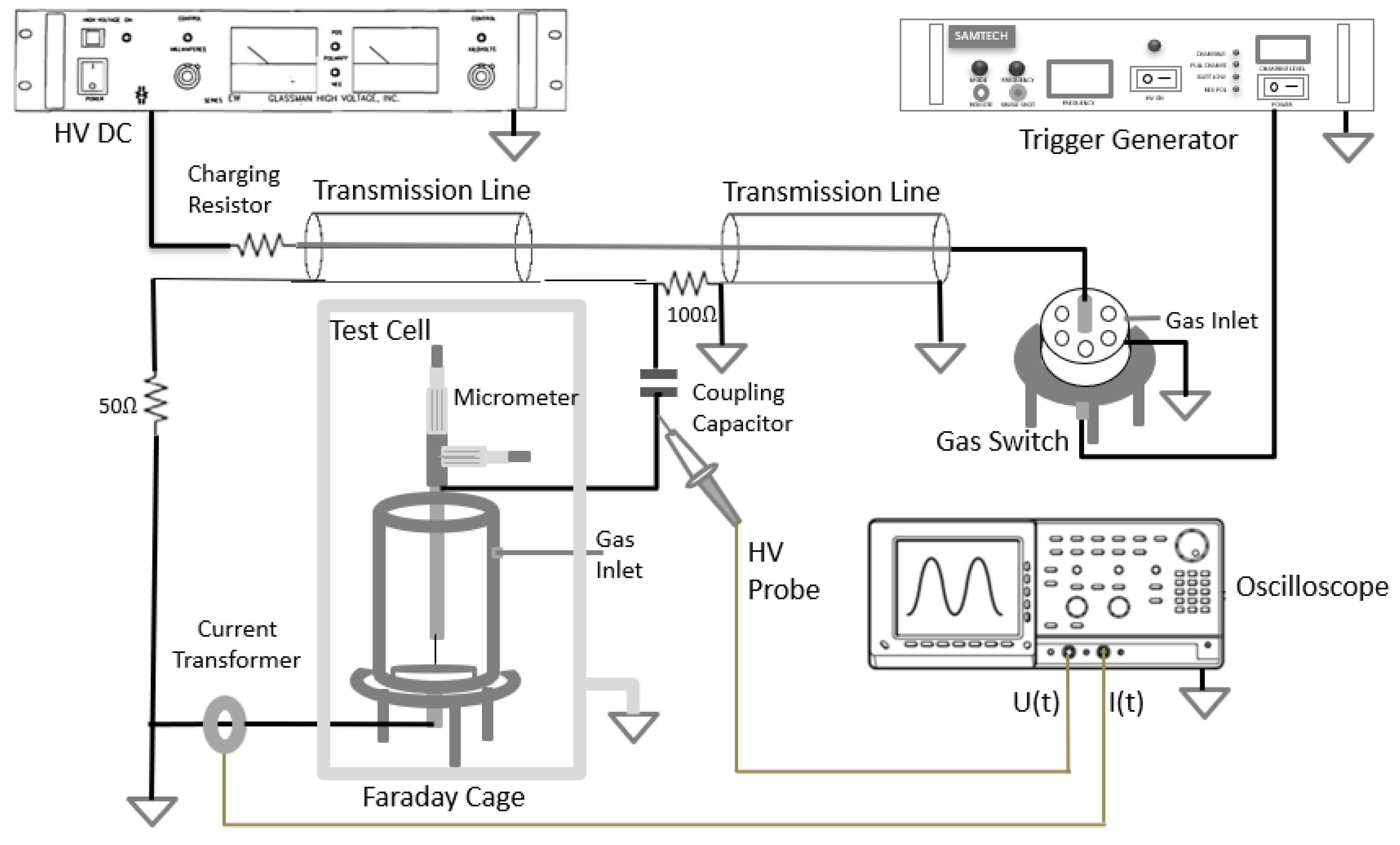
2.3. Pulse Generator and Diagnostic Devices
3. Results
3.1. Simulation of the HV Impulses and Electric Field in the Test Cell
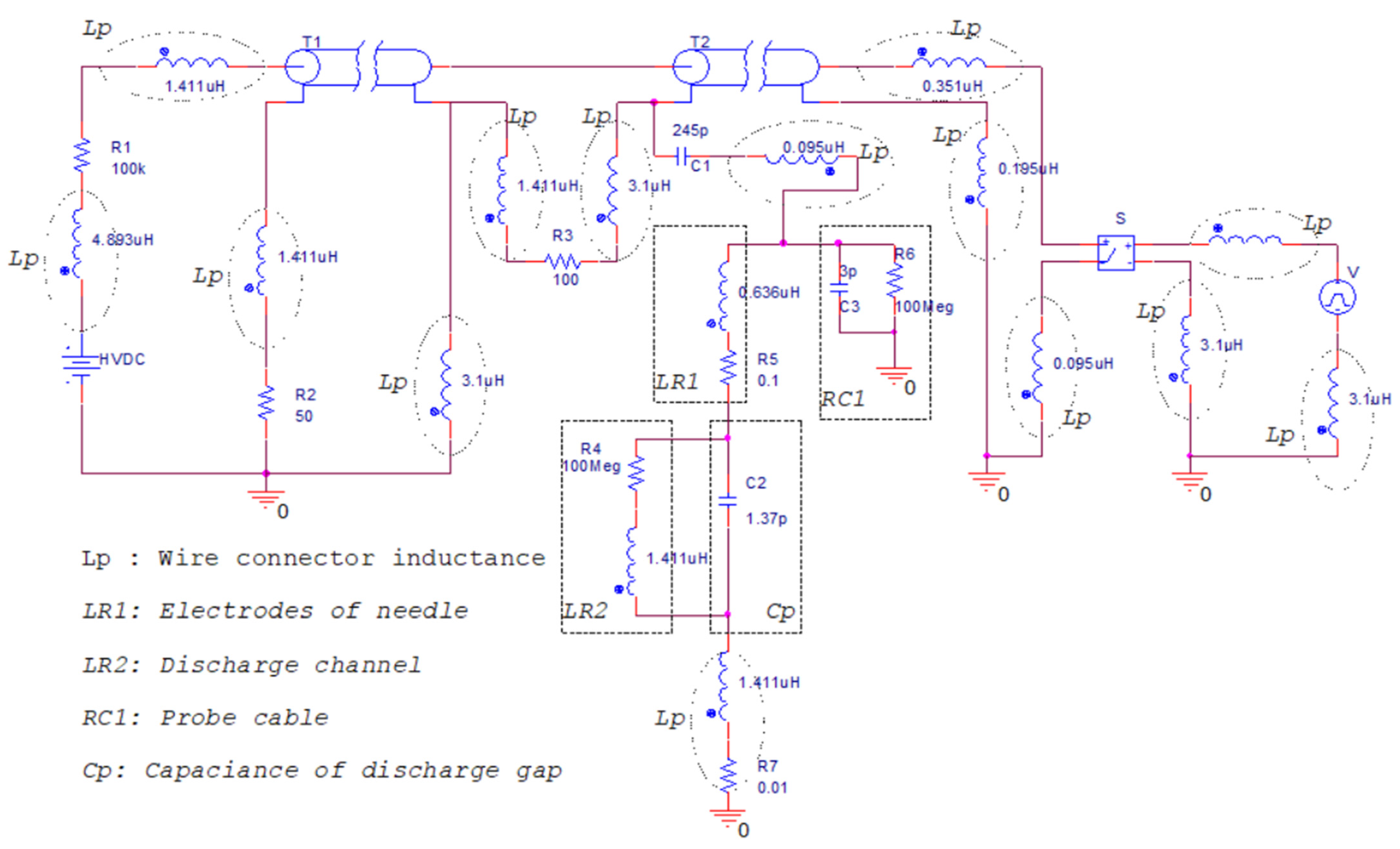
3.1.1. RLC Lumped-Element Equivalent Circuit
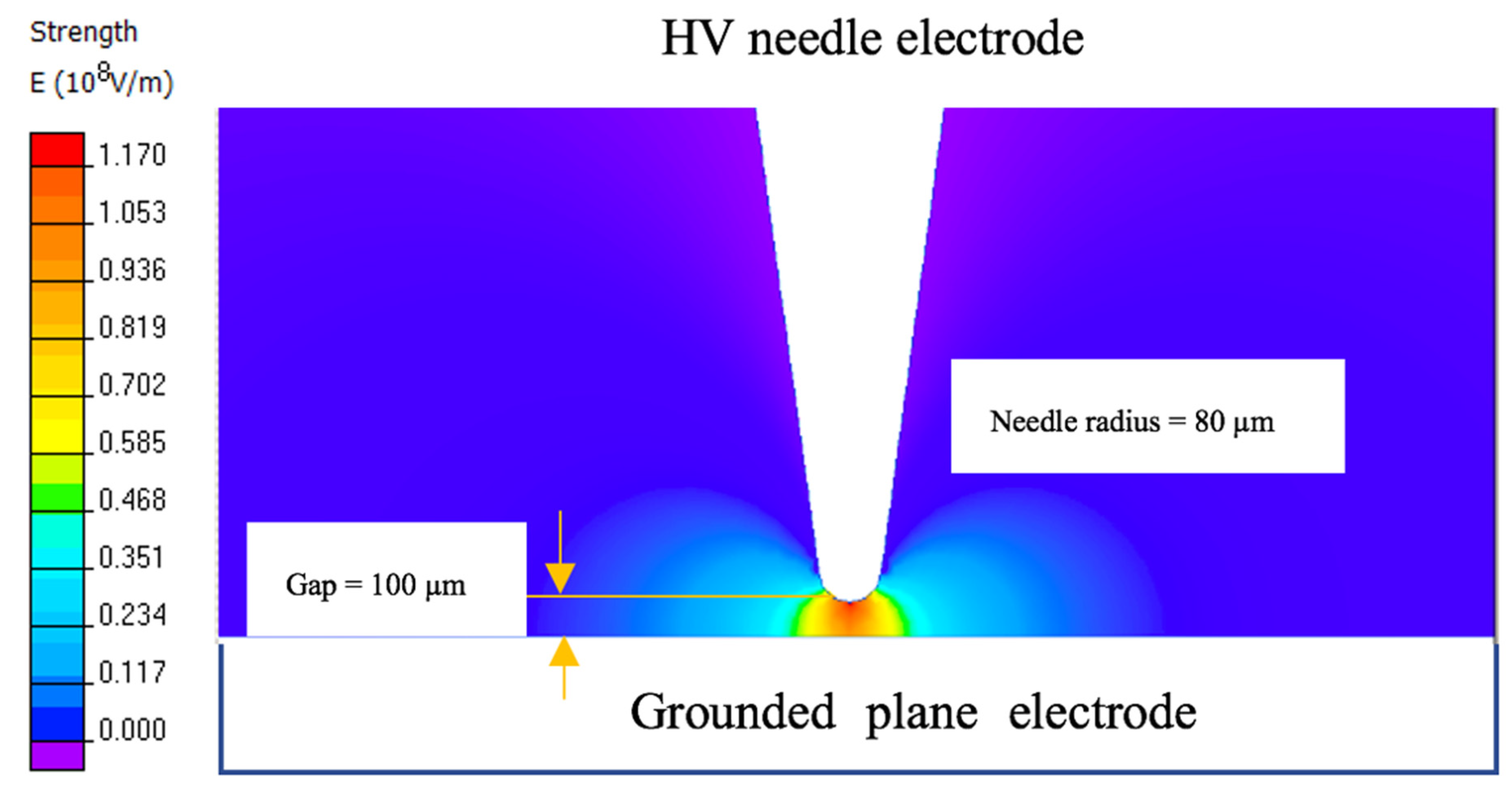
3.1.2. Simulation of Electric Field Distribution Using QuickField Software
3.2. Breakdown Voltage and Time to Breakdown in Investigated Gases
3.3. Scaling Relationships
3.3.1. E/N as a Function of Nd
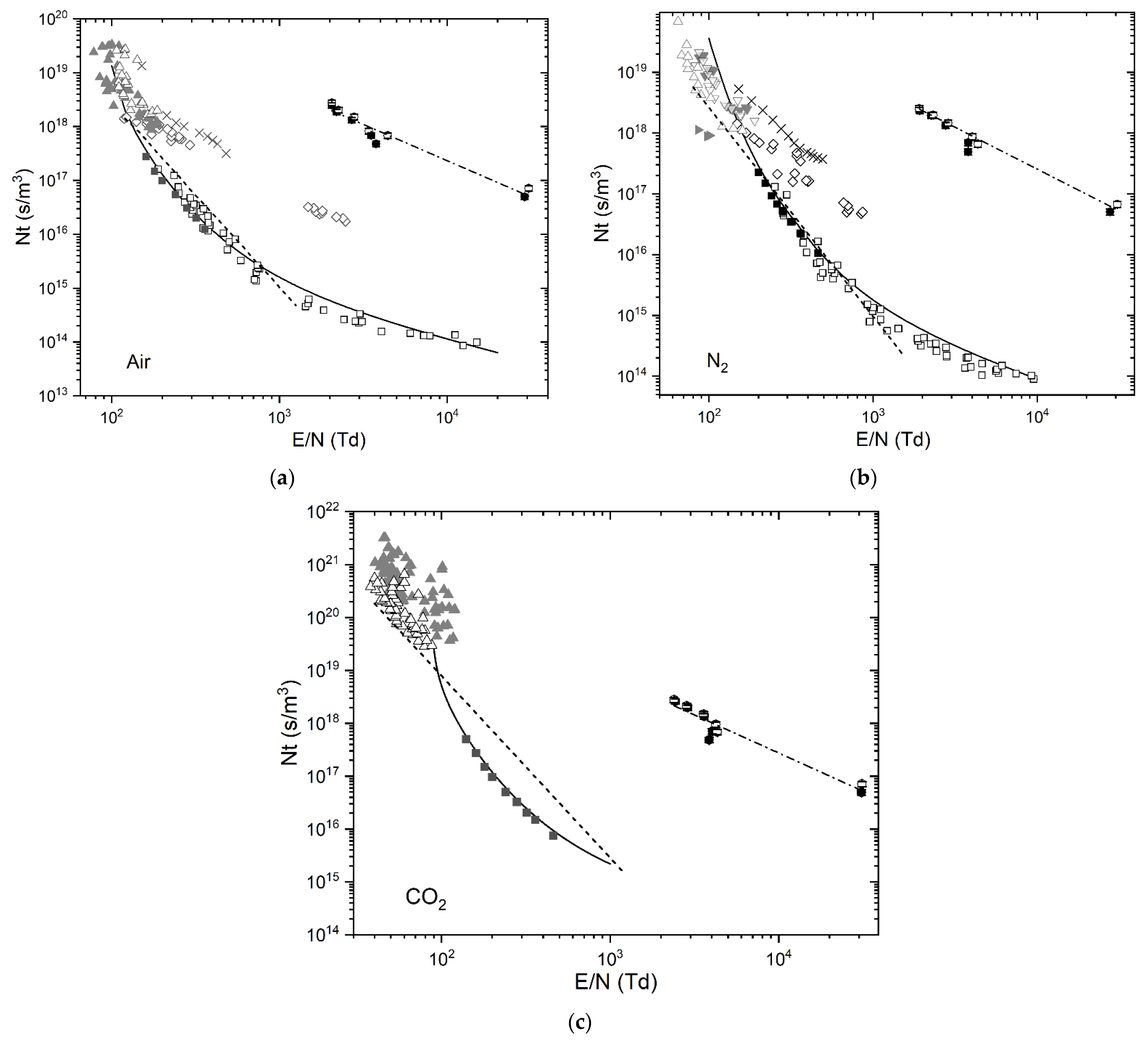
3.3.2. Nt as a Function of E/N
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schaefer, G.; Kristiansen, M.; Guenther, A. Gas Dis-Charge Closing Switches; Springer Science + Business Media: New York, NY, USA, 1990. [Google Scholar]
- Haddad, A.; Warne, D.F. Advances in High Voltage Engineering; The Institution of Engineering and Technology: London, UK, 2007. [Google Scholar]
- Becker, K.H.; Schoenbach, K.H.; Eden, J.G. Microplasmas and applications. J. Phys. D Appl. Phys. 2006, 39, R55–R70. [Google Scholar] [CrossRef]
- Luo, D.; Duan, Y. Microplasmas for analytical applications of lab-on-a-chip. TrAC Trends Anal. Chem. 2012, 39, 254–266. [Google Scholar] [CrossRef]
- Joffrion, J.B.; Mills, D.; Clower, W.; Wilson, C.G. On-Chip Microplasmas for the Detection of Radioactive Cesium Contamination in Seawater. Micromachines 2017, 8, 259. [Google Scholar] [CrossRef] [Green Version]
- Jovović, J.; Konjević, N. Spectroscopic and electric characterization of an atmospheric pressure segmented gas discharge with micro hollow electrodes. Eur. Phys. J. D 2014, 68, 60. [Google Scholar] [CrossRef]
- Niu, G.; Knodel, A.; Burhenn, S.; Brandt, S.; Franzke, J. Review: Miniature dielectric barrier discharge (DBD) in analytical atomic spectrometry. Anal. Chim. Acta 2020, 1147, 211–239. [Google Scholar] [CrossRef]
- Paris Agreement. 2015. Available online: https://unfccc.int/sites/default/files/english_paris_agreement.pdf (accessed on 9 September 2021).
- Eves, M. A Literature Review on SF6 Gas Alternatives for Use on the Distribution Network. Western Power Distribution Innovation. 2018. Available online: https://www.westernpower.co.uk/downloads/5857 (accessed on 9 September 2021).
- Cai, X.; Zou, X.; Wang, X.; Wang, L.; Guan, Z.; Jiang, W. Over-volted breakdown and recovery of short nitrogen spark gaps. Laser Part. Beams 2010, 28, 443–450. [Google Scholar] [CrossRef]
- Kumar, S.; Huiskamp, T.; Pemen, A.; Seeger, M.; Pachin, J.; Franck, C.M. Electrical Breakdown Study in CO2 and CO2-O2 Mixtures in AC, DC and Pulsed Electric Fields at 0.1–1 MPa Pressure. IEEE Trans. Dielectr. Electr. Insul. 2021, 28, 158–166. [Google Scholar] [CrossRef]
- Simeni, M.S.; Goldberg, B.; Gulko, I.; Frederickson, K.; Adamovich, I.V. Sub-nanosecond resolution electric field measurements during ns pulse breakdown in ambient air. J. Phys. D Appl. Phys. 2017, 51, 01LT01. [Google Scholar] [CrossRef] [Green Version]
- Balmelli, M.; Farber, R.; Merotto, L.; Soltic, P.; Bleiner, D.; Franck, C.M.; Biela, J. Experimental Analysis of Breakdown With Nanosecond Pulses for Spark-Ignition Engines. IEEE Access 2021, 9, 100050–100062. [Google Scholar] [CrossRef]
- Starikovskii, A.; Anikin, N.; Kosarev, I.; Mintoussov, E.; Nudnova, M.; Rakitin, A.; Roupassov, D.; Starikovskaia, S.; Zhukov, V. Nanosecond-Pulsed Discharges for Plasma-Assisted Combustion and Aerodynamics. J. Propuls. Power 2008, 24, 1182–1197. [Google Scholar] [CrossRef]
- Drew, D.S.; Pister, K.S.J. Geometric Optimization of Microfabricated Silicon Electrodes for Corona Discharge-Based Electrohydrodynamic Thrusters. Micromachines 2017, 8, 141. [Google Scholar] [CrossRef] [Green Version]
- Park, H.J.; Kim, S.H.; Ju, H.W.; Lee, H.; Lee, Y.; Park, S.; Yang, H.; Park, S.-J.; Eden, J.G.; Yang, J.; et al. Microplasma Jet Arrays as a Therapeutic Choice for Fungal Keratitis. Sci. Rep. 2018, 8, 2422. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Doherty, K.G.; Oh, J.-S.; Unsworth, P.; Bowfield, A.; Sheridan, C.M.; Weightman, P.; Bradley, J.W.; Williams, R.L. Polystyrene Surface Modification for Localized Cell Culture Using a Capillary Dielectric Barrier Discharge Atmospheric-Pressure Microplasma Jet. Plasma Process. Polym. 2013, 10, 978–989. [Google Scholar] [CrossRef]
- Chiang, W.; Mariotti, D.; Sankaran, R.M.; Eden, J.G.; Ostrikov, K. Microplasmas for Advanced Materials and Devices. Adv. Mater. 2019, 32, e1905508. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Garner, A.L.; Meng, G.; Fu, Y.; Loveless, A.M.; Ii, R.S.B.; Darr, A.M. Transitions between electron emission and gas breakdown mechanisms across length and pressure scales. J. Appl. Phys. 2020, 128, 210903. [Google Scholar] [CrossRef]
- Loveless, A.M.; Meng, G.; Ying, Q.; Wu, F.; Wang, K.; Cheng, Y.; Garner, A.L. The Transition to Paschen’s Law for Microscale Gas Breakdown at Subatmospheric Pressure. Sci. Rep. 2019, 9, 5669. [Google Scholar] [CrossRef] [Green Version]
- Levatter, J.; Lin, S.-C. Necessary conditions for the homogeneous formation of pulsed avalanche discharges at high gas pressures. J. Appl. Phys. 1980, 51, 210–222. [Google Scholar] [CrossRef]
- Mankowski, J.; Dickens, J.; Kristiansen, M. High voltage subnanosecond breakdown. IEEE Trans. Plasma Sci. 1998, 26, 874–881. [Google Scholar] [CrossRef]
- Shao, T.; Sun, G.; Yan, P. An experimental investigation of repetitive nanosecond-pulse breakdown in air. J. Phys. D Appl. Phys. 2006, 39, 2192–2197. [Google Scholar]
- Carboni, V.; Lackner, H.; Giri, D.; Lehr, J. The breakdown fields and risetimes of select gases under the conditions of fast charging (~20 ns and less) and high pressures (20-100 atmospheres). In Proceedings of the 28th IEEE International Conference on Plasma Science and 13th IEEE International Pulsed Power Conference. Digest of Papers (Cat. No.01CH37251), Las Vegas, NV, USA, 17–22 June 2001; PPPS-2001 Pulsed Power Plasma Science 2001. Volume 1, pp. 482–486. [Google Scholar] [CrossRef]
- Kiyan, T.; Takade, M.; Namihira, T.; Hara, M.; Sasaki, M.; Goto, M.; Akiyama, H. Polarity Effect in DC Breakdown Voltage Characteristics of Pressurized Carbon Dioxide up to Supercritical Conditions. IEEE Trans. Plasma Sci. 2008, 36, 821–827. [Google Scholar] [CrossRef]
- Babich, L.; Loiko, T.V. Generalized Paschen’s law for overvoltage conditions. IEEE Trans. Plasma Sci. 2016, 44, 3243–3248. [Google Scholar] [CrossRef]
- Beloplotov, D.; Lomaev, M.; Sorokin, D.; Tarasenko, V. Displacement current during the formation of positive streamers in atmospheric pressure air with a highly inhomogeneous electric field. Phys. Plasmas 2018, 25, 083511. [Google Scholar] [CrossRef]
- Rep’ev, A.; Repin, P. Dynamics of the Optical Emission from a High-Voltage Diffuse Discharge in a Rod–Plane Electrode System in Atmospheric-Pressure Air. Plasma Phys. Rep. 2006, 32, 72–78. [Google Scholar] [CrossRef]
- Laity, G.; Neuber, A.; Fierro, A.; Dickens, J.; Hatfield, L. Phenomenology of streamer propagation during pulsed dielectric surface flashover. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 946–953. [Google Scholar] [CrossRef]
- Wilson, M.P. Impulse Breakdown of Liquid-Solid Interfaces. Ph.D. Thesis, University of Strathclyde, Glasgow, UK, 2011. [Google Scholar]
- Passive High-Voltage Probes P5100, P5120, P5122, P6015A Data Sheet. Available online: https://docs.rs-online.com/d2f5/0900766b80e4e715.pdf (accessed on 9 September 2021).
- Grover, F.W. Inductance Calculations: Working Formulas and Tables; Dover Publications, Inc.: New York, NY, USA, 1946. [Google Scholar]
- Krile, J.; Neuber, A.; Dickens, J.; Krompholz, H. DC and Pulsed Dielectric Surface Flashover at Atmospheric Pressure. IEEE Trans. Plasma Sci. 2005, 33, 1149–1154. [Google Scholar] [CrossRef]
- Liu, T.; Timoshkin, I.V.; MacGregor, S.J.; Wilson, M.P.; Given, M.J.; Bonifaci, N.; Hanna, R. Field-Time Breakdown Characteristics of air, N₂, CO₂, and SF₆. IEEE Trans. Plasma Sci. 2020, 48, 3321–3331. [Google Scholar] [CrossRef]
- Dick, A.R.; Macgregor, S.J.; Buttram, M.T.; Pate, R.C.; Rinehart, L.F.; Prestwich, K.R. Breakdown Phenomena in Ultra-Fast Plasma Closing Switches. IEEE Trans. Plasma Sci. 2000, 28, 1456. [Google Scholar] [CrossRef]
- Felsenthal, P.; Proud, J.M. Nanosecond-Pulse Breakdown in Gases. Phys. Rev. 1965, 139, A1796–A1804. [Google Scholar] [CrossRef]
- Martin, T.H. An empirical formula for gas switch breakdown delay. In Proceedings of the 7th Pulsed Power Conference, Monterey, CA, USA, 11–14 June 1989; pp. 73–79. [Google Scholar]
- Kawada, Y.; Sumikazu, S.; Tatsuzo, H. Nanosecond-pulse breakdown of gas-insulated gaps. J. Appl. Phys. 1988, 63, 1877–1881. [Google Scholar] [CrossRef]
- Levko, D.; Arslanbekov, R.; Kolobov, V. Modified Paschen curves for pulsed breakdown. Phys. Plasmas 2019, 26, 064502. [Google Scholar] [CrossRef]



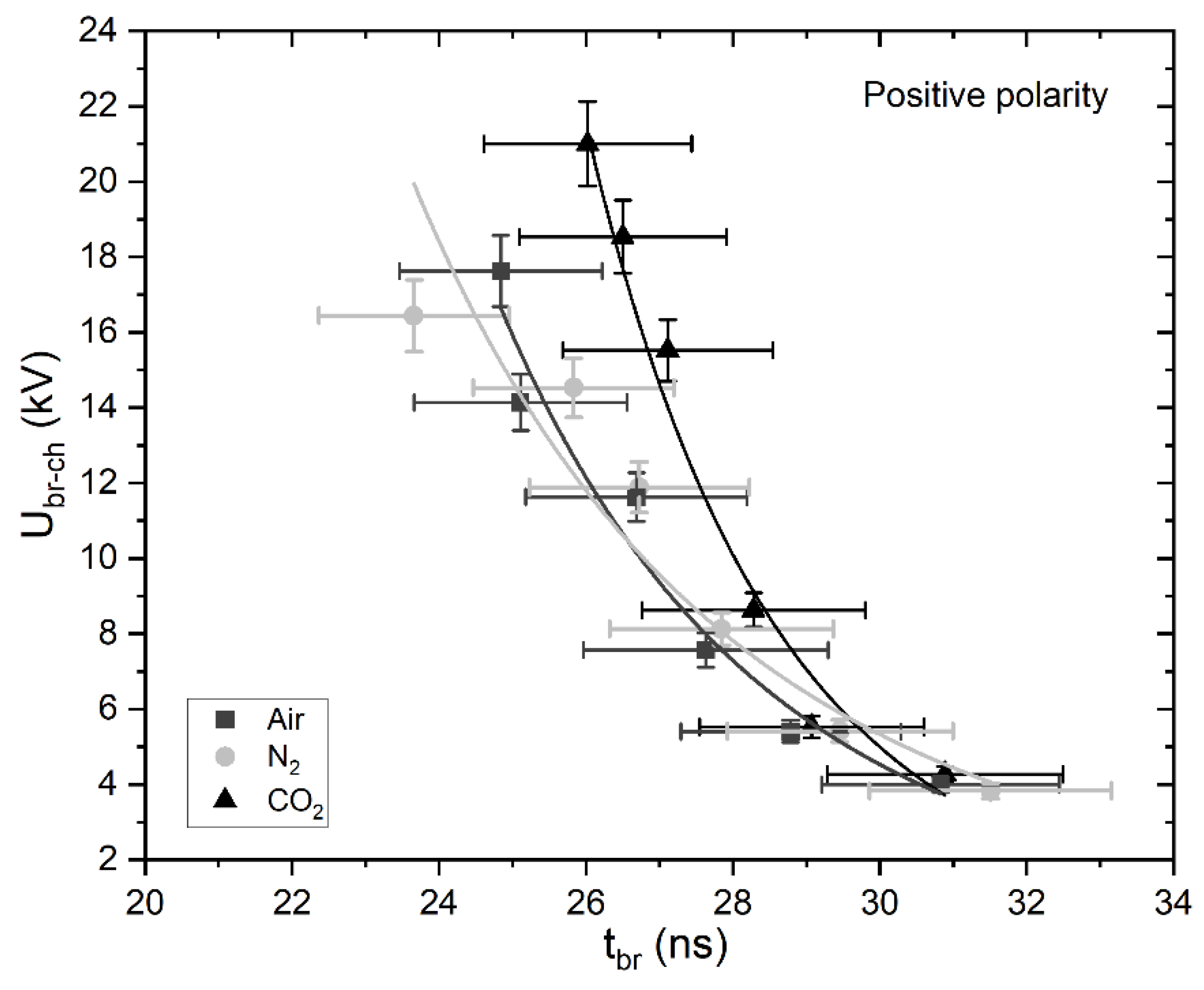
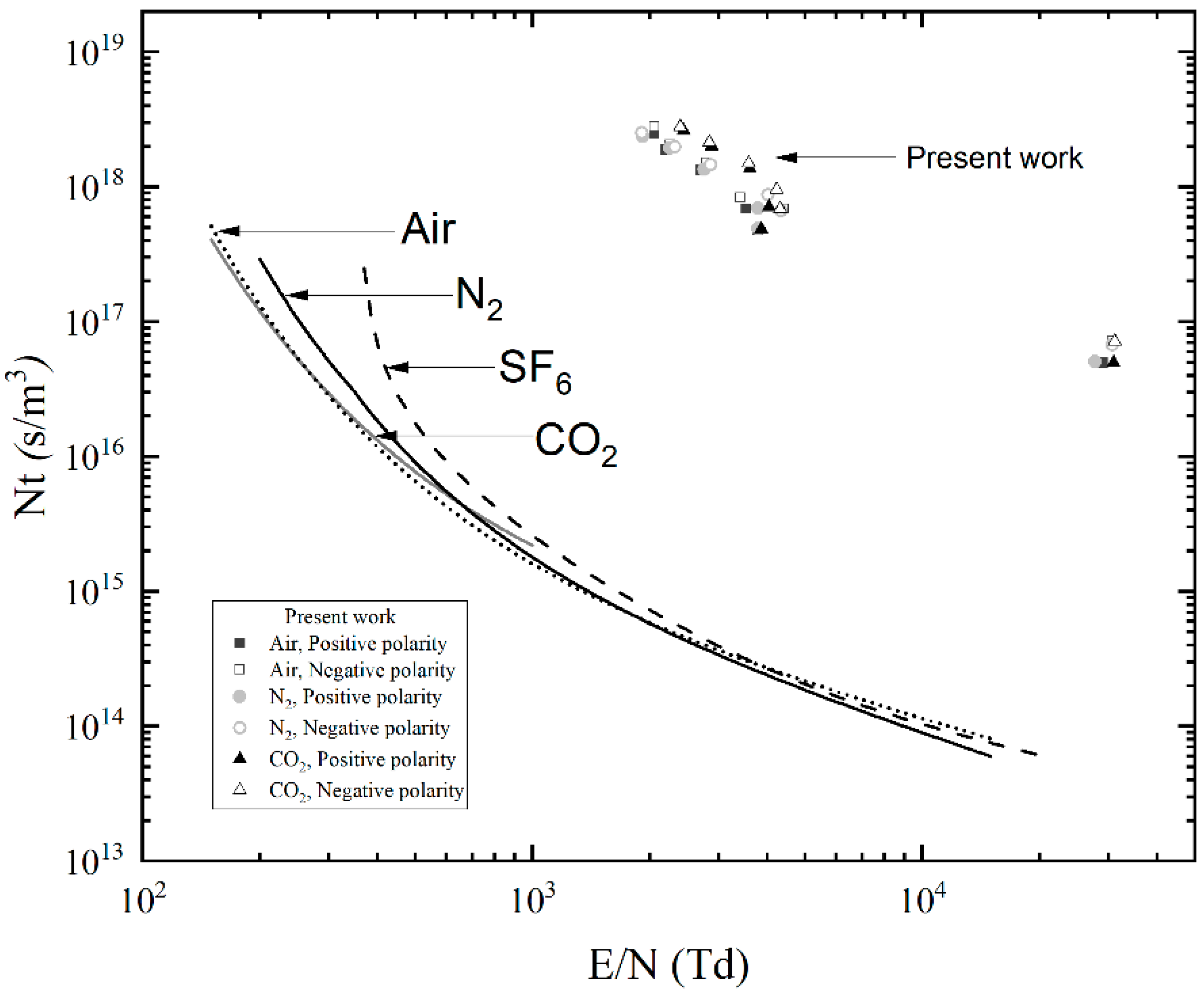
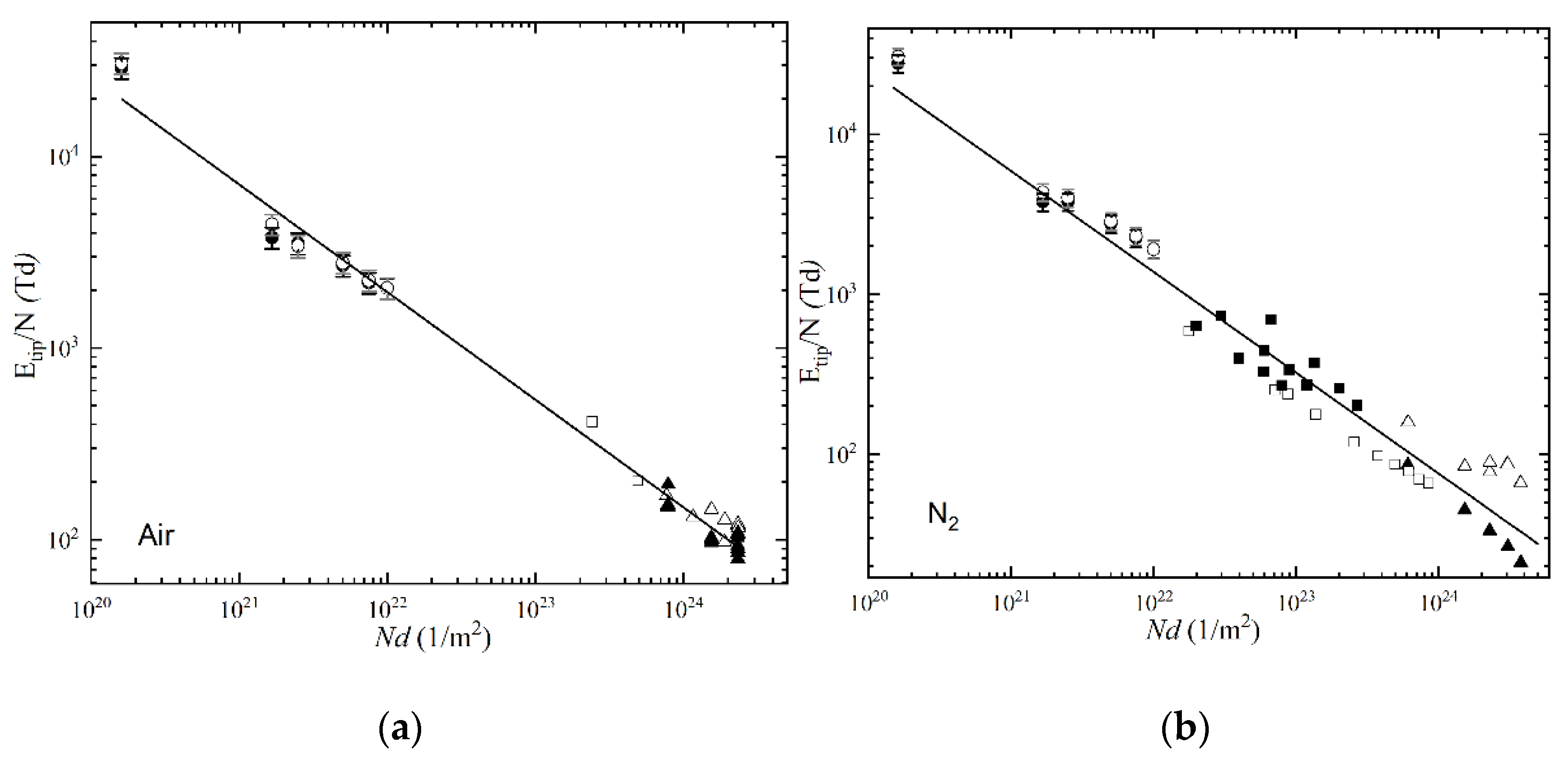
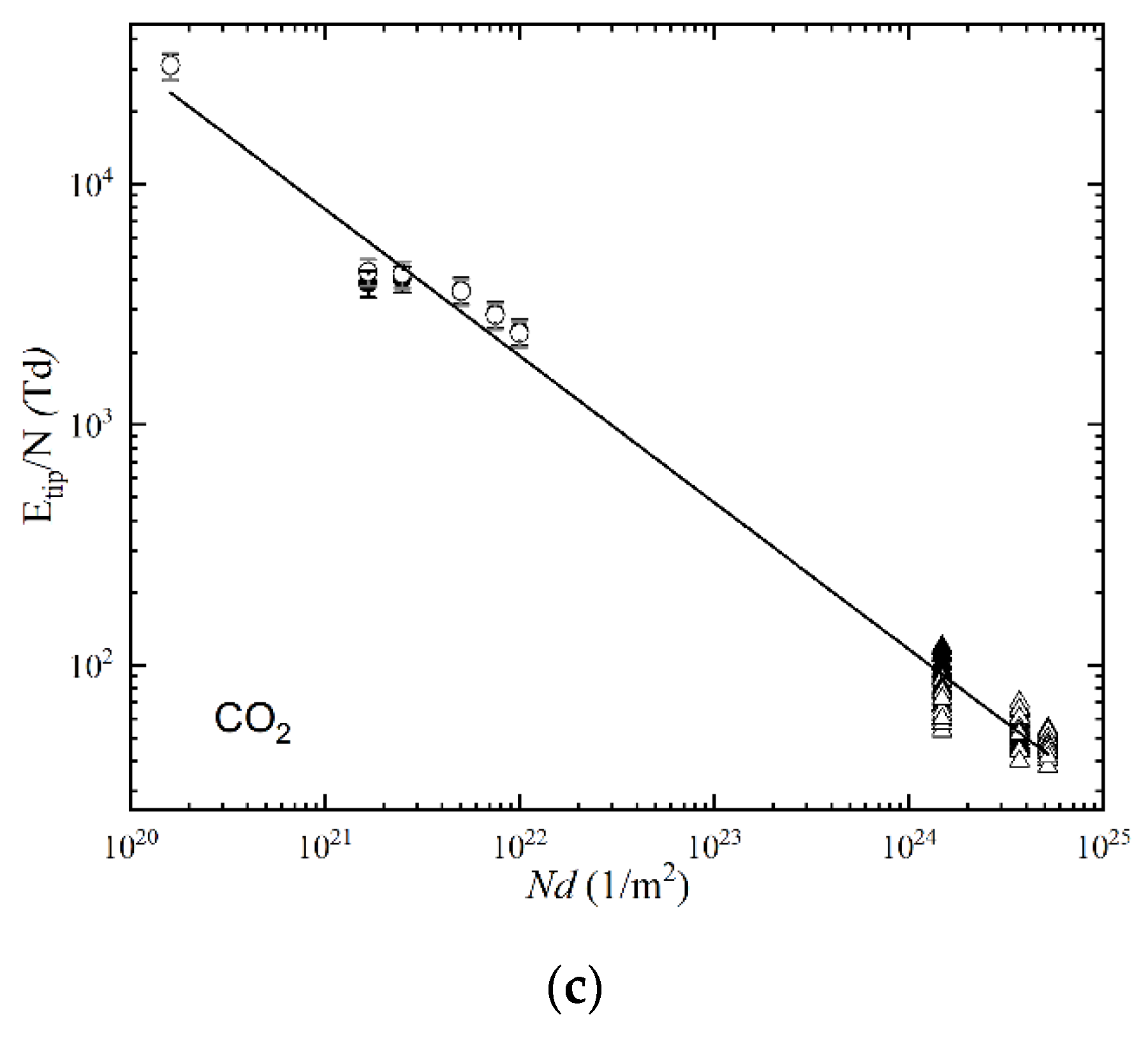
| Ubr-ch = A · (tbr)−B | |||
|---|---|---|---|
| Negative polarity | Air | N2 | CO2 |
| A | 7.09 · 104 | 4.24 · 104 | 5.37 · 105 |
| B | 2.55 | 2.42 | 3.07 |
| Positive polarity | Air | N2 | CO2 |
| A | 6.88 · 1010 | 8.54 · 108 | 5.75 · 1015 |
| B | 6.89 | 5.55 | 10.20 |
| Etip/N = C · (Nd)−D | |||
|---|---|---|---|
| Air | N2 | CO2 | |
| C | 4.51 · 1015 | 1.02 · 1017 | 5.08 · 1016 |
| D | 0.56 | 0.63 | 0.61 |
| Ntbr = K · (Etip/N)−M | |||
|---|---|---|---|
| Air | N2 | CO2 | |
| K | 5.78 · 1022 | 8.05 · 1022 | 1.59 · 1023 |
| M | 1.35 | 1.38 | 1.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Timoshkin, I.; Wilson, M.P.; Given, M.J.; MacGregor, S.J. The Nanosecond Impulsive Breakdown Characteristics of Air, N2 and CO2 in a Sub-mm Gap. Plasma 2022, 5, 12-29. https://doi.org/10.3390/plasma5010002
Liu T, Timoshkin I, Wilson MP, Given MJ, MacGregor SJ. The Nanosecond Impulsive Breakdown Characteristics of Air, N2 and CO2 in a Sub-mm Gap. Plasma. 2022; 5(1):12-29. https://doi.org/10.3390/plasma5010002
Chicago/Turabian StyleLiu, Ting, Igor Timoshkin, Mark P. Wilson, Martin J. Given, and Scott J. MacGregor. 2022. "The Nanosecond Impulsive Breakdown Characteristics of Air, N2 and CO2 in a Sub-mm Gap" Plasma 5, no. 1: 12-29. https://doi.org/10.3390/plasma5010002
APA StyleLiu, T., Timoshkin, I., Wilson, M. P., Given, M. J., & MacGregor, S. J. (2022). The Nanosecond Impulsive Breakdown Characteristics of Air, N2 and CO2 in a Sub-mm Gap. Plasma, 5(1), 12-29. https://doi.org/10.3390/plasma5010002





