A Comprehensive Review on Amplification of Laser Pulses via Stimulated Raman Scattering and Stimulated Brillouin Scattering in Plasmas
Abstract
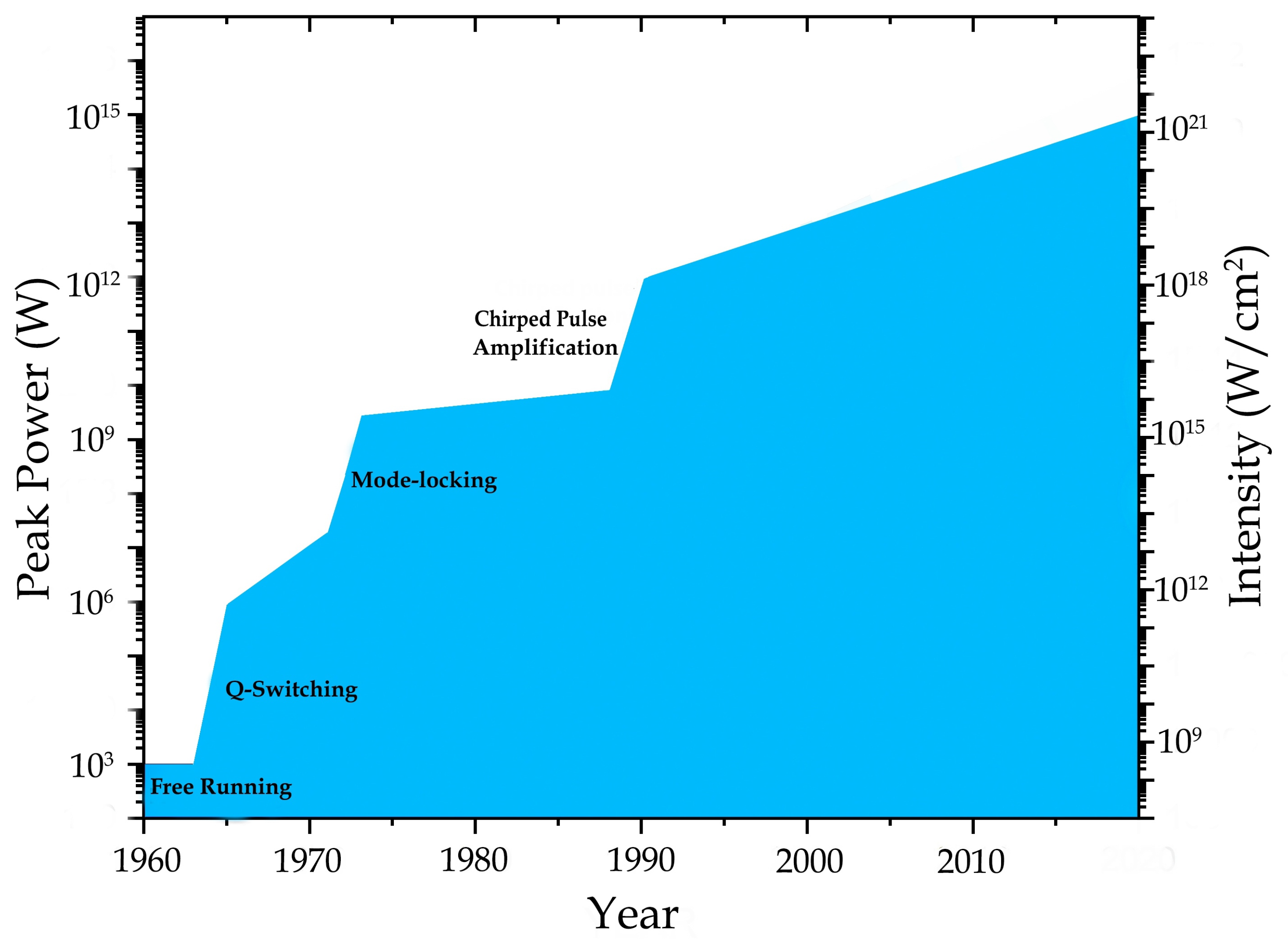
:1. Introduction
2. Stimulated Raman Scattering (SRS)
2.1. Theory
2.2. Factors Limiting Raman Amplification
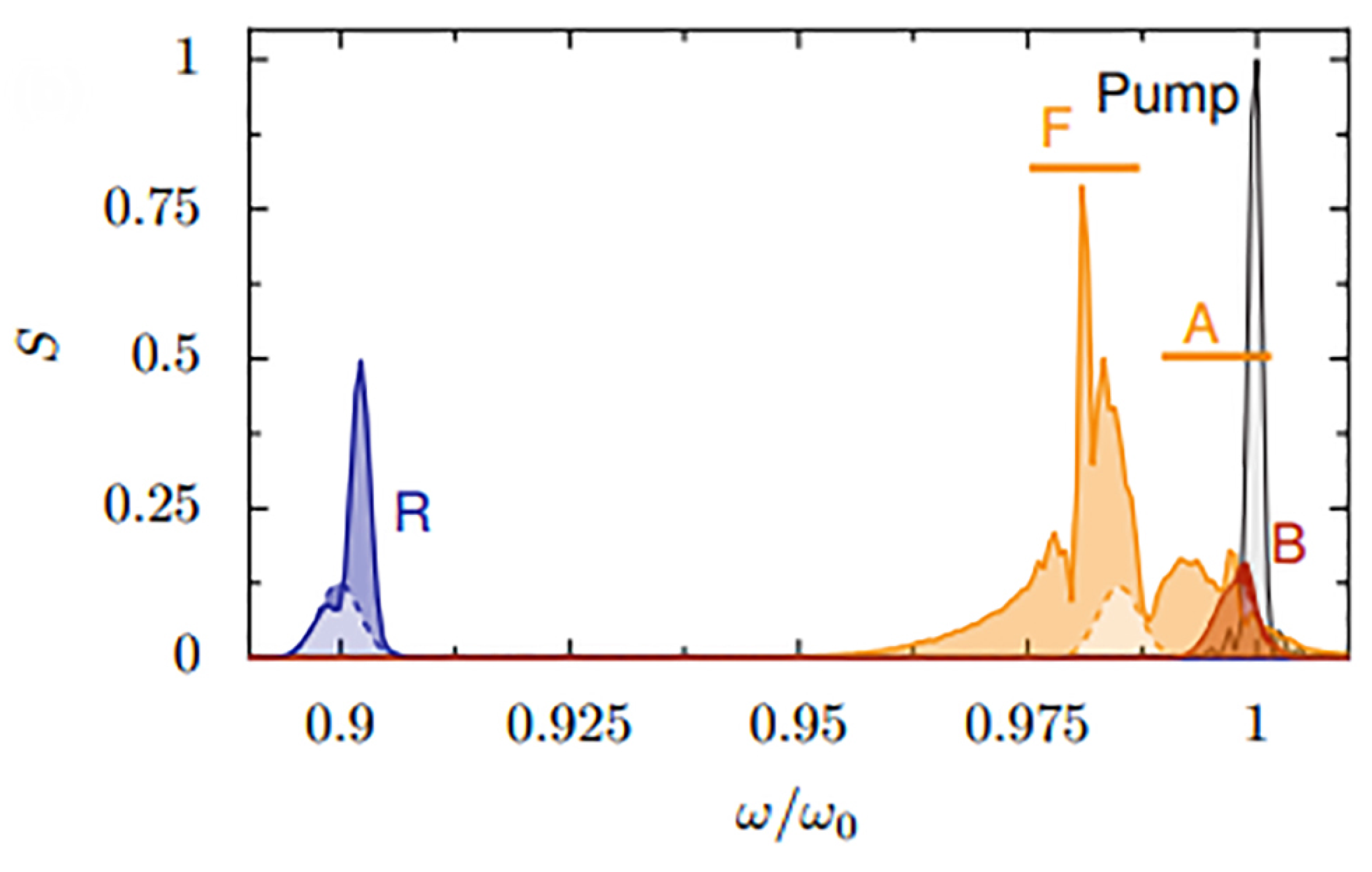
2.2.1. Forward Raman Scattering (FRS)
2.2.2. Langmuir Wave Breaking
2.2.3. Other Factors Limiting Raman Amplification
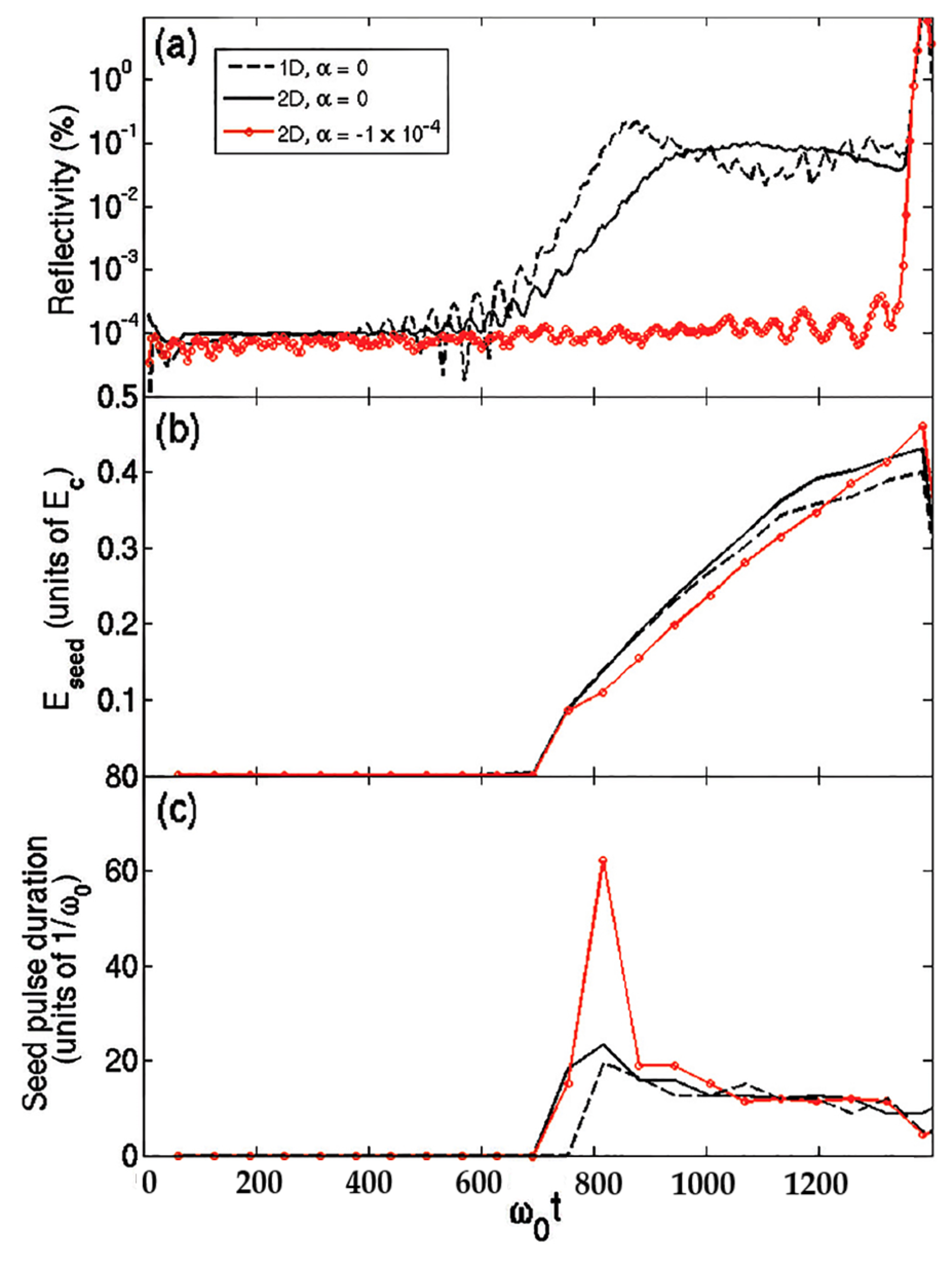
2.3. Mitigating the Limiting Factors of Raman Amplification
3. Stimulated Brilliouin Scattering (SBS)
3.1. Theory
3.2. Factors Limiting Brillouin Scattering
3.2.1. Forward Raman Scattering
3.2.2. Filamentation
3.3. Mitigating the Limiting Factors for Brillouin Amplification
3.3.1. Studies under Subquarter-Critical Plasma Densities
3.3.2. Studies above Subquarter-Critical Densities
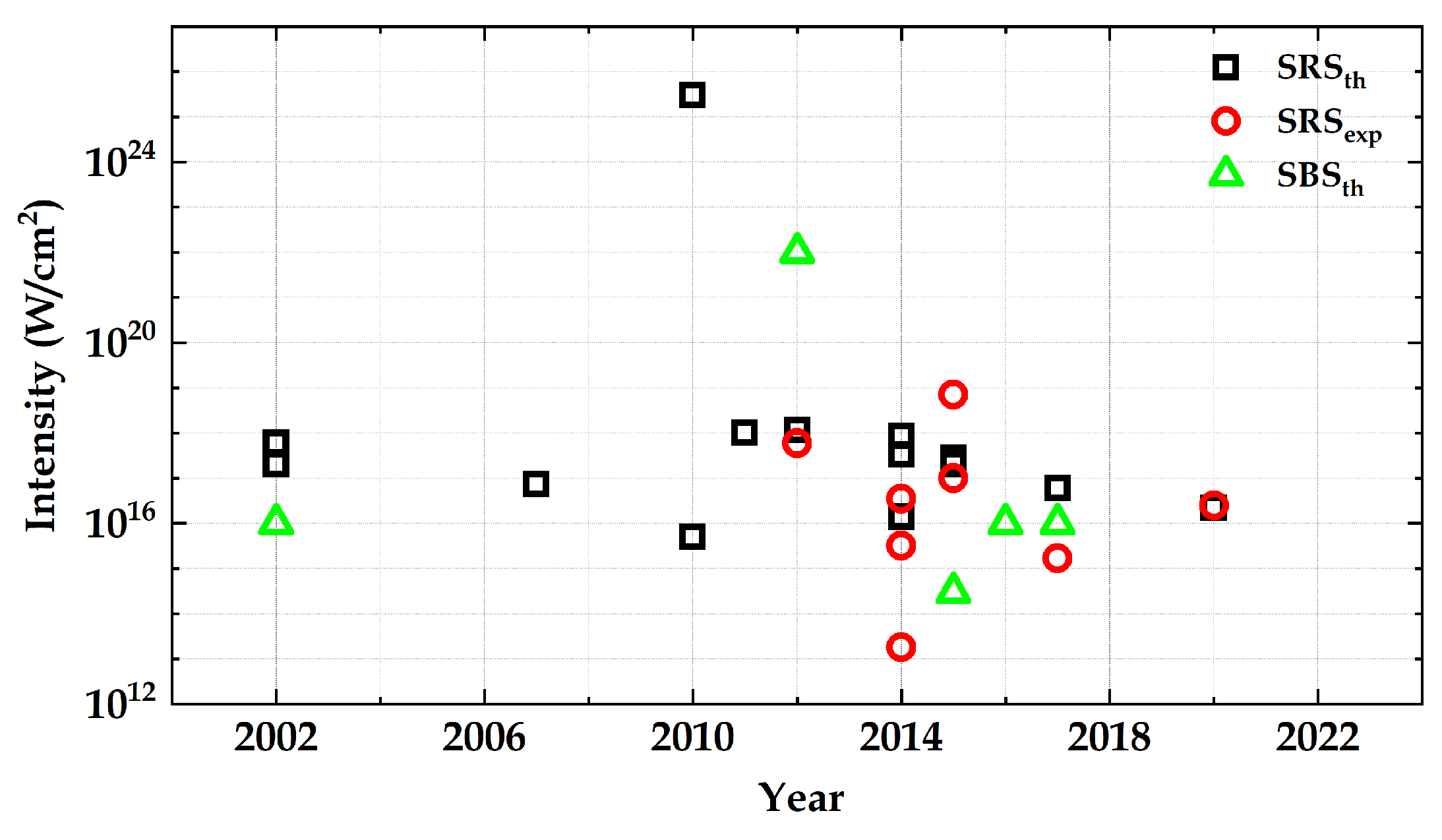
4. A Comparison of Raman and Brillouin Scattering
5. Amplification in Magnetized Plasma
5.1. Theoretical Structure
5.2. Laser Amplification in Strongly Magnetized Plasma
5.3. Laser Pulse Compression Using Magnetised Plasma
5.4. Amplification of Mid-Infrared Lasers via Magnetized Plasma Coupling
5.5. Kinetic Simulations of Laser Parametric Amplification in Magnetized Plasmas
5.6. Laser-Plasma Interactions in Magnetized Environment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BRA | Backward Raman Amplification |
| CPA | Chirped Pulse Amplification |
| CPRA | Chirped Pulse Raman Amplification |
| CWB | Coherent Wave Breaking |
| EBW | Electron Bernstein Waves |
| FEL | Free Electron Lasers |
| FRS | Forward Raman Scattering |
| FWHM | Full Width at Half Maximum |
| GDD | Group Delay Dispersion |
| ICF | Inertial Confinement Fusion |
| ISI | Induced Spatial Incoherence |
| LWFA | Laser Wakefield Acceleration |
| MBRA | Magnetic Backward Raman Amplification |
| MHD | Magneto-hydrodynamic |
| MLF | Magnetic Low Frequency |
| OAM | Orbital Angular Momentum |
| PIC | Particle-in-cell |
| SBS | Stimulated Brillouin Scattering |
| SMI | Self Modulation Instability |
| SM-LWFA | Self-modulated Laser Wakefield Acceleration |
| SPM | Self Phase Modulation |
| SRA | Stimulated Raman Amplification |
| SRS | Stimulated Raman Scattering |
| SRSS | Stimulated Raman Side Scattering |
| sc-SBS | Strongly Coupled-Stimulated Brillouin Scattering |
| wc-SBS | Weakly Coupled-Stimulated Brillouin Scattering |
| RBS | Raman Backscattering |
| sc-SBS | Strongly Coupled-Stimulated Brillouin Scattering |
| wc-SBS | Weakly Coupled-Stimulated Brillouin Scattering |
| RBS | Raman Backscattering |
| UH | Ultra Hybrid |
References
- Maiman, T. Optical and microwave-optical experiments in ruby. Phys. Rev. Lett. 1960, 4, 564. [Google Scholar] [CrossRef]
- Bloembergen, N. Nonlinear optics and spectroscopy. Rev. Mod. Phys. 1982, 54, 685. [Google Scholar] [CrossRef] [Green Version]
- Sheehy, B.; DiMauro, L. Atomic and molecular dynamics in intense optical fields. Annu. Rev. Phys. Chem. 1996, 47, 463–494. [Google Scholar] [CrossRef] [Green Version]
- Betti, R.; Hurricane, O. Inertial-confinement fusion with lasers. Nat. Phys. 2016, 12, 435–448. [Google Scholar] [CrossRef]
- Keefe, D. Inertial confinement fusion. Annu. Rev. Nucl. Part. Sci. 1982, 32, 391–441. [Google Scholar] [CrossRef]
- Craxton, R.; Anderson, K.; Boehly, T.; Goncharov, V.; Harding, D.; Knauer, J.; McCrory, R.; McKenty, P.; Meyerhofer, D.; Myatt, J.; et al. Direct-drive inertial confinement fusion: A review. Phys. Plasmas 2015, 22, 110501. [Google Scholar] [CrossRef] [Green Version]
- Lianqiang, S.; Fengjuan, W.; Zongqiang, Y.; Weiwu, W.; Hongbo, C.; Chao, T.; Feng, Z.; Tiankui, Z.; Zhigang, D.; Wenshuai, Z.; et al. Research progress of kinetic effects in laser inertial confinement fusion. High Power Laser Part. Beams 2020, 33, 012004. [Google Scholar]
- Gao, Y.; Cui, Y.; Ji, L.; Rao, D.; Zhao, X.; Li, F.; Liu, D.; Feng, W.; Xia, L.; Liu, J.; et al. Development of low-coherence high-power laser drivers for inertial confinement fusion. Matter Radiat. Extrem. 2020, 5, 065201. [Google Scholar] [CrossRef]
- Wang, G. A brief review of the progress of laser inertial confinement fusion in recent years. Chin. J. Nucl. Sci. Eng. 1997, 17, 266–269. [Google Scholar]
- Bingham, R.; Mendonca, J.; Shukla, P. Plasma based charged-particle accelerators. Plasma Phys. Control. Fusion 2003, 46, R1. [Google Scholar] [CrossRef]
- Malka, V.; Faure, J.; Gauduel, Y.A.; Lefebvre, E.; Rousse, A.; Phuoc, K.T. Principles and applications of compact laser–plasma accelerators. Nat. Phys. 2008, 4, 447–453. [Google Scholar] [CrossRef]
- Katsouleas, T. Progress on plasma accelerators: From the energy frontier to tabletops. Plasma Phys. Control. Fusion 2004, 46, B575. [Google Scholar] [CrossRef]
- Bingham, R. Basic concepts in plasma accelerators. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 559–575. [Google Scholar] [CrossRef] [PubMed]
- Esarey, E.; Schroeder, C.; Leemans, W. Physics of laser-driven plasma-based electron accelerators. Rev. Mod. Phys. 2009, 81, 1229. [Google Scholar] [CrossRef]
- Downer, M.; Zgadzaj, R.; Debus, A.; Schramm, U.; Kaluza, M. Diagnostics for plasma-based electron accelerators. Rev. Mod. Phys. 2018, 90, 035002. [Google Scholar] [CrossRef] [Green Version]
- Katsouleas, T. Plasma accelerators race to 10 GeV and beyond. Phys. Plasmas 2006, 13, 055503. [Google Scholar] [CrossRef]
- Umstadter, D.P. All-laser-driven Thomson X-ray sources. Contemp. Phys. 2015, 56, 417–431. [Google Scholar] [CrossRef] [Green Version]
- Schoenlein, R.; Elsaesser, T.; Holldack, K.; Huang, Z.; Kapteyn, H.; Murnane, M.; Woerner, M. Recent advances in ultrafast X-ray sources. Philos. Trans. R. Soc. A 2019, 377, 20180384. [Google Scholar] [CrossRef] [Green Version]
- Corde, S.; Phuoc, K.T.; Lambert, G.; Fitour, R.; Malka, V.; Rousse, A.; Beck, A.; Lefebvre, E. Femtosecond X rays from laser-plasma accelerators. Rev. Mod. Phys. 2013, 85, 1. [Google Scholar] [CrossRef]
- Wang, S.; Baumgarten, C.M.; Wang, Y.; Reagan, B.A.; Rockwood, A.P.; Wang, H.; Yin, L.; Wernsing, K.; Bravo, H.; Luther, B.M.; et al. High-power ultrashort pulse lasers to pump plasma-based soft X-ray lasers. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1–15. [Google Scholar] [CrossRef]
- Albert, F.; Thomas, A.G. Applications of laser wakefield accelerator-based light sources. Plasma Phys. Control. Fusion 2016, 58, 103001. [Google Scholar] [CrossRef] [Green Version]
- Liang, E. Gamma-ray and pair creation using ultra-intense lasers and astrophysical applications. High Energy Density Phys. 2013, 9, 425–427. [Google Scholar] [CrossRef]
- Remington, B.A.; Drake, R.P.; Ryutov, D.D. Experimental astrophysics with high power lasers and Z pinches. Rev. Mod. Phys. 2006, 78, 755. [Google Scholar] [CrossRef] [Green Version]
- Takabe, H.; Kuramitsu, Y. Recent progress of laboratory astrophysics with intense lasers. High Power Laser Sci. Eng. 2021, 9, e49. [Google Scholar] [CrossRef]
- Ditmire, T.; Edens, A.D. Laboratory simulations of astrophysical blast waves with high energy lasers. Laser Photonics Rev. 2008, 2, 400–416. [Google Scholar] [CrossRef]
- Burns, F. High-power lasers their performance, limitations, and future. IEEE Spectr. 1967, 4, 115–120. [Google Scholar] [CrossRef]
- Fork, R.; Shank, C.; Yen, R. Amplification of 70-fs optical pulses to gigawatt powers. Appl. Phys. Lett. 1982, 41, 223–225. [Google Scholar] [CrossRef]
- Pogorelsky, I.V.; Fischer, J.; Kusche, K.; Babzien, M.; Kurnit, N.; Bigio, I.; Harrison, R.; Shimada, T. Subnanosecond multi-gigawatt CO/sub 2/laser. IEEE J. Quantum Electron. 1995, 31, 556–566. [Google Scholar] [CrossRef]
- Malkin, V.; Shvets, G.; Fisch, N. Ultra-powerful compact amplifiers for short laser pulses. Phys. Plasmas 2000, 7, 2232–2240. [Google Scholar] [CrossRef]
- Mourou, G.A.; Barty, C.; Perry, M.D. Ultrahigh-Intensity Laser: Physics of the Extreme on a Tabletop. USA. 1997. Available online: https://physicstoday.scitation.org/doi/10.1063/1.882131 (accessed on 9 November 2022).
- Bahk, S.W.; Rousseau, P.; Planchon, T.; Chvykov, V.; Kalintchenko, G.; Maksimchuk, A.; Mourou, G.; Yanovsky, V. Generation and characterization of the highest laser intensities (1022 W/cm2). Opt. Lett. 2004, 29, 2837–2839. [Google Scholar] [CrossRef]
- Yu, T.J.; Lee, S.K.; Sung, J.H.; Yoon, J.W.; Jeong, T.M.; Lee, J. Generation of high-contrast, 30 fs, 1.5 PW laser pulses from chirped-pulse amplification Ti: Sapphire laser. Opt. Express 2012, 20, 10807–10815. [Google Scholar] [CrossRef] [PubMed]
- Vaupel, A.; Bodnar, N.; Webb, B.; Shah, L.; Richardson, M.C. Concepts, performance review, and prospects of table-top, few-cycle optical parametric chirped-pulse amplification. Opt. Eng. 2013, 53, 051507. [Google Scholar] [CrossRef]
- Tabak, M.; Hammer, J.; Glinsky, M.E.; Kruer, W.L.; Wilks, S.C.; Woodworth, J.; Campbell, E.M.; Perry, M.D.; Mason, R.J. Ignition and high gain with ultrapowerful lasers. Phys. Plasmas 1994, 1, 1626–1634. [Google Scholar] [CrossRef] [Green Version]
- Lehmann, G. Plasma-Based Methods for Amplification and Manipulation of High-Power Laser Pulses. In Proceedings of the NIC Symposium 2018; No. FZJ-2018-02948; John von Neumann-Institut für Computing: Jülich, Germany, 2018. [Google Scholar]
- Seres, J.; Seres, E.; Hochhaus, D.; Ecker, B.; Zimmer, D.; Bagnoud, V.; Kuehl, T.; Spielmann, C. Laser-driven amplification of soft X-rays by parametric stimulated emission in neutral gases. Nat. Phys. 2010, 6, 455–461. [Google Scholar] [CrossRef]
- Dai, J.; Xie, X.; Zhang, X.C. Terahertz wave amplification in gases with the excitation of femtosecond laser pulses. Appl. Phys. Lett. 2007, 91, 211102. [Google Scholar] [CrossRef]
- Kuwahara, K.; Takahashi, E.; Matsumoto, Y.; Kato, S.; Owadano, Y. Short-pulse generation by saturated KrF laser amplification of a steep Stokes pulse produced by two-step stimulated Brillouin scattering. JOSA B 2000, 17, 1943–1947. [Google Scholar] [CrossRef]
- Gorbunov, V.A.; Papernyĭ, S.; Petrov, V.; Startsev, V. Time compression of pulses in the course of stimulated Brillouin scattering in gases. Sov. J. Quantum Electron. 1983, 13, 900. [Google Scholar] [CrossRef]
- Capjack, C.; James, C.; McMullin, J. Plasma KrF laser pulse compressor. J. Appl. Phys. 1982, 53, 4046–4053. [Google Scholar] [CrossRef]
- Milroy, R.; Capjack, C.; James, C. A plasma-laser amplifier in the 11–16 μm wavelength range. Plasma Phys. 1977, 19, 989. [Google Scholar] [CrossRef]
- Maier, M.; Kaiser, W.; Giordmaine, J. Intense light bursts in the stimulated Raman effect. Phys. Rev. Lett. 1966, 17, 1275. [Google Scholar] [CrossRef]
- Gudzenko, L.I.; Shelepin, L.A.; Yakovlenko, S.I. Amplification in recombining plasmas (plasma lasers). Sov. Phys. Uspekhi 1975, 17, 848. [Google Scholar] [CrossRef]
- Hora, H. Self-focusing of laser beams in a plasma by ponderomotive forces. Z. Phys. A Hadron. Nucl. 1969, 226, 156–159. [Google Scholar] [CrossRef]
- Hora, H. Theory of relativistic self-focusing of laser radiation in plasmas. JOSA 1975, 65, 882–886. [Google Scholar] [CrossRef]
- Esarey, E.; Sprangle, P.; Krall, J.; Ting, A. Self-focusing and guiding of short laser pulses in ionizing gases and plasmas. IEEE J. Quantum Electron. 1997, 33, 1879–1914. [Google Scholar] [CrossRef]
- Sakai, O.; Tachibana, K. Plasmas as metamaterials: A review. Plasma Sources Sci. Technol. 2012, 21, 013001. [Google Scholar] [CrossRef]
- Sakai, O.; Sakaguchi, T.; Tachibana, K. Verification of a plasma photonic crystal for microwaves of millimeter wavelength range using two-dimensional array of columnar microplasmas. Appl. Phys. Lett. 2005, 87, 241505. [Google Scholar] [CrossRef] [Green Version]
- Lehmann, G.; Spatschek, K. Plasma-based polarizer and waveplate at large laser intensity. Phys. Rev. E 2018, 97, 063201. [Google Scholar] [CrossRef] [PubMed]
- Forslund, D.; Kindel, J.; Lindman, E. Theory of stimulated scattering processes in laser-irradiated plasmas. Phys. Fluids 1975, 18, 1002–1016. [Google Scholar] [CrossRef]
- Milroy, R.; Capjack, C.; James, C. Plasma laser pulse amplifier using induced Raman or Brillouin processes. Phys. Fluids 1979, 22, 1922–1931. [Google Scholar] [CrossRef]
- Andreev, A.A.; Sutyagin, A. Feasibility of optical pulse compression by stimulated Brillouin scattering in a plasma. Sov. J. Quantum Electron. 1989, 19, 1579. [Google Scholar] [CrossRef]
- Marquès, J.R.; Lancia, L.; Gangolf, T.; Blecher, M.; Bolaños, S.; Fuchs, J.; Willi, O.; Amiranoff, F.; Berger, R.; Chiaramello, M.; et al. Joule-level high-efficiency energy transfer to subpicosecond laser pulses by a plasma-based amplifier. Phys. Rev. X 2019, 9, 021008. [Google Scholar] [CrossRef] [Green Version]
- Malkin, V.; Shvets, G.; Fisch, N. Fast compression of laser beams to highly overcritical powers. Phys. Rev. Lett. 1999, 82, 4448. [Google Scholar] [CrossRef]
- Lancia, L.; Giribono, A.; Vassura, L.; Chiaramello, M.; Riconda, C.; Weber, S.; Castan, A.; Chatelain, A.; Frank, A.; Gangolf, T.; et al. Signatures of the self-similar regime of strongly coupled stimulated Brillouin scattering for efficient short laser pulse amplification. Phys. Rev. Lett. 2016, 116, 075001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moody, J.; MacGowan, B.; Glenzer, S.; Kirkwood, R.; Kruer, W.; Schmitt, A.; Williams, E.; Stone, G. First measurement of short length-scale density fluctuations in a large laser plasma. Phys. Rev. Lett. 1999, 83, 1783. [Google Scholar] [CrossRef]
- Toroker, Z.; Malkin, V.; Fisch, N. Seed laser chirping for enhanced backward Raman amplification in plasmas. Phys. Rev. Lett. 2012, 109, 085003. [Google Scholar] [CrossRef] [Green Version]
- Malkin, V.; Shvets, G.; Fisch, N. Detuned Raman amplification of short laser pulses in plasma. Phys. Rev. Lett. 2000, 84, 1208. [Google Scholar] [CrossRef]
- Trines, R.; Fiuza, F.; Bingham, R.; Fonseca, R.; Silva, L.; Cairns, R.; Norreys, P. Simulations of efficient Raman amplification into the multipetawatt regime. Nat. Phys. 2011, 7, 87–92. [Google Scholar] [CrossRef]
- Ping, Y.; Cheng, W.; Suckewer, S.; Clark, D.S.; Fisch, N.J. Amplification of ultrashort laser pulses by a resonant Raman scheme in a gas-jet plasma. Phys. Rev. Lett. 2004, 92, 175007. [Google Scholar] [CrossRef]
- Lancia, L.; Marquès, J.R.; Nakatsutsumi, M.; Riconda, C.; Weber, S.; Hüller, S.; Mančić, A.; Antici, P.; Tikhonchuk, V.; Héron, A.; et al. Experimental evidence of short light pulse amplification using strong-coupling stimulated Brillouin scattering in the pump depletion regime. Phys. Rev. Lett. 2010, 104, 025001. [Google Scholar] [CrossRef]
- Ping, Y.; Kirkwood, R.; Wang, T.L.; Clark, D.; Wilks, S.; Meezan, N.; Berger, R.; Wurtele, J.; Fisch, N.; Malkin, V.; et al. Development of a nanosecond-laser-pumped Raman amplifier for short laser pulses in plasma. Phys. Plasmas 2009, 16, 123113. [Google Scholar] [CrossRef] [Green Version]
- Ren, J.; Cheng, W.; Li, S.; Suckewer, S. A new method for generating ultraintense and ultrashort laser pulses. Nat. Phys. 2007, 3, 732–736. [Google Scholar] [CrossRef]
- Lehmann, G.; Spatschek, K.; Sewell, G. Pulse shaping during Raman-seed amplification for short laser pulses. Phys. Rev. E 2013, 87, 063107. [Google Scholar] [CrossRef]
- Trines, R.M.; Alves, E.; Webb, E.; Vieira, J.; Fiúza, F.; Fonseca, R.; Silva, L.; Cairns, R.A.; Bingham, R. New criteria for efficient Raman and Brillouin amplification of laser beams in plasma. Sci. Rep. 2020, 10, 19875. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, G.; Spatschek, K. Nonlinear Brillouin amplification of finite-duration seeds in the strong coupling regime. Phys. Plasmas 2013, 20, 073112. [Google Scholar] [CrossRef]
- Sadler, J.D.; Trines, R.M.; Tabak, M.; Haberberger, D.; Froula, D.H.; Davies, A.S.; Bucht, S.; Silva, L.O.; Alves, E.P.; Fiúza, F.; et al. Optimization of plasma amplifiers. Phys. Rev. E 2017, 95, 053211. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lehmann, G.; Spatschek, K. Non-filamentated ultra-intense and ultra-short pulse fronts in three-dimensional Raman seed amplification. Phys. Plasmas 2014, 21, 053101. [Google Scholar] [CrossRef]
- Chiaramello, M.; Amiranoff, F.; Riconda, C.; Weber, S. Role of frequency chirp and energy flow directionality in the strong coupling regime of Brillouin-based plasma amplification. Phys. Rev. Lett. 2016, 117, 235003. [Google Scholar] [CrossRef]
- Edwards, M.R.; Mikhailova, J.M.; Fisch, N.J. X-ray amplification by stimulated Brillouin scattering. Phys. Rev. E 2017, 96, 023209. [Google Scholar] [CrossRef] [Green Version]
- Sadler, J.D.; Nathvani, R.; Oleśkiewicz, P.; Ceurvorst, L.A.; Ratan, N.; Kasim, M.F.; Trines, R.M.; Bingham, R.; Norreys, P.A. Compression of X-ray free electron laser pulses to attosecond duration. Sci. Rep. 2015, 5, 16755. [Google Scholar] [CrossRef] [Green Version]
- Lehmann, G.; Spatschek, K. Control of Brillouin short-pulse seed amplification by chirping the pump pulse. Phys. Plasmas 2015, 22, 043105. [Google Scholar] [CrossRef]
- Schluck, F.; Lehmann, G.; Spatschek, K. Parametric pulse amplification by acoustic quasimodes in electron-positron plasma. Phys. Rev. E 2017, 96, 053204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qu, K.; Barth, I.; Fisch, N.J. Plasma wave seed for Raman amplifiers. Phys. Rev. Lett. 2017, 118, 164801. [Google Scholar] [CrossRef]
- Moody, J.; Michel, P.; Divol, L.; Berger, R.; Bond, E.; Bradley, D.; Callahan, D.; Dewald, E.; Dixit, S.; Edwards, M.; et al. Multistep redirection by cross-beam power transfer of ultrahigh-power lasers in a plasma. Nat. Phys. 2012, 8, 344–349. [Google Scholar] [CrossRef]
- Kruer, W.L.; Wilks, S.C.; Afeyan, B.B.; Kirkwood, R.K. Energy transfer between crossing laser beams. Phys. Plasmas 1996, 3, 382–385. [Google Scholar] [CrossRef]
- Hinkel, D.; Rosen, M.; Williams, E.; Langdon, A.; Still, C.; Callahan, D.; Moody, J.; Michel, P.; Town, R.; London, R.; et al. Stimulated Raman scatter analyses of experiments conducted at the National Ignition Facility. Phys. Plasmas 2011, 18, 056312. [Google Scholar] [CrossRef]
- Williams, E.; Cohen, B.; Divol, L.; Dorr, M.; Hittinger, J.; Hinkel, D.; Langdon, A.; Kirkwood, R.; Froula, D.; Glenzer, S. Effects of ion trapping on crossed-laser-beam stimulated Brillouin scattering. Phys. Plasmas 2004, 11, 231–244. [Google Scholar] [CrossRef]
- Michel, P.; Glenzer, S.; Divol, L.; Bradley, D.; Callahan, D.; Dixit, S.; Glenn, S.; Hinkel, D.; Kirkwood, R.; Kline, J.; et al. Symmetry tuning via controlled crossed-beam energy transfer on the National Ignition Facility. Phys. Plasmas 2010, 17, 056305. [Google Scholar] [CrossRef]
- Michel, P.; Divol, L.; Williams, E.; Thomas, C.; Callahan, D.; Weber, S.; Haan, S.; Salmonson, J.; Meezan, N.; Landen, O.; et al. Energy transfer between laser beams crossing in ignition hohlraums. Phys. Plasmas 2009, 16, 042702. [Google Scholar] [CrossRef]
- Glenzer, S.; MacGowan, B.; Michel, P.; Meezan, N.; Suter, L.; Dixit, S.; Kline, J.; Kyrala, G.; Bradley, D.; Callahan, D.; et al. Symmetric inertial confinement fusion implosions at ultra-high laser energies. Science 2010, 327, 1228–1231. [Google Scholar] [CrossRef] [Green Version]
- Tanaka, K.; Goldman, L.; Seka, W.; Richardson, M.; Soures, J.; Williams, E. Stimulated Raman scattering from UV-laser-produced plasmas. Phys. Rev. Lett. 1982, 48, 1179. [Google Scholar] [CrossRef]
- Michel, P.; Divol, L.; Dewald, E.; Milovich, J.; Hohenberger, M.; Jones, O.; Hopkins, L.B.; Berger, R.; Kruer, W.; Moody, J. Multibeam stimulated Raman scattering in inertial confinement fusion conditions. Phys. Rev. Lett. 2015, 115, 055003. [Google Scholar] [CrossRef] [Green Version]
- Walsh, C.; Villeneuve, D.; Baldis, H. Electron plasma-wave production by stimulated Raman scattering: Competition with stimulated Brillouin scattering. Phys. Rev. Lett. 1984, 53, 1445. [Google Scholar] [CrossRef]
- Froula, D.; Divol, L.; Meezan, N.; Dixit, S.; Neumayer, P.; Moody, J.; Pollock, B.; Ross, J.; Suter, L.; Glenzer, S. Laser beam propagation through inertial confinement fusion hohlraum plasmas. Phys. Plasmas 2007, 14, 055705. [Google Scholar] [CrossRef] [Green Version]
- Villeneuve, D.; Baldis, H.; Bernard, J. Suppression of stimulated Raman scattering by the seeding of stimulated Brillouin scattering in a laser-produced plasma. Phys. Rev. Lett. 1987, 59, 1585. [Google Scholar] [CrossRef] [PubMed]
- Hinkel, D.; Schneider, M.; Baldis, H.; Bonanno, G.; Bower, D.; Campbell, K.; Celeste, J.; Compton, S.; Costa, R.; Dewald, E.; et al. Laser coupling to reduced-scale hohlraum targets at the Early Light Program of the National Ignition Facility. Phys. Plasmas 2005, 12, 056305. [Google Scholar] [CrossRef]
- Baldis, H.; Villeneuve, D.; La Fontaine, B.; Enright, G.; Labaune, C.; Baton, S.; Mounaix, P.; Pesme, D.; Casanova, M.; Rozmus, W. Stimulated Brillouin scattering in picosecond time scales: Experiments and modeling. Phys. Fluids B Plasma Phys. 1993, 5, 3319–3327. [Google Scholar] [CrossRef]
- Lindl, J.D.; Amendt, P.; Berger, R.L.; Glendinning, S.G.; Glenzer, S.H.; Haan, S.W.; Kauffman, R.L.; Landen, O.L.; Suter, L.J. The physics basis for ignition using indirect-drive targets on the National Ignition Facility. Phys. Plasmas 2004, 11, 339–491. [Google Scholar] [CrossRef] [Green Version]
- Baton, S.; Rousseaux, C.; Mounaix, P.; Labaune, C.; La Fontaine, B.; Pesme, D.; Renard, N.; Gary, S.; Louis-Jacquet, M.; Baldis, H. Stimulated Brillouin scattering with a 1 ps laser pulse in a preformed underdense plasma. Phys. Rev. E 1994, 49, R3602. [Google Scholar] [CrossRef]
- Langdon, A.; Hinkel, D. Nonlinear evolution of stimulated scatter in high-temperature plasmas. Phys. Rev. Lett. 2002, 89, 015003. [Google Scholar] [CrossRef]
- Mori, W.; Decker, C.; Hinkel, D.; Katsouleas, T. Raman forward scattering of short-pulse high-intensity lasers. Phys. Rev. Lett. 1994, 72, 1482. [Google Scholar] [CrossRef]
- Matsuoka, T.; McGuffey, C.; Cummings, P.; Horovitz, Y.; Dollar, F.; Chvykov, V.; Kalintchenko, G.; Rousseau, P.; Yanovsky, V.; Bulanov, S.; et al. Stimulated Raman side scattering in laser wakefield acceleration. Phys. Rev. Lett. 2010, 105, 034801. [Google Scholar] [CrossRef] [PubMed]
- Gordon, D.; Tzeng, K.; Clayton, C.; Dangor, A.; Malka, V.; Marsh, K.; Modena, A.; Mori, W.; Muggli, P.; Najmudin, Z.; et al. Observation of electron energies beyond the linear dephasing limit from a laser-excited relativistic plasma wave. Phys. Rev. Lett. 1998, 80, 2133. [Google Scholar] [CrossRef]
- Rousseaux, C.; Malka, G.; Miquel, J.; Amiranoff, F.; Baton, S.; Mounaix, P. Experimental validation of the linear theory of stimulated Raman scattering driven by a 500-fs laser pulse in a preformed underdense plasma. Phys. Rev. Lett. 1995, 74, 4655. [Google Scholar] [CrossRef] [PubMed]
- Tzeng, K.C.; Mori, W. Suppression of electron ponderomotive blowout and relativistic self-focusing by the occurrence of Raman scattering and plasma heating. Phys. Rev. Lett. 1998, 81, 104. [Google Scholar] [CrossRef]
- Krushelnick, K.; Ting, A.; Burris, H.; Fisher, A.; Manka, C.; Esarey, E. Second harmonic generation of stimulated Raman scattered light in underdense plasmas. Phys. Rev. Lett. 1995, 75, 3681. [Google Scholar] [CrossRef]
- Jia, Q.; Barth, I.; Edwards, M.R.; Mikhailova, J.M.; Fisch, N.J. Distinguishing Raman from strongly coupled Brillouin amplification for short pulses. Phys. Plasmas 2016, 23, 053118. [Google Scholar] [CrossRef]
- Lehmann, G.; Spatschek, K.H. Transient plasma photonic crystals for high-power lasers. Phys. Rev. Lett. 2016, 116, 225002. [Google Scholar] [CrossRef]
- Cairns, R. Raman amplification in plasma. In Harnessing Relativistic Plasma Waves as Novel Radiation Sources from Terahertz to X-rays and Beyond II; SPIE: Bellingham, WA, USA, 2011; Volume 8075, pp. 58–67. [Google Scholar]
- Malkin, V.; Fisch, N.J. Key plasma parameters for resonant backward Raman amplification in plasma. Eur. Phys. J. Spec. Top. 2014, 223, 1157–1167. [Google Scholar] [CrossRef]
- Tsidulko, Y.A.; Malkin, V.M.; Fisch, N.J. Suppression of superluminous precursors in high-power backward Raman amplifiers. Phys. Rev. Lett. 2002, 88, 235004. [Google Scholar] [CrossRef] [Green Version]
- Solodov, A.; Malkin, V.; Fisch, N. Random density inhomogeneities and focusability of the output pulses for plasma-based powerful backward Raman amplifiers. Phys. Plasmas 2003, 10, 2540–2544. [Google Scholar] [CrossRef] [Green Version]
- Solodov, A.; Malkin, V.; Fisch, N. Pump side scattering in ultrapowerful backward Raman amplifiers. Phys. Rev. E 2004, 69, 066413. [Google Scholar] [CrossRef] [Green Version]
- Malkin, V.; Tsidulko, Y.A.; Fisch, N. Stimulated Raman scattering of rapidly amplified short laser pulses. Phys. Rev. Lett. 2000, 85, 4068. [Google Scholar] [CrossRef] [PubMed]
- Trines, R.; Fiúza, F.; Bingham, R.; Fonseca, R.; Silva, L.; Cairns, R.; Norreys, P. Production of picosecond, kilojoule, and petawatt laser pulses via raman amplification of nanosecond pulses. Phys. Rev. Lett. 2011, 107, 105002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yampolsky, N.A.; Malkin, V.; Fisch, N. Finite-duration seeding effects in powerful backward Raman amplifiers. Phys. Rev. E 2004, 69, 036401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Malkin, V.; Toroker, Z.; Fisch, N. Laser duration and intensity limits in plasma backward Raman amplifiers. Phys. Plasmas 2012, 19, 023109. [Google Scholar] [CrossRef]
- Malkin, V.; Fisch, N. Relic crystal-lattice effects on Raman compression of powerful X-ray pulses in plasmas. Phys. Rev. Lett. 2007, 99, 205001. [Google Scholar] [CrossRef] [PubMed]
- Fraiman, G.M.; Yampolsky, N.A.; Malkin, V.M.; Fisch, N.J. Robustness of laser phase fronts in backward Raman amplifiers. Phys. Plasmas 2002, 9, 3617–3624. [Google Scholar] [CrossRef]
- Clark, D.S.; Fisch, N.J. Operating regime for a backward Raman laser amplifier in preformed plasma. Phys. Plasmas 2003, 10, 3363–3370. [Google Scholar] [CrossRef] [Green Version]
- Berger, R.L.; Clark, D.S.; Solodov, A.A.; Valeo, E.J.; Fisch, N.J. Inverse bremsstrahlung stabilization of noise in the generation of ultrashort intense pulses by backward Raman amplification. Phys. Plasmas 2004, 11, 1931–1937. [Google Scholar] [CrossRef] [Green Version]
- Balakin, A.; Fisch, N.; Fraiman, G.; Malkin, V.; Toroker, Z. Numerical modeling of quasitransient backward Raman amplification of laser pulses in moderately undercritical plasmas with multicharged ions. Phys. Plasmas 2011, 18, 102311. [Google Scholar] [CrossRef]
- Malkin, V.; Fisch, N.; Wurtele, J. Compression of powerful X-ray pulses to attosecond durations by stimulated Raman backscattering in plasmas. Phys. Rev. E 2007, 75, 026404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Farmer, J.; Ersfeld, B.; Jaroszynski, D. Raman amplification in plasma: Wavebreaking and heating effects. Phys. Plasmas 2010, 17, 113301. [Google Scholar] [CrossRef]
- Malkin, V.; Fisch, N. Quasitransient regimes of backward Raman amplification of intense X-ray pulses. Phys. Rev. E 2009, 80, 046409. [Google Scholar] [CrossRef] [PubMed]
- Malkin, V.; Fisch, N. Quasitransient backward Raman amplification of powerful laser pulses in dense plasmas with multicharged ions. Phys. Plasmas 2010, 17, 073109. [Google Scholar] [CrossRef]
- Phillion, D.; Banner, D.; Campbell, E.; Turner, R.; Estabrook, K. Stimulated Raman scattering in large plasmas. Phys. Fluids 1982, 25, 1434–1443. [Google Scholar] [CrossRef] [Green Version]
- Prince, R.C.; Frontiera, R.R.; Potma, E.O. Stimulated Raman scattering: From bulk to nano. Chem. Rev. 2017, 117, 5070–5094. [Google Scholar] [CrossRef]
- Liu, C.; Tripathi, V. Stimulated Raman scattering in a plasma channel. Phys. Plasmas 1996, 3, 3410–3413. [Google Scholar] [CrossRef]
- Vieux, G.; Cipiccia, S.; Grant, D.; Lemos, N.; Grant, P.; Ciocarlan, C.; Ersfeld, B.; Hur, M.; Lepipas, P.; Manahan, G.; et al. An ultra-high gain and efficient amplifier based on Raman amplification in plasma. Sci. Rep. 2017, 7, 2399. [Google Scholar] [CrossRef] [Green Version]
- Bogatskaya, A.; Volkova, E.; Popov, A. Unipolar terahertz pulse formation in a nonequilibrium plasma channel formed by an ultrashort uv laser pulse. Phys. Rev. E 2021, 104, 025202. [Google Scholar] [CrossRef]
- Cheng, W.; Avitzour, Y.; Ping, Y.; Suckewer, S.; Fisch, N.J.; Hur, M.S.; Wurtele, J.S. Reaching the nonlinear regime of Raman amplification of ultrashort laser pulses. Phys. Rev. Lett. 2005, 94, 045003. [Google Scholar] [CrossRef] [Green Version]
- Vieira, J.; Trines, R.M.; Alves, E.P.; Fonseca, R.; Mendonça, J.; Bingham, R.; Norreys, P.; Silva, L. Amplification and generation of ultra-intense twisted laser pulses via stimulated Raman scattering. Nat. Commun. 2016, 7, 10371. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chapman, T.; Hüller, S.; Masson-Laborde, P.; Heron, A.; Pesme, D.; Rozmus, W. Driven spatially autoresonant stimulated Raman scattering in the kinetic regime. Phys. Rev. Lett. 2012, 108, 145003. [Google Scholar] [CrossRef] [PubMed]
- Edwards, M.R.; Toroker, Z.; Mikhailova, J.M.; Fisch, N.J. The efficiency of Raman amplification in the wavebreaking regime. Phys. Plasmas 2015, 22, 074501. [Google Scholar] [CrossRef]
- Obenschain, S.; Pawley, C.; Mostovych, A.; Stamper, J.; Gardner, J.; Schmitt, A.; Bodner, S. Reduction of Raman scattering in a plasma to convective levels using induced spatial incoherence. Phys. Rev. Lett. 1989, 62, 768. [Google Scholar] [CrossRef]
- Marchand, R.; Capjack, C.; James, C. Stimulated scattering and self-modulation of an intense laser beam in a plasma waveguide. J. Phys. D Appl. Phys. 1985, 18, 795. [Google Scholar] [CrossRef]
- Farmer, J.; Ersfeld, B.; Jaroszynski, D. Raman Amplification in Plasma: Influence of Heating. In Proceedings of the 37th EPS Conference on Plasma Physics, Helix Arts Centre, Dublin City University Campus, Dublin, Ireland, 21–25 June 2010; Volume 1, p. O4.416. [Google Scholar]
- Sharma, A.; Kourakis, I. Laser pulse compression and amplification via Raman backscattering in plasma. Laser Part. Beams 2009, 27, 579–585. [Google Scholar] [CrossRef] [Green Version]
- Clark, D.; Fisch, N. Raman laser amplification in preformed and ionizing plasmas. Laser Part. Beams 2005, 23, 101–106. [Google Scholar] [CrossRef] [Green Version]
- Coffey, T. Breaking of large amplitude plasma oscillations. Phys. Fluids 1971, 14, 1402–1406. [Google Scholar] [CrossRef]
- Kim, J.; Lee, H.J.; Suk, H.; Ko, I.S. Characteristics of pulse compression in laser pulse amplification by stimulated Raman backscattering. Phys. Lett. A 2003, 314, 464–471. [Google Scholar] [CrossRef]
- Büchner, J. Vlasov-code simulation. In Proceedings of the ISSS, Cancun, Mexico, 1–5 July 2005; Volume 7, pp. 26–31. [Google Scholar]
- Atzeni, S.; Meyer-ter Vehn, J. The Physics of Inertial Fusion: Beam Plasma Interaction, Hydrodynamics, Hot Dense Matter; OUP Oxford: Oxford, UK, 2004; Volume 125. [Google Scholar]
- Schiavi, A. Study of Laser Produced Plasmas by X-ray and Proton Radiography; Imperial College of Science, University of London: London, UK, 2003. [Google Scholar]
- Vieux, G.; Lyachev, A.; Yang, X.; Ersfeld, B.; Farmer, J.P.; Brunetti, E.; Issac, R.; Raj, G.; Welsh, G.H.; Wiggins, S.; et al. Chirped pulse Raman amplification in plasma. New J. Phys. 2011, 13, 063042. [Google Scholar] [CrossRef]
- Jia, Q.; Qu, K.; Fisch, N.J. Optical phase conjugation in backward Raman amplification. Opt. Lett. 2020, 45, 5254–5257. [Google Scholar] [CrossRef] [PubMed]
- Balakin, A.; Fraiman, G.; Fisch, N.; Malkin, V. Noise suppression and enhanced focusability in plasma Raman amplifier with multi-frequency pump. Phys. Plasmas 2003, 10, 4856–4864. [Google Scholar] [CrossRef]
- Farmer, J.P.; Pukhov, A. Raman amplification in the coherent wave-breaking regime. Phys. Rev. E 2015, 92, 063109. [Google Scholar] [CrossRef] [Green Version]
- Pai, C.H.; Lin, M.W.; Ha, L.C.; Huang, S.T.; Tsou, Y.C.; Chu, H.H.; Lin, J.Y.; Wang, J.; Chen, S.Y. Backward Raman amplification in a plasma waveguide. Phys. Rev. Lett. 2008, 101, 065005. [Google Scholar] [CrossRef] [PubMed]
- Sadler, J.D.; Silva, L.O.; Fonseca, R.A.; Glize, K.; Kasim, M.F.; Savin, A.; Aboushelbaya, R.; Mayr, M.W.; Spiers, B.; Wang, R.H.; et al. Advantages to a diverging Raman amplifier. Commun. Phys. 2018, 1, 19. [Google Scholar] [CrossRef] [Green Version]
- Trines, R.M.; Fiuza, F.; Fonseca, R.A.; Silva, L.O.; Bingham, R.; Cairns, R.A.; Norreys, P.A. Numerical simulation of plasma-based Raman amplification of laser pulses to Petawatt powers. IEEE Trans. Plasma Sci. 2011, 39, 2622–2623. [Google Scholar] [CrossRef]
- Moore, C.; Ting, A.; Krushelnick, K.; Esarey, E.; Hubbard, R.; Hafizi, B.; Burris, H.; Manka, C.; Sprangle, P. Electron trapping in self-modulated laser wakefields by Raman backscatter. Phys. Rev. Lett. 1997, 79, 3909. [Google Scholar] [CrossRef]
- Sadler, J.D.; Sliwa, M.; Miller, T.; Kasim, M.F.; Ratan, N.; Ceurvorst, L.; Savin, A.; Aboushelbaya, R.; Norreys, P.A.; Haberberger, D.; et al. Robustness of raman plasma amplifiers and their potential for attosecond pulse generation. High Energy Density Phys. 2017, 23, 212–216. [Google Scholar] [CrossRef]
- Ping, Y.; Geltner, I.; Fisch, N.; Shvets, G.; Suckewer, S. Demonstration of ultrashort laser pulse amplification in plasmas by a counter-propagating pumping beam. Phys. Rev. E 2000, 62, R4532. [Google Scholar] [CrossRef]
- Ping, Y.; Geltner, I.; Morozov, A.; Fisch, N.; Suckewer, S. Raman amplification of ultrashort laser pulses in microcapillary plasmas. Phys. Rev. E 2002, 66, 046401. [Google Scholar] [CrossRef] [Green Version]
- Ping, Y.; Geltner, I.; Suckewer, S. Raman backscattering and amplification in a gas jet plasma. Phys. Rev. E 2003, 67, 016401. [Google Scholar] [CrossRef] [PubMed]
- Dreher, M.; Takahashi, E.; Meyer-ter Vehn, J.; Witte, K.J. Observation of superradiant amplification of ultrashort laser pulses in a plasma. Phys. Rev. Lett. 2004, 93, 095001. [Google Scholar] [CrossRef] [PubMed]
- Balakin, A.A.; Kartashov, D.V.; Kiselev, A.M.; Skobelev, S.A.; Stepanov, A.N.; Fraiman, G.M. Laser pulse amplification upon Raman backscattering in plasma produced in dielectric capillaries. J. Exp. Theor. Phys. Lett. 2004, 80, 12–16. [Google Scholar] [CrossRef]
- Shvets, G.; Fisch, N.; Pukhov, A.; Meyer-ter Vehn, J. Superradiant amplification of an ultrashort laser pulse in a plasma by a counter-propagating pump. Phys. Rev. Lett. 1998, 81, 4879. [Google Scholar] [CrossRef] [Green Version]
- Fisch, N.; Malkin, V. Generation of ultrahigh intensity laser pulses. Phys. Plasmas 2003, 10, 2056–2063. [Google Scholar] [CrossRef] [Green Version]
- Grech, M.; Riazuelo, G.; Pesme, D.; Weber, S.; Tikhonchuk, V. Coherent forward stimulated-brillouin scattering of a spatially incoherent laser beam in a plasma and its effect on beam spray. Phys. Rev. Lett. 2009, 102, 155001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kirkwood, R.; Montgomery, D.; Afeyan, B.; Moody, J.; MacGowan, B.; Joshi, C.; Wharton, K.; Glenzer, S.; Williams, E.; Young, P.; et al. Observation of the nonlinear saturation of Langmuir waves driven by ponderomotive force in a large scale plasma. Phys. Rev. Lett. 1999, 83, 2965. [Google Scholar] [CrossRef] [Green Version]
- Turnbull, D.; Li, S.; Morozov, A.; Suckewer, S. Simultaneous stimulated Raman, Brillouin, and electron-acoustic scattering reveals a potential saturation mechanism in Raman plasma amplifiers. Phys. Plasmas 2012, 19, 083109. [Google Scholar] [CrossRef]
- Yang, X.; Vieux, G.; Brunetti, E.; Ersfeld, B.; Farmer, J.P.; Hur, M.S.; Issac, R.; Raj, G.; Wiggins, S.; Welsh, G.; et al. Chirped pulse Raman amplification in warm plasma: Towards controlling saturation. Sci. Rep. 2015, 5, 13333. [Google Scholar] [CrossRef] [Green Version]
- Bullock, A.B.; Bolton, P.R.; Mayer, F.J. Time-integrated reflectivity of laser-induced back-ablated aluminum thin film targets. J. Appl. Phys. 1997, 82, 1828–1831. [Google Scholar] [CrossRef]
- Perkins, F.; Oberman, C.; Valeo, E. Parametric instabilities and ionospheric modification. J. Geophys. Res. 1974, 79, 1478–1496. [Google Scholar] [CrossRef]
- Kirkwood, R.; Dewald, E.; Niemann, C.; Meezan, N.; Wilks, S.; Price, D.; Landen, O.; Wurtele, J.; Charman, A.; Lindberg, R.; et al. Amplification of an ultrashort pulse laser by stimulated Raman scattering of a 1 ns pulse in a low density plasma. Phys. Plasmas 2007, 14, 113109. [Google Scholar] [CrossRef]
- Chiaramello, M. Laser Amplification via Stimulated Brillouin Scattering in the Strongly Coupled Regime: Towards Control and Optimization. Ph.D. Thesis, Université Pierre et Marie Curie, Paris, France, 2016. [Google Scholar]
- Guillaume, E.; Humphrey, K.; Nakamura, H.; Trines, R.; Heathcote, R.; Galimberti, M.; Amano, Y.; Doria, D.; Hicks, G.; Higson, E.; et al. Demonstration of laser pulse amplification by stimulated Brillouin scattering. High Power Laser Sci. Eng. 2014, 2, e33. [Google Scholar] [CrossRef] [Green Version]
- Gorbunov, L. Perturbation of a medium by a field of a strong electromagnete wave. Sov. Phys. JETP 1969, 28, 1220–1225. [Google Scholar]
- Liu, C.; Kaw, P. Parametric instabilities in homogeneous unmagnetized plasmas. Adv. Plasma Phys. 1976, 6, 83–119. [Google Scholar]
- Zakharov, V.; Musher, S.; Rubenchik, A. Hamiltonian approach to the description of non-linear plasma phenomena. Phys. Rep. 1985, 129, 285–366. [Google Scholar] [CrossRef]
- Liu, C.; Rosenbluth, M.N.; White, R.B. Raman and Brillouin scattering of electromagnetic waves in inhomogeneous plasmas. Phys. Fluids 1974, 17, 1211–1219. [Google Scholar] [CrossRef]
- Schluck, F.; Lehmann, G.; Spatschek, K. Amplification of a seed pumped by a chirped laser in the strong coupling Brillouin regime. Phys. Plasmas 2015, 22, 093104. [Google Scholar] [CrossRef]
- Andreev, A.; Riconda, C.; Tikhonchuk, V.; Weber, S. Short light pulse amplification and compression by stimulated Brillouin scattering in plasmas in the strong coupling regime. Phys. Plasmas 2006, 13, 053110. [Google Scholar] [CrossRef]
- Edwards, M.R.; Jia, Q.; Mikhailova, J.M.; Fisch, N.J. Short-pulse amplification by strongly coupled stimulated Brillouin scattering. Phys. Plasmas 2016, 23, 083122. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Zuo, Y.; Su, J.; Yang, S. The filamentation effect in short pulse amplification by strong-coupling stimulated Brillouin scattering. Phys. Plasmas 2019, 26, 093102. [Google Scholar] [CrossRef]
- Alves, P.; Trines, R.; Humphrey, K.; Bingham, R.; Cairns, A.; Fiuza, F.; Fonseca, R.; Silva, L.; Norreys, P. A robust plasma-based laser amplifier via stimulated Brillouin scattering. arXiv 2013, arXiv:1311.2034v3. [Google Scholar] [CrossRef]
- Clark, D.S.; Fisch, N.J. Particle-in-cell simulations of Raman laser amplification in preformed plasmas. Phys. Plasmas 2003, 10, 4848–4855. [Google Scholar] [CrossRef] [Green Version]
- Humphrey, K.; Trines, R.; Fiuza, F.; Speirs, D.; Norreys, P.; Cairns, R.; Silva, L.; Bingham, R. Effect of collisions on amplification of laser beams by Brillouin scattering in plasmas. Phys. Plasmas 2013, 20, 102114. [Google Scholar] [CrossRef]
- Trines, R.; Alves, E.; Humphrey, K.; Bingham, R.; Cairns, R.; Fiuza, F.; Fonseca, R.; Silva, L.; Norreys, P. Boosting the performance of Brillouin amplification at sub-quarter-critical densities via reduction of parasitic Raman scattering. arXiv 2014, arXiv:1406.5424. [Google Scholar] [CrossRef]
- Gibbon, P. Short Pulse Laser Interactions with Matter: An Introduction; Imperial College Press: London, UK; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2005. [Google Scholar]
- Kruer, W. The Physics of Laser Plasma Interactions; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2019. [Google Scholar]
- Kaw, P.; Schmidt, G.; Wilcox, T. Filamentation and trapping of electromagnetic radiation in plasmas. Phys. Fluids 1973, 16, 1522–1525. [Google Scholar] [CrossRef]
- Max, C.E.; Arons, J.; Langdon, A.B. Self-modulation and self-focusing of electromagnetic waves in plasmas. Phys. Rev. Lett. 1974, 33, 209. [Google Scholar] [CrossRef]
- Ting, A.; Moore, C.; Krushelnick, K.; Manka, C.; Esarey, E.; Sprangle, P.; Hubbard, R.; Burris, H.; Fischer, R.; Baine, M. Plasma wakefield generation and electron acceleration in a self-modulated laser wakefield accelerator experiment. Phys. Plasmas 1997, 4, 1889–1899. [Google Scholar] [CrossRef]
- Perkins, F.; Valeo, E. Thermal self-focusing of electromagnetic waves in plasmas. Phys. Rev. Lett. 1974, 32, 1234. [Google Scholar] [CrossRef]
- Epperlein, E.M. Kinetic theory of laser filamentation in plasmas. Phys. Rev. Lett. 1990, 65, 2145. [Google Scholar] [CrossRef]
- Weber, S.; Riconda, C.; Lancia, L.; Marques, J.R.; Mourou, G.; Fuchs, J. Amplification of ultrashort laser pulses by Brillouin backscattering in plasmas. Phys. Rev. Lett. 2013, 111, 055004. [Google Scholar] [CrossRef]
- Shvets, G.; Wurtele, J.; Shadwick, B. Analysis and simulation of Raman backscatter in underdense plasmas. Phys. Plasmas 1997, 4, 1872–1880. [Google Scholar] [CrossRef] [Green Version]
- Nuter, R.; Tikhonchuk, V. Prepulse suppression and optimization of backward Raman amplification with a chirped pump laser beam. Phys. Rev. E 2013, 87, 043109. [Google Scholar] [CrossRef]
- Vieux, G.; Ersfeld, B.; Farmer, J.P.; Hur, M.S.; Issac, R.; Jaroszynski, D. Plasma density measurements using chirped pulse broad-band Raman amplification. Appl. Phys. Lett. 2013, 103, 121106. [Google Scholar] [CrossRef]
- Ersfeld, B.; Jaroszynski, D. Superradiant linear Raman amplification in plasma using a chirped pump pulse. Phys. Rev. Lett. 2005, 95, 165002. [Google Scholar] [CrossRef] [PubMed]
- Chiaramello, M.; Riconda, C.; Amiranoff, F.; Fuchs, J.; Grech, M.; Lancia, L.; Marquès, J.R.; Vinci, T.; Weber, S. Optimization of interaction conditions for efficient short laser pulse amplification by stimulated Brillouin scattering in the strongly coupled regime. Phys. Plasmas 2016, 23, 072103. [Google Scholar] [CrossRef]
- Riconda, C.; Weber, S.; Lancia, L.; Marquès, J.R.; Mourou, G.; Fuchs, J. Spectral characteristics of ultra-short laser pulses in plasma amplifiers. Phys. Plasmas 2013, 20, 083115. [Google Scholar] [CrossRef]
- Edwards, M.R.; Shi, Y.; Mikhailova, J.M.; Fisch, N.J. Laser amplification in strongly magnetized plasma. Phys. Rev. Lett. 2019, 123, 025001. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Wu, Z.; Zuo, Y.; Zeng, X.; Wang, X.; Wang, X.; Mu, J.; Hu, B.; Su, J. Boosting strong-coupling stimulated Brillouin amplification performance using an external magnetic field. Phys. Plasmas 2021, 28, 013107. [Google Scholar] [CrossRef]
- Trines, R.; Alves, E.; Webb, E.; Vieira, J.; Fiuza, F.; Fonseca, R.; Silva, L.; Sadler, J.; Ratan, N.; Ceurvorst, L.; et al. Essential criteria for efficient pulse amplification via Raman and Brillouin scattering. arXiv 2016, arXiv:1611.04485. [Google Scholar]
- Trines, R.M.; Alves, E.P.; Humphrey, K.; Bingham, R.; Cairns, R.A.; Fiúza, F.; Fonseca, R.; Silva, L.O. Boosting the performance of Brillouin amplification at sub-quarter-critical densities via reduction of parasitic Raman scattering. Plasma Phys. Control. Fusion 2021, 63, 124003. [Google Scholar] [CrossRef]
- Krupke, W. Rare earth vapor laser studies. In Proceedings of the 13th Rare Earth Research Conference, Olgebay Park, WV, USA, 16 October 1977. [Google Scholar]
- Yablonovitch, E.; Goldhar, J. Short CO2 laser pulse generation by optical free induction decay. Appl. Phys. Lett. 1974, 25, 580–582. [Google Scholar] [CrossRef]
- Fisher, R.A.; Feldman, B. Generation of single ultrashort CO2 laser pulses in a Fabry–Perot interferometer. Opt. Lett. 1977, 1, 161–163. [Google Scholar] [CrossRef] [PubMed]
- Cohen, B.I.; Kaufman, A.N. Effects of beat-wave electron trapping on stimulated Raman and Thomson scattering. Phys. Fluids 1978, 21, 404–412. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Zhang, B.; Hong, W.; Deng, Z.; Teng, J.; He, S.; Zhou, W.; Gu, Y. Generation of high-power few-cycle lasers via Brillouin-based plasma amplification. Phys. Plasmas 2017, 24, 113104. [Google Scholar] [CrossRef]
- Turnbull, D.; Bucht, S.; Davies, A.; Haberberger, D.; Kessler, T.; Shaw, J.; Froula, D. Raman amplification with a flying focus. Phys. Rev. Lett. 2018, 120, 024801. [Google Scholar] [CrossRef] [Green Version]
- Afeyan, B.; Hüller, S. Optimal control of laser plasma instabilities using Spike Trains of Uneven Duration and Delay (STUD pulses) for ICF and IFE. In EPJ Web of Conferences; EDP Sciences: Les Ulis, France, 2013; Volume 59, p. 05009. [Google Scholar]
- Lehmberg, R.; Obenschain, S. Use of induced spatial incoherence for uniform illumination of laser fusion targets. Opt. Commun. 1983, 46, 27–31. [Google Scholar] [CrossRef]
- Mostovych, A.; Obenschain, S.; Gardner, J.; Grun, J.; Kearney, K.; Manka, C.; McLean, E.; Pawley, C. Brillouin scattering measurements from plasmas irradiated with spatially and temporally incoherent laser light. Phys. Rev. Lett. 1987, 59, 1193. [Google Scholar] [CrossRef]
- Shoucri, M.; Matte, J.P.; Vidal, F. Relativistic Eulerian Vlasov simulations of the amplification of seed pulses by Brillouin backscattering in plasmas. Phys. Plasmas 2015, 22, 053101. [Google Scholar] [CrossRef]
- Lehmann, G.; Spatschek, K. Temperature dependence of seed pulse amplitude and density grating in Brillouin amplification. Phys. Plasmas 2016, 23, 023107. [Google Scholar] [CrossRef]
- Humphrey, K.; Trines, R.; Alves, E.; Fiúza, F.; Speirs, D.; Bingham, R.; Cairns, R.; Fonseca, R.; Silva, L.; Norreys, P. Production of petawatt laser pulses of picosecond duration via Brillouin amplification of nanosecond laser beams. arXiv 2013, arXiv:1311.2034v1. [Google Scholar]
- Kirkwood, R.; Michel, P.; London, R.; Moody, J.; Dewald, E.; Yin, L.; Kline, J.; Hinkel, D.; Callahan, D.; Meezan, N.; et al. Multi-beam effects on backscatter and its saturation in experiments with conditions relevant to ignition. Phys. Plasmas 2011, 18, 056311. [Google Scholar] [CrossRef] [Green Version]
- Edwards, M.R.; Fisch, N.J.; Mikhailova, J.M. Strongly enhanced stimulated Brillouin backscattering in an electron-positron plasma. Phys. Rev. Lett. 2016, 116, 015004. [Google Scholar] [CrossRef] [Green Version]
- Guo, Q.; Lu, Z.; Wang, Y. Highly efficient Brillouin amplification of strong Stokes seed. Appl. Phys. Lett. 2010, 96, 221107. [Google Scholar] [CrossRef]
- Bel’dyugin, I.; Efimkov, V.; Mikhailov, S.; Zubarev, I. Amplification of weak Stokes signals in the transient regime of stimulated Brillouin scattering. J. Russ. Laser Res. 2005, 26, 1–12. [Google Scholar] [CrossRef]
- Lu, Z.; Gao, W.; He, W.; Zhang, Z.; Hasi, W. High amplification and low noise achieved by a double-stage non-collinear Brillouin amplifier. Opt. Express 2009, 17, 10675–10680. [Google Scholar] [CrossRef]
- Sternklar, S.; Jackel, S.; Chomsky, D.; Zigler, A. Coherent beam and image amplification by Brillouin two-beam coupling in CS 2. Opt. Lett. 1990, 15, 616–618. [Google Scholar] [CrossRef]
- Yin, L.; Albright, B.; Rose, H.; Bowers, K.; Bergen, B.; Kirkwood, R.; Hinkel, D.; Langdon, A.; Michel, P.; Montgomery, D.; et al. Trapping induced nonlinear behavior of backward stimulated Raman scattering in multi-speckled laser beams. Phys. Plasmas 2012, 19, 056304. [Google Scholar] [CrossRef]
- Kirkwood, R.; MacGowan, B.; Montgomery, D.; Afeyan, B.; Kruer, W.; Moody, J.; Estabrook, K.; Back, C.; Glenzer, S.; Blain, M.; et al. Effect of ion-wave damping on stimulated Raman scattering in high-Z laser-produced plasmas. Phys. Rev. Lett. 1996, 77, 2706. [Google Scholar] [CrossRef]
- Ren, J.; Li, S.; Morozov, A.; Suckewer, S.; Yampolsky, N.; Malkin, V.; Fisch, N. A compact double-pass Raman backscattering amplifier/compressor. Phys. Plasmas 2008, 15, 056702. [Google Scholar] [CrossRef]
- Mishra, S.; Andreev, A. Amplification of ultra-short laser pulses via resonant backward Raman amplification in plasma. Phys. Plasmas 2016, 23, 083108. [Google Scholar] [CrossRef]
- Mardahl, P.; Lee, H.J.; Penn, G.; Wurtele, J.; Fisch, N. Intense laser pulse amplification using Raman backscatter in plasma channels. Phys. Lett. A 2002, 296, 109–116. [Google Scholar] [CrossRef]
- Yampolsky, N.; Fisch, N.; Malkin, V.; Valeo, E.; Lindberg, R.; Wurtele, J.; Ren, J.; Li, S.; Morozov, A.; Suckewer, S. Demonstration of detuning and wavebreaking effects on Raman amplification efficiency in plasma. Phys. Plasmas 2008, 15, 113104. [Google Scholar] [CrossRef] [Green Version]
- Turnbull, D.; Li, S.; Morozov, A.; Suckewer, S. Possible origins of a time-resolved frequency shift in Raman plasma amplifiers. Phys. Plasmas 2012, 19, 073103. [Google Scholar] [CrossRef]
- Depierreux, S.; Yahia, V.; Goyon, C.; Loisel, G.; Masson-Laborde, P.E.; Borisenko, N.; Orekhov, A.; Rosmej, O.; Rienecker, T.; Labaune, C. Laser light triggers increased Raman amplification in the regime of nonlinear Landau damping. Nat. Commun. 2014, 5, 4158. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Toroker, Z.; Malkin, V.; Fisch, N. Backward Raman amplification in the Langmuir wavebreaking regime. Phys. Plasmas 2014, 21, 113110. [Google Scholar] [CrossRef]
- Edwards, M.R.; Qu, K.; Mikhailova, J.M.; Fisch, N.J. Beam cleaning of an incoherent laser via plasma Raman amplification. Phys. Plasmas 2017, 24, 103110. [Google Scholar] [CrossRef]
- Lehmann, G.; Schluck, F.; Spatschek, K. Regions for Brillouin seed pulse growth in relativistic laser-plasma interaction. Phys. Plasmas 2012, 19, 093120. [Google Scholar] [CrossRef]
- Jia, Q.; Shi, Y.; Qin, H.; Fisch, N.J. Kinetic simulations of laser parametric amplification in magnetized plasmas. Phys. Plasmas 2017, 24, 093103. [Google Scholar] [CrossRef]
- Matsuo, K.; Nagatomo, H.; Zhang, Z.; Nicolai, P.; Sano, T.; Sakata, S.; Kojima, S.; Lee, S.H.; Law, K.F.F.; Arikawa, Y.; et al. Magnetohydrodynamics of laser-produced high-energy-density plasma in a strong external magnetic field. Phys. Rev. E 2017, 95, 053204. [Google Scholar] [CrossRef]
- Stix, T.H. Waves in Plasmas; Springer: New York, NY, USA, 1992. [Google Scholar]
- Sprangle, P.; Esarey, E.; Ting, A. Nonlinear theory of intense laser-plasma interactions. Phys. Rev. Lett. 1990, 64, 2011. [Google Scholar] [CrossRef] [PubMed]
- Laqua, H.P. Electron Bernstein wave heating and diagnostic. Plasma Phys. Control. Fusion 2007, 49, R1. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.; Qin, H.; Fisch, N.J. Laser-pulse compression using magnetized plasmas. Phys. Rev. E 2017, 95, 023211. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arber, T.; Bennett, K.; Brady, C.; Lawrence-Douglas, A.; Ramsay, M.; Sircombe, N.; Gillies, P.; Evans, R.; Schmitz, H.; Bell, A.; et al. Contemporary particle-in-cell approach to laser-plasma modelling. Plasma Phys. Control. Fusion 2015, 57, 113001. [Google Scholar] [CrossRef]
- Shi, Y.; Fisch, N.J. Amplification of mid-infrared lasers via magnetized-plasma coupling. arXiv 2019, arXiv:1904.05536. [Google Scholar]
- Shi, Y.; Qin, H.; Fisch, N.J. Laser-plasma interactions in magnetized environment. Phys. Plasmas 2018, 25, 055706. [Google Scholar] [CrossRef]




| Raman Amplification | Brillouin Amplification | |
|---|---|---|
| Frequency of pump and seed | Never identical | May or may not be identical |
| Energy loss to plasma wave | Comparatively low | Comparatively high |
| Plasma density ratio | Forbidden for density ratios > 0.25 | Allowed in density ratios below and above 0.25 |
| Contact length of plasma wave and seed pulse | Long | Short |
| Peak Intensities | Comparatively lower | Comparatively higher |
| Major Limitations | Forward Raman scattering, Langmuir wave breaking, super-luminous precursor of the amplified pulse, pulse scattering by plasma density inhomogeneties, parasitic effects of plasma noise on Raman scattering | Forward Raman Scattering, Filamentation |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miriam Cheriyan, R.; Varghese, N.; Sooraj, R.S.; Rao, K.H.; Smijesh, N. A Comprehensive Review on Amplification of Laser Pulses via Stimulated Raman Scattering and Stimulated Brillouin Scattering in Plasmas. Plasma 2022, 5, 499-539. https://doi.org/10.3390/plasma5040037
Miriam Cheriyan R, Varghese N, Sooraj RS, Rao KH, Smijesh N. A Comprehensive Review on Amplification of Laser Pulses via Stimulated Raman Scattering and Stimulated Brillouin Scattering in Plasmas. Plasma. 2022; 5(4):499-539. https://doi.org/10.3390/plasma5040037
Chicago/Turabian StyleMiriam Cheriyan, Renju, Nikhil Varghese, R. S. Sooraj, Kavya H. Rao, and N. Smijesh. 2022. "A Comprehensive Review on Amplification of Laser Pulses via Stimulated Raman Scattering and Stimulated Brillouin Scattering in Plasmas" Plasma 5, no. 4: 499-539. https://doi.org/10.3390/plasma5040037
APA StyleMiriam Cheriyan, R., Varghese, N., Sooraj, R. S., Rao, K. H., & Smijesh, N. (2022). A Comprehensive Review on Amplification of Laser Pulses via Stimulated Raman Scattering and Stimulated Brillouin Scattering in Plasmas. Plasma, 5(4), 499-539. https://doi.org/10.3390/plasma5040037









