Validating the Multi-Mode Model’s Ability to Reproduce Diverse Tokamak Scenarios
Abstract
:1. Introduction
2. Multi-Mode Anomalous Transport Module
3. TRANSP
4. Simulation Results
4.1. EAST
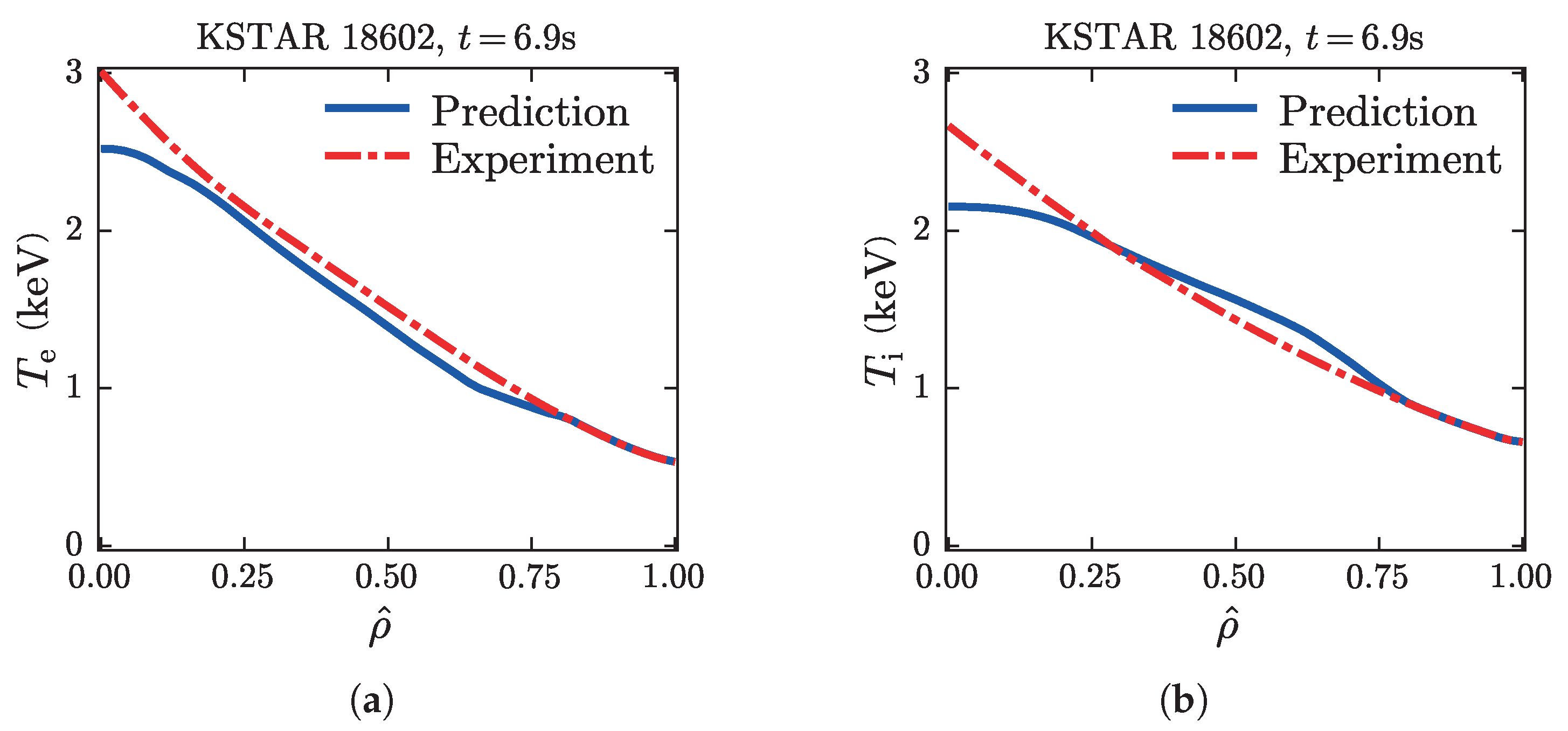
4.2. KSTAR
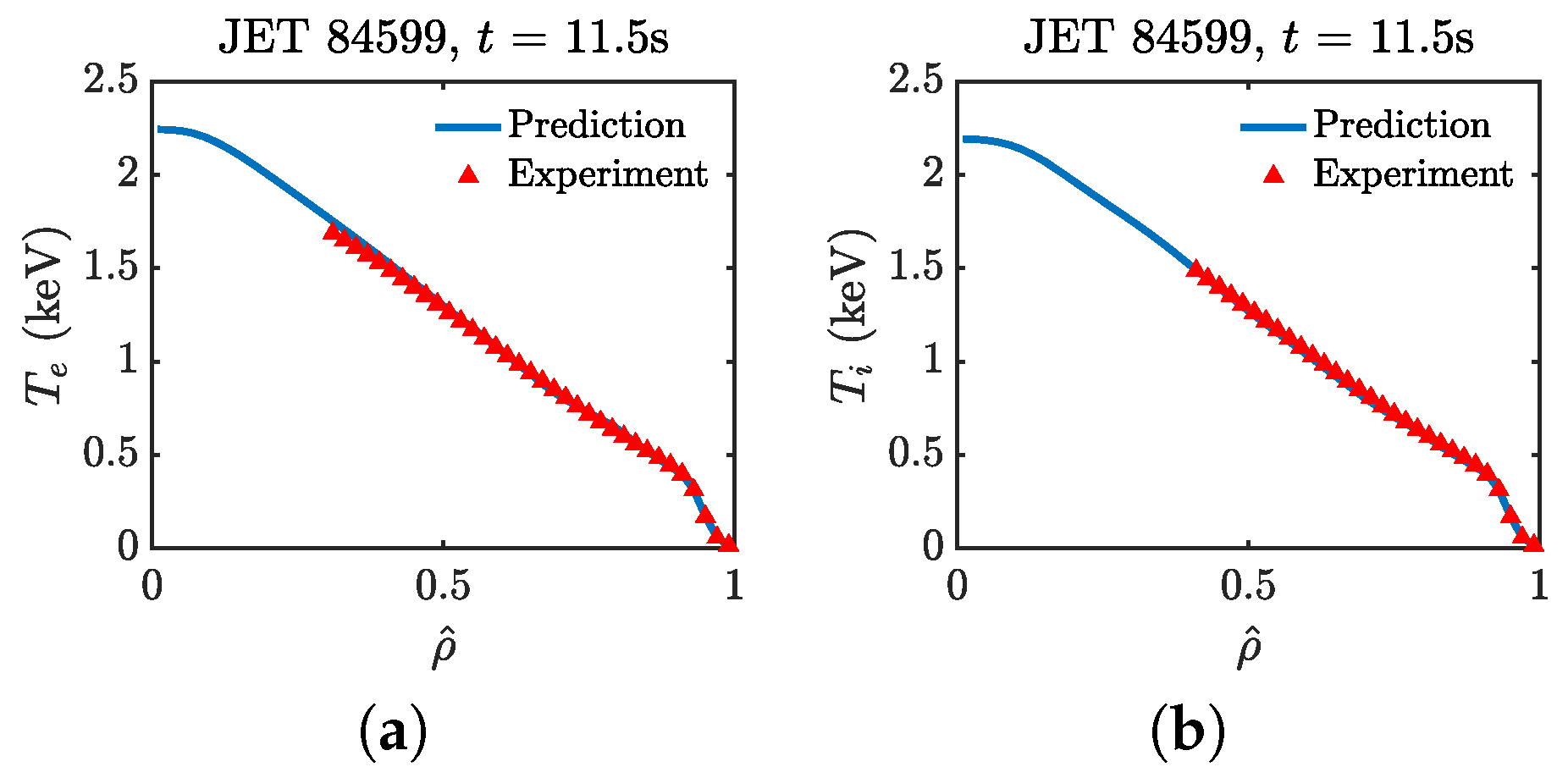
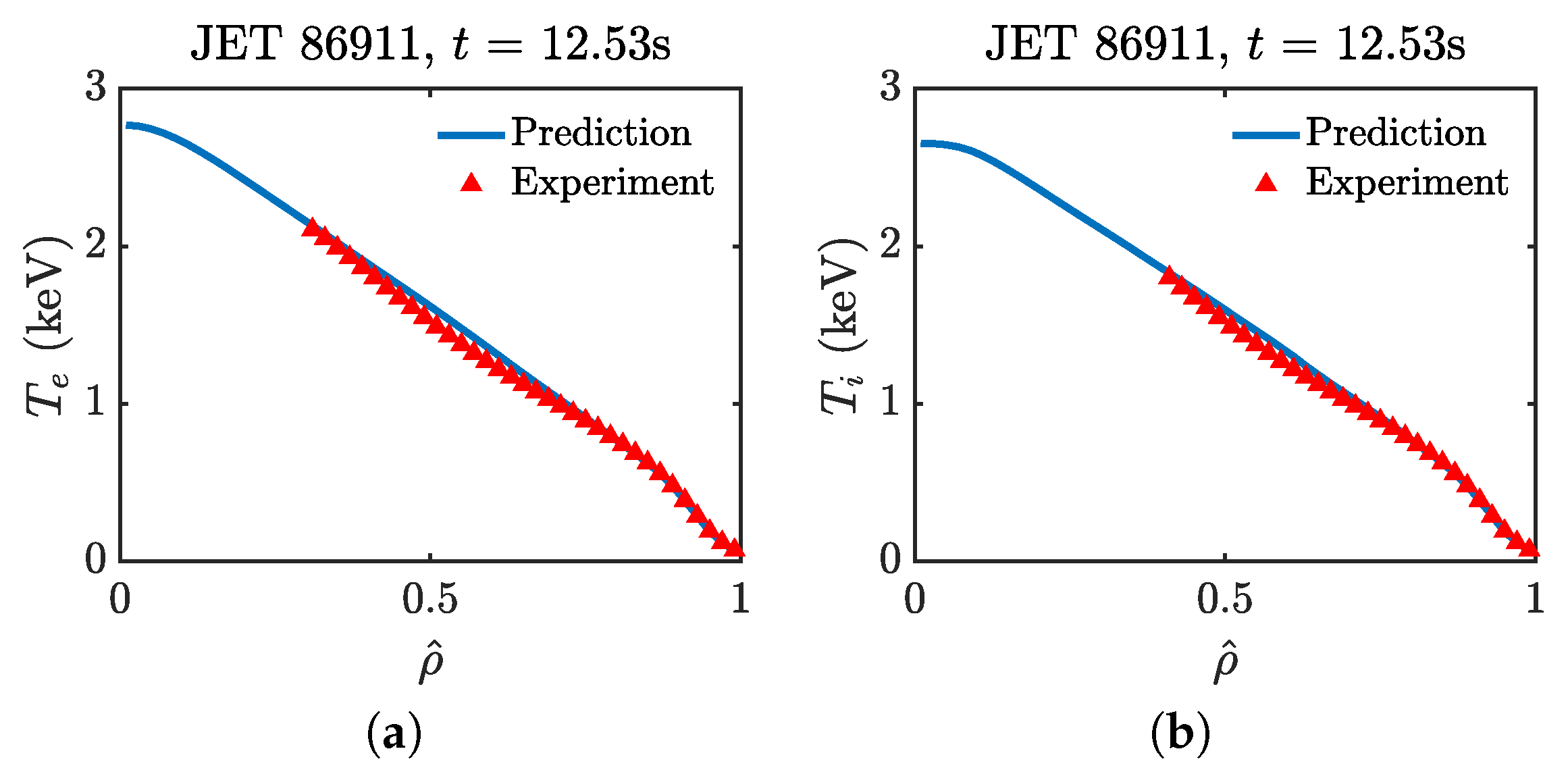
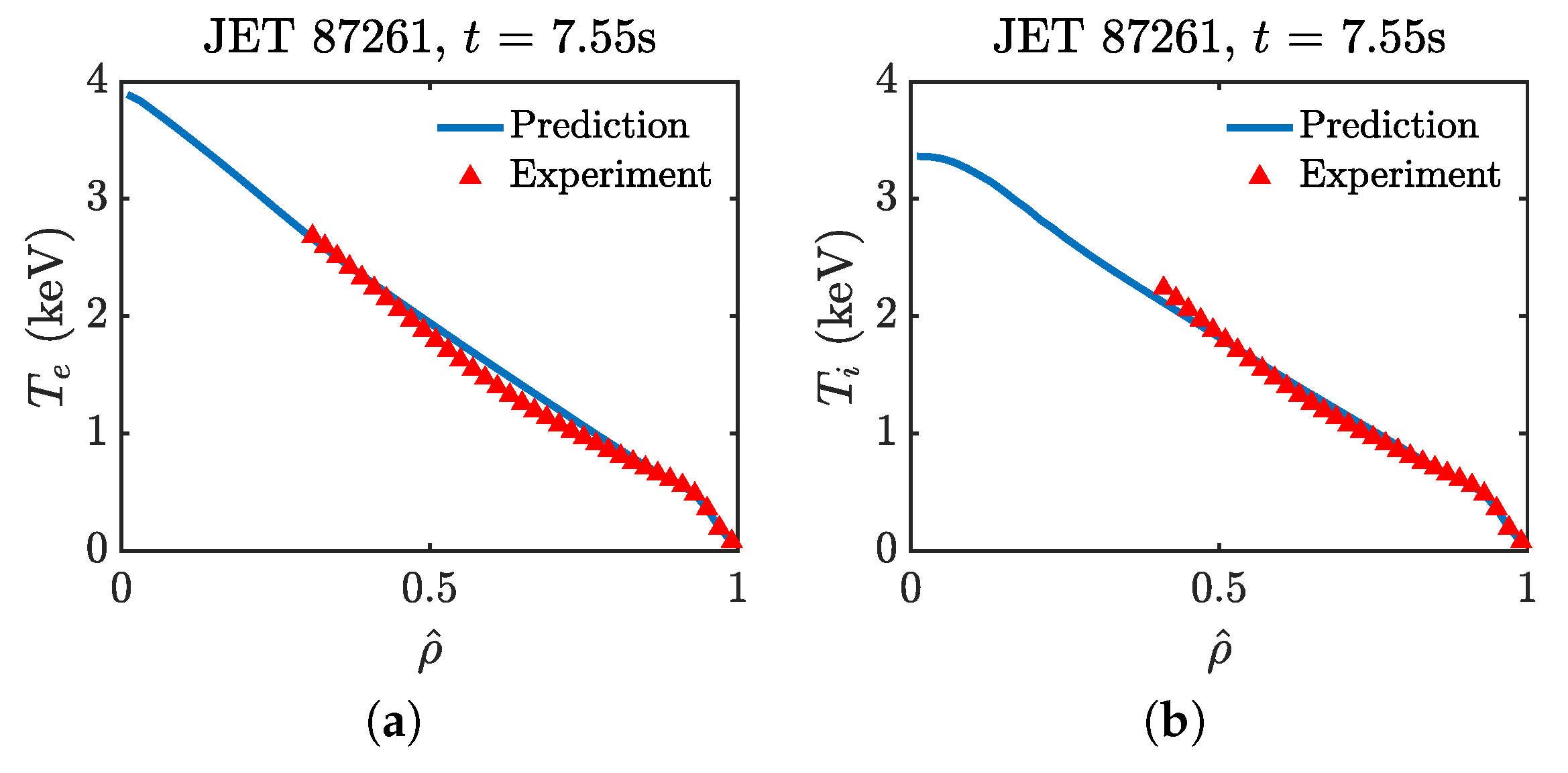
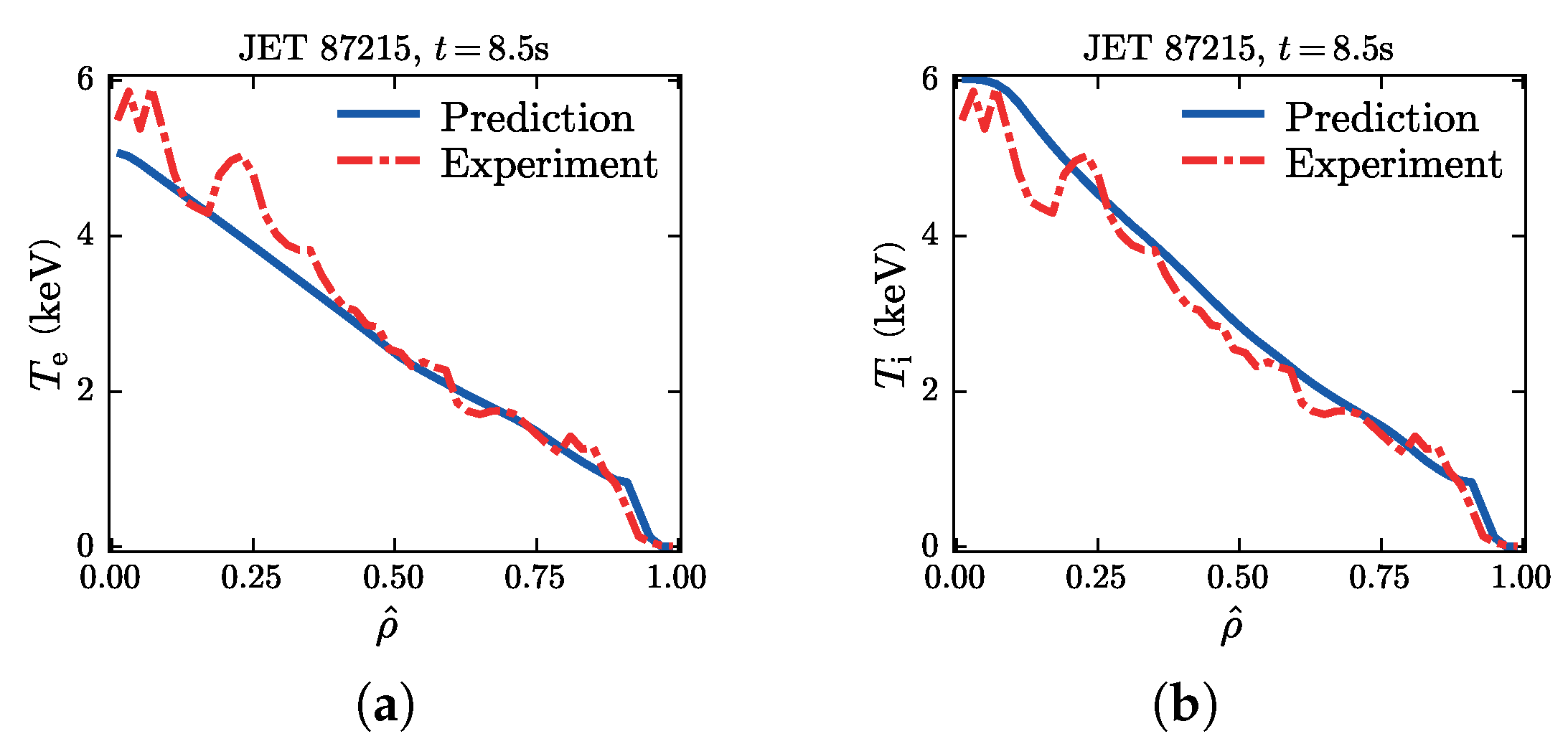
4.3. JET
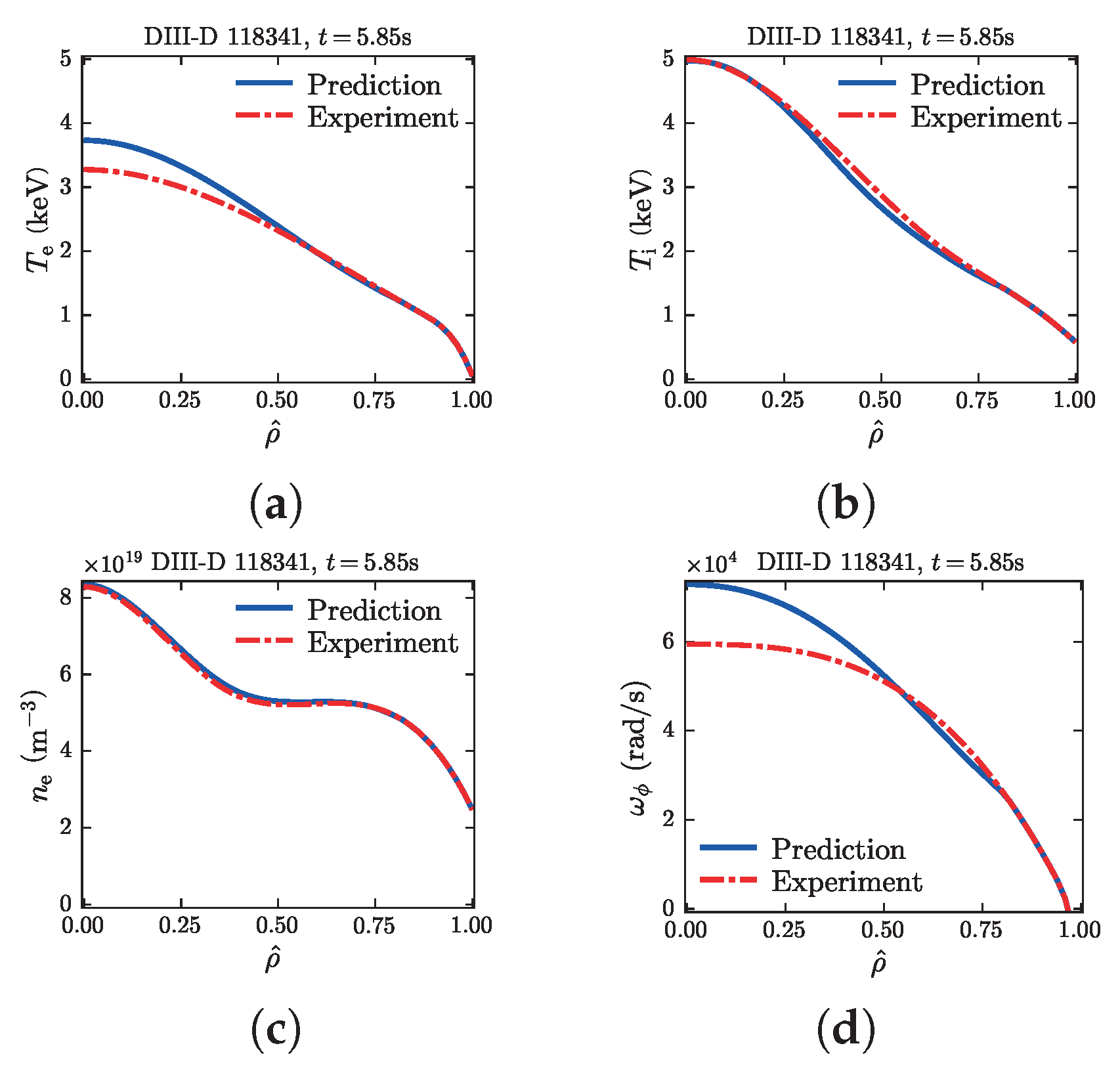
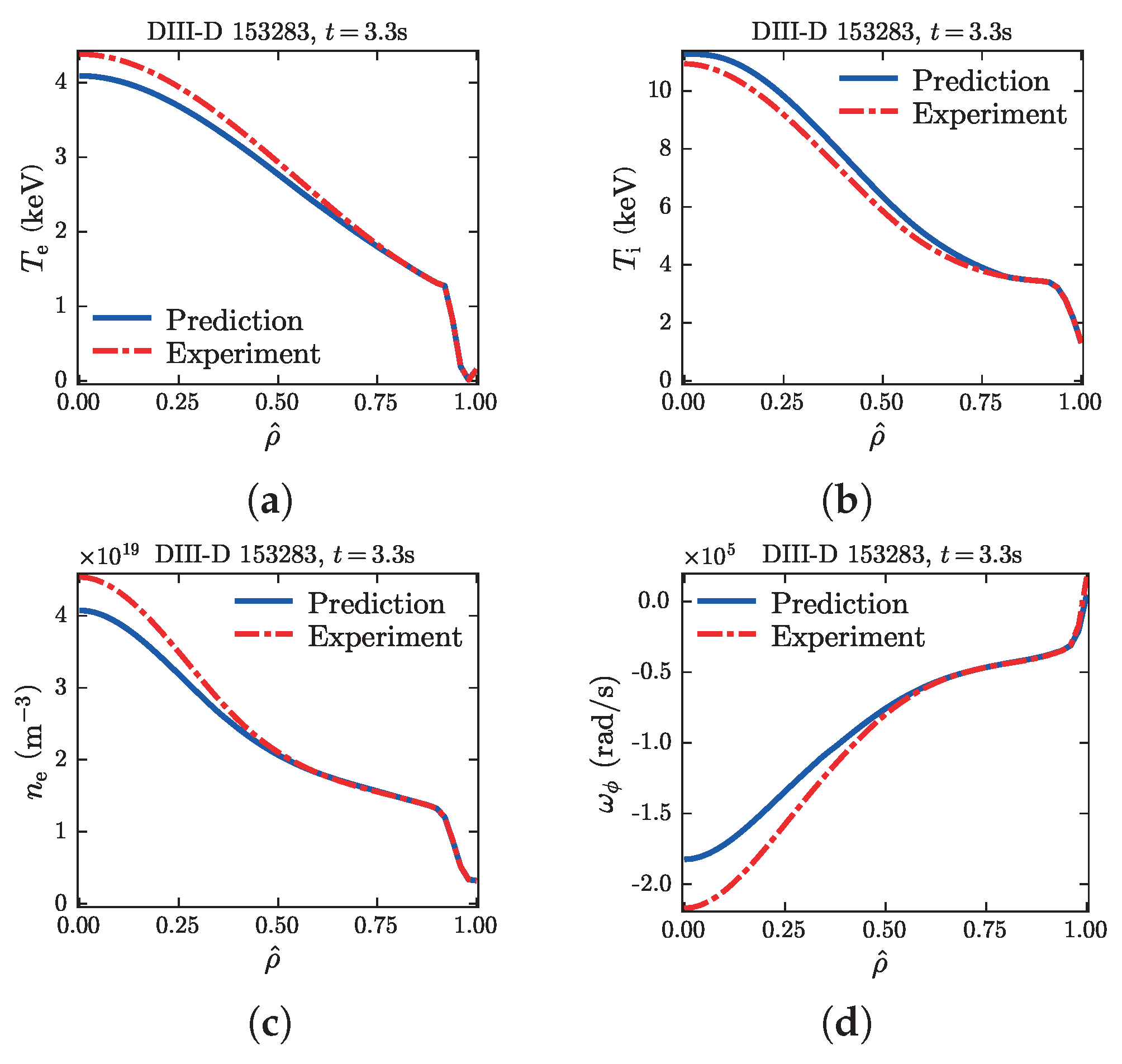
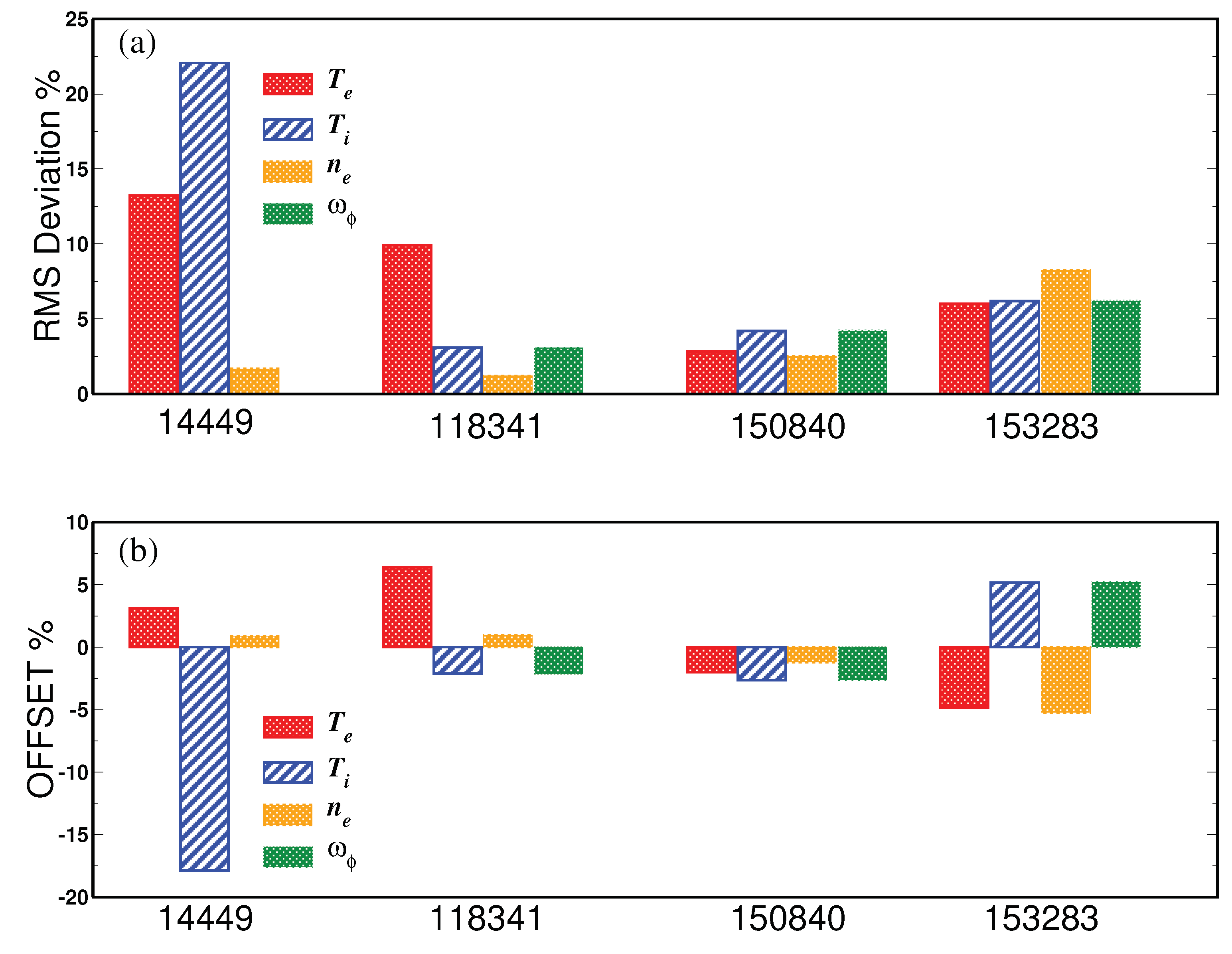
4.4. DIII-D
5. Summary and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rafiq, T.; Kritz, A.H.; Weiland, J.; Pankin, A.Y.; Luo, L. Physics basis of Multi-Mode anomalous transport module. Phys. Plasmas 2013, 20, 032506. [Google Scholar] [CrossRef] [Green Version]
- Luo, L.; Rafiq, T.; Kritz, A. Improved Multi-Mode anomalous transport module for tokamak plasmas. Comput. Phys. Commun. 2013, 184, 2267–2276. [Google Scholar] [CrossRef]
- Hawryluk, R. An empirical approach to tokamak transport. In Physics of Plasmas Close to Thermonuclear Conditions; Coppi, B., Leotta, G., Pfirsch, D., Pozzoli, R., Sindoni, E., Eds.; Pergamon: Oxford, UK, 1981; pp. 19–46. [Google Scholar] [CrossRef]
- Weiland, J. Stability and Transport in Magnetic Confinement Systems; Springer: New York, NY, USA; Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Horton, W.; Hong, B.G.; Tang, W.M. Toroidal electron temperature gradient driven drift modes. Phys. Fluids 1988, 31, 2971–2983. [Google Scholar] [CrossRef]
- Rafiq, T.; Weiland, J.; Kritz, A.H.; Luo, L.; Pankin, A.Y. Microtearing modes in tokamak discharges. Phys. Plasmas 2016, 23, 062507. [Google Scholar] [CrossRef] [Green Version]
- Rafiq, T.; Kritz, A.H.; Weiland, J.; Luo, L.; Schuster, E. Study of the parametric dependence of linear and nonlinear microtearing modes in conventional tokamak discharges. Phys. Plasmas 2018, 25, 012504. [Google Scholar] [CrossRef] [Green Version]
- Rafiq, T.; Kaye, S.; Guttenfelder, W.; Weiland, J.; Schuster, E.; Anderson, J.; Luo, L. Microtearing instabilities and electron thermal transport in low and high collisionality NSTX discharges. Phys. Plasmas 2021, 28, 022504. [Google Scholar] [CrossRef]
- Rafiq, T.; Bateman, G.; Kritz, A.H.; Pankin, A.Y. Development of drift-resistive-inertial ballooning transport model for tokamak edge plasmas. Phys. Plasmas 2010, 17, 082511. [Google Scholar] [CrossRef]
- Jenko, F.; Dorland, W.; Hammett, G.W. Critical gradient formula for toroidal electron temperature gradient modes. Phys. Plasmas 2001, 8, 4096–4104. [Google Scholar] [CrossRef] [Green Version]
- Bateman, G.; Halpern, F.; Kritz, A.; Pankin, A.; Rafiq, T.; Budny, R.; McCune, D.; Kinsey, J.; Voitsekhovitch, I.; Weiland, J. Integrated modeling simulations of toroidal momentum transport in tokamaks. In Proceedings of the 2008 IAEA Fusion Energy Conference, Geneva, Switzerland, 13–18 October 2008. [Google Scholar]
- Weiland, J.; Zagorodny, A.; Rafiq, T. Theory for transport in magnetized plasmas. Phys. Scr. 2020, 95, 105607. [Google Scholar] [CrossRef]
- Weiland, J.; Zagorodny, J. Drift wave theory for transport in tokamaks. Rev. Mod. Plasma Phys. 2019, 3, 8. [Google Scholar] [CrossRef] [Green Version]
- Weiland, J.; Rafiq, T.; Schuster, E. Fast particles in drift wave turbulence. Phys. Plasmas 2023, 30, 042517. [Google Scholar] [CrossRef]
- Zagorodny, A.; Weiland, J. Statistical theory of turbulent transport (non-Markovian effects). Phys. Plasmas 1999, 6, 2359–2372. [Google Scholar] [CrossRef]
- Connor, J.W.; Pogutse, O.P. On the relationship between mixing length and strong turbulence estimates for transport due to drift turbulence. Plasma Phys. Control. Fusion 2001, 43, 155. [Google Scholar] [CrossRef]
- Rafiq, T.; Kritz, A.H.; Tangri, V.; Pankin, A.Y.; Voitsekhovitch, I.; Budny, R.V. Integrated modeling of temperature profiles in L-mode tokamak discharges. Phys. Plasmas 2014, 21, 122505. [Google Scholar] [CrossRef]
- Howard, N.T.; White, A.E.; Greenwald, M.; Holland, C.; Candy, J. Multi-scale gyrokinetic simulation of Alcator C-Mod tokamak discharges. Phys. Plasmas 2014, 21, 032308. [Google Scholar] [CrossRef]
- Weiland, J. Review of mixing length estimates and effects of toroidicity in a fluid model for turbulent transport in tokamaks. Plasma Phys. Rep. 2016, 42, 502. [Google Scholar] [CrossRef]
- Weiland, J. Analytical eigenvalue solution for ηi modes of general mode width. Phys. Plasmas 2004, 11, 3238–3241. [Google Scholar] [CrossRef]
- Wade, M.; Luce, T.; Jayakumar, R.; Politzer, P.; Hyatt, A.; Ferron, J.; Greenfield, C.; Murakami, M.; Petty, C.; Prater, R.; et al. Development, physics basis and performance projections for hybrid scenario operation in ITER on DIII-D. Nucl. Fusion 2005, 45, 407. [Google Scholar] [CrossRef] [Green Version]
- Rafiq, T.; Kritz, A.H.; Bateman, G.; Kessel, C.; McCune, D.C.; Budny, R.V. Effect of pedestal height and internal transport barriers on International Thermonuclear Experimental Reactor target steady state simulations. Phys. Plasmas 2011, 18, 112508. [Google Scholar] [CrossRef]
- Rafiq, T.; Kritz, A.H.; Kessel, C.E.; Pankin, A.Y. Fusion power production in International Thermonuclear Experimental Reactor baseline H-mode scenarios. Phys. Plasmas 2015, 22, 042511. [Google Scholar] [CrossRef]
- Kritz, A.; Rafiq, T.; Kessel, C.; Bateman, G.; McCune, D.; Budny, R.; Pankin, A. Integrated modelling for prediction of optimized ITER performance. Nucl. Fusion 2011, 51, 123009. [Google Scholar] [CrossRef]
- Snyder, P.B.; Groebner, R.J.; Leonard, A.W.; Osborne, T.H.; Wilson, H.R. Development and validation of a predictive model for the pedestal height. Phys. Plasmas 2009, 16, 056118. [Google Scholar] [CrossRef]
- Rafiq, T.; Weiland, J. Self-consistent core-pedestal ITER scenario modeling. Nucl. Fusion 2021, 61, 116005. [Google Scholar] [CrossRef]
- Rafiq, T.; Wilson, C.; Luo, L.; Weiland, J.; Schuster, E.; Pankin, A.Y.; Guttenfelder, W.; Kaye, S. Electron temperature gradient driven transport model for tokamak plasmas. Phys. Plasmas 2022, 29, 092503. [Google Scholar] [CrossRef]
- Chang, C.S.; Hinton, F.L. Effect of impurity particles on the finite-aspect ratio neoclassical ion thermal conductivity in a tokamak. Phys. Fluids 1986, 29, 3314–3316. [Google Scholar] [CrossRef]
- Houlberg, W.A.; Shaing, K.C.; Hirshman, S.P.; Zarnstorff, M.C. Bootstrap current and neoclassical transport in tokamaks of arbitrary collisionality and aspect ratio. Phys. Plasmas 1997, 4, 3230–3242. [Google Scholar] [CrossRef]
- Pankin, A.; McCune, D.; Andre, R.; Bateman, G.; Kritz, A. The tokamak Monte Carlo fast ion module NUBEAM in the National Transport Code Collaboration library. Comput. Phys. Commun. 2004, 159, 157–184. [Google Scholar] [CrossRef]
- Smirnov, A.P.; Harvey, R.W.; Kupfer, K. A general ray tracing code GENRAY. Bull. Am. Phys. Soc. 1994, 39, 1626. [Google Scholar]
- Harvey, R.W.; McCoy, M.G. The CQL3D Code. In Proceedings of the IAEA Technical Committee on Advances in Simulation and Modelling of Thermonuclear Plasmas, Montreal, QC, Canada, 15–17 June 1992; IAEA: Vienna, Austria, 1992. [Google Scholar]
- Kritz, A.; Hsuan, H.; Goldfinger, R.; Batchelor, D. Ray Tracing Study of Electron Cyclotron Heating in Toroidal Geometry. In Proceedings of the 3rd Joint Varenna-Grenoble International Symposium on Heating in Toroidal Plasmas, Commission of the European Communities, Grenoble, France, 22–26 March 1982; Volume 2, pp. 707–723. [Google Scholar]
- LoDestro, L.L.; Pearlstein, L.D. On the Grad–Shafranov equation as an eigenvalue problem, with implications for q solvers. Phys. Plasmas 1994, 1, 90–95. [Google Scholar] [CrossRef]
- Lao, L.; John, H.S.; Stambaugh, R.; Kellman, A.; Pfeiffer, W. Reconstruction of current profile parameters and plasma shapes in tokamaks. Nucl. Fusion 1985, 25, 1611–1622. [Google Scholar] [CrossRef]
- Kim, H.T.; Romanelli, M.; Yuan, X.; Kaye, S.; Sips, A.; Frassinetti, L.; Buchanan, J.; JET Contributors. Statistical validation of predictive TRANSP simulations of baseline discharges in preparation for extrapolation to JET D–T. Nucl. Fusion 2017, 57, 066032. [Google Scholar] [CrossRef]
- ITER Physics Expert Group on Confinement and Transport; ITER Physics Expert Group on Confinement Modelling and Database; ITER Physics Basis Editors. Chapter 2: Plasma confinement and transport. Nucl. Fusion 1999, 39, 2175. [Google Scholar] [CrossRef]
- Wan, B.; Liang, Y.; Gong, X.; Li, J.; Xiang, N.; Xu, G.; Sun, Y.; Wang, L.; Qian, J.; Liu, H.; et al. Overview of EAST experiments on the development of high-performance steady-state scenario. Nucl. Fusion 2017, 57, 102019. [Google Scholar] [CrossRef]
- Huang, J.; Qian, J.; Garofalo, A.; Gong, X.; Wu, C.; Chang, J.; Zhang, J.; Du, H.; Wu, M.; Hao, B.; et al. Improved high-performance fully non-inductive discharge by optimizing the fast-ion confinement on EAST. Nucl. Fusion 2019, 60, 016002. [Google Scholar] [CrossRef]
- Choi, W.; Poli, F.; Li, M.; Baek, S.; Gorenlenkova, M.; Ding, B.; Gong, X.; Chan, A.; Duan, Y.; Hu, J.; et al. Observation of synergy between lower hybrid waves at two frequencies in EAST. Phys. Plasmas 2021, 28, 072506. [Google Scholar] [CrossRef]
- Poli, F.M.; Bonoli, P.T.; Chilenski, M.; Mumgaard, R.; Shiraiwa, S.; Wallace, G.M.; Andre, R.; Delgado-Aparicio, L.; Scott, S.; Wilson, J.R.; et al. Experimental and modeling uncertainties in the validation of lower hybrid current drive. Plasma Phys. Control. Fusion 2016, 58, 095001. [Google Scholar] [CrossRef]
- Zang, Q.; Zhao, J.; Yang, L.; Hu, Q.; Xi, X.; Dai, X.; Yang, J.; Han, X.; Li, M.; Hsieh, C. Upgraded multipulse laser and multipoint Thomson scattering diagnostics on EAST. Rev. Sci. Instrum. 2011, 82, 063502. [Google Scholar] [CrossRef]
- Han, X.; Hu, A.; Li, D.; Xiao, S.; Tian, B.; Zang, Q.; Zhao, J.; Hsieh, C.; Gong, X.; Hu, L.; et al. Multiple laser system for high-resolution thomson scattering diagnostics on the EAST tokamak. IEEE Trans. Plasma Sci. 2018, 46, 406–409. [Google Scholar] [CrossRef]
- Zhang, S.; Gao, X.; Ling, B.; Wang, Y.; Zhang, T.; Han, X.; Liu, Z.; Bu, J.; Li, J. Density profile and fluctuation measurements by microwave reflectometry on EAST. Plasma Sci. Technol. 2014, 16, 311. [Google Scholar] [CrossRef]
- Zhen, Z.; Zhang, T.; Mingfu, W.; Kaixuan, Y.; Zhong, F.; Huang, J.; Kangning, G.; Yukai, L.; Gongshun, L.; Xiang, H.; et al. Experimental study of core and edge fluctuations by reflectometry on EAST tokamak. Plasma Sci. Technol. 2021, 23, 075101. [Google Scholar]
- Xu, M.; Xu, X.; Wen, Y.; Ma, J.; Xie, J.; Gao, B.; Lan, T.; Liu, A.; Yu, Y.; He, Y.; et al. Electron cyclotron emission imaging on the EAST tokamak. Plasma Sci. Technol. 2011, 13, 167. [Google Scholar] [CrossRef]
- Liu, H.; Qian, J.; Jie, Y.; Ding, W.; Brower, D.; Zou, Z.; Li, W.; Lian, H.; Wang, S.; Yang, Y.; et al. Initial measurements of plasma current and electron density profiles using a polarimeter/interferometer (POINT) for long pulse operation in EAST. Rev. Sci. Instrum. 2016, 87, 11D903. [Google Scholar] [CrossRef]
- Zou, Z.; Liu, H.; Li, W.; Lian, H.; Wang, S.; Yao, Y.; Lan, T.; Zeng, L.; Jie, Y. Optical configuration optimization and calibration for the POINT system on EAST. Rev. Sci. Instrum. 2016, 87, 11E121. [Google Scholar] [CrossRef]
- Huang, Y.; Xiao, B.; Luo, Z.; Qian, J.; Li, S.; Chen, Y.; Liu, H.; Xu, L.; Yuan, Y.; Yuan, Q. Development of real-time plasma current profile reconstruction with POINT diagnostic for EAST plasma control. Fusion Eng. Des. 2017, 120, 1–8. [Google Scholar] [CrossRef]
- Zhu, X.; Zeng, L.; Liu, H.; Qian, J.; Zang, Q.; Jie, Y.; Zou, Z.; Li, W.; Yao, Y.; Gao, X. Improvement of q profile by the polarimeter/interferometer system on EAST tokamak. J. Instrum. 2017, 12, C12060. [Google Scholar] [CrossRef]
- Singh, R.; Tangri, V.; Nordman, H.; Weiland, J. Fluid description of electron temperature gradient driven drift modes. Phys. Plasmas 2001, 8, 4340–4350. [Google Scholar] [CrossRef]
- Chung, J.; Kim, H.; Jeon, Y.; Kim, J.; Choi, M.; Ko, J.; Lee, K.; Lee, H.; Yi, S.; Kwon, J.; et al. Formation of the internal transport barrier in KSTAR. Nucl. Fusion 2017, 58, 016019. [Google Scholar] [CrossRef]
- Kim, J.; Choi, M.; Lee, J. Reversed Ip operation with counter neutral beam injection in KSTAR. In Proceedings of the 27th IAEA Fusion Energy Conference (FEC 2018), Gandhinagar, India, 22–27 October 2018. [Google Scholar]
- Park, Y.; Sabbagh, S.; Ko, W.; Bak, J.; Berkery, J.; Bialek, J.; Choi, M.; Hahn, S.; In, Y.; Jardin, S.; et al. Investigation of instabilities and rotation alteration in high beta KSTAR plasmas. Phys. Plasmas 2017, 24, 012512. [Google Scholar] [CrossRef]
- Na, D.; Yang, S.; Shi, Y.; Hahm, T.; Na, Y.; Lee, S.; Kwon, J.; Jhang, H.; Ko, W.; Angioni, C.; et al. Rotation Reversal in KSTAR and its Turbulence and Transport Characteristics. In Proceedings of the 26th IAEA Fusion Energy Conference (FEC 2016), Kyoto, Japan, 17–22 October 2016. [Google Scholar]
- Yoon, S.; Jeon, Y.; Kim, H.; Kang, J.; Rhee, T.; Oh, Y.; Park, J. The effect of electron cyclotron heating on thermal and fast-ions transport in high beta-poloidal discharges at KSTAR. In Proceedings of the IAEA Fusion Energy Conference, Gandhinagar, India, 22–27 October 2018. [Google Scholar]
- Kwak, J.G.; Rhee, T.; Han, H.; Kang, J.; Bak, J.; Ahn, H.; Nam, Y.; Kim, H.; Kim, M.; Ko, W.; et al. KSTAR status and upgrade plan toward fusion reactor. IEEE Trans. Plasma Sci. 2020, 48, 1388–1395. [Google Scholar] [CrossRef]
- Park, H.K.; Choi, M.; Hong, S.; In, Y.; Jeon, Y.; Ko, J.; Ko, W.; Kwak, J.; Kwon, J.; Lee, J.; et al. Overview of KSTAR research progress and future plans toward ITER and K-DEMO. Nucl. Fusion 2019, 59, 112020. [Google Scholar] [CrossRef]
- Sips, A.; Kessel, C.; Joffrin, E.; Rimini, F.; Jackson, G.; Urano, H.; Nunes, I.; Hobirk, J.; Stober, J.; Schweinzer, J.; et al. Assessment of the baseline scenario at q95∼3 for ITER Preprint. In Proceedings of the 2016 IAEA Fusion Energy Conference, Kyoto, Japan, 17–22 October 2016. [Google Scholar]
- Frassinetti, L.; Saarelma, S.; Lomas, P.; Nunes, I.; Rimini, F.; Beurskens, M.N.A.; Bilkova, P.; Boom, J.E.; de la Luna, E.; Delabie, E.; et al. Dimensionless scalings of confinement, heat transport and pedestal stability in JET-ILW and comparison with JET-C. Plasma Phys. Control. Fusion 2016, 59, 014014. [Google Scholar] [CrossRef]
- Kim, H.T.; Romanelli, M.; Voitsekhovitch, I.; Koskela, T.; Conboy, J.; Giroud, C.; Maddison, G.; Joffrin, E. Comparative analysis of core heat transport of JET high density H-mode plasmas in carbon wall and ITER-like wall. Plasma Phys. Control. Fusion 2015, 57, 065002. [Google Scholar] [CrossRef]
- Pasqualotto, R.; Nielsen, P.; Gowers, C.; Beurskens, M.; Kempenaars, M.; Carlstrom, T.; Johnson, D. High resolution Thomson scattering for Joint European Torus (JET). Rev. Sci. Instrum. 2004, 75, 3891–3893. [Google Scholar] [CrossRef]
- Giroud, C.; Meigs, A.G.; Negus, C.R.; Zastrow, K.D.; Biewer, T.M.; Versloot, T.W. Impact of calibration technique on measurement accuracy for the JET core charge-exchange system. Rev. Sci. Instrum. 2008, 79, 10F525. [Google Scholar] [CrossRef] [PubMed]
- Mast, K.F.; Krause, H.; Behringer, K.; Bulliard, A.; Magyar, G. Bolometric diagnostics in JET. Rev. Sci. Instrum. 1985, 56, 969–971. [Google Scholar] [CrossRef]
- Meister, H.; Fischer, R.; Horton, L.D.; Maggi, C.F.; Nishijima, D.; Giroud, C.; Zastrow, K.D.; Zaniol, B. Zeff from spectroscopic bremsstrahlung measurements at ASDEX Upgrade and JET. Rev. Sci. Instrum. 2004, 75, 4097–4099. [Google Scholar] [CrossRef]
- Brambilla, M. ‘Quasi-local’ wave equations in toroidal geometry with applications to fast wave propagation and absorption at high harmonics of the ion cyclotron frequency. Plasma Phys. Control. Fusion 2002, 44, 2423–2443. [Google Scholar] [CrossRef]
- Staebler, G.M.; Kinsey, J.E.; Waltz, R.E. A theory-based transport model with comprehensive physics. Phys. Plasmas 2007, 14, 055909. [Google Scholar] [CrossRef] [Green Version]
- Kiefer, C.; Angioni, C.; Tardini, G.; Bonanomi, N.; Geiger, B.; Mantica, P.; Pütterich, T.; Fable, E.; Schneider, P.; Team, A.U.; et al. Validation of quasi-linear turbulent transport models against plasmas with dominant electron heating for the prediction of ITER PFPO-1 plasmas. Nucl. Fusion 2021, 61, 066035. [Google Scholar] [CrossRef]
- Solomon, W.; Politzer, P.; Buttery, R.; Holcomb, C.; Ferron, J.; Garofalo, A.; Grierson, B.; Hanson, J.; In, Y.; Jackson, G.; et al. Access to high beta advanced inductive plasmas at low injected torque. Nucl. Fusion 2013, 53, 093033. [Google Scholar] [CrossRef]
- Grierson, B.; Burrell, K.; Garofalo, A.; Solomon, W.; Diallo, A.; O’Mullane, M. Response of impurity particle confinement time to external actuators in QH-mode plasmas on DIII-D. Nucl. Fusion 2014, 54, 114011. [Google Scholar] [CrossRef]
- Jackson, G.; Luce, T.; Solomon, W.; Turco, F.; Buttery, R.; Hyatt, A.; deGrassie, J.; Doyle, E.; Ferron, J.; Haye, R.L.; et al. Long-pulse stability limits of the ITER baseline scenario. Nucl. Fusion 2015, 55, 023004. [Google Scholar] [CrossRef] [Green Version]


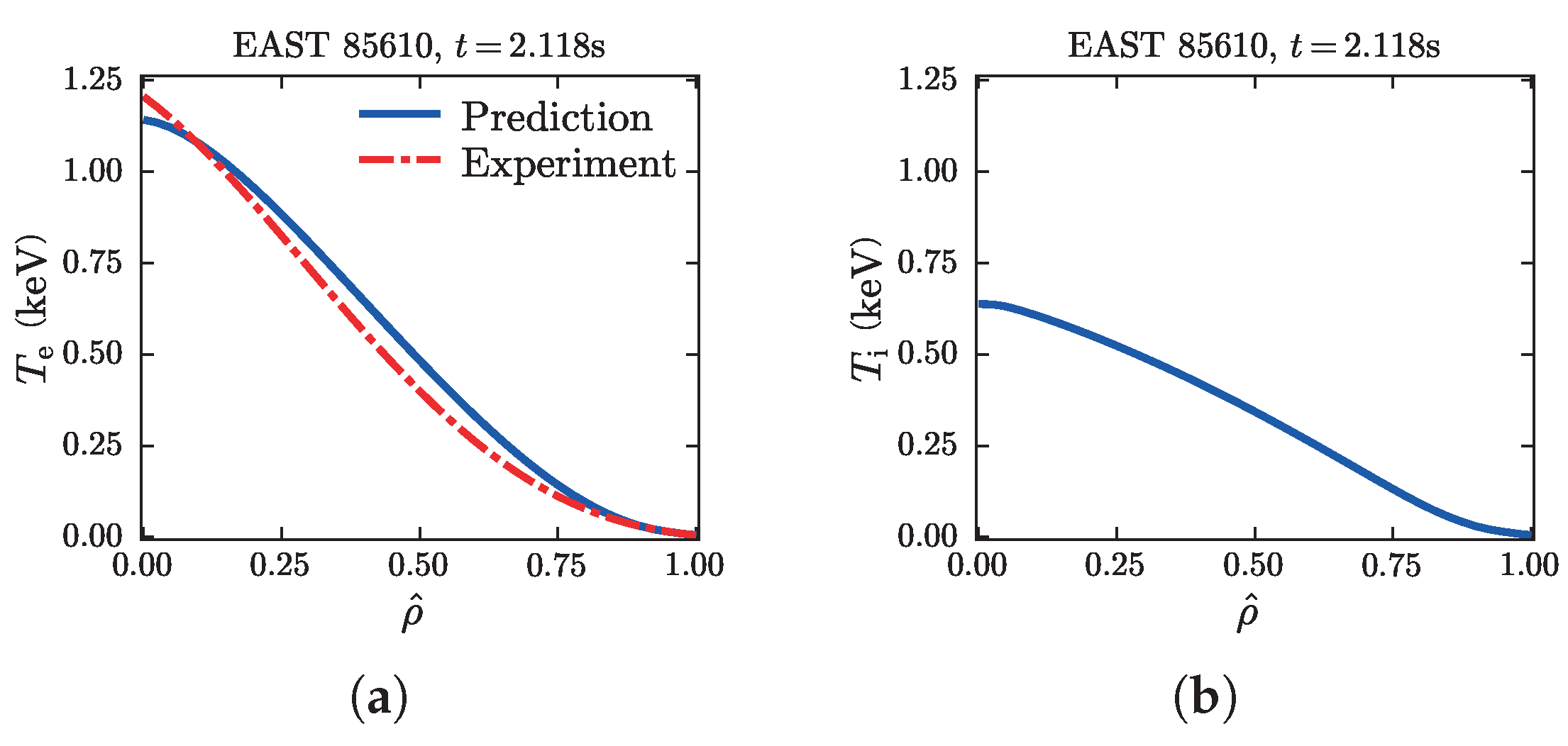

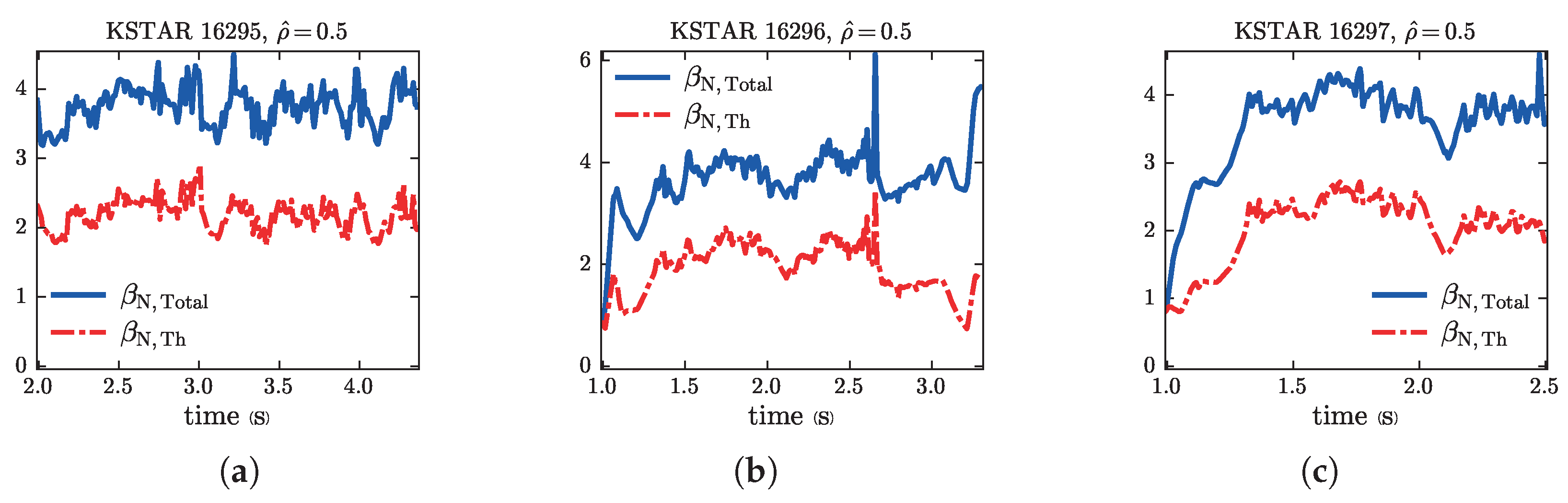

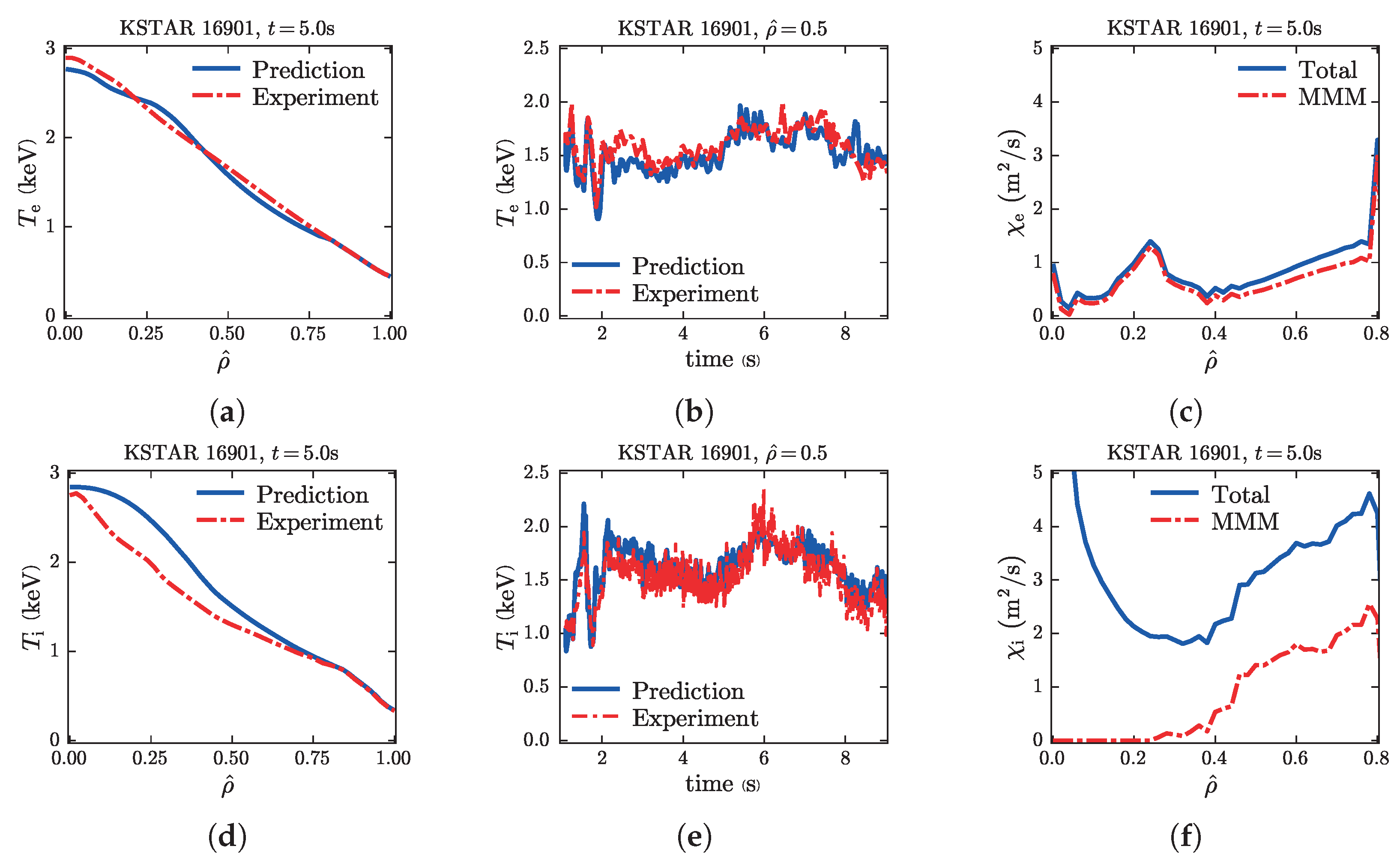
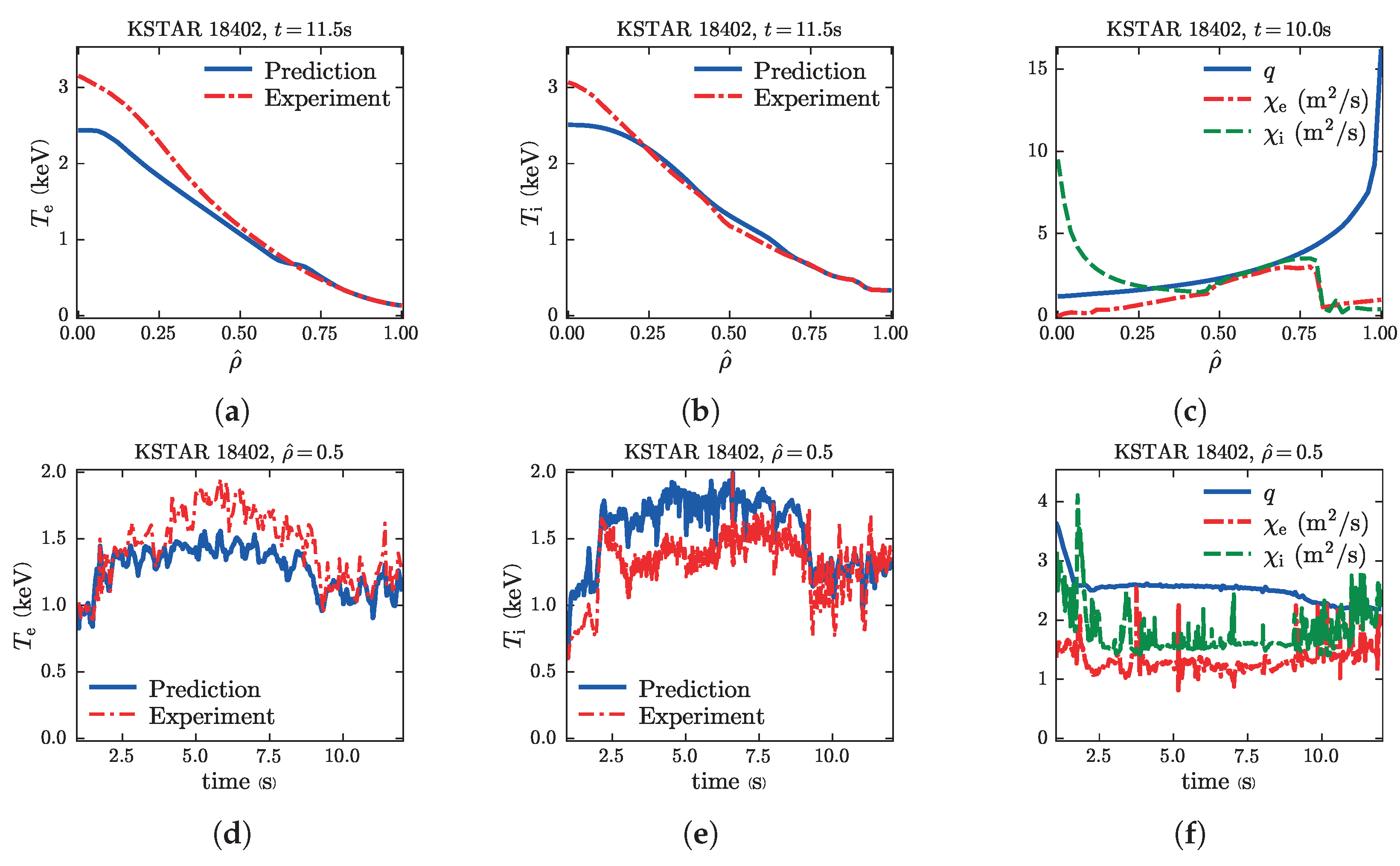




| Discharge | 80208 a | 85122 | 85124 a | 85126 a | 85610 a | 90328 |
|---|---|---|---|---|---|---|
| R (m) | 1.85 | 1.87 | 1.87 | 1.87 | 1.87 | 1.88 |
| a (m) | 0.46 | 0.45 | 0.45 | 0.45 | 0.45 | 0.46 |
| 1.61 | 1.65 | 1.67 | 1.64 | 1.67 | 1.66 | |
| 0.39 | 0.41 | 0.41 | 0.41 | 0.41 | 0.40 | |
| (T) | 2.48 | 2.41 | 2.41 | 2.41 | 2.40 | 2.42 |
| (MA) | 0.44 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| (m−3) | 2.10 | 3.06 | 3.06 | 3.05 | 1.92 | 1.78 |
| (MA) | 2.5 | 1.54 | 1.43 | 1.57 | 1.73 | 1.64 |
| (MW) | 1.00 (1.0–6.0 s) | 0.98 (2.8–4.8 s) | 1.08 (5.8–6.8 s) | 0.39 (2.8–4.0 s) | 0.60 (2.5–7.4 s) | 1.36 (2.5–4.0 s) |
| 0.85 (1.1–6.0 s) | 1.08 (5.8–6.8 s) | 0.73 (3.0–7.5 s) | 0.57 (2.7–7.3 s) | 0.33 (2.6–7.4 s) | 1.44 (6.0–7.5 s) | |
| (MW) | 1.00 (3.0–6.0 s) | |||||
| (s) | 3.5, 4.0 | 2.17 | 2.076 | 2.175 | 2.188 | 1.997 |
| Discharge | RMS | Offset | q RMS | q Offset |
|---|---|---|---|---|
| 85126 | 6.9 | −2.2 | 8.4 | −0.7 |
| 85610 | 8.8 | 6.4 | 11.3 | −3.5 |
| 85122 | 13.6 | −7.3 | 7.7 | −4.4 |
| 85124 | 14.0 | −8.6 | 6.6 | −2.6 |
| 90328 | 11.9 | −2.7 | 15.9 | −12.6 |
| Average | 11.0 | −2.9 | 10.0 | −4.8 |
| Discharge | Type | R (m) | a (m) | (T) | (MA) | (m−3) | (MW) | (MW) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 16295 | high- | 2.7 (1–1.5 s), 4.5 (1.5–4.5 s) | ||||||||
| 16296 | high- | 2.7 (1–1.5 s), 4.5 (1.5–3.5 s) | ||||||||
| 16297 | high- | 2.7 (1–1.5), 4.5 (1.5–2.6 s) | ||||||||
| 16299 | high- | 2.7 (1–1.5), 4.5 (1.5–3 s) | ||||||||
| 16325 | high- | 4.5 (1.5–14 s) | ||||||||
| 16901 | moderate- | 3.5 (1.1–10 s) | ||||||||
| 16949 | high- | 3.5 (1.5–12 s) | ||||||||
| 18399 | high- | 3.5 (1.5–10 s) | ||||||||
| 18400 | high- | 3.5 (1.5–12 s) | ||||||||
| 18402 | high- | 3.5 (1.5–12 s) | ||||||||
| 18404 | high- | 3.5 (1.5–5.5 s), 4.2 (5.5–12 s) | 0.8 (1.8–6 s) | |||||||
| 18476 | 4.9 (1.2–7 s) | |||||||||
| 18477 | 4.9 (1.1–7 s) | 0.8 (1.8–6 s) | ||||||||
| 18492 | 5.1 (4–7 s) | 0.75 (4–7 s) | ||||||||
| 18495 | 5.1 (4–7 s) | 0.75 (4–7 s) | ||||||||
| 18499 | 5.1 (4–7 s) | |||||||||
| 18602 | high- | 4.8 (4–8 s) |
| Type | RMS | RMS Range | RMS | RMS Range | Offset | Offset Range | Offset | Offset Range |
|---|---|---|---|---|---|---|---|---|
| ITB | 8.5 | 3.2–13.7 | 14.8 | 4.6–24.0 | 5.7 | −3.0–12.2 | 14.3 | 0.2–30.0 |
| High | 4.8 | 4.2–6.3 | 8.3 | 4.5–13.7 | −0.5 | −2.7–1.5 | −0.45 | −4.8–11.8 |
| High | 11.5 | 3.3–17.2 | 15.1 | 4.6–36.0 | −6.1 | −12.2–2.3 | 12.1 | −0.3–31.0 |
| High | 7.1 | — | 6.3 | — | −6.8 | — | 4.6 | — |
| moderate | 5.0 | — | 20.1 | — | −1.1 | — | 16.5 | — |
| Discharge | R (m) | a (m) | (T) | (MA) | (MW) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 84599 | ||||||||||||
| 86911 | ||||||||||||
| 87215 | ||||||||||||
| 87261 |
| Type | RMS | RMS Range | RMS | RMS Range | Offset | Offset Range | Offset | Offset Range |
|---|---|---|---|---|---|---|---|---|
| low | 10.4 | 4.0–18.0 | 10.5 | 3.0–18.8 | −6.2 | −24.0–8.2 | −5.7 | −18.5–4.6 |
| 11.5 | 3.6–25.6 | 8.2 | 6.8–9.8 | −6.5 | −22.0–3.7 | −7.6 | −17.0–2.0 | |
| 9.7 | 3.0–15.3 | 6.2 | 1.0–14.4 | −3.9 | −12.7–11.6 | −1.3 | −9.3–9.9 | |
| Confinement [61] | 12.8 | 7.6–21.3 | 14.8 | 8.6–22.8 | −8.9 | −19.9–10.1 | −12.1 | −21.3–5.4 |
| Discharge | R (m) | a (m) | (T) | (MA) | (m−3) | (MW) | (MW) | ||
|---|---|---|---|---|---|---|---|---|---|
| 144449 | 5.51 (1.8–3.0 s), 7.88 (3.0–4.6 s) | ||||||||
| 118341 | 9.20 (5.4–5.9 s) | ||||||||
| 150840 | 1.06 (3.0–4.0 s) | 2.76 (3.0–4.0 s) | |||||||
| 153283 | 5.91 (1.0–1.5 s), 5.33 (1.5–5.0 s) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rafiq, T.; Wang, Z.; Morosohk, S.; Schuster, E.; Weiland, J.; Choi, W.; Kim, H.-T. Validating the Multi-Mode Model’s Ability to Reproduce Diverse Tokamak Scenarios. Plasma 2023, 6, 435-458. https://doi.org/10.3390/plasma6030030
Rafiq T, Wang Z, Morosohk S, Schuster E, Weiland J, Choi W, Kim H-T. Validating the Multi-Mode Model’s Ability to Reproduce Diverse Tokamak Scenarios. Plasma. 2023; 6(3):435-458. https://doi.org/10.3390/plasma6030030
Chicago/Turabian StyleRafiq, Tariq, Zibo Wang, Shira Morosohk, Eugenio Schuster, Jan Weiland, Wilkie Choi, and Hyun-Tae Kim. 2023. "Validating the Multi-Mode Model’s Ability to Reproduce Diverse Tokamak Scenarios" Plasma 6, no. 3: 435-458. https://doi.org/10.3390/plasma6030030
APA StyleRafiq, T., Wang, Z., Morosohk, S., Schuster, E., Weiland, J., Choi, W., & Kim, H.-T. (2023). Validating the Multi-Mode Model’s Ability to Reproduce Diverse Tokamak Scenarios. Plasma, 6(3), 435-458. https://doi.org/10.3390/plasma6030030






