Investigation of Plasma Propagation in Packed-Bed Dielectric Barrier Discharge Based on a Customized Particle-in-Cell/Monte Carlo Collision Model
Abstract
:1. Introduction
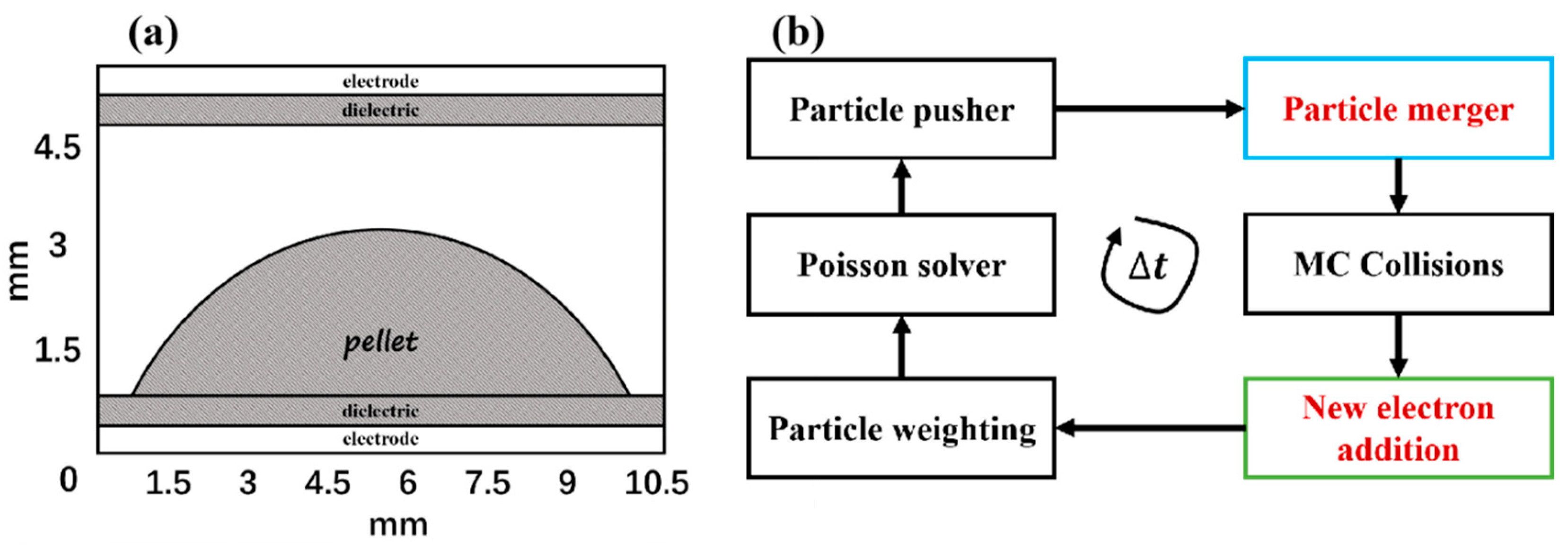
2. Computational Model
3. Results and Discussion
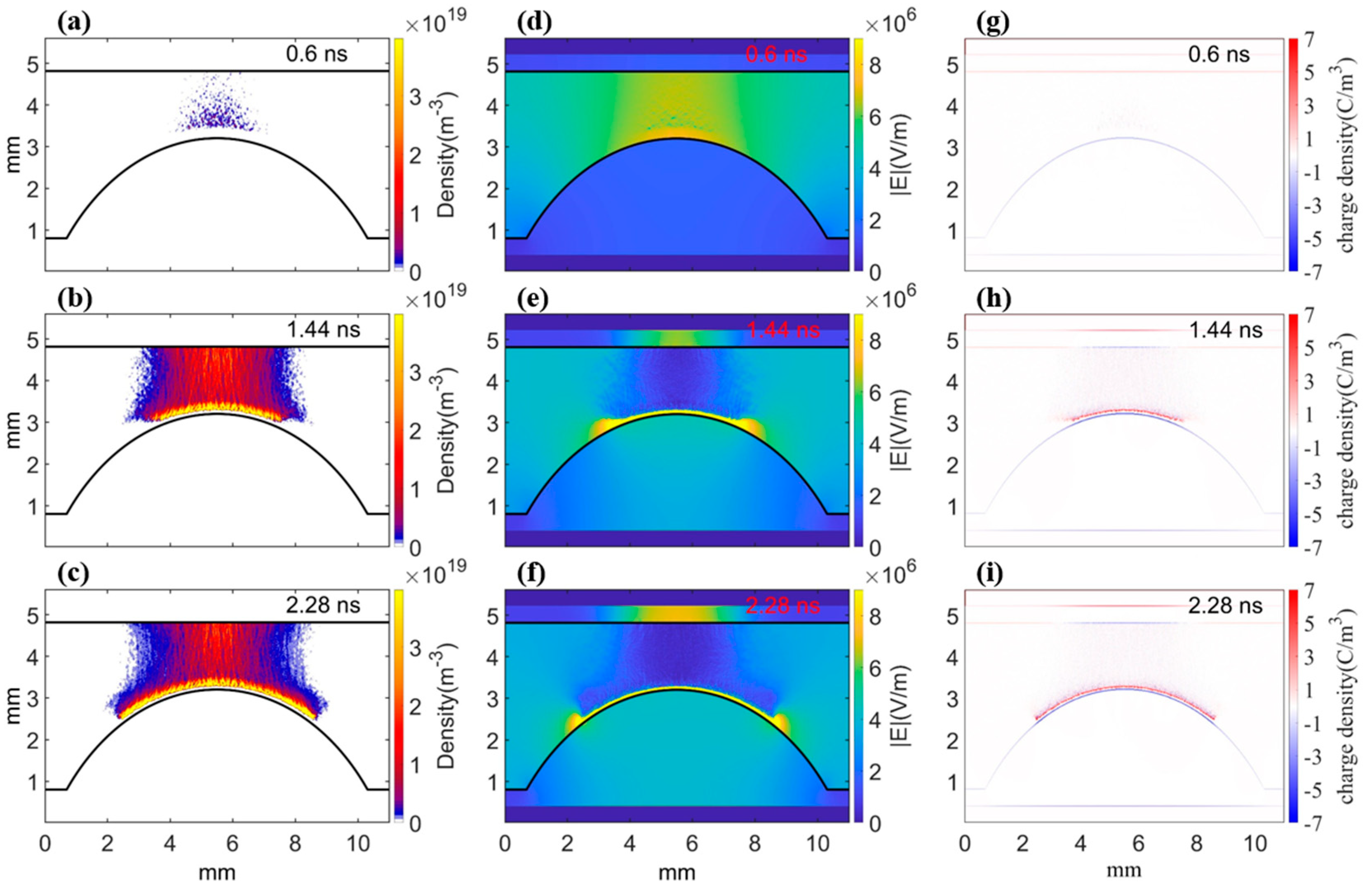
3.1. Plasma Streamer Evolution in Packed-Bed DBD
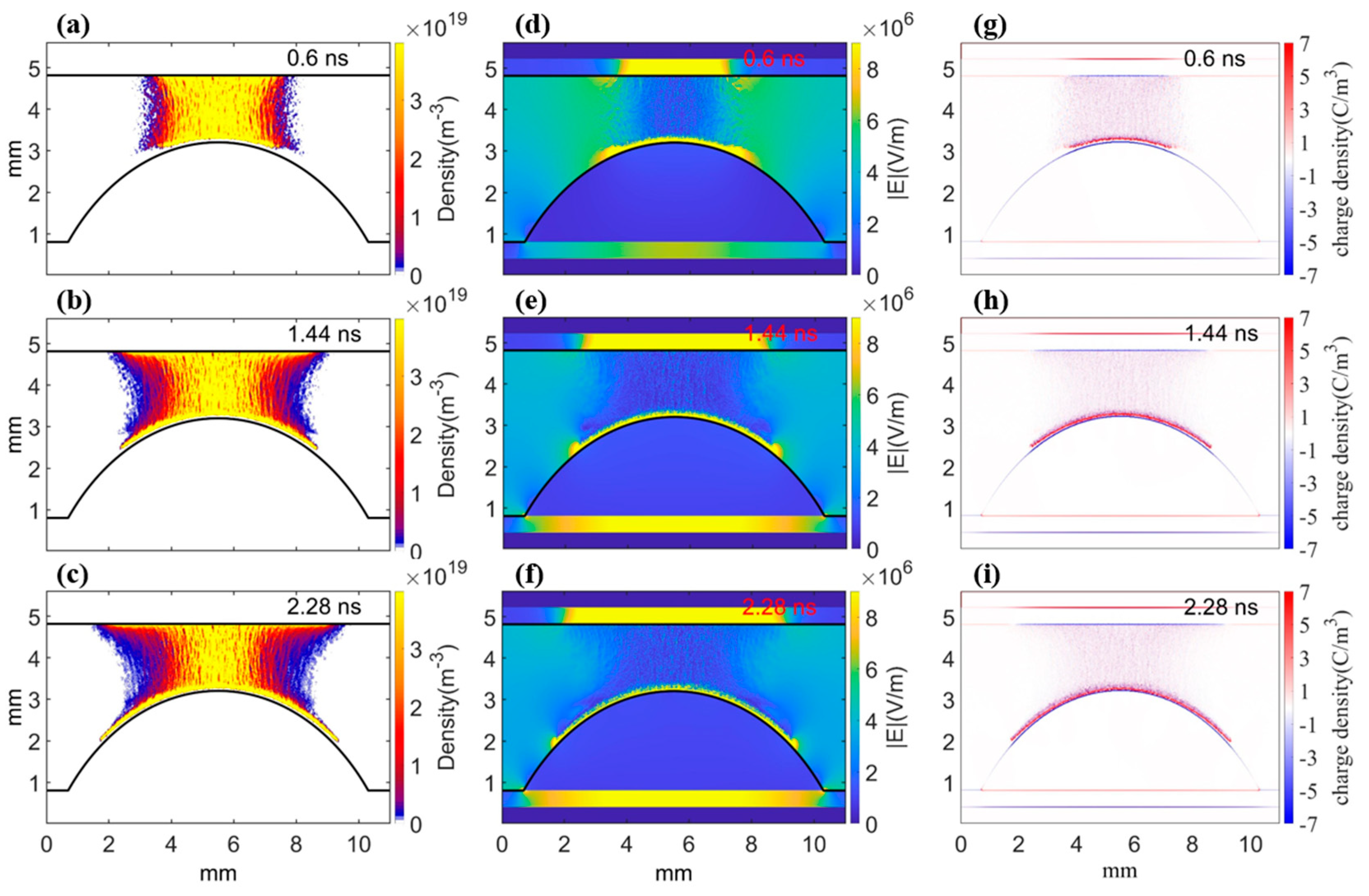
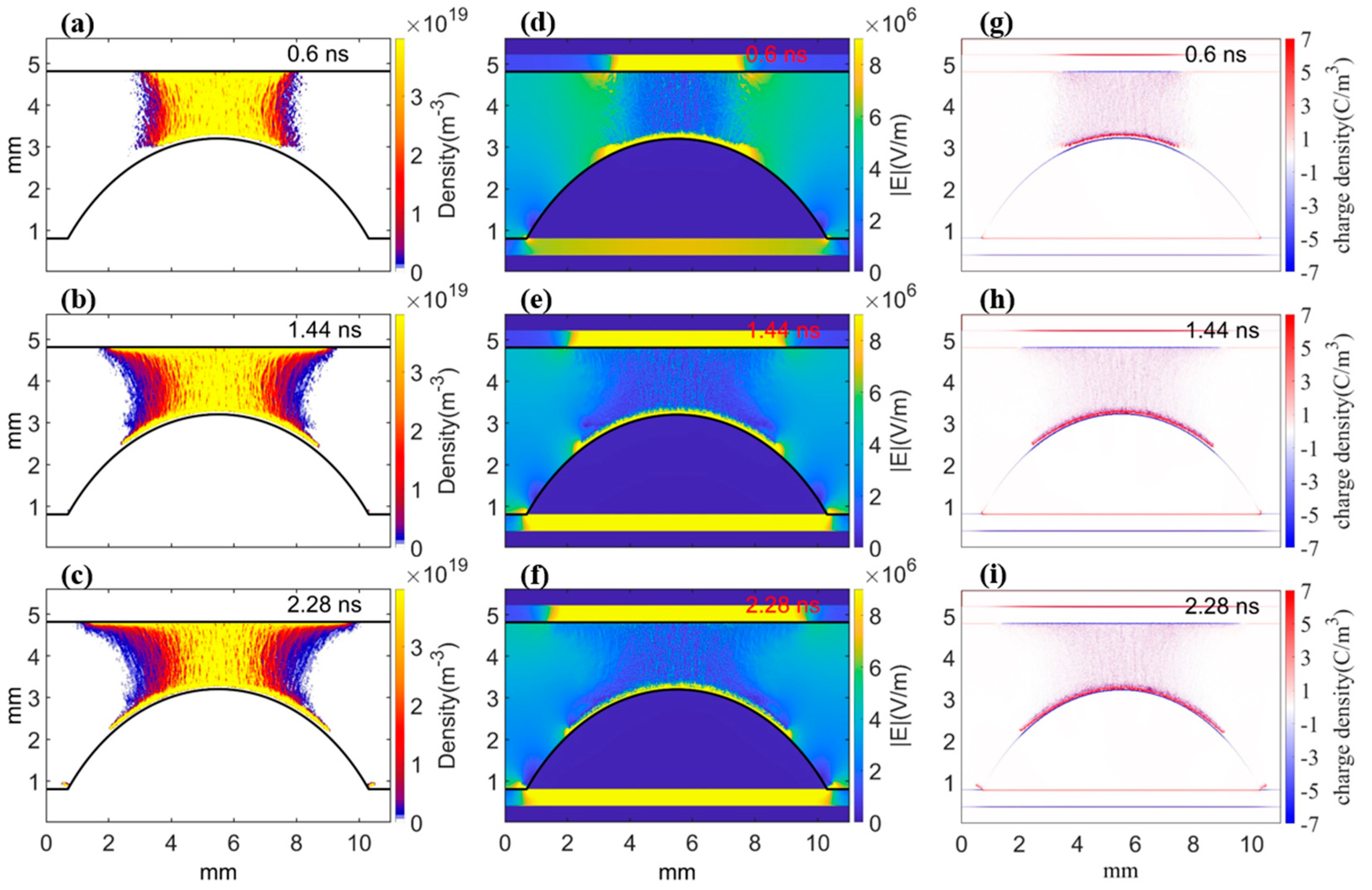
3.2. Effect of Pellet Material on Plasma Streamer Propagation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Adamovich, I.; Baalrud, S.D.; Bogaerts, A.; Bruggeman, P.J.; Cappelli, M.; Colombo, V.; Czarnetzki, U.; Ebert, U.; Eden, J.G.; Favia, P.; et al. The 2017 Plasma Roadmap: Low temperature plasma science and technology. J. Phys. D Appl. Phys. 2017, 50, 323011. [Google Scholar] [CrossRef]
- Bogaerts, A.; Neyts, E.C. Plasma Technology: An Emerging Technology for Energy Storage. ACS Energy Lett. 2018, 3, 1013. [Google Scholar] [CrossRef]
- Snoeckx, R.; Bogaerts, A. Plasma technology—A novel solution for CO2 conversion? Chem. Soc. Rev. 2017, 46, 5805. [Google Scholar] [CrossRef] [PubMed]
- Patil, B.S.; Cherkasov, N.; Lang, J.; Ibhadon, A.O.; Hessel, V.; Wang, Q. Low temperature plasma-catalytic NOx synthesis in a packed DBD reactor: Effect of support materials and supported active metal oxides. Appl. Catal. B 2016, 194, 123–133. [Google Scholar] [CrossRef]
- Neyts, E.C.; Bogaerts, A. Understanding plasma catalysis through modelling and simulation—A review. J. Phys. D Appl. Phys. 2014, 47, 224010. [Google Scholar] [CrossRef]
- Chen, H.L.; Lee, H.M.; Chen, S.H.; Chao, Y.; Chang, M.B. Review of plasma catalysis on hydrocarbon reforming for hydrogen production—Interaction, integration, and prospects. Appl. Catal. B Environ. 2008, 85, 1–9. [Google Scholar] [CrossRef]
- Van Laer, K.; Bogaerts, A. Fluid modelling of a packed bed dielectric barrier discharge plasma reactor. Plasma Sources Sci. Technol. 2016, 25, 015002. [Google Scholar] [CrossRef]
- Van Laer, K.; Bogaerts, A. How bead size and dielectric constant affect the plasma behaviour in a packed bed plasma reactor: A modelling study. Plasma Sources Sci. Technol. 2017, 26, 085007. [Google Scholar] [CrossRef]
- Hensel, K.; Sato, S.; Mizuno, A. Electrical discharge in honeycomb monolith. Chem. Listy 2008, 102, S1318–S1321. [Google Scholar]
- Kirkpatrick, M.J.; Odic, E.; Leininger, J.P.; Blanchard, G.; Rousseau, S.; Glipa, X. Plasma assisted heterogeneous catalytic oxidation of carbon monoxide and unburned hydrocarbons: Laboratory-scale investigations. Appl. Catal. B 2011, 106, 160–166. [Google Scholar] [CrossRef]
- Brandenburg, R. Dielectric barrier discharges: Progress on plasma sources and on the understanding of regimes and single filaments. Plasma Sources Sci. Technol. 2017, 26, 053001. [Google Scholar] [CrossRef]
- Kim, H.H. Nonthermal Plasma Processing for Air-Pollution Control: A Historical Review, Current Issues, and Future Prospects. Plasma Process. Polym. 2004, 1, 91–110. [Google Scholar] [CrossRef]
- Neyts, E.C.; Ostrikov, K.; Sunkara, M.K.; Bogaerts, A. Plasma Catalysis: Synergistic Effects at the Nanoscale. Chem. Rev. 2015, 115, 13408. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.H.; Ogata, A.; Futamura, S. Oxygen partial pressure-dependent behavior of various catalysts for the total oxidation of VOCs using cycled system of adsorption and oxygen plasma. Appl. Catal. B. 2008, 79, 356. [Google Scholar] [CrossRef]
- Van Durme, J.; Dewulf, J.; Leys, C.; Van Langenhove, H. Combining non-thermal plasma with heterogeneous catalysis in waste gas treatment: A review. Appl. Catal. B. 2008, 78, 324. [Google Scholar] [CrossRef]
- Whitehead, J.C. Plasma–catalysis: The known knowns, the known unknowns and the unknown unknowns. J. Phys. D Appl. Phys. 2016, 49, 243001. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, L.; Yang, D.; Schulze, J.; Wang, Y.; Bogaerts, A. Positive and negative streamer propagation in volume dielectric barrier discharges with planar and porous electrodes. Plasma Process. Polym. 2021, 18, e2000234. [Google Scholar] [CrossRef]
- Nijdam, S.; van de Wetering, F.M.J.H.; Blanc, R.; van Veldhuizen, E.M.; Ebert, U. Probing photo-ionization: Experiments on positive streamers in pure gases and mixtures. J. Phys. D Appl. Phys. 2010, 43, 145204. [Google Scholar] [CrossRef]
- Ebert, U.; Montijn, C.; Briels, T.M.P.; Hundsdorfer, W.; Meulenbroek, B.; Rocco, A.; van Veldhuizen, E.M. The multiscale nature of streamers. Plasma Sources Sci. Technol. 2006, 15, S118. [Google Scholar] [CrossRef]
- Ningyu, L.; Victor, P.P. Effects of photoionization on propagation and branching of positive and negative streamers in sprites. J. Geophys. Res. Sp. Phys. 2004, 109, A 04301. [Google Scholar]
- van Veldhuizen, E.M.; Rutgers, W.R. Pulsed positive corona streamer propagation and branching. J. Phys. D Appl. Phys. 2002, 35, 2169. [Google Scholar] [CrossRef]
- Nijdam, S.; Takahashi, E.; Markosyan, A.H.; Ebert, U. Investigation of positive streamers by double-pulse experiments, effects of repetition rate and gas mixture. Plasma Sources Sci. Technol. 2014, 23, 25008. [Google Scholar] [CrossRef]
- Chen, H.L.; Lee, H.M.; Chen, S.H.; Chang, M.B. Review of Packed-Bed Plasma Reactor for Ozone Generation and Air Pollution Control. Ind. Eng. Chem. Res. 2008, 47, 2122–2130. [Google Scholar] [CrossRef]
- Butterworth, T.; Elder, R.; Allen, R. Effects of particle size on CO2 reduction and discharge characteristics in a packed bed plasma reactor. Chem. Eng. J. 2016, 293, 55–67. [Google Scholar] [CrossRef]
- Uytdenhouwen, Y.; Van Alphen, S.; Michielsen, I.; Meynen, V.; Cool, P.; Bogaerts, A. A packed-bed DBD micro plasma reactor for CO2 dissociation: Does size matter? Chem. Eng. J. 2018, 348, 557–568. [Google Scholar] [CrossRef]
- Kim, H.H.; Teramoto, Y.; Negishi, N.; Ogata, A. A multidisciplinary approach to understand the interactions of nonthermal plasma and catalyst: A review. Catal. Today 2015, 256, 13–22. [Google Scholar] [CrossRef]
- Kim, H.H.; Teramoto, Y.; Sano, T.; Negishi, N.; Ogata, A. Effects of Si/Al ratio on the interaction of nonthermal plasma and Ag/HY catalysts. Appl. Catal. B Environ. 2015, 166, 9–17. [Google Scholar] [CrossRef]
- Tu, X.; Gallon, H.J.; Twigg, M.V.; Gorry, P.A.; Whitehead, J.C. Dry reforming of methane over a Ni/Al2O3 catalyst in a coaxial dielectric barrier discharge reactor. J. Phys. D Appl. Phys. 2011, 44, 274007. [Google Scholar] [CrossRef]
- Butterworth, T.; Allen, R.W.K. Plasma-catalyst interaction studied in a single pellet DBD reactor: Dielectric constant effect on plasma dynamics. Plasma Sources Sci. Technol. 2017, 26, 065008. [Google Scholar] [CrossRef]
- Wang, W.; Kim, H.-H.; Van Laer, K.; Bogaerts, A. Streamer propagation in a packed bed plasma reactor for plasma catalysis applications. Chem. Eng. J. 2018, 334, 2467–2479. [Google Scholar] [CrossRef]
- Zhang, Q.Z.; Bogaerts, A. Plasma streamer propagation in structured catalysts. Plasma Sources Sci. Technol. 2018, 27, 105013. [Google Scholar] [CrossRef]
- Zhang, Q.-Z.; Wang, W.-Z.; Bogaerts, A. Importance of surface charging during plasma streamer propagation in catalyst pores. Plasma Sources Sci. Technol. 2018, 27, 065009. [Google Scholar] [CrossRef]
- Zhang, Q.Z.; Bogaerts, A. Propagation of a plasma streamer in catalyst pores. Plasma Sources Sci. Technol. 2018, 27, 035009. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.Y.; Zhang, Y.R.; Bogaerts, A. Formation of microdischarges inside a mesoporous catalyst in dielectric barrier discharge plasmas. Plasma Sources Sci. Technol. 2017, 26, 054002. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.-Y.; Jiang, W.; Bogaerts, A. Two-dimensional particle-in cell/Monte Carlo simulations of a packed-bed dielectric barrier discharge in air at atmospheric pressure. New J. Phys. 2015, 17, 083056. [Google Scholar] [CrossRef]
- Nieter, C.; Cary, J.R. VORPAL: A versatile plasma simulation code. J. Comput. Phys. 2004, 196, 448–473. [Google Scholar] [CrossRef]
- Kuhfeld, J.; Lepikhin, N.D.; Luggenhölscher, D.; Czarnetzki, U.; Donkó, Z. PIC/MCC simulation for a ns-pulsed glow discharge in nitrogen at sub-atmospheric pressure and analysis of its quasi-steady state physics. Plasma Sources Sci. Technol. 2023, 32, 084001. [Google Scholar] [CrossRef]
- Hong, Y.J.; Yoon, M.; Iza, F.; Kim, G.C.; Lee, J.K. Comparison of fluid and particle-in-cell simulations on atmospheric pressure helium microdischarges. J. Phys. D Appl. Phys. 2008, 41, 245208. [Google Scholar] [CrossRef]
- Zhang, Q.-Z.; Nguyen-Smith, R.T.; Beckfeld, F.; Liu, Y.; Mussenbrock, T.; Awakowicz, P.; Schulze, J. Computational study of simultaneous positive and negative streamer propagation in a twin surface dielectric barrier discharge via 2D PIC simulations. Plasma Sources Sci. Technol. 2021, 30, 075017. [Google Scholar] [CrossRef]
- Lichtenberg, A.J.; Lieberman, M.A. Principles of Plasma Discharges and Materials Processing, 2nd ed.; Wiley: New York, NY, USA, 2005. [Google Scholar]
- Furman, M.A.; Pivi, M.T.F. Probabilistic model for the simulation of secondary electron emission. Phys. Rev. Spec. Top. Accel. Beams 2002, 5, 124404. [Google Scholar] [CrossRef]
- Phelps, A.V.; Petrovic, Z.L. Cold-cathode discharges and breakdown in argon: Surface and gas phase production of secondary electrons. Plasma Sources Sci. Technol. 1999, 8, R21. [Google Scholar] [CrossRef]
- Pancheshnyi, S.; Biagi, S.; Bordage, M.C.; Hagelaar, G.J.M.; Morgan, W.L.; Phelps, A.V.; Pitchford, L.C. The LXCat project: Electron scattering cross sections and swarm parameters for low temperature plasma modeling. Chem. Phys. 2012, 398, 148–153. [Google Scholar] [CrossRef]
- Biagi v8.9 Database. 2015. Available online: www.lxcat.net (accessed on 2 November 2021).
- Alexandre, L.; Mikhail, S.; Dmitry, O.; Richard, M.; Sergey, M. Limitations of the DBD effects on the external flow. In Proceedings of the 48th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010. [Google Scholar]
- Qiu, Y.; Xian, Y.; Lu, X.; Ostrikov, K. Effect of background ionization on plasma ignition dynamics. Phys. Plasmas 2017, 24, 033503. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhang, L.; Shahzad, A.; Attri, P.; Zhang, Q. Investigation of Plasma Propagation in Packed-Bed Dielectric Barrier Discharge Based on a Customized Particle-in-Cell/Monte Carlo Collision Model. Plasma 2023, 6, 637-648. https://doi.org/10.3390/plasma6040044
Li X, Zhang L, Shahzad A, Attri P, Zhang Q. Investigation of Plasma Propagation in Packed-Bed Dielectric Barrier Discharge Based on a Customized Particle-in-Cell/Monte Carlo Collision Model. Plasma. 2023; 6(4):637-648. https://doi.org/10.3390/plasma6040044
Chicago/Turabian StyleLi, Xufeng, Leiyu Zhang, Aamir Shahzad, Pankaj Attri, and Quanzhi Zhang. 2023. "Investigation of Plasma Propagation in Packed-Bed Dielectric Barrier Discharge Based on a Customized Particle-in-Cell/Monte Carlo Collision Model" Plasma 6, no. 4: 637-648. https://doi.org/10.3390/plasma6040044
APA StyleLi, X., Zhang, L., Shahzad, A., Attri, P., & Zhang, Q. (2023). Investigation of Plasma Propagation in Packed-Bed Dielectric Barrier Discharge Based on a Customized Particle-in-Cell/Monte Carlo Collision Model. Plasma, 6(4), 637-648. https://doi.org/10.3390/plasma6040044






