Toroidal CO2 Plasma Sources with Low- and High-Frequency Power Coupling Configurations for Improved Energy Transfer Efficiencies
Abstract
:1. Introduction
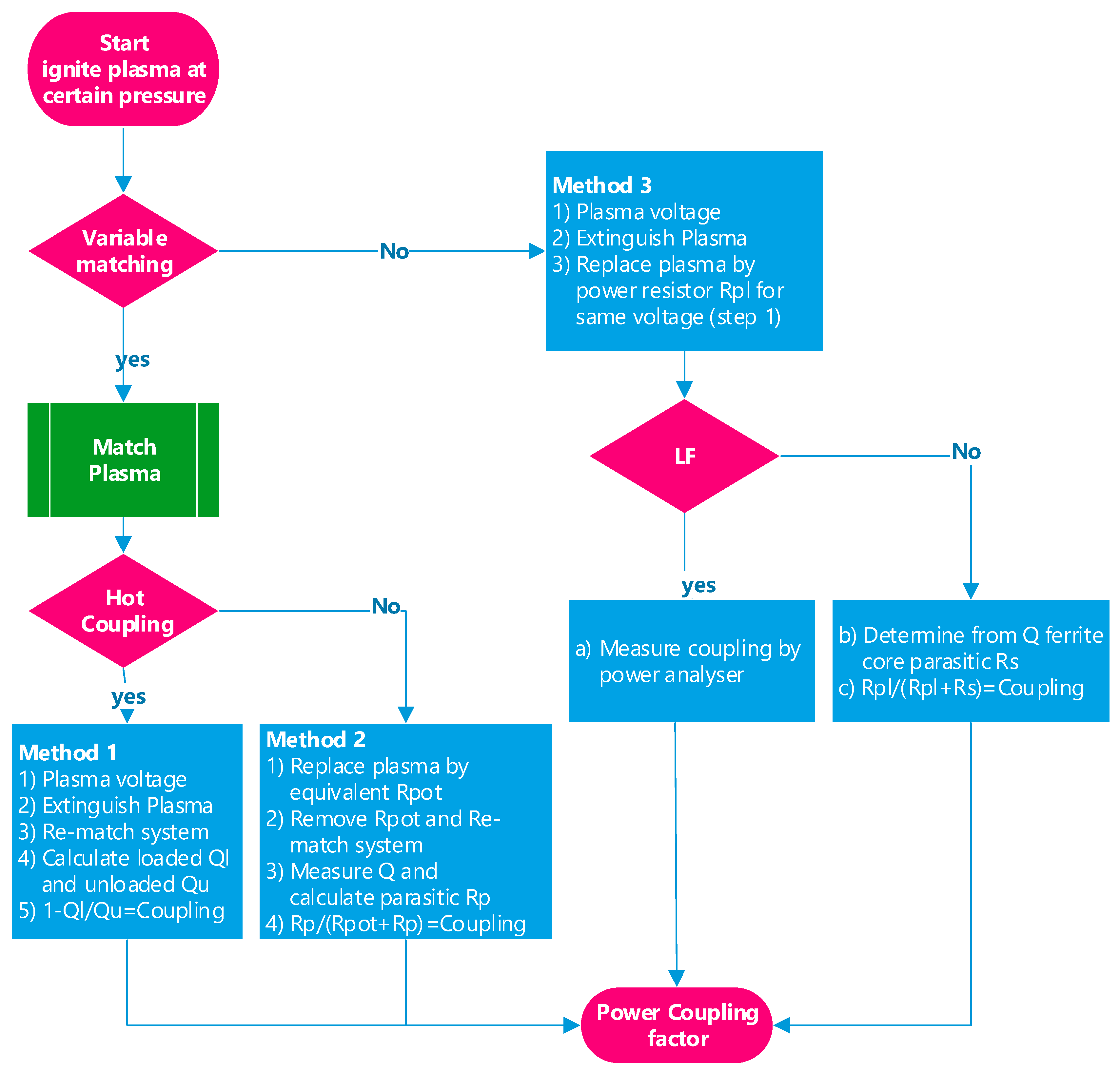
2. Power Coupling Efficiency Recipes
- Method 1 is employed to measure the energy transfer in a fully powered (hot), HF plasma:
- The voltage is measured with plasma inside the inductor (as an alternative to this, a less invasive 50 Ω coupling loop field probe at a certain distance from the coil can be used to determine a voltage proportional to the magnetic field strength for in situ monitoring purposes).
- The plasma is extinguished by increasing the pressure to 1 bar.
- After re-tuning to zero reflecting power (if necessary), the voltage over the inductor is measured again (or using the field probe described in point 2).
- The Q factor ratio is calculated with and without plasma from the ratio of the voltages (or the fields) at the same power.
- The Q factor ratio determines the loss of energy via radiation to the environment or heating of the coil. One minus this Q factor ratio represents the power absorbed by the plasma.
- Method 2 was performed in the case of a high frequency (HF) plasma in hybrid hot/cold conditions:
- Without plasma, an additional resistance is placed parallel to the coil and varied until full matching (zero reflection) is again obtained; this resistance represents the equivalent plasma resistance, Rpot.
- Now, this resistance is removed and the system is re-matched (still without plasma), and the unloaded Q of this system is measured by measuring the resonant frequency and bandwidth through the reflected power (i.e.,|S11|2) on the vector network analyzer with a bandwidth of −3 dB points of the resonance dip
- Using the (unloaded) Q, the parasitic parallel resistance, Rp, is determined. If an uncooled coil is used and its temperature changes dramatically during the plasma (e.g., at a glowing condition), then the increase in the parasitic series resistance of the coil can be determined to calculate the loaded Q. In this case, this should be used to recalculate the Rp for a better approximation.
- The coupling factor is the ratio of loaded equivalent (plasma) resistance (from step 1) over the total resistance (step 1) and parasitic resistance (step 3), i.e., Rp/(Rp + Rpot).
- Method 3 is used when there is no variable active matching circuit available (see Scheme 1, the path to method 3):
- The voltage is measured over the plasma by an additional single winding parallel to the plasma in the transformer.
- The plasma is extinguished (i.e., by increasing the pressure to atmospheric pressure or removing the whole plasma chamber).
- The plasma is replaced by a low-inductance-variable power resistor that is adjusted until the voltage is the same as that of the plasma (i.e., the plasma impedance) as in step 1.If an LF circuit is used,
- With a two-channel-power analyzer (measuring the complex amplitudes of all voltages and currents) connected to both the primary and secondary side of the transformer, the coupling is measured.
If an HF circuit is used,- b.
- The Q factor of the original ferrite transformer core is measured at the right frequency, and this gives the equivalent loss resistance in series, Rs.
- c.
- The loss resistance is compared with the plasma impedance of CO2, where the ratio of the two gives the power coupling.
3. Results and Discussion
3.1. Fluorescent Plasma Lamp
3.2. CO2 Plasma Torus Reactor with Two Ferrite Transformer Toroid Cores
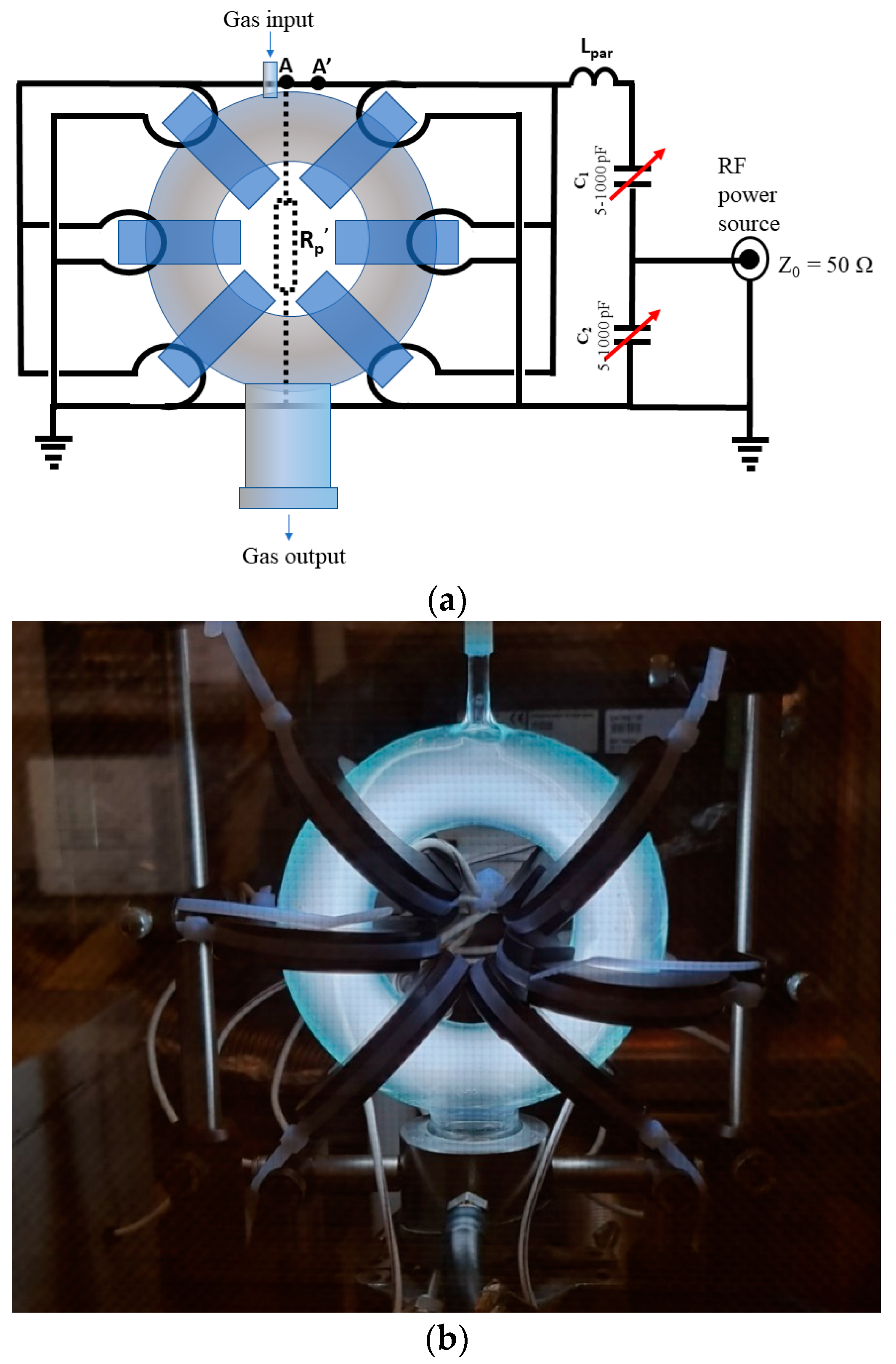
3.3. HF Toroidal Plasma Reactor Employing Six Parallel Ferrite Transformer Cores in CO2
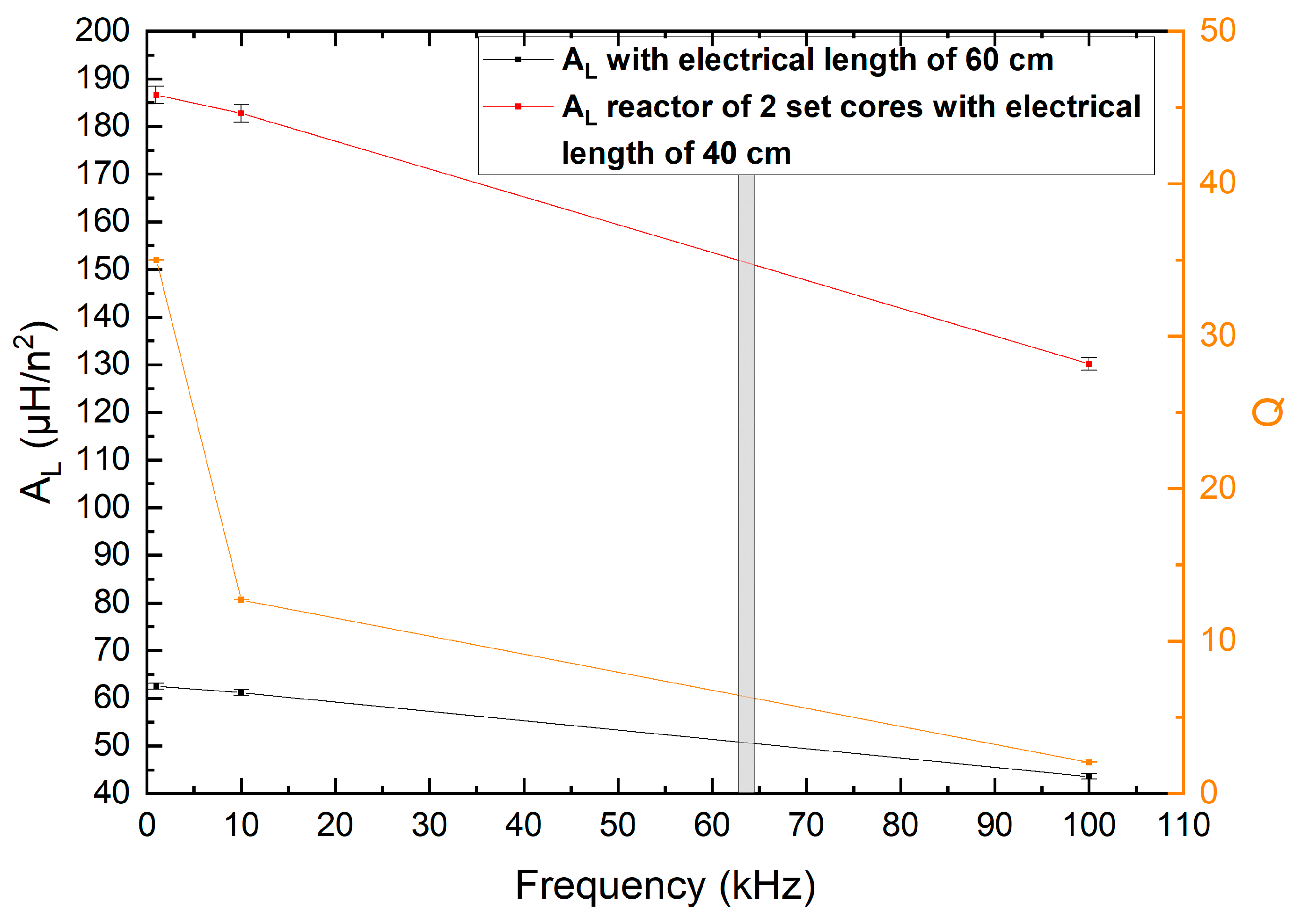
3.4. Low-Frequency Plasma Reactor with High-AL-Value Transformer Cores
3.5. HF (10.1 MHz) Poloidal Plasma Coupling Configuration
3.6. HF (21.7 MHz) Toroidal Coil Plasma Coupling Configuration
4. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Piovesan, N.; Gambin, A.F.; Miozzo, M.; Rossi, M.; Dini, P. Energy sustainable paradigms and methods for future mobile networks: A survey. Comput. Commun. 2018, 119, 101–117. [Google Scholar] [CrossRef]
- Nikoo, M.S.; Jafari, A.; Perera, N.; Zhu, M.; Santoruvo, G.; Matioli, E. Nanoplasma-enabled picosecond switches for ultrafast electronics. Nature 2020, 579, 534–539. [Google Scholar] [CrossRef] [PubMed]
- Godyak V, Ferromagnetic enhanced inductive plasma sources. J. Phys. D Appl. Phys. 2013, 46, 283001. [CrossRef]
- Boulos, M.I. The inductively coupled R.F. (radio frequency) plasma. Pure Appl. Chem. 1985, 57, 1321–1352. [Google Scholar] [CrossRef]
- Rauner, D.; Mattei, S.; Briefi, S.; Fantz, U.; Hatayama, A.; Lettry, J.; Nishida, K.; Tran, M.Q. Investigation of the RF efficiency of Inductively CoupledHydrogen Plasmas at 1 MHz. AIP Conf. Proc. 2017, 1869, 030035. [Google Scholar]
- Kamada, Y.; Barabaschi, P.; Ishida, S. the JT-60SA Team and JT-60SA Research Plan Contributors, Progress of the JT-60SA project. Nucl. Fusion 2013, 53, 104010. [Google Scholar] [CrossRef]
- Smith, D.K.; Chen, X.; Holber, W.M.; Georgelis, E. Toroidal Low-Field Reactive Gas Source. U.S. Patent 6,150,628, 21 November 2000. [Google Scholar]
- Onenga, J. Fusion: A true challenge for an enormous reward. EPJ Web Conf. 2022, 268, 00011. [Google Scholar] [CrossRef]
- Paranjpe, A.P. Plasma Sources Employing Spiral RF Coil and Method for Using Same. U.S. Patent 5,436,528, 25 July 1995. [Google Scholar]
- Wang, Y.; Wang, Z.; Dong, L.; Zhou, Y.; Sun, R.; Li, C. Micro inductively coupled plasma excitation source based on the three-dimensional spiral-shaped coil. In Proceedings of the 2010 International Conference on Measuring Technology and Mechatronics Automation, Changsha, China, 13–14 March 2010; pp. 660–663. [Google Scholar]
- Munsat, T.; Hooke, W.M.; Bozeman, S.P.; Washburnd, S. Two new planar coil designs for a high pressure radio frequency plasma source. Appl. Phys. Lett. 1995, 66, 2180–2182. [Google Scholar] [CrossRef]
- Dijk, J.; Peerenboom, K.S.C.; Jimenez-Diaz, M.; Mihailova, D.B.; Mullen, J.J.A.M. The plasma modelling toolkit. J. Phys. D Appl. Phys. 2009, 42, 1940121. [Google Scholar]
- Hagelaar, G.J.M.; Pitchford, L.C. Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models. Plasma Sources Sci. Technol. 2005, 14, 722. [Google Scholar] [CrossRef]
- BOLSIG+ Version 12-2019. Available online: https://www.bolsig.laplace.univ-tlse.fr/index.html (accessed on 22 March 2024).
- Janssen, J.F.J. Equilibrium and Transport in Molecular Plasmas. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2016. [Google Scholar]
- Phelps Database. Available online: www.lxcat.net (accessed on 22 March 2019).
- Hake, R.D.; Phelps, A.V. Momentum-Transfer and Inelastic-Collision Cross Sections for Electrons in O2, CO, and CO2. Phys. Rev. 1967, 158, 70. [Google Scholar] [CrossRef]
- Phelps Database, CO2 cross Sections. Available online: www.lxcat.net (accessed on 22 March 2024).
- Phelps Satabase, CO cross Sections. Available online: www.lxcat.net (accessed on 22 March 2024).
- Phelps Database, O2 cross Sections. Available online: www.lxcat.net (accessed on 22 March 2024).
- Blaha, M.; Davis, J. Elastic scattering of electrons by oxygen and nitrogen at intermediate energies. Phys. Rev. A 1975, 12, 2319. [Google Scholar] [CrossRef]
- Viegas, P.; Vialetto, L.; Wolf, A.J.; Peeters, F.J.J.; Groen, P.W.C.; Righart, T.W.H.; Bongers, W.A.; van de Sanden, M.C.M.; Diomede, P. Insight into contraction dynamics of microwave plasmas for CO2 conversion from plasma chemistry modelling. Plasma Sources Sci. Technol. 2020, 29, 105014. [Google Scholar] [CrossRef]
- Hecimovic, A.; Mayer, M.T.; De Haart, L.G.J.; Gupta, S.; Kiefer, C.K.; Navarrete, A.; Schulz, A.; Fantz, U. Benchmarking microwave-induced CO2 plasma splitting against electrochemical CO2 reduction for a comparison of promising technologies. J. CO2 Util. 2024, 83, 102825. [Google Scholar] [CrossRef]



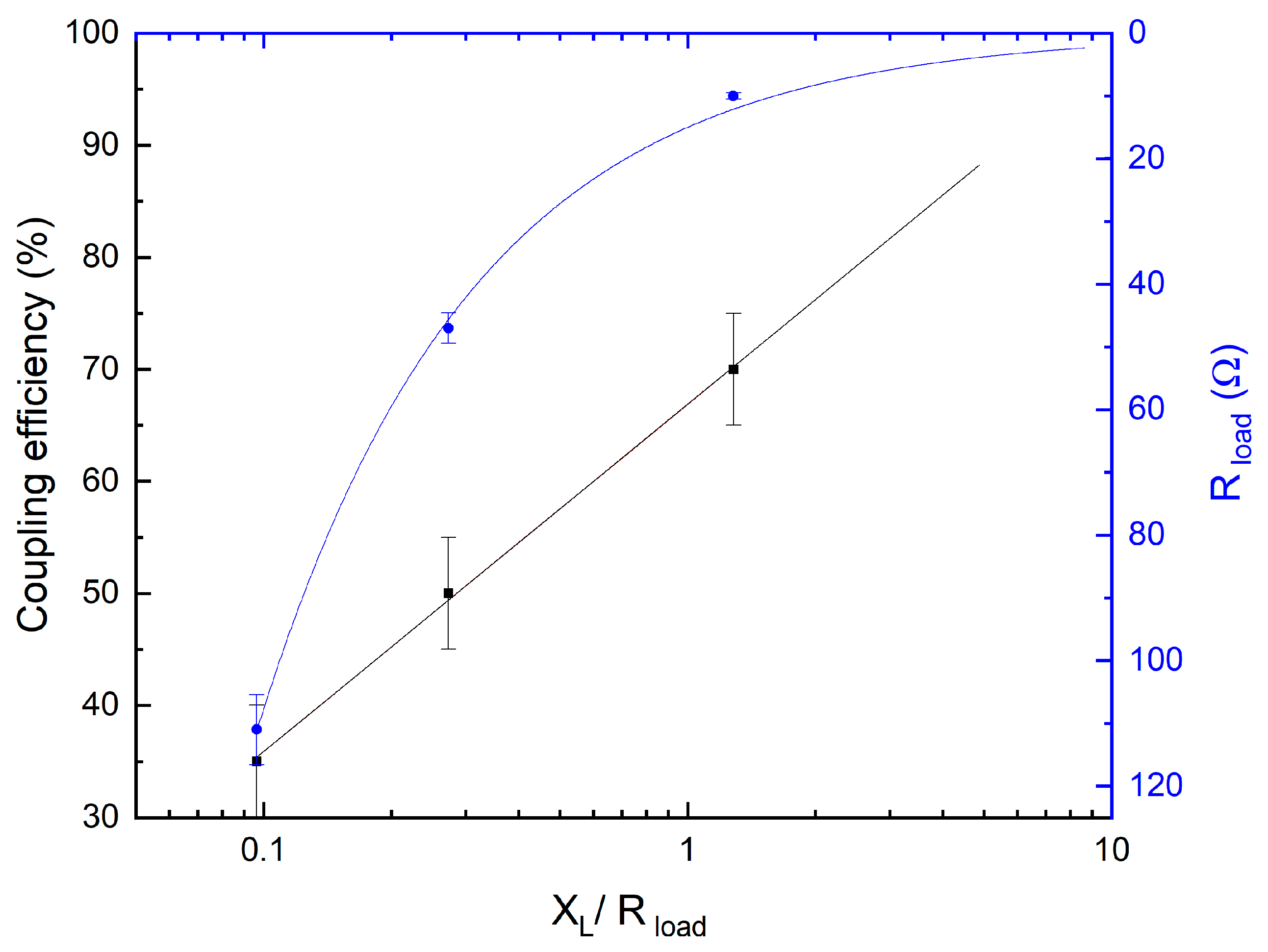


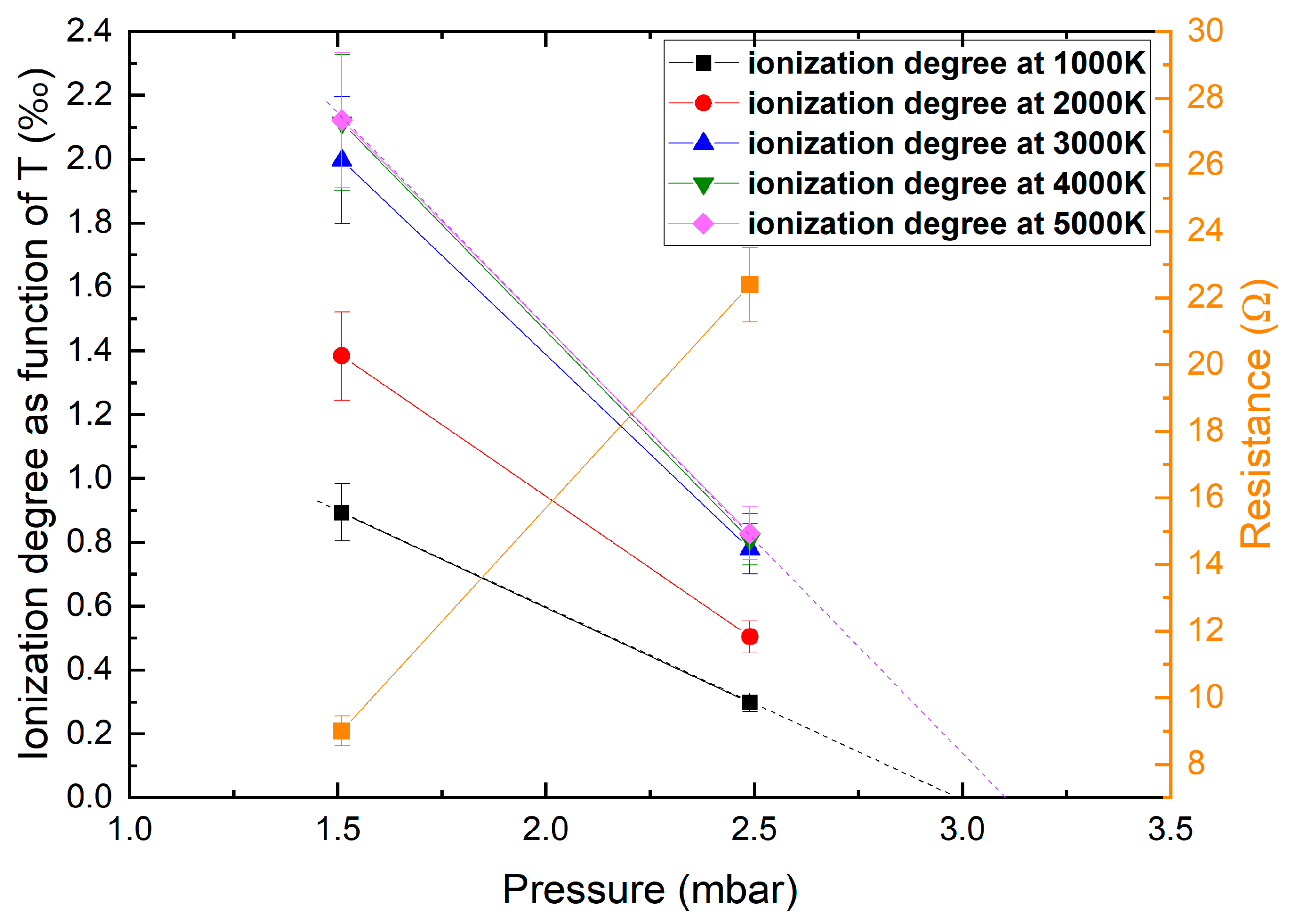

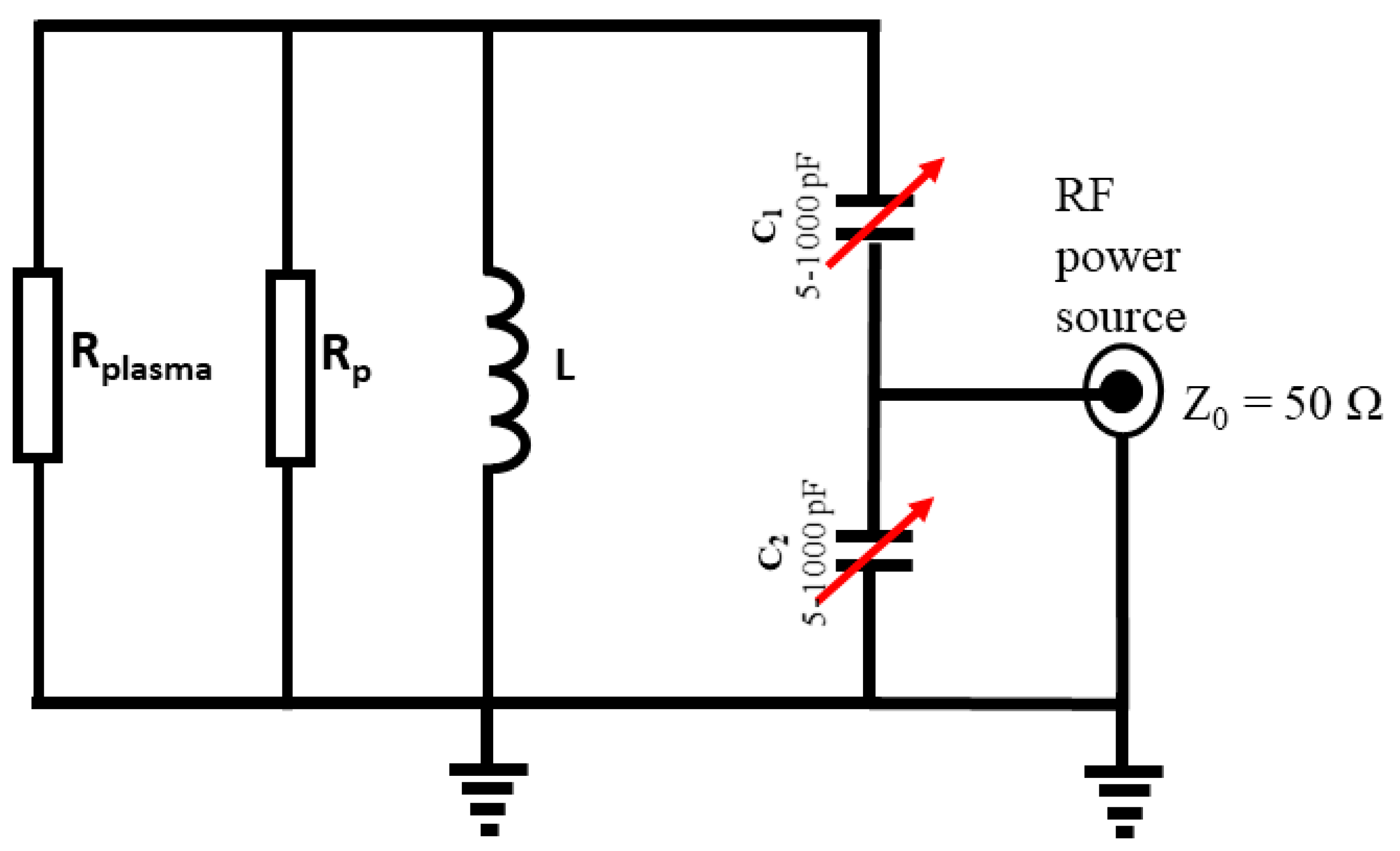

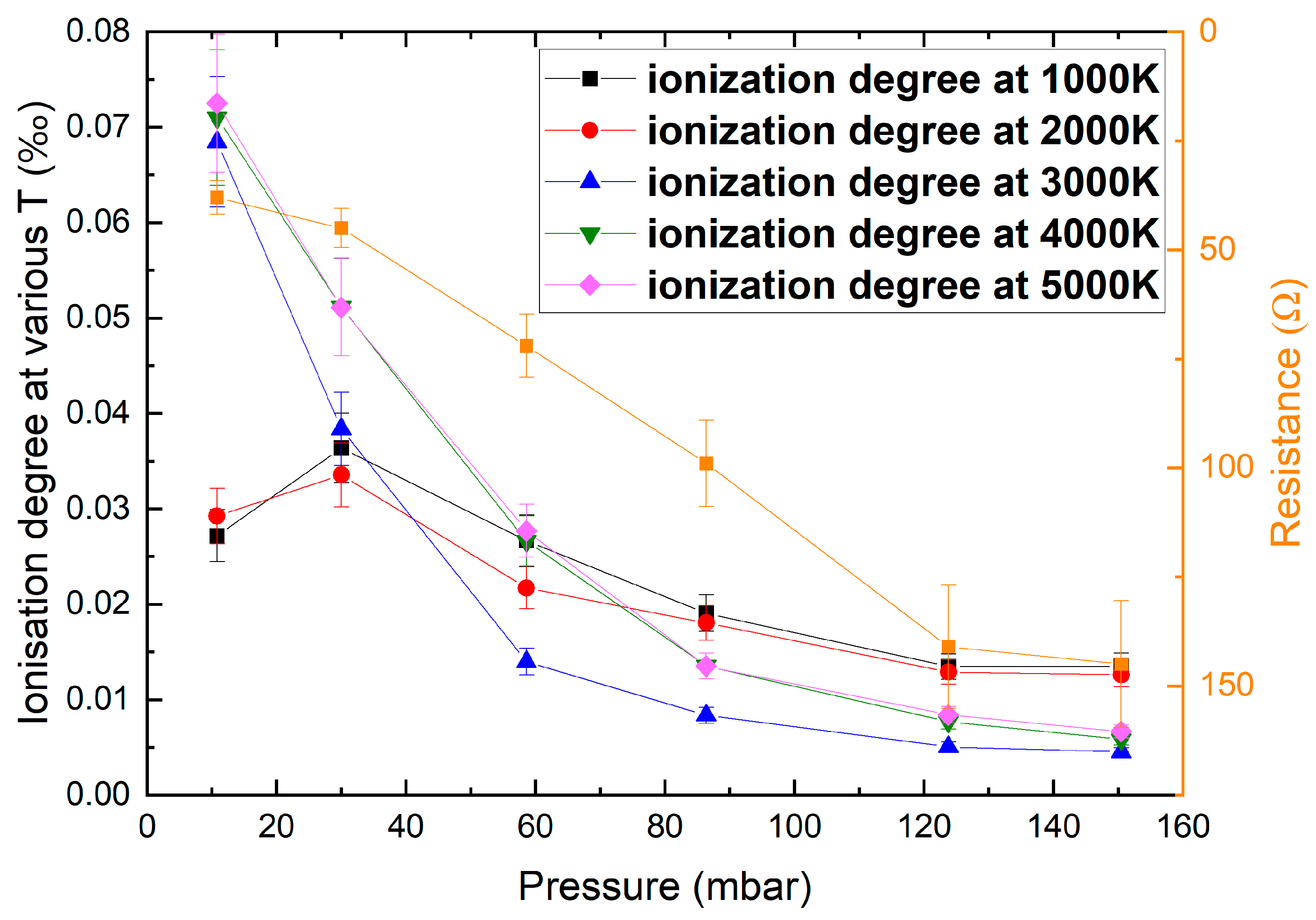
| CO2 Flow (SLM) | p (mbar) | f (kHz) | Pprimary (W) | Psecondary (W) | XL (Ω) | XL/Rplasma | Rplasma (Ω) | U RMSplasma (V) | Coupling Efficiency |
|---|---|---|---|---|---|---|---|---|---|
| 0.51 | 1.51 | 66.1 | 3546 | 3120 | 29.08 | 3.2 | 9.0 | 181.4 | 88% |
| 0.96 | 2.49 | 62.8 | 3944 | 3125 | 27.62 | 1.23 | 22.4 | 254.6 | 79% |
| CO2 Flow (SLM) | p (mbar) | Pr (W) | Po (W) | Rpot (Ω) | Rp (Ω) | Pab (W) | Rplasma (Ω) | U RMSplasma (V) | Coupling Efficiency |
|---|---|---|---|---|---|---|---|---|---|
| 0.10 | 0.53 | 1 | 530 | 4990 | 548 | 52.4 | 493.58 | 160.86 | 9.9% |
| 0.27 | 5.05 | 8 | 571 | 17,720 | 548 | 17.1 | 531.33 | 95.38 | 3.0% |
| 0.27 | 10.4 | 7 | 596 | 71,300 | 548 | 4.5 | 543.58 | 49.70 | 0.8% |
| 0.27 | 15 | 2 | 691 | 136,700 | 548 | 2.8 | 545.57 | 38.79 | 0.4% |
| p (mbar) | P Total (W) | Pabsorbed (W) | Rp temperature compensated (kΩ) | Rpot (kΩ) | Rplasma (Ω) | U RMSplasma (V) | Coupling Efficiency |
|---|---|---|---|---|---|---|---|
| 10.8 | 500 | 430 | 32.8 | 5.38 | 38.2 | 128.2 | 86% |
| 30 | 500 | 445 | 47.9 | 6.17 | 45.2 | 141.8 | 89% |
| 58.6 | 508 | 422 | 50.0 | 10.57 | 72.1 | 174.4 | 83% |
| 86.4 | 499 | 294 | 29.0 | 20.41 | 99.1 | 170.8 | 59% |
| 123.8 | 515 | 216 | 29.3 | 41.10 | 141.3 | 174.8 | 42% |
| 150.5 | 504 | 146 | 24.8 | 60.00 | 145.1 | 145.6 | 29% |
| Type CO2 Plasma Source | Vessel, Size (cm) | Core (y/n) | Power (W) | Freq. (MHz) | Pressure Range (mbar) | Max. Coupling (%) |
|---|---|---|---|---|---|---|
| Modified Plasma lamp 1 | QT, 7 × 3.4 | y, ×2 | 600 | 0.22 | 0.5–0.6 | 66–60 |
| 6 parallel Ferrite | QT, 7 × 3.4 | y, ×6 | 1000 | 10.19 | 1.4 | 33 |
| High AL 2 | RT, 20.4 × 10.4 × 5.2 | y, ×2 | 3100 | 0.064 | 1.5–2.5 | 88–79 |
| Poloidal | QT, 2.1 × 1.9 | n | 596 | 27.70 | 0.5–15 | 10–0.4 |
| Toroidal | QT, 2.1 × 1.9 | n | ~500 | 21.7 | 11–124 | 86–29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Devid, E.J.; Bongers, W.A.; Groen, P.W.C.; van Ginkel, M.; Doyle, S.J.; Smits, F.M.A.; van Deursen, C.F.A.M.; Serras, K.; Labeur, S.; Gleeson, M.A.; et al. Toroidal CO2 Plasma Sources with Low- and High-Frequency Power Coupling Configurations for Improved Energy Transfer Efficiencies. Plasma 2024, 7, 566-584. https://doi.org/10.3390/plasma7030030
Devid EJ, Bongers WA, Groen PWC, van Ginkel M, Doyle SJ, Smits FMA, van Deursen CFAM, Serras K, Labeur S, Gleeson MA, et al. Toroidal CO2 Plasma Sources with Low- and High-Frequency Power Coupling Configurations for Improved Energy Transfer Efficiencies. Plasma. 2024; 7(3):566-584. https://doi.org/10.3390/plasma7030030
Chicago/Turabian StyleDevid, E. J., W. A. Bongers, P. W. C. Groen, M. van Ginkel, S. J. Doyle, F. M. A. Smits, C. F. A. M. van Deursen, K. Serras, S. Labeur, M. A. Gleeson, and et al. 2024. "Toroidal CO2 Plasma Sources with Low- and High-Frequency Power Coupling Configurations for Improved Energy Transfer Efficiencies" Plasma 7, no. 3: 566-584. https://doi.org/10.3390/plasma7030030
APA StyleDevid, E. J., Bongers, W. A., Groen, P. W. C., van Ginkel, M., Doyle, S. J., Smits, F. M. A., van Deursen, C. F. A. M., Serras, K., Labeur, S., Gleeson, M. A., & van de Sanden, M. C. M. (2024). Toroidal CO2 Plasma Sources with Low- and High-Frequency Power Coupling Configurations for Improved Energy Transfer Efficiencies. Plasma, 7(3), 566-584. https://doi.org/10.3390/plasma7030030








